Dynamic response of pipes conveying two-phase flow based on Timoshenko beam model

Abstract

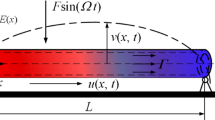
The dynamic behavior of pipes subjected to internal gas–liquid two-phase flow has been studied using the Timoshenko beam model and the slip-ratio factor model. In this paper, the governing equations were carried out using the generalized integral transform technique (GITT) by transforming the governing partial differential equations into a set of second-order ordinary differential equations. The comparison between Timoshenko beam model and Euler–Bernoulli beam model has been conducted through parametric study on dimensionless frequencies and amplitudes over various aspect ratios, internal fluid flow rates, and volumetric gas fractions. The results show that the frequencies of Timoshenko beam model are less and the amplitude is larger than that of Euler–Bernoulli beam model at low aspect ratio. In addition, the amplitude for Timoshenko beam model increases more dramatically than that of Euler–Bernoulli beam model when the pipe is about to lose stability. The high flow rate leads to the divergence of the dynamic system, as well as the two-phase flow accelerates the instability and has significant influence on the dynamic response when the pipe is long and the internal liquid flows fast.

Appendix

The dynamic equations of Timoshenko beam are derived through following closely the work by Païdoussis and Issid [18] and applying Newtons second law. In the derivation process, the small deflection approximation was adopted. Then the curvilinear coordinate s may be interchanged by the coordinate x. Conduct the force analysis of the two elements $\delta s$ of fluid and pipe, as shown in Fig. 14.

For fluid element, it is subjected to pressure p, which is measured above the ambient pressure and due to the friction loss, reaction force F of the pipe on the fluid normal to the fluid, wall shear stress q between the fluid and the pipe tangential to the fluid element as well as gravity force Mg. Then the force and moment equilibrium equations in the x and w directions yield

$$\begin{aligned} -A\frac{\partial p}{\partial x}-q+Mg+F\frac{\partial w}{\partial x}=M{{a}_{fx}} \end{aligned}$$

(36)

$$\begin{aligned} -F-A\frac{\partial }{\partial x}(p\frac{\partial w}{\partial x})-q\frac{\partial w}{\partial x}=M{{a}_{fw}} \end{aligned}$$

(37)

$$\begin{aligned} pA\Upsilon ={{I}_{f}}\ddot{\theta } \end{aligned}$$

(38)

where ${{a}_{fx}}$ and ${{a}_{fw}}$ are the acceleration in the x and w direction of the fluid element, which were derived by Païdoussis [16] with the assumption that the fluid flow was approximated as a plug flow, yield

$$\begin{aligned} {{a}_{fx}}=\frac{dU}{dx} \end{aligned}$$

(39)

$$\begin{aligned} {{a}_{fw}}={{\left[ \frac{\partial }{\partial t}+U\frac{\partial }{\partial x} \right] }^{2}}w=\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}+2U\frac{{{\partial }^{2}}w}{\partial x\partial t}+{{U}^{2}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+\frac{dU}{dt}\frac{\partial w}{\partial x} \end{aligned}$$

(40)

For the pipe element, it subjected to reactive force F and shear stress q from fluid element as well as gravity force mg, longitudinal tension T, transverse shear force Q, bending moment H and damping due to friction with surrounding fluid $c\frac{\partial w}{\partial t}$. Projection of the forces on the x and w direction and consideration of moments, gives

$$\begin{aligned} \frac{\partial T}{\partial x}+q+mg-F\frac{\partial w}{\partial x}=0 \end{aligned}$$

(41)

$$\begin{aligned} \frac{\partial Q}{\partial x}+F+\frac{\partial }{\partial x}\left(T\frac{\partial w}{\partial x}\right)+q\frac{\partial w}{\partial x}-c\frac{\partial w}{\partial t}=m\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}} \end{aligned}$$

(42)

$$\begin{aligned} \frac{\partial H}{\partial x}+Q-T\Upsilon ={{I}_{p}}\frac{{{\partial }^{2}}\theta }{\partial {{t}^{2}}} \end{aligned}$$

(43)

Combining Eqs. (37, 42) and the equation of shear force, it can be obtained that

$$\begin{aligned}&{{k}^{'}}G{{A}_{p}}\left(\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}-\frac{\partial \theta }{\partial x}\right)+\frac{\partial }{\partial x}\left[(T-pA)\frac{\partial w}{\partial x}\right] \nonumber \\&-c\frac{\partial w}{\partial t}=M{{a}_{fw}}+m{{a}_{fw}} \end{aligned}$$

(44)

Adding Eqs. (36) and (41), one can obtained

$$\begin{aligned} \frac{\partial }{\partial x}(T-pA)=M\frac{dU}{dt}-(M+m)g \end{aligned}$$

(45)

Païdoussis [16] intergrated from x to L and derived the expression $T-pA$ at $x=L$, which yields

$$\begin{aligned}&T-pA=\bar{T}-\bar{p}A(1-2\nu \delta )+ \nonumber \\&\left[(M+m)g-M(dU/dt)\right](L-x) \end{aligned}$$

(46)

Substitution of Eqs. (46) into (44) gives the equation of Timoshenko beam conveying fluid in w direction.

$$\begin{aligned}&m\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}+c\frac{\partial w}{\partial t}+M\left( \frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}+2U\frac{{{\partial }^{2}}w}{\partial x\partial t}+{{U}^{2}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}} \right) \nonumber \\&={{k}^{'}}G{{A}_{p}}\left(\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}-\frac{\partial \theta }{\partial x}\right)+\left\{\left[\bar{T}-\bar{p}A(1-2\nu \delta )\right]- \right.\nonumber \\&\left.\left[M\frac{dU}{dt}-(M+m)g\right](L-x)\right\}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}-(M+m)g\frac{\partial w}{\partial x} \end{aligned}$$

(47)

Adding Eqs.(38) and (43) and substituting the bending moment and transverse shear force, the moment equation can be derived.

$$\begin{aligned}&({{\rho }_{p}}{{I}_{P}}+{{\rho }_{f}}{{I}_{f}})\ddot{\theta }=E{{I}_{p}}\frac{{{\partial }^{2}}\theta }{\partial {{x}^{2}}}+{{\kappa }^{'}}G{{A}_{p}}\left(\frac{\partial w}{\partial x}-\theta\right ) \nonumber \\&-\left\{\left[\bar{T}-\bar{p}A(1-2\nu \delta )\right]-\right. \nonumber \\&\left.\left[M\frac{dU}{dt}-(M+m)g\right](L-x)\right\}\left(\frac{\partial w}{\partial x}-\theta \right) \end{aligned}$$

(48)