Analyzing Congestion Propagation on Urban Rail Transit Oversaturated Conditions: A Framework Based on SIR Epidemic Model

Abstract

Simulating the congestion propagation of urban rail transit system is challenging, especially under oversaturated conditions. This paper presents a congestion propagation model based on SIR (susceptible, infected, recovered) epidemic model for capturing the congestion prorogation process through formalizing the propagation by a congestion susceptibility recovery process. In addition, as congestion propagation is the key parameter in the congestion propagation model, a model for calculating congestion propagation rate is constructed. A gray system model is also introduced to quantify the propagation rate under the joint effect of six influential factors: passenger flow, train headway, passenger transfer convenience, time of congestion occurring, initial congested station and station capacity. A numerical example is used to illustrate the congestion propagation process and to demonstrate the improvements after taking corresponding measures.

1 Introduction

Congestion, along with the expansion of urban transit networks, is becoming one of the major concerns of the transportation system agencies, especially under the oversaturated conditions. The initiatives in the transportation system consist of various management strategies and effective restrictive measures which aim to reduce congestion and avoid accidents. The analysis of congestion in road networks includes macroscopic [1, 2], medium [3, 4] and microscopic [5, 6] levels. The rearrangement of demand in the network once an element fails is a particular focus of some studies [7,8,9]. Generally, there is an overlook on the dynamic properties of traffic in previous papers, such as the propagation of congestion. The congestion propagation process on highway has been studied by Sundara [10] and Zhang [11], whom both depicted the characteristics of congestion propagation under a highway traffic incident. Based on this research, Zang [12] proposed a model to calculate the boundary and recovery rate of the congestion in the light of the traffic flow theory. Nevertheless, research in the propagation of the congestion in rail transit networks is limited in the following two categories: the propagation mechanism and the congestion simulation.

Research on the accident delay of the high-speed railway can be classified into two aspects: emergency rescheduling and delay propagation. Emergency rescheduling methods manage to minimize operation conflicts and train delay to optimize rescheduling strategies and predict influence according to accident characteristics. Meng and Zhou [13] developed an innovative integer programming model for train dispatching on an N-track network by means of simultaneously rerouting and rescheduling trains. Wang and Goverde [14] have determined a timetable constraints set with accessibility and non-conflict under delay accidents of single-track railway, upon which a train rescheduling model was established aiming to reduce global delay time and energy consumption. Carey and Kwieciński [15] conducted a stochastic simulation of trains on line section to establish an approximation model between scheduled headway and secondary delay for the coefficient modification and schedule optimization of current operation plan. Louwerse and Huisman [16] studied the rescheduling methods to seek a higher service level based on event-activity network using integer programming. Cadarso and Ángel [17] presented an approach to optimize timetable and rolling stock assignment with special consideration of passenger demand under large-scale disruptions in rapid transit network. Delay propagation models help to combine micro-propagation model with mathematical statistics to predict and estimate the service performance and transport efficiency, and max-plus algebra [18] and stochastic distribution [19] are often used in this kind of research. In the max-plus algebra, by viewing the operation plan under periodic timetable as a discrete event dynamic system, a recursion function considering buffer time and recovery time can be formulated to describe the train operating status and further reveal the time–space propagation mechanism. In the stochastic distribution model, activity graph theory is applied to describe primary delay and secondary delay and construct relevant cumulative distribution function by considering delay as a random variable.

Some of the current studies emphasized on how the congestion spreads and grows in the urban rail networks. Zhou [20] proposed the concept of the propagation of passenger flow during peak hours for the first time, and Zhou analyzed the mechanism and influential factors of the congestion propagation. Stephen [21] described the transmission under the oversaturated conditions in rail transit based on the combustion theory, and he proposed that the congestion propagation is similar to the ripple effect. Other researchers focused on the congestion simulation and the model construction. Duan [22] classified the urban railway stations into 3 categories: the starting, the intermediate and the terminal stations, and he extracted certain features of the oversaturated conditions. He then proposed the model of the influence of passenger densities in the station waiting areas. Li [23] proposed a model based on the transmission dynamics of the complex network and compared the influencing factors of the congestion propagation, including the capacity of the stations, the number of the initial congested stations, the propagation rate and the dissipation rate. The two aspects: propagation mechanism of the complex network and influential factors of the congestion propagation, are combined by li [24] who proposed a coordination game model for the traffic congestion propagation and explored the influential factors (e.g., road structure and station distribution). Liu [25] proposed a rail transit model for the oversaturated conditions.

The details of the influential factors of the congestion propagation are clearly analyzed, and the models for the congestion propagation are constructed with brevity. However, the quantitative research in the congestion propagation process and the influential factors like the propagation rate is limited. Wu [26] calculated the approximate rate of propagation based on time algorithm, but Wu has applied an assumed value of the congestion propagation rate in the simulation instead of calculating the value with accuracy.

In previous research, however, there is an overlook of the dynamic properties of traffic, such as the propagation of congestion [2]. Furthermore, quantitative research in the congestion propagation process is very limited [3, 4]. This paper aims to provide extensive analyses and simple formulations to help understand the behavior of the congestion propagation in urban rail networks. We propose a congestion propagation model in the urban rail networks by making some simplified assumptions about the traffic behavior. It is important to reflect the decision-making process of traffic controllers who need simple and applicable formulations to help react in real time.

This paper is organized as follows: The problem statement is delineated in Sect. 2 to illustrate the purpose of the research. The congestion propagation model is dedced and constructed in Sect. 3, and it is modeled as a susceptible-congested-recovered process. The method for calculating the congestion propagation rate is described in Sect. 4. Numerical simulation on a real-world network with the field measurement data is presented in Sect. 5. Comparing the proposed model with the previous model presented in the literature survey part is discussed in Sect. 6. The conclusion of this study is summarized in Sect. 7.

2 Problem Statement

The classical SIR model [27] for disease outbreaks considers a population split into three compartments: the susceptible individuals S, the infected individuals I and the recovered individuals R. The model is commonly called the susceptible-infected-recovered (SIR) model. The model contains two parameters: the transmission rate k, i.e., the contact rate times the probability of infection [28], and the recovery rate r, i.e., the rate at which infective individuals recover. The model equations are defined as follows.

$$S^{\prime}(t) = -\, kI(t)S(t)$$

(1)

$$I^{\prime}(t) = kI(t)S(t) - rI(t)$$

(2)

$$R^{\prime}(t) = rI(t)$$

(3)

In the classical SIR model it is assumed that S, I and R are the fraction of the population. The parameters k and r reflect some external forces that influence the course of the disease outbreak, for example, changes in the environment (seasonality) or changes in contact rates. Investigations of this model and extensions have been developed by many researchers, including Dietz and Heesterbeek [29], Anderson and May [30], Bailey [31], Brauer [32], Diekmann [33], Keeling and Rohani [34] and Thieme [28].

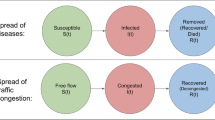
This modeling metaphor can be gainfully employed to examine the congestion propagation. Figure 1 shows a simple propagation congestion process among an urban rail transit network based on three categories of SIR epidemic model. The first station on the left-hand side represents susceptible station (susceptible individual), that is, station which is usually adjacent to the initial congested stations is easily affected and delayed by congestion. When train runs to the next station, susceptible stations are affected by oversaturated station (infectious individual) and become oversaturated themselves (they become infected). Also over time, a proportion of stations will become recovered stations (recovered individuals). In the SIR model, the infectious population will recover and develop immunity to infection.

Fig. 1

Comparison between epidemic propagation and congestion propagation

This paper aims to fill the gap of previous research by providing a research on congestion propagation based on SIR epidemic model. We propose a congestion propagation model and use the increment of the number of congested stations to evaluate the congestion incidence of the network. As a result, the model generates the proper measurements for different oversaturated conditions. Furthermore, in order to simulate the congestion propagation process, we propose a separate method to calculate the value of congestion propagation rate. The outcome of this model produces a quantitative analysis of the efficiency of measurements taken to relieve the oversaturated conditions

3 Congestion Propagation Model

Based on the SIR epidemic model, stations that are easily affected by the congestion are categorized under susceptible stations. Stations that were previously susceptible stations and were affected by the congestion are categorized under congested stations. The recovered stations are those which have recovered from the congestion. Theoretically, for the statement simplicity, stations after recovery from congestion obtain permanent immunity from congestion.

Table 1 lists the definition of indices, sets and parameters used in the mathematical formulations of congestion propagation model.

Table 1 Notation of congestion propagation model

These variables $S(t)$, $I(t)$ and $R(t)$ represent three different types of stations at a particular time, respectively. $S(t)$ represents the number of susceptible stations, $I(t)$ represents the number of congested stations, and $R(t)$ represents the number of recovered stations.

Assume that the congestion propagation rate is k and recovery rate is r. During the time period [t, t + Δt], the congested station increment is $kI(t)S(t)\Delta t$ and the recovered station increment is $rI(t)\Delta t$. The state transition equations can be formulated as follows, and Fig. 2 shows the congestion propagation.

$$S(t + \Delta t) - S(t) = - kI(t)S(t)\Delta t$$

(4)

$$I(t + \Delta t) - I(t) = kI(t)S(t)\Delta t - rI(t)\Delta t$$

(5)

$$R(t + \Delta t) - R(t) = rI(t)\Delta t$$

(6)

where $S(t{}_{0}) = S_{0} > 0,I(t{}_{0}) = I_{0} > 0,R(t{}_{0}) = R_{0} = 0$.

Fig. 2

Congestion propagation between t and t + Δt

The increment of the number of congested stations is applied to evaluate the congestion propagation. It can be defined as follows:

$$\Delta I(t + \Delta t )= N_{p} k - rI(t)$$

(7)

where p represents the departure station of the metro line.

These formulas describe the increment or decrement of the number of stations among three different categories over time, which can be used to simulate the congestion propagation process.

4 The Method for Calculating Propagation Rate

In SIR model, the transmission rate of an infectious disease is the rate of infection given contact. It is the epidemiological analogue of a rate constant in chemical reactions. The direct measurement of the transmission rate is essentially impossible for most infections. But if we wish to predict the changes caused by public health programs, we need to know the transmission rate [30]. The transmission rate of many acute infectious diseases varies significantly in time and frequently exhibits significant seasonal dependence [35,36,37]: Some epidemic cases peak in winter, while other cases peak in spring or in summer. The transmission rate of many acute infectious diseases varies significantly in time, but the underlying mechanisms are usually uncertain. They may include seasonal changes in the environment, contact rate, immune system response. The transmission rate has been thought difficult to measure directly.

Similarly, in urban rail transit, propagation rate represents the congestion probability between two adjacent stations when one of them encounters oversaturated condition. There are various influential factors of the propagation rate. In order to compute the propagation rate, these factors are classified into six classes: passenger flow characteristic, train departure interval, passenger transfer convenience, the time of congestion occurring, the initial congested station and station capacity [38]. We divided these parameters into two classes: parameter A associated with passenger transfers and parameter B associated with time.

4.1 Formula Construction

We use the total passenger flow in one station and the transfer passenger flow to represent the five influential factors: passenger flow characteristic, average passenger transfer time for transfer convenience, congestion occurring time t, the station capacity F_j at station j and the average train headway. The passenger arrival is set homogeneous for the station so that the application of the average train headway to represent the passenger waiting time is feasible (e.g., 2 min).

Table 2 lists the general indices, sets and parameters used in the mathematical formulation for calculating propagation rate.

Table 2 Notations for congestion propagation rate model

The quantitative model was constructed as follows:

$$k = \alpha \frac{{\sum\nolimits_{i = 1}^{{N_{j} }} {{\text{Flow}}_{i,j} x_{1} } + \left( {{\text{Flow}}_{j} - \sum\nolimits_{i = 1}^{{N_{j} }} {{\text{Flow}}_{i,j} } } \right)x_{2} }}{{{\text{Flow}}_{j} }} + \beta \frac{{{\text{Transfer}}_{i,j} x_{1} + {\text{Travel}}_{j,k} + W_{j} }}{T_{\rm ll}}$$

(8)

s.t.

$$x_{1} = \left\{ {\begin{array}{ll} 1 & {{\text{passengers}}\;{\text{coming}}\;{\text{from}}\;{\text{other}}\;{\text{metro}}\;{\text{lines}}} \\ 0 & {{\text{passenger}}\;{\text{coming}}\;{\text{directly}}\;{\text{to}}\;{\text{station}}\;{\text{without}}\;{\text{transfer}}} \\ \end{array} } \right.$$

(9)

$$x_{ 2} = \left\{ {\begin{array}{ll} 1 & {{\text{passengers}}\;{\text{coming}}\;{\text{directly}}\;{\text{to}}\;{\text{station}}\;{\text{without}}\;{\text{transfer}}} \\ 0 & {{\text{passenger}}\;{\text{coming}}\;{\text{from}}\;{\text{other}}\;{\text{metro}}\;{\text{lines}}} \\ \end{array} } \right.$$

(10)

$$x_{1} + x_{2} = 1$$

(11)

$${\text{Flow}}_{j} \le F_{j}$$

(12)

where $\frac{{\sum\nolimits_{i = 1}^{{N_{j} }} {{\text{Flow}}_{i,j} } }}{{{\text{Flow}}_{j} }}$ represents passenger transfer rate, and $\frac{{\left( {{\text{Flow}}_{j} - \sum\nolimits_{i = 1}^{{N_{j} }} {{\text{Flow}}_{i,j} } } \right)}}{{{\text{Flow}}_{j} }}$ represents the rate without transfer. ${\text{Travel}}_{j,k} + W_{j}$ is for the time spent between two adjacent stations in the same metro line. If passengers come from another metro line, we add ${\text{Transfer}}_{i,j} x_{1}$, namely walking time in the transfer channel to formula (8).

We define passenger-transfer-associated parameter A and time-associated parameter B as follows:

$$A = \frac{{\sum\nolimits_{i = 1}^{{N_{j} }} {{\text{Flow}}_{i,j} x_{1} } + \left( {{\text{Flow}}_{j} - \sum\nolimits_{i = 1}^{{N_{j} }} {{\text{Flow}}_{i,j} } } \right)x_{2} }}{{{\text{Flow}}_{j} }}$$

(13)

$$B = \frac{{{\text{Transfer}}_{i,j} x_{1} + {\text{Travel}}_{j,k} + W_{j} }}{T_{\rm ll}}$$

(14)

4.2 Parameter Calibration

There are three methods for the weight analysis of the parameter calibration: analytic hierarchy process, expert scoring method and variation coefficient method. However, in the previous research, there are few literatures on the definition of the interrelation among parameters.

To elaborate the relationship among different parameters, we deduct the gray system model to calculate the values of $\alpha$ and $\beta$.

The gray system model aims to calculate the degree of association between the behavior factor (i.e., congestion propagation) and the relevant factors (i.e., passenger flow and passenger behavior). If the developing trend between the behavior and the relevant factors is consistent, the degree of gray incidence would be large. If the trend is less well defined, the degree of gray incidence would be small [39]. The gray system model is considered to be an analysis of the geometric proximity among different factor sequences and the behavior sequence. The proximity is described by the degree of gray incidence, which is regarded as a measure of the similarities of data that can be arranged in sequential order. In this model, data are collected for behavior sequence X₀ and relevant factor sequence X_i over the same time period.

The notation for parameter calibration is shown in Table 3.

Table 3 Notation for parameter calibration

Definition 1

According to the notation, we can define $\alpha$ and $\beta$ as follows:

$$\alpha = \gamma (X_{0} ,X_{\text{A}} )$$

(15)

$$\beta = \gamma (X_{0} ,X_{\text{B}} )$$

(16)

Definition 2

Assume that the behavior data sequence is defined as follows:

$$X_{0} = (x_{0} (1),x_{0} (2), \ldots ,x_{0} (n))^{T}$$

(17)

Besides, $X_{0}$ is equal to k when $\alpha$ and $\beta$ are equal to 1 (refer to [39]).

And the correlation factor data sequence is assumed to be:

$$\begin{aligned} X_{i} = (x_{i} (1),x_{i} (2), \ldots ,x_{i} (n))^{T} \hfill \\ \vdots \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots \hfill \\ X_{m} = (x_{m} (1),x_{m} (2), \ldots ,x_{m} (n))^{T} . \hfill \\ \end{aligned}$$

(18)

where $x_{i} (j) > 0,\,i = 0,1,2 \ldots m,j = 1,2 \ldots n.$.

$${\text{Suppose}}\,{\text{ that}}\,\gamma (X_{0} ,X_{i} ) = \frac{1}{n}\sum\limits_{j = 1}^{n} {\gamma (x_{0} (j),x_{i} (j))}$$

(19)

It satisfies the following four properties:

$$\left( {\text{i}} \right) \, \,{\text{Normality}}{:}\,0 < \gamma (X_{0} ,X_{i} ) \le 1,when\;X_{0} = X_{i} \Leftrightarrow \gamma (X_{0} ,X_{i} ) = 1$$

(20)

$$\left( {\text{ii}} \right)\,{\text{ Integrity}}{:}\,\gamma (X_{p} ,X_{q} ) \ne \gamma (X_{q} ,X_{p} )when\;p \ne q,$$

(21)

where $X_{p} ,X_{q} \in X = \{ x_{k} |k = 0,1,2 \cdots m,m \ge 2\}.$

$$\left( {\text{iii}} \right){\text{ Even symmetry}}{:}\,\gamma (X_{p} ,X_{q} ) = \gamma (X_{q} ,X_{p} ) \Leftrightarrow x = \{ X_{p} ,X_{q} \}$$

(22)

$$\left( {\text{iv}} \right){\text{ Proximity}}{:}{\text{ the smaller}}\,|x_{0} (j) - x_{i} (j)|,{\text{ the bigger}}\,\gamma (x_{0} (j),x_{i} (j)).$$

(23)

Then, $\gamma (X_{0} ,X_{i} )$ is called the gray correlation degree of $X_{0}$ and $X_{{_{i} }}$,$\gamma (x_{0} (j),x_{i} (j))$ represents the correlation coefficient of $X_{0}$ and $X_{i}$ at the jth point, and the four properties (i), (ii), (iii) and (iv) are called four axioms of the gray correlation(refer to [39]).

Definition 3

Assume that $X_{i} = (x_{i} (1),x_{i} (2), \ldots ,x_{i} (n))$ which is defined by the above Definition 1, where $i = 0, 1, 2 \ldots m$. We define:

$$\Delta_{0i} (j) = |x_{0} (j) - x_{i} (j)|$$

(24)

$$\Delta_{\hbox{min} } = \mathop {\hbox{min} }\limits_{i} \mathop {\hbox{min} }\limits_{j} \Delta_{0i} (j)$$

(25)

$$\Delta_{\hbox{max} } = \mathop {\hbox{max} }\limits_{i} \mathop {\hbox{max} }\limits_{j} \Delta_{0i} (j)$$

(26)

Then, $\Delta_{0i} (j)$ represents absolute deviation of $x_{0} (j)$ and $x_{i} (j)$, and $\Delta_{\hbox{min} }$ and $\Delta_{\hbox{max} }$ represent bipolar minimum deviation and bipolar maximum deviation, respectively(refer to [39]).

Theorem 1

For an arbitrary given number $\lambda \in (0,1)$ , we define:

$$\gamma (X_{0} (j),X_{i} (j)) = \frac{{\Delta_{\hbox{min} } + \lambda \Delta_{\hbox{max} } }}{{\Delta_{0i} (j) + \lambda \Delta_{\hbox{max} } }}$$

(27)

$$\gamma = \gamma (X_{0} ,X_{i} ) = \frac{1}{n}\sum\limits_{j = 1}^{n} {\gamma (x_{0} (j),x_{i} (j))}$$

(28)

Then, the value $\gamma = \gamma (X_{0} ,X_{i} )$ can be calculated by using formula (28).

5 Case Study

In this section, we focus on how to use the congestion propagation model and the propagation rate to conduct the quantitative analysis of the above proposed model. Such analysis can bring about clearity of the operation condition of the urban railway network. The congestion propagation rate model can be used to generate measures to solve the oversaturated condition, improve congestion and finally enable us to analyze the incidents for future reference.

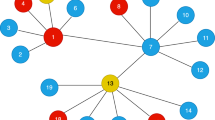
The case study takes the oversaturated condition occurred at Beijing Xizhimen Station which is a big interchange station of line 2, line 4 and line 13. The rail transit network is shown in Fig. 3. The calculation results by using the model is to verify the effectiveness of the SIR epidemic model. 

Fig. 3

A part of Beijing metro network

5.1 Data Preparation

The data collected on September 8, 2014, at Xizhimen Station are applied to calibrate $\alpha$ and $\beta$. The data measured and collected include the passenger number, average passenger walking speed, the railway departure interval, the running time between two stations and the total running time from the origin to the destination. These data and various comparisons with other research are shown in Tables 4, 5 and 6.

Table 4 Value of the passenger transfer rate

Table 5 Value of the time-associated parameters

Table 6 Passenger walking speed in transfer channel in peak hours

The transfer rate from line 4 to line 2 differs greatly compared to the data obtained by Li [40], while the other transfer rates are similar. The collected data of the project evaluation report published by China Metro Engineering Consulting Company [41] are more accurate than the data obtained from Li. As a result, the collected data are selected as the basis to calibrate the parameters. Table 5 displays the value of parameters associated with time from three lines in Xizhimen Station.

In Table 6 the transfer walking speed in Beijing metro line 5 and Haidian Huangzhuang Station which is an interchange station of line 10 and line 4 are also list  for a comparison with the data collected at Xizhimen Station. 

The calculation resulst for calibration model is shown in Table 7.

Table 7 The input data for calibration value calculation

5.2 Calibration Value Calculation

In this section, we use MATLAB to calculate the value of α and β.

According to Definition 2, when the value of parameters α and β is equal to 1, the behavior data sequence X₀ is equal to the value of k.

Equation (8) can be written as:

$$k = \frac{{\sum\nolimits_{i = 1}^{{N_{j} }} {{\text{Flow}}_{i,j} x_{1} } + \left( {{\text{Flow}}_{j} - \sum\nolimits_{i = 1}^{{N_{j} }} {{\text{Flow}}_{i,j} } } \right))x_{2} }}{{{\text{Flow}}_{j} }} + \frac{{{\text{Transfer}}_{i,j} x_{1} + {\text{Travel}}_{j,k} + W_{j} }}{Tll}$$

(29)

By using the data shown in Tables 4 and 5, the relevant factor sequences can be calculated as follows:We assume $\lambda$ = 0.5; by using formulae (23–26), the calibration degree can be calculated as follows:

$$\alpha_{\text{peak}} = \gamma_{\text{peak}} (X_{0} ,X_{\text{A}} ) = 0.54.$$

$$\alpha_{\text{normal}} = \gamma_{\text{normal}} (X_{0} ,X_{\text{A}} ) = 0.57.$$

$$\beta_{\text{peak}} = \gamma_{\text{peak}} (X_{0} ,X_{\text{B}} ) = 0.46.$$

$$\beta_{\text{normal}} = \gamma_{\text{normal}} (X_{0} ,X_{B} ) = 0.43.$$

5.3 Propagation Simulation

In the literature, the methods of calculating recovery rate r are limited. In order to simulate the propagation rate, we assume that the congestion recovery rate is 0.10, by referring to Ref. [22]. From the network graph, some parameters are given, N_Xizhimen =  5, I₀ = 1, r = 0.10. In the aims to calculate the propagation rate, we refer to formula (8); the correlation degrees α and β are given by Sect. 5.2 (α_peak = 0.54, α_normal = 0.57, β_peak = 0.46,β_normal = 0.43). Considering the oversaturated situation, the parameters in peak hours are chosen for the following calculation so that Eq. (8) can be written as:

$$k_{\rm peak} = 0.54 \times \frac{{\sum\nolimits_{i = 1}^{{N_{j} }} {{\rm Flow}_{i,j} x_{1} } + ({\rm Flow}_{j} - \sum\nolimits_{i = 1}^{{N_{j} }} {{\rm Flow}_{i,j} } )x_{2} }}{{{\rm Flow}_{j} }} + 0.46 \times \frac{{{\rm Transfer}_{i,j} x_{1} + {\rm Travel}_{j,k} + W_{j} }}{{{T}}_{\rm ll}}$$

(30)

Using the data shown in Tables 4 and 5, the value of propagation rate k_peak can be calculated, which is shown in Table 8.

Table 8 Congestion propagation rate k_peak at different lines

The peak-hour propagation rate k_peak is selected, and in this case the propagation rate of line 4 is used in simulation $k_{{^{{_{line\; 4} }} }}$= 28.7% by considering the oversaturated conditions. The input of these values into the above formula (8) simulates the congestion propagation process as follows:

The process of congestion propagation in Fig. 4 illustrates that the increment of congested stations increases rapidly within the first 5 min and that there is a decline at time step 8 and a slight decline between time step 8 and 25. We adjust the parameter N_i in order to compare the result with the actual circumstances, and the simulation is shown in Fig. 5a. Figure 4 illustrates the alternatives of measures taken by operators which include traveling past stations 1 and 3 without stopping, and the adjacent stations of the initial congested station (N₁) reduce time step from 5 to 3; as a result, the number of congested stations declines to 6 within 25 min, and the increment begins to stabilize between time step 10 and 25. The adjustment of its value (e.g., 5, 4, 3, 2) provides a better illustration of the impact of parameter N_i, and the simulation is shown in Fig. 5a.

Fig. 4

Process of congestion propagation

Fig. 5

Congestion propagation simulation under different values of parameters

Figure 5b shows the evolutions of propagation rate equal to 0.23, 0.20, 0.16 and 0.10, respectively. A conclusion can be drawn from this figure; the total number of congested stations will decline if the propagation rate is reduced. However, by comparing (b) with (a), it is clear that the reduction in adjacent stations will significantly reduce the increase in the total number of congested stations and the corresponding improvement is more efficient.

It is shown that when combined with the above analysis of the propagation rate, the propagation of congested station will expand when the propagation rate increases. Thus, it is more efficient to reduce the number of adjacent stations (reduce N_i) by traveling past some of the stations without stopping. Furthermore, there are other measures that can improve the oversaturated condition by reducing the propagation rate k, which includes restricting passenger flow at the station entrance, adjusting the train interval, improving transfer convenience and facilitating access to stations.

6 Comparison

Liu [40] introduced the time algorithm to calculate the congestion propagation rate.

$$k = \frac{{t_{1} - t_{2} }}{T}$$

(31)

In this equation, T represents the train operating time in the network, t₁ represents the time point when an oversaturated condition begins at a station (e.g., Xizhimen Station), and t₂ represents the time point when an oversaturated condition begins at the connected station (e.g., Chegongzhuang Station).

It is challenging to apply this formulation to practical use as the value of parameters t₁ and t₂ is difficult to measure. Hence, the result may lack accuracy. Moreover, the data of parameters cannot be collected before the occurrence of oversaturated conditions. Consequently, this method is not available and lacks the ability to prevent oversaturated conditions.

By comparison, the method proposed in Sect. 4 can be used in a variety of applications and the data of parameters can be collected more easily. For example, the method can be used in generating effective measures for the oversaturated condition. Firstly, the parameter data and possible measures are the input. Secondly, the operators can calculate the propagation rate and the cumulative number of congested stations. Finally, the operators can select the most effective measure, by referring to the value of congestion propagation rate and the simulated number of congested stations.

7 Conclusion

This paper presents a model based on SIR epidemic model that comprises a congestion propagation model and a propagation rate calculation method to utilize the propagation theories of the oversaturated conditions in rail transit. The application of the congestion propagation model aims to simulate the propagation process of the whole network under oversaturated conditions. In this paper, a new approach consisting of a separate method that calculates the congestion propagation rate is studied and presented. The congestion propagation rate model is used to generate measures to solve the oversaturated condition, improve congestion and finally enable us to analyze the incidents for future reference. The two models establish a solid foundation for the study of large-scale network congestion propagation. The influential factors of the propagation rate can be classified into six classes: passenger flow characteristic, train departure interval, passenger transfer convenience, the time of congestion occurring, the initial congested station and station capacity. Nevertheless, there are some other influential factors for these models. Hence, further research on other influential factors is suggested to extend the models. The congestion propagation model provides an extensive analysis of the propagation process related to congestion. Moreover, the model depicts the forecasting and trends of congestion so that traffic controllers obtain a quantitative observation of the process. The congestion propagation rate model distinguishes the efficiency of the alternatives related to congestion improvement measures. As a result, traffic controllers evaluate the outcome and subsequently select the optimal measure to resolve the oversaturated conditions. The expansion of urban transit networks magnifies the propagation of congestion and oversaturated conditions. The goal of the comprehensive quantitative model is to integrate congestion propagation analysis with efficiency differentiation of propagation rate to promote effective congestion recovery measures. The paper hopes to initialize a new approach in the quantitative model of the congestion propagation through the utilization of the two models and integrate the two results for the development of urban transit. Thus, the models proposed in this paper optimize the recovery measures and more importantly simulate the current circumstances and forecast the propagation trends in urban transit systems.