Abstract
Urban transit system is an important part of city transportation, which is an interdisciplinary industry, including traffic engineering, operation research, and computer science. To provide smart services for passengers while applying the new technologies, it is necessary to build an optimal transit network and transit service. A smart transit system is processed from strategic planning, tactical planning, operational planning, transit evaluation to marketing and policy. For each stage, large quantities of related literature have been introduced from different perspectives. The aim of this research is to document the main smart urban transit models, topics and implementations for future references and research in each stage. For the planning part, this paper first summarized the objectives, constraints, algorithms, and implications of the models currently in use and classified the objectives and constraints with classic category and new category. The prominent topics and potential research were captured clearly when comparing the two categories. The methodologies for solving those models were proposed and the genetic algorithm and simulated annealing have been mostly used, which will be helpful for filling the gaps for further research. Despite of the model updates, this study also summarized the application trends such as integrated network design in strategic planning, synchronization and timetable recovery from disruption in tactical and operational planning. To improve the transit system and service, evaluation models on service reliability, service accessibility, timetable robustness, and energy consuming are proposed, which highlight the gap between the idealized service and the real service. Some flexible fare scheme, investments, and commercial strategies are discussed in the financial part. The conclusion highlighted the future scope of the smart urban transit in passenger demand management, travel information service, facility and service optimization and shared mobility, in order to make it more convenient for the passengers and more friendly to the environment.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Transportation influences the form of cities and their livability, their economic, social, and environmental characteristics. The increasing transportation demand creates more and more mobility-related problems. Most of the big cities are facing the problem of traffic congestion [1,2,3,4]. As urban transit has great possibilities for reducing traffic congestion, offering alternative transportation modes, and contributing greatly to the quality of urban life, urban transit system (bus system, rail transit system, and mass transit system) has begun to grow [5, 6]. The set of urban rail systems can be roughly subdivided into the tram, light rail, rapid transit (underground, subway, metro), monorail, commuter rail, and other types such as rail-guided buses in Nancy, France [7].
Transit system is a complex industry including several majors and perspectives, as shown in Fig. 1. Here is a question, how to build the smart transit system considering all the related perspectives? The global problem is not tractable. Not only the technologies but also the transit network and service planning are needed to make the system more smart and intelligent. A set of subproblems including traffic design problem, transit evaluation, and marketing and policy models are proposed to build the smart transit system.
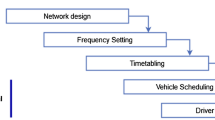
The transit plan is the foundation for a smart urban transit system. Transit network planning problem (TNP) spans every decision that should be taken before the operation of the system. Due to its complexity and objectives, TNP could be divided into strategic planning (network design), tactical planning (frequency setting, timetabling), and operational planning (vehicle scheduling, driver scheduling, and maintenance) [8,9,10]. On the basis of transit planning, a smart urban transit system also required attractive marketing policy to attract more residents and also reasonable evaluating methods evaluating to improve the system. In this way, the urban transit system can be classified into these five parts which are connected and interacted with each other as shown in Fig. 2.
1.1 Strategic Planning (SP)
Strategic planning problems are the initial stage of every smart urban transit system. It defines the network layouts and associated operational characteristics such as rolling stock types and distance between stops. The objective is maximizing the service quality under budgetary restrictions or minimizing the weighted sum of operators’ and users’ costs [9].
1.2 Tactical Planning (TP)
Tactical planning is a way of transferring the transit design to the transportation service, which is a connection between the passengers and operators. Tactical problems focus on the decisions related to services provided to the public, namely the frequencies of service along the routes and the timetables, which could maximize the quality of service [11,12,13]. These problems are usually solved on a seasonal basis with occasional updates [8].
1.3 Operational Planning (OP)
Operational planning problems focused on providing the proposed service at minimum cost. This topic includes a variety of problems such as vehicle scheduling, driver scheduling, rolling stock schedule, and maintenance schedule.
1.4 Transit Evaluation (TE)
Transit evaluation is a kind of way to obtain the service feedback from the passengers and operators. It also highlights the places where the operators can improve their service. Usually, the transit evaluation contains the transit accessibility, network reliability, timetable robustness, and energy-consuming evaluation.
1.5 Marketing and Policy (MP)
In order to make more profit for the society and residents, some works on marketing strategies such as fare policy, investment strategies and trade-offs, and cooperation with other transportation modes are studied.
The aim of this paper is to review state-of-the-art models and approaches for solving these urban transit problems. This review is not exhaustive as it aims to mostly cover the recent contributions that have been applied or have potential to be applied from our viewpoint. Other than reviewing the topics and technology, we also review the solution methods for a different aspect of the urban transit system. This allows comparisons of solution methods of different problems in various classes of the urban transit system and proposes new algorithmic research directions.
The rest of the paper is organized as follows: Sect. 2 reviews the urban transit network planning problem studied in the literature. Section 3 mainly depicts the timetable optimization problems from different perspectives. Section 4 describes the methods evaluating the transit service. Section 5 presents the research on transit marketing and policy. Section 6 depicts the solution method used in Sects. 3 and 4. Finally, the overall view of the research and further research directions are presented in Sect. 7.
2 Strategic Planning: Sustainable Urban Transit Network Design
Network design was firstly formulated by Dantzig [14] as a fixed charge transshipment problem. This problem has been well studied with a full spectrum of strategic, tactical, and operational decision-making situations [9, 14,15,16]. The aim for the network design problem is to find an optimal allocation and utilization of resources to achieve a certain goal [17], such as improving traveler mobility, reducing air/noise pollution, avoiding accidents, and increasing accessibility to meet passengers’ movement requirements [9]. Generally, the objective of network design problem is to minimize the total travel time or the generalized travel cost.
In addition to basic objectives, several other perspectives are considered in practice. These perspectives include: (1) ensuring adequate coverage in the network; (2) ensuring minimum frequencies of service; and (3) any other design considerations such as the availability of infrastructure or right-of-way for routes [18, 19].
A summary of urban transit planning studies ordered by time is presented in Table 1 and Fig. 3. From the beginning of Table 1, budget and passenger demand are main constraints for network design model. Transit planning aims to find a balance between passengers benefit and operation cost [20,21,22]. Recently, based on the abundant data provided by data collection systems, it has become possible to analyze the passenger demand in various dimensions such as time-dependent demand and service reliability, which provide new aspects to design a better network. Some attempts are proposed to solve the flexible demand models [21, 23,24,25]. For the passengers, they hope the transit network could cover a larger service area and have high accessibility [26,27,28] and fewer transfers [22]. In addition to travel demand and accessibility, the stochastic travel time [29, 30], robustness of network [31], and multi-route transit lines [32] are taken into consideration in network design models.
2.1 Discussion
2.1.1 “Passenger-Environmental Friendly” Design
There is a big change in network designing concept. In the past few decades, facilities and infrastructures, civil construction, and budgets have become the priorities. In the last 10 years, the passenger demand and travel experience have raised more attention. Network designers are trying to build a passenger-friendly and environmental-friendly network. In the passenger-friendly network design model, the objective is not only the travel demand, but also the travel cost, which means fewer transfers in the path and more direct shortest path for the passengers are designed to enhance the accessibility of the network. To reduce the emission of the transportation, the environmental costs are addressed in those models. Some research examined how the operational characteristics of urban transit systems affect both costs and greenhouse gas emissions, which could be used to optimize the network design of existing bus service or help to select a mode for minimizing both costs [33].
2.1.2 Dynamic and Detailed Design
To represent a more realistic network, vehicle stochasticity and travel stochasticity are considered in recent network design work. Considering the stochastic characters of travel time can help securing transfer possibilities and minimizing passengers’ transfer time. In spite of travel time stochasticity, some more detailed criteria are taken into consideration such as the network robustness and the time-dependent passenger demand. All these detailed information in the network design could represent passenger profits in the network, and the design will provide better service for the passengers [18].
2.1.3 Integrated Network Design
The network design relates to the timetable scheduling and train/bus operation. In order to make the design satisfy and facilitate the operation tasks, integrated design ideas became very popular. The integrated design also can be taken as a network optimization that combines transit network, vehicle headways, and timetables [34,35,36,37]. This problem is more difficult and complex than the normal network design problem. A heuristic method combined with simulated annealing, tabu, and greedy search methods could be used to solve this problem.
3 Tactical and Operational Planning: Transit Operation and Services
3.1 Timetable Design and Optimization
Timetable generation is the following process of transit network strategic planning, in which the departure time of each trip is determined. For most of timetable optimization problems, the objectives are to minimize the passenger waiting time or transfer time [50,51,52,53], despite meeting with the flexible travel demand [54,55,56,57,58,59,60,61]. Meanwhile, a major complication in transit network timetabling occurs when schedules are intended to be coordinated at a transfer stop or terminals, named timetable synchronization [16, 62, 63]. The objectives of these models are to maximize the number of synchronizations in the transfer stations or maximize the direct transfer passengers and to minimize the passengers’ transfer time and waiting time in the transfer station. A special case in timetable synchronization is the first and last train organization [6, 64, 65]. When generating the timetable, it is also important for the operators to minimize the operation cost and build up the environmentally friendly timetable [66,67,68,69,70,71,71]. For the models mentioned in those papers, most of them share same constraints, including: (1) dwell time in the station; (2) the time window of the train, which gives out the upper and lower departure time of the train in any station; and (3) train consecutive trip, which gives out the order of the first train and consecutive train. For tram systems, which has the correlation with road traffic their timetabling models have to consider the intersection signal timing and the trade-offs between the tram travel time and the roadway traffic delay [72, 73]. Table 2 and Fig. 4 summarize the related literature on obtaining passenger travel time, schedule synchronization, first and last train optimization, and energy consumption, respectively. Summarizing from the related literature, there are two research directions that have become popular in recent years: cyclic timetables and timetable recovery from disruption.
-
1.
Cyclic Timetable A cyclic timetable repeated every standard period [74, 75]. The cyclic timetable is widely used in Europe railway system. Serafini and Ukovich [76] firstly introduced the Periodic Event Scheduling Problem (PESP), by which periodic timetabling instances may be formulated in a very compact way and was applied widely later [51, 77, 78, 82]. Sels et al. [79] derived a PESP model to minimize the total passengers’ travel time in cyclic timetables, and macroscopic simulations were utilized to generate a robust railway timetable. The new periodic timetable is able to save 3.8% of passenger average journey time in Belgian railway. Liebchen and Möhring [80] extended PESP by two features, a linear objective function and a symmetry requirement. Kroon et al. [81] considered the stochastic disturbances in operation and described a Stochastic Optimization Model (SOM) that can be used to allocate the time supplements and the buffer times in a given timetable in such a way that the timetable became maximally robust against stochastic disturbances, and Maróti [83] used a branch-and-bound approach to shorten the computation time of SOM.
-
2.
Timetable Recovery from Disruption Considering the bus or train delay, the real-time rescheduling problems and disruption management for rolling stocks and crew schedule become important [84,85,86,87,88,89,89]. Cacchiani et al. [90] presented an overview of recovery models and algorithms for real-time railway disturbance and disruption management. Weng et al. [91] developed a maximum likelihood regression tree-based model to predict subway incident delays, which is beneficial for subway engineers looking to propose effective strategies for reducing subway incident delays, especially in cities with huge public travel demand. Albrecht et al. [92] described how the Problem Space Search (PSS) metaheuristic can be used for large-scale problems to create quality timetables in which both train movements and scheduled track maintenance are simultaneously considered. Veelenturf et al. [93] formulated an integer linear programming model for solving the timetable rescheduling problem, which minimizes the number of canceled and delayed train services while adhering to infrastructure and rolling stock capacity constraints. Kroon et al. [94] considered the passenger flow change in the large-scale disruption. They described an iterative heuristic for solving the rolling stock rescheduling model with dynamic passenger flows. Yin et al. [95] proposed the static disruption management problems and three levels of attack strategies. Jin [96] presented an optimization-based approach that responds to degradations of urban transit rail networks by introducing smartly designed bus bridging services.
3.2 Discussion
3.2.1 Integrated Timetable Design
Timetable generation is correlated with other scheduling phases (timetable, rolling stock, and crew rescheduling). Most of the research considers one scheduling phase. Only few of them integrated two phases, such as timetable and rolling stock scheduling or vehicle and duty scheduling [37, 97,98,99,100,101,102,102]. For the future research, a nonlinear multi-objective model for optimal schedule could be designed, which is able to maximize schedule reliability and minimize energy consumption, rolling stock, and crew deployment. Another possible strategy for obtaining a full integration is to design a framework that consists of a closed loop in which each rescheduling phase is solved by an efficient algorithm to find a feasible solution and get feedback from the other phases in order to obtain a better feasible solution for the whole system [90].
3.2.2 Synchronization Management
The target of optimizing operation is to reduce transfer time and provide convenience for the passengers. For recent studies, transfers are usually synchronized in one point of the network [103, 104]. In the network, synchronization management is not only required for different lines, which minimize the transfer for the passenger, but also between different modes, the connection between the metro and feeder bus. In this way, the network-mode-wide optimization of the transfer and synchronization would be desirable.
3.2.3 Schedule-Free Operation
High-frequency transit systems are essential for the socioeconomic and environmental well-being of large and dense cities. Based on the high frequency of the transit, Sánchez-Martínez et al. [105] developed a schedule-free paradigm for high-frequency transit operations, in which trip sequences and departure times are optimized to maximize service quality while satisfying operator resource constraints.
4 Transit Service Evaluation from Both Design and Operation Perspectives
Service evaluation is the way to find out the weak point of the schedule and operation strategy [115] and improvements for the social efficiency [116]. Service evaluation contains comfort, convenience, travel conditions, environment, etc. [117, 118]. Litman [119] studied how transit service quality factors affect travel time values and transit ridership. The evaluation analysis is mostly based on the survey data or operation data. Awasthi et al. [120] presented a three-step hybrid approach based on SERVQUAL and fuzzy TOPSIS for evaluation which could provide solution under partial or lack of quantitative information from the survey. Based on the passenger data to evaluate the drawbacks of scheduled timetables, Jiang et al. proposed a simulation-based model to estimate the passenger delays in transit network [121, 122]. Reviewing the recent research about transit evaluation, they can be categorized as service reliability and accessibility, timetable robustness, and energy evaluation.
4.1 Accessibility Evaluation of Transit Network and Services
Accessibility is essential to ensure equal opportunities for all people in society [123,124,125,126,126]. Improving the accessibility of transit system has the potential to increase the attractiveness of public transit to current and prospective riders. Xu et al. [127] defined the Expected Locational Accessibility (ELA) of urban transit networks for commuters, measured by the sample-test-statistics method and the topological analysis method. De Oña et al. [128] proposed a Structural Equation Model (SEM) approach for evaluating the quality of service perceived by users of a bus transit service with 1200 collected surveys. The results showed the service has the highest weight, while comfort and personnel parameters have little weight in the model. And conventional evaluation practices generally assign the same time value regardless of travel conditions, and the impacts of comfort and convenience are underestimated.
4.2 Reliability Evaluation of Timetable
An understanding of service reliability, which includes routes, stops, punctuality, deviation, and evenness [129], is necessary to develop strategies that help transit agencies provide better services [129,130,131,131]. Diab et al. [132] made up the gap between passengers’ and transit agencies’ perspectives on service reliability. Chang et al. [133] analyzed the bus traffic signal priority strategies with their own INTEGRATION simulation package. Simulation results indicated that the improvements of 3.2% in bus service reliability will increase 0.9% for bus efficiency. Van Oort [134] considered the additional travel time as the indicators for the service reliability and demonstrated that traditional indicators lead to wrong indications. The approach proposed in Eklund and Cook [135], which has the capability of handling the uncertainty of transit operations based on a multi-objective evolutionary algorithm using a dynamic Bayesian network, applies preventive strategies to forestall bus unreliability.
4.3 Robustness Evaluation of Timetable
Urban transit systems experience high capacity consumption during large parts of the day resulting in delay-sensitive traffic systems. One fundamental challenge is, therefore, to assess the robustness and find strategies to decrease the sensitivity to disruptions [136,137,138,138]. Andersson et al. [139] proposed a new robustness measure based on Robustness Critical Points (RCP) in the timetable and applied the new model to the Swedish railway line. Goerigk et al. [140] analyzed the impact of different line planning models by comparing their impact on timetables and their robustness against delays. For the Dutch railway network, Corman et al. [141] evaluated the “shuttle” timetable reliability with a thorough assessment and Goverde [142] described a stability theory to analyze timetables on sensitivity and robustness to delays based on a linear system description of a railway timetable in max-plus algebra. Dewilde et al. [143] introduced the minimizing the real travel time as a practical robustness measure. The results indicate an average improvement in robustness of 6.2% together with a decrease in delay propagation of about 25%.
5 Marketing and Policy from an Industry Perspective
Passengers are quite sensitive to the price strategy [144,145,146,147,148,148]. Analyzing the passenger behavior before and after new price scheme, the acceptability of urban transport pricing strategies could help to make more reasonable price policy [149,150,151,151]. Delbosc and Currie [152] focused on the fare evasion. They used a quantitative cluster analysis to segment fare evasion behaviors into three categories, which show distinct personality and behavioral characteristics. A model built by Bianchi et al. [153] tested the impact of different price levels on patronage by period based on the new price strategy of Santiago Metro. Li et al. [154] proposed a network-based model for investigating the optimal transit fare structure under monopoly and oligopoly market regimes with uncertainty in the network. Wang et al. [155] assessed the influence of ridership and revenue of Beijing metro new distance-based fare policy. Instead of flat fare, researchers try to make a flexible pricing strategy which will attract more passengers and make higher revenue [156, 157]. Some special ticket schemes are put forward for the university student [158, 159], for example, students and faculty from University of Minnesota; twin cities could enjoy three stations free ride in the campus. Brown et al. [160] evaluated the results of the Un-limited Access Program at the University of California, Los Angeles (UCLA), which provides fare-free transit service for all students.
In order to get more investments for the urban transit system, some marketing strategies are studied [161,162,163,163]. Schmekel [164] analyzed the strategic importance of retail investment in Asia and its implications for the Metro Group in Asia. Chakrabarti and Giuliano [165] took Los Angeles Metro bus system to analyze the transit patronage from service reliability.
Transit is not the only mode that provides transportation supply. Parking and Ride (P + R) is a good way to achieve the cooperation between cars and transit. Hamre and Buehler [166] evaluated the relationship between commuter benefits and mode choice for the commute to work using revealed preference data on 4630 regular commuters, including information about free car parking, public transportation benefits, and bike parking at work in the Washington, DC region. Chen et al. [167] developed the location-based service application to help P + R riders choose the best depart train station. Du et al. [168] modeled park and ride services in a multi-commodity discrete/continuum transport system with elastic demand.
6 Review of Solution Techniques Solving Smart Urban Transit Models
Transit planning models are usually considered as an optimization problem. Solutions about these models are listed in Tables 1 and 2. In this section, we only discussed the solution used in optimization problems in Sects. 2 and 3. Normally, the solution can be classified into three categories: (1) exact or mathematical methods, (2) heuristics, and (3) metaheuristics. Exact methods, such as the branch-and-bound method and Lagrangian decomposition method, highly rely on the model mathematical properties. Although some of them have been applied to realistic and large networks, the computation efficiency is still a big shortage to solve the real-size network problem. Heuristics are usually developed for the large network application because of short computation time, but the one thing need to consider is the convergence. Metaheuristics such as simulated annealing and the use of a genetic algorithm were proposed based on analogies to physical, chemical, or biological process [18]. Metaheuristics process could identify the nearly global optimal solutions more efficiently. Figure 2 summarizes the applications of some metaheuristics and mathematical methods in the literature in Sects. 2 and 3.
Figure 5 shows that the heuristics and metaheuristics are mostly used to solve the planning problems in the urban transit system. Although a large collection of metaheuristic application to these problems can be found in the literature, the applications are very limited to a very few numbers of classical metaheuristic such as GA and SA and none classical metaheuristics such as TS and AC. Among these methods, the GAs and SAs have been mostly used. Further research on testing those methods hasn’t been applied and could be studied in the later research. There are limited studies that have employed a mathematical method for obtaining solutions. For example, the branch-and-bound algorithm and MIP solver in the Cplex are used to solve some mixed integer problem. Although they can provide an exact solution, they can usually be applied to some small network.
A summary of methods used in urban transit planning. IM iterated local search, GA genetic algorithm, H heuristic, SS scatter search algorithm, MCS Monte-Carlo simulation, L Lagrangian decomposition/relaxation, AC ant colony optimization, SA simulated annealing, TS tabu search, HC hill climbing, BB branch-and-bound algorithm, F fuzzy mathematical programming, PSO particle swarm optimization
7 Discussion and Conclusion
A smart transit system contains sustainable urban transit network design, high-level operation service, reasonable evaluation, flexible marketing and policy. This study focused and summarized the models and research in each part. In the network design process, this research listed the objectives, constraints and algorithms for network design model. Despite satisfying the traffic demand and accessibility, designers consider more on the environment, social profits, and the operation schedule. To provide better service after summarizing and analyzing the operational updating model, the schedule synchronization, cyclic timetable, minimal energy consumption, and timetable recovery from the disruption are considered as new aspects for the tactical and operational planning stage. To improve the transit system and service, this study summarized the evaluation models on service reliability, service accessibility, timetable robustness, and energy consuming are proposed, which highlight the gap between the idealized service and the real service. Meanwhile, the urban transit system is a complex industry and needs financial investments. Some flexible fare scheme, investments, and commercial strategies are applied to the transit system to support the sustainable development. From travel demand, system synchronization to operation control, the transit systems are facing challenges on how to improve the travel efficiency and decrease travel energy consumption. There are several research topics that are necessary for the future study.
7.1 Passenger Demand Management and Travel Information Service
7.1.1 Passenger Behavior Analysis and Rescheduling for Transit Interruption
A lot of research has focused on passenger behavior and transit service for normal daily transit operation. However, transit system is not always stable and train delay or signal failures may happen. To deal with those disruptions, it is necessary to learn the passenger behavior pattern such as the behavior in the station and route choice in the network. Following the spatial and temporal passenger flow on the network, it is possible to provide temporary and emergency rescheduling model and algorithm for the delayed passengers.
7.1.2 Data-Driven Passenger Demand and Behavior Analysis
With the development of the communication technology and computer science, the passenger travel data and operation data can be collected and updated in a short time interval [169]. For the transit system, the automated vehicle location (AVL) systems, automatic fare collection (AFC), and automatic passenger collection (APC) opened new venues in operations and system monitoring. The various uses of the data could be classified into three levels: strategic, tactical, and operational level. For the strategic level, data can be very useful to transit planners, from the day-to-day operation of the transit system to the strategic long-term network planning [170]. In the tactical level, the data can be the input for the service adjustments and network development. In the operational one, it is possible for the operators to evaluate the operation performance, service level, and service reliability [171,172,173,174,175,175]. Meanwhile, those huge amount of data provide better opportunity for the researchers to track and estimate passenger behaviors in the network [176, 177], such as the spatial–temporal density [178, 179], path choice [180, 181], trip pattern and trip chain [182,183,184,184], and transfers [185]. Operation agencies could provide better and smarter operation strategy for passengers, such as a reinforcement learning-based coordinated passenger inflow control strategy [186].
7.1.3 Heterogeneous–Homogeneous Passenger Forecasting Models
Detailed spatial and temporal passenger distribution patterns are the foundation for the passenger forecasting model. A pile of research has been worked on the spatial and temporal passenger behavior from statistical to dynamic. From those studies, most of them focus on the commuters in transit system during the peak hour, which is the majority proportion of passengers. The research results provide nice homogeneous passenger forecasting models. For the off-peak hour, the passenger classifications are more vivid. It is more diversity in route choice, spatial distribution, and temporal distribution. In this case, it is necessary to provide heterogeneous forecasting models to cover the passenger diversity.
7.1.4 Real-Time Service Information
Real-time information helps the passengers to update their trip plan. Watkins et al. [187] developed the OneBusAway system which can estimate the bus arrival time [188] and analyze the passenger perceived and actual wait time impacted by real-time information. Zhang et al. [189] analyzed the impact of Stockholm metro with the real-time crowding information. Though these services are widely used and improved the performance of the public transportation, there are some blanks need to fill. For instance, it is still challenging to calculate the overall transit ridership.
7.2 Transit Facility and Service Optimization
7.2.1 Operation Energy Consumption Control
The transit system is motivated by electricity. In Beijing, compared with other industries, Beijing metro is on the top place on energy consumption. To reduce the energy consumption, it is necessary to optimize the train operation speed based on the traction curve. From the research above, some researchers have been working on the schedule optimization with consideration of environmental costs. Meanwhile, some technologies for train and network design such as regenerative breaking technology, energy-saving slope, and automatic train operation and control system have been applied in the transit system.
7.2.2 Data-Driven Rescheduling Models
In addition to passenger analysis, AVL provides bus and train real-time position and makes the real-time control and real-time information (RTI) possible [190, 191]. The passengers could use RTI to change their path in time based on the congestion condition in the network, and for the operators, they could deal with unexpected variations in the schedule and improve the performance of the system. Nesheli et al. [192] invested and analyzed the benefit from real-time operational tactics. In 2015, collaborating with Ceder they proposed transfer synchronization to improve the reliability of public transportation [193].
Over the years, Geographic Information System (GIS) technology has been implemented for a variety of purposes within the transit industry. Recently, the GIS has been widely used in accessibility analysis such as the walking accessibility between alternative neighborhood designs [194] and transport accessibility disadvantage [123]. The data and results in transit have the spatial characteristic. To demonstrate the data more clearly and directly, some visualization tools based on GIS have been developed to explore spatial variations in data [195]. The visualization results also provide a better way to find out the character of the data and a better understanding of the data.
7.2.3 Integrated Operation Design
Transit network is the combination of passengers, stations, transit lines, trains, and service staff. Timetables, rolling stock plans, maintenance planning, and crew scheduling are dominated operation schedules for the transit system. All of these components have correlations with others. While there are some classical models which performed well in each part individually, it is still necessary and challenging to propose an integrated optimization model to consider all of these components together and provide efficient and environmental-friendly transit service for passengers.
7.3 Shared Mobility and Emergency Control
7.3.1 Emergency Control
While most of the models showed excellent results in improving the schedule and operation performance, most of the applications are off-line or post-evaluation. Transit system needs a quick response to the accident and disruption. It is necessary and will be a large challenge to apply the academic models and algorithms into the real-time operation facing the interruption in the system.
7.3.2 Shared Mobility
Technology is transforming transportation. Bike sharing, car sharing, and rider sourcing services provided by companies such as Uber and Lyft are all shared modes, which have a strong relationship with the public transit [196, 197]. The shared mobility, especially the bike sharing, could efficiently solve the last one-kilometer problem. Jin et al. [198] showed out that the metro network resilience to disruptions can be enhanced significantly from localized integration with feeder bus services. In recent 3 years, another kind of “public mode,” bicycle-sharing programs, such as Mobike (Beijing), CityCycle [199], and NiceRide (Minneapolis), has received increasing attention with initiatives to increase bike usage, better meet the demand of a more mobile demand, and lessen the environmental impacts of our transportation activities [200,201,202,203,203]. After studied 7 cities (Austin, Boston, Chicago, Los Angeles, San Francisco, Seattle, and Washington, DC.), shared modes complement public transit, enhancing urban mobility, especially when public transit runs infrequently or is not available and will continue to grow significantly. In the future, the public entities such as buses, tram, and metro should collaborate with the shared mobility modes to ensure that benefits could be widely and equitably shared. Technology and emerging approaches are urgent for public sector and private operators’ collaboration to improve paratransit services [196, 197].
References
Ahmed QI, Lu H, Ye S (2008) Urban transportation and equity: a case study of Beijing and Karachi. Transp Res Part A Policy Pract 42(1):125–139
Ingvardson JB, Jensen JK, Nielsen OA (2017) Analysing improvements to on-street public transport systems: a mesoscopic model approach. Public Transp 9:385–409
Miller P, de Barros AG, Kattan L, Wirasinghe SC (2016) Analyzing the sustainability performance of public transit. Transp Res Part D Transp Environ 44:177–198
Miller P, de Barros AG, Kattan L, Wirasinghe SC (2016) Public transportation and sustainability: a review. KSCE J Civ Eng 20(3):1076
Vuchic VR (2005) Urban transit: operations, planning, and economics. Wiley, London
Kang L, Wu J, Sun H, Zhu X, Gao Z (2015) A case study on the coordination of last trains for the Beijing subway network. Transp Res Part B Methodol 72:112–127
Desaulniers G, Hickman M (2007) Public transit. In: Barnhart C, Laporte G (eds) Handbooks in operations research and management science: transportation, vol 14. North-Holland, Amsterdam, pp 69–128. https://www.sciencedirect.com/science/article/pii/S0927050706140025
Ibarra-Rojas OJ, Delgado F, Giesen R, Muñoz JC (2015) Planning, operation, and control of bus transport systems: a literature review. Transp Res Part B Methodol 77:38–75
Ceder A (2007) Public transit planning and operation: theory modeling and practice. Elsevier, Butterworth-Heinemann, Oxford
Bussieck MR, Kreuzer P, Zimmermann UT (1997) Optimal lines for railway systems. Eur J Oper Res 96:54–63
Odoni AR, Rousseau J-M, Wilson NHM (1994) Models in urban and air transportation. In: Pollock SM, Rothkopf MH, Barn A (eds) Handbooks in OR & MS: operations research and the public sector, vol 8. North Holland, Amsterdam
Binder S, Maknoon Y, Bierlaire M (2017) The multi-objective railway timetable rescheduling problem. Transp Res Part C Emerg Technol 78:78–94
Dantzig G (1963) Linear programming and extensions. Princeton University Press, Princeton
Kepaptsoglou K, Karlaftis M (2009) Transit route network design problem: review. J Transp Eng 135(8):491–505
Ceder A (2001) Operational objective functions in designing public transport routes. J Adv Transp 35(2):125–144
Crainic TG (2000) Service network design in freight transportation. Eur J Oper Res 122(2):272–288
Farahani RZ, Miandoabchi E, Szeto WY, Rashidi H (2013) A review of urban transportation network design problems. Eur J Oper Res 229(2):281–302
Quan Y, Liu J (2017) Issues and thoughts on regional rail transit planning. Urban Transp China 15(1):12–19
Current JR, Revelle CS, Cohon JL (1987) The median shortest path problem: a multiobjective approach to analyze cost vs. accessibility in the design of transportation networks. Transp Sci 21:188–197
Fan W, Machemehl RB (2006) Optimal transit route network design problem with variable transit demand: genetic algorithm approach. J Transp Eng 132(1):40–51
Guihaire V, Hao JK (2008) Transit network design and scheduling: a global review. Transp Res Part A Policy Pract 42(10):1251–1273
Baaj MH, Mahmassani HS (1991) An AI-based approach for transit route system planning and design. J Adv Transp 25(2):187–209
Cipriani E, Gori S, Petrelli M (2012) A bus network design procedure with elastic demand for large urban areas. Public Transp 4(1):57–76
Hassannayebi E, Sajedinejad A, Mardani S (2014) Urban rail transit planning using a two-stage simulation-based optimization approach. Simul Model Pract Theory 49:151–166
Tong L, Zhou X, Miller HJ (2015) Transportation network design for maximizing space–time accessibility. Transp Res Part B Methodol 81:555–576
Yu B, Yang ZZ, Jin PH, Wu SH, Yao BZ (2012) Transit route network design-maximizing direct and transfer demand density. Transp Res Part C Emerg Technol 22:58–75
Ziari H, Keymanesh MR, Khabiri MM (2007) Locating stations of public transportation vehicles for improving transit accessibility. Transport 22(2):99–104
Yan Y, Liu Z, Meng Q, Jiang Y (2013) Robust optimization model of bus transit network design with stochastic travel time. J Transp Eng 139(6):625–634
Yao B, Hu P, Lu X, Gao J, Zhang M (2014) Transit network design based on travel time reliability. Transp Res Part C Emerg Technol 43:233–248
Ukkusuri SV, Mathew TV, Waller ST (2007) Robust transportation network design under demand uncertainty. Comput Aided Civ Infrastruct Eng 22(1):6–18
Wan QK, Lo HK (2003) A mixed integer formulation for multiple-route transit network design. J Math Model Algorithms 2(4):299–308
Griswold JB, Madanat S, Horvath A (2013) Tradeoffs between costs and greenhouse gas emissions in the design of urban transit systems. Environ Res Lett 8(4):044046
Zhao F, Zeng X (2008) Optimization of transit route network, vehicle headways and timetables for large-scale transit networks. Eur J Oper Res 186(2):841–855
Burggraeve S, Bull SH, Vansteenwegen P, Lusby RM (2017) Integrating robust timetabling in line plan optimization for railway systems. Transp Res Part C Emerg Technol 77:134–160
Schöbel A (2017) An eigenmodel for iterative line planning, timetabling and vehicle scheduling in public transportation. Transp Res Part C Emerg Technol 74:348–365
Lidén T, Joborn M (2017) An optimization model for integrated planning of railway traffic and network maintenance. Transp Res Part C Emerg Technol 74:327–347
Kuah GK, Perl J (1989) The feeder-bus network-design problem. J Oper Res Soc 40(8):751–767
Chien S, Yang Z, Hou E (2001) Genetic algorithm approach for transit route planning and design. J Transp Eng 127(3):200–207
Ceder A (2003) Chapter 3: designing public transport network and routes. In: Lam W, Nell M (eds) Advanced modeling for transit operations and service planning. Elsevier, New York (Pergamon Imprint, 59–91)
Lee YJ, Vuchic VR (2005) Transit network design with variable demand. J Transp Eng 131(1):1–10
Fan W, Machemehl RB (2008) A tabu search based heuristic method for the transit route network design problem. Computer-aided systems in public transport. Springer, Berlin, pp 387–408
Lium AG, Crainic TG, Wallace SW (2009) A study of demand stochasticity in service network design. Transp Sci 43(2):144–157
Fan L, Mumford CL (2010) A metaheuristic approach to the urban transit routing problem. J Heuristics 16(3):353–372
Fan W, Machemehl R (2011) Bi-level optimization model for public transportation network redesign problem: accounting for equity issues. Transp Res Rec J Transp Res Board 2263:151–162
Gallo M, Montella B, D’Acierno L (2011) The transit network design problem with elastic demand and internalisation of external costs: an application to rail frequency optimisation. Transp Res Part C Emerg Technol 19:1276–1305
Cipriani E, Gori S, Petrelli M (2012) Transit network design: a procedure and an application to a large urban area. Transp Res Part C Emerg Technol 20(1):3–14
Miandoabchi E, Farahani RZ, Dullaert W, Szeto WY (2012) Hybrid evolutionary metaheuristics for concurrent multi-objective design of urban road and public transit networks. Netw Spat Econ 12:441–480
Zarrinmehr A, Saffarzadeh M, Seyedabrishami S, Nie YM (2016) A path-based greedy algorithm for multi-objective transit routes design with elastic demand. Public Transp 8(2):261–293
Wong RC, Yuen TW, Fung KW, Leung JM (2008) Optimizing timetable synchronization for rail mass transit. Transp Sci 42(1):57–69
Liebchen C (2008) The first optimized railway timetable in practice. Transp Sci 42(4):420–435
Shafahi Y, Khani A (2010) A practical model for transfer optimization in a transit network: model formulations and solutions. Transp Res Part A Policy Pract 44(6):377–389
Chang YH, Yeh CH, Shen CC (2000) A multiobjective model for passenger train services planning: application to Taiwan’s high-speed rail line. Transp Res Part B Methodol 34(2):91–106
Sun L, Jin JG, Lee DH, Axhausen KW, Erath A (2014) Demand-driven timetable design for metro services. Transp Res Part C Emerg Technol 46:284–299
Niu H, Zhou X (2013) Optimizing urban rail timetable under time-dependent demand and oversaturated conditions. Transp Res Part C Emerg Technol 36:212–230
Barrena E, Canca D, Coelho LC, Laporte G (2014) Exact formulations and algorithm for the train timetabling problem with dynamic demand. Comput Oper Res 44:66–74
Barrena E, Canca D, Coelho LC, Laporte G (2014) Single-line rail rapid transit timetabling under dynamic passenger demand. Transp Res Part B Methodol 70:134–150
Cai Z, Pang B, Diao H (2017) Optimization of urban rail transit timetable with dynamic demand. Railw Transp Econ 2017(1):95–100
Li D, Ding S, Zhang Q, Li S (2017) Improved dynamic demand oriented timetabling model for intercity railway. J Transp Syst Eng Inf Technol 17(3):157–164
Shang P, Li R, Liu Z, Yang L, Wang Y (2018) Equity-oriented skip-stopping schedule optimization in an oversaturated urban rail transit network. Transp Res Part C Emerg Technol 89:321–343
Shi J, Yang L, Yang J, Gao Z (2018) Service-oriented train timetabling with collaborative passenger flow control on an oversaturated metro line: an integer linear optimization approach. Transp Res Part B Methodol 110:26–59
Ceder A, Golany B, Tal O (2001) Creating bus timetables with maximal synchronization. Transp Res Part A Policy Pract 35(10):913–928
Eranki A (2004) A model to create bus timetables to attain maximum synchronization considering waiting times at transfer stops. Doctoral dissertation, University of South Florida
Dou X, Meng Q, Guo X (2015) Bus schedule coordination for the last train service in an intermodal bus-and-train transport network. Transp Res Part C Emerg Technol 60:360–376
Guo X, Wu J, Sun H, Liu R, Gao Z (2016) Timetable coordination of first trains in urban railway network: a case study of Beijing. Appl Math Model 40(17):8048–8066
Albrecht T, Oettich S (2002) A new integrated approach to dynamic schedule synchronization and energy-saving train control. WIT Trans Built Environ 61:847–856
Peña-Alcaraz M, Fernández A, Cucala AP, Ramos A, Pecharromán RR (2012) Optimal underground timetable design based on power flow for maximizing the use of regenerative-braking energy. Proc Inst Mech Eng Part F J Rail Rapid Transit 226:397–408
Li X, Lo HK (2014) An energy-efficient scheduling and speed control approach for metro rail operations. Transp Res Part B Methodol 64:73–89
Cucala AP, Fernández A, Sicre C, Domínguez M (2012) Fuzzy optimal schedule of high speed train operation to minimize energy consumption with uncertain delays and driver’s behavioral response. Eng Appl Artif Intell 25:1548–1557
Zhao N, Roberts C, Hillmansen S, Tian Z, Weston P, Chen L (2017) An integrated metro operation optimization to minimize energy consumption. Transp Res Part C Emerg Technol 75:168
Tian Z, Weston P, Zhao N, Hillmansen S, Roberts C, Chen L (2017) System energy optimisation strategies for metros with regeneration. Transp Res Part C Emerg Technol 75:120–135
Shi J, Sun Y, Schonfeld P, Qi J (2017) Joint optimization of tram timetables and signal timing adjustments at intersections. Transp Res Part C Emerg Technol 83:104–119
Jiang Z, Xu R (2016) Scheduling optimization of tram operation diagram under signal passive priority condition. J Traffic Transp Eng 16(3):100–107
Robenek T, Azadeh SS, Maknoon Y, Bierlaire M (2017) Hybrid cyclicity: combining the benefits of cyclic and non-cyclic timetables. Transp Res Part C Emerg Technol 75:228–253
Li D, Ding S (2017) Research on establishment of periodic train working diagram for high speed railway based on improved PESP model. China Railw Sci 38(1):132–137
Serafini P, Ukovich W (1989) A mathematical model for periodic scheduling problems. SIAM J Discrete Math 2(4):550–581
Odijk MA (1996) A constraint generation algorithm for the construction of periodic railway timetables. Transp Res Part B Methodol 30(6):455–464
Kümmling M, Großmann P, Nachtigall K, Opitz J, Weiß R (2015) A state-of-the-art realization of cyclic railway timetable computation. Public Transp 7(3):281–293
Sels P, Dewilde T, Cattrysse D, Vansteenwegen P (2016) Reducing the passenger travel time in practice by the automated construction of a robust railway timetable. Transp Res Part B Methodol 84:124–156
Liebchen C, Möhring RH (2007) The modeling power of the periodic event scheduling problem: railway timetables—and beyond. Algorithmic methods for railway optimization. Springer, Berlin, pp 3–40
Peeters L, Kroon L (2001) A cycle based optimization model for the cyclic railway timetabling problem. In: Computer-aided scheduling of public transport. Springer, Berlin, pp 275–296
Kroon L, Maróti G, Helmrich MR, Vromans M, Dekker R (2008) Stochastic improvement of cyclic railway timetables. Transp Res Part B Methodol 42(6):553–570
Maróti G (2017) A branch-and-bound approach for robust railway timetabling. Public Transp 9:73–94
Walker CG, Snowdon JN, Ryan DM (2005) Simultaneous disruption recovery of a train timetable and crew roster in real time. Comput Oper Res 32(8):2077–2094
Gao Y, Yang L, Gao Z (2017) Real-time automatic rescheduling strategy for an urban rail line by integrating the information of fault handling. Transp Res Part C Emerg Technol 81:246–267
Veelenturf LP, Kroon LG, Maróti G (2017) Passenger oriented railway disruption management by adapting timetables and rolling stock schedules. Transp Res Part C Emerg Technol 80:13
Lee WH, Yen LH, Chou CM (2016) A delay root cause discovery and timetable adjustment model for enhancing the punctuality of railway services. Transp Res Part C Emerg Technol 73:4
Teng J, Xu R (2010) Bus dispatching strategies in urban rail emergent events. J China Railw Soc 32(5):13–17
Wang L (2012) Fuzzy random optimization for train operation in emergency. Beijing Jiaotong University, Beijing
Cacchiani V, Huisman D, Kidd M, Kroon L, Toth P, Veelenturf L, Wagenaar J (2014) An overview of recovery models and algorithms for real-time railway rescheduling. Transp Res Part B Methodol 63:15–37
Weng J, Zheng Y, Qu X, Yan X (2015) Development of a maximum likelihood regression tree-based model for predicting subway incident delay. Transp Res Part C Emerg Technol 57:30–41
Albrecht AR, Panton DM, Lee DH (2013) Rescheduling rail networks with maintenance disruptions using problem space search. Comput Oper Res 40(3):703–712
Veelenturf LP, Kidd MP, Cacchiani V, Kroon LG, Toth P (2015) A railway timetable rescheduling approach for handling large-scale disruptions. Transp Sci 50(3):841–862
Kroon L, Maróti G, Nielsen L (2014) Rescheduling of railway rolling stock with dynamic passenger flows. Transp Sci 49(2):165–184
Yin H, Han B, Li D (2016) Evaluating disruption in rail transit network: a case study of Beijing subway. Proc Eng 137:49–58
Jin JG, Teo KM, Odoni AR (2015) Optimizing bus bridging services in response to disruptions of urban transit rail networks. Transp Sci 50(3):790–804
Borndörfer R, Löbel A, Weider S (2008) A bundle method for integrated multi-depot vehicle and duty scheduling in public transit. In: Computer-aided systems in public transport. Springer, Berlin, pp 3–24
Borndörfer R, Grötschel M, Pfetsch ME (2007) A column-generation approach to line planning in public transport. Transp Sci 41(1):123–132
Haase K, Desaulniers G, Desrosiers J (2001) Simultaneous vehicle and crew scheduling in urban mass transit systems. Transp Sci 35(3):286–303
Luan X, Miao J, Meng L, Corman F, Lodewijks G (2017) Integrated optimization on train scheduling and preventive maintenance time slots planning. Transp Res Part C Emerg Technol 80:329–359
Wang S (2016) Study on integrated train timetabling and rolling stock scheduling model and algorithm based on time-dependent demand for urban rail transit. Beijing Jiaotong University, Beijing
Zhou Y, Tang J, Xu X, Xiao H (2013) Research on integrated theoretical frame of networked train operation for urban rail transit. Urban Rapid Rail Transit 26(4):63–67
Luo X, Jiang Y (2017) Timetable transfer-coordination optimization based on transit data mining. J Transp Syst Eng Inf Technol 17(5):173–178
Ning Q, Zhao P, Xu W, Qiao K, Yao X (2016) Timetable synchronization optimization for urban rail transit in the last trains’ hour. J Transp Syst Eng Inf Technol 16(6):108–114
Sánchez-Martínez GE, Wilson NH, Koutsopoulos HN (2016) Schedule-free high-frequency transit operations. Public Transp 9:285–305
Cevallos F, Zhao F (2006) A genetic algorithm for bus schedule synchronization. In: Applications of advanced technology in transportation, pp 737–742
Ibarra-Rojas OJ, Rios-Solis YA (2012) Synchronization of bus timetabling. Transp Res Part B Methodol 46(5):599–614
Wu J, Liu M, Sun H, Li T, Gao Z, Wang DZ (2015) Equity-based timetable synchronization optimization in urban subway network. Transp Res Part C Emerg Technol 51:1–18
Wu D, Wang S, Liang W (2016) Impact of financing modes on the overall efficiency of urban rail transit projects. Urban Rapid Rail Transit 29(1):26–29
Guo X, Sun H, Wu J, Jin J, Zhou J, Gao Z (2017) Multiperiod-based timetable optimization for metro transit networks. Transp Res Part B Methodol 96:46–67
Kang L, Zhu X (2017) Strategic timetable scheduling for last trains in urban railway transit networks. Appl Math Model 45:209–225
Kang L, Zhu X, Sun H, Puchinger J, Ruthmair M, Hu B (2016) Modeling the first train timetabling problem with minimal missed trains and synchronization time differences in subway networks. Transp Res Part B Methodol 93:17–36
Su S, Li X, Tang T, Gao Z (2013) A subway train timetable optimization approach based on energy-efficient operation strategy. IEEE Trans Intell Transp Syst 14(2):883–893
Yang X, Chen A, Li X, Ning B, Tang T (2015) An energy-efficient scheduling approach to improve the utilization of regenerative energy for metro systems. Transp Res Part C Emerg Technol 57:13–29
Eboli L, Mazzulla G (2011) A methodology for evaluating transit service quality based on subjective and objective measures from the passenger’s point of view. Transp Policy 18(1):172–181
Morisugi H (2000) Evaluation methodologies of transportation projects in Japan. Transp Policy 7(1):35–40
Vickerman R (2000) Evaluation methodologies for transport projects in the United Kingdom. Transp Policy 7(1):7–16
Fielding GJ, Babitsky TT, Brenner ME (1985) Performance evaluation for bus transit. Transp Res Part A Gen 19(1):73–82
Litman T (2008) Valuing transit service quality improvements. J Public Transp 11(2):3
Awasthi A, Chauhan SS, Omrani H, Panahi A (2011) A hybrid approach based on SERVQUAL and fuzzy TOPSIS for evaluating transportation service quality. Comput Ind Eng 61(3):637–646
Jiang Z, Hsu CH, Zhang D, Zou X (2016) Evaluating rail transit timetable using big passengers’ data. J Comput Syst Sci 82(1):144–155
Jiang Z, Li F, Xu R, Gao P (2012) A simulation model for estimating train and passenger delays in large-scale rail transit networks. J Cent South Univ 19(12):3603–3613
Wu BM, Hine JP (2003) A PTAL approach to measuring changes in bus service accessibility. Transp Policy 10(4):307–320
Prasertsubpakij D, Nitivattananon V (2012) Evaluating accessibility to Bangkok Metro Systems using multi-dimensional criteria across user groups. IATSS Res 36(1):56–65
Liu Y, Song R, Li Z (2014) Evaluating of the accessibility to rail transit based on spatial syntax. Urban Rapid Rail Transit 27(6):70–74
Li S, An Z, He L (2013) Research on interaction between rail transit and city land development. Urban Rapid Rail Transit 26(5):25–29
Xu W, Zhang W, Li L (2017) Measuring the expected locational accessibility of urban transit network for commuting trips. Transp Res Part D Transp Environ 51:62–81
De Oña J, de Oña R, Eboli L, Mazzulla G (2013) Perceived service quality in bus transit service: a structural equation approach. Transp Policy 29:219–226
Chen X, Yu L, Zhang Y, Guo J (2009) Analyzing urban bus service reliability at the stop, route, and network levels. Transp Res Part A Policy Pract 43(8):722–734
Liu Z, Song R (2010) Reliability analysis of Guangzhou rail transit with complex network theory. J Transp Syst Eng Inf Technol 10(5):194–200
Chen J (2010) Reliability study on urban rail transit network based on complex network theories. Urban Rapid Rail Transit 23(2):18–21
Diab EI, Badami MG, El-Geneidy AM (2015) Bus transit service reliability and improvement strategies: integrating the perspectives of passengers and transit agencies in North America. Transp Rev 35(3):292–328
Chang J, Collura J, Dion F, Rakha H (2003) Evaluation of service reliability impacts of traffic signal priority strategies for bus transit. Transp Res Rec J Transp Res Board 1841:23–31
Van Oort N (2014) Incorporating service reliability in public transport design and performance requirements: international survey results and recommendations. Res Transp Econ 48:92–100
Eklund P, Cook C (2015) Toward real-time multi-criteria decision making for bus service reliability optimization. In: International symposium on methodologies for intelligent systems, pp 371–378
De-Los-Santos A, Laporte G, Mesa JA, Perea F (2012) Evaluating passenger robustness in a rail transit network. Transp Res Part C Emerg Technol 20(1):34–46
Cao Z, Yuan Z, Li D, Zhang S, Ma L (2017) Robust optimization model for train working diagram of urban rail transit. China Railw Sci 38(3):130–136
Sun Y, Liu X, Jing C, Song R, Nie T (2015) Robust optimization for rail transit network under uncertainty demand. J Transp Syst Eng Inf Technol 15(4):181–186
Andersson EV, Peterson A, Krasemann JT (2013) Quantifying railway timetable robustness in critical points. J Rail Transp Plan Manag 3(3):95–110
Goerigk M, Schachtebeck M, Schöbel A (2013) Evaluating line concepts using travel times and robustness. Public Transp 5(3):267–284
Corman F, D’Ariano A, Hansen IA (2014) Evaluating disturbance robustness of railway schedules. J Intell Transp Syst 18(1):106–120
Goverde RM (2007) Railway timetable stability analysis using max-plus system theory. Transp Res Part B Methodol 41(2):179–201
Dewilde T, Sels P, Cattrysse D, Vansteenwegen P (2014) Improving the robustness in railway station areas. Eur J Oper Res 235(1):276–286
Ros D, Tuffin B (2004) A mathematical model of the Paris metro pricing scheme for charging packet networks. Comput Netw 46(1):73–85
Ivaldi M, Vibes C (2008) Price competition in the intercity passenger transport market: a simulation model. J Transp Econ Policy 42(2):225–254
Deng L, Wang F, Zhang L, Wang Q, Lai T (2016) Fare optimization for urban rail line. Syst Eng Theory Pract 36(6):1568–1575
Yang W (2016) Urban rail transit peak and off-peak periods variable logging ticket pricing strategies study based on elastic coefficient. Beijing Jiaotong University, Beijing
Liu M, Wang J (2017) Pricing method of urban rail transit considering the optimization of passenger transport structure. J Transp Syst Eng Inf Technol 17(3):53–59
Schade J, Schlag B (2003) Acceptability of urban transport pricing strategies. Transp Res Part F Traffic Psychol Behav 6(1):45–61
Tirachini A (2013) Estimation of travel time and the benefits of upgrading the fare payment technology in urban bus services. Transp Res Part C Emerg Technol 30:239–256
De Palma A, Kilani M, Proost S (2015) Discomfort in mass transit and its implication for scheduling and pricing. Transp Res Part B Methodol 71:1–18
Delbosc A, Currie G (2016) Cluster analysis of fare evasion behaviours in Melbourne, Australia. Transp Policy 50:29–36
Bianchi R, Jara-Díaz SR, Ortúzar JDD (1998) Modelling new pricing strategies for the Santiago Metro. Transp Policy 5(4):223–232
Li ZC, Lam WH, Wong SC (2009) The optimal transit fare structure under different market regimes with uncertainty in the network. Netw Spat Econ 9(2):191–216
Wang ZJ, Li XH, Chen F (2015) Impact evaluation of a mass transit fare change on demand and revenue utilizing smart card data. Transp Res Part A Policy Pract 77:213–224
Hetrakul P, Cirillo C (2014) A latent class choice based model system for railway optimal pricing and seat allocation. Transp Res Part E Logist Transp Rev 61:68–83
Zhang X, Ma L, Zhang J (2017) Dynamic pricing for passenger groups of high-speed rail transportation. J Rail Transp Plan Manag 6(4):346–356
Wang Q, Wang L, Wang S, Zhao L, Cheng X, Chen X (2011) Study on student ticket distribution model and its particle swarm optimization algorithm. In: 2011 international conference on internet computing & information services (ICICIS)
Jomnonkwao S, Sangphong O, Khampirat B, Siridhara S, Ratanavaraha V (2016) Public transport promotion policy on campus: evidence from Suranaree University in Thailand. Public Transp 8(2):185–203
Brown J, Hess DB, Shoup D (2003) Fare-free public transit at universities: an evaluation. J Plan Educ Res 23(1):69–82
Eliasson J, Börjesson M (2014) On timetable assumptions in railway investment appraisal. Transp Policy 36:118–126
Yuan L, Wang Y (2017) Evaluation optimization on urban rail transit project in-vestment and financing structure based on entropy theory. Urban Mass Transit 20(8):92–97
Wu Y, Yang H, Tang J, Yu Y (2016) Multi-objective re-synchronizing of bus timetable: model, complexity and solution. Transp Res Part C Emerg Technol 67:149–168
Schmekel V (2005) The strategic importance of retail investment in Asia and its implications for the Metro Group in Asia. J Glob Mark 18(1–2):133–150
Chakrabarti S, Giuliano G (2015) Does service reliability determine transit patronage? Insights from the Los Angeles Metro bus system. Transp Policy 42:12–20
Hamre A, Buehler R (2014) Commuter mode choice and free car parking, public transportation benefits, showers/lockers, and bike parking at work: evidence from the Washington, DC Region. J Public Transp 17:4
Chen Z, Xia JC, Irawan B, Caulfied C (2014) Development of location-based services for recommending departure stations to park and ride users. Transp Res Part C Emerg Technol 48:256–268
Du Y, Zhao C, Zhang H, Wong SC, Liao F (2017) Modeling park-and-ride services in a multi-commodity discrete/continuum transport system with elastic demand, No. 17-02785
Van Oort N, Sparing D, Brands T, Goverde RM (2015) Data driven improvements in public transport: the Dutch example. Public Transp 7(3):369–389
Pelletier MP, Trépanier M, Morency C (2011) Smart card data use in public transit: a literature review. Transp Res Part C Emerg Technol 19(4):557–568
El-Geneidy AM, Horning J, Krizek KJ (2011) Analyzing transit service reliability using detailed data from automatic vehicular locator systems. J Adv Transp 45(1):66–79
Strathman JG, Kimpel TJ, Dueker KJ, Gerhart RL, Callas S (2002) Evaluation of transit operations: data applications of Tri-Met’s automated bus dispatching system. Transportation 29(3):321–345
Eom JK, Choi MH, Lee J (2012) Evaluation of metro service quality using transit smart card data. In: Transportation Research Board 91st annual meeting, No. 12-1314
Lee DH, Sun L, Erath A (2012) Study of bus service reliability in Singapore using fare card data. In: 12th Asia-Pacific Intelligent Transportation Forum
Sun Y, Shi J, Schonfeld PM (2016) Identifying passenger flow characteristics and evaluating travel time reliability by visualizing AFC data: a case study of Shanghai Metro. Public Transp 8(3):341–363
Asakura Y, Iryo T, Nakajima Y, Kusakabe T (2012) Estimation of behavioural change of railway passengers using smart card data. Public Transp 4(1):1–16
Kusakabe T, Asakura Y (2014) Behavioural data mining of transit smart card data: a data fusion approach. Transp Res Part C Emerg Technol 46:179–191
Sun L, Lee DH, Erath A, Huang X (2012) Using smart card data to extract passenger’s spatio-temporal density and train’s trajectory of MRT system. In: Proceedings of the ACM SIGKDD international workshop on urban computing
Tao S, Corcoran J, Mateo-Babiano I, Rohde D (2014) Exploring bus rapid transit passenger travel behaviour using big data. Appl Geogr 53:90–104
Sun Y, Schonfeld PM (2015) Schedule-based rail transit path-choice estimation using automatic fare collection data. J Transp Eng 142(1):04015037
Sun Y, Xu R (2012) Rail transit travel time reliability and estimation of passenger route choice behavior: analysis using automatic fare collection data. Transp Res Rec J Transp Res Board 2275:58–67
Nassir N, Khani A, Lee S, Noh H, Hickman M (2011) Transit stop-level origin-destination estimation through use of transit schedule and automated data collection system. Transp Res Rec J Transp Res Board 2263:140–150
Ma X, Wu YJ, Wang Y, Chen F, Liu J (2013) Mining smart card data for transit riders’ travel patterns. Transp Res Part C Emerg Technol 36:1–12
Sun L, Axhausen KW, Lee DH, Huang X (2013) Understanding metropolitan patterns of daily encounters. Proc Natl Acad Sci 110(34):13774–13779
Nassir N, Hickman M, Ma ZL (2015) Activity detection and transfer identification for public transit fare card data. Transportation 42(4):683–705
Jiang Z, Fan W, Liu W, Zhu B, Gu J (2018) Reinforcement learning approach for coordinated passenger inflow control of urban rail transit in peak hours. Transp Res Part C Emerg Technol 88:1–16
Watkins KE, Ferris B, Borning A, Rutherford GS, Layton D (2011) Where is my bus? Impact of mobile real-time information on the perceived and actual wait time of transit riders. Transp Res Part A Policy Pract 45:839–848
Rahman MM, Wirasinghe SC, Kattan L (2016) The effect of time interval of bus location data on real-time bus arrival estimations. Transp A Transp Sci 12(8):700–720
Zhang Y, Jenelius E, Kottenhoff K (2016) Impact of real-time crowding information: a Stockholm metro pilot study. Public Transp 9:483–499
Brakewood C, Macfarlane GS, Watkins K (2015) The impact of real-time information on bus ridership in New York City. Transp Res Part C Emerg Technol 53:59–75
Corsar D, Edwards P, Nelson J, Baillie C, Papangelis K, Velaga N (2017) Linking open data and the crowd for real-time passenger information. Web Semant Sci Serv Agents World Wide Web 43:18–24
Nesheli MM, Ceder AA, Ghavamirad F, Thacker S (2017) Environmental impacts of public transport systems using real-time control method. Transp Res Part D Transp Environ 51:216–226
Nesheli MM, Ceder AA (2015) Improved reliability of public transportation using real-time transfer synchronization. Transp Res Part C Emerg Technol 60:525–539
Aultman-Hall L, Roorda M, Baetz BW (1997) Using GIS for evaluation of neighborhood pedestrian accessibility. J Urban Plan Dev 123(1):10–17
Mesbah M, Currie G, Lennon C, Northcott T (2012) Spatial and temporal visualization of transit operations performance data at a network level. J Transp Geogr 25:15–26
Shared-Used Mobility Center (SUMC) (2016) Shared mobility and the transformation of public transit. Research Analysis No. TCRP J-11/TASK 21
UC Berkeley (2018) Innovative mobility: carsharing outlook
Jin JG, Tang LC, Sun L, Lee DH (2014) Enhancing metro network resilience via localized integration with bus services. Transp Res Part E Logist Transp Rev 63:17–30
Fishman E, Washington S, Haworth N (2012) Barriers and facilitators to public bicycle scheme use: a qualitative approach. Transp Res Part F Traffic Psychol Behav 15(6):686–698
DeMaio P, Gifford J (2004) Will smart bikes succeed as public transportation in the United States? J Public Transp 7(2):1
Lin JR, Yang TH (2011) Strategic design of public bicycle sharing systems with service level constraints. Transp Res Part E Logist Transp Rev 47(2):284–294
Shu J, Chou MC, Liu Q, Teo CP, Wang IL (2013) Models for effective deployment and redistribution of bicycles within public bicycle-sharing systems. Oper Res 61(6):1346–1359
Khani A, Livshits V, Dutta A (2014) Modeling regional bicycle travel in Phoenix Metropolitan Area. In: Transportation Research Board 93rd annual meeting, No. 14-4881
Acknowledgements
This study was supported by the National Natural Science Foundation of China (U1434207) of People’s Republic of China, and the Beijing Municipal Natural Science Foundation (8162033). The authors would also like to thank Professor Zijia Wang from Beijing Jiaotong University, Rebekah, an international student from Beijing Jiaotong University, and Yan Sun from Shandong University of Finance and Economics for helping us edit and polish the language of this paper.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor: Jing Teng.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lu, K., Han, B. & Zhou, X. Smart Urban Transit Systems: From Integrated Framework to Interdisciplinary Perspective. Urban Rail Transit 4, 49–67 (2018). https://doi.org/10.1007/s40864-018-0080-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40864-018-0080-x