Abstract
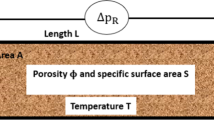
In this paper, we study the solute transport through a semi-infinite channel filled with a fluid saturated sparsely packed porous medium. A small perturbation of magnitude \(\varepsilon \) is applied on the channel’s walls on which the solute particles undergo a first-order chemical reaction. The effective model for solute concentration in the small-Péclet-number regime is derived using asymptotic analysis with respect to the small parameter \(\varepsilon \). The obtained mathematical model clearly indicates the effects of porous medium, chemical reaction and boundary distortion. In particular, the effect of porous medium parameter on the dispersion coefficient is discussed.

Similar content being viewed by others
References
Adler, P.M.: Porous Media: Geometry and Transports. Butterworth-Heinermann Series in Chemical Engineering, Boston (1992)
Allaire, G.: Homogenization of the Navier-Stokes equations in open sets perforated with tiny holes I. Abstract framework, a volume distribution of holes. Arch. Rational. Mech. Anal. 113, 209–259 (1991)
Darcy, H.: Les fontaines publiques de la ville de Dijon. Victor Darmon, Paris (1856)
Bolster, D., Dentz, M., Le Borgne, T.: Solute dispersion in channels with periodically varying apertures. Phys. Fluids 21, 056601 (2009)
Brinkman, H.: A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A1, 27–34 (1947)
Chandrasekhara, B.C., Rudraiah, N., Nagaraj, S.T.: Velocity and dispersion in porous media. Int. J. Eng. Sci. 18, 921–929 (2009)
Cussler, E.L.: Diffusion: Mass Transfer in Fluid Systems, 2nd edn. Cambridge University Press, New York (1997)
John Lee, S.-J., Sundararajan, N.: Microfabrication for Microfluidics. Artech House, Boston (2010)
Marušić-Paloka, E.: Effects of small boundary perturbation on flow of viscous fluid. ZAMM -J. Appl. Math. Mech. 96, 1103–1118 (2016)
Marušić-Paloka, E., Pažanin, I.: On the reactive solute transport through a curved pipe. Appl. Math. Lett. 24, 878–882 (2011)
Marušić-Paloka, E., Pažanin, I., Radulović, M.: Flow of a micropolar fluid through a channel with small boundary perturbation. Z. Naturforsch. A 71, 607–619 (2016)
Marušić-Paloka, E., Pažanin, I.: On the Darcy–Brinkman flow through a channel with slightly perturbed boundary. Transp. Porous Media 117, 27–44 (2017)
Marušić-Paloka, E., Pažanin, I., Marušić, S.: Comparison between Darcy and Brinkman laws in a fracture. Appl. Math. Comput. 218, 7538–7545 (2012)
Mikelic, A., Devigne, V., van Duijn, C.J.: Rigorous upscaling of the reactive flow through a pore, under dominant Péclet and Damkohler numbers. SIAM J. Math. Anal. 38, 1262–1287 (2006)
Ng, C.-O., Wang, C.Y.: Darcy-Brinkman flow through a corrugated channel. Transp. Porous Media 85, 605–618 (2010)
Nunge, R.J., Lin, T.-S., Gill, W.N.: Laminar dispersion in curved tubes and channels. J. Fluid Mech. 51, 363–383 (1972)
Pal, D.: Effect of chemical reaction on the dispersion of a solute in a porous medium. Appl. Math. Model. 23, 557–566 (1999)
Rosencrans, S.: Taylor dispersion in curved channels. SIAM J. Appl. Math. 57, 1216–1241 (1997)
Taylor, G.I.: Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. Roy. Soc. Lond. Sect. A 219, 186–203 (1953)
Rubinstein, J., Mauri, R.: Dispersion and convection in periodic porous media. SIAM J. Appl. Math. 46, 1018–1023 (1986)
Rudraiah, N., Ng, C.-O.: Dispersion in porous media with and without reaction: a review. J. Porous Media 10, 219–248 (2007)
Sanchez-Palencia, E.: On the asymptotics of the fluid flow past an array of fixed obstacles. Int. J. Eng. Sci. 20, 1291–1301 (1982)
Valdes-Parada, F.J., Aguiar-Madera, C.G., Alvarez-Ramirez, J.: On diffusion, dispersion and reaction in porous media. Chem. Eng. Sci. 66, 2177–2190 (2011)
Woolard, H.F., Billingham, J., Jensen, O.E., Lian, G.: A multiscale model for solute transport in a wavy-walled channel. J. Eng. Math. 64, 25–48 (2009)
Acknowledgements
The author has been supported by the Croatian Science Foundation (Project 3955: Mathematical modeling and numerical simulations of processes in thin or porous domains). The author would like to thank the referees for their helpful comments and suggestions that helped to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Ahmad Izani Md. Ismail.
Appendix: Darcy–Brinkman Velocity
Appendix: Darcy–Brinkman Velocity
It is well known that the stationary flow of an incompressible, viscous fluid through a porous media is described by the conservation of mass and conservation of linear momentum principles. Conservation of mass is expressed by the continuity equation
satisfied by the fluid velocity, while different models have been proposed over the past sixteen decades to describe the conservation of the linear momentum. Without any doubt, the Darcy law [3] is the most popular one stating that the filtration velocity is proportional to the driving pressure gradient. However, one of its major drawbacks is that it cannot sustain the (physically relevant) no-slip boundary condition imposed on an impermeable wall. Thus, if one wants to consider a sparse porous medium, the Darcy–Brinkman equation [5] would represent a suitable choice (see, e.g., [2, 13, 22]):
Here \(\mathbf {u}^{*}\) and \(p^{*}\) denote (dimensional) filter velocity and pressure, \(\mu \) is the physical viscosity of the fluid, K stands for the permeability of the porous medium, while \(\mu _e\) denotes the effective viscosity for the Brinkman term. It should be mentioned that, in Chandrasekhara et al. [6], it is assumed that \(\mu =\mu _e\). However, in general, those two viscosities are not equal (see, e.g., [13]). Being the second-order PDE for the velocity, Eq. (48) can handle the presence of a boundary on which the no-slip condition for the velocity can be imposed. Thus, the Darcy–Brinkman model represents an essential generalization of the Darcy law which is capable of successfully describing numerous situations naturally arising in industry and geophysical problems.
For the sake of reader’s convenience, let us derive the zero-order asymptotic solution of the system (47)–(48) entering in the starting convection–diffusion equation (1). It is natural to assume that the flow is governed by a constant pressure gradient \(\frac{\partial p^{*}}{\partial x^{*}}=-\,\delta \) in the \(x^{*}\)-direction. Consequently, we deduce that the flow is purely in the longitudinal direction, i.e., \(\mathbf {u}^{*}=u^{*}(x,y)\mathbf {e}_1\). Introducing
we get the dimensionless form of Eqs. (47)–(48) as
Here
is the non-dimensional parameter characterizing the porous medium which is proportional to the inverse square root of the Darcy number \({ Da}=\frac{K}{H^{2}}\). Note that \(k=0\) corresponds to classical Stokes flow. Now, we plug the expansion
in the Darcy–Brinkman Eq. (50) and also in the no-slip boundary condition
Using Taylor series approach (see, e.g., [15] for details), from (54), we deduce
After collecting the terms with equal powers of \(\varepsilon \), we obtain
Due to the divergence-free condition (50), the solution of (57) is independent of x and, thus, given by
Finally, applying (49) we can easily recover the dimensional velocity \(u_0^{*}\) which enters in the governing Eq. (1).
Rights and permissions
About this article
Cite this article
Pažanin, I. A Note on the Solute Dispersion in a Porous Medium. Bull. Malays. Math. Sci. Soc. 42, 729–741 (2019). https://doi.org/10.1007/s40840-017-0508-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-017-0508-6