Introduction

The consumption of metal resources in the world is growing rapidly [1]. In the next few decades, the demand for natural resources is expected to be several times higher than the current reserves [2, 3]. In such global situation, since natural resources are scarce in Japan, Japanese industries have constantly faced supply risks [4,5,6]. Moreover, since the mining and refining of raw natural resources require a large amount of energy in response to the expansion of those demands, the global environment faces the challenge of massive CO2 and other greenhouse gas emissions [7, 8]. On the other hand, Japan could have accumulated a large amount of metal resources [9,10,11]. Those resources, which are present in the form of substrates and household appliances, have the potential to have apparent reserves and higher grades than natural ores [12, 13]. With increasing resource accumulation, which is called an ‘urban mine (UM)’, the recycling of those resources has come to play a crucial role in the circular economy [3]. It will be advantageous for energy and the economy if spent valuable metals can be recovered efficiently from UM [10, 14]. In addition, the global environment, which is affected by the exploitation of natural resources, can be protected by recovering [15]. Therefore, recovering and recycling of metal elements is a key technology for the construction of a sustainable society. For example, there is a typical high-temperature process where scrap material is melted, oxidized, and reduced to separate metal phase, which contains valuable elements such as gold, silver, lead, and tin [16]. This metal phase is divided into each metallic element by electrorefining and/or multistage extraction [17].

The minable reserve of Sn is so small [18] that Sn is one of the valuable metals whose recovery from scrap materials is being attempted [19]. To recycle Sn from scrap materials, especially Waste from Electrical and Electronic Equipment (WEEE) used mainly as solder, they are fed to copper smelter and then the furnace specialized for recycling [20, 21]. When recovering Sn by the process, Sn is distributed to Cu-based metal phase and slag phase. In the latter, Sn is dissolved in the form of SnO. For the efficient recovery of Sn in this process, it is required to maximize the Sn distribution to the metal phase. In contrast, Fe, which is an impurity in the metal phase, should be removed by its distribution to the slag phase. When the slag reduction is simply enhanced, FeO is reduced simultaneously with SnO, and the Fe concentration in the metal phase increases [22] and eventually metallic iron is solidified and suspended. This leads to poor fluidity and workability. Therefore, the reduction of only SnO in the slag phase is preferred in practical operation. For this specific reduction, it is necessary to evaluate the optimum conditions concerning slag composition, temperature and oxygen partial pressure by using the activity coefficient of SnO in slag.

Distribution behavior and thermodynamic data of Sn in ordinary Sn and Pb smelting process are well studied [23,24,25,26,27,28,29,30]. In WEEE recycling, CaO–SiO2–FetO(–Al2O3) slag system is applied for operating [31]. Some of researchers have reported a Sn distribution between copper metal and slag and activity coefficient of SnO in the slag. Takeda et al. investigated using the slags saturated with calcium ferrite or iron silicate [32]. Anindya et al. also studied using this slag system under the flow of CO–CO2 mixture [33]. Nagamori et al. reported the Sn distribution between FeO–Fe2O3–SiO2–Al2O3–CuO0.5 slag and copper [34]. In all of those studies, slag liquids equilibrated with molten Cu-based metal, and the activity coefficient of SnO was calculated using the data of Sn activity coefficient in Cu metal [35, 36].

To discuss a Sn migration from slag to metal without Fe-oxide reduction, the elucidation of Sn distribution behavior between slag and metal under the saturation of solid Fe is required, because it is the most reducible condition suitable for the deposition of solid Fe. However, there is currently insufficient research investigating the effect of slag composition on Sn distribution under this experimental condition.

Against those backgrounds, this study measured the activity coefficients of SnO and FetO in CaO–SiO2–FetO(–Al2O3) molten slag saturated with solid Fe at 1573 K by equilibrium experiments. Moreover, the activity coefficient PbO was also measured by using Pb–Sn alloy as metal phase, since Pb is contained in WEEE along with Sn and the recovery of Pb is also required. From the results obtained as functions of slag basicity, FetO and alumina concentrations in CaO–SiO2–FetO slag, and oxygen potentials, the operation condition suitable for reducing SnO and PbO but not FeO was discussed.

Experimental

Slag Preparation

Table 1 shows the target compositions of slag and Pb–Sn alloy used in this equilibrium experiment.

Table 1 Target composition of this study's synthetic slags (mass%) and gas conditions
Full size table

In this table, to simplify the description of the slag compositions, the symbols C/S and RF, which are defined by Eqs. (1) and (2), respectively, are introduced, referring to a previous report [37].

$$C/S = \, \left( {{\text{mass}}\% {\text{ CaO}}} \right) \, / \, \left( {{\text{mass}}\% {\text{ SiO}}_{{2}} } \right)$$
(1)
$$RF = \, \left( {{\text{mass}}\% {\text{ Fe}}_{t} {\text{O}}} \right) \, / \, \left\{ {\left( {{\text{mass}}\% {\text{ Fe}}_{t} {\text{O}}} \right) \, + \, \left( {{\text{mass}}\% {\text{ CaO}}} \right) \, + \, \left( {{\text{mass}}\% {\text{ SiO}}_{{2}} } \right)} \right\}$$
(2)

herein C/S is called ‘slag basicity’, and RF is the FetO mass ratio in CaO–SiO2–FetO pseudo-ternary system, where (mass% FetO) is the FeO mass concentration calculated assuming that all Fe oxides in slag is present as FeO.

Using the No. 1 sample as the reference, the following three experimental conditions with varying C/S, RF, and Al2O3 concentrations were chosen to achieve slag compositions applicable to actual operations. As an actual WEEE recycling slag composition, C/S, RF, and mass%Al2O3 are 0.53, 0.28, and 31.6, respectively [31]. However, depending on adapted process, operability, feed stock, and so on, the contents of CaO, SiO2, FeO, and Al2O3 vary. Therefore, by changing those variables, their effects were evaluated in this study.

  1. (I)

    The values of C/S were changed to 0.45, 0.7, 0.9, and 1.1 with RF ≈ 0.5 (Nos. 1 to 4). Since RF is automatically determined in equilibrium with CO–CO2 gas, PCO/PCO2 ratio was adjusted so that the equilibrium composition became RF ≈ 0.5.

  2. (II)

    The values of RF were changed from 0.5 (No. 1) to 0.4 and 0.6 (Nos. 5 and 6) with C/S = 0.45.

  3. (III)

    The Al2O3 content was increased from 0 mass% (No. 1) to 5, 10, and 15 mass% with C/S = 0.45 and RF ≈ 0.5 (Nos. 7 to 9).

From the phase diagram of the CaO–SiO2–FetO system [37] and that of the CaO–SiO2–Al2O3 pseudo-ternary system at RF = 0.5, which were drawn by the thermodynamic equilibrium calculation software ‘FactSage 8.1’ [38], all experimental points listed in Table 1 are in the range of liquid phase.

Reagents CaCO3 (99.5% up, FUJIFILM Wako pure chemical), SiO2 (99.9% up, FUJIFILM Wako pure chemical), FeO (99.5% up, HAYASHI pure chemical), and Al2O3 (99% up, KANTO chemical) were applied for slag preparation. In this study, a CaO–SiO2–FetO master slag was first prepared as follows: CaCO3 and SiO2 reagents were mixed and pressed to a cylindrical shape by applying a pressure of 2 tons cm−2. Then, the mixture was calcined by holding it in a Pt crucible at 1273 K under an air atmosphere for more than 10 h to remove CO2 and pre-sinter the mixture of CaO and SiO2. This pellet was crushed, mixed with FeO, and melted in a Fe crucible at 1573 K under an Ar (G1 grade, TAIYO NIPPON SANSO JFP) atmosphere. By using a Fe crucible during the pre-melting of slag, it is possible to suppress the Fe2O3 generation as much as possible due to the Fe/FeO equilibrium. After melting, the crucible was taken out of the furnace, and poured the molten slag onto a stainless steel plate for quenching with He gas blowing. The obtained master slag was crushed to less than 0.1 mm and mixed with SiO2, FeO, and Al2O3 reagents to achieve the respective composition. Finally, the mixture was pressed to a cylindrical shape by applying a pressure of 2 tons cm−2.

Procedure

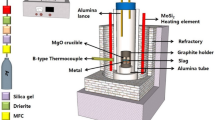
The CaO–SiO2–FetO slag containing the respective Al2O3 concentration (12 g) was equilibrated with Pb–Sn alloy (18 g), which was prepared by granular Pb (99.5% up, KANTO chemical) and Sn (99.5% up, FUJIFILM Wako pure chemical), in a pure Fe crucible (ϕ32 × ϕ27 × 50 mm) at 1573 K for 5 h while blowing CO–CO2 mixed gas (300 mL min−1) on the surface of molten slag. The reason for using Pb–Sn alloy is its low solubility in Fe crucible. Copper alloy and pure Sn cannot be used because they would melt Fe crucible. Furthermore, by using the Pb–Sn alloy, the activity coefficients of SnO and PbO in the slag can be simultaneously measured. This experimental temperature (1573 K) is close to the actual operating conditions and the same as previous research [39]. Kato et al. reported that the equilibrium of Fe crucible/slag melt/Pb melt/CO–CO2 gas was achieved in 5 h and the change of slag composition was not observed [40]. Based on this report, the holding time at high temperature was determined to be 5 h in this study.

In equilibrium experiments, Fe crucible containing metal and slag was inserted to the soaking zone of a vertical furnace with silicon carbide heating element under an Ar flow (500 mL min−1) using Mo rod. After then, the Ar flow was stopped, and the mixture of CO and CO2 gases was blown on the surface of molten slag to control the partial oxygen pressure, PO2. The flow rates of CO (G1 grade, TAIYO NIPPON SANSO JFP) and CO2 (G1 grade, TAIYO NIPPON SANSO JFP) gases were fixed by separate mass flow controllers, which were calibrated with a soap film flow meter. The CO/CO2 equilibrium and its standard Gibbs free energy, ∆G°, are written by Eqs. (3) and (4), respectively [41].

$${\text{CO}}\left( {\text{g}} \right) \, + { 1}/{\text{2 O}}_{{2}} \left( {\text{g}} \right) \, = {\text{ CO}}_{{2}} \left( {\text{g}} \right)$$
(3)
$$\Delta G^\circ_{{({3})}} = \, - {28258}0 \, + { 86}.0{15} \; T \, \left[ {{\text{Joule}}} \right] \, \left( {{298} - {3}000 \, {\text{ K}}} \right)$$
(4)

where T is absolute temperature [K]. From Eq. (4), PCO/PCO2 ratio is represented by Eq. (5), where PCO and PCO2 are CO and CO2 partial pressure [atm], respectively.

$${\text{log }}\left( {P_{{{\text{CO}}}} /P_{{{\text{CO2}}}} } \right) \, = \, - {14761}/T + { 4}.{493 } - { 1}/{\text{2 log}} \, P_{{{\text{O2}}}}$$
(5)

The following method was applied to maintain the desired FeO concentration in slag. When the FeO in slag equilibrates with solid Fe according to Eq. (6), the FeO activity, aFeO, is derived from Eqs. (7) and (8) [41].

$${\text{Fe}}\left( {\text{s}} \right) \, + { 1}/{\text{2 O}}_{{2}} \left( {\text{g}} \right) \, = {\text{ FeO}}\left( {\text{s}} \right)$$
(6)
$$\Delta G^\circ_{{({6})}} = \, - {26433}0 \, + { 64}.{73} \, T \, \left[ {{\text{Joule}}} \right] \, \left( {{298} - {165}0 \, {\text{ K}}} \right)$$
(7)
$$= \, - RT{\text{ln }}\left\{ {\left( {a_{{{\text{FeO}}({\text{s}})}} } \right)/\left( {a_{{{\text{Fe}}({\text{s}})}} \cdot\;P_{{{\text{O2}}}}^{{{1}/{2}}} } \right)} \right\}$$
(8)

where R is the gas constant [J K−1 mol−1]. Since the Fe crucible was used in this experiment, the Fe activity is unity. The FeO activity, aFeO(s), can be expressed by Eq. (9) using the activity coefficient, γFeO(s), and mole fraction, XFeO, of FeO.

$$a_{{{\text{FeO}}\left( {\text{s}} \right)}} = \gamma_{{{\text{FeO}}({\text{s}})}} \cdot\;X_{{{\text{FeO}}}}$$
(9)

From Eqs. (7) to (9), the relationship between XFeO and PO2 is given by Eq. (10).

$${\text{log}} \, P_{{{\text{O2}}}} = \, - {27615}/T + { 6}.{762 } + {\text{ 2 log}} \, \gamma_{{{\text{FeO}}({\text{s}})}} + {\text{ 2 log}} \, X_{{{\text{FeO}}}}$$
(10)

The values of γFeO(s) are evaluated from γFeO(l) reported by Kudo et al. [37], whose standard state was liquid, after converting from liquid to solid using ∆G°(11) [42].

$${\text{FeO}}\left( {\text{l}} \right) \, = {\text{ FeO}}\left( {\text{s}} \right)$$
(11)
$$\Delta G^\circ_{{({11})}} = \, - {2211}0 + {13}.{{5T}}$$
(12)

The PCO/PCO2 ratio to achieve the desired FetO concentration can be estimated by Eqs. (5) and (10). The calculated PO2 and PCO/PCO2 ratio for each slag sample are also given in Table 1. It is expected that more accurate γFeO will be obtained in this study.

After 5 h, the Fe crucible was quickly removed from the furnace using Mo rod and immersed in water to cool the sample from the outside of the Fe crucible. Simultaneously, the surface of the slag, which covered metal phase, was cooled by He gas blowing. After confirming a solidification of the slag surface, the Fe crucible was completely immersed in water and rapidly cooled.

After cooling, the Fe crucible was cut vertically along with slag and metal. A cross-sectioned surface of cut piece was mirror-polished and observed by Scanning Electron Microscope and Electron Probe Micro Analyzer (JEOL, JXA-8200) to confirm the absence of the micro metal particles dispersed in slag phase and the micro slag particles in metal phase. From the cross-sectioned sample of another cut piece, approximately 1 g of slag and metal samples were taken for chemical analysis. After dissolving 0.1 g of them with hot 0.2 v/v% HF-mineral acids, the compositions of slag and metal phases were determined using Inductively Coupled Plasma‒Atomic Emission Spectroscopy (SPECTRO, ARCOS EOP system). Three to four standard solutions with various concentrations of Sn, Pb, Si, Ca, Fe, and Al were prepared by diluting 1000 mg/L elemental standard solutions [Sn in 3 mol/L HCl, Pb(NO3)2 in 0.1 mol/L HNO3, Na2SiO3 in 0.2 mol/L Na2CO3, CaCO3 in 0.1 mol/L HNO3, Fe in 0.2 mol/L HNO3, and Al in 0.2 mol/L HNO3, FUJIFILM Wako pure chemical].

Results and Discussion

Observation of Samples

The photos of the sample after quenching are shown in Fig. 1. It is found from Fig. 1a that the surface of Pb–Sn alloy in the Fe crucible is covered with the slag layer. In Fig. 1b, the slag phase is observed at the upper part and the metal phase at the lower part. Although Pb and Sn in molten metal are thermodynamically less oxidizable, and the equilibrium vapor pressures of Pb, Sn and their compounds are higher than iron, it is believed that only a small amount of Pb and Sn evaporated, but enough remained due to slag covering.

Fig. 1
figure 1

Photos of the sample after equilibrium experiments: a slag surface, b cross-section

Full size image

Because of the possibility of spinel (FeAl2O4) formation in sample No. 9, whose Al2O3 concentration is highest in the samples given in Table 1, SEM and EPMA observations were made at the area of slag/metal boundary and that away from the boundary. Figure 2a shows an SEM image of the slag phase away from the slag/metal boundary. It is confirmed that there is no spinel formation and undissolved reagents, and the slag phase is homogeneous. No significant particle suspension was also observed in the metal phase. An SEM image near the slag/metal boundary is shown in Fig. 2b. Suspension of fine Fe particles is observed in the metal phase. Fe particles, which are considered to generate by the reaction (13) between Pb metal and FeO in slag, are suspended in the Pb phase near the interface.

$${\text{Pb}}\left( {\text{l}} \right) \, + \, \left( {{\text{FeO}}} \right) \, = \, \left( {{\text{PbO}}} \right) \, + {\text{ Fe}}\left( {\text{s}} \right)$$
(13)
Fig. 2
figure 2

SEM images of the cross-section of the slag phase away from the slag/metal interface (a) and that of the interface (b) in sample No. 9

Full size image

It is suggested that the equilibrium compositions of slag and metal could be obtained by sampling at the areas away from the slag/metal interface.

Activity Coefficients of SnO, PbO, and FetO

The analyzed chemical compositions after equilibrium experiments are listed in Table 2. The same sample solution was measured three times by ICP-AES, and additional sample solutions for Nos. 1, 5, and 9 in Table 2 were prepared and measured. As a result, the analytical errors (relative values) were ± 3% for Sn and Pb and ± 2% for the other elements. The values of C/S and RF after the equilibrium experiment are only slightly different from those in Table 1. Therefore, it can be said that the PCO/PCO2 ratios evaluated from Eqs. (5) and (10) were appropriate, and the equilibrium experiments were performed under the predicted conditions, although Pb, Sn, and their compounds are volatile and susceptible to PO2.

Table 2 Analyzed chemical compositions of samples after equilibration
Full size table

Although the tin oxide in slag is mainly composed of tin monoxide, with a small amount of tin dioxide, it is assumed in this study that all tin oxide is present as SnO [43]. The Sn(l)/SnO(l) equilibrium is written by Eq. (14) [41].

$${\text{Sn}}\left( {\text{l}} \right) \, + { 1}/{\text{2 O}}_{{2}} \left( {\text{g}} \right) \, = {\text{ SnO}}\left( {\text{l}} \right)$$
(14)
$$\Delta G^\circ_{{({14})}} = \, - {258195 } + { 77}.0{8} \, T \, \left[ {{\text{Joule}}} \right] \, \left( {{125}0 - {15}00{\text{ K}}} \right)$$
(15)

The effective temperature range of ∆G°(14) is 1250–1500 K, but it is assumed in this study that ∆G°(14) can also be valid at 1573 K. The activity of SnO in slag, aSnO(l), and that of Sn in metal, aSn(l), are expressed by Eqs. (16) and (17), respectively, using activity coefficient, γi, and mole fraction, Xi, of i.

$$a_{{{\text{SnO}}\left( {\text{l}} \right)}} = \gamma_{{{\text{SnO}}({\text{l}})}} \cdot\;X_{{{\text{SnO}}}}$$
(16)
$$a_{{{\text{Sn}}\left( {\text{l}} \right)}} = \gamma_{{{\text{Sn}}({\text{l}})}} \cdot\;X_{{{\text{Sn}}}}$$
(17)

The values of XSnO and XSn are calculated from the compositions of slag and metal given in Table 2. Therefore, γSnO(l) can be obtained by Eq. (18).

$${\text{log}} \, \gamma_{{{\text{SnO}}({\text{l}})}} = { 13487}/T - { 4}.0{26 } + { 1}/{\text{2 log}} \, P_{{{\text{O2}}}} - {\text{ log}} \, X_{{{\text{SnO}}}} + {\text{ log}} \, a_{{{\text{Sn}}({\text{l}})}}$$
(18)

The value of aSn(l) in Pb–Sn melt has been reported at 1173 K by Goto and Pierre [44], as shown by data points and a broken line in Fig. 3. By applying a regular solution approximation to their γSn(l) value, that at T is derived by Eq. (19).

$${\text{log}} \, \gamma_{{{\text{Sn}}\left( {\text{l}} \right){\text{ at}} \, T[{\text{K}}]}} = { 1173}/T \, \cdot{\text{log}}\gamma_{{{\text{Sn}}\left( {\text{l}} \right){\text{ at 1173 K}}}}$$
(19)
Fig. 3
figure 3

Activity of Sn in Pb–Sn liquid at 1573 K plotted against XSn

Full size image

The Sn activity in Pb–Sn melt at 1573 K is shown by a solid line in Fig. 3.

Since Pb–Sn liquid was equilibrated with the molten slag containing SnO, PbO, and FetO in a pure Fe crucible, the activity coefficients of PbO and FetO can also be obtained.

The Pb(l)/PbO(l) equilibrium is written by Eq. (20) [41].

$${\text{Pb}}\left( {\text{l}} \right) \, + { 1}/{\text{2 O}}_{{2}} \left( {\text{g}} \right) \, = {\text{ PbO}}\left( {\text{l}} \right)$$
(20)
$$\Delta G^\circ_{{({2}0)}} = \, - {18444}0 \, + { 69}.{79} \, T \, \left[ {{\text{Joule}}} \right] \, \left( {{1159} - {\text{1897 K}}} \right)$$
(21)

From ∆G°(20), γPbO(l) can be obtained by Eq. (22).

$${\text{log}} \, \gamma_{{{\text{PbO}}({\text{l}})}} =\, { 9635}/T - { 3}.{646 } + { 1}/{\text{2 log}} \, P_{{{\text{O2}}}} - {\text{ log}} \, X_{{{\text{PbO}}}} + {\text{ log}} \, \gamma_{{{\text{Pb}}({\text{l}})}} + {\text{ log}} \, X_{{{\text{Pb}}}}$$
(22)

The Pb–Sn metal phase in this study contains a small amount of Sn, as shown in Table 2. Therefore, it is possible to assume γPb(l) = 1 by applying Raoul’s Law. From ∆G°(6), γFetO(s) can be calculated by Eq. (23).

$${\text{log}} \, \gamma_{{{\text{Fe}}t{\text{O}}({\text{s}})}} = { 138}0{8}/T - { 3}.{381 } + { 1}/{\text{2 log}} \, P_{{{\text{O2}}}} - {\text{ log}} \, X_{{{\text{Fe}}t{\text{O}}}}$$
(23)

Figure 4 shows the activity coefficients of SnO, PbO, and FetO of CaO–SiO2–FetO slags with RF = 0.51 to 0.52 at 1573 K plotted against the C/S value. The activity coefficients of PbO and FetO increased with the C/S value. On the other hand, SnO increased up to C/S = 0.7 but remained constant above it. Kudo et al. [37] reported that the PbO activity coefficient at 1573 K increased with C/S in the same slag system saturated with Fe. The trend shown in Fig. 4 is consistent with it. It can be said that the higher basicity, the easier SnO, PbO, and FetO contained in the slag are reduced. Higher γSnO(l) and γPbO(l) are necessary to distribute Sn and Pb in the metal phase, while lower γFetO(s) to prevent FeO reduction. Therefore, a C/S value around 0.7 might be appropriate from Fig. 4.

Fig. 4
figure 4

The relationships between γSnO(l), γPbO(l), γFetO(s), and C/S at 1573 K

Full size image

It can be seen from Fig. 4 that the present γPbO(l) and γFetO(s) values are different from those estimated using the data reported by Kudo et al. [37] The major difference in experimental methods is that they used ZrO2–MgO solid electrolyte to measure the oxygen potential of the system, whereas CO–CO2 mixed gas was used to determine the oxygen potential in this study. There may be other causes, but the reason for those differences of γPbO(l) and γFetO(s) is not clear from this study, so it will be a subject of future investigation.

To obtain the FetO concentration that favors SnO reduction, some experiments have been performed with varying the RF value, as described in (II) of Sect. “Slag Preparation”. The activity coefficients of SnO, PbO, and FeO in the slag with C/S = 0.41 to 0.47 at 1573 K are plotted against RF value in Fig. 5. It is found that those activity coefficients increase with RF value. According to Eq. (10), a decrease in FetO concentration corresponds to that in PO2. Therefore, this trend suggests that SnO and PbO become difficult to be reduced as PO2 decreases in the reduction process, although such phenomena in actual operation had not been reported. Conversely, the activity coefficients of PbO and SnO become higher with FetO concentration, so it can be said that the higher FetO concentration is, the easier SnO and PbO reduction becomes. For comparison, the activity coefficients of PbO and FeO at 1573 K obtained by Kudo et al. [37], whose slag was also a CaO–SiO2–FetO system with C/S = 0.42 to 0.45, are plotted against RF value by closed circles in the same figure. Their trend, similar to this study, is observed in the relations between γPbO(l) and RF, but their γFetO(s) becomes almost constant at high RF. The reason for the different trends in γPbO(l) and γFeO(s) is thought to be that the slag in this study contained SnO, but currently under investigation.

Fig. 5
figure 5

The relationships between γSnO(l), γPbO(l), γFetO(s), and RF at 1573 K

Full size image

Finally, to investigate the effect of alumina addition on the activity coefficients of SnO, PbO, and FeO in slags was investigated using CaO–SiO2–FetO slag containing 5 to 15 mass% Al2O3. The activity coefficients of SnO, PbO, and FetO in the slags with C/S = 0.45 to 0.50 and RF = 0.49–0.51 at 1573 K are plotted against the mole fraction of alumina, XAl2O3, in Fig. 6. They tend to decrease with increasing XAl2O3. Therefore, it is suggested that a lower alumina concentration is advantageous for SnO and PbO reduction.

Fig. 6
figure 6

The relationships between γSnO(l), γPbO(l), γFetO(s), and XAl2O3 at 1573 K

Full size image

Although the slag composition range in this study is narrow, an empirical equation was derived by multiple regression analysis for the effects of C/S, RF, and XAl2O3 on each activity coefficient. They are represented by Eqs. (24) to (26), where r is the correlation coefficient.

$${\text{log}} \, \gamma_{{{\text{SnO}}({\text{l}})}} = \, 0.{31}C/S + \, 0.{62}RF{-}{ 1}.{29}X_{{{\text{Al2O3}}}} + \, 0.00{4 } \, \left( {r = \, 0.{912}} \right)$$
(24)
$${\text{log}} \, \gamma_{{{\text{PbO}}({\text{l}})}} = { 1}.0{7}C/S + { 3}.{69}RF{-}{ 6}.{86}X_{{{\text{Al2O3}}}} {-}{ 2}.0{62 } \, \left( {r = \, 0.{97}0} \right)$$
(25)
$${\text{log}} \, \gamma_{{{\text{Fe}}t{\text{O}}({\text{s}})}} = \, 0.{37}C/S + \, 0.{62}RF{-} \, 0.{35}X_{{{\text{Al2O3}}}} {-} \, 0.{444 } \, (r = \, 0.{973)}$$
(26)

The relations between the activity coefficients obtained by Eqs. (18), (22), and (23) and those calculated by Eqs. (24) to (26) are shown in Figs. 7, 8 and 9, respectively. Both are considered to be in good agreement from each figure and correlation coefficient. It is clear from these equations that C/S and RF affect positively and Al2O3 concentration negatively on the activity coefficients of SnO, PbO, and FetO. From the coefficients of each function, the factor that most affects the activity coefficient is Al2O3 concentration for γSnO(l), γPbO(l), and RF for γFetO(s). These trends can be explained by the following characteristics and interactions: In the experimental composition range of slag, it is considered that Sn, Pb and Fe behave as basic elements and Al behaves as an acidic element. Focusing on the variables in the regression equation, C/S and RF are related to slag basicity, and XAl2O3 to slag acidity. Therefore, the basic elements such as Sn, Pb and Fe are repelled under a more basic slag and attracted under a more acidic slag. Comparing three variables, Pb seems to be the most basic element from the coefficients of the regression equation.

Fig. 7
figure 7

The relation between the activity coefficient of SnO(l) obtained by Eq. (18) and calculated by Eq. (25)

Full size image
Fig. 8
figure 8

The relation between the activity coefficient of PbO(l) obtained by Eq. (22) and calculated by Eq. (25)

Full size image
Fig. 9
figure 9

The relation between the activity coefficient of FetO(s) obtained by Eq. (23) and calculated by Eq. (26)

Full size image

Preferential Reduction of SnO and PbO

For the efficient recovery of valuable metals such as Sn and Pb in Cu recycling, it is important to suppress the FeO reduction as much as possible to prevent the Fe transfer to the metal phase.

The equilibrium reaction of Sn/SnO/Fe/FetO is indicated by Eq. (27), whose ∆G°(27) is calculated by ∆G°(6) and ∆G°(14).

$${\text{Sn}}\left( {\text{l}} \right) \, + {\text{ Fe}}_{t} {\text{O}}\left( {\text{s}} \right) \, = {\text{ SnO}}\left( {\text{l}} \right) \, + {\text{ Fe}}\left( {\text{s}} \right)$$
(27)
$$\Delta G^\circ_{{({27})}} = \Delta G^\circ_{{({14})}} - \Delta G^\circ_{{({6})}} = { 6135 } + { 12}.{35} \, T \, \left[ {{\text{Joule}}} \right]$$
(28)
$$= \, - RT{\text{ln }}\left\{ {\left( {\gamma_{{{\text{SnO}}({\text{l}})}} \cdot\;X_{{{\text{SnO}}}} \cdot\;a_{{{\text{Fe}}({\text{s}})}} } \right)/\left( {a_{{{\text{Sn}}({\text{l}})}} \cdot\;\gamma_{{{\text{Fe}}t{\text{O}}({\text{s}})}} \cdot\;X_{{{\text{Fe}}t{\text{O}}}} } \right)} \right\}$$
(29)

The relation between the distribution ratio of Sn between metal and slag, aSn(l)/XSnO, and that of Fe, aFe(s)/XFetO, at 1573 K is represented by Eq. (30) using Eqs. (24), (26) and (29), and shown in Fig. 10 as functions of C/S and XAl2O3, whose variation range is 0.4–1.2 and 0–0.1, respectively, from Figs. 4 and 6.

$${\text{log }}\left( {a_{{{\text{Sn}}({\text{l}})}} /X_{{{\text{SnO}}}} } \right) = {\text{ log }}\left( {a_{{{\text{Fe}}({\text{s}})}} /X_{{{\text{Fe}}t{\text{O}}}} } \right) + { 1}.{296 } - \, 0.0{6}C/S - \, 0.{94}X_{{{\text{Al2O3}}}}$$
(30)
Fig. 10
figure 10

Relationships between the distribution ratio of Sn between metal and slag and that of Fe at 1573 K as functions of C/S and XAl2O3

Full size image

Comparing aSn(l)/XSnO values at the same aFe(s)/XFetO value, aSn(l)/XSnO decreases with increasing C/S and XAl2O3. However, since aSn(l)/XSnO value is much larger than aFe(s)/XFetO value, it can be said that Sn moves more easily from slag to metal than Fe.

From ∆G°(31) of Eq. (31), which is the equilibrium reaction of Pb/PbO/Fe/FetO, the relation between the distribution ratio of Pb between metal and slag, aPb(l)/XPbO, and that of Fe, aFe(s)/XFetO, at 1573 K is represented by (34) using Eqs. (25), (26) and (33), and shown in Fig. 11 as functions of C/S, RF, and XAl2O3.

$${\text{Pb}}\left( {\text{l}} \right) \, + {\text{ Fe}}_{t} {\text{O}}\left( {\text{s}} \right) \, = {\text{ PbO}}\left( {\text{l}} \right) \, + {\text{ Fe}}\left( {\text{s}} \right)$$
(31)
$$\Delta G^\circ_{{({31})}} = \Delta G^\circ_{{({18})}} - \Delta G^\circ_{{({6})}} = { 7989}0 \, + { 5}.0{6} \, T \, \left[ {{\text{Joule}}} \right]$$
(32)
$$= \, - RT{\text{ln }}\left\{ {\left( {\gamma_{{{\text{PbO}}({\text{l}})}} \cdot\;X_{{{\text{PbO}}}} \cdot\;a_{{{\text{Fe}}({\text{s}})}} } \right)/\left( {a_{{{\text{Pb}}({\text{l}})}} \cdot\;\gamma_{{{\text{Fe}}t{\text{O}}({\text{s}})}} \cdot\;X_{{{\text{Fe}}t{\text{O}}}} } \right)} \right\}$$
(33)
$${\text{log }}\left( {a_{{{\text{Pb}}({\text{l}})}} /X_{{{\text{PbO}}}} } \right) = {\text{ log }}\left( {a_{{{\text{Fe}}({\text{s}})}} /X_{{{\text{Fe}}t{\text{O}}}} } \right) + { 1}.{299 } + \, 0.{7}0C/S + { 3}.0{8}RF - { 6}.{51}X_{{{\text{Al2O3}}}}$$
(34)
Fig. 11
figure 11

Relationships between the distribution ratio of Pb between metal and slag and that of Fe at 1573 K as functions of C/S, RF, and XAl2O3

Full size image

When comparing aPb(l)/XPbO values at the same aFe(s)/XFetO value, aPb(l)/XPbO increases with C/S and RF, while that decreased with increasing XAl2O3. However, since aPb(l)/XPbO value is extremely larger than both aSn(l)/XSnO and aFe(s)/XFetO values, it is expected that PbO is reduced more easily than SnO and FetO.

In this study, the slag composition suitable for reducing SnO and PbO was thermodynamically discussed using activity coefficients. However, in practical operation, in addition to the equilibrium reduction degree of target oxides, their mass transfer rates in the slag, which are affected by slag viscosity, also influence the reduction rate. The relationship between SnO reduction rate and slag viscosity will be reported in a separate paper.

Conclusions

Activity coefficients of SnO, PbO, and FetO in CaO–SiO2–FetO–Al2O3 slag were determined at 1573 K with varying slag basicities and the concentrations of FetO and Al2O3. The results obtained can be summarized as follows.

  1. (1)

    The activity coefficients of PbO and FetO increased with the C/S value. On the other hand, SnO increased to C/S = 0.7 but remained constant above it.

  2. (2)

    The activity coefficients of SnO, PbO, and FetO increased with increasing FetO concentration and decreasing Al2O3 concentration.

  3. (3)

    The activity coefficients were represented by the following empirical equations.

    $${\text{log}} \, \gamma_{{{\text{SnO}}({\text{l}})}} = \, 0.{31}C/S + \, 0.{62}RF{-}{ 1}.{29}X_{{{\text{Al2O3}}}} + \, 0.00{4}$$
    $${\text{log}} \, \gamma_{{{\text{PbO}}({\text{l}})}} = { 1}.0{7}C/S + { 3}.{69}RF{-}{ 6}.{86}X_{{{\text{Al2O3}}}} {-}{ 2}.0{62}$$
    $${\text{log}} \, \gamma_{{{\text{Fe}}t{\text{O}}({\text{s}})}} = \, 0.{37}C/S + \, 0.{62}RF{-} \, 0.{35}X_{{{\text{Al2O3}}}} {-} \, 0.{444}$$
  4. (4)

    The order of reducibility was PbO > SnO >> FetO when comparing aSn(l)/XSnO, aPb(l)/XPbO and aFe(s)/XFetO.

  5. (5)

    The slag condition favorable to SnO and PbO reduction is higher basicity, around 50 mass% FetO, and lower Al2O3 content.

It is expected that this slag composition can help optimizing the WEEE recycling process in the Sn and Pb recovery from the slag.