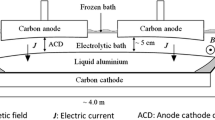
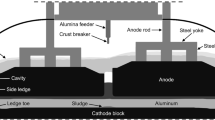
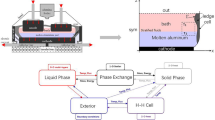
Abstract
The research project SynErgie aims to adapt large scale industrial processes to a volatile supply of renewable energy which is expected for the future. The aluminum electrolysis process is one of the biggest consumers of electric energy in Germany. The aim is to vary its nominal process power by ± 25%. This numerical study focuses on the magnetohydrodynamic (MHD) behavior of the electrolysis cells of Trimet Aluminum SE in Essen. To capture the MHD driven flow and electrodynamics inside the electrolysis cells a computational fluid dynamics (CFD) model is developed in the OpenFOAM® framework. This accounts for the influence of neighboring electrolysis cells, the magnetization of ferromagnetic materials, a static ledge profile and the dynamic changes of anode shape caused by the carbon consumption. The simulation predictions show the heave of the aluminum cryolite interface for different line currents. To analyze the behavior of flexible process operation, shifts of the line currents are studied in detail. After shifting the line current, the interface heave changes directly whereas the shape of the anode bottom reacts with a delay in time. This leads to a locally uneven anode cathode distance (ACD) followed by a disturbed current distribution inside the electrolysis cell after shifting the line current. The anodic current distribution is quantified by the model, which can help process operators to identify whether increased anode currents are caused by the line current shift or potential abnormalities like spikes.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
As the number of renewable electricity sources is increasing, the volatility of electric energy in the grid rises. This trend also affects large scale industrial processes, as the availability and the price of electric energy become more relevant. Trimet Aluminum SE aims to design the aluminum electrolysis pot lines flexible in terms of current input. To adapt the technology of the electrolysis cells, magnetic compensation of the cells has been installed by means of a modification to the pot busbars, which allows higher line currents and reduces problems related to cell control. Moreover, to maintain the thermal balance of the electrolysis cells, shell heat exchangers have been installed [1].
Despite of these actions, shifts of the line current still impact the process operation. These impacts and its consequences are the subject of the current study. It focuses on the operating condition after shifting the line current by ± 25%. The results help process operators to understand the dynamics of the electrolysis cells and to adapt their actions regarding process operation accordingly.
Modeling the MHD phenomena in Hall-Héroult cells has been studied for many years. CFD has been shown to be a powerful tool to deal with these challenges. The following articles contribute to this field. They focus on different aspects, which are summarized below. One of the early contributors to the study of aluminum-cryolite interface waves was Potocnik [2]. He developed and applied a custom CFD model based on a commercial software tool. This allowed to calculate the flow field and the aluminum-cryolite interface. Other commercial software packages have been used and have been accompanied by in-house software developed by Severo et al [3]. Their tools can also take into account the shape of the anode bottom to calculate the flow field and the metal pad heave. Another model has been implemented by Wang et al [4]. In addition to MHD, their model also considers the motion caused by gas bubbles. It is used to develop a new cathode design. This leads to a lower bath velocity and a higher frequency of gas release. Another MHD model is proposed by Hua et al [5] which considers the influence of different ledge profiles. The MHD stability is focused by Bojarevics and Dupuis [6]. A specially developed model updates the magnetic field at all time steps. Metal pad instabilities are also analyzed by Mohammad et al [7, 8]. Their study is on the topic of waves at the aluminum-cryolite interface. The addition of oscillatory components to the line current can prevent instabilities and increase cell efficiency. The only known contribution to focus directly on load shifts in aluminum electrolysis cells is by Dupuis and Bojarevics [9]. They analyze cell stability by calculating interface oscillations after load shifts.
Many different aspects of MHD in aluminum electrolysis have been studied by various authors. However, details of the current distribution, the metal pad heave and the transient evolution of the velocity field after a line current shift in aluminum electrolysis cells have not been published so far. This is the motivation for the current study to be carried out. The transient dynamics and the electrical behavior of aluminum electrolysis cells are presented in the application case of electrolysis cells at Trimet in Essen, Germany.
Physical Background
In this section, the relevant equations to describe electrodynamics, magnetic fields and the resulting fluid mechanics are described. These are the basis of the implemented solvers, which were employed to execute the current study.
The electric potential of a system without free charges can be described by:
where \(\sigma\) is the electric conductivity, \(\Phi\) is the electric potential, \({\textbf {u}}\) is the velocity and \({\textbf {B}}\) is the magnetic flux density.
This equation implies that the current density must be divergence free. The current density can be expressed by:
where \({\textbf {J}}\) is the current density.
Both the electric potential \(\Phi\) and the current density \({\textbf {J}}\) can be divided into a velocity dependent and a velocity independent part. Ampere’s Circuit Law, which denotes the relationship between current density and the magnetic flux density induced by it, can be expressed as:
where \(\mu _0\) is the magnetic permeability of free space.
In this study, \({\textbf {B}}\) is determined from the current density with the help of Biot-Savart Law, given by Eq. 4. Note that subscripts r and \(r'\) indicate that a given parameter is evaluated at that particular spatial location (e.g., \({\textbf {B}}_{\textbf {r}}\)).
where V is the volume, \(r'\) is the location of current source and r is the location of the evaluation point.
B is related to magnetic vector potential by:
where A is the magnetic vector potential.
Combining Eqs. 4 and 5, the magnetic vector potential can be written as:
Equation 6 is discretized and then solved as a volume integral at the boundaries for the magnetic vector potential \({\textbf {A}}\) with the help of the Burnes-Hut method [10], which is grouping grid cells into different nodes in an octree structure. The advantage of this procedure is that only the contribution of nearby grid cells has to be calculated directly. Grid cells with a far distance are approximated as large groups. This clearly reduces the numerical efforts. Solving Biot-Savart Law directly would result in a number of computations of \(O(N^2)\), with N as the number of grid cells. With the help of the Barnes-Hut method this can be reduced to a number of computations of \(O(N_B log(N))\), with \(N_B\) as the number of boundary faces. The described method allows a computation of \({\textbf {A}}\) without adding a surrounding volume of air saving a lot of computational efforts. Boundaries are all outer surfaces of the different electrolysis cell components. The internal values of the magnetic vector potential \({\textbf {A}}\) can be determined by combining Eqs. 3 and 5, leading to \(-\nabla ^2 {\textbf {A}} = \mu _0 {\textbf {J}}\). The boundary condition for solving this equation is determined using the Barnes-Hut method resulting in fixed values at the boundaries.
For the cases where ferromagnetic materials are considered, the magnetic flux density is the sum of two contributions \({\textbf {B}} = {\textbf {B}}_{I} + {\textbf {B}}_{M}\), where subscript I relates to current and M, to magnetization [11]. The magnetic vector potential is then calculated as:
where \({\textbf {M}}\) is the magnetization matrix.
This equation can be split into a free part including free currents \({\textbf {J}}_{r}\) and a bounded part including the magnetization \(\nabla \times {\textbf {M}}_{r'}\). The magnetization matrix can be written as:
where \({\textbf {H}}\) is the magnetic field strength and \(\mu _r\) is the relative magnetic permeability.
Finally, total magnetic flux density B (i.e., both contributions \({\textbf {B}}_{\textbf {I}} + {\textbf {B}}_{\textbf {M}}\)) is calculated according to Eq. 5.
The source for acceleration of the fluid phases is the Lorentz Force, defined by:
where \({\textbf {F}}_{L}\) is the Lorentz force.
The governing equations to describe the fluid flow for MHD problems are presented next. The velocity and pressure fields of the incompressible fluids are obtained by the momentum equation expressed by:
where t is the time, \(\rho\) is the density, p is the pressure and \(\mu\) is the dynamic viscosity. Surface tension is neglected.
The continuity equation ensures the conservation of mass. For incompressible fluids it is:
To capture both fluids arising in Hall-Héroult cells, the volume of fluid (VOF) approach is utilized. Therein, the momentum equation is only solved once for all fluids. To differentiate the fluids \(\alpha\) is used as a phase fraction variable. It is updated every timestep with the help of the following equation:
where \(\alpha\) is the phase fraction variable.
Numerical Model
The physics described above is implemented in the OpenFoam® framework (version 7). This framework is based on the Finite Volume Method and is implemented in C++ language. The basis of the currently employed algorithms was developed by [12].
The global workflow for this study is presented in Fig. 1. The first step is to calculate a static current distribution within the electrolysis cell while ignoring fluid motion. In this step the neighboring electrolysis cells are considered. The current distribution is then mapped into the next simulation (second step), which determines the magnetization of the ferromagnetic materials. The magnetized material influences the magnetic fields in the electrolysis cells. Here, the potshell is magnetized. The result of this step is B distribution which is applied as external magnetic flux density to the MHD simulations, the third step, including the prediction of the consumed anode profile in steady-state operating conditions. The resulting anode profile is the basis for the last analysis step.
Anode Consumption
The dynamic anode consumption model is based on the following assumption: the interface between aluminum and bath (cryolite) bulges due to action of electromagnetic forces (heave). The anodes blocks, consisting of carbon, are permanently consumed according to the alumina reduction equation. The local anode-cathode distance (ACD) is assumed uniform in the whole electrolysis cell, as this balances out the ohmic voltage drop of the electrolytic bath. As a result, the bottom surface of the anodes blocks has necessarily to conform to the resulting metal pad-bath interface. Similar anode shape is reported by [6].
This mechanism is implemented in the numerical model in the same way as it is described above. The simulation has ACD as boundary condition and local anode height is adjusted to match it. All grid cells corresponding to the anode blocks are marked with the attribute “anode” by the solver and their electric conductivity is set accordingly. This is done every timestep until convergence of the numerical model is reached.
The resulting profiles from that model have an increased current density at the corners of the carbon blocks. This condition is present after the first step of shape determination. As an increased current density also means more carbon consumption, the carbon at these locations is consumed faster. This leads to rounded anodes edges. This mechanism is also respected by the model in the second step of anode shape determination. For this, the model removes said “anode” attribute of all grid cells which have a current density above a given threshold. The threshold value is chosen so that the rounded corners of the anode correspond to the measurements. A value of 1.7 leads to the presented results. Figure 2 shows a photograph of an anode which was removed from an electrolysis cell and the corresponding fitted shape by the numerical model.
Electrolysis Cell Geometry at Trimet
The simulations are executed using electrolysis cells of the type EPT14, which are installed in two reduction halls at Trimet in Essen. The electrolysis cells are designed in an end-to-end fashion and have originally been planned for a line current of 140 kA. Now, the electrolysis cells are able to cope with higher line currents as they have been upgraded in terms of both magnetic and thermal behavior [1, 13].
Figure 3 shows the numerical domain for the cell of interest consisting of 15 regions. Here, regions mean all components of the electrolysis cells like steel shell, busbars, anodes, cathode and lining materials. The adjacent electrolysis cells are considered by the Burnes-Hut algorithm using tree-structured division of geometry into cubic cells [10]. In this study three cells are considered in the upstream and downstream direction, respectively. Moreover, the opposite side in the same potroom is also included with the same amount of electrolysis cells plus the direct opposite electrolysis cell. This results in 13 neighboring electrolysis cells taken into account.
The authors are aware that, by not considering the neighboring rows of pots in their entirety leads to some error of the bias of the vertical component of the magnetic flux density \(\Delta {\textbf {B}}_magnetic flux density{Z}\), leading to some error of the velocity distribution in the metal. Nevertheless, given that the metal pad heave is mostly dependent on the divergence of the horizontal components of the Lorentz forces \(\nabla \cdot {\textbf {F}}_{\textbf {L,XY}}\) it is rationalized that the absence of the (mostly) uniform contribution of \(\Delta {\textbf {B}}_{\textbf {Z}}\) should not considerably impact the prediction of the metal pad heave.
The mesh consists of 15.3 million grid cells which are mostly hexahedral. The mesh density, especially important for the fluid region where the VOF-method is applied, is chosen according to the findings of former studies executed by Gutt et al. [12]. The inlet and outlet for \({\textbf {J}}\) are applied on the downstream and upstream ends of the busbar system as outlined. The outer boundaries of the simulation domain have Neumann boundary conditions. The gradient of J is zero, which means that the current cannot pass these boundaries. The internal boundaries between the different regions are coupled to those of their neighbors. The current distribution inside the electrolysis cell is dominated by the electric conductivities of the individual components.
Results
Standard Operation at 165 kA and Validation of Simulation Results
Nowadays, the EPT14 electrolysis cells are operated with a line current of 165 kA, which is the standard operating condition. The first simulation treats this situation. The resulting interface heave is presented in Fig. 4. The total metal upheaval is approximately 8 cm and there are two positions of highest heave at both long outsides. These are -2 m and 1 m away from the cell center. According to the assumption described in Sect. Anode Consumption", the anode bottom surfaces conform to this shape, resulting in a uniform local ACD.
The data which has been generated with the help of the simulations is validated using measurement data from the electrolysis process at Trimet in Essen. The interface height was measured at six different positions in the electrolysis cells from the side facing outside of the potline—refer to Fig. 4. To allow for the measurements, the crust was broken between the anodes. The distance to the interface was determined using steel rods. As a consistent vertical reference, the horizontal bar holding the anodes was selected. The measurements were executed in February 2022 at six different electrolysis cells. The results are presented in Fig. 5. The plot shows the average values from all electrolysis cells considered in the measurements and the simulation data. A good agreement between simulation data and measurements can be seen.
Line Current Shifting by ± 25%
The standard operating condition described before is shifted to a ± 25% higher and lower line current in the next step. This means, that the new line currents of 124 and 206 kA cause a new interface shape directly after shifting the line current. The interface shapes after shifting the line current can be observed in Fig. 6. Decreasing the line current leads to a smoother interface shape and increasing leads to an accentuation of local maxima of the interface. As expected, the maximum metal upheaval decreases at lower line current (5 cm at 124 kA) and increases at higher load (11 cm at 206 kA).
The anode currents are permanently monitored in some electrolysis cells at Trimet in Essen. This can help to identify process abnormalities like spikes [14].
Figure 7 presents the individual anode currents after a decrease of the line current to 124 kA. The individual anode currents tend to increase at the corner anodes due to the flattening of the interface. That leads to increased anode currents up to 16 kA compared to the average anode current. The two regions with the highest heave at 165 kA and 206 kA have decreased anode currents also due to the flattening of the interface. All in all, the situation at 124 kA is by tendency the opposite to the situation of 206 kA.
Figure 8 presents the individual anode currents after an increase of the line current. There are mainly two regions in the electrolysis cell, which have increased anode currents immediately after increasing current by ± 25%. The regions correspond to the maxima in the interface bulge presented in Fig. 4. They cause an increase of the individual anode currents up to + 10% compared to the average anode current.
The magnetic flux density fields for the situations with increased and decreased line currents are presented in Fig. 9. The qualitative distribution of magnetic fields remains mostly the same. The intensity of magnetic flux density rises with increasing line current.
The transient evolution of the flow field in the electrolysis cell is presented in Fig. 10. To highlight the effect of changed line current, the coloring presents the relative deviation of flow velocity magnitude at the shifted line current compared to the flow velocity magnitude at the standard operating condition of 165 kA line current. This can be written as \(\frac{|\mathbf {U_{new}} |}{|\mathbf {U_{165 \, kA}} |}\). The direction of the flow velocity (presented by the arrows) stays almost the same compared to the situation before line current shift. The magnitude of the flow velocity changes depending on the line current. Lower line current leads to decreased flow velocity magnitude and higher amperage leads to increased flow velocity magnitude. The maximum velocity decreases by 23.6% at 124 kA and increases by 29.5% at 206 kA line current compared to an amperage of 165 kA. Eighty seconds after the line current shifts, the conversion of the flow field to the new operating condition is completed.
Conclusion
In the present numerical study, our MHD model for the simulation of Hall-Héroult cells is presented and applied to industrial EPT14 cells used at Trimet in Essen. The focus of the study is to analyze load shifting scenarios occurring at flexible operating conditions of aluminum electrolysis. The motivation for current modulation is to adapt industrial processes to a volatile supply of renewable electricity sources. The numerical model is able to consider the influence of neighboring electrolysis cells, the magnetization of ferromagnetic materials, a static ledge profile and the dynamic changes of anode shape caused by the carbon consumption. Two load shifting scenarios are studied in detail. The standard line current of 165 kA is shifted to 124 kA and 206 kA which corresponds to a 25% decrease or increase. The model predicts a flatter bath-aluminum interface during the decreased line current situation. Combined with the anode bottom shape which was formed at the standard operation of 165 kA, this situation leads to relatively increased anode currents at the corner anodes of up to 16%. After increasing the line current to 206 kA, the interface deformation is reinforced, which leads to an increase of local current density maxima. Certain anodes have up to 10% higher currents compared to the average anode current. The technical implications of this study are more in the sense of deepening understanding and forecasting process control rather than recommending hardware retrofits. With the help of the presented results process operators are able to understand why certain areas or anodes have increased currents after load shifts. This may help to distinguish the impacts of load shifts from effects like spikes, incorrectly inserted anodes or anode drop-offs.
References
Düssel R, Mulder A, Bugnion L (2019) Transformation of a potline from conventional to a full flexible production unit. In: Chesonis C (ed) Light metals 2019. Springer, Cham, pp 533–541
Potocnik V (1989) Modelling of metal-bath interface waves in hall-heroult cells using ester/phoenics. Light Metals: Proceedings of Sessions, AIME Annual Meeting (Warrendale, Pennsylvania), 227–235
Severo D, Schneider A, Pinto E, Gusberti V, Potocnik V (2005) Modeling magnetohydrodynamics of aluminum electrolysis cells with ansys and cfx. In: Kvande H. (ed) Light metals 2005. TMS
Wang Q, Li B, He Z, Feng N (2014) Simulation of magnetohydrodynamic multiphase flow phenomena and interface fluctuation in aluminum electrolytic cell with innovative cathode. Metall Mater Trans B 45(1):272–294. https://doi.org/10.1007/s11663-013-0001-z
Hua J, Rudshaug M, Droste C, Jorgensen R, Giskeodegard N-H (2018) Numerical simulation of multiphase magnetohydrodynamic flow and deformation of electrolyte-metal interface in aluminum electrolysis cells. Metall Mater Trans B 49(3):1246–1266. https://doi.org/10.1007/s11663-018-1190-2
Bojarevics V, Dupuis M (2021) Application and adaptability of MHD stability computation for modern aluminium reduction cells at extreme conditions of low acd. In: Perander L (ed) Light metals 2019. Springer, Cham, pp 565–571
Mohammad I, Dupuis M, Funkenbusch P, Kelley D (2022) Stabilizing electrolysis cells with oscillating currents: amplitude, frequency, and current efficiency, 551–559. https://doi.org/10.1007/978-3-030-92529-1_73
Mohammad I, Dupuis M, Funkenbusch PD, Kelley DH (2022) Oscillating currents stabilize aluminum cells for efficient, low carbon production. JOM 74(5):1908–1915. https://doi.org/10.1007/s11837-022-05254-8
Dupuis M, Bojarevics V (2021) Analyzing the impact on the cell stability power modulation on a scale of minutes. In: Aluminium smelting industry, 54–57
Barnes J, Hut P (1986) A hierarchical o(n log n) force-calculation algorithm. Nature 324(6096):446–449. https://doi.org/10.1038/324446a0
Dupuis M, Bojarevics V, Freibergs J (2004) Demonstration thermo-electric and mhd mathematical models of a 500 ka aluminum electrolysis cell: Part 2. In: Tabereaux A.T. (ed) Light metals 2004. TMS
Gutt R, Nandana V, Janoske U (2018) A numerical study of metal pad rolling instability in a simplified Hall-Héroult cell. Paper presented at the 6th European Conference on Computational Mechanics (ECCM 6), Glasgow, UK, 11–15 June
Düssel R (2017) Entwicklung eines Regelungskonzepts für Aluminium-Elektrolysezellen unter Beruecksichtigung einer variablen Stromstaerke und eines regelbaren Waermeverlusts. PhD Thesis at TRIMET Aluminium SE & Bergische Universitaet Wuppertal, Lehrstuhl für Mess-, Steuerungs-, Regelungstechnik
Kremser R, Grabowski N, Düssel R, Mulder A, Tutsch D (2021) Comparison of different spike detection methods in hall-héroult cells. Automation 2021, Band 2392
Acknowledgements
This research is financed by the Bundesministerium für Bildung und Forschung under the project SynErgie II (03SFK3B1-2), whose support is gratefully acknowledged by the authors.
Funding
Open Access funding enabled and organized by Projekt DEAL. This research is financed by the Bundesministerium für Bildung und Forschung under the project SynErgie II (03SFK3B1-2).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.
Additional information
The contributing editor for this article was Adam Clayton Powell.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gesell, H., Janoske, U. Magnetohydrodynamic Analysis of Load Shifting in Hall-Héroult Cells. J. Sustain. Metall. 9, 459–467 (2023). https://doi.org/10.1007/s40831-023-00670-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40831-023-00670-9