Introduction

With the ongoing technical evolution of medical devices to high-performance products, not only the corresponding design and structure is becoming more important. Also the material requirements are getting more complex and lead to a shift of the optimization focus onto the properties of the material. Herein, the fatigue behavior and the related understanding in damage mechanisms play a key role in the field of technical evolution, especially for high-risk implantable devices subjected to increasing lifetime requirements.

Due to the deformation behavior of Nitinol, this material finds its preferred use in the field of stents or heart valve frames, for example. This is mainly related to the superelastic deformation behavior of this shape-memory-alloy (SMA), which enables significant dimensional changes of such devices during the implantation and minimizes the invasive procedure. During the subsequent lifetime, those implants are subjected to in vivo cyclic loadings, which lead inevitably to questions of fatigue damages. Minimizing the risks of fatigue failure and pushing the tolerable loads to increase the fatigue lifetime were targeted not only by various studies on structural optimization or optimization of manufacturing processes [1,2,3,4], but also by numerous studies on the material properties (e.g., [5,6,7,8]). In the scope of the latter studies, fatigue damages and their initiation were primarily attributed to local load peaks at structural imperfections in Nitinol [9,10,11,12,13,14,15]. The classification of imperfections includes several different types which basically originate from non-metallic inclusions. Such inclusions emerge during metallurgical processes in the ingot production and subsequent manufacturing procedures [16, 17]. Along with these manufacturing procedures, as for example to the final tubing, these inclusions are subjected to deformations beyond the corresponding ultimate strength. This situation, in combination with the plastic deformations of the surrounding Nitinol matrix, leads to the formation of fractured inclusions. Along with the inclusion fracturing voids emerge at the remains. These particle-void-assemblies (PVA) show a vast variance in shape along with a geometrical alignment to the deformation direction, i.e., drawing direction [18].

In terms of the above-mentioned fatigue damage initiation at inclusions, PVAs play a key role for the crack initiation mechanism [11,12,13,14,15]. Extensive work was done to investigate the role of these inclusion types for the fatigue behavior in an analogous manner to other high strength materials [19,20,21]. These studies primarily confirmed the well-known inclusion size effect on the fatigue life and on the corresponding limiting fatigue threshold for Nitinol. Urbano et al. [14] have shown that the size effect on the fatigue strength follows the phenomenological correlation of Kitagawa by Muramaki’s \(\surd\)area-approach. In addition to the stated size effect, Adler et al. [3] and Salajegheh et al. [22] found evidence for an inclusion orientation effect on the local fatigue strain situation. Adler et al. concluded further that based on findings of Murakami et al. [19], other structural characteristics, like particle–matrix-bonding or inclusion shape, are also from essential importance for the local fatigue strain configuration. To the authors` knowledge up to now the detailed fatigue mechanisms for cyclically loaded inclusions and the corresponding interaction of fundamental geometrical inclusion characteristics are not fully understood. Along with the experimental findings, simulative studies for inclusions in Nitinol by Senthilnathan et al. [23] and Gu et al. [24] confirmed the significant fatigue strain and stress effect emanating by idealized inclusions. Gu et al. showed that the inclusion shape and the orientation with respect to the load axis have strong and synergetic effects on the fatigue stress in the vicinity of the inclusion in steel. Despite numerous other studies on the generalized effect of inclusion of the fatigue stress or strain, just a small number considered extended geometrical inclusion properties, whereby even less are based on superelastic material behavior. For example, Bonsignore et al. [25] emphasized the significance of the link between fatigue strain results determined by fatigue simulations and the material inherited imperfections, like PVAs, which are in general neglected for fatigue simulations. Using the fatigue strain limits by Pelton et al. [26], they identified regions of high risk for fatigue damage. In the context of medical devices, several questions arise on additional effects of inclusions like orientation and shape and the resulting local fatigue strains in SMA’s, which can be summarized as

  • Local fatigue strain sensitivity for orientation relative to load axis

    1. •

      Existence of critical orientation

    2. •

      Difference for loaded PVAs and fully embedded particles

  • Local fatigue strain sensitivity for inclusion shape variation

    1. •

      Existence of critical shape

    2. •

      Difference for loaded PVAs and fully embedded particles

  • Synergetic effects of shape and orientation of the inclusion on local fatigue strain

  • Under which circumstances are PVAs less critical for the local fatigue strain

  • How strong is the strain localization and distribution around inclusions on macroscopic evaluation scale in dependence on the shape and orientation

From the authors` view, answering those questions are mandatory to any discussion on fatigue behavior improvement on the materials level. In the scope of the underlying study, first steps toward these answers are discussed in the following.

Numerical Modeling and Methods

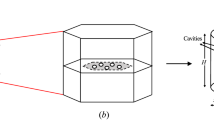
Geometrical and structural characteristics of inclusions in a standard grade Nitinol tube according to ASTM F2063 were evaluated based on metallographic analysis by scanning electron and light microscopy. As reported in literature, the fatigue relevant inclusion types are fully embedded particles or cracked particles accompanied by voids. Both types additionally exhibit strong variations in shape which can range from almost perfectly round to elongated and sharp. Figure 1 shows an exemplary metallographic analysis perpendicular to the drawing direction of the tube of particles and PVAs along with a strong variance in shape and size. Based on these findings, the inclusion shape and size were defined as the first parameters to investigate in this numerical study. In the scope of this study, the pure size effect of the inclusion on the local fatigue strain is excluded due to a dimensionless modeling approach by using a consistent mesh quality and the resulting scalability of the simulated unit cell.

Fig. 1
figure 1

Metallographic analysis on the geometrical properties of inclusion types of particles and PVAs. Strong variance in shape and size for the inclusions (appear in white) is apparent

Full size image

Along with the geometric constraints of the inclusion orientation and the drawing direction, further aspects were suspected to affect the local fatigue strains. Several fatigue strain analyses based on FEM have shown that cyclic loading in combination with increasing complexity of the design structures leads to complex local fatigue strain configurations in highly strained regions (see [27]). These complex fatigue strain configurations result in a broad variation of principal strain directions with respect to the drawing direction. An exemplary fatigue load situation is shown in Fig. 2 by a cyclic flat plate crush load and the resulting varying principal fatigue strain directions, indicated by red arrows. The combination of material inherited inclusion alignment and the complex fatigue strain configuration results in a wide variance of relative inclusion orientation and the fatigue load direction.

Fig. 2
figure 2

Exemplary fatigue load case (cyclic flat compression) and the corresponding strain amplitude distribution with principal direction

Full size image

For a holistic and representative evaluation of geometric and structural parameters of inclusions on fatigue strain situation, the parameters are defined as following:

  • Inclusion structure consisting of fully embedded particle or accompanied by voids

  • Shape of PVA or particle

  • Orientation of longitudinal axis of PVA or particle

  • applied global fatigue load differentiated by strain amplitude and mean strain

For the simulation model, a void-to-particle ratio of 0.35 for the PVA was used. The geometrical definition of the inclusion shape was done by using an ellipticity parameter, which describes the relation between longitudinal and transversal length. In Eq. 1, this ellipticity parameter is defined and ranges from Eq. 1 for a perfectly round shape up to 0, which describes an infinite thin inclusion.

$$E \, = \, 1 - \left( {b/a} \right)$$
(1)

Here a and b are the longitudinal and transversal length of the ellipsoid shape, respectively. Along with geometrical parameters, the fatigue strain configuration defined by global applied strain amplitude and mean strain are also essential to study locally resulting fatigue loads. Based on these main parameters the design space was defined and is shown in Table 1. For sake of efficiency, a small number of parameter sub-settings were defined. These parameter settings cover critical and significant definitions and provide adequate resolution for a first discussion of the effect of inclusion characteristics on the local fatigue situation. The parameter set for the applied global strain amplitude and mean strain was defined in correspondence to commonly observed fatigue loads for medical devices subjected to low cycle and high cycle fatigue [27, 28]. However, in terms of numerical stability, the applied range for global fatigue strains was capped and thus represents a restricted scope of typical fatigue loads. The combination of all parameters with the sub-settings led 240 unique models and simulations were conducted and analyzed.

Table 1 Overview of used parameters with all sub-settings for the current numerical study
Full size table

The Simulation Model

The unit cell model consists of the particle or PVA with the different structural configurations and the surrounding NiTi matrix. This unit cell represents a plain strain configuration of a cross section through the inclusion. This two-dimensional model consists of a square-shaped deformable body, representing the NiTi matrix and a rigid debonded particle embedded in a void (see Fig. 3a). The relative dimensions of the unit cell and the particle or PVA were defined to minimize the effects of the surrounding boundary conditions on the centered region of interest. This led to an edge length of the unit cell of about five times the particle’s longitudinal length. By this approach, any other environmental effects emanating from free surfaces, theoretical adjacent inclusions, or other inhomogeneities were also neglected. For the superelastic material response of the NiTi matrix, the standard implementation for superelasticity in ABAQUS [29] at 21°C was applied. Additionally, the standard implementation for kinematic hardening behavior after fully martensitic transformation was used to take into account plastic deformation during the cyclic loading. In Table 2, the generic material model parameters are listed as well as the corresponding absolute stress–strain data for the kinematic hardening calibration. The applied continuum material model uses constitutive equations with macroscopic variables to describe the isotropic superelastic deformation by the phase transformation. This results in a homogenized material response during stress-induced phase transformation, instead of a distinct local resolved transformation effect around the wandering transition layer between the two phases. Consequently, all results and deformations within this unit cell represent a homogeneous material response and neglect also any microstructural effects, like grain size and crystallographic orientation. No frictional and cohesive contact behavior was assumed in the contact modeling between particle and NiTi matrix due to the lack of experimental data. This frictionless behavior leads to unconstrained motions of the particle within the void, which was stabilized during the simulation by a very weak spring system for translatory and rotatory degrees of freedom.

Fig. 3
figure 3

Idealized structure of unit cell with embedded particle and void in a and the corresponding applied boundary conditions for the fatigue simulation (b)

Full size image
Table 2 Overview of used generic material parameters
Full size table

Symmetry boundary conditions were applied to the unit cell. The outer edges were defined to stay in the same plane in horizontal direction (ux,left, ux,right) and in vertical direction (uy,bottom). To apply the global strain amplitude and global mean strain, the upper edges were subjected to a cyclic uniform displacement (see Fig. 3b). To ensure a precise and reliable evaluation of fatigue strains, the mesh strategy as well as the mesh quality was from crucial importance. Based on a prior conducted mesh sensitivity study, an element size of about 0.3% of particle longitudinal length was used for a uniform meshed layer circumferential to the contact zone with a thickness of five elements (Fig. 4a). For high contact accuracy, a “hard” contact formulation with geometric smoothing algorithms provided by ABAQUS 2022 was used between the much finer mesh of the particle and the NiTi bulk material.

Fig. 4
figure 4

Element size definition based on results of mesh sensitivity study (bottom) (a). The modified tensor method is shown in b with the alignment of the mean strain tensor with respect to the strain amplitude tensor

Full size image

The fatigue strain evaluation at integration points of the reduced integrated solid continuum elements (C3D8R) was conducted by extracting the tensors of the strain amplitude and the mean strain between the maximum and minimum peak load after five simulation cycles. The maximum principal strain of the strain amplitude tensor was evaluated within the inclusion contact region of the NiTi matrix. Results by Marrey et al. [30] or Tripathy et al. [31] suggest to take into account large rotations by aligning the mean strain tensor with the principal directions of the strain amplitude tensor. Despite no large rotations are expected during the simulations, this approach is followed in this study. Along with the rotation of the directions of the mean tensor (see Fig. 4b) the evaluation of the fatigue strain state was conducted by using the highest strain amplitude linked with a positive mean strain.

Results and Discussion

For the evaluation of the simulation results, two detail levels were defined to access essential characteristics of the underlying data sets. The main level for evaluations comprises the careful re-organization of all fatigue data and differentiates between major study parameters. This approach is based on the categorization of the observed local maximum principal strain amplitudes and corresponding mean strains into global applied fatigue load, orientation, or shape, i.e., ellipticity. Within each parameter category, the fatigue strain configuration is then evaluated with respect to all remaining parameter sets. Additionally, each parameter set was extended by a corresponding representative average value, which results in a more general consideration for the effect analysis. The secondary evaluation level includes a more detailed view on some specific results which are not fully represented by the main evaluation.

General Overview

A general overview for the local strain situation at inclusions under varying global strain loads is shown in Fig. 5. This graph provides a generalized impression of maximum local strain amplitudes occurring in inclusion surroundings [particle in (a) and PVA in (b)] for different levels of applied global fatigue strains. In Fig. 5 top graph, a monotonically increasing local strain amplitude is apparent due to increasing global applied strain amplitude. Despite the fact that the observed maximum local strain amplitude occurred at different locations and under varying parameter sets, these summarized results show a visible averaged correlation. This effect on the resulting local strain amplitude can be observed for particles as well as for PVAs in a very comparable manner. The main difference between both results is the higher overall strain amplitude level, which was found for cyclic loaded PVAs. This fatigue strain effect attributed to the existence of voids is in good agreement with results by Moore et al. [32] and Kafka et al. [33], which observed a strong drop in fatigue initiation lifetime based on numerical evaluation methods for PVAs. By analyzing the effect of varying mean strain on the strain amplitude in the bottom of Fig. 5, a significantly different relationship can be observed. The set averages are showing a slow increasing behavior for global applied mean strain rising up to 0.6%. This can be qualitatively observed for both inclusion types under cyclic loading. For global applied mean strains beyond this apparent threshold, the resulting strain amplitude shows a strong decreasing characteristic. A quantitative comparison of this behavior between cyclic loaded particles and PVAs shows a significantly higher strain amplitude level for PVAs. The observed sudden decrease of the local maximum strain amplitude correlates well with the emergence of plastic deformation in the contact region around the particle for both inclusion types.

Fig. 5
figure 5

Visualization of all results for particles (a) and PVA (b) regarding local strain amplitude and clustered into corresponding sets of applied strain amplitude as well as mean strain. For each parameter set, the corresponding average is additionally marked by red closed diamond (Color figure online)

Full size image

Effect of Orientation

Breaking down the above shown results into several different evaluations for the remaining parameter categories is done in Figs. 6 and 7. In Fig. 6, a correlation between the orientation of the inclusion with respect to the load direction and the resulting local strain amplitude is shown. This graph comprises all result of Fig. 5 and distinguishes between the different inclusion orientations. As in the evaluation above, the parameter set averages are marked by red dashes and provide a more generalized insight. These set averages show increasing local strain amplitude by ranging the orientation from 0° to 45° relative to the load direction. Beyond this orientation, the local strain amplitudes are mainly scattered around a constant level of about 3.50% for particles and 4.30% for PVAs. The significantly higher strain amplitude level for cyclic loaded PVAs originates from the much higher strain and the strong localization within the contact region between particle edges and the NiTi matrix. For a more detailed understanding of the underlying data structure and the complex effect relationship of combined parameters, a second evaluation level is applied in Fig. 6. To highlight the additional effect of the applied global strain amplitude, different amplitude levels are visualized by a color scale. By this color coding, a weak sensitivity of the orientation effect characteristics for different applied strain amplitudes becomes apparent. For both inclusion types, this relationship of initially increasing and subsequently saturating local strains is apparent for all different levels of applied strain amplitudes. However, an increasing applied strain amplitude results in a general shift of the resulting local strain amplitude toward higher strains. This is in good agreement with results in Fig. 5, regarding the effect of increasing applied strain amplitude on the local strain amplitude.

Fig. 6
figure 6

Classification of observed maximum local strain amplitudes for particles (a) and PVA (b) regarding the corresponding orientation with respect to the fatigue load direction. The set average is marked by red dash as well as the corresponding applied global strain amplitude by gray-to-black color scale for all results within each category (Color figure online)

Full size image
Fig. 7
figure 7

Visualization of the shape effect on resulting local strain amplitudes for all results of different applied mean strain, applied strain amplitude, and different orientations of particle (a) and PVA (b). Additionally, the globally applied strain amplitudes for all results are shown by gray-to-black color scale (Color figure online)

Full size image

Effect of Shape

Besides the above shown effect of orientation on the local strain amplitude, the shape or ellipticity shows also interesting effect characteristics. For this purpose, the resulting maximum local strain amplitudes are plotted based on the similar strategy as in Fig. 6. All observed local strain amplitudes are plotted in Fig. 7 with respect to the ellipticity, complemented by the averages of each cluster of inclusion ellipticity. Similarly, to results in Fig. 5, the observed local strain amplitudes show a monotonically increasing behavior for inclusions of narrowing characteristic. This means that ranging from round spherical inclusions to very thin and elongated shapes the resulting strain amplitudes increase. The observed effect is mainly related to the size of the contact zone between the Nitinol matrix and the rigid particle. For round particles, the contact zone and the resulting interaction region are significantly larger during compressive load cycles compared to the one evoked by very thin and elongated particles. This leads to a more homogeneously distributed strain situation under comparable global load conditions, instead of the strictly localized strain situation with a much higher strain level for elongated inclusions. It follows, a broken particle with sharp edges accompanied by a void leads to even stronger strain localizations and higher resulting local fatigue strains, as indicated in Fig. 7b. This observed effect of inclusion shape is in contrast with experimentally observed fatigue damages emanated from inclusions by Rahim et al. [11]. They found no clear evidence for shape effects by comparing the resulting crack length. The resulting crack length, however, is not only affected by the initiation phase but also by the subsequent crack propagation mechanisms, which are highly sensitive to various additional microstructural effects. For visualizing the additional effect of the applied strain amplitude, in Fig. 7 a, corresponding color coding was applied on the displayed results. The significantly higher level of resulting local strain amplitudes for inclusions under increasing global strain amplitude becomes apparent in Fig. 7. The amplifying parameter dependence can be observed throughout all investigated simulations for both inclusion types. The increasing scatter of local strain amplitude in Fig. 7 indicates significant interaction relationships of several geometrical parameters for both inclusion types.

Synergetic Parameter Effects

The above discussed results and evaluations lead to the secondary evaluation level, which focuses on a more detailed view for the synergetic parameter effects. For this purpose, the results are categorized into different sub-sets of identical parameter values, and the sub-set averages are plotted in Fig. 8. For example, there are three different sub-sets with identical ellipticities and three sub-sets with identical orientations. Plotting these averages for both inclusion types with respect to the global applied strain amplitude (top graphs) shows a monotonically increasing behavior under rising global applied strain amplitudes. Comparing the order of the strain levels between the effects of orientation and shape, an effect dominance of the shape (ellipticity) is apparent. This effect behavior on the local strain amplitude was observed for fully embedded particles and PVAs. Additionally, every observed effect behavior in Figs. 5 and 6 is also visible in this graph. Resulting from this graph, it becomes clear inclusions of strong elliptical shape create high local fatigue strains. This effect dominance is more pronounced for cyclic strained PVAs than for fully embedded particles.

Fig. 8
figure 8

Detailed view on the specific averages of results for different orientation sets or ellipticity sets with respect to global strain amplitudes (top) and global mean strain (bottom) for fully embedded particles (a) and PVAs (b). The main averages per main parameter (global strain amplitude or global mean strain) as introduced in Fig. 5 are highlighted with red dashes (Color figure online)

Full size image

This clear effect hierarchy for particles and PVAs with respect to the applied global strain amplitude is in strong contrast to the results of varying global applied mean strain. Here, the hierarchy of effect dominance on local strain amplitudes is strongly dependent on the inclusion type as well as on the global mean strain level. Regarding the local strain amplitude of cyclic strained particles, Fig. 8 shows that round particles lead to higher fatigue strains when subjected to negative or low global mean strains. Furthermore, under the same load conditions, the particle orientation shows a secondary effect role. This behavior is inverted after passing the threshold of 0.6% global applied mean strain, and the sub-set averages show a collapsing behavior. As mentioned in the discussion of the fatigue strain effects in Fig. 5, the threshold of 0.6% correlates with the emergence of plastic deformations. With respect to the applied global mean strain, fully embedded particles while still in elastic deformation show an inverse shape effect compared to the observed global strain amplitude dependency. The resulting local strain amplitudes at PVAs show a significant different sensitivity for ellipticity and orientation. PVAs subjected to global mean strains between 0.0 and 0.6% show high local strain amplitudes preferably around very thin and elongated inclusion shapes. For negative global applied mean strains, the above observed dominant effect role of the shape for applied global strain amplitude can be confirmed. But along with the appearance of plasticity in the contact region of PVAs at global applied mean strains above 0.6%, the orientation with respect to the load direction becomes more important. With respect to the applied global mean strain, no clear and universal effect hierarchy can be derived.

Total Implications

To discuss the above introduced results and effects in the context of a fatigue relevant visualization, the local strain amplitude and the corresponding mean strain are plotted in Fig. 9. In sub-figure (a), all cyclic strain results are differentiated by the inclusion type, regardless of any additional geometric parameter. With this graph, the strong difference between cyclic strained particles and PVAs becomes clear, especially in the regime for low fatigue strains. Fatigue strain situations emanating from particles show a more concentrated strain field in this regime, whereby PVAs under identical conditions show a broad scattering instead. This different scattering pattern can be attributed to the above discussed effect relationships, which are highly dependent on the inclusion type. A more detailed evaluation of the corresponding global fatigue strain loading is shown in sub-figure (b). In this graph, the effect of inclusion type is neglected and just the applied fatigue strains are taken into account. To emphasize the observed effect on the local fatigue strain, qualitative tendencies based on the result sets averages for both global applied load parameters are shown in Fig. 9b. Based on this graph, one can conclude that, besides the general trivial relationship between global and local strains, the global strain amplitude is of dominant importance. This result is also present in Fig. 9c, where additionally the extensive effect of the ellipticity regarding the local strain load is shown. By the fatigue strain results of different ellipticities and applied strain amplitudes, the resulting local fatigue strain situation shows a high sensitivity to this geometric parameter. As indicated by the quantitative tendency, the local fatigue strains are increasing along with larger ellipticities. In comparison to the effect of the inclusion orientation in Fig. 9d, supplementary to those results shown in Fig. 6, the slightly weaker parameter effect on the local strain situation becomes apparent. Furthermore, the saturation of the orientation effect on the local fatigue strain, introduced Fig. 6, manifests in the heterogeneity of the fatigue strain results for orientations above 45° in the high strain regime.

Fig. 9
figure 9

a Resulting local strain amplitudes with corresponding local mean strains of particles (black closed diamonds) and PVAs (open squares). b Simulation results (local strain amplitude and mean strain) correlated with the corresponding global loads (global strain amplitude and mean strain) by color coding and size-scaled closed circles. c Visualization of all simulation results regarding applied global strain amplitude (highlighted by color coding) and the corresponding ellipticity by size-scaled circles. d Visualization of all simulation results regarding applied global strain amplitude (highlighted by color coding) and the corresponding orientation by size-scaled circles (Color figure online)

Full size image

Another aspect to discuss is the spatial dimension of the highly strained region around the inclusion, which must be considered in terms of microstructural fatigue damage mechanisms in this study. In the light of the current evaluated maximum fatigue strains, the strain distribution with respect to the size of the overstrained region as well as fatigue strain profile within is not considered. With respect to several commonly used and successfully applied fatigue damage schemes, the fatigue load distribution and the corresponding overloaded volume are from crucial importance, especially regarding the inclusion size effect on the local fatigue strain situation (see [22, 32,33,34,35]). Therefore, it can be assumed that there is a difference for the fatigue damage mechanism between very localized and more expanded overloaded microstructural regions. The definition of a high-risk region of potential fatigue damage is the key factor to the evaluation of the inclusion size effect and is directly related to the fundamentals of fracture mechanics. Apart from the definition of an evaluation region, the evaluation of a fatigue indication parameter (FIP) is commonly an effective way for the assessment of the fatigue damage potential [32, 33]. But this demands the accurate and precise definition of the fatigue damage threshold, which is highly dependent on the underlying material state as well as on a broad range of microstructural effects. Therefore, this fatigue damage threshold has to be chosen very carefully. To the current state of this study and the underlying results, the evaluation based on the spatial homogenized FIP is not yet considered, due to the lack of a specific damage initiation threshold. This missing additional evaluation step must be considered in every discussion of the underlying results.

Finally, one crucial characteristic of the applied simulation method, specifically the applied material model, must be emphasized regarding the above results discussion. As mentioned in Sect. "Numerical Modelling and Methods," the material model applied is based on a macroscopic framework and thus represents not the microstructural material behavior. The microscopic material behavior, especially during phase transformation, has a significant impact on the local strain situation in the scale of the parent microstructure. Effects, like local softening due to phase transformation or strong strain shifts due to phase transition layers or retained martensite, have to bear in mind for all discussions of explicit strain situations around inclusions, with magnitude of the parent microstructure. Numerous studies faced these microstructural issues by using representative volume elements (RVE), which incorporate a representative number of microstructural relevant entities, e.g., grains, in combination with crystal plasticity models. The efficiency and the costs of this simulation method are strongly related to the number of considered microstructural entities and restrict therefore the dimensions of the region of interest. In this context, this study is focused on a more mesoscopic level and thus excludes any size scale relationship for the fatigue strain situation around inclusions in combination with superelastic material behavior.

Numerical Effects

Besides the effect synergy and all specific effects on local fatigue strains, these results must be discussed regarding numerical simulation effects. Prior to the main body of this investigation, extensive numerical studies were carried out to minimize any numerical effects by element size or mesh quality. The outcome of this mesh sensitivity study (see Fig. 4a) led to the application of a structured mesh around the inclusion. Furthermore, the used element size leads in compressive load cycles to an estimated relative numerical error of about 5%, based on the results of the mesh sensitivity study (Fig. 4a). To reduce this effect of mesh size on the evaluation results, the above-mentioned spatial homogenization around the peak values provides in general an effective solution (see [32,33,34]), but was not yet applied in this study. A much higher impact on the numerical precision and the physical interpretation was found for the applied boundary conditions and the size of the unit cell. Due to the study objective, to investigate the material response around one single imperfection and hence neglecting any additional environmental impacts, the application of periodic boundary conditions was not reasonable. Instead, the modeling of plane boundaries with specific degrees of freedom around a unit cell in combination with sufficient spatial dimensions provided an efficient solution. The applied unit cell dimensions of five times the inclusion length lead to an estimated numerical error of 0.7% in the fatigue load dominant compressive cycle, based on the results of the mesh sensitivity study. In addition to the above-mentioned impact of mesh quality on the results precision, the interaction modeling plays an important role. In common, interactions between surfaces or bodies are modeled with interaction approaches which allow small portions of surface penetrations to optimize the numerical solving stability and in turn accepting errors in contact stresses. This behavior and the related numerical error were minimized by using a hard contact approach and increase the precision of contact stresses and strains between fine meshed bodies.

Conclusion

Motivated by the importance of inclusions on the fatigue life of Nitinol-based medical devices, a numerical study was conducted to evaluate the critical inclusion properties and the corresponding effects on the fatigue strain levels. Based on metallographic investigations, shape of the inclusion and orientation with respect to the loading direction were defined. Global boundary conditions on the surrounding NiTi matrix were defined based on commonly applied fatigue loads. Additionally, the effect of the existence of a void in combination with a broken particle was investigated.

The major findings of this study suggest that, besides the trivial correlation between global and local fatigue strains, the shape and the orientation are of essential importance for the local fatigue strain situation. According to the summarizing Fig. 9 in combination with Figs. 6 and 7, it can be observed that the inclusion shape shows a slightly larger effect on the local strain level than the orientation. Based on an additional statistical evaluation of the data, the influence of the parameters on the local strain level can be ranked:

  1. 1.

    Global strain amplitude

  2. 2.

    Ellipticity

  3. 3.

    Orientation

  4. 4.

    Global mean strain

A significant difference in the local fatigue strain level between particles and PVAs was observed, along with the parameter hierarchy shown above. The resulting fatigue strains are higher in the PVA, than for fully embedded particles, due to strong strain localization in the contact region of the remaining particle in the PVA. Furthermore, the highest risk for a high fatigue strain increase was found for thin and elongated PVAs, especially with significant misorientation to the load axis. Regarding any material quality requirements for high-performance medical devices, the above stated findings can be rephrased: a NiTi-material structure with round fully embedded particles is less prone to high global fatigue strain than with broken particles accompanied by elongated voids.

The maximum local strain amplitude and the modified re-orientated mean strains were used for strain evaluation in this study. This approach, though, neglects the spatial dimension and distribution of the overstrained region, which means that, to the current state of this study the influence of the inclusion size on the local fatigue strain configuration is still not fully understood. This remaining question is strongly linked to the fundamentals in fracture mechanics and requires a more detailed evaluation procedure. For the future work, this missing evaluation factor will be established by considering the highly strained volume at the inclusion, as well as the homogenization of region of peak strains. Furthermore, the underlying study parameters will be extended regarding the void-to-particle ratios and further PVA geometries. In terms of simulation validation, additional experimental investigations, like [35,36,37,38] based on in situ experiments, will be conducted and should provide a reliable data base for this missing link.