Finite Strain Constitutive Modelling of Shape Memory Alloys Considering Partial Phase Transformation with Transformation-Induced Plasticity

Abstract

This paper presents a unified modelling effort to describe partial phase transformation during cyclic thermo-mechanical loading in Shape Memory Alloys (SMA). To this purpose, a three-dimensional (3D) finite strain constitutive model considering TRansformation-Induced Plasticity (TRIP) is combined with a modified hardening function to enable the accurate and efficient prediction of partial transformations during cyclic thermo-mechanical loading. The capabilities of the proposed model are demonstrated by predicting the behavior of the material under pseudoelastic and actuation operation using finite element analysis. Numerical results of the modified model are presented and compared with the original model without considering the partial transformation feature as well as with uniaxial actuation experimental data. Various aspects of cyclic material behavior under partial transformation are analyzed and discussed for different SMA systems.

Introduction

Shape memory alloys (SMAs) are smart alloys possessing the unique behaviors known as Pseudo-Elasticity (PE), one-way and two-way Shape-Memory Effect (SME). After being subjected to mechanical deformation while at the high temperature austenitic phase, the alloy is able to recover the original shape through a solid-state, diffusion-less phase transformation caused by the imposition of a stress (i.e., PE) and/or temperature (i.e., SME) field [1]. The physical mechanism behind SMA properties is attributed to such solid-state, diffusionless phase transformation between a high-temperature, high-symmetry austenitic phase and a low-temperature, low-symmetry martensitic phase, that takes place when the alloy is subjected to certain thermo-mechanical loading conditions [2].

Fig. 1

Schematic example of a PT formation during thermal actuation, determining one closed loop with two reversal points. FR and RF denote the reversal points passing, respectively, from forward to reverse transformation and from reverse to forward

Table 1 Material parameters used for the numerical simulations

Fig. 2

Uniaxial pseudoelastic tests. a Applied stress-loading step parameter, c stress–strain, e strain-loading step parameter curve for the first test; b Applied stress-loading step parameter, d stress–strain, and f strain-loading step parameter curve for the second test

Fig. 3

Biaxial non-proportional pseudoelastic tests. a Applied stress path, b strain component 11 versus 33 curve

Fig. 4

First uniaxial actuation test. Model actuation response for a constant tensile stress of 200 MPa. a Applied temperature history, b strain-temperature, and c strain-loading step parameter curve

Fig. 5

Second uniaxial actuation test. Model actuation response for a constant tensile stress of 200 MPa. a Applied temperature history, b strain-temperature, and c strain-loading step parameter curve

Fig. 6

Third uniaxial actuation test. Model actuation response for a constant tensile stress of 200 MPa. a Applied temperature history, b strain-temperature, and c strain-loading step parameter curve

Fig. 7

Tube actuator. Analyzed geometry and applied boundary conditions

Fig. 8

Tube actuator test. a Shear strain-temperature curve, c twist angle-temperature curve, and b–d comparison between the original and proposed model for selected full transformation (FT) and partial transformation (PT) cycles

Fig. 9

Uniaxial actuation test on a $\hbox {Ni}_{50.3}\hbox {Ti}_{29.7}\hbox {Hf}_{20}$ HTSMA under a 395 MPa constant tensile stress. Comparison between experimental and numerical strain-temperature curves for the a proposed model formulation and the b original model formulation by Xu et al. [31]

Such unique behavioral characteristics make SMAs largely employed in a wide range of innovative applications [3]. Particularly, thanks to PE, good biocompatibility, and high corrosion resistance, SMAs are extensively used in the biomedical field, as stents, occluders, or surgical tools, while thanks to the SME and high output energy density, coupled with several advantages for system miniaturization (e.g., high power-to-mass ratio, maintainability, reliability, clean and silent actuation), SMAs are largely investigated as actuators in various engineering industries including, e.g., aerospace [4], civil [5], automotive [6], and recently wind energy [7,8,9,10].

When SMAs are subjected to cyclic loading, either thermal or mechanical, they most often present two important characteristics, i.e. TRansformation Induced Plasticity (TRIP) strains and partial transformation.

The first characteristic is generally exhibited during the so-called training procedure, which is typically employed to stabilize the cyclic response of SMAs before their use [11,12,13]. During this procedure, permanent microstructural changes are often introduced in the alloy, which leads to the generation of an internal stress field and large irrecoverable TRIP strains. Consequently, cyclic loading tremendously affects SMA characteristics and most importantly the performance (e.g., actuation work) and fatigue life of the SMA component. As an example, Phillips et al. [13] showed that the internal damage in a SMA actuator subjected to actuation fatigue evolves in a non-linear manner, with a rapid damage nucleation during the training period associated to the irrecoverable strain accumulation. Moreover, the training process can be used to induce the so-called two-way SME in actuators [14], that is the capability of a SMA to change its shape reversibly during subsequent thermal cycles between its transformation temperatures without applying any external mechanical load.

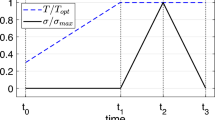
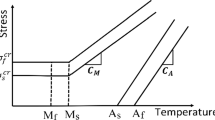
The second characteristic is exhibited when SMAs are subjected to a mechanical or thermal load that is reversed before the completion of phase transformation. Reversal of transformation direction while the alloy is in a mixed phase state leads to the formation of a Partial Transformation (PT) branch. In this case, SMAs are capable of “remembering” their previous states associated with the transformation reversal prior to a complete phase transformation [15]. Such a feature is also known as reversal memory. Depending on the applied loading history, different PT situations may arise, including partial loops with one single reversal point, closed loops with two reversal points (see Fig. 1), and partial loops with multiple reversal points. From a microstructural point of view, such phenomenon is associated to an ordered alteration of the material microstructure, dictated by the achievement of a critical threshold energy value by each grain [16]. When a threshold is reached, a certain group of grains is transformed, and the phase of the SMA is changed. In case of a transformation reversal, alternations take place depending on this threshold. Assumed that the same energy level state is achieved after a series of loadings, the material also obtains the respective microstructure and, consequently, the same phase. Based on these assumptions, the formation of closed PT cycles and memory wipe-out phenomenon can be explained. As a result, PT largely affects the amount of generated transformation strains, the actuation frequency [15, 17], and most importantly the fatigue life of the component [18]. In fact, it has been shown in ref. [12] that operation in PT conditions enhances the actuation frequency of antagonistic SMA wire actuators and reduces the developed stresses and activation temperatures, which can be translated to a possible energy efficient operation with prolonged thermo-mechanical fatigue life. Catoor et al. [19] showed that Nitinol stents experience cyclic loading from cardiac cycles and musculoskeletal movements in the mixed-phase state and their lifetime is affected by operation in PT conditions.

It is clear from the above discussion that these two features are very likely to be coupled during cyclic loading and their consideration is fundamental for the successful design of SMA-based structures with increased performance and fatigue lives. Accordingly, it becomes essential an associated accurate modeling to support the design.

To date, several modeling efforts have been dedicated to the first characteristic, i.e., to predicting the evolving properties of SMAs under cyclic thermo-mechanical loading, caused by repeated phase transformations under material yielding point [20,21,22,23,24,25,26,27,28,29,30,31,32]. However, these efforts have been restricted to the prediction of the full transformation loops and not to an accurate modeling of PT (i.e., the second characteristic).

The second characteristic is generally accounted for by describing the behavior of conventional SMAs without considering irrecoverable strains and damage, which is sufficient for the design of components where the operating temperatures, maximum stress levels, and number of actuation cycles are relatively low. These contributions include differential equations and Duhem-Madelung type models [15, 33, 34], Preisach-type models [35,36,37,38,39], purely phenomenological models and state equations based on principles of thermodynamics and/or plasticity [20, 40,41,42,43,44].

To the authors’ knowledge, the modeling of the complex behaviour of SMAs under the two described characteristics, accounted simultaneously in thermal and/or mechanical cycles, is still missing in the current literature.

Motivated by the described framework, the aim of the present work is to address SMA features under such two important characteristics through a unified modelling effort.

To this purpose, the proposed formulation starts from the three-dimensional phenomenological model recently published in ref. [31], that has been validated against experimental data on NiTi and NiTiHf SMA materials. The choice of dealing with the model by Xu et al. [31] is motivated by the following reasons: (i) the model is formulated in a finite strain framework, which is well suited in case of SMA actuators experiencing 30% or higher TRIP strains during their lifetime or in the presence of cracks [45]; (ii) the model describes the two-way SME exhibited by trained SMAs at load-free conditions; (iii) the model considers stress-dependent TRIP evolution under multiaxial stress state. Despite these advantages, the model by Xu et al. [31] is limited to an accurate and efficient description of only full phase transformation.

Accordingly, an efficient and easy-to-implement modified hardening function [15] is introduced in the present paper to account for PT behaviour under cyclic loading. This constitutive modeling approach has been inspired by the models presented in refs [46] and [41] and combines some of their characteristics. However, it does not require the determination of any additional material parameters rendering the calibration process easier and more straightforward. In fact, the model can be calibrated by using the same data extracted from uniaxial characterization processes often followed in the literature.

In order to evaluate model accuracy and reliability, several numerical simulations are performed, including uniaxial pseudoelastic and actuation tests and the finite element analysis of a tube-shaped actuator where the effect of geometric non-linearity is quite evident due to the large rotations involved. Results from numerical simulations of uniaxial actuation tests are validated through a comparison with few data from a conducted experimental test on a NiTiHf high temperature SMA. Various aspects of SMA behavior including TRIP and PT are analyzed and discussed.

The paper is organized as follows. Section “Model Formulation” presents model equations, while Sect. “Numerical Results” shows the results of numerical simulations. Section “Comparison with Experiments for NiTiHf High Temperature SMA” reports the comparison with experiments. Finally, conclusions and summary are given in Sect. “Conclusions”.

Model Formulation

The present section focuses on the formulation of the proposed model. The extension proposed herein starts from the thermodynamically-consistent finite strain model formulation recently presented by Xu et al. [47], and its continuous development considering TRIP strain and load-free two-way SME after cyclic loading [31]. The interested reader may refer to [31, 47] for details about the original model formulation and to Appendix A for modeling preliminaries.

Kinematic Assumption

In the framework of macroscopic modeling and of finite strain continuum mechanics, an additive decomposition of the rate of deformation tensor ${\mathbf{D}}$ into an elastic part ${\mathbf{D}}^{e}$, a transformation part ${\mathbf{D}}^{t r}$, and a TRIP part ${\mathbf{D}}^{t p}$, is considered as follows [31]:

$$\begin{aligned} {\mathbf{D}}={\mathbf{D}}^{e}+{\mathbf{D}}^{t r}+{\mathbf{D}}^{t p} \end{aligned}$$

(1)

Combing Eqs (A.12)–(A.15), the total logarithmic strain tensor ${\mathbf{h}}$ (or true strain) can be additively split into an elastic part ${\mathbf{h}}^{e}$, a transformation part ${\mathbf{h}}^{t r}$, as well as a TRIP part ${\mathbf{h}}^{t p}$:

$$\begin{aligned} {\mathbf{h}}={\mathbf{h}}^{e}+{\mathbf{h}}^{t r}+{\mathbf{h}}^{t p} \end{aligned}$$

(2)

Here, ${\mathbf{h}}^{t r}$ is the transformation logarithmic strain tensor accounting for the recoverable inelastic strain associated with phase transformation, while ${\mathbf{h}}^{t p}$ is the TRIP logarithmic strain tensor describing the irrecoverable transformation-induced plastic strain.

Thermodynamic Potential

Based on the work by Xu et al. [31] and within the classical thermodynamic framework for dissipative materials, the Kirchhoff stress tensor $\varvec{\tau }$ and temperature T are assumed as external state variables, while $\lbrace \xi , {\mathbf{h}}^{t r}, {\mathbf{h}}^{t p}, \varvec{\beta }\rbrace$ is assumed as a set of internal state variables. Particularly, $\xi$ is the martensitic volume fraction ranging between 0 (pure austenitic phase) and 1 (pure martensitic phase) and $\varvec{\beta }$ is the internal stress tensor defining the internal stress field generated as a consequence of the training process. Accordingly, the Gibbs free energy G depends on such variables as follows:

$$\begin{aligned} G= & {} -\dfrac{1}{2 \rho _{0}} \varvec{\tau }: {\mathcal {S}} \varvec{\tau }-\dfrac{1}{\rho _{0}} \varvec{\tau }:\left[ \varvec{\alpha }\left( T-T_{0}\right) +{\mathbf{h}}^{t r}+{\mathbf{h}}^{t p}\right] \\&-\dfrac{1}{\rho _{0}} \displaystyle \int _{0}^{\xi }\left( \varvec{\beta }: \dfrac{\partial {\mathbf{h}}^{t r}}{\partial \tau }\right) d \tau +c\left[ (T- T_{0})\right. \\&\left. -T \ln \left( \dfrac{T}{T_{0}}\right) \right] -s_{0} T+u_{0}+\dfrac{1}{\rho _{0}} f(\xi ) \end{aligned}$$

(3)

where ${\mathcal {S}}$, $\varvec{\alpha }$, c, $s_0$, and $u_0$ denote the effective compliance fourth order tensor, thermal expansion second order tensor, specific heat, specific entropy at the reference state, and specific internal energy at the reference state (defined at temperature $T_0$), respectively, while f is the hardening function. Particularly, ${\mathcal {S}}$, $\varvec{\alpha }$, c, $s_0$, and $u_0$ are evaluated in terms of the martensitic volume fraction $\xi$ by means of rule of mixtures. The specific form adopted for f allows for an accurate and efficient description of PT, as detailed in the next subsection. Finally, it is noted that the Kirchhoff stress tensor $\varvec{\tau }$ is related to the Cauchy or true stress tensor $\varvec{\sigma }$ by means of the relationship $\varvec{\tau }=J\varvec{\sigma }$. Here, J is the determinant of the deformation gradient ${\varvec{F}}$ (see Appendix A for details) and is approximately equal to 1 since phase transformation is assumed to be volume preserving [31, 47].

Hardening Function for PT Loops

An hardening function is included in the Gibbs free energy (3) proposed by Xu et al. [31] to account for the polycrystalline hardening effects.

In order to describe SMA behavior under PT during cyclic thermo-mechanical loading, including reversal point memory and the associated memory wipe-out, the hardening function is here modified according to the approach proposed by Karakalas et al. [15]. Such an approach considers the scaling hypothesis by Ivshin and Pence [46] on the value of the martensitic volume fraction that is used only in the expression of the hardening function and uses interpolation functions for the approximation of the martensitic volume fraction. Therefore, after the material exhibits a transformation reversal, the value of the martensitic volume fraction is stored and a set of linear interpolation functions are defined. The two reversal values are distinguished since each one has different effect on the evolution of the respective hardening expression.

Accordingly, the hardening function is updated introducing a pair of interpolation functions to scale the martensitic volume fraction, as follows:

$$\begin{aligned} \dfrac{\partial f}{\partial \xi }=\left\{ \begin{array}{l} \dfrac{1}{2} a_{1}\left( 1+\left( {\tilde{\xi }}_{\text{ fwd }}\right) ^{n_{1}}-\left( 1-{\tilde{\xi }}_{\text{ fwd }}\right) ^{n_{2}}\right) +a_{3},\ \ {\dot{\xi }}\ge 0\\ \dfrac{1}{2} a_{2}\left( 1+\left( {\tilde{\xi }}_{\text{ rev }}\right) ^{n_{3}}-\left( 1-{\tilde{\xi }}_{\text{ rev }}\right) ^{n_{4}} \right) -a_{3}, \ \ {\dot{\xi }}<0 \end{array}\right. \end{aligned}$$

(4)

where $a_1$, $a_2$, and $a_3$ are material parameters and the four smoothing parameters $n_1$, $n_2$, $n_3$, and $n_4$ are introduced to effectively treat the smooth transition characteristics at the initiation and completion during phase transformation.

The modified value for $\xi$ in the expression of f for the forward transformation is of the following form:

$$\begin{aligned} {\tilde{\xi }}_{f w d}=\left\{ \begin{array}{l} \left[ \xi -\left( \dfrac{\xi -\xi _{FR}}{1-\xi _{RF}}\right) \right] \left( \dfrac{\xi -\xi _{RF}}{\xi _{FR}-\xi _{RF}}\right) , \quad \xi _{RF} \leqslant \xi \leqslant \xi _{FR} \\ \xi , \quad \xi >\xi _{FR} \end{array}\right. \end{aligned}$$

(5)

where $\xi _{FR}$ and $\xi _{RF}$ are the reversal point passing, respectively, from forward to reverse transformation and from reverse to forward. For the purpose of illustration, the reader may refer to points FR and RF in Fig. 1.

Similarly, the modified values for $\xi$ in the expression of f for the reverse transformation is of the following form:

$$\begin{aligned} {\tilde{\xi }}_{r e v}=\left\{ \begin{array}{l} \left( \dfrac{\xi }{\xi _{FR}-\xi _{RF}}\right) \left[ \left( \xi _{FR}-\xi \right) +\left( \dfrac{\xi -\xi _{RF}}{\xi _{FR}}\right) \right] , \quad \xi _{RF} \leqslant \xi \leqslant \xi _{FR} \\ \xi , \quad \xi <\xi _{RF} \end{array}\right. \end{aligned}$$

(6)

Constitutive Equations

Following the classic thermodynamic principles and Coleman-Noll procedure, constitutive equations can be derived from the Gibbs free energy (3). Accordingly, the following relationships between the Kirchhoff stress and logarithmic strain and the entropy and temperature are obtained:

$$\begin{aligned} {\mathbf{h}}= & {} -\rho _{0} \frac{\partial G}{\partial \varvec{\tau }}={\mathcal {S}} \varvec{\tau }+\varvec{\alpha }\left( T-T_{0}\right) +{\mathbf{h}}^{t r}+{\mathbf{h}}^{t p} \end{aligned}$$

(7)

$$\begin{aligned} s= & {} -\rho _{0} \frac{\partial G}{\partial T}=\frac{1}{\rho _{0}} \varvec{\tau }: \varvec{\alpha }+{\text {cln}}\left( \frac{T}{T_{0}}\right) -s_{0} \end{aligned}$$

(8)

A reduced form of dissipation inequality can be derived by substituting the above constitutive equations into the Clausius-Planck inequality [31, 47]:

$$\begin{aligned} -\rho _{0} \frac{\partial G}{\partial {\mathbf{h}}^{t r}}: \mathring{{\mathbf{h}}}^{t r}-\rho _{0} \frac{\partial G}{\partial {\mathbf{h}}^{t p}}: \mathring{{\mathbf{h}}}^{t p}-\rho _{0} \frac{\partial G}{\partial \xi } {\dot{\xi }} \geqslant 0 \end{aligned}$$

(9)

Transformation Strain Evolution Law

The evolution law for transformation strain is described as follows [31]:

$$\begin{aligned} \mathring{{\mathbf{h}}}^{t r}=\varvec{\Lambda } {\dot{\xi }}, \quad \varvec{\Lambda }=\left\{ \begin{array}{l} \varvec{\Lambda }_{f w d},\ \ {\dot{\xi }}\ge 0 \\ \varvec{\Lambda }_{r e v},\ \ {\dot{\xi }}<0 \end{array}\right. \end{aligned}$$

(10)

where $\varvec{\Lambda }_{f w d}$ and $\varvec{\Lambda }_{r e v}$ are, respectively, the forward and reverse transformation direction tensor, defined as:

$$\begin{aligned} \varvec{\Lambda }_{f w d}=\frac{3}{2} H^{c u r} \frac{\varvec{\tau }^{{\text{eff}}^{\prime }}}{\widetilde{\varvec{\tau }}^{{\text{eff}}}} ; \quad \varvec{\Lambda }^{r e v}=\frac{{\mathbf{h}}^{t r-r}}{\xi ^{r}} \end{aligned}$$

(11)

Here, ${\mathbf{h}}^{t r-r}$ and $\xi ^{r}$ represent the value of transformation strain and the martensitic volume fraction at the reversal point, respectively; $\varvec{\tau }^{{\text{eff}}}=\varvec{\tau }+\varvec{\beta }$ is the effective stress tensor that can be used to achieve the two-way SME of trained SMAs under load-free conditions, $\varvec{\tau }^{{\text{eff}}^{\prime }}$ and ${\bar{\tau }}^{{\text{eff}}}$ being its deviatoric part and von Mises equivalent effective stress; $H^{{\text{cur}}}$ is an exponential function introduced to calculate the value of current transformation strain given an effective stress state [48]:

$$\begin{aligned} H^{{\text{cur}}}\left( {\tau }^{{\text{eff}}}\right) =\left\{ \begin{array}{ll} H^{m i n}+\left( H^{\max }-H^{\min }\right) \left( 1-e^{-{\text{k}}_{t}\left( {\bar{\tau }}^{{\text{eff}}}-\tau _{{\text{crit}}}\right) }\right) ,\ \ &{} \overline{{\tau }}^{{\text{eff}}}>\tau _{{\text{crit}}} \\ H^{\min },\ \ &{} \overline{{\tau }}^{{\text{eff}}}\le \tau _{{\text{crit}}} \end{array}\right. \end{aligned}$$

(12)

where $H^{\min }$ corresponds to an observable two-way SME strain for pre-trained SMAs or some SMAs experiencing particular production process such as extrusion and aging under stress, $\tau _{{\text{crit}}}$ denotes a critical stress value below which only $H^{\min }$ is observed, ${\text{k}}_{t}$ is a curve-fitting material parameter, and $H^{\max }$ is the maximum (or saturated) value of transformation strain, defined as:

$$\begin{aligned} H^{\max }=H_{f}^{\max }+\left( H_{i}^{\max }-H_{f}^{\max }\right) e^{-\lambda _{1} \zeta ^{d}} \end{aligned}$$

(13)

Here, $\zeta ^{d}$ is the accumulation of orientated martensitic volume fraction which is defined in the next section, while $H_{i}^{\max }$ and $H_{f}^{\max }$ are the values of $H^{\max }$ before and after the cyclic loading. The definition of $H^{\max }$ takes into account for a degradation phenomenon that sometimes exists for the value of maximum transformation strain as a result of the accumulation of retained martensite [49].

TRIP Strain Evolution Law

The evolution law for the TRIP strain, considering the effect of stress multiaxiality, is as follows [31]:

$$\begin{aligned} \mathring{{\mathbf{h}}}^{t p}=\varvec{\Lambda }^{t p} {\dot{\xi }}, \quad \varvec{\Lambda }^{t p}=\left\{ \begin{array}{ll} \varvec{\Lambda }_{f w d}^{t p}, &{} {\dot{\xi }}\ge 0 \\ \varvec{\Lambda }_{r e v}^{t p}, &{} {\dot{\xi }}<0 \end{array}\right. \end{aligned}$$

(14)

where $\varvec{\Lambda }_{f w d}^{t p}$ and $\varvec{\Lambda }_{r e v}^{t p}$ are the forward and reverse TRIP direction tensor, respectively, defined as:

$$\begin{aligned} \varvec{\Lambda }_{r e v}^{t p}=-\left( \frac{H^{c u r}}{H^{m a x}}\right) ^{2} \frac{{\mathbf{h}}^{t r-r}}{\xi ^{r}} \frac{C_{1}^{p} C_{2}^{p}}{1+C_{2}^{p} \zeta ^{d}} \end{aligned}$$

(15)

$$\begin{aligned} \varvec{\Lambda }_{f w d}^{t p}=\frac{3}{2}\left( \frac{H^{c u r}}{H^{m a x}}\right) ^{2} \frac{\varvec{\tau }^{{\text{eff}}^{\prime }}}{{\overline{\tau }}^{{\text{eff}}}} \frac{C_{1}^{p} C_{2}^{p}}{1+C_{2}^{p} \zeta ^{d}} \end{aligned}$$

(16)

Here, $C_{1}^{p}$ and $C_{2}^{p}$ are material parameters dictating the magnitude and evolving trend for TRIP during cyclic thermo-mechanical loading, while $\zeta ^{d}$ is the accumulation of oriented martensitic volume fraction, defined as follows:

$$\begin{aligned} \zeta ^{d}=\int _{0}^{t}\left| {\dot{\xi }}^{d}(t)\right| d t \end{aligned}$$

(17)

in which the oriented martensitic volume fraction is calculated as:

$$\begin{aligned} \xi ^{d}=\frac{H^{c u r}}{H^{m a x}} \xi \end{aligned}$$

(18)

Internal Stress Evolution Law

The following exponential evolution law is used for the internal stress [31]:

$$\begin{aligned} \varvec{\beta }=\sigma _{b} \frac{H^{c u r}}{H^{m a x}} \frac{\varvec{\tau }^{{\text{eff}}}}{{\overline{\tau }}^{{\text{eff}}}}\left( 1-e^{-\lambda _{1} \zeta ^{d}}\right) \end{aligned}$$

(19)

$\sigma _{b}$ being a model parameter representing the maximum (or saturated) magnitude of the internal stress and $\lambda _{1}$ being a material parameter controlling the evolution trend.

Transformation Function

The following transformation function is adopted [31]:

$$\begin{aligned} \Phi (\varvec{\tau }, T, \xi )=\left\{ \begin{array}{c} \pi -Y,\ \ \ {\dot{\xi }}\ge 0 \\ -\pi -Y,\ \ \ {\dot{\xi }}<0 \end{array}\right. \end{aligned}$$

(20)

where $\pi$ is the general thermodynamic driving force conjugated to $\xi$:

$$\begin{aligned} \begin{aligned} \pi =&(\varvec{\tau }+\varvec{\beta }): \varvec{\Lambda } +\varvec{\tau }: \varvec{\Lambda }^{t p}+\frac{1}{2} \varvec{\tau }: \Delta {\mathcal {S}} \varvec{\tau }+\varvec{\tau }: \Delta \varvec{\alpha }\left( T-T_{0}\right) \\&\left. +\rho \Delta s_{0} T-\rho \Delta c[T -T_{0}-T \ln \left( \frac{T}{T_{0}}\right) \right] -\rho \Delta u_{0}-\dfrac{\partial f}{\partial \xi } \end{aligned} \end{aligned}$$

(21)

and the critical value Y is constructed to be stress-dependent quantity with a reference critical value $Y_0$ and an additional parameter D:

$$\begin{aligned} Y(\varvec{\sigma })=\left\{ \begin{array}{l} Y_{0}+D \varvec{\sigma }: \varvec{\Lambda }_{f w d},\ \ \ {\dot{\xi }}\ge 0 \\ Y_{0}+D \varvec{\sigma }: \varvec{\Lambda }_{r e v},\ \ \ {\dot{\xi }}<0 \end{array}\right. \end{aligned}$$

(22)

It is worth noting that Eq. (21) can be obtained by substituting the evolution laws (10) and (14) into the reduced form of dissipation inequality (9). Accordingly:

$$\begin{aligned} \left( \varvec{\tau }: \varvec{\Lambda }+\varvec{\beta }: \varvec{\Lambda }+\varvec{\tau }: \varvec{\Lambda }^{t p}-\rho _{0} \frac{\partial G}{\partial \xi }\right) {\dot{\xi }}=\pi {\dot{\xi }} \geqslant 0 \end{aligned}$$

(23)

The model is completed by the Kuhn-Tucker conditions, defined as follows:

$$\begin{aligned} \begin{array}{lll} {\dot{\xi }} \geqslant 0 ; &{} \Phi =\pi -Y \leqslant 0 ; &{} \Phi {\dot{\xi }}=0 \\ {\dot{\xi }} \leqslant 0 ; &{} \Phi =-\pi -Y \leqslant 0 ; &{} \Phi {\dot{\xi }}=0 \end{array} \end{aligned}$$

(24)

Advantages of the Proposed Model Formulation

It is worth highlighting that the proposed formulation considering both TRIP and PT description under finite strain has several advantages.

From the modeling point of view, the modification of the hardening function in Eq. (4) is simple and allows for an accurate description of PT loops (as demonstrated by the numerical tests in the next sections). Moreover, it is worth highlighting that the proposed hardening function ensures a thermodynamic consistent model formulation. This means that, for a closed partial transformation cycle, the Gibbs free energy should also return to its initial value after a loading cycle (isothermal, iso-stress, or combined thermomechanical one) to preserve the thermodynamic consistency of the model, as largely discussed, e.g., in ref. [48]. In the absence of TRIP and assuming a small strain framework, our formulation recovers the modeling formulation proposed by Karakalas et al. [12]. Following the analytical definitions reported in Appendix A of this work [12] and by means of numerical integration, it can be verified that the Gibbs free energy returns to its initial value for closed partial transformation cycle in case of both isothermal and isobaric loading cycles. Therefore, the introduction of the proposed hardening function does not affect the thermodynamic consistency of the original model formulation.

From the calibration point of view, no additional model parameters are introduced. Accordingly, model parameters are all physical and can be derived from experimental data by following the procedure described in [31].

From the numerical point of view, the algorithmic treatment of model equations within a finite element framework is efficient and effective for our case. In fact, the elastic predictor/inelastic corrector scheme proposed in [31] is here applied to compute the variables at the current load step based on the variables known from the previous one. Compared to the implementation proposed in [31], the modification of the hardening function implies the introduction of two additional variables, i.e., $\xi _{FR}$ and $\xi _{RF}$ (see Sect. “Hardening Function for PT Loops”). These variables need to be stored, for each integration point of the finite element mesh, at the beginning of the scheme if a transformation reversal is detected. The numerical advantages of the proposed formulation compared to the one proposed in [41], where the martensite fraction values and the direction of the transformation have to be checked before and after each load increment, are thus clear.

Numerical Results

To demonstrate the capabilities of the proposed model to capture SMA behavior under training and PT thermo-mechanical cycles, several boundary value problems considering different loading conditions are investigated. Particularly, we consider various loading conditions typical of pseudoelastic wires for biomedical applications or linear and torsional actuators. For the simulation, the commercial finite element software ABAQUS/Standard is used, after having implemented the algorithm, described in [31] and modified with the proposed hardening function, into a user-defined material subroutine (UMAT).

Uniaxial Pseudoelastic Tests

At first, three pseudoelastic tests on a single eight-node hexahedral element under force control and prescribed homogeneous temperature are simulated. We adopt material parameters reported in Set 1 of Table 1 [31] related to $\hbox {Ni}_{40}\hbox {Ti}_{50}$Cu$_{10}$ (at.%) SMA. Since the coefficient of thermal expansion for NiTi is calculated to obtain a very low value and because its effect is negligible compared to phase transformation, it was assumed to be equal to zero. The material properties selected for this example were used to verify that the unified model was able to predict the material behavior presented by Xu et al. [31] under complete transformation pseudoelastic cycles. It is remarked that the proposed formulation does not require additional parameters to describe minor loops.

The first pseudoelastic test involves 25 tension cycles, where the applied stress varies between 0 and 550 MPa (see Fig. 2a), and the temperature is set equal to 360 K. During cycling, PT, coupled with TRIP, takes place. Figure 2c and e show the stress–strain and strain-loading step parameter curve, respectively, where the results from the original model by Xu et al. [31] and the proposed model are reported and compared. As it can be observed, the loading is reversed before full trasformation is achieved, determining a clear different behavior during reverse transformation for the two models. A large amount of irrecoverable TRIP strain is accumulated from the first cycle to the 25th cycle. Moreover, due to the specific loading history, TRIP strain does not stabilizes and a typical ratcheting behavior is evident.

The second pseudoelastic test involves five tension cycles at a temperature of 360 K. First, a stress of 750 MPa is applied and unloaded back to 350 MPa. Then, the applied stress varies cyclically between 350 and 560 MPa (see Fig. 2b), inducing PT and TRIP. Figure 2d and f compare the stress–strain and strain-loading step parameter curves, respectively, obtained with the two models. The loading history causes full transformation during the first loading up to 750 MPa, followed by PT during subsequent cycles. Models’ responses overlap for the major transformation loop, while differ for the loops caused by PT.

The third pseudoelastic test involves two non-proportional cycles at a temperature of 360 K. The biaxial loading consists in a square path, where the axial components 11 and 33 of the applied stress vary between 0 and 550 MPa (see Fig. 3a). Figure 3b compares model formulations in terms of true strain component 11 versus component 33 curve. The path induces only PT and the difference between the two model formulations is clear when reverse transformation takes place. It is also noted that the considered loading path induces a limited, but different, amount of TRIP strain in the two model predictions.

Uniaxial Actuation Tests

Different actuation tests are simulated considering a single, eight-node hexahedral finite element in order to demonstrate the response of the constitutive model. The tests are simulated by applying a tensile stress of 200 MPa at constant temperature of 438 K (above critical A_f temperature) to ensure that the material is initially at the pure parent phase of austenite, followed by thermal cycling between a maximum and a minimum value under a 200 MPa constant stress. For all these tests, material parameters from Set 2 of Table 1 [31] are adopted, related to $\hbox {Ni}_{49.9}\hbox {Ti}_{50.1}$(at.%) SMA. Since the coefficient of thermal expansion for NiTi is calculated to obtain a very low value ($\sim 10^{-5}$) and because its effect is negligible compared to phase transformation, it is assumed to be equal to zero. As for pseudoelastic tests, the material properties selected for this example were used to verify that the unified model was able to predict the material behavior presented by Xu et al. [31] under complete transformation cycles.

The first actuation test is performed by applying three thermal cycles between 303 and 438 K to ensure full transformation, followed by two thermal cycles between 303 and 373 K to cause PT (see Fig. 4a). The second actuation test is performed by applying two thermal cycles between 303 and 438 K to ensure full transformation, followed by three thermal cycles between 340 and 438 K to cause PT (see Fig. 5a). The third actuation test is performed by applying two thermal cycles between 303 and 438 K to ensure full transformation, followed by three thermal cycles between 340 and 380 K to cause PT (see Fig. 6a). Figures 4b–c, 5b–c, and 6b–c show the strain-temperature and strain-loading step parameter curves for the three tests, respectively, where the results from the original model by Xu et al. [31] and the proposed model are reported. For all the tests models’ predictions are equal for major transformation branches and in agreement with the results published in [31], while differ for minor loops. Particularly, the first, second, and third test show model response for PT during heating, cooling, and both heating-cooling, respectively. In all cases, the proposed model shows a gradual and smooth PT description compared to the original model.

Tube Actuator

To demonstrate the predictive capabilities of the developed model, a more complex actuation test is simulated, i.e. a SMA torque tube to be used as rotational actuator. The torque tube has a inner radius r equal to 3 mm and a thickness t equal to 0.1$\cdot$r mm. To reduce computational cost, only a tube segment of length L = 2/3$\cdot$r is studied, as shown in Fig. 7. The segment is meshed with 640 eight-node hexahedral finite elements (denoted as C3D8 in the Abaqus library). For the simulation, we adopt material parameters from Set 2 of Table 1. The tube segment is fixed at one end, while at the other end a torque load is applied. Figure 7 shows the analyzed geometry and the applied boundary conditions. The test is simulated by applying, first, a torque load of 3 N m at constant temperature of 410 K to ensure that the material is initially at the pure parent phase of austenite; then, 50 thermal cycles between 300 and 410 K are applied to cause full transformation, followed by five thermal cycles between 340 and 380 K at constant applied torque load to ensure PT.

Figure 8a and c show, respectively, the shear strain-temperature and twist angle-temperature curves obtained with the proposed model. The first 50 thermal cycles are applied to train the material and induce full transformation and clearly shown that the actuator undergoes large strains and rotations. Accordingly, models’ responses are completely matching for these major loops. The latter five cycles induce PT in the tube actuator. The comparison between the proposed and original model for the PT cycles in terms of shear strain and twist angle is shown in Fig. 8b and d. During PT, TRIP strain slightly increases. The comparison between the two models again shows a clear difference between the predicted minor loops. The stabilization of the TRIP strain leads to PT loops demonstrating the reversal memory property of SMAs.

Comparison with Experiments for NiTiHf High Temperature SMA

In order to validate the proposed modelling approach, an experimental test involving partial cooling was conducted on dog-bone specimens of $\hbox {Ni}_{50.3}\hbox {Ti}_{29.7}\hbox {Hf}_{20}$ High Temperature SMA (HTSMA). The particular SMA is intended for actuators used in aerospace applications because they present high stability under cyclic thermal activation. However, their response under PT operation has not been investigated in detail.

The experimental apparatus consists of a MTS Insight testing machine, which is equipped with a MTS loadcell with a 30 kN load capacity. After the specimen was aligned with the grips and positioned, a high temperature Epsilon extensometer of a 1-inch gauge length was attached on the specimen. Moreover, two type K thermocouples were also attached on the specimen to measure its temperature during the experiment. The specimen along with the grips was enclosed to a properly insulated Thermcraft thermal chamber. A controller was responsible for the determination of the heating and cooling rate. Heating of the specimen was performed by heating the air inside the chamber, while cooling was performed by allowing cold liquid nitrogen vapor to enter the chamber. An electric valve opened during the cooling phase and the flow of liquid nitrogen was manually controlled through a valve regulator. Experimental measurements from the thermocouple and the extensometer were transferred into a Windows 7 workstation where they were stored.

The experimental test consisted in applying a tensile stress of 395 MPa at constant temperature of 493 K (to ensure fully austenite state), followed by thermal cycling at constant applied mechanical load. Particularly, one major thermal cycle between 493 and 373 K was performed to induce the full transformation from austenite to martensite and back, followed by seven minor cycles between 493 and 427 K to induce PT during cooling phase.

To simulate this test, we adopt material parameters from Set 3 of Table 1, calibrated on experimental data related to the major hysteresis cycle. Experimental data related to the minor loops are used to validate the model, since the behavior under complete transformation cycles has been already verified. As it can be observed in Fig. 9, both experiments and numerical simulations highlight a small amount of inelastic strain during partial cycling, that accumulates as the number of cycles increase. Yet, when the reverse transformation is fully completed, this strain seems to not affect the strain level exhibited at the pure phase in the experimental data. The proposed model formulation (see Fig. 9a) shows good agreement with experiments compared to the original model formulation (see Fig. 9b).

Conclusions

This paper presented a unified modeling framework for the simultaneous description of TRIP as well as PT characteristic in SMAs subjected to cyclic thermo-mechanical loading. The capabilities of the proposed model extension have been demonstrated through numerical simulations of several boundary value problems, representative of various loading conditions for linear and torsional actuators and pseudoelastic biomedical devices and related to different SMA systems, including $\hbox {Ni}_{40}\hbox {Ti}_{50}\hbox {Cu}_{10}$ and $\hbox {Ni}_{49.9}\hbox {Ti}_{50.1}$(at.%) SMAs and $\hbox {Ni}_{50.3}\hbox {Ti}_{29.7}\hbox {Hf}_{20}$ High Temperature SMAs. The prediction capabilities of the unified approach are first verified by simulating full transformation cycles for the SMA material considered in the original work of Xu et al. [31]. Following that, the prediction of the baseline line model for partial phase transformation cycles are compared with ones predicted by adopting the modified hardening function proposed by Karakalas et al. [15]. To demonstrate the difference between the two different approaches three minor loop cases were considered: (i) partial transformation reversal is initiated on the major heating branch and evolves till fully martensitic state is reached, (ii) partial transformation is initiated on the major cooling branch and heating continues till the material is at the fully austenitic state and (iii) starting from the major cooling branch partial transformation loops are performed without reaching either purely austenite or martensite phase. Particularly, the comparison with the original model published by Xu et al. [31] has demonstrated the successful capability of the model in accounting both for PT reversal point memory and the associated memory wipe-out in the case of PTs coupled with the generation and saturation of TRIP strains, without the need of additional model parameters. Moreover, the comparison with experimental data under uniaxial conditions demonstrates that the proposed modeling approach is promising for the description of these phenomena. It is worth highlighting that a comprehensive experimental and numerical investigation of the coupling between the two described features under both proportional and non-proportional loading is still missing in the current literature. Accordingly, future work will focus on the validation of the proposed model on an ad-hoc experimental campaign.

Appendix A: Summary of Preliminaries for Model Formulation

Considering a deformable body B, the deformation process of a material point P from reference (undeformed) configuration to current (deformed) configuration can be described by using the deformation gradient second order tensor:

$$\begin{aligned} {\mathbf{F}}({\mathbf{x}}, t)=\dfrac{\partial {\mathbf{x}}}{\partial {\mathbf{X}}}=\mathbf{U R}=\mathbf{V R} \end{aligned}$$

(A.1)

Here, ${\mathbf{X}}$ and ${\mathbf{x}}$ denote the position vector of P, respectively, in the reference configuration at time $t_0$ and in the current configuration at time t, ${\mathbf{U}}$ and ${\mathbf{V}}$ are the right and left stretch tensors, respectively, and ${\mathbf{R}}$ is a proper orthogonal rotation tensor. The right and left Cauchy-Green deformation tensors are then, respectively, defined as:

$$\begin{aligned} {\mathbf{C}}={\mathbf{F}}^{{\text{T}}} {\mathbf{F}}={\mathbf{U}}^{2}, \ \ \ {\mathbf{b}}={\mathbf{F}} {\mathbf{F}}^{{\mathbf{T}}}={\mathbf{V}}^{2} \end{aligned}$$

(A.2)

The velocity gradient ${\mathbf{L}}$ can be additively decomposed into a symmetric part, i.e., the rate of deformation tensor ${\mathbf{D}}$, and an anti-symmetric part, i.e., the spin tensor ${\mathbf{W}}$, as follows:

$$\begin{aligned} {\mathbf{L}}=\frac{\partial {\mathbf{v}}}{\partial {\mathbf{x}}}=\dot{{\mathbf{F}}} {\mathbf{F}}^{-1}={\mathbf{D}}+{\mathbf{W}} \end{aligned}$$

(A.3)

where ${\mathbf{v}}=d {\mathbf{x}}/d t=\dot{{\mathbf{x}}}$ is the velocity field of P and

$$\begin{aligned} {\mathbf{W}}=\frac{1}{2}\left( {\mathbf{L}}-{\mathbf{L}}^{{\mathbf{T}}}\right) , \ \ \ {\mathbf{D}}=\frac{1}{2}\left( {\mathbf{L}}+{\mathbf{L}}^{{\text{T}}}\right) \end{aligned}$$

(A.4)

The material and spatial Hencky (logarithmic) strain tensors ${\mathbf{H}}$ and ${\mathbf{h}}$ are, respectively, defined as:

$$\begin{aligned} {\mathbf{H}}=\frac{1}{2} \ln ({\mathbf{C}})=\ln ({\mathbf{U}}) \end{aligned}$$

(A.5)

and

$$\begin{aligned} {\mathbf{h}}=\frac{1}{2} \ln ({\mathbf{B}})=\ln ({\mathbf{V}}) \end{aligned}$$

(A.6)

while the engineering or nominal strain tensor $\varvec{\varepsilon }$ as:

$$\begin{aligned} \varvec{\varepsilon }=\frac{1}{2} \left( Grad{\mathbf{U}} +(Grad{\mathbf{U}})^T\right) \end{aligned}$$

(A.7)

where ${\mathbf{U}}={\mathbf{x}}-{\mathbf{X}}$ is the displacement vector and Grad is the gradient.

Based on the works [50,51,52,53], it is proven that the corotational rate of the logarithmic strain ${\mathbf{h}}$ associated with the so-called logarithmic spin $\varvec{\Omega }^{l o g}$ is identical to the rate of deformation tensor ${\mathbf{D}}$:

$$\begin{aligned} \mathring{{\mathbf{h}}}^{l o g}=\dot{{\mathbf{h}}}+{\mathbf{h}} \varvec{\Omega }^{l o g}-\varvec{\Omega }^{l o g} {\mathbf{h}}={\mathbf{D}} \end{aligned}$$

(A.8)

where:

$$\begin{aligned} \varvec{\Omega }^{l o g}={\mathbf{W}}+\sum _{i \ne j}^{n}\left( \frac{1+\left( \lambda _{i} / \lambda _{j}\right) }{1-\left( \lambda _{i} / \lambda _{j}\right) }+\frac{2}{\ln \left( \lambda _{i} / \lambda _{j}\right) }\right) {\mathbf{b}}_{i} {\mathbf{D}} {\mathbf{b}}_{j} \end{aligned}$$

(A.9)

$\lambda _{i}, \lambda _{j} (i, j = 1, 2, 3)$ being the eigenvalues of left Cauchy-Green tensor ${\mathbf{B}}$, and ${\mathbf{b}}_{i}, {\mathbf{b}}_{j}$ being the corresponding subordinate eigenprojections. Eq. (A.8) can be integrated by using the corotational integration scheme [54] into the following equation:

$$\begin{aligned} {\mathbf{h}}=\int _{\text{ corot. } } {\mathbf{D}} {\text{d}} t=\left( {\mathbf{R}}^{l o g}\right) ^{T}\left( \int _{0}^{t} {\mathbf{R}}^{l o g} {\mathbf{D}}\left( {\mathbf{R}}^{l o g}\right) ^{T} {\text{d}} t^{\prime }\right) {\mathbf{R}}^{l o g} \end{aligned}$$

(A.10)

where ${\mathbf{R}}^{l o g}$ is a second-order rotation tensor such that $\varvec{\Omega }^{l o g}=\dot{{\mathbf{R}}}^{l o g}\left( {\mathbf{R}}^{l o g}\right) ^{T}$.

Based on Eq. (A.8) and (1), the following equation can be recovered:

$$\begin{aligned} \mathring{{\mathbf{h}}}^{l o g}=\mathring{{\mathbf{h}}}^{e-l o g}+\mathring{{\mathbf{h}}}^{tr-l o g}+\mathring{{\mathbf{h}}}^{t p-l o g} \end{aligned}$$

(A.11)

where:

$$\begin{aligned} \mathring{{\mathbf{h}}}^{e-l o g}={\mathbf{D}}^{e}, \ \ \ \mathring{{\mathbf{h}}}^{t p-l o g}={\mathbf{D}}^{t p}, \ \ \ \mathring{{\mathbf{h}}}^{t r-log} ={\mathbf{D}}^{t r} \end{aligned}$$

(A.12)

Applying corotational integration (A.10) on Eq. (A.12) gives:

$$\begin{aligned} {\mathbf{h}}^{e}=\int _{\text{ corot. } } {\mathbf{D}}^{e} \quad {\text{d}} t=\left( {\mathbf{R}}^{l o g}\right) ^{T}\left( \int _{0}^{\tau } {\mathbf{R}}^{l o g} {\mathbf{D}}^{e}\left( {\mathbf{R}}^{l o g}\right) ^{T} {\text{d}} \tau \right) {\mathbf{R}}^{l o g} \end{aligned}$$

(A.13)

$$\begin{aligned} {\mathbf{h}}^{t r}=\int _{\text{ corot. } } {\mathbf{D}}^{t r} {\text{d}} t=\left( {\mathbf{R}}^{l o g}\right) ^{T}\left( \int _{0}^{T} {\mathbf{R}}^{l o g} {\mathbf{D}}^{t r}\left( {\mathbf{R}}^{l o g}\right) ^{T} {\text{d}} \tau \right) {\mathbf{R}}^{l o g} \end{aligned}$$

(A.14)

$$\begin{aligned} {\mathbf{h}}^{t p}=\int _{\text{ corot. } } {\mathbf{D}}^{t p} {\text{d}} t=\left( {\mathbf{R}}^{l o g}\right) ^{T}\left( \int _{0}^{\tau } {\mathbf{R}}^{l o g} {\mathbf{D}}^{t p}\left( {\mathbf{R}}^{l o g}\right) ^{T} {\text{d}} \tau \right) {\mathbf{R}}^{l o g} \end{aligned}$$

(A.15)