Abstract
Superelastic Nitinol micromechanics are studied well into plastic deformation regimes using neutron diffraction. Insights are made into the nature of initial transformation, bulk transformation, plastic deformation, and unloading. Schmid factor predictions based on habit plane variants are found to best describe the very first grains that transform, prior to the transformation plateaus. However, the bulk transformation behavior that gives rise to transformation plateaus violates single crystal Schmid factor analyses, indicating that in bulk polycrystals, it is the effect of grain neighborhoods, not the orientations of individual grains, that drives transformation behaviors. Beyond the plateaus, a sudden shift in micromechanical deformation mechanisms is observed at ~8.50 %/4.75 % tension/compression engineering strain. This mechanism results in reverse-phase transformation in both cases, indicating a strong relaxation in internal stresses of the samples. It is inferred that this mechanism is most likely initial bulk plastic flow, and postulated that it is the reason for a transition from fatigue life enhancement to detriment when pre-straining superelastic Nitinol. The data presented in this work provide critical datasets for development and verification of both phenomenological internal variable-driven and micromechanical theories of transformation-plasticity coupling in shape memory alloys.
Similar content being viewed by others
Introduction
The micromechanics of shape memory alloys (SMAs), especially near equiatomic compositions of nickel–titanium (“Nitinol”), have fascinated and perplexed researchers and engineers for many decades. One of the earliest crowning achievements in the field was the Phenomenological Theory of Martensite of Wechsler, Lieberman, and Read (“WLR Theory”) [1], which provided mathematical means to solve for geometrically possible austenite–martensite interfaces at the microscopic scale, and also related them to shape recovery strains at the macroscopic scale. It is still the basis for most modern day micromechanical models and theories. The current era of micromechanical modeling is largely rooted in a framework that uses the “habit plane variants (HPVs)” of WLR theory, or martensite twin pairs that form geometrically compatible interfaces with an austenite lattice, as the geometric building blocks for microstructure. It was developed in the early 1990s by Patoor et al. [2, 3], with incarnations that include simplified treatments of interaction energies [4] or additions of crystal plasticity [5, 6] implemented within finite element and self-consistent numerical frameworks. More recently, a second approach has emerged that simply uses variants of martensite or “correspondence variants (CVs),” and implementation approaches have been extended to finite differences and phase-field finite elements [7, 8]. Micromechanical models have been used to explore many phenomena, including topics, we will discuss in this work such as martensite reorientation, tension–compression asymmetry, and transformation-plasticity interactions. However, micro-scale assumptions and predictions of these frameworks were largely unverified, mostly because the creation of experiments to quantify the physical mechanisms used in the models lagged in development.
Today, however, this is no longer the case. The advent of non-destructive in situ experiments is providing data that elucidate physics at the length scales of micromechanical theories. In situ microscopy techniques, together with digital image correlation, provide a means for visually studying the bridges between microscopic scales and macroscopic responses and are unequivocally well suited for observing films, strips, sheets, and other geometries where surface effects dominate the structural response of components [9–12]. In situ neutron diffraction, on the other hand, provides a means to simultaneously probe the conglomerate responses of millions to billions of crystals in bulk samples of several millimeters to centimeters in size, concurrent with macroscopic behaviors [13–18]. There is a gap between these techniques in an ability to study the responses of bulk components whose sample length scales of interest are of several hundred microns to several millimeters. Here, high-energy X-ray powder diffraction provides a solution to study SMA micromechanics with micron resolution in a manner parallel to neutron diffraction, but with finer focus [19–23], while new high-energy diffraction microscopy (HEDM) techniques promise to create new three-dimensional means that allow for simultaneous observations of the individual responses of thousands of individual crystals at once [24, 25].
In this work, we present new micromechanical investigations into transformation-plasticity interactions of SMAs using in situ neutron diffraction. The new work we present is most directly related to recent works coupling neutron diffraction and modeling to study transformation asymmetry of superelastic Nitinol wires [26], austenite plasticity in thermal martensitic Ni49.9Ti50.1 [13], as well as the accommodation mechanisms responsible for the four regimes of monotonic tension and compression stress–strain behaviors of thermal martensitic Ni49.9Ti50.1 [17, 18]. The general descriptions of these four regimes are
-
Regime i effectively elastic, traditionally modeled using linear elasticity
-
Regime ii accommodation twinning and/or phase transformation, traditionally modeled using thermodynamics of martensitic phase transformations and reorientation mechanics
-
Regime iii a return to effectively elastic behavior, traditionally modeled using linear elasticity
-
Regime iv plastic deformation, traditionally modeled using conventional plasticity theories.
We now present a parallel study of monotonic deformation through these four regimes, plus unloading events, of state of the art superelastic Nitinol rods used primarily for biomedical implants. In doing so, we aim to provide critical understanding that may be used to verify, validate, and improve both research and engineering models of SMAs. Furthermore, building upon a previous in situ study of shape-setting Nitinol [14], the current work provides some fundamental insight into another important processing issue: the effect of pre-strain and plasticity on Nitinol microstructures, and why pre-straining a device into Regime iii or iv may lead to improvements in fatigue lives of components [27, 28]. We further explore this issue in a parallel work investigating the effects of different amounts of tension pre-strain on Nitinol microstructures and mechanics [29].
Methods
Materials
Commercial-scale low-oxygen grade (extra low inclusion, or “ELI”) Ni50.8Ti49.2 (in atomic percent) was manufactured by multi-cycle vacuum-arc remelt processing at ATI Metals, Wah Chang (Albany, Oregon, USA). The chemical composition and inclusion distribution was characterized in the wrought material at a 25.4 mm diameter bar size in accordance with ASTM F2063 [30]. ELI Nitinol has a significantly lower oxygen (< 60 mass ppm) and carbon (< 20 mass ppm) content than the ASTM specification that results in maximum inclusion length of 17 µm and area fraction of non-metallic inclusions of 0.28 %. The fully annealed Af of the bars was −11 °C.
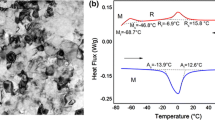
The ELI Nitinol bars were then cold drawn with successive 35 % cross-sectional area reductions and subsequent stress-relief heat treatments at 510 °C for 5 min prior to machining the tension–compression specimens from 10 mm diameter rods. Cylindrical dogbone specimens with 8 mm diameter threaded grip sections and gage sections of 5.10 mm diameter × 15.25 mm long were machined on a lathe and used for both the tension and compression experiments. A 20.3 mm radius was used to taper the grip sections to the gages. The compression/tension specimens were then stress relieved at 520 °C/525 °C for 5 min, respectively, to achieve an Af of approximately 17 °C, evident in the digital scanning calorimetry (DSC) curves shown in Fig. 1. The DSC thermograms also reveal the presence of peaks associated with the distinct forward transformations of austenite to R-Phase, and then to martensite upon cooling, whereas the reverse transformations from martensite to R-Phase and R-Phase to austenite occur (nearly) concurrently upon heating. The target Af temperature is approximately 10 °C below the in situ deformation and diffraction temperature of ~30 °C, allowing for study of stress-induced martensite.
Diffraction Instrument
The SMARTS instrument at the Manuel Lujan Jr. Neutron Scattering Center of Los Alamos National Laboratories has been reviewed elsewhere [31]. We used the same SMARTS configuration as in previous works [15–18]. In review, we used a horizontal load frame oriented at 45° relative to the incident beam of neutrons. Boron-nitride slits masked the beam to a 5 × 5 mm2 cross-sectional area. The detectors on either side of the specimen recorded data with diffraction vectors within 0° to 11° alignments of parallel (Q||, −90° bank) and perpendicular (Q⊥, +90° bank) to the applied load. Diffraction spectra (effective range of 0.6 to 3.5 Å) were recorded simultaneously in each detector. In the ensuing work, we document uniaxial deformation in the direction of the applied load, thus we report data from the Q||, −90° bank. These spectra contain the reflections indicated with markers on inverse pole figures (IPFs) in Fig. 2.
Inverse pole figures showing the experimental coverage for (a) B2 (austenite) and (b) B19′ (martensite) measurements. Each dot indicates a peak contained within the diffraction spectra. All measured reflections are labeled for B2 (considering material symmetry), while low-index reflections are labeled for B19′
Loadings and Measurements
Two specimens were mechanically loaded at RT (~30 °C) in the beam’s path. Macroscopic strain was measured using a mechanical extensometer that spanned the irradiated region. A single high-resolution CCD camera was used to monitor the specimens for bending and bulging during the compression experiment, and they were not observed on the samples used to generate the data reported in this work. Diffraction patterns were recorded for roughly 40 min at the following points for tension: 0.00 to 1.00 % engineering strain in 0.20 % intervals, a point was taken at 1.25 %, then data were collected in 0.50 % intervals from 1.50 to 11.00 %, and during unload, data were collected in −0.20 % intervals between 10.90 and 10.50 %, then −0.50 % intervals to 5.50 %. For compression, we attempted an analogous, opposite program only with a maximum intended strain of 8.00 %, but experienced slight extensometer slippage near peak load due to surface roughness changes caused by martensitic transformation. We corrected the data using the local crosshead displacement vs. load relations for this material (i.e., the relations just before and after each crosshead slip event). The actual program was the same, but opposite sign up to −4.00 %, then data were recorded at −4.25, −4.75, −5.25, −6.04, −6.54, −7.04, −7.22, −7.78 −8.28 %, and then in +0.50 % increments to −0.28 % engineering strain upon unload. The mechanical loading and unloading engineering strain rate was 5 × 10−4 s−1 in all cases, except when the extensometer slipped in compression. Mechanical loading paths were carried out in engineering strain control unless otherwise noted.
Neutron Data Analysis
Neutron data were binned and fits to 0.6 to 3.6 Å diffraction patterns were refined using the SMARTSware [32] routine SMARTSRunRep, which performs sequences of Rietveld refinements [33], which are used to calculate IPFs, by calling sequences of the GSAS programs EXPEDT, RAWPLOT, POWPREF, and GENLES [32, 34, 35]. We used the crystal structures reported by Kudoh et al. [36] for initializing each the monoclinic and cubic phases in the refinements. Atomic positions and thermal motions were held fixed during the refinements. Austenite diffraction patterns were refined using space group Pm\( \bar{3} \)m and a tenth order spherical harmonics model for texture; monoclinic diffraction patterns were refined using space group P11\( 2_{1/m} \), and an eighth order spherical harmonics texture model. Lower-order texture models were used in cases where phase fractions of austenite or martensite were less than 5 %. Our threshold for being able to meaningfully refine the martensite phase was around 2.5 % weight fraction. For data points with less than 2.5 % martensite, we use a 0 % mean weight fraction with an errorbar of 3 %. Lattice strains of B2 reflections were calculated using the SMARTSware routine SMARTSSPF to fit individual reflections using the GSAS time of flight profile function 3 (TOF-3).
In this work, we report some IPFs plotted in volume fraction, in addition to other using the traditional multiples of random distribution (MRD) measure. This additional measure allows for understanding of the magnitude of material that is transforming, in addition to phase-specific orientation comparisons. To make this calculation, we adopt our previous strategy for extracting volume fractions from IPFs [15–17], only we now also weight the IPFs of each phase by the total phase fraction. Thus, the volume fraction \( f \) is calculated for each data point indicated in Fig. 2 from its refined, relative intensity measured in MRD according to:
where \( \lambda \) is the martensite phase fraction determined at each data point from the Rietveld refinement.
Results
The tension and compression “true” stress–strain responses are shown in Fig. 3a, with the strain response denoted \( \varepsilon^{ \log } \) since it is calculated by taking the natural logarithm of one plus the engineering strain. The monotonic deformations are characterized by four regimes, labeled in figure, as briefly reviewed in the Introduction and discussed in more detail in a previous work [18]. The material transitions from Regime i to ii at approximately 1.0 %/−0.8 % strain, Regime ii to iii at 6.0 %/−4.2 %, and iii to iv at 8.5 %/−6.0 % in tension/compression, respectively. Unloading responses are also shown. The tension sample did not exhibit an unloading plateau, but rather a residual strain of about 7.0 %, while the compression sample did show an unloading plateau, but also a residual strain of about −1.0 %. The widths of inelastic deformation plateaus are indicated, as well as rehardening and initial unloading effective moduli. Figure 3b documents the martensite phase fraction evolution as a function of macroscopic strain.
Figures 4, 5, 6, and 7 are additional data from Regime i; Figure 4 shows lattice strain evolutions of several B2 reflections, Fig. 5 selected segments of the diffraction spectra at each measurement point, and Fig. 7 IPFs in the load direction of volume fractions and volume fraction differences of orientation distributions in this regime. The initial IPFs (Fig. 7a, e) are consistent with {111}A fiber symmetry texture with a stronger intensity of {111}A grains oriented along the fiber than in transverse directions (grains with their {110}A axes aligned with the load direction), which we have confirmed for ELI Nitinol rods in separate measurements made at the advanced photon source (APS). The compression specimen had stronger initial texture than the tension specimen. The heat treatments used to process this material resulted in a small volume fraction of Ni4Ti3 precipitates, indicated by labeled reflections in Fig. 4. Figure 6 depicts (a) the stress–strain response and (b) selected diffraction spectra of a different Nitinol specimen that will be used to contrast the Regime i behavior of the material we studied versus the possible Regime i behaviors of superelastic Nitinol.
Volume fraction distributions of austenite (B2) orientations during loading in Regime i. All differences are taken with respect to the first IPF in each column. [The data in this figure are from previously unpublished measurements made by D.J. Bronfenbrenner, A.R. Pelton, and A. Mehta at the Stanford Linear Accelerator (SLAC)]
Figures 8, 9, 10, and 11 show the evolution in volume fractions of B2 and B19′ orientation distributions aligned with the sample load axes through Regimes ii-iv, as well as unload. Load-direction IPFs and differences of IPFs at initial loading, transitions between the monotonic regimes, and also initial and final unloading are shown in MRD in Fig. 12. Finally, Schmid factors for transformation and slip of B2 orientations are given for each tension and compression, and each transformation to a single martensite variant and HPVs in Fig. 13. We provide further discussion of observations and interpretations of the data in Figs. 8, 9, 10, 11,12, and 13 in the next section.
Probability distributions of austenite (B2) and martensite (B19′) orientations during critical points in the load and unload paths. Differences are calculated with respect to the previous IPF, except for: (c, q) B2 at 1.50 %/−0.80 % strain tension/compression, which are shown with respect to (a, o) initial, and (h, n, v, bb) 7.00 %/−0.28 % strain, which are shown with respect to peak loads (f, l, t, z) respectively. Note that different scales are used for B19′ than for B2 due to much stronger martensite textures
Inverse pole figures for B2 orientations are shown for (a, d) Schmid factors required to transform to the most preferred habit plane variant (HPV) and (b, e) the most preferred martensite correspondence variant for each (compression, tension). c The Schmid factors for uniaxial slip and (f) stiffness (E hkl) according to the elastic constants of Mercier et al. [51] are also represented
Discussion
Regime i: Elastic Loading and Initial Transformation
It is apparent that on average, the bulk material behaves linear-elastically between approximately −400 and 250 MPa applied uniaxial stress; as the macroscopic stress–strain (Fig. 3a) and microscopic stress–strain (Fig. 4a–e) responses are linear, as is the strain–strain (Fig. 4f) response during this same deformation. The one exception is that grains contributing to the (100)A reflection show a stiffening from ~50 GPa to 80 GPa in their effective modulus in compression between −150 and −400 MPa (Fig. 4a). Considering that their initial population in the sample is nearly zero (Figs. 7a, 12o), it is not surprising that this non-linear behavior does not have macroscopic manifestations or a dramatic effect on other grain populations. The most likely mechanism causing this non-linear excursion is that the few {100}A grains that are present are starting to transform. In this event, because they are accommodating the macroscopic deformation with transformation strain instead of elastic strain, the rate of accumulation of \( \varepsilon_{100} \) slows with respect to the macroscopic load. This event results in an apparent increase in \( E_{100} \) according to Hooke’s Law using an engineering definition of stress and strain together with the micromechanical assumption that the load is, on average, initially experience equally by all grains:
After a previous derivation given in [16], these same micromechanical assumptions (in engineering stress and strain) would also require
Using the moduli indicated in Figs. 3a and 4a, this means the ratio \( \frac{{\varepsilon_{\text{macro}} }}{{\varepsilon_{\text{hkl}} }} \) should increase from 0.71 to 1.14. In measuring the response of the (100)A reflection in Fig. 4f, the ratio increases from 0.85 to 1.09 in this regime. Note that deviations in slopes of responses in Fig. 4f are much more subtle, visually, than those in Fig. 4a–e. So indeed, this mechanism is supported, realizing that some of the quantitative difference is due to limitations of applying the linear-elastic micromechanical assumption of load distribution to the non-linear behavior. The few {100}A grains are likely shedding some load to their neighbors as they transform, but their neighbors continue to elastically load. This finding is analogous to observations previously made by Barney et al. of Ni50.8Ti49.2 with synchrotron X-ray microdiffraction under tensile loading conditions [37]. Aside from this one exception, all other grains predominantly exhibit behaviors consistent with linear elasticity, including the expected trend in \( E_{\text{hkl}} \) given in Fig. 13f. The small quantitative differences between this figure and the values indicated in Fig. 4a are most likely due to our material having different transformation temperatures and therefore elastic constants than that studied by Mercier et al., with an additional possible contribution coming from the grains in the real material not exactly sharing the load equally on average.
While our results indicate that linear elasticity is an appropriate model for the mechanics in this regime, we do see that micromechanics of the material do not completely follow the bulk behavior as austenite grains do transform. This behavior is indicated by only decreases, with no accompanying increases in volume fraction distributions in the difference IPFs shown in Fig. 7b–d, f–g. In comparing the first orientations to transform in the bulk material with expectations from Schmid factor analyses (Fig. 13a, b, d, e), Habit Plane Variant transformation seems to describe the initial transformation events better than Correspondence Variant transformation. For example, in tension, the difference plots include grains around {111}A, but not {111}A itself (Figs. 7b, 12b, again refer to Fig. 2 for orientation labels). In compression {110}A to {210}A orientations decrease in population while {211}A populations do not change (Figs. 7f, 12p), which is more consistent with Fig. 13a than Fig. 13b. However, in compression, {111}A grains are also observed to initially decrease in population in compression, which is not expected from either transformation Schmid factor prediction. This result speaks to the fact that in a polycrystal, it is not just grain orientations that drive transformation, but rather the grain neighborhoods also have influences that may dominate preferred orientation predictions. This has been shown in other recent works through both experiments [38] and modeling [8, 39].
Obvious asymmetry exists in the “transformation stresses” that define the transition from Regime i to ii, the source of which has been well established in previous theory and experiments on Nitinol [40–43] and is further discussed in the next section. In addition, there is another interesting and familiar macroscopic anomaly that distinguishes tension from compression in Regime i. Prior to the pronounced plateaus, the material remains predominantly linear-elastic in compression, in spite of some initial transformation of grains, while in tension, a very pronounced, gradual softening leading into the plateau is observed to start around 250 MPa applied stress (Fig. 3a). The softening we observe is somewhat different in nature than the more sudden “shift” in the initial loading response documented in Fig. 6a and previously studied by Sittner et al. [44]. From the diffraction spectra shown in Fig. 6b and the work of Sittner et al. on highly textured Nitinol wires, it is clear that the pre-plateau inelastic deformation is due to R-phase transformation. However, in the presently studied ELI Nitinol samples, the answer is not so clear. In the initial diffraction patterns, we would expect to see (300)R and (112)R reflections split out from the left and right of the (110)A reflection, respectively, and eventually consume it. They have the highest texture-free relative intensities of the R-phase structure by 5 times, with the next most-intense R-phase reflection being \( (\bar{2}\bar{2}2)_{\text{R}} \) with a stress-free d-spacing of approximately 1.52 Å. However, in our initial diffraction patterns, we see no signature of the \( (\bar{2}\bar{2}2)_{\text{R}} \) (Fig. 5a), but the (110)A does noticeably broaden and it is possible there is a (300)R peak being masked or overlapping in this deformation region due to both the instrument resolution and peak broadening caused by small R-phase domain size, though it is not obvious in the data (Fig. 5b). This is the most reasonable conclusion considering the pronounced 2-step forward transformation in the DSC data (Fig. 1), though it is also possible that under stress, the material is bypassing the R-phase and going straight to monoclinic. Considering the \( \varepsilon_{\text{hkl}} \) behaviors in Fig. 4, regardless of 1-step or 2-step forward transformation, what is evident is that {210}A then {110}A grains transform and shed their loads to their neighbors, which results in the effective modulus softening of \( \varepsilon_{111} \) and \( \varepsilon_{211} \). This follows the rationale given above for {100}A grains in compression. The reason that these early transformation events lead to bulk softening in tension is that these orientations are significant in volume fraction (Fig. 7a).
Regime ii: The Transformation Plateaus
The difference in the magnitude of the plateau strains in tension (4.89 %) versus compression (3.28 %) as seen in Fig. 3a can be qualitatively rationalized on the basis of the crystallographic theory of martensite, as summarized by Bhattacharya [45]. In tension, the most efficient HPV for a {111}A orientation consists of CVs 8 and 5 in the Bhattacharya notation. It is capable of producing ~5.7 % strain in tension. Additional strain can be produced by subsequent reorientation of martensite. Since [111]A is a highly symmetric direction, multiple HPVs can be produced in such a grain to accommodate constraints from the neighboring grains. These factors suggest that a material with {111}A fiber texture realize ~6 % transformation strain [41].
In compression, on the other hand, the most efficient HPV for {111}A can produce a strain of −4.0 %. This means that transformation in compression has a lower Schmid factor compared to that in tension. This lower Schmid factor has three consequences. First the stress for forward transformation is higher versus tension—not coincidently 600 versus 400 MPa—the same as the ratio of the maximum strains (which are proportional to the Schmid factors). Second, potentially less efficient HPVs need to be activated to meet the inter-granular constraints and produce a macro strain of ~4.0 %. Third, plasticity can more effectively compete with transformation in compression, since the Schmid factor for slip (Fig. 13c) of {111}A is the same irrespective of tension or compression. This rationale explains the higher hardening in Regime ii compression than tension in Fig. 3a, and is consistent with the previous finding of Stebner et al. in studying thermal martensite, that higher activity of plasticity in Regime ii leads to higher asymmetry in plateau hardening rates [18].
While the first grains to transform (as detected by the bulk neutron diffraction technique) were evident in the volume fraction IPFs of Regime i, the dominant behaviors of initiation of the transformation plateaus are most evident in Fig. 4f. Here we see that in tension, the (210)A and (110)A reflection populations participate in bulk transformation first, while (100)A then finally (111)A are the last reflection populations to give way to bulk transformation. This observation is indicated from the shift from elastic-like relations according to Eq. 3 to inelastic deformation, indicated by non-linear, stagnant-like \( \varepsilon_{hkl} \) behavior relative to the macroscopic deformation. In compression, {111}A grains are the first to wholly participate in bulk transformation, while {100}A are the last, though the transformation points are much more closely clustered, indicating that transformation has a more homogenous nature in compression than in tension, consistent with surface observations of Reedlunn et al. [46]. More interestingly, perhaps, is that while a Schmid factor analysis is reasonable for most of the “first grain to transform” analysis in Regime i, these orderings of bulk transformation defy such an approach for both HPV or CV transformation. This result indicates that such analysis can provide qualitative insight into concepts such as tension–compression asymmetry of transformation stresses and strains. However, in bulk polycrystalline material, the grain neighborhoods have a stronger influence over bulk transformation than the grain orientations themselves.
Another interesting observation regarding the transformation plateaus can be observed in studying the populations of martensite orientations in Figs. 8 and 12. Note from Fig. 3b, that transformation is always increasing in this regime. However, in the martensite difference IPFs, it is clear that throughout the regime, some martensite orientation populations decrease. A decrease in the difference IPFs while the bulk phase fraction is increasing necessarily indicates martensite reorientation. This reorientation is especially active of the first orientations to form, in examining Figs. 8j, k, z, aa and 12j, x, and again as the transformation plateau begins to saturate in Fig. 8o, ee, ff. Regarding initiation, this orientation population phenomenon indicates that initially, some grains transform to martensite orientations that are not elastically preferred, and then those orientations immediately twin to new orientations. This highlights a competition between elastic energy minimization, which indicates that most open-packed planes (near \( (\bar{1}50)_{\text{M}} \)) should align with the load in tension and closest-packed planes (near \( (100)_{\text{M}} \)) in compression, and the geometric restrictions of austenite–martensite interfaces. The latter do not allow the material to transform directly to the elastically preferred martensite orientations, but rather force a transformation of some grains to non-optimal orientations, for example, near \( (\bar{1}21)_{\text{M}} \), \( (\bar{2}10)_{\text{M}} \), \( (102)_{\text{M}} \) in tension (Fig. 12i) and \( (\bar{1}21)_{\text{M}} \), \( (\bar{2}10)_{\text{M}} \), \( (001)_{\text{M}} \), \( (\bar{1}50)_{\text{M}} \) in compression (Fig. 12w), which then reorient to elastically preferred orientation as they are able. After the initial reorientation, this mechanism is relatively dormant during the middle of the transformation plateaus. Then, as the transformation plateaus saturate, martensite reorientation again becomes stronger. These findings indicate that the plateau strain is not solely defined by transformation strains, but also martensite twinning and detwinning make contributions. Still, the relative volume fraction of reorientation is much smaller than the ultimate transforming volumes, thus it is still right to say that transformation is the dominant driver of the plateaus.
One final observation in this regime is that transformation is not complete at the end of the plateaus. This is in contrast to previous work on NiTi single crystals, where theoretical transformation strains were obtained during the plateau, thus transformation almost certainly did complete before rehardening [47]. Thus, incomplete transformation during the plateau is a reality of polycrystalline effects in Nitinol. Some of these effects could be due to processing—the cold work in these samples was not fully annealed, thus initial dislocation structures in the material could promote slip and inhibit transformation in some grains. However, Brinson et al. studied annealed superelastic Nitinol, and found the same result—transformation was not completed throughout the whole polycrystal during the transformation plateau [12]. Richards et al. reached the same conclusion theoretically, simulating an initially pristine polycrystal [8]. They showed that transformation fronts put stress on grains under conditions where some grains are more favorable to slip than transformation, thus plasticity helps to connect competing transformation fronts. It is this same plasticity that then leads to (1) non-transforming material as well as (2) a need for higher stress to transform surrounding material that had not yet transformed or slipped.
Regime iii: Rehardening
It is no surprise to find that the rate of transformation drastically slows into Regime iii (Fig. 3b). Still, bulk transformation of the material is not complete—only 85 %/65 % of the material has transformed coming into this regime in tension/compression. Furthermore, the loading deformation of this material still has significant contributions from transformation through this regime—moreso in compression (15 % further transformation) than tension (10 %). Subtly, but perhaps more interestingly, are the noticeable non-monotonic behaviors in the volume fraction kinetics in this regime, highlighted with red arrows in Fig. 3b, which are more pronounced in compression, with an ~7 % decrease in phase fraction occurring around −5 % macroscopic strain, than in tension, where an ~3 % decrease in phase fraction is observed around 8 % strain (note, these are logarithmic strain values, which correspond to ~4.75 and 8.50 % engineering strain, respectively). This shift in mechanisms is further affirmed by the dramatically different nature of the microstructure changes observed in the difference IPFs of Fig. 9h, j (changes in orientation distributions leading into this anomaly) versus Fig. 10h, p (changes immediately thereafter). These difference IPFs are almost completely opposite in nature—orientations that increased in population before these events decrease in population thereafter. While slip is difficult to directly identify via peak broadening amidst large amounts of transformation and reorientation, these volume fraction kinetics indicate a sudden shift in inelastic deformation mechanisms; most probably the bulk material yields to gross plastic flow since further reorientation of martensite, even on new twin systems, would not likely cause reverse-phase transformation. This conclusion is consistent with, but not the only possible explanation for the fragmentation of the remaining B2 orientation distributions from Fig. 9b to c and j to k, in tension and compression, respectively. Thus, in addition to some grains transforming before the transformation plateaus, in addition some local slip occurs before bulk plastic flow. The retention of {111}A grains in both tension and compression is consistent with both 1) there being more of these grains than any other population initially in each sample (i.e., preferred orientation) and 2) {111} orientations having the highest Schmid factor for slip (Fig. 13c), in that it is more likely that {111}A grains would plastically deform instead of transform, especially in compression, as discussed in “Regime ii: The Transformation Plateaus” section.
This anomalous result is likely the reason for a sudden shift on the effect of pre-strain on fatigue life of superelastic Nitinol. It has been empirically documented that approximately 8 % tensile pre-strain leads to an increase in fatigue performance [27], while 8–10 % bending degrades fatigue performance [28]. It has been hypothesized that the reason for worse fatigue life in bending is compressive pre-strain damage [28]. We propose that it is the sudden shift in mechanisms documented in the previous paragraph that is likely the reason for a transition from fatigue enhancement to fatigue degradation. Our results also suggest the idea that perhaps not all compressive pre-strain microstructure changes are damaging—it is very likely that ~4.5 % compressive pre-strain could have the same effect on fatigue life as ~8.0 % tensile pre-strain, if the mechanism that relaxes stresses to the extent that reverse transformation occurs is the true indicator of the line between fatigue enhancement and degradation. They also support the conclusion that in bending a wire, the detrimental deformation would occur in compression due to the large strain asymmetry found in this mechanistic transition. These factors will be explored in more detail in the companion paper [29].
Generally the changes in orientation populations are too convoluted to uniquely identify contributions from phase transformation and unique monoclinic twinning mechanisms to reorientation events. However, Fig. 9f exhibits one case of a clear twinning event, as a clearly unique and equal volume fraction of the material twins from near \( (\bar{1}00)_{\text{M}} \) to \( (\bar{1}50)_{\text{M}} \). Since this sample is being loaded in tension, this twin could be explained by [100]\( (010)_{\text{M}} \) compound twinning, according to the calculations in Figs. 4 and 5 of [18]. Alternatively, detwinning of either Type I or II, Mode C twins or else (131) deformation twinning are better candidate mechanisms.
Another likely twin is evident given the nature of the increase in \( (010)_{\text{M}} \)/\( (100)_{\text{M}} \) orientations in compression/tension. Twinning from near \( (\bar{1}00)_{\text{M}} \) and \( (\bar{1}50)_{\text{M}} \) to these orientations in tension and compression via [120]\( (\bar{2}10)_{\text{M}} \) compound twinning, respectively, provides a maximum of twinning strain of known monoclinic twin systems. Thus these changes in populations are strong indicators of such deformation twinning in the martensite, as has been previously observed of thermal Nitinol martensites [18, 48].
Regime iv: Plastic Flow
In Regime iv, very little additional transformation occurs, again with a bit more in compression (~5 %) than tension (~1 %) (Fig. 3b). It can be concluded that deformation in this regime is dominated by some combination of martensite reorientation together with martensite and/or austenite slip, though it is not possible to arrive at unique, proposed mechanisms from our data—there are too many possibilities. However, the martensite difference plots (Figs. 10h, p, 12l, z) are of a different nature than for the previous regime, indicating the same deformations do not dominate Regime iv relative to Regime iii. Ambiguity in the interpretations highlights a limitation of bulk techniques and a need for in situ investigations of these same behaviors on a more local scale.
Unloading
The first unloading step in compression shows clear reverse transformation, while very little reverse transformation occurs while initially unloading from tension, even if the same 0.50 % strain intervals are considered (Fig. 3b). Thus, the initial reorientation of B2 in tension (Fig. 11b–d) is likely due primarily to a plasticity Bauschinger effect [49]. Twinning or reverse transformation would show an increase in some of the B2 orientation volume fraction populations in the difference plots, as in compression for Fig. 11r. The B19′ changes in Figs. 11j–l, z are complementary—in tension it appears a reorientation Bauschinger effect dominates—while in compression reverse transformation is prevalent. Still, all of these results indicate that the initial macroscopic unloading moduli are measures of effective, not elastic stiffness, as these initial unloading deformations have moderate inelastic deformation contributions. A similar conclusion can be drawn for the initial rehardening moduli in Regime iii, also indicated in Fig. 3a. The reason for tension–compression asymmetry in these moduli can be understood through three mechanisms: (1) the volume fractions of austenite and martensite are modestly different in tension and compression, thus the contributions of each phase to the bulk elastic response is different; (2) in all cases, the material is predominantly martensitic, and martensite elastic properties may vary substantially with texture due to strong crystal anisotropy [16, 17, 50]. The tensile martensite textures indicate a more compliant martensite microstructure than the compressive (see Fig. 4 of [17]), which is consistent with the moduli trends in Fig. 3a; (3) different inelastic mechanisms are active in tension versus compression, thus the differences between the true bulk elastic stiffness and the effective stiffness we observe are likely greater in compression, where transformation is playing a larger role.
Beyond initial unloading, most interesting observation in this regime is that the material reverse transforms by ~65 % in compression but only 10 % in tension. This is in spite of loading the material well beyond a very clear macroscopic yield in compression, but only to a semi-ambiguous macroscopic yield point in tension. This indicates that even though the Schmid factors for slip are identical for tension and compression, because plasticity is coupled to transformation and transformation is asymmetric, plasticity is also asymmetric. This is evident as the sample macroscopically flowed at a true stress of ~1.6 GPa in compression, yet at only a stress of ~1.1 GPa in tension. Also, backstress and/or friction were introduced by plastic deformation that favored a much higher retained phase fraction of martensite upon unloading in tension. An argument could be made that this plastic asymmetry arises from material processing—this material was cold drawn and partially recrystallized. However, the plastic asymmetry completely contradicts such an argument—cold drawing introduces tensile-like plasticity. The resulting Bauschinger effect would be a higher plastic flow stress in tension, lower in compression. Furthermore, we have observed the same plastic asymmetry of hot-extruded, near-random textured NiTi thermal martensite [18]. Thus, it is the coupling of phase transformation with plasticity that dominates the plastic yield asymmetry, not processing and residual stress, as in traditional elastic–plastic metals.
Still, not all of the unloading strain in the compression plateau during this event is from reverse transformation—the plateau exhibits 25 % more strain, yet ~20 % of the volume of martensite does not reverse transform (Fig. 3). Figures 11ff and 12bb indicate that substantial reorientation occurs simultaneous with reverse transformation as the compressive load is removed, thus it is the presence of more reorientation than occurred during the forward transformation plateau (Regime ii) that gives rise to the larger unloading plateau.
Conclusion
We have presented a micromechanical investigation of the bulk behavior and average microstructural response of millions to billions of grains in the gage of superealstic ELI Nitinol material deformed well into plasticity regimes. While the neutron diffraction technique provided new insights into the deformation mechanisms, it was limited in an ability to quantify the roles of individual mechanisms, as was possible for monotonic deformations of monoclinic NiTi [18]. In the present study, reorientation and transformation events simultaneously occurred throughout the deformations and each clouded the direct identification of the other, as well as quantifiable signatures of slip. Still, we did qualitatively verify recent micromechanical reports using theories and surface observations that grain neighborhoods are equally, if not more important, than the orientations of grains themselves in bulk polycrystals. We were also able to quantify the kinetics of phase fraction in these deformations, which allows these data to serve as a benchmark for internal variable theories that assume constitutive behavior as a function of martensite volume fraction. Furthermore, the lattice strain and inverse pole figure evolutions provide benchmarking targets for micromechanical models, especially of self-consistent or grain-scale finite element implementations. Full-field and phase-field micromechanical implementations likely desire quantified data at more local scales.
References
Wechsler MS, Lieberman DS, Read TA (1953) On the theory of the formation of martensite. Trans Am Inst Min Metall Eng 197(11):1503–1515
Patoor E, Bensalah MO, Eberhardt A, Berveiller M (1993) Micromechanical aspects of the shape memory behaviour. Proceedings of the International Conference on Martensitic Transformations (Icomat-92), p. 401–406
Patoor E, Eberhardt A, Berveiller M (1994) Mechanics of phase transformation and shape memory alloys. Micromechanical modelling of the shape memory behavior. ASME, New York
Gao X, Brinson LC (2002) A simplified multivariant SMA model based on invariant plane nature of martensitic transformation. J Intell Mater Syst Struct 13:795–810
Manchiraju S, Anderson PM (2010) Coupling between martensitic phase transformations and plasticity: a microstructure-based finite element model. Int J Plast 26(10):1508–1526
Thamburaja P, Anand L (2001) Polycrystalline shape-memory materials: effect of crystallographic texture. J Mech Phys Solids 49(4):709–737
Paranjape HM (2014) Modeling of shape memory alloys: phase transformation/plasticity interaction at the nano scale and the statistics of variation in pseudoelastic performance. The Ohio State University
Richards AW, Lebensohn RA, Bhattacharya K (2013) Interplay of martensitic phase transformation and plastic slip in polycrystals. Acta Mater 61(12):4384–4397
Ezaz T, Sehitoglu H, Abuzaid W, Maier HJ (2012) Higher order twin modes in martensitic NiTi-The (20(1)over-bar) case. Mater Sci Eng A 558:422–430
Kammers AD, Daly S (2013) Digital image correlation under scanning electron microscopy: methodology and validation. Exp Mech 53(9):1743–1761
Kimiecik M, Jones JW, Daly S (2013) Quantitative studies of microstructural phase transformation in nickel-titanium. Mater Lett 95:25–29
Brinson LC, Schmidt I, Lammering R (2004) Stress-induced transformation behavior of a polycrystalline NiTi shape memory alloy: micro and macromechanical investigations via in situ optical microscopy. J Mech Phys Solids 52(7):1549–1571
Benafan O, Noebe R, Padula S, Garg A, Clausen B, Vogel S, Vaidyanathan R (2013) Temperature dependent deformation of the B2 austenite phase of a NiTi shape memory alloy. Int J Plast 51:103–121
Benafan O, Padula S, Noebe R, Brown D, Clausen B, Vaidyanathan R (2013) An in situ neutron diffraction study of shape setting shape memory NiTi. Acta Mater 61(10):3585–3599
Stebner A, Gao X, Brown DW, Brinson LC (2011) Neutron diffraction studies and multivariant simulations of shape memory alloys: empirical texture development—mechanical response relations of martensitic nickel-titanium. Acta Mater 59(7):2841–2849
Stebner AP, Brown DW, Brinson LC (2013) Measurement of elastic constants of monoclinic nickel-titanium and validation of first principles calculations. Appl Phys Lett 102(211908):211908-1–211908-5
Stebner AP, Brown DW, Brinson LC (2013) Young’s modulus evolution and texture based elastic-inelastic strain partitioning during large uniaxial deformations of monoclinic nickel-titanium. Acta Mater 61:1944–1956
Stebner AP, Vogel SC, Noebe RD, Sisneros TA, Clausen B, Brown DW, Garg A, Brinson LC (2013) Micromechanical quantification of elastic, twinning, and slip strain partitioning exhibited by polycrystalline, monoclinic nickel-titanium during large uniaxial deformations measured via in situ neutron diffraction. J Mech Phys Solids 61(11):2302–2330
Cai S, Schaffer J, Daymond M, Yu C, Ren Y (2014) Effect of heat treatment temperature on nitinol wire. Appl Phys Lett 105(7):071904
Cai S, Schaffer J, Ren Y, Yu C (2013) Texture evolution during nitinol martensite detwinning and phase transformation. Appl Phys Lett 103(24):241909
Daymond MR, Young ML, Almer JD, Dunand DC (2007) Strain and texture evolution during mechanical loading of a crack tip in martensitic shape-memory NiTi. Acta Mater 55(11):3929–3942
Young ML, Gollerthan S, Baruj A, Frenzel J, Schmahl WW, Eggeler G (2013) Strain mapping of crack extension in pseudoelastic NiTi shape memory alloys during static loading. Acta Mater 61(15):5800–5806
Robertson S, Mehta A, Pelton A, Ritchie R (2007) Evolution of crack-tip transformation zones in superelastic Nitinol subjected to in situ fatigue: a fracture mechanics and synchrotron X-ray microdiffraction analysis. Acta Mater 55(18):6198–6207
Bernier JV, Barton NR, Lienert U, Miller MP (2011) Far-field high-energy diffraction microscopy: a tool for intergranular orientation and strain analysis. J Strain Anal Eng Des 46(7):527–547
Lienert U, Li S, Hefferan C, Lind J, Suter R, Bernier J, Barton N, Brandes M, Mills M, Miller M (2011) High-energy diffraction microscopy at the advanced photon source. JOM 63(7):70–77
Šittner P, Lukáš P, Novák V, Daymond M, Swallowe G (2004) In situ neutron diffraction studies of martensitic transformations in NiTi polycrystals under tension and compression stress. Mater Sci Eng A 378(1):97–104
Dooley BA, Lasley CC, Mitchell MR, Steele RR, Tittelbaugh EM (2012) Method of making shape memory alloy articles with improved fatigue performance. Google Patents
Gupta S, Pelton AR, Weaver JD, Gong X-Y, Nagaraja S (2014) High compressive pre-strains reduce the bending fatigue life of nitinol wire. J Mech Behav Biomed Mater 44:96–108
Pelton AR, Clausen B, Stebner AP (2015) In-situ neutron diffraction studies of the micromechanics of increasing tension pre-strain amplitudes of superelastic nickel-titanium. Shape Mem Superelasticity 1(1) (in review)
ASTM-F2063-12 (2010) Standard specification for wrought nickel-titanium shape memory alloys for medical devices and surgical implants. F2063-12
Bourke MAM, Dunand DC, Ustundag E (1995) SMARTS—a spectrometer of strain measurement in engineering materials. Appl Phys 74:s1707–s1709
Clausen B (1998) SMARTSware Manual. Los Alamos National Laboratory
Rietveld HM (1966) A method for including line profiles of neutron powder diffraction peaks in determination of crystal structures. Acta Crystallographica S 21:A228
Larson AC, VonDreele RB (1986) GSAS. Los Alamos National Laboratory
VonDreele RB (1997) Quantitative texture analysis by Rietveld refinement. J Appl Crystallogr 30:517–525
Kudoh Y, Tokonami M, Miyazaki S, Otsuka K (1985) Crystal-structure of the martensite in Ti-49.2 at-percent-Ni alloy analyzed by the single-crystal X-ray-diffraction method. Acta Metall 33(11):2049–2056
Barney MM, Xu D, Robertson SW, Schroeder V, Ritchie RO, Pelton AR, Mehta A (2011) Impact of thermomechanical texture on the superelastic response of Nitinol implants. J Mech Behav Biomed Mater 4(7):1431–1439
Kimiecik M, Jones JW, Daly S (2015) Grain orientation dependence of martensitic phase transformation in polycrystalline shape memory alloys. Acta Mater (in press)
Paranjape H, Anderson PM (2014) Texture and grain neighborhood effects on Ni-Ti shape memory alloy performance. Modell Simul Mater Sci Eng 22(7):075002
Bhattacharya K, Kohn RV (1996) Symmetry, texture and the recoverable strain of shape-memory polycrystals. Acta Mater 44(2):529–542
Shu YC, Bhattacharya K (1998) The influence of texture on the shape-memory effect in polycrystals. Acta Mater 46(15):5457–5473
Gall K, Sehitoglu H (1999) The role of texture in tension-compression asymmetry in polycrystalline NiTi. Int J Plast 15(1):69–92
Gall K, Sehitoglu H, Chumlyakov YI, Kireeva IV (1999) Tension-compression asymmetry of the stress-strain response in aged single crystal and polycrystalline NiTi. Acta Mater 47(4):1203–1217
Šittner P, Landa M, Lukáš P, Novak V (2006) R-phase transformation phenomena in thermomechanically loaded NiTi polycrystals. Mech Mater 38(5):475–492
Bhattacharya K (2003) Microstructure of martensite : why it forms and how it gives rise to the shape-memory effect, vol xi., Oxford series on materials modellingOxford University Press, Oxford, p 288
Reedlunn B, Churchill CB, Nelson EE, Shaw JA, Daly SH (2014) Tension, compression, and bending of superelastic shape memory alloy tubes. J Mech Phys Solids 63:506–537
Miyazaki S, Kimura S, Otsuka K, Suzuki Y (1984) The Habit Plane and Transformation Strains Associated with the Martensitic-Transformation in Ti-Ni Single-Crystals. Scr Metall 18(9):883–888
Nishida M, Ii S, Kitamura K, Furukawa T, Chiba A, Hara T, Hiraga K (1998) New deformation twinning mode of B19′ martensite in Ti-Ni shape memory alloy. Scripta Mater 39(12):1749–1754
Bauschinger J (1886) On the change of position of the elastic limit of iron and steel under cyclic variations of stress. Mitt Mech Tech Lab München 13:1–115
Wagner MFX, Windl W (2008) Lattice stability, elastic constants and macroscopic moduli of NiTi martensites from first principles. Acta Mater 56(20):6232–6245
Mercier O, Melton K, Gremaud G, Hägi J (1980) Single-crystal elastic constants of the equiatomic NiTi alloy near the martensitic transformation. J Appl Phys 51(3):1833–1834
Acknowledgments
We thank D.J. Bronfenbrenner, A.R. Pelton, and A. Mehta for providing the previously unpublished stress–strain and high-energy X-ray data shown in Fig. 6, collected from measurements made at the Stanford Linear Accelerator (SLAC). LCB and HMP thank DOE BES support under grant number DE-SC0010594. We thank Nitinol Devices and Components (NDC) for donating the samples for this research; in particular, Max Launey and Lot Vien for assistance with the materials. We also acknowledge Thomas Sisneros of Los Alamos National Laboratory for assistance with the tension experiment, and Gang Chen of the Northwest Institute for Nonferrous Metal Research (NIN, Xi’an, Shaan Xi, China) for assistance with the compression experiment during his time as a visiting scholar at Northwestern University. This work has benefitted from the use of the Lujan Neutron Scattering Center, which was funded by the Office of Basic Energy Sciences of the Department of Energy under contract DE-AC52-06NA25396.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Stebner, A.P., Paranjape, H.M., Clausen, B. et al. In Situ Neutron Diffraction Studies of Large Monotonic Deformations of Superelastic Nitinol. Shap. Mem. Superelasticity 1, 252–267 (2015). https://doi.org/10.1007/s40830-015-0015-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40830-015-0015-2