Local Mechanical Response of Superelastic NiTi Shape-Memory Alloy Under Uniaxial Loading

Abstract

In this paper, we focus on the local mechanical response of superelastic NiTi SMA at different temperatures under uniaxial loading. In situ DIC is applied to measure the local strain of the specimen. Based on the experimental results, two types of mechanical response, which are characterized with localized phase transformation and homogenous phase transformation, are identified, respectively. Motivated by residual strain accumulation phenomenon of the superelastic mechanical response, we conduct controlled experiments, and infer that for a given material point, all (or most) of the irreversibility is accumulated when the transformation front is traversing the material point. A robust constitutive model is established to explain the experimental phenomena and we successfully simulate the evolution of local strain that agrees closely with the experimental results.

Introduction

Shape-memory alloys (SMAs), such as NiTi, have been applied widely in the aviation, mechanical, and medical fields [1–3]. Basically, NiTi has two stable phases, an austenite phase with higher symmetry and a martensitic phase with lower symmetry. It is widely accepted that the free energy of these two phases is stress and temperature dependent that gives access to stress-induced phase transformation and temperature-induced phase transformation [4]. NiTi demonstrates different macroscopic stress–strain responses under different temperatures, which can be categorized into two main groups: superelasticity properties (i.e., NiTi is able to recover from the large stress-induced deformation after unloading) and shape-memory effect properties (i.e., NiTi is able to recover from residual strain at stress-free condition after heating or cooling). Numerous experiments have been conducted to observe macroscopic global strain–stress behavior and the evolution of the phase transformation under uniaxial tension [5–9]. Many theoretical models have been developed to explain the experimental phenomena based on thermomechanics and continuum theory [10–12]. However, little attention is paid to local mechanical response especially local strain until Daly and Bhattacharya [13, 14] first introduced the digital image correlation (DIC) method to observe the phenomenon of stress-induced localized phase transformation of NiTi. Then, some important results were reported by several groups. Churchill et al. [15] presented their experimental observations on the isothermal mechanical responses of NiTi wires. Saletti et al. [16] applied in situ DIC to follow the uniaxial growth rate of the stress-induced martensite at three different levels of velocity. Lackmann et al. [17] employed in situ DIC and electron back scatter diffraction (EBSD) to reveal the relation between grain orientations, local strain concentrations, and resulting topographical changes in NiTi on the meso- and microscale. Using custom-designed fixturing and stereo DIC, Reedlunn et al. [18] performed isothermal experiments on superelastic NiTi tubes in tension, compression, and large rotation, pure bending to quantify the local strain field and eliminate grip effects.

The aim of the work was to provide a sound analysis on the local mechanical response of superelastic NiTi SMA at different temperatures under uniaxial tension from perspective of experimental investigation and theoretical deduction. The paper is structured as follows: The material properties and experiment procedures are introduced briefly in “Material and Experimental Procedure” section. In “Experimental Results” section, with the help of DIC, we obtain the local strain field of the specimen and identify two types of superelastic mechanical response characterized with localized phase transformation and homogeneous phase transformation. In “Analysis and Discussion” section, based on reasonable assumptions, we develop a constitutive model and provide the simulation of local strain with the discussion of the accumulation of irreversibility. Summary and conclusions are given in “Summary and Conclusions” section.

Material and Experimental Procedure

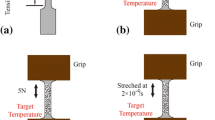
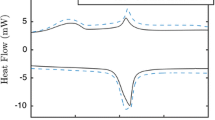
The as-received NiTi (55.6 wt% Ni) SMA thin sheets with the thickness of 0.2 mm (Memry Corp.) were chosen in the current research. As shown in Fig. 1a, the microstructure of the material is characterized by regular grains with a diameter of 120 nm. Differential scanning calorimetry (DSC) was conducted to measure the transformation temperature of the specimen. The austenite finish temperature of the virgin sample is A _f = 12.6 °C, indicating that the material demonstrates superelastic property at and above room temperature, as shown in Fig. 1b. The specimen was line-cut into the dog-bone shape. During the experiment, we focus on the central part of the specimen whose size is 40 mm × 6.6 mm, as shown in Fig. 2a.

Fig. 1

a TEM image of the austenite phase of NiTi; b DSC results of NiTi

Fig. 2

a Dog-bone shape specimen and the size of focus area; b DIC photo of the sprayed sample

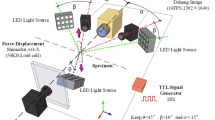
A temperature chamber was designed to render a stable experiment environment temperature. The specimen was placed in the chamber and stretched/unloaded under displacement control at the strain rate whose magnitude is $10^{ - 5} /s$, which can be regarded as a quasi-static condition. Black speckles with white texture were sprayed on the surface of the specimen, as shown in Fig. 2b. A CCD camera was put in front of the specimen and the DIC photo was captured through the optical glass of the temperature chamber. Data were stored and post-processed with the commercial software NCM-2D^® in the computer terminal. The maximum error of NCM-2D is up to 0.2 μm, which can meet the experimental requirements of accuracy. A schematic of the top view of the experimental setup is shown in Fig. 3.

Fig. 3

Schematic of the top view of the experimental setup

Experimental Results

From the global stress–strain response shown in Fig. 4, we find that all four specimens have produced a stress plateau during forward transformation, while with increasing temperature, the stress plateau associated with the reverse transformation tends to disappear and the irreversible strain increases. The physical reason for the transition from the perfect SE to the partial SE in NiTi can be attributed to the opposite change trend of transformation yield stress and true yield stress with temperature. On one hand, The relation between transformation stress and temperature keeps to the Clausius–Clapeyron relation. So, the transformation yield stress increases as the temperature increases. On the other hand, true yield stress of NiTi decreases with increasing temperature [19, 20]. So, there must exists a critical temperature M_c at which the transformation yield stress equals to true yield stress. If M_c locates in the superelastic temperature regime and the environmental temperature is above M_c, NiTi will yield during forward transformation and demonstrates partial SE property.

Fig. 4

Global strain–stress response of NiTi at 25, 50, 75, and 100 °C

After analyzing the mechanical response and the local longitudinal strain evolution of the four NiTi samples through in situ DIC, we extract the longitudinal strain along the central line of the specimen, and obtain the contour plot of the local longitudinal strain evolution, as shown in Figs. 5a, 6a, 7a, and 8a. Choosing three material points along the central line of the specimen, i.e., N, L, and M, we can obtain the longitudinal strain evolution of these three material points from the DIC results, as shown in Figs. 5b, 6b, 7b, and 8b. Choosing five time points, i.e., (i) to (v), on the time axis, we can then obtain the longitudinal strain distribution along the central line of the specimen at these five time points, as shown in Figs. 5c, 6c, 7c, and 8c. The longitudinal strain field of the specimen in these five time points is shown in Figs. 5d, 6d, 7d, and 8d.

Figs. 5–8

The phase transformation modes of NiTi SMA under T = 25 °C, 50, 75, and 100 °C, respectively. a The contour plot of the evolution of the longitudinal strain along the central line. The white line represents the stress evolution; b the longitudinal strain evolution of the selected three material points, i.e., N, L, and M; c the longitudinal strain distribution along the central line of the specimen at the selected five time points, i.e., (i) to (v); d the longitudinal strain field of the specimen at the selected five time points, i.e., (i) to (v) (Color figure online)

Along the tensile direction, the heterogeneous strain state of the specimen can be recognized clearly in Fig. 5, 6, 7, 8. In view of the work of Saletti et al. [16], Reedlunn et al. [21], and Bewerse et al. [22], the sharp transition between high-strain and low-strain regions is attributed to transformation fronts associated with the local martensite transformation, and thus regions undergoing different magnitudes of local strain (large vs. small) are corresponding to regions with different phases (martensite vs. austenite). As is demonstrated in Fig. 5d, several declining transformation boundaries, which are also referred to as Lüders deformation bands (LDBs), pass through the width of the sample. In light of the in situ EBSD studies of Mao et al. [21, 22], it is pointed out that LDB does not purely keep to the principal of the maximum shear stress, but is possibly a result of the interaction between the mechanics and the martensite crystallography. In the present experiments, the declining angle of the LDB ranges from 57° to 62°, which agrees with the detailed studies indicating that shear angle of the LDB varies from 48° to 61° [23–25].

For T = 25 and 50 °C, the phase transformation is associated with the extending of the phase transformation band, and we can detect easily the transformation band front both for forward and reverse phase transformations in Figs. 5 and 6. In this paper, it is called localized phase transformation. For T = 100 °C, when the specimen is unstrained, the strain distribution is uniform, and we cannot ascertain the localized reverse phase transformation band and the corresponding band front in Fig. 8. In this paper, it is called homogeneous reverse phase transformation. Taking the residual strain into account, we identify two typical superelastic mechanical responses of NiTi that are characterized with different forms of phase transformation and the amount of the residual strain:

• (I) Forward and reverse phase transformations are both localized and there is no (or very little) residual strain (typically T = 25 and 50 °C).

• (II) Forward phase transformation is localized, while reverse phase transformation is homogeneous and with considerable residual strain (typically T = 100 °C).

For T = 75 °C, when the specimen is unstrained, it demonstrates a characterization combined with both homogeneous and localized phase transformations, which can be viewed as an intermediate state. So, we infer that with the increasing temperature, Type I mechanical response will gradually transform to Type II mechanical response.

Analysis and Discussion

Constitutive Model for NiTi

The constitutive model used in this research is based on the work of Machado and Lagoudas [26]. The Gibbs free energy of the SMA is given by

$$G\left( {\varvec{\sigma},T,\xi ,\varvec{\varepsilon}^{T} } \right) = - \frac{1}{2\rho }\varvec{\sigma}:\varvec{S}:\sigma - \frac{1}{\rho }\varvec{\sigma}:\varvec{\varepsilon}^{T} + c\left[ {\left( {T - T_{0} } \right) - T\ln \left( {\frac{T}{{T_{0} }}} \right)} \right] - s_{0} T + u_{0},$$

(1)

where $\varvec{\sigma}$ is the stress, $\varvec{\varepsilon}^{T}$ is the transformation strain, T ₀ is the reference temperature, s ₀ is the reference effective specific entropy, and u ₀ is the reference effective specific internal energy. The material parameters S and c refer to effective compliance tensor and effective specific heat, respectively. Here, $\varvec{\varepsilon}$ is designated as the local strain of the material point, and it can be decomposed into two parts, the elastic part $\varvec{\varepsilon}^{\text{e}}$ and the plastic part $\varvec{\varepsilon}^{pl}$.

$$\varvec{\varepsilon}=\varvec{\varepsilon}^{\text{e}} +\varvec{\varepsilon}^{\text{pl}}$$

(2)

We can obtain the $\varvec{\varepsilon}^{\text{e}}$ via the following constitutive equation:

$$\varvec{\varepsilon}^{\text{e}} = - \rho \frac{\partial G}{{\partial\varvec{\sigma}}} = \varvec{S}:\varvec{\sigma}+\varvec{\varepsilon}^{T}.$$

(3)

Substituting Eq. (3) into Eq. (2), we get

$$\varvec{\varepsilon}= \varvec{S}:\varvec{\sigma}+\varvec{\varepsilon}^{T} +\varvec{\varepsilon}^{\text{pl}}.$$

(4)

Theoretically, $\varvec{\sigma}$ in Eq. (4) should be the local stress. However, it is difficult to measure the local stress with current techniques. Considering the homogeneity of the sample, we assume that the local stress is the same throughout the specimen, and hence the local stress is identical to the global stress due to the uniaxial loading condition. To simplify the problem, Eq. (4) is reduced to 1D form (along the tensile direction):

$$\varepsilon = S\sigma + \varepsilon^{T} + \varepsilon^{\text{pl}}$$

(5)

The effective coefficients S and c are defined according to the rule-of-mixture approach:

$$S = S_{\text{A}} + \xi \left( {S_{\text{M}} - S_{\text{A}} } \right) = S_{\text{A}} + \xi \delta S_{\text{MA}}$$

(6)

$$c = c_{\text{A}} + \xi \left( {c_{\text{M}} - c_{\text{A}} } \right) = c_{\text{A}} + \xi \delta c_{\text{MA}},$$

(7)

where S _A and c _A denote the compliance coefficient and specific heat of austenite phase, respectively and S _M and c _M denote the compliance coefficient and specific heat of martensite phase, respectively. Then, $\delta S_{\text{MA}}$ and $\delta c_{\text{MA}}$ denote the difference of the compliance coefficient and specific heat between austenite phase and martensite phase.

Following Boyd and Lagoudas [27], we assume that the evolution of the transformation strain is proportional to the change of the martensite volume fraction. Thus, we obtain

$$\dot{\varepsilon }^{T} = H\dot{\xi },$$

(8)

where $\dot{X}$ denotes the time derivative of X, H is the total strain transformation when austenite is completely transformed to martensite, and $\xi$ is the martensite volume fraction. The time derivative of Eq. (5) is given by

$$\dot{\varepsilon } = \dot{S}\sigma + S\dot{\sigma } + \dot{\varepsilon }^{T} + \dot{\varepsilon }^{\text{pl}}.$$

(9)

Substituting Eq. (6) into Eq. (9), we get

$$\dot{\varepsilon } = \dot{\xi }\delta S_{\text{MA}} \sigma + \left( {S_{\text{A}} + \xi \delta S_{\text{MA}} } \right)\dot{\sigma } + H\dot{\xi } + \dot{\varepsilon }^{\text{pl}}.$$

(10)

Analysis on Type I Mechanical Response

For convenience of analysis, material point (denoted as A) is chosen as the observation point of the specimen. As stated above, no (or very little) residual strain is observed in Type I mechanical response, so the plastic deformation $\varepsilon^{\text{pl}}$ is ignored. Thus, the constitutive Eq. (10) can be modified as follows:

$$\dot{\varepsilon } = \dot{\xi }\delta S_{\text{MA}} \sigma + \left( {S_{\text{A}} + \xi \delta S_{\text{MA}} } \right)\dot{\sigma } + H\dot{\xi }.$$

(11)

All the experiments are performed at the temperature far above A _f, so the virgin specimen is fully austenite, that is, $\xi = 0$ at the beginning stress-free state. In this paper, we assume that in Type I mechanical response, the phase transformation will only occur in the transformation band and the material points within the phase transformation band have undergone phase transformation completely. The evolution of Type I mechanical response can be divided into nine stages and the corresponding time point from $t_{1}^{I}$ to $t_{6}^{I}$ can be defined, as shown in Fig. 9. The phase transformation front is traversing point A at stages (c) and (g).

Fig. 9

Schematic of Type I mechanical response. Blue part represents austenite phase and red part represents martensitic phase. Stage (a): $0 < t < t_{1}^{I}$, elastic loading; stage (b)–(d): $t_{1}^{I} < t < t_{3}^{I}$, localized forward transformation; stage (e): $t_{3}^{I} < t < t_{4}^{I}$, elastic unloading; stage (f)–(h): $t_{4}^{I} < t < t_{6}^{I}$, localized reverse transformation; stage (i): $t > t_{6}^{I}$, elastic unloading (Color figure online)

Based on constitutive Eq. (11) and the given assumptions, the result and description are listed in Table 1. Most of the result and the description are intuitive and easy to obtain. The only two stages we need to pay attention to are stages (c) and (g), and they are discussed in detail as follows.

Table 1 Solution to the proposed model of Type I mechanical response

During stage (c), the phase transformation front is traversing point A. Since the stress is still at the plateau state, we have

$$\dot{\sigma } = 0.$$

(12)

Substituting Eq. (13) into (12), we obtain

$$\dot{\varepsilon } = \left( {H + \delta S_{\text{MA}} \sigma } \right)\dot{\xi }$$

(13)

In this model, the phase transformation front is simplified as a boundary between austenite and martensite with infinitesimal width. Based on this key assumption, we come safely to the conclusion that $\xi$ and $\varepsilon$ change instantaneously and simultaneously when the transformation front traverses the material point. Once there is a jump of local strain during phase transformation, the time derivative of $\xi$ and $\varepsilon$ must be infinitely great to satisfy Eq. (13). It is viewed as the mathematical explanation on the well-known material-level instabilities that give rise to the appearance (or the move) of the macroscopic transformation band [28]. Integrating Eq. (13) with respect to t in the neighborhood of $t_{2}^{I}$, we obtain

$$\int_{{t_{2}^{I-}}}^{{t_{2}^{I+}}} {\left({H + \delta S_{\text{MA}} \sigma} \right)\dot{\xi}dt} = \int_{{t_{2}^{I -}}}^{{t_{2}^{I+}}} {\dot{\varepsilon}dt}$$

(14)

$$\int_{{\xi (t_{2}^{I-})}}^{{\xi (t_{2}^{I+})}} {\left({H + \delta S_{\text{MA}} \sigma} \right)d\xi} = \int_{{\varepsilon (t_{2}^{I-})}}^{{\varepsilon (t_{2}^{I+})}} {d\varepsilon},$$

(15)

where $\sigma_{\text{f}}$ is the forward critical stress and $\Delta \varepsilon_{\text{f}}$ is the value change of the local strain change before and after forward phase transformation.

$$\Delta \varepsilon_{f} = \;\varepsilon \left({t_{2}^{I +}} \right) - \left({t_{2}^{I -}} \right)$$

(16)

Noting that $\xi \left( {t_{2}^{I - } } \right) = 0$, we obtain

$$\Delta \varepsilon_{\text{f}} = \left( {H + \delta S_{\text{MA}} \sigma_{\text{f}} } \right)\xi \left( {t_{2}^{I + } } \right).$$

(17)

The phase transformation occurred in the material point is assumed to be complete,

$$\xi \left( {t_{2}^{I + } } \right) = 1$$

(18)

Substituting Eq. (18) into (17), we have

$$H + \delta S_{\text{MA}} \sigma_{\text{f}} = \Delta \varepsilon_{\text{f}}$$

(19)

After undergoing the forward phase transformation, local strain of the material point A reaches the peak. We then obtain

$$\varepsilon_{\text{peak}} = H + S_{\text{M}} \sigma_{\text{f}}$$

(20)

Similar to stage (c), during stage (g) ($t = t_{5}^{I}$), the material point A is undergoing the reverse phase transformation, and we obtain the following conditions:

$$\xi \left( {t_{5}^{I + } } \right) = 1,\,\,\,\,\xi \left( {t_{5}^{I - } } \right) = 0$$

(21)

$\sigma_{\text{r}}$ is the critical stress of reverse transformation and $\Delta \varepsilon_{\text{r}}$ is the value change of the local strain before and after reverse transformation:

$$\Delta \varepsilon_{r} = \varepsilon \left( {t_{5}^{I - } } \right) - \varepsilon \left( {t_{5}^{I - } } \right)$$

(22)

Thus, we find

$$H + \delta S_{\text{MA}} \sigma_{\text{r}} = \Delta \varepsilon_{\text{r}}$$

(23)

It is evident that $\sigma_{\text{f}} > \sigma_{\text{r}}$, we obtain

$$\Delta \varepsilon_{\text{f}} > \Delta \varepsilon_{\text{r}}$$

(24)

that agrees well with the experiment result in Figs. 5b and 6b.

The results listed in Table 1 are plotted in Fig. 10, and we find that it is in good accordance with the experimental results shown in Fig. 5.

Fig. 10

The simulation of the local strain evolution of the material point. All the stage is separated with each other by black dash line. Stage (c) and stage (d) are highlighted with the red dash line (Color figure online)

Analysis on Type II Mechanical Response

Similar to the analysis on Type I mechanical response, point A is chosen as the observation point, and Type II mechanical response is divided into five stages and the corresponding time point from $t_{1}^{II}$ to $t_{3}^{II}$ can be defined, as shown in Fig. 11. The phase transformation front is traversing point A at stage (c).

Fig. 11

Schematic of Type II mechanical response. Blue part represents austenite phase, red part represents martensitic phase, and orange part represents the mixture of austenite and martensitic phase. Stage (a): $0 < t < t_{1}^{II}$, elastic loading; stage (b)–(d): $t_{1}^{II} < t < t_{3}^{II}$, localized forward transformation; stage (e): $t > t_{3}^{II}$, homogeneous reverse transformation (Color figure online)

With the increasing temperature, the residual strain increases after unloading. The residual strain is up to 2 % at 100 °C. So, plasticity must be taken into consideration in the analysis on Type II mechanical response. In order to reveal the mechanism of irreversibility, two controlled experiments were conducted at 75 °C.

• (i) The specimen is under uniaxial tension and unloaded when the forward transformation band has covered 50 % of the surface when t = t _peak.

• (ii) The specimen is under uniaxial tension and unloaded when the forward transformation band has covered the complete surface.

The result of experiment (i) is shown in Fig. 12, and the result of experiment (ii) is shown in Fig. 7.

Fig. 12

The strain evolution contour plot with 50 % phase transformation band coverage at T = 75 °C. The white line represents the stress evolution (Color figure online)

As can be seen in Fig. 13, the blue dash line gives the strain distribution of experiment (i) when t = t _peak, we can determine the strain plateau and distinguish those material points having undergone the phase transformation from those that have not. The blue solid line gives the residual strain distribution of experiment (i). For the material points having undergone the phase transformation, the residual strain is up to 1 % after unloading, while for those not undergoing the phase transformation, the residual strain is less than 0.1 %. This means the deformation is reversible. Comparing the residual strain of experiment (i) (blue solid line in Fig. 13) with that of experiment (ii) (green solid line in Fig. 11), we find that the residual strain within the phase transformation zone of these two experiments coincides. Hence we come to the conclusion that the length of the stress plateau contributes little to irreversibility. Besides, as shown in Figs. 7a and 12, the plateau stress of the reverse phase transformation maintains constant or slightly decreases, so it is impossible to accumulate much plastic deformation in the presence of increasing dislocation slip during reverse phase transformation [29]. Thus, we arrive at the conclusion that the irreversible deformation is mainly accumulated instantaneously due to the significant strain gradient when the phase transformation front traversing the material point, which is same as the conclusion drawn from the microscopic experiments [30, 31].

Fig. 13

The local strain distribution along the centerline under T = 75 °C. The blue dash line represents the strain distribution of experiment (i) when t = t _peak. The blue solid line represents the residual strain distribution of experiment (i). The green solid line represents the residual strain distribution of experiment (ii) (Color figure online)

Fig. 14

Schematic of the local strain and stress evolution of Type II mechanical response

Similar to the analysis on Type I mechanical response, the evolution of local strain and the evolution of local martensitic volume fraction can be derived through the constitutive Eq. (11). Using the same techniques and conditions as those of Type I, we can obtain a mathematical explanation at the first four stages of Type II mechanical response. Due to the homogeneous reverse transformation, we cannot presume the evolution of $\xi$ when the specimen is unloaded. Based on the experimental results shown in Fig. 8, we make the assumption that when the specimen is unloaded, and $\dot{\sigma}$ and $\dot{\varepsilon}$ keep constant. The results and the descriptions are listed in Table 2. The evolution of local strain and stress deduced from the model is illustrated in Fig. 14.

Table 2 Solution to the proposed model of Type II mechanical response from stage (a) to stage (d)

Summary and Conclusion

The present study focused mainly on the local mechanical response of superelastic NiTi SMA under uniaxial tension. In situ DIC was applied to measure the local strain of specimens. A series of quasi-static experiments and two controlled experiments were conducted. Localized and homogenous phase transformations were observed. A constitutive model was developed to explain the experiment phenomena. From the results of the present study, the following conclusions are drawn:

• (1) Two types of mechanical response of NiTi SMA phase transformation were identified. With increasing temperature, Type I mechanical response will gradually transform to Type II mechanical response.

• (2) As for Type I mechanical response, it is proven theoretically and experimentally in this paper that the coupling between local strain and local martensitic volume fraction gives rise to the appearance (or the movement) of the macroscopic transformation band.

• (3) As for Type II mechanical response, it is characterized with the homogeneous reverse transformation. We conclude that the residual strain is accumulated instantaneously when the forward transformation front is traversing the material point.