1 Introduction

Efficient investments in and effective navigation of financial markets require knowledge of not only various types of assets but also an understanding of the relationships among many dimensions, such as price, volume, volatility, risk, and others. One of the most widely used and analyzed dimensions is the relationship between price and volume. Weinstein (1988) wrote: Never trust a breakout that isn’t accompanied by a significant increase in volume. Volume analysis allows for understanding the source of the price change and confirms or negates a given trend direction and trend quality. The volume reveals when professional investors with huge portfolios buy and sell stocks. No increase in turnover when overcoming a significant price level might be an indicator for the false signals coming from the market, which might point out that smart money is attempting to distribute stocks at a low cost. Volume–price dynamics are commonly used by investors who trade currencies, equities, and commodities on all types of markets—mature and developed—by speculators playing derivatives, such as futures or options, and by persons investing in bonds, among others.

The observations of the relationship between trading volume and asset prices have been focused on by many scientists during the last few decades. Technical analysts and traders expect that price changes are positively correlated with volume; hence, the volume should increase during an upward trend and should decrease during a downward correction. In contrast, during a downward trend, the volume should increase as prices decline and should decrease as growth increases. Research within this scope does not confirm fully such a relationship. The volume–price dependency might change depending on the market investigated and the assets considered.

Research on price–volume relationships started in 1966 when Ying (1966) proved an asymmetric relationship between the absolute value of a daily price change and daily volume, which stated that strong volume increases are associated with either strong price decreases or increases. In the next years, similar conclusions were formulated by many authors, such as Crouch (1970a, b), Westerfield (1977), Tauchen and Pitts (1983) and Harris and Gurel (1986). Positive relationships were also confirmed on the basis of the investigated relationships between price variance and volume, such as by Morgan (1976), Epps and Epps (1976), Cornell (1981), Rutledge (1984), Bessembinder and Seguin (1993), Brailsford (1996), Cooper et al. (2000), Llorente et al. (2002), Statman et al. (2006), Griffin et al. (2007), Glaser and Weber (2009), Israeli (2015) Tran and Mai (2015), Plastun et al. (2019) and Ndjadingwe and Radikoko (2015). A positive relationship between price and volume is in line with the expectations of technical traders. One of many explanations might be observed through the information flow in the market after receiving the information of traders’ generated volume, which directly translates into price movements (Copeland 1976; Jennings et al. 1981). However, other authors found a negative relationship between price and volume, such as Smirlock and Starks (1985), Wood et al. (1985), Moosa and Korczak (1999), Moosa et al. (2003), Kocagil and Shachmurove (1998), Mcmillan and Speight (2002) and Chen et al. (2004). Despite the wide range of different papers on the reverse relationship between price and volume, no unique explanation exists for this fact; for example, Black (1976) and Christie (1982) argued that the explanation might be found in a firm’s increasing equity market value, which negatively impacts its financial ratio and consequently reduces stock return volatility. Glosten et al. (1993) and Chen and Ghysels (2007) assumed that bad news negatively affects volume. No or weak dependency was observed by, for example, Granger and Morgenstern (1963), Godfrey et al. (1964), James and Edmister (1983), Harris and Raviv (1993) and Ji and Zhang (2019). Other authors noticed mixed results, including Wang and Huang (2012), Giot et al. (2010) and Amatyakul (2010), who observed a positive relationship between price and volume on the basis of a continuous component; however, during jumps, which the authors associated with private trading, the relationship was negative.

Researchers use different statistical and quantitative methods to capture and interpret the volume–price relation. For example, Gulia (2019) and Park (2010) applied the GARCH method and found a positive relationship between price volatility and volume on the Indian Stock Exchange. Wei et al. (2019) used Granger causality tests to examine the volume–price relationship in the context of the spillover effect on the two Chinese exchanges—the Shenzhen Stock Exchange and the Shanghai Stock Exchange—during the bull market phase. They showed that, in both markets, the price is followed by the volume, and no spillover effect was recognized during the consolidation phase. Fleming and Kirby (2011) used fractionally integrated time series models and noted that a long memory in volatility and volume dynamics exists. Shi et al. (2018) used a Tobit model and found a positive relationship between volume and price volatility on the Chinese copper and aluminum futures market. They concluded that expected trading volume has a weak ability to interpret price volatility relative to unexpected trading volume, which has a stronger explanatory effect. Similar to other authors, they observed an asymmetric effect that revealed a stronger sensitivity to the appearance of positive than negative information on the market.

Relatively little attention was placed on investigating the volume–price relationship in the cryptocurrency market. For example, Sahoo et al. (2019), based on the Granger causality developed by Toda and Yamamoto (1995) and the non-linear Granger causality proposed by Diks and Panchenko (2005), received mixed results when analyzing the relationships between volume and price and volume and price variability. The application of linear Granger causality showed a significant causality between bitcoin returns and volume; hence, the authors found that price can be used to predict volume. The adoption of Toda–Yamamoto linear causality implies that volume causes volatility. Both relationships are unidirectional. However, the application of the non-linear Granger causality test indicated bidirectional causality between bitcoin’s log returns and volume and showed that no linear causality exists between volume and volatility. The obtained differences suggest the superiority of non-linear models when modeling price–volume dependency. Wang et al. (2019) verified the mixture of the distribution hypothesis and sequential information arrival hypothesis and used a non-linear causality test with data on fifteen foreign currencies from more than sixty platforms and found a causal negative price–volume relationship. Balcilar et al. (2017) used the nonparametric causality-in-quantiles test and data collected from only one exchange and claimed that no dependency exists between volume and price in bearish and bullish periods.

The purpose of our analysis is to investigate the long-term and short-term dynamics between the strength of a trend measured by the Average Directional Movement Index (ADX) and the volume in bullish and bearish periods using the vector error correction model (VECM). Such a context with regard to bitcoin was considered as an example by Ciaian et al. (2018), who used the autoregressive distributed lag method (ARDL) in the context of the bitcoin–altcoin price relationship. The same technique was applied by Sovbetov (2018) and Sriyana (2019), who searched for determinants that might affect bitcoin prices. He claimed, inter alia, that cryptocurrency prices depend on the market’s beta, trading volume, and volatility in both the short- and long-term perspectives. Moreover, for bitcoin, the convergence speed to a long-term equilibrium is 23.68%. Ciaian et al. (2016) and Czapliński and Nazmutdinova (2019) applied vector-autoregressive (VAR), VECM, and ARDL to model bitcoin price formation. They found that the Dow Jones Index, the exchange rate, and oil prices affect bitcoin prices only in the short-term. However, investors’ speculative behavior affects bitcoin prices in both the short and long terms. Kristoufek (2020) detected a long-term equilibrium using VECM between bitcoin prices and mining costs.

This research is limited to bitcoin, which is the prominent representative of the cryptocurrency market. Worth mentioning is that bitcoin—the oldest and still active cryptocurrency and other cryptocurrencies—has yet to gain status as money; thus, these currencies are considered financial assets. Both practitioners and theorists of financial markets have problems with the clear classification of cryptocurrencies and with indicating that universal mechanisms influence and explain the behavior of cryptocurrencies in the financial space. For further information on bitcoin and other cryptocurrencies, please refer to Liu et al. (2015), Szetela et al. (2016, 2020), Urquhart (2017), Corbet et al. (2018).

Our study contributes to the current literature in two ways: by setting an interdependency analysis using the VECM in the context of technical analysis, which is difficult to find in the literature, and by separately investigating the bullish and bearish cryptocurrency market, which guarantees more accurate results. The obtained results might be used to determine the extent to which agents who are active in the bitcoin market are long-term players and to which investors view bitcoin only as a speculative asset and react oversensitively to negative news. The combination of the ADX and volume strengthens the capability of the investment signal to go short or long, which might be desirable for investors when setting their investment strategies. The intention of this research is not to present investment schemes based on ADX; therefore, for details on the application of ADX for investment purposes, please refer to Wilder Jr. (1978).

The remainder of this paper is structured as follows. The second section is devoted to theoretical considerations of the techniques and methodology used. A description of the data used and the results of the empirical research are included in the third section. All of the considerations are summarized in the last section.

2 Methodology

The focus of our research is on the bidirectional relationship between bitcoin’s strength as a trend and its volume in bullish and bearish periods. First, we used daily bitcoin prices to construct an ADX, described in detail in Sect. 2.1, which is an indicator of trend strength. The assistance of two supportive lines—a positive and a negative—provides information on the direction of a trend. In the next step, the VECM, described in Sect. 2.2, was applied to establish and test the long- and short-term relationships between the calculated trend strength and volume.

2.1 Average Directional Movement Index

As a basis of our research, the ADX, which was constructed by Wilder Jr. (1978), is used. This indicator has some advantages, which are observed as desirable for cryptocurrencies. ADX was designed to technically support commodity trading but can also be used for financial assets. The ADX was designed to manage market volatility based on a price range and, together with the two supportive lines—positive and negative directional movement lines—can be used to detect and measure a trend’s strength and direction. Its prime application is to decide whether to take a long or short position in trend markets. In this research, possible trading strategies resulting from the signals produced by the ADX are not discussed but are used to detect possible differences in trends magnitude across markets.

The ADX is a complex tool constructed on the basis of other indicators, such as directional movement (DM), average true rate, directional indicator (DI), and true directional movement (TDM). Wilder Jr. (1978) described in his book the detailed steps that need to be taken to calculate ADX. First, plus and minus DM and True Range (TR) are calculated, which are the basis for other indicators from which ADX results directly, such as plus and minus DI. A detailed description of the procedure to calculate ADX is presented as follows.

TR is understood as the largest difference between today’s high and today’s low, an absolute value of today’s high and yesterday’s close, or an absolute value of today’s low and yesterday’s close. Formally, a TR is described in Eq. (1):

$${TR}_{t}=max\left\{\begin{array}{c}{high}_{t}-{low}_{t}\\ \left|{high}_{t}-{close}_{t-1}\right|\\ \left|{low}_{t}-{close}_{t-1}\right|\end{array}\right.$$
(1)

A comparison of the differences between two consecutive lows with the difference between their respective highs indicates the DM. The plus DM (+ DM) is a situation in which the current high minus the prior high is greater than the previous low minus the current low (see Eq. 2). The opposite relationship points at the minus DM (− DM). Therefore, the DM equals the current high minus the prior high, and the – DM equals the prior low minus the current low (see Eq. 3). By assumption, the DM is positive; therefore, when an indicator is a negative number, then it is set to zero. Formally:

$${+DM}_{t}=\mathrm{max}\left\{0; \; {high}_{t}-{high}_{t-1}\right\}$$
(2)
$${-DM}_{t}=\mathrm{max}\left\{0; \; {low}_{t-1}-{low}_{t}\right\}$$
(3)

When both – DM and + DM equal zero, then an inside day is noted, which is when no DM is observed.

To capture a real tendency in the trend change, introducing a smoothing parameter is necessary. In this work, Wilder’s original assumptions are followed, and the indicators over 14 days are averaged. In notation, 14 in a low index is used to signal the number of days over which the smoothing is performed.

The initial value of a smoothed TR (\({TR}_{{t}_{0}}\)) is a simple sum of a TR over a number of days (see Eq. 4). The same rule applies to the initial DM (\({DM}_{{t}_{0}}\)) values (see Eq. 6).

$${TR}_{14({t}_{0})}=\sum_{i=1}^{14}{TR}_{i}$$
(4)

The values of a smoothed TR for the next periods are calculated as the sum of thirteen times the previous TR value and the value of a TR of a current period divided by fourteen (see Eq. 5).

$${TR}_{14({t}_{i})}={TR}_{14({t}_{i-1})}-\frac{{TR}_{14\left({t}_{i-1}\right)}}{14}+{TR}_{{t}_{i}}$$
(5)

This smoothing technique has application to other smoothed indicators used in the paper that are calculated as in Eqs. (7–10):

$${DM}_{14({t}_{0})}=\sum_{i=1}^{14}{DM}_{i}$$
(6)
$$+{DM}_{14({t}_{1})}={+DM}_{14({t}_{0})}-\frac{{+DM}_{14({t}_{0})}}{14}{+ +DM}_{{t}_{1}}$$
(7)
$$+{DM}_{14({t}_{i})}=+{DM}_{14({t}_{i-1})}-\frac{+{DM}_{14({t}_{i-1})}}{14}{+ +DM}_{{t}_{i}}$$
(8)
$$-{DM}_{14({t}_{1})}={-DM}_{14({t}_{0})}-\frac{{-DM}_{14({t}_{0})}}{14}{+ -DM}_{{t}_{1}}$$
(9)
$${-DM}_{14({t}_{i})}={-DM}_{14({t}_{i-1})}-\frac{{-DM}_{14({t}_{i-1})}}{14}{+ -DM}_{{t}_{i}}$$
(10)

The directional indicator (DI) is calculated as a quotient of smoothed plus or minus DM and smoothed TR (see Eqs. 11–12); thus, it reflects the percent of the TR that is up or down for the day. Important to notice is that, on a specific day, only one from both states finds application + DI or – DI because having DMs in opposite directions on one day is impossible.

$${+DI}_{14\left(t\right)}=\frac{{+DM}_{14\left(t\right)}}{{TR}_{14\left(t\right)}}\bullet 100\%$$
(11)
$${-DI}_{14\left(t\right)}=\frac{{-DM}_{14\left(t\right)}}{{TR}_{14\left(t\right)}}\bullet 100\%$$
(12)

True DM (TDM) is calculated as the difference between + DI and – DI (see Eq. 13). TDM provides information on part of the price movement, which is a non-DM.

$${TDM}_{t}={+DI}_{14(t)}-{-DI}_{14(t)}$$
(13)

The DM index (DX) is the quotient of a TDM and the sum of a + DI and a – DI (see Eq. 14).

$${DX}_{t}=\frac{{TDM}_{t}}{{+DI}_{14(t)}+{-DI}_{14(t)}}\bullet 100\%$$
(14)

After smoothing the DX over 14 days, we received an ADX. The applied technique is analogous to that previously described (see Eqs. 15–16).

$${ADX}_{14({t}_{0})}=\sum_{i=1}^{14}{ADX}_{i}$$
(15)
$${ADX}_{({t}_{i})}=\frac{13\times {ADX}_{({t}_{i-1})}+{DX}_{{t}_{i}}}{14}$$
(16)

The ADX is normalized between 0 and 100. If the ADX is higher than 25, then prices are accepted as following a strong trend. + DI and – DI are used as support lines for ADX. Both lines are an indicator of a direction of the DM and complement the ADX indicator, which reflects the strength of the DM and, thus, is important to interpreting both the ADX and DI indicators together. If the DM is up—the upper trend is considered—then + DI > – DI. If the direction is down, then + DI < – DI.

2.2 VAR and VECM

To analyze the relationship between a given time series, we used a VAR formulated by Sims (1980). An analysis of the relationship between time series is complex and complicated. Often, the dependent variables are modeled not only by a set of explanatory variables but also might depend on their historical observations and/or historical values of the independent variables. VARs allow for a simultaneous analysis of this type of relationship. An important advantage of this model is a lack of restrictions concerning the division of variables into endogenous and exogenous. This model also allows for an analysis of the bidirectional relation, that is, when two variables interact with each other. Following Lütkepohl (2005), a VAR model of order p (VAR(p)) can be described as follows:

$${y}_{t}=v+{A}_{1}{y}_{t-1}+\dots +{A}_{p}{y}_{t-p}+{u}_{t}; t=0,\pm 1,\pm 2,\dots$$

where:

\(v={\left({v}_{1},\dots ,{v}_{K }\right)}^{^{\prime}}\) is a (Kx1) intercept vector, Ai is the coefficient matrix, \({y}_{t}={\left({y}_{1t},\dots ,{y}_{Kt }\right)}^{^{\prime}}\) is a (Kx1) random vector, \({u}_{t}={\left({u}_{1t},\dots ,{u}_{Kt }\right)}^{^{\prime}}\) is a K-dimensional white noise or an innovation process.

Vector-autoregressive models can be applied to stationary time series. A process is assumed to be strict stationarity if the joint distribution of consecutive vectors remains unchanged at each point in time. This process can be described as stationary in a broader sense if all yt have the same mean vector μ and the autocovariances of the process do not depend on time but solely on the distance between them.

To investigate whether a considered time series follows a stationary process, a Dickey–Fuller test is applied, which verifies the presence of a unit root under the null hypothesis (\({H}_{0}: \delta =0\)) versus an alternative hypothesis, which assumes process stationarity (\({H}_{1}: \delta <0)\). However, the financial time series are often not stationary and are characterized by, for example, trends. The detection of the existence of a unit root points at the non-stationary, and further differentiation is required. If an underlying non-stationary time series can be brought to a stationary one as a result of d-times differentiation, then the process is assumed to be integrated of order d. A vector time series is integrated of order d if at least one time series is integrated of order d (Lau 1999). Following Engle and Granger (1987), if two time series yt and xt are integrated of order d, then the combination of these two time series are also integrated of order d [I(d)]. Two time series are cointegrated of order (d, b) if their combination can be written in the form \({z}_{t}={y}_{t}-\alpha -\beta {x}_{t}\), which is I(d-b) and b > 0.

The error correction model (ECM) is a concept presented by Engle and Granger (1987). They proved that if yt and xt are cointegrated of order (1,1), an ECM written in the following form must exist:

$$\Delta {y}_{t}={\theta }_{0}+{\theta }_{1}{z}_{t-1}+\sum {\theta }_{2i}\Delta {x}_{t-i}+\sum {\theta }_{3i}\Delta {y}_{t-i}+{\varepsilon }_{t} ()$$

where:

\(\Delta {y}_{t}={y}_{t}-{y}_{t-1}\) and \(\Delta {x}_{t}={x}_{t}-{x}_{t-1}\)

$${\varepsilon }_{t}\sim iid(0, {\sigma }_{\varepsilon }^{2})$$

Zt−1–disequilibrium between yt and xt in the period t − 1.

A K-dimensional process is assumed to be cointegrated if of order (d,b), if all yt are integrated of order d, and a linear combination \({z}_{t}={\beta }^{^{\prime}}{y}_{t}\) exists, with \({\beta }^{^{\prime}}\ne 0\), such that \({z}_{t}\sim I(d-b)\). The ECM assumes that every economic process tends to its equilibrium in either the short or long-term. The concept of cointegration is used to investigate the issue of long-term equilibrium. If there exists a long-term relationship between xt and yt, then zt is assumed to be an equilibrium error, which is understood as a deviation from the equilibrium for any point in time. Through the error correction mechanism, this error is corrected in the short-term, meaning between two successive periods.

3 Empirical results

3.1 Data

We analyzed daily bitcoin prices and volume from 14.01.2015 to 22.12.2019. All of the data were obtained from the Coinbase exchange, one of the largest and most popular cryptocurrency exchanges. The ADX was calculated on the basis of prices and following Wilder’s algorithm described in detail in Sect. 2.1. To ensure data comparability for further analyses, a similar logic was adopted for the volume data. In Table 1, the main descriptive statistics for the two variables used in the VECM calculated separately for up and down price movements were presented. The time series for the downward price movement (1,163) is observed to be almost twice as long as for the upward price movement (603), which indicates that bitcoin is much more sensitive to bad news that appears on the market. In contrast, getting back to equilibrium after a price decline might also take longer and might point to investors’ limited trust in financial assets such as cryptocurrencies.

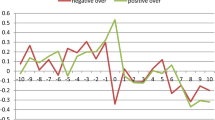
Table 1 Descriptive statistics for two variables used in VECM calculated separately for up and down price movements
Full size table

Figures 1, 2 and 3 present ADX and VOL development between 09.02.2015 and 22.12.2019 in the full sample (Fig. 1) separately for the upward (Fig. 2) and downward trends (Fig. 3). All figures show some co-movement between volume and the strength of a trend reflected by the ADX. However, differences are observed between the trends. Larger ADX fluctuations occur in the upward trend but are shorter and not always supported by volume development. Different situations are observed for the bearish market. Trends last longer, and only a few strong picks are observed throughout the entire period. In the first few years of bitcoin development before 2017, the ADX and VOL were not substantially interconnected. During this period, stronger volume fluctuations were observed in connection with the upward trend, which points to the boom optimism and speculative trend among investors. The period after 2016 supports the opinion that the cryptocurrency market is developing and becoming more mature. For both trends, the volume increased was more strongly interconnected with price changes.

Fig. 1
figure 1

Source: own calculations

ADX and VOL development between 09.02.2015 and 22.12.2019.

Full size image
Fig. 2
figure 2

Source: own calculations

ADX and VOL development between 09.02.2015 and 22.12.2019 for the upward trend.

Full size image
Fig. 3
figure 3

Source: own calculations

ADX and VOL development between 09.02.2015 and 22.12.2019 for the downward trend.

Full size image

3.2 Model estimation

The VAR model was selected for the analysis, which is extended by the ECM when detecting non-stationarity (Hunter et al. 2017). First, we performed a Dickey–Fuller test to check for the unit roots. Three types of tests were performed: (1) test for a unit root, (2) test for a unit root with drift, and (3) test for a unit root with drift and deterministic time trend. The null hypothesis assuming non-stationarity was verified. The results, which are summarized in Table 2, indicate that both variables for both trends are characterized by unit roots (p > 0.05). Therefore, the second test for the first differences was performed, according to which it can be assumed that the analyzed time series are integrated of order 1.

Table 2 Results of Dickey–Fuller unit root test for original time series and after one differentiation for both upward and downward trends
Full size table

The assumption for the application of the VECM is that the series is integrated of the same order d (d(I)) and at least one cointegrating vector exists, such as the combination of the time series after differentiation is stationary (Stock 1987). Therefore, to detect the rank order of the cointegration, the Johansen Cointegration rank test using trace is performed. The results are summarized in Table 3 and show that, in both cases, one cointegration vector of order 1 exists. Moreover, the processes have a linear drift before differencing, and the ECM is characterized by the constant drift.

Table 3 Cointegration rank test using trace
Full size table

The aforementioned results were considered, and the VECM was applied. The order of VECM was estimated based on the minimal information criterion (Table 4). For the downward trend, the VECM(4) was a fit, and the VECM(3) was a fit for the upward trend. The model estimation results are summarized in Table 5. The results indicate that the fit models are statistically significant at the 1% level and moderate, with no autocorrelation among the residuals.

Table 4 Minimal information criterion for VECM estimation
Full size table
Table 5 Vector error correction model estimation results
Full size table

The long-term equilibrium parameter estimates and adjustment coefficient estimates of VAR(4) for the downward trend and VAR(3) for the upward trend are summarized in Table 6. The model estimation results are summarized in Tables 7 and 8. The adjustment coefficients are used to control for the transitory deviation in the estimation of the long-term equations. β = 1 points to the normalized variable. For the estimated parameters, we received desirable signs for the beta parameters, which points to stable adjustments toward equilibrium. The cointegration vector for the downward and upward trends for the ADX and VOL variables, respectively, have the form \(\widehat{{\beta }_{1ADX}}=\left(1, -0.0003\right), \widehat{{\beta }_{2ADX}}=(1, -0.0000)\), \(\widehat{{\beta }_{1VOL}}=(-30749, 1)\), and \(\widehat{{\beta }_{2VOL}}=(-3329456, 1)\). In both analyzed cases, the ADX reveals a very low adjustment tendency (close to zero) for both bearish and bullish markets.

Table 6 Parameter estimated for VECM including normalization for downward and upward trends
Full size table
Table 7 Estimation results of VECM for the downward trend
Full size table
Table 8 Estimation results of VECM for the upward trend
Full size table

The error correction term for the downward trend has the form:

$${ADX}_{t}={ADX}_{t-1}-0.00044\left({ADX}_{t-1}-0.00003{VOL}_{t-1}\right)$$
$${VOL}_{t}={VOL}_{t-1}+2706({VOL}_{t-1}-0.00003ADX)$$

and has the following form for the upward trend:

$${ADX}_{t}={ADX}_{t-1}-1.3\left({ADX}_{t-1}-0.000{VOL}_{t-1}\right)$$
$${VOL}_{t}={VOL}_{t-1}+81593({VOL}_{t-1}-0.000ADX)$$

Therefore, if no long-term equilibrium exists in t − 1, then the disequilibrium tends to decrease in time t. For the ADX, the adjustment is negligible in both cases. Hence, no long-term relationship between ADX and VOL can be assumed. The volume size adjustment speed is more significant—close to one in a bearish market and very slow in a bullish market, or close to zero.

The short-term dynamic estimation shows differences between the upward and downward trends regarding the interdependence between the ADX and VOL. The model specification for the downward trend has the following form:

$$\begin{array}{c}{\Delta VOL}_{t}\\ \Delta {ADX}_{t}\end{array}=\left( \begin{array}{cc}-0.88& 27 066.44\\ 0& -0.00044\end{array}\right)\begin{array}{c}{VOL}_{t-1}\\ {ADX}_{t-1}\end{array}+\left(\begin{array}{cc}-0.12& -0\\ -0.095& -0\\ -0.05& 0\end{array}\right)\begin{array}{c}{\Delta VOL}_{t-1}\\ \Delta {VOL}_{t-2}\\ {\Delta VOL}_{t-3}\end{array}+\left(\begin{array}{cc}-17 861.94& -0.60\\ -52 723.85& -0.31\\ -24 324.54& -0.13\end{array}\right)\begin{array}{c}{\Delta ADX}_{t-1}\\ \Delta {ADX}_{t-2}\\ {\Delta ADX}_{t-3}\end{array}+{\varepsilon }_{t}$$

and has the following form for the upward trend:

$$\begin{array}{c}{\Delta VOL}_{t}\\ \Delta {ADX}_{t}\end{array}=\left(\begin{array}{cc}-0.02451& 0\\ 81 593.47& -1.299\end{array}\right)\begin{array}{c}{VOL}_{t-1}\\ {ADX}_{t-1}\end{array}+\left(\begin{array}{cc}-0.60323& -0\\ -0.22278& -0\end{array}\right)\begin{array}{c}{\Delta VOL}_{t-1}\\ {\Delta VOL}_{t-2}\end{array}+\left(\begin{array}{cc}-106 646.12& 0.18\\ -63 739.72& 0.03\end{array}\right)\begin{array}{c}{\Delta ADX}_{t-1}\\ {\Delta ADX}_{t-2}\end{array}+{\varepsilon }_{t}$$

In the bearish market, VOL is invariant to changes in the ADX (p > 0.05). Only the first two differences are statistically significant, but their impact on volume is close to zero and, hence, can be neglected. In the bullish market, volume depends on its first two differences. The ADX is statistically insignificant at the 5% level but is significant at the 10% level; hence, volume might be assumed to also be sensitive to changes in the strength of the trend. Therefore, positive information from the cryptocurrency market encourages investors to make stronger entrances into the market, which can cause bubbles and further drive price increases. The strength of the trend in the bullish market is sensitive at the 1% level to the first three differences of ADX and to the differences in VOL; however, the impact of the accommodation on the volume equals zero and, hence, can be neglected. Therefore, the results are comparable with the one for the bullish market. The results of the VECM for ADX suggests that the model should be reduced to VECM(2) instead of VECM(3) because the second differences of both variables are statistically insignificant. The first differences of both variables are significant, but the volume has zero effect on the ADX; hence, the ADX reacts only to its changes. Therefore, the strength of the trend in the bullish market is driven by itself and without support from the change in volume.

To verify the estimated models, we performed a stability test of VECM and checked for the residuals’ autocorrelation and normality. The received results confirmed the stability of the estimated models because only one Eigenvalue was reported, whereas the others are far from one. The autocorrelation among the residuals was not confirmed by the Portmanteau test (p > 0.05). The residuals failed to pass the normality check (p < 0.001). However, such a normality test result does not affect the model’s stability but might signal model improvement (Belsley and Kontoghiorghes 2009).

4 Conclusion

Technical analysts and traders expect that price changes are positively correlated with volume. However, the researcher did not fully confirm such a relationship. The dependency between price and volume might change regarding the investigated markets and considered assets. Our findings support this thesis. The results showed that no long-term relationship exists between the strength of a trend and volume in both bearish and bullish markets. Hence, a trend does not react to changes in volume. However, a long-term relationship exists between volume and trend, but only the downward trend with the adjustment speed of 88%. In the short-term, the strength of a trend and, hence, the price in both bullish and bearish markets is invariant to volume changes; however, the volume is sensitive to price changes, especially for the upward trend. The detected relationship is unidirectional, meaning that positive information from the cryptocurrency market encourages investors to make a stronger entrance into the market, which causes bubbles and further drives price increases. These results are in line with the findings based on the Toda–Yamamoto linear causality presented by, for example, Sahoo et al. (2019) and Balcilar et al. (2017), who also compared bullish and bearish markets and found no dependency between price and volume.

Further research in this field should include more variables that could fully explain bitcoin’s price and volume development.