1 Introduction

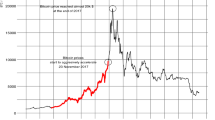
Cryptocurrencies have attracted considerable attention since their recent creation and experienced huge swings. For instance, in 2017 Bitcoin prices rose by more than 20 times, but in early 2018 fell by 70%; similar sharp drops had in fact already occurred 5 times before (June 2011, January 2012, April 2013, November 2013, December 2017). Such significant deviations of asset prices from their average values during certain periods of time are known as overreactions and have been widely analysed in the literature since the seminal paper of De Bondt and Thaler (1985), various studies being carried out for different markets (stocks, FOREX, commodities etc.), countries (developed and emerging), assets (stock prices/indices, currency pairs, oil, gold etc.), and time intervals (daily, weekly, monthly etc.). However, hardly any evidence is available to date on the cryptocurrency market, which is particularly interesting because of its extremely high volatility compared to the FOREX or stock market (see Caporale and Plastun 2018a for details). In the most recent years interest in the cryptocurrency market has increased even further, and price prediction has been investigated in various studies (Ciaian et al. 2016; Balcilar et al. 2017; Khuntia and Pattanayak 2018; Al-Yahyaee et al. 2019 and many others). However, the evidence is still mixed.

The present paper aims to analyse the role of the frequency of overreactions, specifically whether or not it can help predict price behaviour and/or exhibits seasonality, by using daily prices for BitCoin over the period 2013–2018. Overreactions are detected by plotting the distribution of logreturns. Then, the following null hypotheses are tested: (i) the frequency of overreactions is informative about BitCoin price movements (H1), and (ii) it exhibits no seasonality (H2). For this purpose a variety of statistical methods (parametric and non-parametric) are used such as ADF tests, Granger causality tests, correlation analysis, regression analysis with dummy variables, ARIMA and ARMAX models, neural net models, and VAR models.

The remainder of the paper is organised as follows. Section 2 contains a brief review of the literature on price overreactions in the cryptocurrency market. Section 3 describes the methodology. Section 4 discusses the empirical results. Section 5 provides some concluding remarks.

2 Literature review

According to Hileman and Rauchs (2017) there were more than 300 academic papers devoted to the cryptocurrency market published before the crypto boom; their number has increased further since then. The cryptocurrency market is still relatively young and as a result papers have initially analysed some of its general features (Dwyer 2015a, b; Elbahrawy et al. 2017) or properties such as competitiveness (Halaburda and Gandal 2014). There is only a limited number of studies examining instead its long memory and persistence (Caporale et al. 2018c; Bariviera 2017; Urquhart 2016), efficiency (Urquhart 2016; Bartos 2015), correlations between different cryptocurrencies (Halaburda and Gandal 2014), price predictability (Brown 2014), volatility (Cheung et al. 2015; Carrick 2016).

Bariviera (2017) finds evidence of long memory in the daily dynamics of BitCoin; they also show that persistence in the cryptocurrency market is decreasing. Similar conclusions are reached by Bouri et al. (2016) and Catania and Grassi (2017).

Aggarwal (2019) examines Bitcoin returns and finds strong evidence of market inefficiency (see also Urquhart 2016). Calendar anomalies in the cryptocurrency market are analysed by Kurihara and Fukushima (2017) and Caporale and Plastun (2018c), intraday patterns are explored by Eross et al. (2017), the overreaction hypothesis is tested by Caporale and Plastun (2018a).

Ma and Tanizaki (2019) analyse the day-of-the-week effect for both returns and their volatility in the cryptocurrency market, and find significantly high volatilities on Monday and Thursday. Similar results are reported by Aharon and Qadan (2018). Eross et al. (2019) analyse the intraday dynamics of Bitcoin and find that the trade volume in the cryptocurrency market increases during the day and falls from around 4 pm until midnight.

Caporale and Plastun (2018a) explore overreactions in the cryptocurrency market and find price patterns after overreactions: the next-day price changes in both directions are bigger than after “normal” days. Analysing overreactions in the case of the cryptocurrency market is particularly interesting because of its extreme volatility (see Caporale and Plastun 2018a; Cheung et al. 2015 and Dwyer 2015a, b). Also, its average daily price amplitude is up to 10 times higher than in the FOREX or stock market (see Table 1).

Table 1 Comparative analysis of the average daily price amplitude in different financial markets. Source: Caporale and Plastun (2018a)
Full size table

Further, the log return distribution of prices has unusually fat tails (see Table 18), which suggests their being prone to overreactions, which can be helpful to predict future prices and crises. Catania and Grassi (2017) show that price behaviour in the cryptocurrency market is quite complex, with outliers, asymmetries and nonlinearities that are difficult to model.

Al-Yahyaee et al. (2019) try to predict Bitcoin prices using information from a Volatility Uncertainty Index (VIX), whilst Mensi et al. (2019) find evidence of co-movement between Bitcoin and five major cryptocurrencies (Dash, Ethereum, Litecoin, Monero and Ripple). Balcilar et al. (2017) show that information about trade volumes can be used to predict returns in the cryptocurrency market. Aharon and Qadan (2018) show that normally used variables have limited forecasting power for Bitcoin prices. Khuntia and Pattanayak (2018) explore time-varying linear and nonlinear dependence in Bitcoin returns. Kristoufek (2014) finds that the trade-exchange ratio plays an essential role in driving Bitcoin price fluctuations in the long run. Ciaian et al. (2016) show that the total number of unique Bitcoin transactions per day is an important determinant of Bitcoin price fluctuations.

Another issue investigated in the literature is whether overreactions exhibit seasonality. De Bondt and Thaler (1985) show that they tend to occur mostly in a specific month of the year, whilst Caporale and Plastun (2018b) do not find evidence of seasonal behaviour in the US stock market. Note also that according to Khuntia and Pattanayak (2018) market efficiency in the cryptocurrency market is evolving over time. Caporale and Plastun (2018a) find evidence in favour of the overreaction hypothesis, whilst Bartos (2015) report that the cryptocurrency market immediately reacts to the arrival of new information and absorbs it; as a result prices are not affected by overreactions.

Whilst most studies examine abnormal returns and the subsequent price behaviour (in general, contrarian movement) for a given time interval (day, week, and month), the current paper focuses on the frequency of abnormal price changes. Only a few papers have considered this issue in the case of the FOREX or stock market (see Govindaraj et al. 2014; Angelovska 2016), and none in the case of the cryptocurrency market. We will aim to show that the frequency of abnormal price changes can be a useful tool for price predictions in the cryptocurrency market.

3 Methodology

The first step in the analysis of overreactions is their detection. There are two main methods. One is the dynamic trigger approach, which is based on relative values. Wong (1997) and Caporale and Plastun (2018a) in particular propose to define overreactions on the basis of the number of standard deviations to be added to the average return. The other is the static approach which uses actual price changes as an overreaction criterion. For example, Bremer and Sweeney (1991) use a 10% price change as a criterion. Caporale and Plastun (2018b) compare these two methods in the case of the US stock market and show that the static approach produces more reliable results. Therefore, this will also be used here.

The static approach was introduced by Sandoval and Franca (2012) and developed by Caporale and Plastun (2018b). Returns are defined as:

$$ S_{t} = \ln \left( {P_{t} } \right) - \ln \left( {P_{t - 1} } \right) $$
(1)

where \( S_{t} \) stands for returns, and \( P_{t} \) and \( P_{t - 1} \) are the close prices of the current and previous day. The next step is analysing the frequency distribution by creating histograms. We plot values 10% above or below those of the population. Thresholds are then obtained for both positive and negative overreactions, and periods can be identified when returns were above or equal to the threshold.

Such a procedure generates a data set for the frequency of overreactions (at a monthly frequency), which is then divided into 3 subsets including, respectively, the frequency of negative and positive overreactions, and of them all. In this study we also use an additional measure (named the “Overreactions multiplier”), namely the negative/positive overreactions ratio:

$$ {\text{Overreactions}}\;{\text{multiplier}}_{i} = \frac{{{\text{frequency}}\;{\text{of}}\;{\text{negative}}\;{\text{overreactions}}_{i} }}{{{\text{frequency}}\;{\text{of}}\;{\text{positive}}\;{\text{overreactions}}_{i} }} $$
(2)

Then, the following hypotheses are tested:

Hypothesis 1 (H1)

The frequency of overreactions is informative about price movements in the cryptocurrency market.

There is a body of evidence suggesting that typical price patterns appear in financial markets after abnormal price changes. The relationship between the frequency of overreactions and BitCoin prices is investigated here by running the following regressions (see Eqs. 3 and 4):

$$ Y_{t} = a_{0} + a_{1}^{ + } D_{1t}^{ + } + a_{1}^{ - } D_{1t}^{ - } + \varepsilon_{t} $$
(3)

where \( Y_{t} \) are BitCoin log differences on day t; an are BitCoin mean log differences; \( a_{1}^{ + } \;(a_{1}^{ - } ) \) are coefficients on positive and negative overreactions, respectively; \( D_{1n}^{ + } \;\left( {D_{1n}^{ - } } \right) \) is a dummy variable equal to 1 on positive (negative) overreaction days, and 0 otherwise; \( \varepsilon_{t} \) is a random error term at time t.

$$ Y_{t} = a_{0} + a_{1} {{O}}_{t}^{ + } + a_{2} {{O}}_{t}^{ - } + \varepsilon_{t} $$
(4)

where \( Y_{t} \) are BitCoin log differences on day t;\( a_{0} \) are BitCoin mean log differences; a1 (a2) are coefficients on positive and negative overreactions, respectively; \( {{O}}_{t}^{ + } \;\left( {{{O}}_{t}^{ - } } \right) \) is the number of positive (negative) overreaction days during a period t; \( \varepsilon_{t} \) is a random error term at time t.

The size, sign and statistical significance of the coefficients provide information about the possible influence of the frequency of overreactions on BitCoin log returns.

To assess the performance of the regression models a multilayer perceptron (MLP) method will be used (Rumelhart and McClelland 1986). This method is based on neural networks modelling. The algorithm is as follows. The data is divided into 3 groups: the learning group (50%), the test group (25%), and the control group (25%). The learning process in the neural network consists of 2 stages: the first stage is based on an inverse distribution method (number of periods − 100, training speed − 0.01) and the second uses a conjugate gradient method (number of periods − 500). This procedure generates an optimal neural net. The results from the neural net are then compared with those from the regression analysis.

To obtain further evidence an ARIMA(p, d, q) model is also estimated:

$$ Y_{t} = a_{0} + \sum\limits_{i = 1}^{p} {\psi_{t - i} Y_{t - i} } + \sum\limits_{j = 1}^{q} {\theta_{t - j} \varepsilon_{t - j} } + \varepsilon_{t} $$
(5)

where \( Y_{t} \) are BitCoin log differences on day t; a0 is a constant; \( \psi_{t - i} ;\;\theta_{t - j} \) are coefficients of the log differences on day t − i and a random error term at time t − j, respectively; \( Y_{{t - {\text{i}}}} \) are BitCoin log differences on day t − i;\( \varepsilon_{t - j} \) is a random error term at time t − j; \( \varepsilon_{t} \) is a random error term at time t.

To improve the basic ARIMA(p, d, q) specification additional variables are then added, namely the frequency of negative and positive overreactions, respectively:

$$ Y_{t} = a_{0} + \sum\limits_{i = 1}^{p} {\psi_{t - i} Y_{t - i} } + \sum\limits_{i = 1}^{q} {\theta_{t - i} \varepsilon_{t - i} } + \sum\limits_{i = 1}^{{s_{1} }} {a_{t - i} OF_{t - i}^{ - } } + \sum\limits_{i = 1}^{{s_{2} }} {b_{t - i} OF_{t - i}^{ + } + \varepsilon_{t} } $$
(6)

Information criteria, specifically AIC (Akaike 1974) and BIC (Schwarz 1978), are used to select the best ARMAX specification for BitCoin log returns.

As a robustness check, VAR models are also estimated:

$$ y_{t} = a_{0} + \sum\limits_{i = 1}^{p} {A_{i} y_{t - i} } + \varepsilon_{t} $$
(7)

where \( y_{t} = \left( {y_{t}^{1} ,y_{t}^{2} , \ldots ,y_{t}^{k} } \right) \) is a time series vector; At is a time-invariant matrix; a0 is a vector of constants; \( \varepsilon_{t} \) is a vector of error terms. Impulse response functions (IRFs) are then computed and Variance Decomposition (VD) is also carried out. In addition, Granger causality tests (Granger 1969) and Augmented Dickey-Fuller tests (Dickey and Fuller, 1979) are performed.

Hypothesis 2 (H2)

The frequency of overreactions exhibits no seasonality.

We perform a variety of statistical tests, both parametric (ANOVA analysis) and non-parametric (Kruskal–Wallis tests), for seasonality in the monthly frequency of overreactions, which provides information on whether or not overreactions are more likely in some specific months of the year.

4 Empirical results

The data used are BitCoin daily and monthly prices for the period 01.05.2013-31.05.2018; the data source is CoinMarket (https://coinmarketcap.com/). As a first step, the frequency distribution of log returns is analysed (see Table 18 and Fig. 6). As can be seen, two symmetric fat tails are present in the distribution. The next step is the choice of thresholds for detecting overreactions. To obtain a sufficient number of observations we consider values ± 10% of the average from the population, namely − 0.04 for negative overreactions and 0.05 for positive ones. Detailed results are presented in Appendix 2.

Visual inspection of Figs. 7 and 8 suggests that the frequency of overreactions varies over time (see Table 19). To provide additional evidence we carry out ANOVA analysis and Kruskal–Wallis tests (Table 2); both confirm that the differences between years are statistically significant, i.e. that the frequency of overreactions is time-varying.

Table 2 Results of ANOVA and non-parametric Kruskal–Wallis tests for statistical differences in the frequency of overreactions between different years
Full size table

Next we carry out a correlation analysis. Table 3 reports the results for different parameters, namely the number of negative (Over_negative) and positive overreactions (Over_positive), as well as the total number of overreactions (All_over) and the overreactions multiplier (Over_mult) and indicators (BitCoin close prices, BitCoin returns, BitCoin logreturns).

Table 3 Correlation analysis between the frequency of overreactions and different BitCoin series indicators
Full size table

There appears to be a positive (rather than negative, as one would expect) correlation between BitCoin prices and negative overreactions. By contrast, there is a negative correlation in the case of returns and log returns. The overreaction multiplier exhibits a rather strong negative correlation with BitCoin log returns. Finally, the overall number of overreactions has a rather weak correlation with prices.

To make sure that there is no need to shift the data in any direction we carry out a cross-correlation analysis of these indicators at the time intervals t and t + i, where I ∈ {− 10,…,10}. Figure 1 reports the cross-correlation between Bitcoin log returns and the frequency of (both positive and negative) overreactions for the whole sample period for different leads and lags. The highest coefficient corresponds to lag length zero, which means that there is no need to shift the data.

Fig. 1
figure 1

Cross-correlation between Bitcoin log returns and frequency of overreactions over the whole sample period for different leads and lags. This figure displays the correlation coefficients between BitCoin log returns and the frequency of negative overreactions (“negative over”) as well as the frequency of positive overreactions (“positive over”) over the whole sample period with lags in the interval [− 10,…. + 10]

Full size image

To analyse further the relationship between BitCoin log returns and the frequency of overreactions we carry out ADF tests on the series of interest (see Table 4).

Table 4 Augmented Dickey–Fuller test: BitCoin log returns and overreactions frequency data
Full size table

The unit root null is rejected in most cases implying stationarity. The next step is testing H1 by running a simple linear regression and one with dummy variables (see Sect. 3 for details). The results for BitCoin closes, returns and log returns regressed against all overreactions, negative and positive overreactions are presented in Tables 5, 6, and 7, respectively. In all three cases the specification with the highest explanatory power is the one including negative and positive overreactions as separate variables, though in the case of BitCoin closes the positive sign of the coefficient on negative overreactions is not what one would expect.

Table 5 Regression analysis results: BitCoin closes
Full size table
Table 6 Regression analysis results: BitCoin returns
Full size table
Table 7 Regression analysis results: BitCoin log returns
Full size table

To sum up, consistently with the theoretical priors, the total number of overreactions is not a significant regressor in any case. The best specification is the simple linear multiplier regression model with the frequency of positive and negative overreactions as regressors, and the best results are obtained in the case of log returns as indicated by the multiple R for the whole model and the p-values for the estimated coefficients. Specifically, the selected specification is the following:

$$ {\text{Bitcoin}}\;\log \;{\text{return}}_{i} = 0.0645 - 0.0939 \times {{O}}F_{i}^{ - } + 0.1013 \times {{O}}F_{i}^{ + } $$
(8)

which implies a strong positive (negative) relationship between Bitcoin log returns and the frequency of positive (negative) overreactions. On the whole, the above evidence supports H1. The difference between the actual and estimated values of Bitcoin can be seen as an indication of whether Bitcoin is over- or under-estimated and therefore a price increase or decrease should be expected. Obviously, BitCoin should be bought in the case of undervaluation and sold in the case of overvaluation till the divergence between actual and estimated values disappears, at which stage positions should be closed.

As mentioned before, to show that the selected specification is indeed the best linear model we use the multilayer perceptron (MLP) method. Negative and positive overreactions are the independent variables (the entry points) and log returns are the dependent variable (the exit point) in the neural net. The learning algorithm previously described generates the following optimal neural net MLP 2-2-3-1:1 (Fig. 2).

Fig. 2
figure 2

Optimal neural net structure. This figure displays the optimal neural network structure: the entry points (red and pink triangles), neural network methods (learning, control, test; the green, pink and red squares, respectively), and the exit point (BitCoin log returns; the pink square on the right)

Full size image

We compare it with the linear neural net L 2-2-1:1 model, which consists of 2 inputs and 1 output. The results are presented in Tables 8 and 9.

Table 8 Comparative characteristics of neural networks
Full size table
Table 9 Quality comparison of neural networks
Full size table

As can be seen, the neural net based on the multilayer perceptron structure provides better results than the linear neural net: the control error is lower (0.0392 (MLP) vs 0.0801(L)); the standard deviation error and the data ratio are also lower (0.4673 vs 0.5078); the correlation is higher (0.8844 vs 0.8719).

Figure 3 shows the distribution of BitCoin log returns, actual vs estimated (from the regression model and the neural network).

Fig. 3
figure 3

Distribution of BitCoin log returns: actual vs estimated (from the regression model and the neural network). This figure presents estimates and comparison between actual BitCoin log returns (“actual data”) and estimates based both on the regression model (“regression (7)”) and the neural network model (“neural network”) over the sample period considered

Full size image

As can be seen the estimates (from the regression model and the neural network, respectively) are very similar and very close to the actual values, which suggests that the regression model (Eq. 8) captures very well the behaviour of BitCoin prices.

We also estimate ARIMA(p, d, q) models with \( p \le 3;\;q \le 3;\;d = 0 \) choosing the best specification on the basis of the AIC and BIC information criteria. Specifically, we select the following models: ARIMA(2, 0, 2) (on the basis of the AIC criterion); ARIMA(1, 0, 0) and ARIMA(0, 0, 1) (on the basis of the BIC criterion). The parameter estimates are presented in Table 10.

Table 10 Parameter estimates for the best ARIMA models
Full size table

As can be seen, Model 1 captures best the behaviour of BitCoin log returns: all regressors are significant at the 1% level, except \( \psi_{t - i} \), and AIC has the smallest value.

To establish whether this specification can be improved by including information about the frequency of overreactions, ARMAX models (see Eq. 6) are estimated adding as regressors \( {{O}}F_{t}^{ - } \) (negative overreactions) and \( {{O}}F_{t}^{ + } \) (positive overreactions). The estimated parameters are reported in Table 11. Model 4 adds the frequency of negative overreactions and positive overreactions to Model 1. Model 5 is a version of Model 4 chosen on the basis of the AIC and BIC criteria.

Table 11 Estimated parameters for the ARMAX models
Full size table

Clearly, Model 5 is the best specification for modelling BitCoin log returns: all parameters are statistically significant (except \( b_{t - 6} \)), and there is no evidence of misspecification from the residual diagnostic tests. Figure 4 plots the estimated and actual values of BitCoin log returns.

Fig. 4
figure 4

Distribution of BitCoin log returns: actual vs estimated (based on Model 5). This figure presents comparison between actual BitCoin log returns (“actual data”) and estimates based on model 5 (“calculated data”) over the sample period considered

Full size image

Table 12 reports Granger causality tests between BitCoin log returns and both negative (OF−) and positive overreactions (OF+). As can be seen, the null hypothesis of no causality is rejected for negative (OF−) and positive overreactions (OF+), but not for BitCoin log returns (Y), and therefore there is evidence that forecasts of the latter can be improved by including in a VAR specification the two former variables. The optimal lag length implied by both the AIC and BIC criteria is one (see Table 13). The estimates for the VAR(1)-model are reported in Table 14.

Table 12 Granger Causality Tests between BitCoin log returns and both negative (OF−) and positive overreactions (OF +)
Full size table
Table 13 VAR lag length selection criteria
Full size table
Table 14 VAR(1) parameter estimates
Full size table

This model appears to be data congruent: it is stable (no root lies outside the unit circle), and there is no evidence of autocorrelation in the residuals. The IRF analysis (see Appendix 3, Figs. 9, 10 and 11 for details) shows that, in response to a 1-standard deviation shock to log returns, both negative (OF−) and positive overreactions (OF+) revert to their equilibrium value within six periods, whereas it takes log returns only one period to revert to equilibrium. There is hardly any response of log returns to shocks to either positive or negative overreactions, whilst both the latter variables tend to settle down after about six periods. The variance decomposition (VD) results are presented in Table 15. They suggest the following:

Table 15 Variance Decomposition
Full size table

  • The behaviour of Y is mostly explained by its previous dynamics (97.4%); \( {{O}}F^{ - } \) accounts for only 0.2% of its variance, and \( {{O}}F^{ + } \) for only 2.4%.

  • The behaviour of \( {{O}}F^{ - } \) is also mainly determined by its previous dynamics (76.7%), with Y explaining only 22.7% of its variance and \( OF^{ + } \) only 0.6%.

  • The behaviour of \( OF^{ + } \) is mostly accounted for by the \( OF^{ - } \) dynamics (43%), with Y explaining 36.9% of its variance and \( OF^{ + } \) 20.1%.

Finally, we address the issue of seasonality (H2). Figure 5 suggests that the overreactions frequency tends to be higher at the end and the start of the year and lower at other times. Also, there appears to be a mid-year cycle: the frequency starts to increase in April, peaks in June-July and then falls till September with a “W” seasonality pattern.

Fig. 5
figure 5

Monthly seasonality in the overreaction frequency. This figure presents the frequency of price overreactions by month over the whole sample period. “Negative over” represents the frequency of negative overreactions; “Positive over” represents the frequency of positive overreactions; “Overall” represents the overall frequency of overreactions

Full size image

Formal parametric (ANOVA) and non-parametric (Kruskal–Wallis) tests are performed; the results are presented in Tables 16 and 17. As can be seen, there are no statistically significant differences between the frequency of overreactions in different months of the year (i.e. no evidence of seasonality), i.e. H2 cannot be rejected, which is consistent with the visual evidence based on Fig. 3.

Table 16 Parametric ANOVA of monthly seasonality in the overreaction frequency
Full size table
Table 17 Non-parametric Kruskal–Wallis of monthly seasonality in the overreaction frequency
Full size table

5 Conclusion

This paper investigates the role of the frequency of price overreactions in the cryptocurrency market in the case of BitCoin over the period 2013-2018. Specifically, it uses a static approach to detect overreactions and then carries out hypothesis testing by means of a variety of statistical methods (both parametric and non-parametric) including ADF tests, Granger causality tests, correlation analysis, regression analysis with dummy variables, ARIMA and ARMAX models, neural net models, and VAR models. Specifically, the hypotheses tested are whether or not the frequency of overreactions (i) is informative about Bitcoin price movements (H1) and (ii) exhibits no seasonality (H2).

On the whole, the results suggest that the frequency of price overreactions can provide useful information to predict price dynamics in the cryptocurrency market and for designing trading strategies (H1 cannot be rejected) in the specific case of BitCoin. However, these findings are somewhat mixed: stronger evidence of a predictive role for the frequency of price overreactions is found when estimating neural net and ARMAX models as opposed to VAR models. As for the possible presence of seasonality, the evidence is very clear: no seasonal patterns are detected for the frequency of price overreactions (H2 cannot be rejected).