R&D, innovation and firm survival in Chinese manufacturing, 2000–2006

Abstract

This paper examines whether Chinese manufacturing firms survive longer if they innovate. More particularly, it focuses on whether R&D has a greater effect on firm survival than new product innovations. It compares dichotomous and continuous measures of R&D and innovation output, various duration models, heterogeneity in the effects of innovation depending on the industrial environment, and it examines whether risk modifies the effect of innovation on the hazard rate. The analysis is based on data from the National Bureau of Statistics of China, including over 100,000 firms in each year over the period 1999–2006 from all provinces and manufacturing industries in China. It is found that both R&D and product innovation, be it in terms of incidence or intensities, increase the chance of firm survival. As opposed to previous studies, the results indicate that R&D has a greater marginal effect on survival than innovation output and that various measures of risk actually increase the effect of R&D/innovation on survival.

1 Introduction

In order to increase, or merely to save, their market shares firms compete with each other through prices, but also through the introduction of new products or quality improvements in existing products or services (Baumol, 2002; Schumpeter, 1947). Especially on the international market, China has been able to forge a substantial world market share thanks to its low costs reflected in low prices. But as wages increase, price competition through reduced profit margins becomes less of a viable strategy. As competition gets fiercer, Chinese firms may have to turn to R&D and/or innovation in order to survive or continue growing.

The connection between innovation and firm survival has been investigated in many previous papers with different innovation indicators. Some have used the occurrence or the intensity of R&D, others have used the occurrence or the intensity of innovation output measures, and some have related survival to the use of intellectual property rights. Few studies have investigated whether it is the input or the output of innovation that matters more for firms’ survival. Rosenbusch et al. (2011) conducted from a meta-analysis that investing in innovation (e.g., R&D spending) was less connected to firm survival than the output of innovation itself (i.e. patents or innovative products or services). In this paper, we focus on whether it is the actual introduction of new products on the market or rather the conduct of R&D activities that matter more for firm survival. We also examine whether innovation input and output are complements, whether they depend on competition and R&D intensity at the industry level, and whether there is an optimal level of R&D or product innovation beyond which survival is at risk.

Our analysis is based on a large unbalanced panel of Chinese manufacturing firms stretching from 1999 to 2006 from all provinces of China. Since these are Census data for all firms above a certain size, we are able to identify when a firm enters and exits the sample. The dataset contains qualitative and quantitative data on R&D and product innovations.¹, ²

The paper is organized as follows. Section 2 discusses why firms’ survival might depend on R&D more than on innovation or vice versa. Section 3 presents and describes the data. Section 4 presents the econometric estimators and the explanatory variables used to estimate the hazard rate of firm exit. Section 5 analyzes the results and Sect. 6 concludes.

2 Theoretical background and literature review

In the literature on innovation and firm survival, three types of innovation measures have been used: R&D, innovation output (sometimes decomposed into product, process, organizational and marketing innovations), and intellectual property rights (e.g. patents, trademarks, copyrights). They can show up as dummy variables or as continuous variables. As Ugur and Vivarelli (2021) forcefully argue and document there is a lot of heterogeneity in this relationship depending on the type of innovation and the environment in which firms operate. Table 1 gives a synoptic view of the literature. It is not meant to be an exhaustive list nor does it do justice to all the results contained in the papers mentioned and the sources of heterogeneity identified in Colombelli et al. (2016) and Ugur and Vivarelli (2021). The main purpose here is to compare some of the results obtained with the three types of innovation indicators.

Table 1 Synoptic review of studies on innovation and survival

R&D expenditure has frequently been used as a measure of innovative activities. The relationship has been found to be positive with a possible inverse-U shaped curve. Using panel data on publicly traded firms in the US manufacturing sector from 1976 to 1983, Hall (1987) finds that the intensity of R&D expenditure increases the survival probability, and that this effect is stronger for firms that do not patent. In a study of Spanish manufacturing firms, Pérez et al. (2004) confirm that firms that invest in R&D activities experience a 57% lower risk of exit than firms that do not, and that this effect is enhanced by the international orientation of the firms. Fontana and Nesta (2009) report a positive non-linear relationship between the firm’s R&D effort, or its product innovation record, and the probability of surviving. The same positive relationship is found for the survival of Hong Kong owned firms in Guangdong province by Sharif and Huang (2012). Ugur et al. (2016) find that survival time increases with R&D intensity but at a decreasing rate so as to eventually fall with R&D intensity, i.e. an inverted U-relationship between R&D and survival. They also find the effect of R&D intensity on survival time is higher in more concentrated industries and that an increase in the median R&D intensity at the 3-digit SIC level and an increase in the lending premium reduce the effect of R&D intensity on survival time. Yang et al. (2017) find that R&D combined with other internal resources increases the chances of survival in high-tech start-ups in China.

But R&D is actually an investment in innovation, the outcome of which can be new products, new technologies, new ways of doing things. Therefore, a second group of studies has examined the link between survival and innovation output indicators and also uncovered a positive relationship. Christensen et al. (1998) find that firms that innovate in products with new market segments in the disk drive industry have a significantly higher probability of survival than firms that enter established market segments with better performing new components. Banbury and Mitchell (1995) obtain a positive relationship between survival and the number of new products introduced in the market. Greenstein and Wade (1998) find that firms producing older computer models have a lower chance of surviving in the market. Wojan et al. (2018) also report longer survivals for innovative firms.

The relationship between innovation and survival depends very much on the type of innovation, in particular product versus process and risky vs less risky innovations. According to Baldwin and Gu (2004) process innovation is associated with higher plant survival rates while product innovation is related to lower survival rates in Canadian manufacturing. Cefis and Marsili (2005) on Dutch data and Colombelli et al. (2016) on French data also conclude that process innovation has a direct and positive effect on firm survival, while product innovation influences survival only in combination with process innovation. Børing (2015) finds no relation between innovation and the closure of Norwegian firms but well a higher probability of exit through mergers and acquisitions for firms that innovate only in products new to the market. Hyytinen et al. (2015) report that innovation is negatively correlated with survival in Finnish start-up firms. Also in China, according to Howell (2015), innovation increases survival, but risky innovators may disappear earlier. Cefis and Marsili (2019) for the Netherlands find that technological innovation made firms resilient to the financial crisis, whereas non-technological innovations had a detrimental effect on survival.

In order to increase the chances of appropriating the returns from the investment in knowledge, firms may resort to intellectual property (IP) rights instead of, or besides, informal appropriation mechanisms. Patents, copyrights, trademarks or other forms of IP have also been used as measures of innovation, but as a matter of fact they are ways to protect the benefits from inventions more than innovation in the sense of bringing novelties onto the market. But when accompanied by new products or services, IP rights provide a time period of assured monopoly earnings which financially help firms survive longer. Of course, it depends on how well enforced the intellectual protection system is. A third collection of studies has thus linked survival to the use of intellectual property rights. Helmers and Rogers (2010) analyze the survival of the complete cohort of more than 162,000 limited companies incorporated in Britain in 2001 over the subsequent 5-year period. Their results indicate that IP activity is associated with a higher probability of survival. In contrast, using a panel of almost 300,000 Australian companies, Buddelmeyer et al., (2010) show that the degree of uncertainty embodied in different innovation proxies shapes the pattern of company survival. Radical innovation investments (new-to-world), measured by IP applications, are associated with lower survival rates, whereas past successful radical innovations, proxied by the stock of patents, and incremental innovation investment, measured by trademark applications, are associated with higher company survival rates. Ortiz-Villajos and Socota (2018) find that in the top British manufacturing firms that were active during the nineteenth and twentieth century the total patent applications were a good predictor of firm survival in manufacturing but not in services.

Whatever measure of innovation output is chosen, the question is whether it is the input or the output measure that is most relevant for survival. On the one hand, it could be argued that it is when firms manage to successfully bring new products on the market or introduce new production methods that firms gain market shares, make profits and manage to survive longer. The benefit they draw from these successes depends on how the new products were developed—in house, through the purchase of licenses, in a research joint venture—and whether they are patent protected or not. R&D by contrast is a just an investment, and a risky at that, which may never bear fruit, and if so only in a distant future. In the meantime other inventors may come up with better ideas.³

On the other hand, there are various reasons for considering R&D to be more relevant for survival. New products may just replace old products leaving the market share unchanged unless the new products command a higher price than the old products. New products may also fail to meet the customers’ expectations, and if they do, there is a great chance that competitors will quickly come up with similar products unless the initial invention is patent protected. And if they are patent-protected, they can be invented around depending on the strength of the patent protection system. Hence the benefits from innovation can be short lived whereas R&D is an investment in knowledge, which, in addition to yielding innovation outputs in the short run, increases the stock of knowledge, which can lead to innovations in the long run. Moreover, this stock of knowledge increases the absorption capacity, which allows firms to benefit from the R&D done by others and to participate in R&D collaborations (Cohen & Levinthal, 1990). The invention of new products and their successful introduction on the market may be serendipitous, but generally it is the result of many years of research and experimentation. In the end, which one of the two forces predominates is an empirical issue.⁴

Figure 1 builds on Pakes and Griliches (1984, Fig. 3.1) and illustrates the links between R&D, innovation output measures and firm performance. The question is whether the direct link between innovation outputs (we shall concentrate on product innovations) or the indirect link via the knowledge production function works better to explain the survival of firms, or to be more precise whether R&D expenditures or new product innovations are a better predictor of firm survival.

Fig. 1

R&D, innovation and survival

3 Data and descriptive statistics

3.1 Data

Our primary data has been compiled by the National Bureau of Statistics of China. It includes over 100,000 firms in each year over the period 1999–2006, and it has two characteristics that make it particularly suitable for the analysis of new firm survival. First, it is a yearly census of all state-owned firms (whatever their size) and of all non-state-owned firms with sales higher than 5 million RMB (Yuan). Second, it has a longitudinal dimension, i.e., individual firms are identified by an identification code (ID), which allows them to be followed over time. A firm is identified as a new firm when it has a new ID. Similarly, a firm is defined as dead when its ID disappears. That is, a firm is considered to have started in year $t$ if it has no ID from 1999 to $t - 1$, to have died in year $t$ if it has no ID from year $t + {1}$ to 2006, and otherwise its exit date is considered to be a right censored observation.⁵

We performed some data cleaning. First, according to officials at the National Bureau of Statistics, the coverage of the census was extended in 2004. Indeed the data show that there is a sharp increase of entry firms in 2004. To address the concern that entry/exit might be due to a change in coverage, we dropped the small-scale private limited liability corporations and the small-scale other limited liability corporations that were first observed in 2004.

Second, compared with large-, medium- and small-scale firms, micro-enterprises are different regarding creativity, innovation, financial conditions and organization, so we focused on plants with more than 20 employees and 3 million sales throughout the sample period.⁶

Third, because of the absence of R&D and innovation data in 2004 and of R&D data in 2000, the data for those years were constructed by interpolation: if the firm existed in that year, but not in the year before and the year after, its R&D was put equal to zero; if it started to exist in that year R&D was given the same value as in the following year; if it stopped to exist in that year it was given the value of the R&D in the preceding year; and if it existed before and after it was given the mean value of the years just before and just after. For 2000 we extrapolated the R&D using the value of 2001. For innovation output we constructed the data in a similar way for 2004.

Fourth, 25 firms were deleted because they had the same identification number.

3.2 Descriptive statistics

Table 2 informs us about the percentages of the total number of firms surviving over time among those first-observed each year after 2000 and those born before 2000. For instance, 60.73% of the 13,065 firms that first appeared in 2000 survived after 1 year. We notice that every year the number of survivors decreases as expected (since no firm reappears after exiting), but also that after the year 2000 the number of firms that survive 2 years or longer rises over time.

Table 2 Survival rates, manufacturing firms in China, 2000–2006

Among the many reasons why some firms survive longer than others, we shall concentrate on the role of R&D and product innovation. To try and see whether it is the innovation effort or the innovation output that matters more, we have classified firms into four groups: those without any R&D and no innovation output in the form of new products, those with R&D but no product innovations, those with product innovations but no R&D and those with both R&D expenditure and new product sales.

Table 3 gives the number of firms available in our sample overall and by province and the proportion of them that fall into each of our four groupings of innovation activities. The provinces with the largest number of firms are in decreasing order of importance Zhejiang, Guangdong, Jiangsu and Shandong. At the bottom of the ranking are the provinces of Qinghai and Tibet. There is more heterogeneity across provinces in the percentage of firms with only product innovation than in the percentage of firms with only R&D. The ranking in the number of R&D performing firms across provinces is similar to the ranking in the number of firms across provinces, whereas the proportion of product innovators is much more variable across provinces than the proportion of R&D performers. For instance, Henan has a greater number of product innovators that do no R&D than Zhejiang, Guangdong and Jiangsu. It will thus be important to account for some regional heterogeneity or some other sources of heterogeneity that might be more prevalent in Henan than in Zhejiang for instance.

Table 3 Number of firms and their distribution by innovation activities, by province, 2000–2006

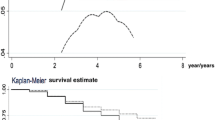
In Fig. 2 the nonparametric Kaplan–Meier estimates of the survival rates are plotted for the four types of firms. There is a clear ordering of the survival rate curves depending on the innovation profiles. The survival curve for firms with R&D and product innovation is always above the one for firms with R&D only, followed by the one with product innovation only and then by the one for non-innovators. We shall now move to a parametric multivariate estimation of the survival rates to see whether we get the same ranking or survival rates when we control for other covariates.

Fig. 2

Kaplan–Meier survival rates depending on the innovation profile. Non-Innovator: firms with no R&D and no new product. R&D: firms with R&D only. New product: firms with new products only. R&D and new product: firms with R&D and new products

4 Model specification

4.1 Choice of parametric models

Since we have annual data we can only observe whether a firm exits in a particular year but not when exactly during that year. What we have are grouped data. Some firms existed already before 1999, others entered later. There is no particular sample selection there. Some died before 2006, while others were still in existence at the end of our sample period. Here we have a problem of right censoring.

Most of the studies on firm survival use the Cox model, because it offers a very convenient interpretation of the estimation results (Audretsch & Mahmood, 1995; Agarwal & Audretsch, 2001; Cefis & Marsili, 2005; Buddelmeyer et al., 2010; Strotmann, 2007; and Deng et al., 2014). However, the Cox model has three shortcomings: it has problems handling ties, it imposes proportional hazards, and it has difficulties to properly control for unobserved heterogeneity. We therefore recommend the use of discrete-time models, which are moreover computationally less demanding than the continuous-time Cox model, especially when analyzing large samples containing heavy ties (Hess & Persson, 2012).⁷

Let us denote by $T_{i} \,$ the time that firm i dies and by $\lambda_{it}$ the continuous time hazard rate that firm i disappears in period j if it has survived up to then:

$$\lambda_{{{\text{it}}}} = {\text{Pr}}\left( {T_{i} = {\text{t}}|T_{i} \ge {\text{t}}} \right).$$

(1)

In discrete time, we have that

$$P\left( {{\text{t}} - {1} \le {\text{T}}_{{\text{i}}} < {\text{t|T}}_{{\text{i}}} \ge {\text{t}} - {1}} \right) = 1 - \exp \left( { - \int\limits_{t - 1}^{t} {\lambda_{is} \;{\text{ds}}} } \right)$$

(2)

and

$$P\left( {{\text{T}}_{{\text{i}}} \ge {\text{t|T}}_{{\text{i}}} \ge {\text{t}} - {1}} \right) = \exp \left( { - \int\limits_{t - 1}^{t} {\lambda_{is} \;{\text{ds}}} } \right).$$

(3)

Having pointed out why it is preferable to apply discrete-time hazard models when analyzing grouped duration data, we shall use a discrete time version of the Cox proportional hazard (PH) model.⁸ Assuming a piecewise continuous proportional hazard function,

$$\lambda_{{{\text{is}}}} = {\text{exp}}\left( {{\text{x}}^{\prime}_{{{\text{it}}}} \beta } \right)\lambda_{{\text{t}}} \quad {\text{t}} - {1} \le {\text{s}} < {\text{t }}$$

(4)

the hazard rate is proportional to a baseline hazard that varies from year to year but that remains constant during the year, and where individual- and period-specific covariates $x_{it}$ determine differences across firms and over time in the hazard rate with respect to the baseline hazard. To be able to estimate the model parameters, a functional form for the hazard rate needs to be specified. The most commonly encountered functional specifications are the normal, logistic, and extreme-value minimum distribution, leading to a probit, logit, or cloglog model, respectively. The cloglog model with period-specific intercepts represents the exact grouped-duration analog of the Cox proportional hazards model (Prentice & Gloeckler, 1978).

In this case the discrete hazard rate $h_{{{\text{it}}}}$ for firm i to die in the period between t − 1 and t is given by

$$h_{it} \left( {x_{it} } \right) = 1 - \exp \left[ { - \exp \left( {x^{\prime}_{it} \beta + \lambda_{t} } \right)} \right]{.}$$

(5)

This specification, which we shall adopt, is also known as the complementary log–log (or cloglog) function (Jenkins, 2005).

If we define a binary variable y_it taking value 1 for spell i when it ends at year t and 0 otherwise, we obtain the following log-likelihood function:

$$\log L\left( {\beta {,}\lambda_{{1}} {,} \ldots \lambda_{{\text{T}}} {; }x_{it} } \right) = \sum\limits_{i = 1}^{N} {\sum\limits_{t = 1}^{{\text{T}}} {\left[ {y_{it} \log h_{it} + \left( {1 - y_{it} } \right)\log \left( {1 - h_{it} } \right)} \right]} } {.}$$

(6)

In this formulation the baseline hazard is very flexible; it is basically a step function estimated by the coefficients of time dummies. We do not assume a parametric time dependence function.

We shall also experiment with an alternative formulation adopted by Han and Hausman (1990), which assumes a continuous proportional hazard function $\lambda_{{\text{o}}} (t)$

$$\lambda_{{{\text{it}}}} = {\text{exp}}\left( {{\text{x}}^{\prime}_{{{\text{it}}}} \beta } \right)\lambda_{{0}} \left( {\text{t}} \right)$$

(7)

and specifies a distribution of the logarithm of the integrated hazard function such that

$${\text{x}}^{\prime}_{{{\text{it}}}} \beta + \delta_{t} = \varepsilon_{it}$$

(8)

where $\varepsilon_{it}$ is a random variable that follows a certain distribution $f(\varepsilon_{it} )$ and $\delta_{t} = \log \int\limits_{0}^{t} {\lambda_{0} {\text{(s)}}\;{\text{ds}}}$. The probability of exit between t − 1 and t is then given by

$$\int\limits_{{\delta_{t - 1} + x^{\prime}_{it} \beta }}^{{\delta_{t} + x^{\prime}_{it} \beta }} {f\left( {\varepsilon_{it} } \right)\;d\varepsilon_{it} } .$$

(9)

If $\varepsilon$ follows an extreme value distribution the likelihood function corresponds to an ordered logit model. The coefficients $\beta ,\delta_{1} ,\delta_{2} , \ldots ,\delta_{T}$ are estimated jointly from the log-likelihood function

$$\log L\left( {\beta {,}\delta_{{1}} {,} \ldots \delta_{{\text{T}}} {; }x_{it} } \right) = \sum\limits_{i = 1}^{N} {\sum\limits_{t = 1}^{{{\text{T}} - {1}}} {y_{it} \int_{{\delta_{t - 1} + x^{\prime}_{it} \beta }}^{{\delta_{t} + x^{\prime}_{it} \beta }} {f\left( {\varepsilon_{it} } \right)\;d\varepsilon_{it} } + } } \, \sum\limits_{i = 1}^{{\text{N}}} {y_{iT} \int_{{\delta_{T} + x^{\prime}_{iT} \beta }}^{\infty } {f\left( {\varepsilon_{iT} } \right)\;d\varepsilon_{iT} } } {.}$$

(10)

We shall also allow for unobserved heterogeneity. Indeed, failure to control for entrepreneurial characteristics or public policy assistance may bias the estimates of our covariates effects. We assume a multiplicative error term in the hazard function with an inverse-Gaussian frailty distribution, with mean 1, and independence with respect to the observed covariates to capture the unobserved heterogeneity. In essence, this boils down to multiplying the right-hand side of Eqs. (4) and (7) by a random error term. The inverse-Gaussian distribution may better handle heavy-tailed distribution (Cameron & Trivedi, 2005).⁹

4.2 Explanatory variables of the hazard rate

We want to explore principally the prominence of R&D and of product innovations on the hazard rate of firm exit.¹⁰ Both can be measured qualitatively (as dummies) or quantitatively (as intensities). In order to compare their relative importance we interact the R&D intensity (rdt), measured by the R&D to sales ratio, with the presence or absence of product innovation (DN0 and DN1), and likewise we interact the product innovation intensity (npt), measured by the fraction of output due to new (to the market) products, with the presence or not of R&D (DR0 and DR1).¹¹ If R&D matters even in the absence of product innovation or vice versa, then we could clearly identify whether it is R&D or product innovation that is most relevant for firm survival.

A firm survival is influenced not only by its innovative efforts, but also by other firm characteristics and industry specificities, which we try to control for. We consider six control variables at the firm level. Large-scale firms could take advantage of scale economies to establish themselves on the market and resist the pressures of competition. To minimize the possibility of an endogeneity bias we control for the initial size rather than the current size. Ample financial resources allow a firm to experiment and impose less stringent requirements for performance. Following studies on slack resources by Greve (2003), Daniel et al. (2004) and Tan and Peng (2004), we control for a firm’s financial constraints using the ratio of administrative, financial, and selling expenses to sales revenue. Advertising expenses also reflect financial resources and are a deliberate strategy to attract customers and increase sales. As exporting firms are likely to be more competitive (Melitz, 2003) they may have lower hazard rates. Therefore we include an export dummy as a control variable. We also control for the ownership status. State-owned firms may be less dynamic than privately owned firms but could also have more means to grow and survive than private firms. Firms from Hong-Kong, Macao, Taiwan and other foreign countries (HMTF) might benefit from connections, complementarities with mother companies and more financial resources to resist competition. We account for firm productivity which is an important theoretical and empirical determinant of plant survival in itself, and which could also be a proxy for other unobservable characteristics favoring plants’ survival.

Instead of including a long list of 4-digit industry dummies, we characterized the sector influence by a number of structural characteristics that might differ from industry to industry. We include the average R&D intensity, the Herfindahl index of concentration of market shares, the entry rate, the capital intensity and the minimum efficient scale of the largest plants, all measured at the 4-digit industry level. We also included at the 2-digit industry level the patent intensity taken from the Yearbook of Science and Technology. Following Audretsch (1991) and Audretsch and Mahmood (1995), we expect firms in highly innovative environments and in industries with scale economies and a high capital intensity to face a higher risk of exit. According to Strotmann (2007), a higher required minimum efficient scale increases the hazard rate. According to Mata et al. (1995) in dynamic industries with many newcomers and a high R&D intensity firms tend to disappear unless they are innovative, hence all other things equal the pressure of competition accelerates failures.

Through year dummies we control for cyclical effects and the age of the firm. A separate dummy controls for firms born before 2000. Province dummies control for institutional differences and framework conditions that may influence the life-spell of a firm. Finally, the age of the firm may have a separate effect irrespective of the year when the exit occurs. We expect an inverse-U relationship: death is more likely for younger firms, but there comes a time where older firms can no longer compete with the latest technologies.

The definitions, abbreviations and means of all the variables are given in Table 4. The average R&D intensity is very low (0.13%) because only 13% of the firms are R&D performers.¹² There are even fewer product innovators (9%) so that the average share in total sales due to new products amounts to only 3.13%. Advertising expenditures are very low (0.07%) so that this variable, if significant, really captures the marketing effort more than the financial resources.7% of the firms in our sample are state-owned firms and 17% are from Macao, Hong Kong, Taiwan or other foreign countries. The average R&D intensity at the industry level is twice as high as the average at the firm level. The Herfindahl index is close to the minimum it can take. On average 23% of the firms in the industry are new entrants. 28% of the firms in our sample were born before 2000. What is also remarkable to notice is that one third of the firms die after 1 year.

Table 4 Variable definitions, measurements and sample averages

5 Empirical results

5.1 The relationship between innovation and survival

In Tables 5 and 6 we present our estimates of the effect of innovation on firm survival using the two specifications presented in Sect. 3, the cloglog model and the ordered logit model. Instead of presenting the coefficients of the estimation, we report directly the more interesting marginal effects of the explanatory variables. Table 5 reports the estimated marginal effects using the qualitative indicators for R&D and innovation, and Table 6 those obtained using the continuous measures of R&D and innovation.

Table 5 Baseline results on innovation and the hazard rate: marginal effects with discrete measure of innovation

Table 6 Baseline results on innovation and the hazard rate: marginal effects with continuous measure of innovation

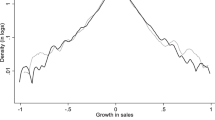
The results are pretty consistent across the two tables. Let us first examine the R&D and innovation variables. Table 5 confirms the Kaplan–Meier survival estimates. There is a clear ranking in the hazard rates depending on the innovation profile: firms that do only product innovation but no R&D have a 3% lower chance of dying than firms that do no R&D and have no product innovations (the reference group); those that do R&D but do not come up with no products on the market have a 5.3% lower hazard rate than the reference group; and those that do both R&D and product innovations have a 6.9% lower hazard rate. The latter effect is, however, smaller than the sum of the marginal effects of doing only R&D and doing only innovation. In that sense we cannot conclude that R&D and the introduction of new products are complementary in terms of firm survival. If we look at Table 6, we see that a 1% higher innovation intensity decreases the hazard rate by a marginal 0.03% in the absence of R&D and by 0.14% in the presence of R&D, whereas a 1% higher R&D intensity decreases the hazard rate by 1.78% in the absence of innovation and by 0.5% in the presence of innovation. The marginal effects of changes in R&D and product innovation intensities on the hazard rate in the presence or in the absence of the other innovation activity are best illustrated graphically. A marginal increase in R&D intensity decreases the hazard rate more than a marginal increase in innovation intensity—in the absence or in the presence of the other innovation activity (compare the left-hand sides or the right-hand sides of Figs. 3 and 4). A small increase in R&D over sales reduces the hazard rate more in the absence than in the presence of product innovation (Fig. 3). However, a marginal increase in the sales of new products relative to total output decreases the hazard rate more in the presence than in the absence of R&D (Fig. 4).The superiority of R&D over product innovation could be interpreted as showing that own R&D efforts have a stronger impact on firm survival than product innovation that could originate inside the firm but also through imitation, licensing or incoming spillovers. Another explanation is that a firm that executes R&D aims not only at producing a new product, but also at introducing process innovations in order to raise productivity and lower cost, and in this way increases its possibility of survival. A third explanation could lie in the errors of measurement in product innovation that would bias downward the estimates of their marginal effects (see Mairesse et al., (2005) for evidence of that).

Fig. 3

Evolution of the average marginal effect of R&D intensity on the hazard rate in the presence and in the absence of product innovation, with a 95% confidence interval. Increases in R&D intensity decrease the hazard rate more quickly in the absence than in the presence of product innovation

Fig. 4

Evolution of the average marginal effect of product innovation intensity on the hazard rate in the presence and in the absence of R&D, with a 95% confidence interval. Increases in product innovation intensity decrease the hazard rate less quickly and less substantially in the absence than in the presence of R&D

If we compare the cloglog and the ordered logit estimates we detect very few differences between the two sets of estimates. By and large, when the marginal effect of a variable in the cloglog model is negative, then the firm tends to survive 3–4 more years following a marginal change in the explanatory variable, and vice versa when the marginal effect is positive. One of the few cases of divergence is for the marginal effect of the minimum efficient scale at the industry level and some of the province specific effects. Notice that the sum of the marginal shifts between dying years is equal to zero. The marginal effects of the ordered logit shows that a firm will die earlier or later, and the flip in signs between the categories tends to occur mostly after 4 years. Notice also that it makes no sense to include duration dummies here since the duration itself is explained by the model.

The signs and the size of the marginal effects of all the other control variables are also similar across the two tables and similar to the results reported in previous studies on Chinese firm data (Bao, 2016; Deng et al., 2014; Howell, 2015).¹³ Most of the firm specific effects have the predicted signs: larger firms, more productive firms, firms with a higher advertisement ratio, private firms, foreign firms and exporters tend to survive longer, whereas higher administrative and financial costs increase the hazard rate. State-owned enterprises (SOE) have a higher failure rate than the reference category of other ownership and hence also indirectly than privately-owned firms or foreign-owned firms. It could indicate a lower efficiency of SOEs but it could also reflect the deliberate effort of the Chinese government in those years to consolidate many small SOEs into large SOEs. As for the industry characteristics, as expected dynamic industries characterized by a high average intensity of R&D, a high percentage of newcomers or a high concentration rate have higher hazard rates. A high capital intensity decreases the hazard rate but the effect is very small. A 1% increase in the minimum efficient scale, i.e. in the relative average first-year firm size industry-normalized, decreases the hazard rate by 7%. The patent intensity is not significant in the cloglog model, but the results of the ordered logit model clearly show that firms tend to survive longer in patent-intensive industries than in industries where patents are less used.

Of the remaining dummy variables that determine the baseline hazard, we have to keep in mind that the reference category comprises firms in Beijing, of year 6 (2005 and after) and duration 6 (a survival period of at least 6 years). Firms born before 2000 have a 0.8% higher probability of dying in the year to come. All other things equal, the lowest hazard rate was observed in 2006 and the highest one in 2001, followed closely by 2004. Quite a few of the province dummies have significant coefficients, showing that the industry variable controls leave some provincial sources of heterogeneity unexplained. Regarding duration, the highest probability of dying is after 1 year, then it goes down for each additional year of survival, it goes up slightly after 4 years, then it decreases sharply after 5 years in existence to rise again after 6 or more years.

5.2 Robustness analysis

Having established that firms tend to survive longer in the presence of R&D and product innovation, we shall now examine how robust our results in the presence of frailty, endogeneity, heterogeneity and riskiness. But first we shall check whether other duration models would have produced different results.

5.2.1 Alternative duration models

The choice between different duration models, be it different parametric specifications of the hazard function or modeling of the failure time, is largely arbitrary. We shall examine to what extent our results on the comparative role of R&D and product innovation are robust to different duration models. In Appendix Table 11 we compare the estimated coefficients and the Akaike Information Criterion for nine different models, for discrete and continuous measures of R&D and innovation. First, it is clear that the rankings of the coefficients of interest does not change across the models and, secondly, on the basis of the Akaike Information Criterion the best fitting model is our cloglog model (the Cox PH model cannot be compared to the others on that criterion).

5.2.2 Frailty

We account for the presence of an individual effect in three ways. In columns (1) and (4) of Table 7 we control for an initial size effect. Since this variable remains constant throughout the lifetime of a firm, it partially captures a fixed individual effect. In columns (2) and (5) we model the individual effect as a random multiplicative error term that follows an inverse Gaussian distribution. In columns (3) and (6) we estimate the correlated random effect by adding the means for each firm of the firm-specific control variables (size, export, finance, productivity and advertisement). Because of convergence problems when estimating the random effects model, due to the small number of observations for some provinces, regional dummies instead of provincial dummies are used, the regions being the Pearl River, the Yangtse region, the Beijing/Hebei/Tianjin circle and the remaining provinces. The results of column 1 are almost the same as those reported in Table 7, column 1. The results are not exactly the same because we have replaced provincial dummies by regional dummies. The ranking of the different R&D/innovation profiles remains unchanged when we control for frailty and also when in addition we control for correlated random effects à la Mundlak.¹⁴ Han and Hausman (1990) also reported that the addition of an individual effect does not make much difference “once a flexible parameter specification of the baseline hazard is used” (p. 28). Manjón-Antolín and Arauzo-Carrod (2008) also report that accounting for unobserved heterogeneity does not make a great difference in the papers they reviewed, and Ugur et al. (2016) as well do not find a significant effect of frailty.¹⁵

Table 7 Robustness analysis: marginal effects controlling for frailty

5.2.3 Endogeneity

To address the endogeneity issue of the contemporaneous R&D or innovation variable, according to which firms do less R&D/innovation in the perspective of near death¹⁶ (hence the marginal effect of R&D/innovation on firm survival gets overestimated), we have also compared specifications with contemporaneous, 1-year lagged and first-year R&D or innovation measurements. As shown in Table 8, the ranking of the different R&D/innovation profiles remains, but the magnitude of the marginal effects varies. They decrease slightly if R&D or innovation is measured at first-year value partly because the initial value may capture the individual effect, partly because the first-year values of R&D and innovation are less relevant than the contemporaneous values. With the values of R&D and innovation lagged one period, the marginal effects are much lower than with the contemporaneous values but also the first year values. If there was a delayed response we would expect a higher effect from a 1-year lagged variation than from a contemporaneous effect. We are inclined to attribute this result to the lower number of observations rather than to a delayed response effect.

Table 8 Robustness: marginal effects allowing for endogeneity of innovation

5.2.4 Industry heterogeneity

Ugur et al. (2016) find for the UK that the positive effect of R&D intensity on firm survival is stronger in concentrated industries, but lower in R&D-intensive industries. We re-examine this issue on Chinese firm data by interacting the firm levels or intensities of R&D and product innovation with two measures of competition at the industry level: the entry rate and the normalized Herfindahl index.¹⁷ Doing R&D or innovating with new products reduces the hazard rate even more in more concentrated industries, but additional effect of concentration is not visible (statistically significant) for the intensities of R&D and innovation. Investing in R&D and/or coming up with new products decreases the chance of dying even more in industries where the proportion of new firms among the total number of firms is high. Competition from newcomers this seems to stimulate firms to do R&D or to innovate in order to survive. This finding goes in the same direction as Kim and Lee’s (2016) finding that current R&D intensity is particularly important for firm survival in industries with high technological opportunity and low R&D appropriability.

In Table 9 we report the marginal effects of R&D and innovation on the hazard rate, in discrete and continuous terms, for four selected industries, which differ in terms of R&D, innovation and patenting (IP). R&D and innovation intensity are high in “medicines” (industry 27) and “chemical raw materials and chemical products” (industry 26) with high patent intensity in the former and low in the latter, and they are low in “articles for culture, education and sport activity” (industry 24) and “textiles” (industry 17), high in the former and low in the latter. Both R&D and coming up with new products decrease the hazard rate in all four industries, but compared to the reference group of firms with no R&D and no innovation output, the reduction in the hazard rate is lower in firms with only R&D than in firms with only innovation, and they reinforce each other. It is difficult to see strong differences between industries and to draw general conclusions about interindustry differences on the basis of 4 particular cases. But what is maybe interesting here is the role of patent intensity. In general, the marginal effects of R&D and innovation output on the hazard rates are higher in industries with low IP protection than in those with high IP protection.

Table 9 Cloglog model of the hazard rate for selected industries (marginal effects)

5.2.5 Riskiness

A few papers argue that innovation is risky and that therefore too much innovation may be harmful for survival. Fernandes and Paunov (2015) estimate a discrete-time hazard model with unobserved plant heterogeneity on Chilean data. They find that risk from a lack of diversification (e.g. relying on a single product) and market risk (innovation from competitors, high-pricing strategy and high sales volatility) diminish survival, but not technical risk (degree of market novelty or level of product sophistication). Bao (2016) introduces interactions between innovation and certain firm characteristics and finds that innovative firms that are financially constrained face a higher risk of exiting the market. He finds some weak signs of an inverted-U relationship between R&D intensity and survival. Ugur et al (2016) find strong evidence of such an inverted-U relationship on UK data.

In order to examine whether innovation is always good for survival or whether too much innovation or risky innovation may instead be detrimental for survival, we make the coefficient of the R&D/innovation profiles vary with different measures of risk. We consider four such measures: (1) a high (low) product innovation proportion dummy taking value 1 (0) when product innovation sales account for more (less) than 50% of total sales, (2) a high (low) R&D variability, taking value 1 (0) when the coefficient of variation of R&D over its duration is above (below) the median value of all firms in the same 4-SIC industry, (3) a many (few) competitors dummy taking value 1 when the number of innovators in the same 4-SIC industry is above (below) the median value for all 4-SIC industries, and (4) a high (low) industry sales volatility dummy if the coefficient of variation of sales in the industry is above (below) the median value for all 4-SIC industries. We have added these interaction terms to the cloglog specification reported in Table 6.¹⁸ The other coefficients hardly change, therefore we only report in Table 10 the coefficients of the interaction terms.

Table 10 Robustness analysis: marginal effects of R&D, innovation on the hazard rate in the presence of risk

We see that the addition of the interaction effects hardly changes the ranking of the effects of R&D/innovation profiles on the hazard rates. Regarding the risk of being too innovative, we confirm the conclusions of Zhang and Mohnen (2013), Fernandes and Paunov (2015) and Howell (2015). Indeed, in column 1 of Table 10 we see that the effect of being a product innovator, with or without R&D, is somewhat lower if new products account for more than 50% of total sales. However, we also find that the other three measures of risk, reflecting some kind of market dynamism, decrease even more the hazard rate when R&D/innovation is performed. Column (2) reveals that firms with more variability in their R&D than the median firm in the industry, whether they innovate or not, tend to have a lower hazard rate when doing R&D than firms with lower R&D volatility than the median firm in the industry. The explanation here could be that firms that adjust their expenditure to cost and demand fluctuations survive longer. Whereas being in an R&D-intensive industry per se increases the hazard rate, it reduces even more the hazard rate when doing R&D or being innovative. This is what column (3) reveals. It confirms the effect of the entry rate reported in Table 9. Somewhat in the same vein, column (4) says that being in a dynamic environment with greater sales variability than in the median industry rewards the R&D and/or innovating firm by lowering even further its hazard rate. The last two findings are contrary to what Fernandes and Paunov (2015) and Howell (2015) report.

6 Conclusion

The main purpose of the paper is to revisit the relationship between innovation and firm survival in Chinese manufacturing firms and focus on whether R&D has a greater effect on firm survival than new product innovations. We do so using dichotomous and continuous measures of R&D and innovation output. We also re-examine the effect of industry characteristics and of various measures of risk on the effect of innovation on the hazard rate.

We use a database from the National Bureau of Statistics of China which includes over 100,000 firms in each year over the period 1999–2006 from all provinces and manufacturing industries in China.

We find that both R&D and product innovation decrease the hazard rate of exit, in other words increase the chance of survival, be it in terms of incidence or intensities. But, R&D has a greater marginal effect on the hazard rate than innovation output. Contrary to some previous studies, we find that being in dynamic industries—R&D-intensive, with high sales or R&D volatility—reduces even more the hazard rate when doing R&D or being innovative.

In terms of innovation policy, our results indicate that China had better stimulate firms to do R&D rather than to introduce new products on the market. Firms could innovate without doing R&D by importing technological know-how, purchasing new machines and licensing frontier technology. However, the mere adoption of outside technology may not be sufficient in order to succeed if firms do not have the appropriate management capability or the brand advantage in marketing. In any case, investments in R&D accumulate into an intangible capital stock, which in addition to serving as an input into the conception of new goods also allow firms to benefit from knowledge spillovers, stay abreast of technological developments and collaborate with other firms at home and abroad. It might be a better strategy for China to reduce its technological gap by investing in R&D rather than promoting all kinds of innovation and to set up the framework conditions that would attract R&D performers to China.

A number of caveats need to be mentioned. First, the data that we have do not allow us to assess the effects of other forms of innovation than product innovation, e.g., process or organizational innovation, on firm survival. Second, if the sample could be extended to more recent years, it would be interesting to examine to what extent R&D and innovation allowed firms to survive the crisis which started in 2007. Third, there may be another channel through which firms survive and yet disappear from our sample, and that is through mergers and acquisition. A firm or a part of it may be merged with another company under a new name. According to our analysis, the old firm would be considered as dead and yet it survived under a different name. Finally, it might be interesting to merge innovation and patent data to examine at the firm level whether intellectual property rights allow Chinese firms to survive longer.

Appendix

See Table 11.

Table 11 Robustness: estimated coefficients and AIC from alternative duration models