Abstract
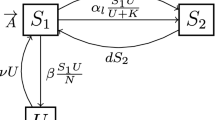
Drug abuse is an issue of considerable concern due to its correlation with negative effects such as delinquency, unemployment, divorce and health problems. Understanding the dynamics of drug abuse is important in developing effective prevention programs. We formulate a mathematical model for the spread of drug abuse using nonlinear ordinary differential equations. Susceptibility to drug use varies, due to differences in behavioral, social and environmental factors. Risk structure is included before initiation and after recovery to help differentiate those more likely (high risk) to abuse drugs and those less likely (low risk) to abuse drugs. The model allows back and forth transition between risk groups. It is shown that the model has multiple equilibria and using the center manifold theory, the model exhibits the phenomenon of backward bifurcation whose implications to rehabilitation are discussed. An epidemic threshold value, \({\mathcal {R}}_a\), termed the abuse reproduction number, is proposed and defined herein in the drug-using context. Sensitivity analysis of the abuse reproduction number and numerical simulations were performed. The results show that education about effective coping response and/or skills to deal with the risky situation may better equip individuals to stand against initiating or re-initiating into drug abuse.





Similar content being viewed by others
References
International Narcotics Control Board (INCB) (2013)
The Naked Truth (TNT). http://www.tnt.org.za (2010)
Arshad, S., Baleanu, D., Bu, W., Tang, Y.: Effects of HIV infection on CD4+ T-cell population based on a fractional-order model. Adv. Differ. Equ. 2017(1), 92 (2017)
Jajarmi, A., Hajipour, M., Baleanu, D.: New aspects of the adaptive synchronization and hyperchaos suppression of a financial model. Chaos Solitons Fractals 99, 285–296 (2017)
Singh, J., Kumar, D., Al Qurashi, M., Baleanu, D.: A new fractional model for giving up smoking dynamics. Adv. Differ. Equ. 2017(1), 88 (2017)
Marin, M.: Generalized solutions in elasticity of micropolar bodies with voids. Rev. Acad. Canar. Cienc. 8(1), 101–106 (1996)
Marin, M.: A temporally evolutionary equation in elasticity of micropolar bodies with voids. Bull. Ser. A Appl. Math. Phys. 60, 3–12 (1998)
Marin, M.: A partition of energy in thermoelasticity of microstretch bodies. Nonlinear Anal. Real World Appl. 11(4), 2436–2447 (2010)
Muchatibaya, G., Fassari, S., Rinaldi, F., Mushanyu, J.: A note on the discrete spectrum of gaussian wells (I): the ground state energy in one dimension. Adv. Math. Phys. Article ID 2125769. https://doi.org/10.1155/2016/2125769 (2016)
Kalula, A.S., Nyabadza, F.: A theoretical model for substance abuse in the presence of treatment. S. Afr. J. Sci. (2012). https://doi.org/10.4102/sajs.v108i3/4.654
Mulone, G., Straughan, B.: A note on heroin epidemics. Math. Biosci. 208, 138–141 (2009)
Mushanyu, J., Nyabadza, F., Muchatibaya, G., Stewart, A.G.R.: Modelling multiple relapses in drug epidemics. Ric. Mat. 65, 37 (2015)
Mushanyu, J., Nyabadza, F., Stewart, A.G.R.: Modelling the trends of inpatient and outpatient rehabilitation for methamphetamine in the Western Cape province of South Africa. BMC Res. Notes 8, 797 (2015b)
Mushanyu, J., Nyabadza, F., Muchatibaya, G., Stewart, A.G.R.: Modelling drug abuse epidemics in the presence of limited rehabilitation capacity. Bull. Math. Biol. 78(12), 2364–2389 (2016)
Njagarah, J.B.H., Nyabadza, F.: Modelling the impact of rehabilitation, amelioration and relapse on the prevalence of drug epidemics. J. Biol. Syst. 21. Article ID 1350001 (2013)
Nyabadza, F., Hove-Musekwa, S.D.: From heroin epidemics to methamphetamine epidemics: modelling substance abuse in a South African Province. Math. Biosci. 225, 132–140 (2010)
Nyabadza, F., Njagarah, J.B.H., Smith, R.J.: Modelling the dynamics of crystal meth (Tik) abuse in the presence of drug-supply chains in South Africa. Bull. Math. Biol. (2012). https://doi.org/10.1007/s11538-012-9790-5
White, E., Comiskey, C.: Heroin epidemics, treatment and ODE modelling. Math. Biosci. 208, 312–324 (2007)
de Alarcón, R.: The spread of heroin abuse in a community. Bull. Narc. (United Nations publication) XXI(3), 17–22 (1969)
Mackintosh, D.R., Stewart, G.T.: A mathematical model of a heroin epidemic: implications for control policies. J. Epidemiol. Community Health 33, 299–304 (1979)
Diekmann, O., Heesterbeek, J.A.P., Metz, J.A.Z.: On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28, 365–382 (1990)
van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)
Capistrána, M.A., Morelesa, M.A., Larab, B.: Parameter estimation of some epidemic models. The case of recurrent epidemics caused by respiratory syncytial virus. ull. Math. Biol. (2009). https://doi.org/10.1007/s11538-009-9429-3
Hsier, Y.H., Wang, Y.S.: Basic reproduction number for HIV model incorporating commercial sex and behavior change. Bull. Math. Biol. 68, 551–575 (2006)
Kodaira, J.Y., de Souza Passos, J.R.: The basic reproduction number in si staged progression model: a probabilistic approach. In: Dynamics Days South America 2010 International Conference on Chaos and Nonlinear Dynamics (2010)
Mastroberardino, T.: Mathematical modeling of the HIV/AIDS epidemic in Cuba. In: AMS Eastern Sectional Meeting University of Maryland/Baltimore County (2014)
van den Driessche, P., Zou, X.: Modeling relapse in infectious diseases. Math. Biosci. 207, 89–103 (2007)
Chitnis, N., Hyman, J.M., Cushing, J.M.: Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 70, 1272–1296 (2008)
Castillo-Chavez, C., Song, B.: Dynamical models of tuberclosis and their applications. Math. Biosci. Eng. 1(2), 361–404 (2004)
Jamison, D.T., Feachmen, R.G., Makgoba, M.W., Bos, E.R., Baingana, F.K., Hofman, K.J., Rogo, K.O.: Disease and mortality in sub-saharan Africa, 2nd edn. World Bank, Washington (2006)
Rossi, C.: The role of dynamic modelling in drug abuse epidemiology. Bull. Narc. LIV(1 and 2), 33–44 (2002)
Acknowledgements
J. Mushanyu acknowledge, with thanks, the support of the Department of Mathematics, University of Zimbabwe. F. Nyabadza acknowledges with gratitude the support from National Research Foundation and Stellenbosch University for the production of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Coefficients of Polynomial (23)
Appendix 2. Number of positive roots of polynomial (23)
Appendix 3. Associated non-zero partial derivatives of F at the drug-free equilibrium
Rights and permissions
About this article
Cite this article
Mushanyu, J., Nyabadza, F. A Risk-Structured Model for Understanding the Spread of Drug Abuse. Int. J. Appl. Comput. Math 4, 60 (2018). https://doi.org/10.1007/s40819-018-0495-9
Published:
DOI: https://doi.org/10.1007/s40819-018-0495-9