1 Introduction

As far as usage of drugs damages the physical, mental, and social well being of individuals, their families and societies, and drug usage turn into a worldwide social and health problem. Police records, rehabilitation centers, and prisons records show the increase in harmful drug uses, and on the other hand, the literature shows expanded studies undertaken to explore various aspects of drugs such as its relation to media and information, campaigns, criminals, etc., see [23, 24].

Among various drug users, heroin users are at high risk of addiction and criminal actions. As indicated in [24], “the number of heroin users increased from 166,000 in 2002 to 335,000 in 2012, and the death rate of drug poisoning involving heroin increased from 0.7 to 2.7 per 100,000 persons during 2002–2013 in the USA. The heroin addiction was first defined as an epidemic in 1981–1983 in Ireland”. White and Comiskey, in [25], have introduced the following epidemic model for the dynamics of heroin users:

$$\begin{aligned} \left\{ \begin{array}{lll} \dfrac{{\text {d}}S}{{\text {d}}t}=\Lambda -\frac{\beta _1 S U_1}{N}-\mu S \\ \dfrac{{\text {d}}U_1}{{\text {d}}t}=\frac{\beta _1 S U_1}{N}+\frac{\beta _3 U_1 U_2}{N}-(\mu +\delta _1+p)U_1 \\ \dfrac{{\text {d}}U_2}{{\text {d}}t}=p U_1-\frac{\beta _3 U_1 U_2}{N}-(\mu +\delta _2)U_2 \end{array} \right. \end{aligned}$$
(1.1)

in which S(t) is the number of susceptible individuals in the population, \(U_1(t)\) is the number of drug users not in treatment; initial and relapsed drug users, and \(U_2(t)\) is the number of drug users in treatment. Their model was revisited by Mulone and Straughan [18].

After White and Comiskey’s work, the epidemiology of drugs has been studied by several authors. For example, Nyabadza and Hove-Muskava in [21] modified (1.1) to a model of the dynamics of methamphetamine use in a South African province. Njagarah and Nyabadza in [19], have studied the impact of rehabilitation, amelioration, and relapse on drug epidemics. Nyabadza, Njagarah, and Smith in [20] have studied the epidemiology of crystal in South Africa. The reader can see also [8, 10, 22].

In many compartmental epidemic models, individuals assumed to be passive persons, that will not respond, i.e., change their behavior during an infectious disease outbreak or in an endemic infection. Now, it is clear that a realistic model must include the feedback that the information about the disease prevalence has on its spreading [6]. In some infectious disease such as sexually transmitted diseases, i.e., STDs, Pandemic Influenza, and SARS, the diffusion of information through targeted campaigns, various media resources and individual to an individual contact, can alert the population to the spreading disease. Most studies of behavior change in epidemic disease models have been carried out in the context of STDs, particularly HIV, see [5, 7, 11, 16, 17, 26].

In the case of drugs, there is a lot of information available about the harm and dangers of drug use in the community. A group of individuals, who can be called responsive individuals, will be safe from the risk of drug abuse, by receiving and understanding such information. In this paper, we will propose modified forms of White–Comiskey’s model, by considering the effect of information transmission, on drug prevalence. Our modification includes the split of the susceptible populations into two compartments, the susceptible individuals \(S_{1}\), and the responsive individuals \(S_{2}\), i.e., the individuals who do not use drugs because of information about the harms and dangers of it. Furthermore, we assume that because of transmission of information, susceptibles will be transmitted from \(S_1\) to \(S_2\). As in [11], we consider two routes for information dissemination, information transmission via direct contact between individuals, and population-wide dissemination of drug-related information.

Our aim is to study the quantitative effect of the coefficients of the model, specially the rate of conversion of susceptible and responsive individuals and the rate of decay of information, on the threshold required for the occurrence of backward bifurcation and stability of equilibrium points. With this study, the mechanism of the effect of changes in these factors on the occurrence or prevention of an epidemic becomes more apparent.

The paper is organized as follows. In Sect. 2, we consider a model without treatment/rehabilitation compartment, compute the basic reproduction number, \(R_0\), of the model, and, by using Lyapunov functions, \(\hbox {Poincare}^{'}\)–Bendixson theorem, and Dulac functions, prove that the drug-free equilibrium \(P_0\) is locally and globally stable if \(R_0<1\), and the unique endemic equilibrium point exists and is locally and globally stable if \(R_0>1\).

In Sect. 3, we consider a model with a compartment for the individuals under treatment/rehabilitation programs with the effect of relapse of drug users under treatment to drug use. We compute \(R_0\), the basic reproduction number of the model and study the local stability of equilibrium points. This model shows more complexity, in fact, although the equation on endemic value \(u^*\) is a polynomial of third order, we have provided a complete analysis which shows that endemic equilibrium may exist (at most 3 points), in cases, \(R_0<1, R_0=1\) and \(R_0>1\). Occurrence of backward bifurcation is also proved for the model which shows, under some conditions, it is not enough to reduce \(R_0\) to the region \(R_0<1\), to control the drug epidemy. In fact, when \(R_0<1\), the drug problem may be persistent. Furthermore, we drive sufficient conditions for the global stability of endemic equilibrium points in some cases, using geometric approach.

2 The first model

2.1 Model formulation and basic properties

As we have mentioned, our goal is to investigate the effect of information on the prevention of drug epidemics. In the White and Comiskey’s model, this effect is not considered. To this end, we add a compartment for the responsive people, to their model. First, in this section, we analyze the model regardless of the effect of treatment/rehabilitation. Then, in the next section, we will consider a more complete model containing a compartment for these people. By doing this, we can see that adding a compartment to the model causes what changes in the analysis process and also the dynamics of the model.

We suppose that the population is divided into three compartments; the susceptible individuals \(S_{1}\), the infected individuals U, i.e., drug users, and the responsive individuals \(S_{2}\), i.e., the individuals who do not use drugs because of information about its harms and dangers. We assume that because of the diffusion of information about the harms and dangers of drug use, susceptibles will be transmitted from \(S_1\) to \(S_2\). In this model, we consider two routes for information dissemination:

  1. (i)

    Information dissemination via direct contact between individuals given by \(f_{1} \), and,

  2. (ii)

    population-wide dissemination of drug-related information given by \( f_{2}\). Contact between individuals is best characterized by frequency dependent contact, and hence, the natural choice for \(f_{1}\) is given by:

    $$\begin{aligned} f_{1}=\frac{\alpha _s S_{1} U}{N}, \end{aligned}$$

where \(\alpha _s\) is the rate of (i.e., the likelihood of) exposure to addicts and taking lessons from the effects of the painful consequences of addiction.

The rate of population-wide transmission of information is assumed to depend on the disease prevalence. This is based on the assumption that more drug users will generate an increased volume and more efficient diffusion of information about its harms and dangers. However, the effect of this will be limited and will saturate for high prevalence with little further impact on individuals’ behavior. Thus, we consider a function of the following form:

$$\begin{aligned} f_{2}=\frac{\alpha _l S_1 U}{K+U}, \end{aligned}$$

where \(\alpha _l\) is, the rate of encouraging people to come to a healthy life together with cautionary behaviors, and K is a positive constant. As a result of either of these two types of information dissemination, susceptible individuals move to the responsive individual’s compartment. However, information that covers the same topic repeatedly will lose its value over time. For example, responsive individuals that avoid using drugs for a certain amount of time are likely to become less cautious. We consider d as the rate of decay of information and cautiousness. In this model, \(\beta \) is the contact rate of susceptibles with infectious individuals, i.e., drug users. The constants \( \nu \), \(\mu \), and A, represent the recovery rate, the natural death rate, and the rate of immigration of susceptibles, respectively. The flowchart of the model is given in the above diagram, Fig. 1, and the model describes by the following system of nonlinear ordinary differential equations:

$$\begin{aligned} \left\{ \begin{array}{lll} \dfrac{{\text {d}}S_{1}}{{\text {d}}t}=A-\alpha _{s}S_{1}\frac{U}{N}-\alpha _{l}S_{1}\left( \frac{U}{U+K}\right) +{\text {d}}S_{2} -\mu S_{1}+\nu U-\beta S_{1}\frac{U}{N}\\ \dfrac{{\text {d}}S_{2}}{{\text {d}}t}=\alpha _{s}S_{1}\frac{U}{N}-{\text {d}}S_{2} +\alpha _{l}S_{1}\left( \frac{U}{U+K}\right) -\mu S_{2}\\ \dfrac{{\text {d}}U}{{\text {d}}t}=\beta S_{1}\frac{U}{N}-\nu U-\mu U \end{array} \right. \end{aligned}$$
(2.1)

The total population \(N(t)=S_1(t)+S_2(t)+U(t)\) satisfies the following equation, \(\frac{{\text {d}}N}{{\text {d}}t}=A - \mu N(t)\), and hence \(\lim _{t \rightarrow \infty } N(t)=\frac{A}{\mu }=N_0\). Following [14, 15], we assume that the population is at equilibrium and study the behavior of the system on the plane \(S_1+S_2+U=N_0=\frac{A}{\mu }\). Let

$$\begin{aligned}&s_1=\frac{S_1}{N_0}, \,\, s_2=\frac{S_2}{N_0},\,\,u=\frac{U}{N_0},\,\,k=\frac{K}{N_0}. \end{aligned}$$
(2.2)

which satisfies \(s_{1}+s_{2}+u=1\). Using this relations, finally, we consider the following two-dimensional system:

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{{\text {d}}s_{1}}{{\text {d}}t}=\mu -\alpha _{s}s_{1}u-\alpha _{l}s_{1}\frac{u}{u+k}+{\text {d}}(1-s_{1}-u) -\mu s_{1}+\nu u-\beta s_{1}u=f(s_1,u)\\ \dfrac{{\text {d}}u}{{\text {d}}t}=\beta s_{1}u-\nu u-\mu u=g(s_1,u). \end{array} \right. \end{aligned}$$
(2.3)

We study (2.3) in the following feasible region:

$$\begin{aligned} \Omega =\{(s_{1},u)\in {\mathbb {R}}_{+}^{2}:s_{1}\ge 0,u\ge 0,s_{1}+u\le 1\}, \end{aligned}$$

which is positively invariant with respect to (2.2).

Fig. 1
figure 1

The flowchart of the model

Full size image

2.2 Stability of the drug-free equilibrium

System (2.3) has the drug-free equilibrium \(P_0=(1,0)\). The Jacobian of the system is given by:

$$\begin{aligned} J(s_{1},u)= \left( \begin{array}{cc} -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u &{} -\alpha _{s}s_{1}-\alpha _{l} s_{1}\left( \frac{k}{(k+u)^{2}}\right) -d+\nu -\beta s_{1}\\ \beta u &{} \beta s_{1}-\nu -\mu \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} J(1,0)= \left( \begin{array}{cc} -d-\mu &{} -\alpha _{s}-\frac{\alpha _{l}}{k} -d+\nu -\beta \\ 0 &{} \beta -\nu -\mu \end{array} \right) . \end{aligned}$$

The eigenvalues of this matrix are \(\lambda _{1}=-d-\mu \) and \(\lambda _{2}=\beta -\nu -\mu \), the first eigenvalue is negative, and the second eigenvalue is negative if \(\beta <\nu +\mu \). We introduce \(R_{0}=\frac{\beta }{\nu +\mu }\), as the basic reproduction number and obtain the following result on the local stability of the drug-free equilibrium.

Theorem 2.1

The drug-free equilibrium \(P_0\) is asymptotically stable when \(R_{0}<1\) and unstable when \(R_{0}>1\).

Furthermore, we can prove the global stability of the drug-free equilibrium point.

Lemma 2.1

The drug-free equilibrium point, \(P_0\), is globally asymptotically stable in \(\Omega \) if \(R_0<1\).

Fig. 2
figure 2

The phase portrait of the system for a: \(\alpha _l=\alpha _s=\beta =\nu =\mu =d=0.5\), \(k=1.2\), and \(R_0=0.5\). b\(\alpha _l=\alpha _s=d=0.5\), \(\nu =\mu =0.25\), \(\beta =0.75\), \(k=1.2\), and \(R_0=1.5\)

Full size image

Proof

Define \(V:\{(s_{1},u)\in \Omega :s_{1}>0\}\rightarrow {\mathbb {R}}\) by:

$$\begin{aligned} V(s_{1},u)=u. \end{aligned}$$

The time derivative of V along the solution curves of (2.3) is:

$$\begin{aligned} \dfrac{{\text {d}}V}{{\text {d}}t}=\dfrac{{\text {d}}u}{{\text {d}}t}\le (\mu +\nu )(R_0-1)u. \end{aligned}$$

Therefore, when \(R_0<1\), \(\dfrac{{\text {d}}V}{{\text {d}}t}\le 0\), and, \(\dfrac{{\text {d}}V}{{\text {d}}t}=0\) if and only if \(u= 0\). Hence, \(P_0\) is global asymptotic stable. \(\square \)

Figure 2 shows the phase portrait of the system, around the equilibrium points, in some cases.

2.3 Endemic equilibrium

Let \(P^*=(s_{1}^*,u^*)\) be the endemic equilibrium point of (2.3); \(u^*\ne 0\) in the second equation imply that:

$$\begin{aligned} s_{1}^{*}=\dfrac{\nu +\mu }{\beta }=\frac{1}{R_0}. \end{aligned}$$
(2.4)

Since in the endemic equilibrium \(s_{1}^*<1\), this relation implies that the endemic equilibrium point exists only when \(R_{0}>1\). Now, substituting this value in the first equation of (2.3), and setting equal to zero, we obtain:

$$\begin{aligned}&\mu -\alpha _{s}\left( \dfrac{\nu +\mu }{\beta }\right) u^*-\alpha _{l}\left( \dfrac{\nu +\mu }{\beta }\right) \left( \frac{u^*}{u^*+k}\right) +d\left( 1-\left( \dfrac{\nu +\mu }{\beta }\right) -u\right) \\&\quad -\mu \left( \dfrac{\nu +\mu }{\beta }\right) +\nu u^*-\beta \left( \dfrac{\nu +\mu }{\beta }\right) u^*=0, \end{aligned}$$

which reduces to:

$$\begin{aligned} A{ u^{*}}^{2}+B u^{*}+C=0. \end{aligned}$$
(2.5)

With the following coefficients:

$$\begin{aligned} A= & {} (\nu +\mu )(-\alpha _{s}-\beta )+\beta (\nu -d)=(\nu +\mu )(-\alpha _{s}-R_{0}(\mu +d)), \\ B= & {} k((\nu +\mu )(-\alpha _{s}-\beta )+\beta (\nu -d))+(\mu +d)(\beta -\nu -\mu ) -\alpha _{l}(\nu +\mu )\\= & {} k(-\alpha _{s}(\nu +\mu )-\beta (\mu +d))+(\mu +d)(\nu +\mu )(R_{0}-1)-\alpha _{l}(\nu +\mu ), \\ C= & {} k(\mu +\nu )(\beta -\nu -\mu )=k(\mu +\nu )^{2}(R_{0}-1). \end{aligned}$$

Since at an endemic equilibrium \(s^{*}_{1}<1\), the endemic equilibrium exists only when, \(R_{0}>1\), and hence C is a positive real number. On the other hand, since A is a negative real number, we have \(\Delta \ge 0\). Solving Eq. (2.5) yields:

$$\begin{aligned} u_{1,2}^{*}=\frac{-B}{2A}\pm \frac{\sqrt{\Delta }}{2A} \end{aligned}$$
(2.6)

and \(u_{1}^{*}=\frac{-B}{2A}-\frac{\sqrt{\Delta }}{2A}\) is the positive root of (2.5). Therefore, in this case:

$$\begin{aligned} P^*=(s_{1}^{*} ,u^{*} )=\left( \dfrac{\nu +\mu }{\beta } ,\frac{-B-\sqrt{\Delta }}{2A}\right) \end{aligned}$$

is the endemic equilibrium point. Now, we investigate the local stability of the endemic equilibrium.

Theorem 2.2

The endemic equilibrium point \(P^*\) is locally asymptotically stable if \(R_0>1\).

Proof

The characteristic equation of the Jacobian matrix of the endemic equilibrium \(P^*\) has the following form:

$$\begin{aligned} \lambda ^{2}-\lambda p+q=0, \end{aligned}$$

where \(p=Trace J(P^*)=-\alpha _{s}u^{*}-\alpha _{l}(\frac{u^{*}}{u^{*}+k})-d-\mu -\beta u^{*}<0\) and \(q=Det J(P^*)=\beta u^{*}\left( \alpha _{s}(\dfrac{\nu +\mu }{\beta })+\alpha _{l} (\dfrac{\nu +\mu }{\beta })(\frac{k}{(k+u^{*})^{2}})+d+\mu \right) >0\). Hence, the linearization theorem shows the local stability of the endemic equilibrium point. Furthermore, if \(\Delta =p^{2}-4q\ge 0\), the endemic equilibrium is a stable node, and if \( \Delta \le 0\), the endemic equilibrium is a stable focus. \(\square \)

For the study of global stability of the endemic equilibrium point, we use the Poincaré–Bendixson theorem.

Theorem 2.3

If \(R_0>1\), the unique endemic equilibrium point \(P^*\) is globally asymptotically stable in \(\Omega \).

Proof

We use the Dulac function \(B(s_{1},u)=\frac{1}{u}\), for which \({\text {div}} (Bf , Bg)=-\alpha _{s}-\alpha _{l}(\frac{1}{u+k})-\dfrac{d}{u}-\frac{\mu }{u}-\beta <0\), in the region \(u>0\). Furthermore, integrating the second equation of (2.3) yields \(u(t)=u(0)e^{\int _{0}^{t}(\beta s_1(\tau )-\nu -\mu ){\text {d}}\tau }\), which shows that the line \(u=0\) is positively invariant, and hence, there are no periodic solutions in this system. Hence, the local stability and the \(\hbox {Poincare}^{'}\)–Bendixson theorem imply the global stability of \(P^*\). \(\square \)

Fig. 3
figure 3

The flowchart of the model with treatment/rehabilitation

Full size image

3 The second model

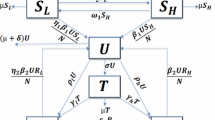
In the previous section, we studied the model (2.1). Now, we developed (2.1) taking into account the effect of treatment and rehabilitation. We add a new compartment T, consist of drug users who become under treatment/rehabilitation to the previous model. We assume that \(\delta _{1}\) represents the treatment/rehabilitation rate and \(\delta _{2}\) is the rate of relapse to drug use. Therefore, we have the following system of nonlinear ordinary differential equations (Fig. 3):

$$\begin{aligned} \left\{ \begin{array}{llll} \dfrac{{\text {d}}S_{1}}{{\text {d}}t}=A-\alpha _{s}S_{1}\frac{U}{N}-\alpha _{l}S_{1}\left( \frac{U}{U+K}\right) +{\text {d}}S_{2} -\mu S_{1}+\nu U-\beta S_{1}\frac{U}{N}\\ \dfrac{{\text {d}}S_{2}}{{\text {d}}t}=\alpha _{s}S_{1}\frac{U}{N}-{\text {d}}S_{2} +\alpha _{l}S_{1}\left( \frac{U}{u+K}\right) -\mu S_{2}\\ \dfrac{{\text {d}}U}{{\text {d}}t}=\beta S_{1}\frac{U}{N}-\nu U-\mu U-\delta _{1}U+\delta _{2}T\frac{U}{N}\\ \dfrac{{\text {d}}T}{{\text {d}}t}=\delta _{1}U-\delta _{2}T\frac{U}{N}-\mu T \end{array} \right. \end{aligned}$$
(3.1)

The total population \(N(t)=S_1(t)+S_2(t)+U(t)+T(t)\) satisfies the following equation: \(\frac{{\text {d}}N}{{\text {d}}t}=A - \mu N(t)\), and hence, \(\lim _{t \rightarrow \infty } N(t)=\frac{A}{\mu }=N_0\). Following [14, 15], we assume that the population is at equilibrium and study the behavior of the system on the hyperplane \(S_1+S_2+U+T=N_0=\frac{A}{\mu }\). Let

$$\begin{aligned}&s_1=\frac{S_1}{N_0}, \,\, s_2=\frac{S_2}{N_0},\,\,u=\frac{U}{N_0},\,\,\tau =\frac{T}{N_0},\,\,k=\frac{K}{N_0}. \end{aligned}$$
(3.2)

which satisfies \(s_{1}+s_{2}+u+\tau =1\). Using this relations, finally, we consider the following system:

$$\begin{aligned} \left\{ \begin{array}{lll} \dfrac{{\text {d}}s_{1}}{{\text {d}}t}=\mu -\alpha _{s}s_{1}u-\alpha _{l}s_{1}\left( \frac{u}{u+k}\right) +{\text {d}}(1-s_{1}-u-\tau )-\mu s_{1}+\nu u-\beta s_{1}u\\ \dfrac{{\text {d}}u}{{\text {d}}t}=\beta s_{1}u-\nu u-\mu u-\delta _{1}u+\delta _{2}\tau u\\ \dfrac{{\text {d}}\tau }{{\text {d}}t}=\delta _{1}u-\delta _{2}\tau u-\mu \tau . \end{array} \right. \end{aligned}$$
(3.3)

We study (3.3) in the following feasible region:

$$\begin{aligned} \Omega _1=\{(s_{1},u,\tau )\in {\mathbb {R}}_{+}^{3}:s_{1}\ge 0,u\ge 0,\tau \ge 0,s_{1}+u+\tau \le 1\}, \end{aligned}$$

Which is positively invariant with respect to (3.3).

3.1 Stability of the drug-free equilibrium

It is easy to see that system (3.3), has a unique drug-free equilibrium \(P_1(1,0,0)\). The Jacobian matrix of this system has the following form:

$$\begin{aligned}&J(s_{1},u,\tau )\\&\quad = \left( \begin{array}{ccc} -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u &{} -\alpha _{s}s_{1}-\alpha _{l} s_{1}\left( \frac{k}{(k+u)^{2}}\right) -d+\nu -\beta s_{1} &{} -d\\ \beta u &{} \beta s_{1}-\nu -\mu -\delta _{1}+\delta _{2}\tau &{} \delta _{2}u \\ 0 &{}\delta _{1}-\delta _{2}\tau &{} -\delta _{2}u-\mu \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} J(1,0,0)= \left( \begin{array}{ccc} -d-\mu &{} -\alpha _{s}-\frac{\alpha _{l}}{k} -d+\nu -\beta &{}-d \\ 0 &{} \beta -\nu -\mu -\delta _{1} &{} 0 \\ 0 &{} \delta _{1} &{}-\mu \end{array} \right) . \end{aligned}$$
(3.4)

The eigenvalues of this matrix are \(\lambda _{1}=-d-\mu \), \(\lambda _{2}=-\mu \), and \(\lambda _{3}=\beta -\nu -\mu -\delta _{1}\). We introduce \(R_{0}=\frac{\beta }{\nu +\mu +\delta _{1}}\) and obtain the following result on the local stability of the drug-free equilibrium.

Theorem 3.1

The drug-free equilibrium \(P_1\) is asymptotically stable when \(R_{0}<1\) and unstable when \(R_{0}>1\).

3.2 Endemic equilibrium

The endemic equilibrium point \((s_{1}^*,u^*,\tau ^*)\) of (3.3) is determined by the following equations:

$$\begin{aligned} \left\{ \begin{array}{lll} \mu -\alpha _{s}s_{1}^*u^*-\alpha _{l}s_{1}^*\left( \frac{u^*}{u^*+k}\right) +d(1-s_{1}^*-u^*-\tau ^*)-\mu s_{1}^*+\nu u^*-\beta s_{1}^*u^*=0\\ \beta s_{1}^*-\nu -\mu -\delta _{1}+\delta _{2}\tau ^*=0\\ \delta _{1}u^*-\delta _{2}\tau ^* u^*-\mu \tau ^*=0 \end{array} \right. \end{aligned}$$
(3.5)

Since \(u^*\ne 0\), the second and third equations yield, \(\tau ^{*}=\frac{\delta _{1}u^{*}}{\delta _{2}u^{*}+\mu }\) and \(s_{1}^{*}=\frac{\nu +\mu +\delta _{1}-\delta _{2}(\frac{\delta _{1}u^{*}}{\delta _{2}u^{*}+\mu })}{\beta }\). Now, by substituting this relations in the first equation of system and setting it equal to zero, we get the following third-order polynomial in terms of \(u^{*}\):

$$\begin{aligned}&\mu -\frac{\alpha _{s}u^{*}}{\beta }\left( \nu +\mu +\delta _{1}-\delta _{2} \left( \frac{\delta _{1}u^{*}}{\delta _{2}u^{*}+\mu }\right) -\alpha _{l} \left( \frac{\nu +\mu +\delta _{1}-\delta _{2}\left( \frac{\delta _{1}u^{*}}{\delta _{2}u^{*}+\mu }\right) }{\beta }\right) \left( \frac{u^{*}}{u^{*}+k}\right) \right. \\&\quad +d\left( 1-\left( \frac{\nu +\mu +\delta _{1}-\delta _{2}\left( \frac{\delta _{1}u^{*}}{\delta _{2}u^{*} +\mu }\right) }{\beta }\right) -u^{*}-\left( \frac{\delta _{1}u^{*}}{\delta _{2}u^{*}+\mu } \right) \right) \\&\quad -\frac{\mu }{\beta }\left( \nu +\mu +\delta _{1}-\delta _{2} \left( \frac{\delta _{1}u^{*}}{\delta _{2}u^{*}+\mu }\right) \right) +\nu u^{*} -u^{*}\left( \nu +\mu +\delta _{1}-\delta _{2}\left( \frac{\delta _{1}u^{*}}{\delta _{2}u^{*}+\mu }\right) \right) =0, \end{aligned}$$

which reduces to

$$\begin{aligned} A{ u^{*}}^{3}+B{u^{*}}^{2}+Cu^{*}+D =0, \end{aligned}$$
(3.6)

where

$$\begin{aligned} A= & {} -\delta _{2}(\mu (\alpha _{s}+\beta )+\nu \alpha _{s}+\beta d), \\ B= & {} (\mu +\nu )(-\alpha _{s}k\delta _{2}-\alpha _{s}\mu -\alpha _{l} \delta _{2}-d\delta _{2}-\mu \delta _{2})+\mu \beta (-\mu -k\delta _{2})\\&+\delta _{1}(-\alpha _{s}\mu -\mu \beta -\beta d)+\delta _{2}\beta (\mu +d-kd)\\= & {} (\mu +\nu )(-\alpha _{s}k\delta _{2}-\alpha _{s}\mu -\alpha _{l}\delta _{2} -d\delta _{2}-\mu \delta _{2})+\delta _{1}(-\alpha _{s}\mu -\mu \beta -\beta d)\\&-{\mu ^{2}\beta +(\mu +d)\beta \delta _{2}(1-k)}, \\ C= & {} \mu (\mu +\nu +\delta _{1})(-\alpha _{s}k-\alpha _{l}-k\beta -d-\mu )+(d+\mu ) (-k(\nu +\mu )\delta _{2}+k\beta \delta _{2} +\beta \mu )\\&+k\beta \nu \mu -kd\beta \nu -kd\beta \delta _{1}, \\ D= & {} k\mu (\mu +d)(\nu +\mu +\delta _1)(R_0-1). \end{aligned}$$

Now, we consider \(f(u)=A u^{3}+Bu^{2}+Cu+D\), with \(f^{\prime }(u)=3Au^{2}+2Bu+C\) and \(f^{\prime \prime }(u)=6Au+2B\). Furthermore since \(A<0\), \(\lim _{u\rightarrow +\infty } f(u)=-\infty \) and \(\lim _{u\rightarrow -\infty } f(u)=+\infty \). For the study of the existence of endemic values \(u^*\), we consider three cases:

Case I: \(R_0>1\), i.e., \(f(0)=D>0\).

And we consider the following subcases:

$$\begin{aligned} I0: \Delta =4B^{2}-12AC<0. \end{aligned}$$

In this case, f(u) is strictly decreasing, and hence, it has a unique positive root:

$$\begin{aligned} I1: \Delta>0, B>0,\hbox { and }C>0. \end{aligned}$$

In this case, according to the second derivative test, \(u_{1}=\frac{-2B+\sqrt{\Delta }}{6A}<0\) is a local minimum and \(u_{2}=\frac{-2B-\sqrt{\Delta }}{6A}>0\) is a local maximum for f(u). Therefore, \(f(u)=A u^{3}+Bu^{2}+Cu+D\), has only one positive real root, \(u^{*}\):

$$\begin{aligned} I2: \Delta >0, B<0\hbox { and }C<0. \end{aligned}$$

In this case, \(u_{1}=\frac{-2B+\sqrt{\Delta }}{6A}<0\) is a local minimum, and \(u_{2}=\frac{-2B-\sqrt{\Delta }}{6A}<0\) is a local maximum, with \(u_{1}<u_{2}\), and therefore, there is only one positive real root for f(u):

$$\begin{aligned} I3: \Delta>0, B>0\hbox { and }C<0. \end{aligned}$$

In this case, \(u_{1}=\frac{-2B+\sqrt{\Delta }}{6A}>0\) is a local minimum, and \(u_{2}=\frac{-2B-\sqrt{\Delta }}{6A}>0\) is a local maximum for f(u) and \(u_{1}<u_{2}\). Hence, \(f(u)=A u^{3}+Bu^{2}+Cu+D\), which has three positive real roots:

$$\begin{aligned} I4: \Delta>0, B<0\hbox { and}, C>0. \end{aligned}$$

In this case, \(u_{1}=\frac{-2B+\sqrt{\Delta }}{6A}<0\) is a local minimum, and \(u_{2}=\frac{-2B-\sqrt{\Delta }}{6A}>0\) is a local maximum for f(u). Thus, \(f(u)=A u^{3}+Bu^{2}+Cu+D\), which has only one positive real root.

It should be noted that if \(\Delta >0\), then B and C are not both zero:

$$\begin{aligned} I5: \Delta >0\hbox { and }B=0. \end{aligned}$$

In this case, \(C>0\), \(u_{1}=\frac{\sqrt{\Delta }}{6A}<0\) is a local minimum, and \(u_{2}=\frac{-\sqrt{\Delta }}{6A}>0\) is a local maximum, and there is only one positive real root for f(u):

$$\begin{aligned} I6: \Delta >0\hbox { and }C=0. \end{aligned}$$

If \(\Delta >0\) and \(C=0\), then \(B\ne 0\). If \(B>0\), the point \(u_{1}=0\) is a local minimum and \(u_{2}=\frac{-2}{3}\frac{B}{A}>0\), is a local maximum. Therefore, there is only one positive real root for f(u).

If \(B<0\), then \(u_{1}=\frac{-2}{3}\frac{B}{A}<0\) is a local minimum and \(u_{2}=\frac{-2}{3}\frac{B}{A}>0\) is a local maximum. Therefore, there is only one positive real root for f(u):

$$\begin{aligned} I7: \Delta =0, B\ne 0\hbox { and }C\ne 0. \end{aligned}$$

If \(\Delta =0\), then, \(C=\frac{B^{2}}{3A}<0\). Therefore we have \(A<0, C<0\). If \(B>0\), then f(u) in \(u=\frac{-B}{3A}>0\) has a horizontal tangent, and if \(B<0\) Then, f(u) has a horizontal tangent in \(u=\frac{-B}{3A}<0\). In both cases, if \(\epsilon >0\) is sufficiently small, then \(f^{\prime }(\frac{-B}{3A}+\epsilon )=\frac{-B^{2}}{3A}+3A\epsilon ^{2}+C=3A\epsilon ^{2}<0\) and \(f^{\prime }(\frac{-B}{3A}-\epsilon )=\frac{-B^{2}}{3A}+3A\epsilon ^{2}+C=3A\epsilon ^{2}<0\). Hence, in this case, there is just one positive real root for f(u):

$$\begin{aligned} I8: \Delta =B=0. \end{aligned}$$

In this case, \(C=0\) and f(u) have a horizontal tangent in \(u=0\) and it is a decreasing function that has \(u^{*}=\root 3 \of {\frac{-D}{A}}>0\) as the only root:

$$\begin{aligned} I9: \Delta =C=0. \end{aligned}$$

If \(\Delta =C=0\), then \(B=0\). With a similar argument as in (8), f(u) has a root \(u^{*}=\root 3 \of {\frac{-D}{A}}>0\).

Figure 4 shows the phase portrait of the system in some cases of I.

Fig. 4
figure 4

The phase portrait of the system for a\(\alpha _s=\alpha _l=d=0.5,\nu =0.125,\mu =0.25\), \(\beta =0.75,\delta _1=0.25,\delta _2=0.5\), and \(k=1.2\). Case I2. b\(\alpha _l=\alpha _s=d=0.01\), \(\nu =\mu =0.01\), \(\beta =0.031\), and \(k=1.2\). Case I4

Full size image

Case II: \(R_0<1\), i.e., \(f(0)=D<0\).

We consider the following subcases:

$$\begin{aligned} II0: \Delta <0. \end{aligned}$$

In this case, f(u) is strictly decreasing, and hence, it does not has any positive root:

$$\begin{aligned} II1: \Delta>0, B>0\hbox { and }C>0. \end{aligned}$$

In this case, according to the second derivative test, \(u_{1}=\frac{-2B+\sqrt{\Delta }}{6A}<0\) is a local minimum and \(u_{2}=\frac{-2B-\sqrt{\Delta }}{6A}>0\) is a local maximum for f(u). If \(f(u_{2})>0\), then f(u) has two positive real roots, and if \(f(u_{2})=0\), then f(u) has only one positive real root, and if \(f(u_{2})<0\), then f(u) has no real positive root:

$$\begin{aligned} II2: \Delta>0, B>0\hbox { and }C<0. \end{aligned}$$

In this case, with an argument similar to the previous case, \(u_{1}=\frac{-2B+\sqrt{\Delta }}{6A}>0\) is a local minimum and \(u_{2}=\frac{-2B-\sqrt{\Delta }}{6A}>0\) is a local maximum for f(u) and \(u_{1}<u_{2}\). If \(f(u_{2})>0\), then f(u) has two positive real roots; if \(f(u_{2})=0\), then f(u) has only one positive real root; and if \(f(u_{2})<0\), then f(u) has no real positive root:

$$\begin{aligned} II3: \Delta>0, B<0\hbox { and }C>0. \end{aligned}$$

In this case, \(u_{1}=\frac{-2B+\sqrt{\Delta }}{6A}<0\) is a local minimum and \(u_{2}=\frac{-2B-\sqrt{\Delta }}{6A}>0\) is a local maximum for f(u). If \(f(u_{2})>0\), then f(u) has two positive real roots and if \(f(u_{2})=0\), then f(u) has only one positive real root; furthermore, if \(f(u_{2})<0\), then f(u) has no real positive root:

$$\begin{aligned} II4: \Delta >0, B<0\hbox { and }C<0. \end{aligned}$$

Clearly, in this case, \(u_{1}=\frac{-2B+\sqrt{\Delta }}{6A}<0\) is a local minimum, \(u_{2}=\frac{-2B-\sqrt{\Delta }}{6A}<0\) is a local maximum and \(u_{1}<u_{2}\), and hence, there is no endemic value for u.

It should be noted that if \(\Delta >0\), then B and C are not both zero:

$$\begin{aligned} II5: \Delta >0\hbox { and }B=0. \end{aligned}$$

If \(\Delta >0\) and \(B=0\), then \(C>0\). In this case, \(u_{1}=\frac{\sqrt{\Delta }}{6A}<0\) is a local minimum and \(u_{2}=\frac{-\sqrt{\Delta }}{6A}>0\) is a local maximum and a similar argument concludes that if \(f(u_{2})>0\), then f(u) has two positive real roots; if \(f(u_{2})=0\), then f(u) only one positive real root; and if \(f(u_{2})<0\), then f(u) has no real positive root:

$$\begin{aligned} II6: \Delta >0, C=0. \end{aligned}$$

If \(\Delta >0\) and \(C=0\), then \(B\ne 0\). If \(B>0\), then \(u_{1}=0\) is a local minimum and \(u_{2}=\frac{-2}{3}\frac{B}{A}>0\) is a local maximum. Therefore, if \(f(u_{2})>0\), then f(u) has two positive real roots; and if \(f(u_{2})=0\), then f(u) has only one positive real root; and if \(f(u_{2})<0\), then f(u) has no real positive root.

If \(B<0\), then \(u_{1}=\frac{-2}{3}\frac{B}{A}<0\) is a local minimum and \(u_{2}=0\) is a local maximum. Therefore, there is only one positive real root for f(u):

$$\begin{aligned} II7: \Delta =0, B\ne 0, C\ne 0. \end{aligned}$$

If \(\Delta =0\), then \( C=\frac{B^{2}}{3A}<0\). Therefore, we have \(A<0 ,C<0 ,D<0\). Now, if \(B>0\), then f(u) in \(u=\frac{-B}{3A}>0\) has a horizontal tangent, and if \(B<0\), then f(u) has a horizontal tangent in \(u=\frac{-B}{3A}<0\). In both cases, if \(\epsilon \) is a sufficiently small positive number, then \(f^{\prime }(\frac{-B}{3A}+\epsilon )=\frac{-B^{2}}{3A}+3A\epsilon ^{2}+C=3A\epsilon ^{2}<0\) and \(f^{\prime }(\frac{-B}{3A}-\epsilon )=\frac{-B^{2}}{3A}+3A\epsilon ^{2}+C=3A\epsilon ^{2}<0\). Therefore, if \(B>0\), there is no positive real root for f(u), and if \(B<0\) for both cases \(f(\frac{-B}{3A})\ge 0\) and \(f(\frac{-B}{3A})< 0\), there is no positive real root for f(u).

$$\begin{aligned} II8: \Delta =0, B=0. \end{aligned}$$

If \(\Delta =0\) and \(B=0\), then \(C=0\). In this case, f(u) has a horizontal tangent in \(u=0\) and it is a decreasing function with the unique root \(u^{*}=\root 3 \of {\frac{-D}{A}}<0\). Therefore, there is no positive real endemic value for u.

$$\begin{aligned} II9: \Delta =0, C=0. \end{aligned}$$

If \(\Delta =0\) and \(C=0\), then \(B=0\), and similar to (II8), f(u) has only one root \(u^{*}=\root 3 \of {\frac{-D}{A}}<0\). Therefore, there is no endemic value for u.

Figure 5 shows the phase portrait of the system in some cases of II.

Fig. 5
figure 5

The phase portrait of the system for a\(\alpha _s=0.9,\alpha _l=0.1,\nu =0.01,\mu =0.01,d=0.9\), \(\beta =0.3333,\delta _1=0.5,\delta _2=0.9\), and \(k=0.01\). Case II2. b\(\alpha _s=0.01,\alpha _l=0.1,\nu =0.01,\mu =0.001,d=0.99\), \(\beta =0.02,\delta _1=0.01,\delta _2=0.14\), and \(k=1.2\). Case II3

Full size image

Case III: \(R_0=1\), i.e., \(f(0)=D=0\), and \(u^{*}\) is the solution of the second-order polynomial:

$$\begin{aligned} g(u^*)=A{ u^{*}}^{2}+Bu^{*}+C=0, \end{aligned}$$
(3.7)

which is a concave parabola in term of \(u^{*}\). Now, if \(\Delta '=B^2-4AC<0\), it does not have any real root. If \(\Delta '\ge 0\), and \(C\ge 0\), it has one positive real root. When \(\Delta '\ge 0\), and \(C\le 0\), if \(B>0\), the parabola \(g(u^*)\) has a positive maximum point \(u_{\max }^*=\frac{-B}{2A}\), and \(g(u_{\max }^*)=\frac{\Delta '}{-4A}\ge 0\). Hence, if \(\Delta '>0\), it has two positive solutions, and if \(\Delta '=0\), it has one positive solution.

Figure 6 shows the phase portrait of the system in some cases of III.

Fig. 6
figure 6

The phase portrait of the system for a\(\alpha _s=0.01,\alpha _l=0.1,\nu =0.005,\mu =0.01,d=0.99\), \(\beta =0.02,\delta _1=0.005,\delta _2=0.14\), and \(k=1.2\). Case III. b\(\alpha _l=\alpha _s=d=0.00001\), \(\mu =0.01\), \(\beta =0.02\), \(\nu =\delta _1=0.005\), \(\delta _2=0.064\), and \(k=0.01\). Case III

Full size image

3.3 Backward bifurcation

Now, we use the Castillo–Chavez and Song theorem, see [4], to determine the conditions for the occurrence of backward bifurcation in (3.3). Let \(s_{1}=x_{1}\), \(u=x_{2}\), and \(\tau =x_{3}\). System (3.3) transforms to the following system:

$$\begin{aligned} \left\{ \begin{array}{lll} \dfrac{{\text {d}}x_{1}}{{\text {d}}t}=\mu -\alpha _{s}x_{1}x_{2}-\alpha _{l}x_{1}\left( \frac{x_{2}}{x_{2}+k}\right) +d(1-x_{1}-x_{2}-x_{3})-\mu x_{1}+\nu x_{2}-\beta x_{1}x_{2}\\ \dfrac{{\text {d}}x_{2}}{{\text {d}}t}=\beta x_{1}x_{2}-\nu x_{2}-\mu x_{2}-\delta _{1}x_{2}+\delta _{2}x_{3}x_{2}\\ \dfrac{{\text {d}}x_{3}}{{\text {d}}t}=\delta _{1}x_{2}-\delta _{2}x_{2} x_{3}-\mu x_{3}. \end{array} \right. \end{aligned}$$
(3.8)

We consider \(\beta ^{*}=\nu +\mu +\delta _{1}\) as the parameter \(\phi \). The Jacobian matrix of the drug-free equilibrium evaluated at \(\beta ^{*}\) has the following form:

$$\begin{aligned} A= \left( \begin{array}{ccc} -d-\mu &{} -\alpha _{s}-\frac{\alpha _{l}}{k} -d+\nu -\beta ^{*} &{}-d \\ 0 &{} \beta ^{*}-\nu -\mu -\delta _{1} &{} 0 \\ 0 &{} \delta _{1} &{}-\mu \end{array} \right) , \end{aligned}$$

which has the eigenvalues, \(\lambda _{1}=-\mu \), \(\lambda _{2}=-d-\mu \) and \(\lambda _{3}=\beta ^{*}-\nu -\mu -\delta _{1} =0\). We compute a right eigenvector w, i.e., \(Aw=0\). By solving this linear system, we found:

$$\begin{aligned} w=\left( \begin{array}{c} \mu (-\alpha _{s}-\frac{\alpha _{i}}{k}-d-\mu -\delta _{1})-\delta _{1}d\\ \mu (d+\mu ) \\ \delta _{1}(d+\mu ) \end{array} \right) . \end{aligned}$$

Furthermore, we need to compute a left eigenvector, i.e., a vector v, with \(vA=0\). Computation shows that \(v=\left( \begin{array}{c} 0\\ 1 \\ 0\end{array} \right) \). Hence:

$$\begin{aligned} a= & {} 2v_{2}w_{2}\left( w_{1}\frac{\partial ^{2}f_{2}}{\partial x_{2}\partial x_{1}}+w_{3}\frac{\partial ^{2}f_{2}}{\partial x_{3}\partial x_{2}}\right) =2v_2w_2(\beta ^*w_1+\delta _2w_3)\\ b= & {} v_{2}w_{2}\frac{\partial ^{2}f_{2}}{\partial x_{2}\partial \beta _{*}}=\mu (d+\mu )>0. \end{aligned}$$

As indicated in [4], Th. 3.2., for the occurrence of backward bifurcation, we need to have \(a>0\) and \(b>0\). The relation \(a>0\), is equivalent to:

$$\begin{aligned} (\mu (-\alpha _{s}-\frac{\alpha _{l}}{k}-d-\mu -\delta _{1})-\delta _{1}d)\beta ^{*} +\delta _{1}(d+\mu )\delta _{2}>0. \end{aligned}$$

The last inequality holds if and only if:

$$\begin{aligned} \delta _{2}>\frac{\mu }{\delta _{1}}\left( \dfrac{\alpha _{s}+\frac{\alpha _{l}}{k} +\delta _{1}}{(d+\mu )}+1\right) +\frac{d}{d+\mu }(\nu +\mu +\delta _{1}). \end{aligned}$$
(3.9)

3.4 Global stability

Now, we obtain sufficient conditions for the global stability of endemic equilibrium points, in cases of unique endemic equilibrium points, using geometric approach introduced in [12, 13], see [2, 3, 9], for applications of this method.

Let \(P=\frac{1}{u}I_{3}\), where \(I_{3}\) is the identity matrix. Then, \(P_{f}P^{-1}=-\frac{1}{u}\dfrac{{\text {d}}u}{{\text {d}}t}I_{3}\), and:

$$\begin{aligned} Q=P_{f}P^{-1}+PJ^{[2]}P^{-1}= \left( \begin{array}{l@{\quad }l@{\quad }l} q_{11} &{} q_{12} &{} q_{13}\\ q_{21} &{}q_{22}&{} q_{23}\\ aq_{31} &{} q_{32} &{} q_{33}\end{array} \right) \end{aligned}$$

in which \(q_{11}=-\alpha _{s}u-\alpha _{l}(\frac{u}{u+k})-d-\mu -\beta u\), \(q_{12}=\delta _{2}u\), \(q_{13}=d\)\(q_{21}=\delta _{1}-\delta _{2}\tau \), \(q_{22}= -\alpha _{s}u-\delta _{2}u-\alpha _{l}(\frac{u}{u+k})-d-\mu -\beta u-\beta s_{1}-\delta _{2}\tau +\delta _{1}+\nu \), \(q_{23}=-\alpha _{s}s_{1} -\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) -d+\nu -\beta s_{1}\), \(q_{31}=0\), \(q_{32}= \beta u\) and \(q_{33}=-\mu -\delta _{2}u \).

For \(z=(z_{1} ,z_{2}, z_{3} )^{T}\), let \(\Vert z\Vert \) be the norm given by:

$$\begin{aligned} \Vert z\Vert =\left\{ \begin{array}{lll} \text{ max }\{\vert z_{1}\vert +\vert z_{2}\vert ,\vert z_{2}\vert +\vert z_{3}\vert \} &{} \text{ if } &{} 0\le z_{2}z_{3} \\ \text{ max }\{\vert z_{1}\vert +\vert z_{3}\vert ,\vert z_{2}\vert \} &{} \text{ if } &{} z_{2}z_{3}\le 0. \end{array}\right. \end{aligned}$$
(3.10)

Lemma 3.1

There exists \(\chi >0\), such that \(D_{+}\Vert z\Vert \le -\chi \Vert z\Vert \) for all \(z\in {\mathbb {R}}^{3}\) and all \(s_{1},u,\tau >0\), where \(D_{+}\Vert z\Vert \) is the right-hand derivative of \( \Vert z\Vert \ \) and z is the solution of \(\dfrac{{\text {d}}z}{{\text {d}}t}=Qz \), provided that:

$$\begin{aligned} \alpha _s+\nu +2\delta _1<d+\mu ,2\delta _1+2\nu +\alpha _s<2d+\mu ,\delta _2<d+\mu ,d<\mu \end{aligned}$$
(3.11)

for some positive constant \(\chi \).

Proof

We demonstrate the existence of some \(\chi >0\), such that:

$$\begin{aligned} D_{+}\Vert z\Vert \le -\chi \Vert z\Vert \end{aligned}$$

for all \(z\in {\mathbb {R}}^{3}\). The proof is divided into eight cases based on the octant and the definition of the norm in (3.10).

Case 1: \(0<z_{1},z_{2},z_{3}\) and \( \vert z_{1}\vert +\vert z_{3}\vert >\vert z_{2}\vert +\vert z_{3}\vert \). In this case, \(\Vert z\Vert = \vert z_{1}\vert +\vert z_{3}\vert \), and

$$\begin{aligned} D_{+}\Vert z\Vert= & {} D_{+}(\vert z_{1}\vert +\vert z_{3}\vert )=\dfrac{{\text {d}}z_{1}}{{\text {d}}t}+\dfrac{{\text {d}}z_{3}}{{\text {d}}t} \\= & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) z_{1}+(\delta _{2}u)z_{2}+{\text {d}}z_{3}\\&+\beta u z_{2}+(-\mu -\delta _{2}u)z_{3}\\= & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) z_{1}+(\beta u+\delta _{2}u)z_{2}+(d-\mu -\delta _{2}u)z_{3}, \end{aligned}$$

since \(z_{1}>z_{2}>0\), we have:

$$\begin{aligned} D_{+}\Vert z\Vert< & {} \left( \delta _{2}u-\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu \right) z_{1} +(d-\mu -\delta _{2}u)z_{3} \\\le & {} \text{ max }\left\{ \delta _{2}u-\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu ,d-\mu -\delta _{2}u\right\} \Vert z\Vert . \end{aligned}$$

Case 2: \(0<z_{1},z_{2},z_{3}\) and \( \vert z_{1}\vert +\vert z_{3}\vert <\vert z_{2}\vert +\vert z_{3}\vert \). In this case, \(\Vert z\Vert = \vert z_{2}\vert +\vert z_{3}\vert \), and

$$\begin{aligned} D_{+}\Vert z\Vert= & {} D_{+}(\vert z_{2}\vert +\vert z_{3}\vert ) =\dfrac{{\text {d}}z_{2}}{{\text {d}}t}+\dfrac{{\text {d}}z_{3}}{{\text {d}}t} =(\delta _{1}-\delta _{2}\tau )z_{1}+\left( -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) \right. \\&\left. -d-\mu -\beta u-\beta s_{1}-\delta _{2}\tau +\delta _{1}+\nu \right) z_{2}+\left( -\alpha _{s}s_{1} -\alpha _{l}s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) \right. \\&\left. -d+\nu -\beta s_{1}\right) z_{3} +( \beta u)z_{2}+ (-\mu -\delta _{2}u)z_{3}\\= & {} (\delta _{1}-\delta _{2}\tau )z_{1}+\left( -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta s_{1}-\delta _{2}\tau +\delta _{1}+\nu \right) z_{2}\\&+\left( -\alpha _{s}s_{1} -\alpha _{l}s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) -d+\nu -\beta s_{1}-\mu -\delta _{2}u\right) z_{3}, \end{aligned}$$

from \(z_{1}<z_{2}\), the above relation becomes:

$$\begin{aligned} D_{+}\Vert z\Vert< & {} \left( \nu +2\delta _{1}-\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta s_{1}-\delta _{2}\tau \right) z_{2}\\&+\left( \nu -\alpha _{s}s_{1} -\alpha _{l}s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) -d-\beta s_{1}-\mu -\delta _{2}u\right) z_{3}\\\le & {} \text{ max }\left\{ \nu +2\delta _{1}-\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta s_{1}-\delta _{2}\tau , \nu \right. \\&\left. -\alpha _{s}s_{1} -\alpha _{l}s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) -d-\beta s_{1}-\mu -\delta _{2}u\right\} \}\Vert z\Vert . \end{aligned}$$

Case 3: \(z_{1}<0<z_{2},z_{3}\) and \( \vert z_{1}\vert +\vert z_{3}\vert >\vert z_{2}\vert +\vert z_{3}\vert \). In this case, \(\Vert z\Vert = \vert z_{1}\vert +\vert z_{3}\vert \), and

$$\begin{aligned} D_{+}\Vert z\Vert= & {} D_{+}(\vert z_{1}\vert +\vert z_{3}\vert ) =-\dfrac{{\text {d}}z_{1}}{{\text {d}}t}+\dfrac{{\text {d}}z_{3}}{{\text {d}}t}\\= & {} \left( \alpha _{s}u+\alpha _{l}\left( \frac{u}{u+k}\right) +d+\mu +\beta u\right) z_{1}-\delta _{2}uz_{2}-{\text {d}}z_{3}+\beta uz_{2}+(-\mu -\delta _{2}u)z_{3} \\= & {} -\left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) z_{1}+(\beta u-\delta _{2}u)z_{2}+(-d-\mu -\delta _{2}u)z_{3}\\= & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) \vert z_{1}\vert +(\beta u-\delta _{2}u)\vert z_{2}\vert + (-d-\mu -\delta _{2}u)\vert z_{3}\vert , \end{aligned}$$

from \(\vert z_{1}\vert >\vert z_{2}\vert \), we have:

$$\begin{aligned} D_{+}\Vert z\Vert< & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu \right) \vert z_{1}\vert +(-d-\mu -\delta _{2}u)\vert z_{3}\vert \\\le & {} \text{ max }\left\{ -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu ,-d-\mu -\delta _{2}u\right\} \Vert z\Vert . \end{aligned}$$

Case 4: \(z_{1}<0<z_{2},z_{3}\) and \( \vert z_{1}\vert +\vert z_{3}\vert <\vert z_{2}\vert +\vert z_{3}\vert \). In this case, \(\Vert z\Vert = \vert z_{2}\vert +\vert z_{3}\vert \), and

$$\begin{aligned} D_{+}\Vert z\Vert= & {} D_{+}(\vert z_{2}\vert +\vert z_{3}\vert ) =\dfrac{{\text {d}}z_{2}}{{\text {d}}t}+\dfrac{{\text {d}}z_{3}}{{\text {d}}t} =(\delta _{1}-\delta _{2}\tau )z_{1}\\&+\left( -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u-\beta s_{1}-\delta _{2}\tau +\delta _{1}+\nu \right) z_{2}\\&+\left( -\alpha _{s}s_{1} -\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) -d+\nu -\beta s_{1}\right) z_{3} +(\beta u)z_{2}\\&+(-\mu -\delta _{2}u)z_{3} (\delta _{2}\tau -\delta _{1})\vert z_{1}\vert +\left( \nu +\delta _{1} -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) \right. \\&\left. -d-\mu -\beta s_{1}-\delta _{2}\tau \right) \vert z_{2}\vert +\left( \nu -\alpha _{s}s_{1} -\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) \right. \\&\left. -d-\beta s_{1}-\mu -\delta _{2}u\right) \vert z_{3}\vert \\\le & {} (\delta _{2}\tau )\vert z_{1}\vert +\left( \nu +\delta _{1} -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta s_{1}-\delta _{2}\tau \right) \vert z_{2}\vert \\&+\left( \nu -\alpha _{s}s_{1} -\alpha _{l} s_{1}\left( \frac{k}{(k+u)^{^{2}}}\right) -d-\beta s_{1}-\mu -\delta _{2}u\right) \vert z_{3}\vert , \end{aligned}$$

from \(\vert z_{1}\vert <\vert z_{2}\vert \), we have:

$$\begin{aligned} D_{+}\Vert z\Vert< & {} \left( \nu +\delta _{1} -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta s_{1}\right) \vert z_{2}\vert \\&+ \left( \nu -\alpha _{s}s_{1} -\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) -d-\beta s_{1}-\mu -\delta _{2}u\right) \vert z_{3}\vert \\\le & {} \text{ max }\left\{ \nu +\delta _{1} -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta s_{1} ,\nu -\alpha _{s}s_{1}\right. \\&\left. -\alpha _{l}s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) -d-\beta s_{1}-\mu -\delta _{2}u\right\} \Vert z\Vert . \end{aligned}$$

Case 5: \(z_{2}<0<z_{1},z_{3}\) and \( \vert z_{1}\vert +\vert z_{3}\vert >\vert z_{2}\vert \). In this case, \(\Vert z\Vert = \vert z_{1}\vert +\vert z_{3}\vert \), and

$$\begin{aligned} D_{+}\Vert z\Vert= & {} D_{+}(\vert z_{1}\vert +\vert z_{3}\vert ) =\dfrac{{\text {d}}z_{1}}{{\text {d}}t}+\dfrac{{\text {d}}z_{3}}{{\text {d}}t}\\= & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) z_{1}+(\delta _{2}u)z_{2}+(d)z_{3}\\&+(\beta u)z_{2}+(-\mu -\delta _{2}u )z_{3}\\= & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) z_{1}+(\delta _{2}u+\beta u)z_{2}+(d-\mu -\delta _{2}u )z_{3} \end{aligned}$$

since \(z_{1}>0\), \(z_{2}<0\):

$$\begin{aligned} D_{+}\Vert z\Vert<(d-\mu -\delta _{2}u )z_{3}<(d-\mu -\delta _{2}u )\Vert z_{3}\Vert . \end{aligned}$$

Case 6: \(z_{2}<0<z_{1},z_{3}\) and \( \vert z_{1}\vert +\vert z_{3}\vert <\vert z_{2}\vert \). In this case, \(\Vert z\Vert = \vert z_{2}\vert \), and

$$\begin{aligned} D_{+}\Vert z\Vert= & {} D_{+}(\vert z_{2}\vert )=-\dfrac{{\text {d}}z_{2}}{{\text {d}}t}= -(\delta _{1}-\delta _{2}\tau )z_{1}\\&-\left( -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u-\beta s_{1}-\delta _{2}\tau +\delta _{1}+\nu \right) z_{2}\\&-\left( -\alpha _{s}s_{1} -\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) +d-\nu -\beta s_{1}\right) z_{3}\\= & {} -(\delta _{1}-\delta _{2}\tau )\vert z_{1}\vert +\left( -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u-\beta s_{1}\right. \\&\left. -\delta _{2}\tau +\delta _{1}+\nu \right) \vert z_{2}\vert +\left( +\alpha _{s}s_{1}+\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) -d+\nu +\beta s_{1}\right) \vert z_{3}\vert \\\le & {} (\delta _{2}\tau )\vert z_{1}\vert +\left( \nu +\delta _{1} -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u-\beta s_{1}-\delta _{2}\tau \right) \vert z_{2}\vert \\&+\left( +\alpha _{s}s_{1}+\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) +\nu -d+\beta s_{1}\right) \vert z_{3}\vert \\\le & {} \left( \delta _{2}\tau +\alpha _{s}s_{1}+\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) +\nu -d+\beta s_{1}\right) (\vert z_{1}\vert +\vert z_{3}\vert )\\&+\left( \nu +\delta _{1} -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u-\beta s_{1}-\delta _{2}\tau \right) \vert z_{2}\vert , \end{aligned}$$

from \(\vert z_{1}\vert +\vert z_{3}\vert < \vert z_{2}\vert \), we have:

$$\begin{aligned} D_{+}\Vert z\Vert\le & {} \left( \alpha _{s}s_{1}+\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) +2\nu +\delta _{1} -\alpha _{s}u-\delta _{2}u\right. \\&\left. -\alpha _{l}\left( \frac{u}{u+k}\right) -\mu -2d-\beta u \right) \vert z_{2}\vert \\= & {} \left( \alpha _{s}s_{1}+\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) +2\nu +\delta _{1} -\alpha _{s}u-\delta _{2}u\right. \\&\left. -\alpha _{l}\left( \frac{u}{u+k}\right) -\mu -2d-\beta u \right) \Vert z\Vert . \end{aligned}$$

Case 7: \(z_{3}<0<z_{1},z_{2}\) and \( \vert z_{1}\vert +\vert z_{3}\vert >\vert z_{2}\vert \). In this case, \(\Vert z\Vert = \vert z_{1}\vert +\vert z_{3}\vert \), and

$$\begin{aligned} D_{+}\Vert z\Vert= & {} D_{+}(\vert z_{1}\vert +\vert z_{3}\vert ) =\dfrac{{\text {d}}z_{1}}{dt}-\dfrac{{\text {d}}z_{3}}{{\text {d}}t}\\= & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) z_{1}+(\delta _{2}u)z_{2}\\&+(d)z_{_{3}}-(\beta u)z_{2}-(-\mu -\delta _{2}u )z_{3} \\= & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) \vert z_{1}\vert +(\delta _{2}u)\vert z_{2}\vert -d \vert z_{3}\vert -(\beta u)\vert z_{2}\vert \\&+(-\mu -\delta _{2}u )\vert z_{3}\vert \\\le & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) \vert z_{1}\vert +(\delta _{2}u)\vert z_{2}\vert \\&-d \vert z_{3}\vert +(-\mu -\delta _{2}u )\vert z_{3}\vert \\\le & {} \left( -\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) \vert z_{1}\vert \\&+(\delta _{2}u)(\vert z_{1}\vert +\vert z_{3}\vert )+(-d-\mu -\delta _{2}u )\vert z_{3}\vert \\= & {} \left( \delta _{2}u-\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u\right) \vert z_{1}\vert +(-d-\mu )\vert z_{3}\vert \\\le & {} \text{ max }\left\{ \delta _{2}u-\alpha _{s}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u ,-d-\mu \right\} \Vert z\Vert . \end{aligned}$$

Case 8: \(z_{3}<0<z_{1},z_{2}\) and \( \vert z_{1}\vert +\vert z_{3}\vert <\vert z_{2}\vert \). In this case, \(\Vert z\Vert =\vert z_{2}\vert \), and

$$\begin{aligned} D_{+}\Vert z\Vert= & {} D_{+}(\vert z_{2}\vert ) =\dfrac{{\text {d}}z_{2}}{{\text {d}}t}\\= & {} (\delta _{1}-\delta _{2}\tau )z_{1}+\left( -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u-\beta s_{1}\right. \\&\left. -\delta _{2}\tau +\delta _{1}+\nu \right) z_{2}+\left( -\alpha _{s}s_{1} -\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) +d-\nu -\beta s_{1}\right) z_{3}\\= & {} (\delta _{1}-\delta _{2}\tau )\vert z_{1}\vert +\left( -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u-\beta s_{1}\right. \\&\left. -\delta _{2}\tau +\delta _{1}+\nu \right) \vert z_{2}\vert -\left( -\alpha _{s}s_{1} -\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) +d-\nu -\beta s_{1}\right) \vert z_{3}\vert \\\le & {} \delta _{1}\vert z_{1}\vert +\left( -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u-\beta s_{1}-\delta _{2}\tau +\delta _{1}+\nu \right) \vert z_{2}\vert \\&+\left( \alpha _{s}s_{1} +\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{^{2}}}\right) +\nu -d+\beta s_{1}\right) \vert z_{3}\vert \\\le & {} \left( \delta _{1}+\alpha _{s}s_{1} +\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{2}}\right) +\nu -d+\beta s_{1}\right) (\vert z_{1}\vert +\vert z_{3}\vert )\\&+\left( -\alpha _{s}u-\delta _{2}u-\alpha _{l}\left( \frac{u}{u+k}\right) -d-\mu -\beta u-\beta s_{1}-\delta _{2}\tau +\delta _{1}+\nu \right) \vert z_{2}\vert , \end{aligned}$$

since \(\vert z_{1}\vert +\vert z_{3}\vert <\vert z_{2}\vert \), we have:

$$\begin{aligned} D_{+}\Vert z\Vert\le & {} \left( 2\nu +2\delta _{1}+\alpha _{s}s_{1} +\alpha _{l} s_{1}\left( \frac{ku}{(k+u)^{2}}\right) -\alpha _{s}u-\delta _{2}u\right. \\&\left. -\alpha _{l}\left( \frac{u}{u+k}\right) -\mu -2d-\beta u-\delta _{2}\tau \right) \Vert z\Vert . \end{aligned}$$

Now, using the supposed inequalities, in all of the above cases, the coefficient of ||z|| is a negative number, and hence, there exists \(\chi >0\), with \(D_{+}\Vert z\Vert \le -\chi \Vert z\Vert \) for all \(z\in {\mathbb {R}}^{3}\). \(\square \)

Lemma 3.1 and a proof similar to corollary 5.4 in [1], implies the following theorem.

Theorem 3.2

If the inequalities (3.11) hold, positive semi-trajectories of system converge to an equilibrium point, i.e., any \(\omega \)-limit point of system in \(\Omega ^{\circ }\), is an equilibrium point.

Finally, the above theorem implies the following result.

Theorem 3.3

Suppose the inequalities (3.11) hold, then:

  1. 1.

    when the only equilibrium point is the drug-free equilibrium \(P_0\), then all solutions tend to \(P_0\);

  2. 2.

    when there is unique endemic equilibrium point, then all solutions of system tends to endemic equilibrium point.

4 Conclusion

The White and Comiskey’s model of heroin epidemics was developed in this paper. The development includes the split of the susceptible populations into two compartments, the susceptible individuals \(S_{1}\), and the responsive individuals \(S_{2}\), i.e., the individuals who do not use drugs because of information about the harms and dangers of it. Furthermore, we assume that because of transmission of information, susceptibles will be transmitted from \(S_1\) to \(S_2\). We considered two routes for information dissemination, information transmission via direct contact between individuals, and population-wide dissemination of drug-related information. At first, we considered a model without treatment/rehabilitation compartment. A complete qualitative study of this model including the existence and local and global stability of the equilibrium points are carried out. The drug-free equilibrium \(P_0\) was shown to be locally and globally stable if \(R_0<1\), and the endemic equilibrium point exists and is locally and globally stable if \(R_0>1\).

Then, we considered a model with a compartment for the individuals under treatment/rehabilitation programs. This model shows more complexity, in fact, endemic equilibrium may exist (up to 3 point), in cases, \(R_0<1, R_0=1\) and \(R_0>1\). Occurrence of backward bifurcation is also proved for the model. The backward bifurcation analysis showed that, if the relapse rate exceeds a certain value, then the backward bifurcation will occur. The occurrence of backward bifurcation makes it harder to control the infection, in fact, to prevent the epidemic from occurring, the reducing of \(R_0\) to the region \(R_0<1\), is not enough.

Formula of \(R_0\) showed that the basic reproduction number is not dependent on information transmission parameters \(\alpha _s,\alpha _l,k,d\), so the role of the other parameters, such as the infection rate and the treatment rate, in the occurrence or elimination of epidemy is of greater impact. However, at the same time, (3.9) showed that increasing the parameters \(\alpha _s\) and \(\alpha _l\), or decreasing the parameters k and d, increases the amount of the threshold necessary for the occurrence of backward bifurcation, which makes the occurrence of backward bifurcation harder, and hence, it makes the infection control easier.