In an attempt to slow the spread of COVID-19, most countries have interrupted formal schooling. This has led to approximately 90% of the world’s student population having their schools closed during varying periods (UNESCO, 2021). The effects of such an unprecedented disruption in school on children’s academic development are unknown. However, it is possible to extrapolate possible effects of the current and ongoing disruptions in school from studies which have examined the effects of the summer hiatus on academic performance. Previous studies have shown that the summer hiatus results in negative effects on children’s educational achievement, with an average decrease of approximately one-tenth of a standard deviation over the summer period (Cooper et al., 1996).

Here we report findings on the effects of the summer hiatus in schooling in a contemporary sample of economically disadvantaged children in a longitudinal study over the first 4 years of school. In addition, we hypothesized and our data support significant ameliorative effects of an intensive evidence-based reading intervention provided during the school year on the summer hiatus. We note that our data were collected prior to the COVID-19 pandemic. These results have important implications for the estimated millions of children who have missed and are currently still missing school because of the coronavirus pandemic.

Methods

Study Oversight

Parents or caretakers provided written consent for their children to participate in the study, and children also provided assent. The Institutional Review Board at the Yale University approved this study. This study was conducted in accordance with the ethical principles that have their origin in the Declaration of Helsinki and are consistent with good clinical practices and applicable laws and regulations.

Participants and Study Design

One hundred and eleven students from two elementary charter schools in New Haven participated in the study (58.6% were girls). Both schools were in districts with high proportions of economically disadvantaged and minority children; 79.0% of the children received free lunches at the beginning of the study; 96.6% were African American, Hispanic, or Latino. All the students in first grade in the two schools were eligible for the study. No students were excluded from the study.

All the participants were tested each year from grade 1 through grade 4, from 2015 through 2018. We used the Phonological Awareness measure of the Comprehensive Test of Phonological Processing (CTOPP-2) (Wagner et al., 2013) as a selection variable for deciding which children were at risk for reading failure. All students below the 25th percentile were considered at risk and were provided with the intervention (n = 20) (designated as intervention). The remaining students served as a comparison group. Among them we selected 18 children closely matched to the intervention cases in sex, age, and the next closest scores on Phonological Awareness (designated as matched comparison group). The remaining children served as a remaining comparison group (n = 73).

All students in the intervention and matched comparison groups were assessed at the beginning and end of each school year (fall and spring test periods). This allowed us to evaluate the effect of the interruption of schooling during the summer. The remaining comparison children were assessed in the fall only, which allowed us to study the overall trend. The mean age (and SD) in months for each group at the first test period were as follows: intervention, 84.2 (SD = 6.8); matched comparison, 78.2 (SD = 3.7); and remaining comparison, 76.4 (SD = 4.3). The sample size available at each wave is reported in Table 1. There was very little attrition in the study, and therefore the sample sizes for the intervention and matched comparison groups show little variation over time. The differences in sample size across time points in the remaining comparison group were due to measuring those students in the fall  waves only.

Table 1 Means (standard deviations) and sample sizes for passage comprehension at all test periods. Age-normed z scores
Full size table

Evidence-Based Intervention

The 20 students in the intervention group received, in addition to their regular reading program, an evidence-based intervention beginning in first grade and continuing in second, third, and fourth grades. The intervention used an Orton-Gillingham approach (Ritchey & Goeke, 2006) and was provided Mondays through Thursday for 90 min each day in small groups of 4 students by instructors trained to administer Orton-Gillingham instruction who worked together with the regular classroom teachers.

Outcome Measure

At every test period, we assessed participants reading comprehension using the Passage Comprehension (PC) component of the Woodcock-Johnson IV Tests of Achievement (WJ IV ACH) (Schrank et al., 2014). We selected reading comprehension as the outcome following long-standing federal guidelines (National Reading Panel, 2000) that reading comprehension represents “… the ‘essence of reading’ that sets the stage for children’s later academic success…” (Gamse et al., 2008) (p. 10).

Because we were interested in the participants’ position relative to their normative population at each test period, we used age-standardized z scores. In this metric, the population mean and standard deviation equal 0 and 1 points, respectively. Therefore, at every test period, a score of zero is exactly at the population’s mean, and scores of −1 and 1 points are one SD below and above the mean, respectively. Note that a student whose score is zero at every test period would show typical development, which would be associated with actual growth in the absolute level of ability. This is because reading ability is expected to increase during the developmental period examined here.

Statistical Analysis

To characterize the longitudinal development of the various constructs, we applied a Latent Change Score (LCS) model (Ferrer & McArdle, 2010; McArdle, 2009; McArdle, 2001). This dynamic structural equation model allows capturing the key elements of change as a set of statistical parameters. A path diagram representing the model is depicted in Figure 1.

Fig. 1
figure 1

Path diagram of the Latent Change Score model applied to characterize the developmental trajectories. Note: Sub index g indicates different estimates for each group. The square boxes represent observed variables. The circles represent latent variables. A triangle represents a constant for the estimation of means. Single-ended arrows represent regression loadings. Double-ended arrows represent variances and covariances. Regression loadings without a value in the diagram were fixed to one.

Full size image

The LCS model includes a measurement structure that makes it possible to separate the variance in the relevant construct from the variance due to measurement error. This allows estimating the latent true trajectory. The measurement occasions (y) are modeled as an auto-regressive system: any given test period yt is a predicted by two components. The first component is the level at the previous test period yt-1, and the second component Δyt captures all the innovations, or changes, from yt-1 to yt. The latent variable y0 (with mean μ0 and variance σ20) allows capturing the initial level (i.e., latent intercept). Another latent variable yS (with mean μS and variance σ2S) characterizes the linear developmental change from each test period to the next (i.e., latent additive component). These two latent variables are allowed to be correlated through the covariance σ0S. Because the system is auto-regressive, any change introduced at one particular test period is propagated to later time points. We specified loadings from the latent additive component to the innovations with a fixed value of 0.5. This parameterization allows interpreting its mean μS as the mean yearly change.

We included a latent variable (summer), with mean γsummer and no variance (i.e., a fixed effect). This latent variable had a specified effect on test periods 3, 5, and 7 only (i.e., the fall of grades 2 through 4, which were taken right after each summer). Because the model is auto-regressive, it allows any effect due to the summer introduced at a given test period to be carried over to later test periods.

To examine differences between the students in intervention and the comparison groups, we applied a two-group SEM including all participants and test periods. Because the same measurement tool was used for the participants in both groups, we constrained the measurement error variance to have the same value for both groups. The rest of the parameters were freely estimated. The R package lavaan was used for model estimation (Rosseel, 2012).

For estimating the model, we used full information maximum likelihood (FIML) (Arbuckle, 1996). This procedure was chosen to deal with unequal sample sizes at each wave. Previous literature has shown that FIML estimation is superior to other methods for dealing with incomplete data in the context of structural equation modeling (Enders & Bandalos, 2001; Schlomer et al., 2010). Given our relatively small sample size, we conducted a power analysis to assess the ability of our model to detect the summer effect in the intervention group. Our analysis indicates that, given our sample size and the effects found in our data, our model would be able to detect such effects at least 63% of the time with samples of size 20 (i.e., 63% power). A power of 80% would be achieved with a sample of size 30. In other words, our sample allows detecting summer effects of the size estimated here.

Results

Descriptive Analysis

Table 1 reports the means and standard deviations of the outcome variable (Passage Comprehension, PC) at each test period. A generalized decline in the z scores is readily apparent from fall ′14 to spring ′18. However, we found marked differences between the intervention group and the two comparison groups. Students in intervention started off with considerably lower mean levels: −.85 (percentile 20). In contrast, both comparison groups had higher initial scores: .58 and .59 (percentile 72). However, intervention students were better able to maintain their relative position from test period 1 to 7, declining by .659 points, whereas the matched and remaining comparison students lost 1.126 and 1.105 points, respectively. Because these are z scores, they can be readily interpreted as standard deviations and as Cohen’s d-indices (Cohen, 1988).

These results are surprising because they show that those students who did not receive the intervention started off above the reference mean but fell behind their reference group from grade 1 to grade 4. They show also that both comparison groups were fairly similar. Note that, because these are z scores, a decrease from one test period to the next indicates a reduction in the group’s standing relative to their reference population, not a decrease in the absolute level. In other words, reading scores in the comparison groups did not decline over time; rather, they did not improve at the rate of their reference population.

Effects of the Summer Interruption on Longitudinal Development

Table 2 includes parameter estimates and fit indices from the LCS models for the intervention and matched comparison groups.

Table 2 Parameters (and standard errors) of the multigroup Latent Change Score model
Full size table

An important feature of the LCS model is that it allows isolating the effect of the summer interruption on the longitudinal trajectories (and, consequently, it makes it possible to estimate what would be the yearly change when such effects are discounted). Figure 2 depicts the total yearly change in reading with and without the summer effects, for each group. A negative (or positive) effect implies that the group decreases (or increases) its mean percentile, relative to the reference population, every year. The gray bars (right side of each pair) depict the estimated yearly change, including the effect of the summer interruption. The black bars (left side of each pair) depict what would be the yearly change if the effect of summer is discounted (i.e., without the summer interruption). The net effect of summer is the difference between the two values and was negative for reading comprehension.

Fig. 2
figure 2

Yearly change in passage comprehension with and without the effect of the summer interruption. Note: Changes expressed in age-normed z scores. A z score of 0 implies that the group keeps its relative position with respect to the reference population from 1 year to the next. Negative and positive scores imply, respectively, that the group falls behind, or learn faster, than the reference population

Full size image

The effect of summer interruption was dsummer,Int = −.32 (95% CI −.60 to −.04) and dsummer,MC = −.20 (95% CI −.47 to .07) for intervention and matched comparison groups, respectively. In other words, the intervention group declined by approximately one-third of a standard deviation every summer, whereas the matched comparison group declined by one-fifth of a standard deviation. The total yearly change was negative for both groups. Note that without the summer disruption, the yearly change would be positive for the intervention students, dyear,AR = .14, and negative but much closer to null for the matched comparison group, dyear,MC = −.16. This implies that, without the summer interruption, the intervention students would gradually reduce their gap with the reference population, whereas the matched comparison would fall behind much more slowly.

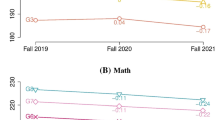
Figure 3 depicts individual trajectories for reading in intervention, matched comparison, and remaining comparison groups, along with the means estimated by the LCS model. This figure indicates that, when compared to their reference population and controlled for age, students in the matched comparison group generally fell behind from grade 1 to grade 4, whereas intervention students were better able to decelerate their decline and maintain their relative standing. The total decline was larger for the matched comparison students. In both cases, the decrease is accelerated during the summer periods.

Fig. 3
figure 3

Longitudinal development of passage comprehension for the intervention and comparison students (summer periods represented by shaded areas). Note: The black line represents the model-implied means. The numbers above and below the line indicate mean percentiles and mean z scores, respectively. The horizontal gray lines indicate values containing the central 50% of the normative population.

Full size image

Discussion

Our findings document a significant negative effect of a school hiatus in economically disadvantaged children in the first 4 years of school. This negative effect, here in a contemporary cohort, is 3–4 times greater than studies over two decades ago had suggested and has serious implications for the millions of children who have missed and may currently still missing school because of the coronavirus pandemic. Of particular relevance, an intensive, evidence-based reading intervention provided to those children most at-risk for reading failure (intervention group) improved their reading during the time they were in school and modified though did not fully reverse the effects of the summer hiatus. On a positive note, even with the negative effects of the summer hiatus, those children who received the intensive reading intervention fared much better than children who did not, whose yearly decline was more than double that observed in the intervention group.

More specifically, our findings suggest that, without the summer interruption, the intervention group, those students at greatest risk (with lower initial scores: mean percentile = 19 in the fall of grade 1), would gradually improve in relation to the normative population. In other words, without the summer disruption, their yearly change in reading would have been positive. However, the interruption in schooling due to the summer hiatus disrupted this process and reversed the net yearly change from positive 0.14 to negative 0.18. This decrease of d = −.32 is more than three times as great as the effects of the summer hiatus reported in previous studies (Cooper et al., 1996). Furthermore, the students at greatest risk for reading failure, who received an evidence-based intervention during the school year, showed, overall, smaller declines in reading regardless of the effect of summer hiatus.

While the positive effects observed in the intervention group provide a degree of optimism, the generalizability of our findings is tempered by the resource intensive nature of the intervention. In particular, children received the reading intervention for 90 min 4 days/week in small groups provided by teachers who had considerable experience and training using the Orton-Gillingham method.

We note that our data were not collected during the COVID-19 pandemic. Two important differences between the schooling disruptions examined in this study and the disruption due to the COVID pandemics are as follows: (a) each of the summer breaks considered here is shorter than the COVID disruption, and (b) summer breaks are an expected part of a normal school year, whereas the COVID disruption is not. Nevertheless, our findings are very useful to inform decisions in the current situation. First, the total disruption time adding the three consecutive summers is approximately 6 months. This period is similar to that in which many school districts have been closed due to the COVID pandemics. Second, even if these types of disruptions are not equivalent, both situations involve children missing school for months. Our results provide support to indicate that the current disruptions in schooling implemented to slow the spread of COVID-19 are likely having a significant detrimental effect on the reading abilities of those students at greatest risk—economically disadvantaged children.

In addition our findings make it imperative that schools put in place programs to compensate for the declines during the period without regular classes. It is critical that vulnerable children are given an opportunity to begin to narrow their yawning achievement gap in reading. These data further suggest that the longer these disruptions persist, the greater will be the negative effects on reading for the most disadvantaged children. They mandate that educational policy makers must both prioritize and implement specific measures to minimize as much as possible these serious consequences. In particular, they must ensure that these most vulnerable students are a major focus of effective, evidence-based reading interventions throughout the school year as well as over the summer. These efforts must be especially proactive in low-income African American and Hispanic populations where identification of academic deficits may be more likely to go unrecognized (Magnusson et al., 2017).

Providing such interventions presents a real challenge since currently, even in school settings with relatively small numbers of students in a class, teachers may have very limited time to help any individual student. Interventions in the current study were provided for 90 min 4 days/week to students in groups of four students or less. In the interests of equity, it is critical that policy makers prioritize the allocation of necessary resources to minimize the negative effects on reading this pandemic has wrought on these most disadvantaged children.