Selection of Appropriate Global Partner for Companies Using q-Rung Orthopair Fuzzy Aczel–Alsina Average Aggregation Operators

Abstract

The term “q-Rung orthopair fuzzy sets ($q^{r}$OFSs)” refers to the collection of the most differentiated ideas for expressing fuzzy data in decision-making rules. The $q^{r}$OFSs can gradually adapt the region of information by adjusting the parameter $q \ge 1$ in response to the fluctuation degree, so assisting in the generation of more numerous possibilities. Aczel–Alsina triangular norm and conorm are superior operations that may create general and adaptable working principles for aggregating arguments. To make use of $q^{r}$OFSs and Aczel–Alsina triangular norms in “multiple attribute decision-making (MADM)” issues, a few q-rung orthopair fuzzy ($q^{r}$OF) Aczel–Alsina aggregation operators: $q^{r}$OF Aczel–Alsina weighted average ($q^{r}$OFAAWA) operator, $q^{r}$OF Aczel–Alsina order weighted average ($q^{r}$OFAAOWA) operator, $q^{r}$OF Aczel–Alsina hybrid average ($q^{r}$OFAAHA) operator for aggregating $q^{r}$OFSs are exhibited in this article to fix the MADM issues based on $q^{r}$OFSs. Some significant properties are additionally demonstrated. A technique for taking care of the MADM issues is proposed based on these created operators. The adequacy of the suggested technique is shown by means of a numerical example on enterprise partner selection, a lot of investigations and correlations with other existing strategies. The sensitivity of the proposed aggregation operators to decision-making findings is investigated. The demonstration outcomes suggest that the suggested technique has fulfilling universality and adaptability in aggregating $q^{r}$OF data and acquiring the correlations of criteria and the attitudes of “decision-makers (DMs)” and is doable and compelling for taking care of the MADM issues dependent on $q^{r}$OFSs.

1 Introduction

While Zadeh [62] initiated the classic fuzzy set (FS) as a way of expressing the vulnerability of choice data, a large number of research accomplishments have been made in this area. With the expanding complexity of decision-making concerns in real-life, the outflow of decision-making data turns out to be more and more diversified. As a speculation of FS, “Atanassov’s intuitionistic fuzzy set (AIFS)” [5] presented by Atanassov is a viable apparatus to communicate complex fuzzy data since it has “membership degrees (MDs)” and “non-membership degrees (NMDs)” simultaneously; along these lines, it has higher adaptability in fuzziness and uncertainty. Be that as it may, the scope of utilizations of AIFS is narrow in light of the fact that DMs may confront circumstances in which the sum of MD and NMD by DMs is bigger than one. Under these conditions, some assessment data cannot be actually communicated by the AIFS. To tackle the circumstance, Yager [57] proposed the Pythagorean fuzzy sets (PFS) in which the sum of the squares of both MD and NMD is less than or equal to one.

On the other hand, the increasing volatility of decision-making concerns and the contrasting attitudes of DMs continue to make it difficult for PFS to provide pertinent data. Along these lines, the jobs of AIFSs and PFSs are constrained. To deal with it, in recent times, Yager presented $q^{r}$OFSs [58] in which the sum of the $q^{th}$ power of MD and the $q^{th}$ power of NMD is equal to or less than 1. AIFSs and PFSs are particular instances of $q^{r}$OFSs when fixing $q=1$ and $q=2$ individually. As q-rung expands, the scope of handling fuzzy data increases. $q^{r}$OFSs permits the DMs to freely relegate the values to MD and the NMD, which gives the DMs more opportunities to communicate the inclination.

Fig. 1

The framework of the study

1.1 Research Gap and Motivation of the Study

Liang et al. [24] defined $q^{r}$OF entropy, $q^{r}$OF cross-entropy and $q^{r}$OF Choquet integral and based on these they proposed a generalized model for the two-sided matching. On the basis of the power mean operator, Ju et al. [17] proposed a few $q^{r}$OF power mean aggregation operators. By utilizing Dombi triangular norms with $q^{r}$OFSs, Jana et al. [16] introduced $q^{r}$OFDWA operator, $q^{r}$OFDWG operator, $q^{r}$OFDOWA operator, $q^{r}$OFDOWG operator, $q^{r}$OFDHWA operator and $q^{r}$OFDHWG operator. Peng together with colleagues [37] proposed a $q^{r}$OF decision-making technique on the basis of the weighted distance-based approximation strategy. $q^{r}$OFS has also been extended to accommodate uncertain linguistic contentions [26], interval values [18].

Liu and Wang [28] proposed for the first time $q^{r}$OF weighted (average, geometric) operator to handle the decision data. On the basis of these operators, they delivered two novel techniques to handle the MADM issues under the fuzzy conditions. Some “$q^{r}$OF Bonferroni mean (BM) operators” have been provided in [29]. Liu et al. [27] developed several power BM operators with linguistic $q^{r}$OF data such as the “$q^{r}$OF BM ($q^{r}$OFBM) operator”, the “$q^{r}$OF weighted BM operator”, the “$q^{r}$OF geometric BM operator”, and the “$q^{r}$OF weighted geometric BM operator”. On the basis of these operators the authors developed several MAGDM techniques. Wei et al. [54] combined $q^{r}$OFS with Heronian mean and provided a few $q^{r}$OF Heronian mean operators. Wei et al. [55] additionally prolonged the MSM operator into the $q^{r}$OFS situation and defined some $q^{r}$OF MSM operators. Likewise, Du [7] proposed the weighted power by utilizing $q^{r}$OF values to improve and develop aggregations on $q^{r}$OFVs. Yang together with Pang [59] developed a few $q^{r}$OF partitioned BM operators. They defined several new $q^{r}$OF BM Dombi operators [60] and applied them to MADM issues. Wang et al. [51] investigated four types of data aggregation operators, for instance, the HM operator, DHM operator, WHM operator, and WDHM operator with the $q^{r}$OFNs.

In terms of the cosine function, Wang together with colleagues [53] suggested the similarity measures of $q^{r}$OFS and utilized them in MADM issues. Peng and Liu [36] developed the organized transformation of distance measure, similarity measure, inclusion measure, and entropy for $q^{r}$OFSs. In order to extend the $q^{r}$OF calculus to a wider area, Ai et al. [2] systematically discussed the $q^{r}$OF double integrals within the context of Archimedean triangular norms and conorms. Combining the idea of soft set and $q^{r}$OFS, Hussain et al. [14] initiated $q^{r}$OF soft set and applied it to MADM issues. Since $q^{r}$OFs have points of interest over existing FSs, $q^{r}$OF values are considered as assessment values in this article.

$q^{r}$OF MADM has seen considerable use in a wide variety of domains, including, but not limited to, supplier selection [38], investment project selection [52], potential assessment of appearing technology development [55], renewable energy sources evaluation [20], assessment of classroom teaching quality [35], stock investment evaluation [47], online shopping [61], credit risk assessment [30], selection of green suppliers [51], smart phone selection [63] and enterprise resource planning systems selection [50]. For different investigates on $q^{r}$OFSs, we would like to refer [3, 13, 25, 31, 32, 34].

In Menger’s theory of stochastic topological spaces, the concept of triangular norms [33] was originally introduced. In the course of research, it became evident that the t-norms with their associated t-conorms are important operations in PFSs and qrOFSs, for example, the “Einstein t-norm and t-conorm” [39], “Archimedean t-norm and t-conorm” [2], “Hamacher t-norm and t-conorm” [6], “Lukasiewicz t-norm and t-conorm” [48]. Klement et al. [19] have carried out considerable research in recent years on the features and process of achieving triangular norms, and their findings have been published in a well-organized manner. It was in 1982 that Aczel–Alsina [1] introduced two new operations, which are referred to as Aczel–Alsina t-norm and Aczel–Alsina t-conorm, and which have a high priority of variability in conjunction with the activities of variables. Based on the Aczel–Alsina triangular norm (AA t-norm), Wang et al. [49] devised a score level hybrid method. In recent times, Senapati et al. [42,43,44,45] have developed “(interval-valued) intuitionistic fuzzy Aczel–Alsina aggregation operators” and implemented them to MADM technique.

After looking at these examples and talking about them, we’ve come to the conclusion that the $q^{r}$OFS is effective and reliable enough to show the credible and debatable data that comes up in real-world situations. The previously stated decision-making challenges in various fuzzy aggregation environments under triangular norm and conorms motivated us to a substantial expanse to produce our present paper. The mathematical procedures that make up the Aczel–Alsina working laws are essential and allow for an advantage to be gained when dealing with faulty and ambiguous information. As a result of these ideas, we decided to implement Aczel–Alsina operations on $q^{r}$OFNs and build certain $q^{r}$OF Aczel–Alsina aggregation operators in order to tackle various $q^{r}$OF MADM problems.

1.2 Contributions of This Study

The purpose of this investigation is to develop a strategic and insightful recommendation technique that will enable the choice of the alternative approach that represents the most appropriate alternative among a repository of alternatives. This will be accomplished by establishing a strategy that will allow for such a preference of the alternative approach that it will enable us to choose the most reasonable alternative. The efficacy of the proposed framework would be ascertained through the use of a $q^{r}$OF AA weighted average aggregation operator, which would be attained via the incorporation of AA working rules into a $q^{r}$OF context. In other words, the effectiveness of the proposed framework would be affirmed through the incorporation of AA operating laws into a $q^{r}$OF context. This is a list of a few of the most important things that have been done as part of this research:

• (1) For the $q^{r}$OFSs, new AA operational rules have been developed and implemented.

• (2) These unique operations have led to the development of various useful aggregation operators, which include the $q^{r}$OF Aczel–Alsina weighted average ($q^{r}$OFAAWA) operator, the $q^{r}$OF Aczel–Alsina order weighted average ($q^{r}$OFAAOWA) operator, and the $q^{r}$OF Aczel–Alsina hybrid average ($q^{r}$OFAAHA) operator.

• (3) Examine the properties of such unique operators, as well as specific examples of their application.

• (4) Construct an algorithm that can deal with MADM issues while also making use of $q^{r}$OF data.

• (5) Create a brand-new MADM method that employs the $q^{r}$OFAAWA operator.

• (6) Comparative and sensitivity assessments are done to show that the approach is strong and reliable.

1.3 Organization of This Work

One may find the information listed below in the article: In Sect. 2, we discuss some preliminary information concerning $q^{r}$OFSs and the Aczel–Alsina operator. This information includes definitions, features, and operating rules. In Sect. 3, we propose Aczel–Alsina operations with respect to $q^{r}$OFNs. We talk about the $q^{r}$OFAAWA operator, $q^{r}$OFAAOWA operator and $q^{r}$OFAAHA operator in Sect. 4. In Sect. 5, we take into consideration a MADM strategy while keeping in mind the $q^{r}$OFAAWA operator. In Sect. 6, we demonstrate the proposed method using a real-world scenario. In Sect. 7, we conduct an analysis of the effect that parameters have on the outcomes of decision-making. In Sect. 8, we look at how the weights of the criteria affect the order in which they are ranked. Section 9 provides a relative investigation of other appropriate methodologies to endorse the sufficiency of the proposed method. In Sect. 10, we give the conclusions.

2 Preliminaries

In this section, we acquaint some essential ideas related with t-norm, t-conorm, Aczel–Alsina t-norm and $q^{r}$OFSs.

2.1 t-Norms, t-Conorms, Aczel–Alsina t-Norms

Definition 1

[19] “A t-norm is a rational function on the unit interval [0,1], that is, a function $T:[0,1] \times [0,1] \rightarrow [0,1]$ designed in such a way the following four axioms are fulfilled,, for all $\varrho , \upsilon , \omega \in [0, 1]$:

• (i) Symmetric: $T(\varrho ,\upsilon ) = T(\upsilon ,\varrho )$;

• (ii) Monotonic: $T(\varrho ,\upsilon )\le T(\varrho , \omega )$ if $\upsilon \le \omega$;

• (iii) Associative: $T(\varrho , T(\upsilon , \omega ))= T(T(\varrho ,\upsilon ), \omega )$;

• (iv) Identity element 1: $T(\varrho , 1) = \varrho$.”

Example 1

[19] “Few prominent examples of t-norms are

• (i) $T_{P}(\varrho ,\upsilon )=\varrho .\upsilon$ (product t-norm)

• (ii) $T_{M}(\varrho ,\upsilon )=\min (\varrho ,\upsilon )$ (minimum t-norm)

• (iii) $T_{L}(\varrho ,\upsilon )=\max (\varrho + \upsilon -1, 0)$ (Lukasiewicz t-norm)

• (iv) $T_D(\varrho ,\upsilon ) =\left\{ \begin{array}{ll} \varrho ,&\quad \text{ if } \upsilon =1\\ \upsilon ,&\quad \text{ if } \varrho =1\\ 0,&\quad \text{ otherwise } \end{array}\right. \text{(Drastic } \text{ t-norm) }$

for all $\varrho , \upsilon \in [0, 1]$.”

Definition 2

[19] “A t-conorm is a rational function on the unit interval [0,1], that is, a function $S:[0,1] \times [0,1] \rightarrow [0,1]$ designed in such a way the following four axioms are fulfilled, for all $\varrho , \upsilon , \omega \in [0, 1]$:

• (i) Symmetric:    $S (\varrho ,\upsilon ) = S (\upsilon ,\varrho )$;

• (ii) Monotonic:   $S (\varrho ,\upsilon )\le S (\varrho , \omega )$ if $\upsilon \le \omega$;

• (iii) Associative:    $S(\varrho , S(\upsilon , \omega ))= S (S(\varrho ,\upsilon ), \omega )$;

• (iv) Identity element   0: $S (\varrho , 0) = \varrho$.”

Example 2

[19] “Few prominent examples of t-conorms are

• (i) $S_{P}(\varrho,\upsilon) = \varrho +\upsilon -\varrho .\upsilon$ (probabilistic sum)

• (ii) $S_{M}(\varrho ,\upsilon )=\max (\varrho ,\upsilon )$ (maximum t-conorm)

• (iii) $S_{L}(\varrho ,\upsilon )=\min (\varrho + \upsilon , 1)$ (Lukasiewicz t-conorm)

• (iv) $S_D(\varrho ,\upsilon )=\left\{ \begin{array}{ll} \varrho , &{} \text{ if } \upsilon =0\\ \upsilon , &{} \text{ if } \varrho =0\\ 1, &{} \text{ otherwise } \end{array}\right. \text{(Drastic } \text{ t-conorm) }$

for all $\varrho , \upsilon \in [0, 1]$.”

Definition 3

[1, 4] “The Aczel–Alsina t-norms $(T_{A}^{\eta })_{\eta \in [0,\infty ]}$ is ascertained by

$$\begin{aligned} T_{A}^{\eta }(\varrho ,\upsilon )=\left\{ \begin{array}{ll} T_D(\varrho ,\upsilon ),&\quad \mathrm{if} \,\, \eta =0\\ \min (\varrho ,\upsilon ),&\quad \mathrm{if} \,\, \eta =\infty \\ e^{-((-\ln \varrho )^\eta +(-\ln \upsilon )^\eta )^{1/\eta }},&\quad \text{otherwise} \end{array}\right. \end{aligned}$$

The Aczel–Alsina t-conorms $(S_{A}^{\eta })_{\eta \in [0,\infty ]}$ is ascertained by

$$\begin{aligned} S_{A}^{\eta }(\varrho ,\upsilon )=\left\{ \begin{array}{ll} S_D(\varrho ,\upsilon ), & \quad \mathrm{if} \,\, \eta =0\\ \max (\varrho ,\upsilon ),&\quad \mathrm{if} \,\, \eta =\infty \\ 1-e^{-((-\ln (1- \varrho ))^\eta +(-\ln (1-\upsilon ))^\eta )^{1/\eta }},&\quad \text{otherwise''} \end{array}\right. \end{aligned}$$

“Limiting values: $T_{A}^{\infty }=\min$, $T_{A}^{0}=T_D$, $T_{A}^{1}=T_P$, $S_{A}^{\infty }=\max$, $S_{A}^{0}=S_D$, $S_{A}^{1}=S_P$.

The t-norm $T_{A}^{\eta }$ and t-conorm $S_{A}^{\eta }$ are dual with regard to each other for all $\eta \in [0,\infty ]$. The Aczel–Alsina t-norms family and Aczel–Alsina t-conorms family are strictly increasing and strictly decreasing, respectively.

It is worth noting that Aczel–Alsina t-norms family are really the only t-norms that satisfy the equivalence $T(\varrho ^\lambda ,\upsilon ^\lambda ) = T(\varrho ,\upsilon )^\lambda$ for any $\lambda > 0$ and $\varrho , \upsilon \in [0,1]$.”

2.2 q-Rung Orthopair Fuzzy Sets

Basic concepts of $q^{r}$OFSs are concisely presented in Sect. [10, 12].

Definition 4

[58] “A $q^{r}$OFS $\psi$ over a fixed set X interpreted as

$$\begin{aligned} \psi =\{\langle x, \zeta _{\psi }(x), \varphi _{\psi }(x)\rangle |x\in X\} \end{aligned}$$

where $\zeta _{\psi }$ and $\varphi _{\psi }$ are functions from X to the closed interval [0, 1], such that $0\le \zeta _{\psi }^{q}(x)+\varphi _{\psi }^{q}(x)\le 1$, for all $x \in X$ and they represent the MD and NMD of x to set $\psi,$ respectively. The value $\pi _{\psi }(x)=\root q \of {1-\zeta _{\psi }^{q}(x)-\varphi _{\psi }^{q}(x)}$ is generally called the indeterminacy degree of the member x to set $\psi$. It is clear that $0\le \pi _{\psi }(x) \le 1$, for all $x \in X$.

For benefit, we called $\psi =\{\langle x, \zeta _{\psi }(x), \varphi _{\psi }(x)\rangle |x\in X\}$ as q-rung orthopair fuzzy number ($q^{r}$OFN) denoted by $\psi =(\zeta _{\psi },\varphi _{\psi })$.”

For contrasting two $q^{r}$OFNs, score function and accuracy function is ascertained as

Definition 5

[28] “The score function $\hat{Z}(\psi )$ and accuracy function $\hat{L}(\psi )$ of a $q^{r}$OFN $\psi =(\zeta _{\psi },\varphi _{\psi })$ can be computed as:

$$\begin{aligned} \hat{Z}(\psi ) &= \zeta _{\psi }^{q}-\varphi _{\psi }^{q},\quad \text{ where } \;\hat{Z}(\psi )\in [-1,1]\end{aligned}$$

(1)

$$\begin{aligned} \hat{L}(\psi ) &= \zeta _{\psi }^{q}+\varphi _{\psi }^{q}, \quad \text{ where }\;\hat{L}(\psi )\in [0,1].'' \end{aligned}$$

(2)

Liu and Wang [28] introduced comparison method on the basis of score and accuracy function for ranking the $q^{r}$OFNs, that is represented as

Definition 6

[28] “Assume that $\psi _1=(\zeta _{\psi _1}, \varphi _{\psi _1})$ and $\psi _2=(\zeta _{\psi _2}, \varphi _{\psi _2})$ are any two $q^{r}$OFNs. Let $\hat{Z}(\psi _1)$, $\hat{Z}(\psi _2)$ be score functions and $\hat{L}(\psi _1)$, $\hat{L}(\psi _2)$ be accuracy functions of $\psi _1$ and $\psi _2$, respectively. Then

• (i) if $\hat{Z}(\psi _1) < \hat{Z}(\psi _2)$, then $\psi _1\prec \psi _2$

• (ii) if $\hat{Z}(\psi _1)> \hat{Z}(\psi _2)$, then $\psi _1\succ \psi _2$

• (iii) if $\hat{Z}(\psi _1)= \hat{Z}(\psi _2)$, then

  • (1) if $\hat{L}(\psi _1) < \hat{L}(\psi _2)$, then $\psi _1\prec \psi _2$.

  • (2) if $\hat{L}(\psi _1) > \hat{L}(\psi _2)$, then $\psi _1\prec \psi _2$.

  • (3) if $\hat{L}(\psi _1)= \hat{L}(\psi _2)$, then $\psi _1\sim \psi _2$.”

Definition 7

[58] Let $\psi =(\zeta _{\psi },\varphi _{\psi })$, $\psi _1=(\zeta _{\psi _1}, \varphi _{\psi _1})$ and $\psi _2=(\zeta _{\psi _2}, \varphi _{\psi _2})$ be three $q^{r}$OFNs. The fundamental operations among them are outlined in the subsequent way:

• (i) $\psi _1\vee \psi _2=(\max \{\zeta _{\psi _1}, \zeta _{\psi _2}\}, \min \{\varphi _{\psi _1},\varphi _{\psi _2}\})$

• (ii) $\psi _1\wedge \psi _2=(\min \{\zeta _{\psi _1},\zeta _{\psi _2}\}, \max \{\varphi _{\psi _1},\varphi _{\psi _2}\})$

• (iii) $\psi _1 \bigoplus \psi _2=\Big (\root q \of {1-\zeta _{\psi _1}^{q}-\zeta _{\psi _2}^{q}}, \varphi _{\psi _1} \varphi _{\psi _2}\Big )$

• (iv) $\psi _1 \bigotimes \psi _2=\Big (\zeta _{\psi _1}\zeta _{\psi _2}, \root q \of {1-\varphi _{\psi _1}^{q}-\varphi _{\psi _2}^{q}}\Big )$

• (v) $\Phi \;\psi =\Big (\root q \of {1-(1-\varphi _{\psi }^{q})^{\Phi }}, \varphi _{\psi }^{\Phi }\Big ), \Phi > 0$

• (vi) $\psi ^{\Phi }=\Big (\zeta _{\psi }^{\Phi },\root q \of {1-(1-\varphi _{\psi }^{q})^{\Phi }}\Big ), \;\Phi > 0$

• (vii) $\psi ^c=(\varphi _{\psi }, \zeta _{\psi })$.

3 Aczel–Alsina Operations on $q^{r}$OFNs

In view of Aczel–Alsina t-norm furthermore Aczel–Alsina t-conorm, we explained Aczel–Alsina operations in relation to $q^{r}$OFNs.

Definition 8

Let $\psi =(\zeta _{\psi },\varphi _{\psi })$, $\psi _1=(\zeta _{\psi _1}, \varphi _{\psi _1})$, and $\psi _2=(\zeta _{\psi _2}, \varphi _{\psi _2})$ be three $q^{r}$OFNs, $\eth \ge 1$ and $\vartheta >0$. Then, the Aczel–Alsina t-norm and t-conorm operations of $q^{r}$OFNs are assigned as:

• (i)
  $$\begin{aligned}&\psi _1\bigoplus \psi _2\\&\quad = \bigg \langle \root q \of {1-e^{-((-\ln (1- \zeta ^{q}_{\psi _1}))^\eth +(-\ln (1-\zeta ^{q}_{\psi _2}))^\eth )^{1/\eth }}}, \\&\qquad \root q \of {e^{-((-\ln \varphi ^{q}_{\psi _1})^\eth +(-\ln \varphi ^{q}_{\psi _2})^\eth )^{1/\eth }}}\bigg \rangle , \end{aligned}$$
• (ii)
  $$\begin{aligned}&\psi _1\bigotimes \psi _2\\&\quad = \bigg \langle \root q \of {e^{-((-\ln \zeta ^{q}_{\psi _1})^\eth +(-\ln \zeta ^{q}_{\psi _2})^\eth )^{1/\eth }}},\\&\qquad \root q \of {1-e^{-((-\ln (1- \varphi ^{q}_{\psi _1}))^\eth +(-\ln (1-\varphi ^{q}_{\psi _2}))^\eth )^{1/\eth }}}\bigg \rangle , \end{aligned}$$

• (iii) $\vartheta \psi =\Big \langle \root q \of {1-e^{-(\vartheta (-\ln (1- \zeta ^{q}_{\psi }))^\eth )^{1/\eth }}}, \root q \of {e^{-(\vartheta (-\ln \varphi ^{q}_{\psi })^\eth )^{1/\eth }}}\Big \rangle$,

• (iv) $\psi ^{\vartheta }=\Big \langle \root q \of {e^{-(\vartheta (-\ln \zeta ^{q}_{\psi })^\eth )^{1/\eth }}}, \root q \of {1-e^{-(\vartheta (-\ln (1- \varphi ^{q}_{\psi }))^\eth )^{1/\eth }}} \Big \rangle$.

Example 3

Let $\psi =(0.67,0.34)$, $\psi _1=(0.27,0.82)$ and $\psi _2=(0.45,0.65)$ be three $q^{r}$OFNs, then based on above-mentioned Aczel–Alsina operation on $q^{r}$OFNs for $\eth =4$, $\vartheta =6$ and $q=5$, we get

• (i)
  $$\begin{aligned}&\psi _1\bigoplus \psi _2\\&\quad =\Big \langle \root 5 \of {1-e^{-((-\ln (1- (0.27)^{5}))^4+(-\ln (1-(0.45)^{5}))^4)^{1/4}}},\\&\qquad \root 5 \of {e^{-((-\ln (0.82)^{5})^4+(-\ln (0.65)^{5})^4)^{1/4}}}\Big \rangle \\&\quad =(0.450000787, 0.646906518). \end{aligned}$$
• (ii)
  $$\begin{aligned}&\psi _1\bigotimes \psi _2 \\&\quad = \Big \langle \root 5 \of {e^{-((-\ln (0.27)^{5})^4+(-\ln (0.45)^{5})^4)^{1/4}}}, \\&\qquad \root 5 \of {1-e^{-((-\ln (1- (0.82)^{5}))^4+(-\ln (1-(0.65)^{5}))^4)^{1/4}}}\Big \rangle \\&\quad =(0.258609103, 0.820161579). \end{aligned}$$
• (iii)
  $$\begin{aligned}&6 \psi =\Big \langle \root 5 \of {1-e^{-(6(-\ln (1- (0.67)^{5}))^4)^{1/4}}},\\&\qquad \root 5 \of {e^{-(6(-\ln (0.34)^{5})^4)^{1/4}}}\Big \rangle \\&\quad =(0.726997934, 0.184809749). \end{aligned}$$
• (iv)
  $$\begin{aligned} \psi ^{6} &= \Big \langle \root 5 \of {e^{-(6(-\ln (0.67)^{5})^4)^{1/4}}},\\&\quad \root 5 \of {1-e^{-(6(-\ln (1- (0.34)^{5}))^4) ^{1/4}}} \Big \rangle \\ &= (0.534308835, 0.371770418). \end{aligned}$$

Theorem 1

Let $\psi =(\zeta _{\psi },\varphi _{\psi })$, $\psi _1=(\zeta _{\psi _1}, \varphi _{\psi _1})$ and $\psi _2=(\zeta _{\psi _2}, \varphi _{\psi _2})$ be three $q^{r}$OFNs, then we have

• (i) $\psi _1 \bigoplus \psi _2=\psi _2 \bigoplus \psi _1$;

• (ii) $\psi _1 \bigotimes \psi _2=\psi _2 \bigotimes \psi _1$;

• (iii) $\vartheta (\psi _1 \bigoplus \psi _2)=\vartheta \psi _1 \bigoplus \vartheta \psi _2$, $\vartheta >0$;

• (iv) $(\vartheta _1+\vartheta _2 )\psi =\vartheta _1 \psi \bigoplus \vartheta _2 \psi$, $\vartheta _1, \vartheta _2 >0$;

• (v) $(\psi _1 \bigotimes \psi _2)^\vartheta =\psi _1^\vartheta \bigotimes \psi _2^\vartheta$, $\vartheta >0$;

• (vi) $\psi ^{\vartheta _1} \bigotimes \psi ^{\vartheta _2}=\psi ^{(\vartheta _1+\vartheta _2 )}$, $\vartheta _1, \vartheta _2 >0$.

Proof

For the three $q^{r}$OFNs $\psi$, $\psi _1$ and $\psi _2$, and $\vartheta , \vartheta _1, \vartheta _2 > 0$, as stated in Definition 8, we can get

(i):

$$\begin{aligned}&\psi _1\bigoplus \psi _2 \\&\quad = \bigg \langle \root q \of {1-e^{-((-\ln (1- \zeta ^{q}_{\psi _1}))^\eth +(-\ln (1-\zeta ^{q}_{\psi _2}))^\eth )^{1/\eth }}}, \\&\qquad \root q \of {e^{-((-\ln \varphi ^{q}_{\psi _1})^\eth +(-\ln \varphi ^{q}_{\psi _2})^\eth )^{1/\eth }}}\bigg \rangle \\&\quad =\bigg \langle \root q \of {1-e^{-((-\ln (1- \zeta ^{q}_{\psi _2}))^\eth +(-\ln (1-\zeta ^{q}_{\psi _1}))^\eth )^{1/\eth }}},\\&\qquad \root q \of {e^{-((-\ln \varphi ^{q}_{\psi _2})^\eth +(-\ln \varphi ^{q}_{\psi _1})^\eth )^{1/\eth }}}\bigg \rangle =\psi _2 \bigoplus \psi _1. \end{aligned}$$

(ii):

It is straightforward.

(iii):

Let $t= \root q \of {1-e^{-((-\ln (1- \zeta ^{q}_{\psi _1}))^\eth +(-\ln (1-\zeta ^{q}_{\psi _2}))^\eth )^{1/\eth }}}$. Then $\ln (1-t^{q})=-((-\ln (1- \zeta ^{q}_{\psi _1}))^\eth +(-\ln (1-\zeta ^{q}_{\psi _2}))^\eth )^{1/\eth }$. Using this, we get

$$\begin{aligned}&\vartheta (\psi _1 \bigoplus \psi _2)\\&\quad =\vartheta \bigg \langle \root q \of {1-e^{-((-\ln (1- \zeta ^{q}_{\psi _1}))^\eth +(-\ln (1-\zeta ^{q}_{\psi _2}))^\eth )^{1/\eth }}}, \\&\qquad \root q \of {e^{-((-\ln \varphi ^{q}_{\psi _1})^\eth +(-\ln \varphi ^{q}_{\psi _2})^\eth )^{1/\eth }}}\bigg \rangle \\&\quad =\bigg \langle \root q \of {1-e^{-(\vartheta ((-\ln (1- \zeta ^{q}_{\psi _1}))^\eth +(-\ln (1-\zeta ^{q}_{\psi _2}))^\eth ))^{1/\eth }}}, \\&\qquad \root q \of {e^{-(\vartheta ((-\ln \varphi ^{q}_{\psi _1})^\eth +(-\ln \varphi ^{q}_{\psi _2})^\eth ))^{1/\eth }}}\bigg \rangle \\&\quad =\bigg \langle \root q \of {1-e^{-(\vartheta (-\ln (1- \zeta ^{q}_{\psi _1}))^\eth )^{1/\eth }}}, \root q \of {e^{-(\vartheta (-\ln \varphi ^{q}_{\psi _1})^\eth )^{1/\eth }}}\bigg \rangle \\&\qquad \bigoplus \bigg \langle \root q \of {1-e^{-(\vartheta (-\ln (1- \zeta ^{q}_{\psi _2}))^\eth )^{1/\eth }}}, \root q \of {e^{-(\vartheta (-\ln \varphi ^{q} _{\psi _2})^\eth )^{1/\eth }}}\bigg \rangle \\&\quad =\vartheta \psi _1 \bigoplus \vartheta \psi _2 \end{aligned}$$

.

(iv):

$$\begin{aligned}&\vartheta _1 \psi \bigoplus \vartheta _2 \psi =\Big \langle \root q \of {1-e^{-(\vartheta _1(-\ln (1- \zeta ^{q}_{\psi }))^\eth )^{1/\eth }}}, \root q \of {e^{-(\vartheta _1(-\ln \varphi ^{q}_{\psi })^\eth )^{1/\eth }}}\Big \rangle \\&\quad \bigoplus \Big \langle \root q \of {1-e^{-(\vartheta _2(-\ln (1- \zeta ^{q}_{\psi }))^\eth )^{1/\eth }}}, \root q \of {e^{-(\vartheta _2(-\ln \varphi ^{q}_{\psi })^\eth )^{1/\eth }}}\Big \rangle \\&\quad =\Big \langle \root q \of {1-e^{-((\vartheta _1+\vartheta _2)(-\ln (1- \zeta ^{q}_{\psi }))^\eth )^{1/\eth }}}, \root q \of {e^{-((\vartheta _ 1+\vartheta _2)(-\ln \varphi ^{q}_{\psi })^\eth )^{1/\eth }}}\Big \rangle \\&\quad =(\vartheta _1+\vartheta _2 )\psi . \end{aligned}$$

(v):

$$\begin{aligned}&(\psi _1 \bigotimes \psi _2)^\vartheta = \Big \langle \root q \of {e^{-((-\ln \zeta ^{q}_{\psi _1})^\eth +(-\ln \zeta ^{q}_{\psi _2})^\eth )^{1/\eth }}}, \\&\quad \root q \of {1-e^{-((-\ln (1- \varphi ^{q}_{\psi _1}))^\eth +(-\ln (1-\varphi ^{q}_{\psi _2}))^\eth )^{1/\eth }}}\Big \rangle ^\vartheta \\&\quad =\Big \langle \root q \of {e^{-(\vartheta ((-\ln \zeta ^{q}_{\psi _1})^\eth +(-\ln \zeta ^{q}_{\psi _2})^\eth ))^{1/\eth }}}, \\&\qquad \root q \of {1-e^{-(\vartheta ((-\ln (1- \varphi ^{q}_{\psi _1}))^\eth +(-\ln (1-\varphi ^{q}_{\psi _2}))^\eth )^{1/\eth }}}\Big \rangle \\&\quad =\Big \langle \root q \of {e^{-(\vartheta (-\ln \zeta ^{q}_{\psi _1})^\eth )^{1/\eth }}}, \\&\qquad \root q \of {1-e^{-(\vartheta (-\ln (1- \varphi ^{q}_{\psi _1}))^\eth )^{1/\eth }}}\Big \rangle \bigoplus \Big \langle \root q \of {e^{-(\vartheta (-\ln \zeta ^{q}_{\psi _2})^\eth )^{1/\eth }}}, \\&\qquad \root q \of {1-e^{-(\vartheta (-\ln (1- \varphi ^{q}_{\psi _2}))^\eth )^{1/\eth }}}\Big \rangle =\psi _1^\vartheta \bigotimes \psi _2^\vartheta . \end{aligned}$$

(vi):

$$\begin{aligned}&\psi ^{\vartheta _1} \bigotimes \psi ^{\vartheta _2} =\Big \langle \root q \of {e^{-(\vartheta _1(-\ln \zeta ^{q}_{\psi })^\eth )^ {1/\eth }}}, \root q \of {1-e^{-(\vartheta _1(-\ln (1- \varphi ^{q}_{\psi }))^\eth )^{1/\eth }}} \Big \rangle \\&\quad \bigotimes \Big \langle \root q \of {e^{-(\vartheta _2(-\ln \zeta ^{q}_{\psi })^\eth )^{1/\eth }}}, \root q \of {1-e^{-(\vartheta _2(-\ln (1- \varphi ^{q}_{\psi }))^\eth )^{1/\eth }}} \Big \rangle \\&\quad =\Big \langle \root q \of {e^{-((\vartheta _1+\vartheta _2)(-\ln \zeta ^{q}_{\psi })^\eth )^{1/\eth }}}, \root q \of {1-e^ {-((\vartheta _1+\vartheta _2)(-\ln (1- \varphi ^{q}_{\psi }))^\eth )^{1/\eth }}}\Big \rangle \\&\quad =\psi ^{(\vartheta _1+\vartheta _2 )}. \end{aligned}$$

$\square$

4 $q^{r}$OF Aczel–Alsina Average Aggregation Operators

In this section, we suggest Aczel–Alsina average aggregation operators with $q^{r}$OFNs, for example, $q^{r}$OFAAWA operator, $q^{r}$OFAAOWA operator, and $q^{r}$O- FAAHA operator.

Definition 9

Let $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ be several $q^{r}$OFNs. Then $q^{r}$OF Aczel–Alsina weighted average ($q^{r}$OFAAWA) operator is a function $q^{r}O-$ $FAAWA: q^{r}OFN^{\tau }\rightarrow q^{r}OFN$ such that

$$\begin{aligned}&q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _{\tau })={\mathop {\bigoplus }\limits _{\xi =1}^{\tau }}(\gamma _\xi \psi _\xi )\\&\quad =\gamma _1\psi _1 \bigoplus \gamma _2\psi _2 \bigoplus \cdots \bigoplus \gamma _{\tau }\psi _{\tau } \end{aligned}$$

where $\gamma =(\gamma _1,\gamma _2,\ldots ,\gamma _{\tau })^{T}$ be the weight vector of $\psi _\xi$ $(\xi =1,2,\ldots ,\tau )$ with $\gamma _{\psi }> 0$ and $\mathop {\sum } _{\xi =1}^{\tau }\gamma _\xi =1$.

We develop the succeeding theorem that follows the Aczel–Alsina operations on $q^{r}$OFNs.

Theorem 2

Let $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ be several $q^{r}$OFNs, then their values aggregated by $q^{r}$OFAAWA operator is also a $q^{r}$OFN, and

$$\begin{aligned}&q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _{\tau }) \\ & \quad ={\mathop {\bigoplus }\limits _{\xi =1}^{\tau }}(\gamma _\xi \psi _\xi ) \\&\quad =\Biggl \langle \root q \of {1-e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln (1- \zeta ^{q}_{\psi _\xi }))^\eth \big )^{1/\eth }}}, \root q \of {e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln \varphi ^{q}_{\psi _\xi })^\eth \big )^{1/\eth }}}\Bigg \rangle \end{aligned}$$

(3)

where $\gamma =(\gamma _1,\gamma _2,\ldots ,\gamma _{\tau })$ be the weight vector of $\psi _\xi$ $(\xi =1,2,\ldots ,\tau )$ so that $\gamma _\xi > 0$, and ${\mathop {\sum } _{\xi =1}^{\tau }}\gamma _\xi =1$.

Proof

Using the mathematical induction method, we can show that Theorem 2 is true in the following way:

(I) When $\tau =2$, we get by applying the Aczel–Alsina operations to the $q^{r}$OFNs

$\gamma _1 \psi _1=\Big \langle \root q \of {1-e^{-(\gamma _1(-\ln (1- \zeta ^{q}_{\psi _1}))^\eth )^{1/\eth }}}, \root q \of {e^{-(\gamma _1(-\ln \varphi ^{q}_{\psi _1})^\eth )^{1/\eth }}}\Big \rangle$,

$\gamma _2 \psi _2=\Big \langle \root q \of {1-e^{-(\gamma _2(-\ln (1- \zeta ^{q}_{\psi _2}))^\eth )^{1/\eth }}}, \root q \of {e^{-(\gamma _2(-\ln \varphi ^{q}_{\psi _2})^\eth )^{1/\eth }}}\Big \rangle$.

Based on Definition 8, we obtain

$$\begin{aligned}&q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2)=\gamma _1 \psi _1\bigoplus \gamma _2 \psi _2\\&\quad =\Big \langle \root q \of {1-e^{-(\gamma _1(-\ln (1- \zeta ^{q}_{\psi _1}))^\eth )^{1/\eth }}}, \\&\qquad \root q \of {e^{-(\gamma _1(-\ln \varphi ^{q}_{\psi _1})^\eth )^{1/\eth }}}\Big \rangle \bigoplus \Big \langle \root q \of {1-e^{-(\gamma _2(-\ln (1- \zeta ^{q}_{\psi _2}))^\eth )^{1/\eth }}},\\&\qquad \root q \of {e^{-(\gamma _2(-\ln \varphi ^{q}_{\psi _2})^\eth )^{1/\eth }}}\Big \rangle \\&\quad =\Bigg \langle \root q \of {1-e^{-\big (\gamma _1(-\ln (1- \zeta ^{q}_{\psi _1}))^\eth +\gamma _2(-\ln (1- \zeta ^{q}_{\psi _2})) ^\eth \big )^{1/\eth }}},\\&\qquad \root q \of {e^{-\big (\gamma _1(-\ln \varphi ^{q}_{\psi _1})^\eth +\gamma _2(-\ln \varphi ^{q}_{\psi _2})^\eth \big )^{1/\eth }}}\Bigg \rangle \\&\quad =\Bigg \langle \root q \of {1-e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{2}}\gamma _\xi (-\ln (1- \zeta ^{q}_{\psi _\xi }))^\eth \big )^{1/\eth }}}, \\&\qquad \root q \of {e^{-\big ({\mathop {\sum }_{\xi =1}^{2}}\gamma _\xi (-\ln \varphi ^{q}_{\psi _\xi })^\eth \big )^{1/\eth }}}\Bigg \rangle . \end{aligned}$$

Hence, (3) is right for $\tau =2$.

(II) If (3) holds true for $\tau =k$, then we have

$$\begin{aligned}&q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _k) ={\mathop {\bigoplus }\limits _{\xi =1}^{k}}(\gamma _\xi \psi _\xi ) \\&\quad =\Bigg \langle \root q \of {1-e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{k}}\gamma _\xi (-\ln (1- \zeta ^{q}_{\psi _\xi }))^\eth \big )^{1/\eth }}}, \root q \of {e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{k}}\gamma _\xi (-\ln \varphi ^{q}_{\psi _\xi })^\eth \big )^{1/\eth }}}\Bigg \rangle . \end{aligned}$$

Now for $\tau =k+1$, then

$q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _k,\psi _{k+1})$ $={\mathop {\bigoplus }\limits _{\xi =1}^{k}}(\gamma _\xi \psi _\xi )\bigoplus$ $(\gamma _{k+1}\psi _{k+1})$

$=\Bigg \langle \root q \of {1-e^{-\big ({\mathop {\sum}_{\xi =1}^{k}}\gamma _\xi (-\ln (1- \zeta ^{q}_{\psi _\xi }))^\eth \big )^{1/\eth }}}, \root q \of {e^{-\big ({\mathop {\sum }_{\xi =1}^{k}}\gamma _\xi (-\ln \varphi ^{q}_{\psi _\xi })^\eth \big )^{1/\eth }}}\Bigg \rangle$

$\bigoplus \Bigg \langle \root q \of {1-e^{-\big (\gamma _{k+1}(-\ln (1-\zeta ^{q}_{\psi _{k+1}}))^\eth \big )^{1/\eth }}}, \root q \of {e^{-\big (\gamma _{k+1}(-\ln \varphi ^{q}_{\psi _{k+1}})^\eth \big )^{1/\eth }}}\Bigg \rangle$

$=\Bigg \langle \root q \of {1-e^{-\big ({\mathop {\sum }_{\xi =1}^{k+1}}\gamma _\xi (-\ln (1- \zeta ^{q}_{\psi _\xi }))^\eth \big )^{1/\eth }}}, \root q \of {e^{-\big ({\mathop {\sum }_{\xi =1}^{k+1}}\gamma _\xi (-\ln \varphi ^{q}_{\psi _\xi })^\eth \big )^{1/\eth }}}\Bigg \rangle$.

Thus, (3) is true for $\tau =k+1$.

On the basis of (I) and (II), we have come to the realisation that (3) is correct for any $\tau$. $\square$

We prove easily the subsequent properties using the $q^{r}$OFAAWA operator.

Theorem 3

(Idempotency Property) If $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ be several equal $q^{r}$OFNs, i.e., $\psi _\xi =\psi$ for all $\xi$, then

$$\begin{aligned} q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _{\tau })=\psi . \end{aligned}$$

Proof

Since $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })=\psi$ $(\xi =1,2,\ldots ,\tau )$, then we have by equation (3), $q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _{\tau })={\mathop {\bigoplus }\limits _{\xi =1}^{\tau }}(\gamma _\xi \psi _\xi )$

$=\Bigg \langle \root q \of {1-e^{-\big ({\mathop {\sum }_{\xi =1}^{\tau }}\gamma _\xi (-\ln (1- \zeta ^{q}_{\psi _\xi }))^\eth \big )^{1/\eth }}}, \root q \of {e^{-\big ({\mathop {\sum } _{\xi =1}^{\tau }}\gamma _\xi (-\ln \varphi ^{q}_{\psi _\xi })^\eth \big )^{1/\eth }}}\Bigg \rangle$

$=\Bigg \langle \root q \of {1-e^{-\big ((-\ln (1- \zeta ^{q}_{\psi }))^\eth \big )^{1/\eth }}}, \root q \of {e^{-\big ((-\ln \varphi ^{q}_{\psi })^\eth \big )^{1/\eth }}}\Bigg \rangle$

$=\Big \langle \root q \of {1-e^{\ln (1- \zeta ^{q}_{\psi })}}, \root q \of {e^{\ln \varphi ^{q}_{\psi }}}\Big \rangle$ $=\Big (\root q \of {\zeta ^{q}_{\psi }}, \root q \of {\varphi ^{q}_{\psi }}\Big )=(\zeta _{\psi },\varphi _{\psi })=\psi .$

Thus, $q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _{\tau })=\psi$ holds. $\square$

Theorem 4

(Boundedness Property) Let $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ be several $q^{r}$OFNs. Let $\psi ^{-}=\min (\psi _1,\psi _2,\ldots , \psi _{\tau })$ and $\psi ^{+}=\max (\psi _1,\psi _2,$ $\ldots ,\psi _{\tau })$. Then, $\psi ^{-}\le q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _{\tau })\le \psi ^{+}.$

Proof

Let $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ be a number of $q^{r}$OFNs. Let $\psi ^{-}=\min (\psi _1,\psi _2,\ldots , \psi _{\tau })=(\zeta _{\psi }^{-}, \varphi _{\psi }^{-})$ and $\psi ^{+}=\max (\psi _1,\psi _2,\ldots , \psi _{\tau })=(\zeta _{\psi }^{+}, \varphi _{\psi }^{+})$. We have, $\zeta _{\psi }^{-}=\min \limits _{\xi }\{\zeta _{\psi _\xi }\}$, $\varphi _{\psi }^{-}=\max \limits _{\xi }\{\varphi _{\psi _\xi }\}$, $\zeta _{\psi }^{+}=\max \limits _{\xi }\{\zeta _{\psi _\xi }\}$, and $\varphi _{\psi }^{+}=\min \limits _{\xi }\{\varphi _{\psi _\xi }\}$. As a consequence of this, there are now additional inequities,

$$\begin{aligned}&\root q \of {1-e^{-\Big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln (1- (\zeta _{\psi }^{-})^{q}))^\eth \Big )^{1/\eth }}}\\&\quad \le \root q \of {1-e^{-\Big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln (1- \zeta ^{q}_{\psi _\xi }))^\eth \Big )^{1/\eth }}}\\&\quad \le \root q \of {1-e^{-\Big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln (1- (\zeta _{\psi }^{+})^{q}))^\eth \Big )^{1/\eth }}},\\&\quad \root q \of {e^{-\Big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln (\varphi _{\psi }^{+})^{q})^\eth \Big )^{1/\eth }}} \le \root q \of {e^{-\Big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln \varphi ^{q}_{\psi _\xi })^\eth \Big )^{1/\eth }}} \\&\quad \le \root q \of {e^{-\Big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln (\varphi _{\psi }^{-})^{q})^\eth \Big )^{1/\eth }}}. \end{aligned}$$

Therefore, $\psi ^{-}\le q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _{\tau })\le \psi ^{+}.$ $\square$

Theorem 5

(Monotonicity Property) Suppose that $\psi _\xi$ and $\psi ^{\prime}_\xi$ $(\xi =1,2,\ldots ,\tau )$ are two sets of $q^{r}$OFNs, if $\psi _\xi \le \psi ^{\prime}_\xi$ for every $\xi$, then

$$\begin{aligned} q^{r}OFAAWA_{\gamma }(\psi _1,\psi _2,\ldots ,\psi _{\tau })\le q^{r}OFAAWA_{\gamma }(\psi ^{\prime}_1,\psi ^{\prime}_2,\ldots ,\psi ^{\prime}_{\tau }). \end{aligned}$$

(4)

Now, we introduce $q^{r}$OF Aczel–Alsina ordered weighted averaging ($q^{r}$OF- AAOWA) operator.

Definition 10

Assume that $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ are an arrangement of $q^{r}$OFNs. A $\tau$-dimensional $q^{r}$OFAAOWA operator is a mapping $q^{r}OFAAOWA: q^{r}OFN^{\tau }$ $\rightarrow q^{r}OFN$ along with associated vector $\wp =(\wp _1,\wp _2,$ $\ldots ,\wp _{\tau })^{T}$ in order to allow $\wp _\xi >0$, and ${\mathop {\sum } _{\xi =1}^{\tau }}\wp _\xi =1$. Therefore,

$$\begin{aligned}&q^{r}OFAAOWA_{\wp }(\psi _1,\psi _2,\ldots ,\psi _{\tau })={\mathop {\bigoplus }\limits _{\xi =1}^{\tau }}(\wp _\xi \psi _{\phi (\xi )})\\&\quad =\wp _1\psi _{\phi (1)} \bigoplus \wp _2\psi _{\phi (2)} \bigoplus \cdots \bigoplus \wp _{\tau }\psi _{\phi (\tau )} \end{aligned}$$

where $(\phi (1),\phi (2),\ldots ,\phi (\tau ))$ are the permutation of $(\xi =1,2,\ldots ,\tau )$, with the property that $\psi _{\phi (\xi -1)}\ge \psi _{\phi (\xi )}$ for all $\xi =1,2,\ldots ,\tau.$

The Aczel–Alsina product operation on $q^{r}$OFNs is used as the basis for building the following theorem.

Theorem 6

Suppose that $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ is arrangement of $q^{r}$OFNs. A $\tau$-dimensional $q^{r}$OF Aczel–Alsina ordered weighted average ($q^{r}$OFAAOWA) operator is a mapping $q^{r}OFAAOWA: q^{r}OFN^{\tau }\rightarrow q^{r}OFN$ with associated vector $\wp =(\wp _1,\wp _2,\ldots ,\wp _{\tau })^{T}$ such that $\wp _\xi >0$, and ${\mathop {\sum}_{\xi =1}^{\tau }}\wp _\xi =1$. Then,

$$\begin{aligned}&q^{r}OFAAOWA_{\wp }(\psi _1,\psi _2,\ldots ,\psi _{\tau }) \\ & = {\mathop {\bigoplus }\limits _{\xi =1}^{\tau }}(\wp _\xi \psi _{\phi (\xi )})\\&= \Bigg \langle \root q \of {1-e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\wp _\xi \big (-\ln \big (1- \zeta ^{q}_{\psi _{\phi (\xi )}}\big )\big )^\eth \big )^{1/\eth }}}, \root q \of {e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\wp _\xi \big (-\ln \varphi ^{q}_{\psi _{\phi (\xi )}}\big )^\eth \big )^{1/\eth }}}\Bigg \rangle \end{aligned}$$

(5)

where $(\phi (1),\phi (2),\ldots ,\phi (\tau ))$ are the permutation of $(\xi =1,2,\ldots ,\tau )$, with the property that $\psi _{\phi (\xi -1)}\ge \psi _{\phi (\xi )}$ for all $\xi =1,2,\ldots ,\tau$.

The subsequent properties may be shown by $q^{r}$OFAAOWA operator without any problem.

Theorem 7

(Idempotency Property) If $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ are all equal, i.e. $\psi _\xi =\psi$ for all $\xi$, then ${q^{r}OFAAOWA}_{\wp }(\psi _1,\psi _2,\ldots ,\psi _{\tau })=\psi .$

Theorem 8

(Boundedness Property) Let $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ be a number of $q^{r}$OFNs. Let $\psi ^{-}=\min \limits _{\xi }\psi _\xi$, and $\psi ^{+}=\max \limits _{\xi }\psi _\xi$. Then

$$\begin{aligned} \psi ^{-}\le {q^{r}OFAAOWA}_{\wp }(\psi _1,\psi _2,\ldots ,\psi _{\tau })\le \psi ^{+}. \end{aligned}$$

Theorem 9

(Monotonicity Property) Let $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ and $\psi ^{\prime}_\xi =(\zeta ^{\prime}_{\psi _\xi },$ $\varphi ^{\prime}_{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ be two sets of $q^{r}$OFNs, if $\psi _\xi \le \psi ^{\prime}_\xi$ for all $\xi$, then

$$\begin{aligned} {q^{r}OFAAOWA}_{\wp }(\psi _1,\psi _2,\ldots ,\psi _{\tau })\le {q^{r}OFAAOWA}_{\wp }(\psi ^{\prime}_1,\psi ^{\prime}_2,\ldots ,\psi ^{\prime}_{\tau }). \end{aligned}$$

Theorem 10

(Commutativity Property) Let $\psi _\xi =(\zeta _{\psi _\xi }, \varphi _{\psi _\xi })$ and $\psi ^{\prime}_\xi =(\zeta ^{\prime}_{\psi _\xi },$ $\varphi ^{\prime}_{\psi _\xi })$ $(\xi =1,2,\ldots ,\tau )$ be two sets of $q^{r}$OFNs, then ${q^{r}OFAAOWA}_{\wp }(\psi _1,$ $\psi _2,$ $\ldots ,\psi _{\tau })= {q^{r}OFAAOWA}_{\wp }(\psi ^{\prime}_1,\psi ^{\prime}_2,\ldots ,\psi ^{\prime}_{\tau })$ where $\psi ^{\prime}_\xi$ is any permutation of $\psi _\xi$ $(\xi =1,2,\ldots ,\tau )$.

In Definition 9, we observe that $q^{r}$OFAAWA operator weights $q^{r}$OF values. At the same time from Definition 10, we get $q^{r}$OFAAOWA operator weights ordered positions of the $q^{r}$OF values. In such a way, weights indicate in these two operators $q^{r}$OFAAWA and $q^{r}$OFAAOWA have been in two different situations. However, they can be represented by a single operator. To avoid this difficulties, we exhibit $q^{r}$OF Aczel–Alsina hybrid averaging ($q^{r}$OFAAHA) operator.

Definition 11

Let $\psi _\xi$ $(\xi =1,2,\ldots ,\tau )$ be an arrangement of $q^{r}$OFNs. A $\tau$-dimensional $q^{r}$OF Aczel–Alsina hybrid average ($q^{r}$OFAAHA) operator is a mapping $q^{r}OFA-$ $AHA: q^{r}OFN^{\tau }\rightarrow q^{r}OFN$, in such a way as to allow

$$\begin{aligned}&q^{r}OFAAHA_{\gamma ,\wp }(\psi _1, \psi _2, \ldots , \psi _{\tau })= \bigoplus ^{\tau }_{\xi =1}(\wp _\xi \dot{\psi }_{\phi (\xi )})\\&\quad = \wp _1 \dot{\psi }_{\phi (1)} \bigoplus \wp _2 \dot{\psi }_{\phi (2)} \bigoplus \cdots \bigoplus \wp _{\tau } \dot{\psi }_{\phi (\tau )} \end{aligned}$$

where $\wp =(\wp _1, \wp _2, \ldots , \wp _{\tau })^T$ would be the weighted vector directly related to $q^{r}$OFAAHA operator, and where $\wp _\xi \in [0, 1]$ $(\xi =1,2,\ldots ,\tau )$ and $\sum_{\xi =1}^{\tau }\wp _\xi =1$; $\dot{\psi }_\xi =\tau \gamma _\xi \psi _\xi$, $\xi =1,2,\ldots ,\tau$, $(\dot{\psi }_{\phi (1)}, \dot{\psi }_{\phi (2)}, \ldots , \dot{\psi }_{\phi (\tau )})$ is any permutation of a number of the weighted $q^{r}$OFNs $(\dot{\psi }_1, \dot{\psi }_2, \ldots , \dot{\psi }_{\tau })$, so as to allow $\dot{\psi }_{\phi (\xi -1)} \ge \dot{\psi }_{\phi (\xi )}$ $(\xi =1,2,\ldots ,\tau )$; $\gamma = (\gamma _1, \gamma _2, \ldots , \gamma _{\tau })^T$ is the weight vector of $\psi _\xi$, with $\gamma _\xi \in [0, 1]$ and $\sum_{\xi =1}^{\tau } \gamma _\xi = 1$, and $\tau$ is the balancing coefficient, which has played a significant role in maintaining balance.

Using Aczel–Alsina operations on $q^{r}$OFNs data, it is possible to prove the underlying theorem.

Theorem 11

Let $\psi _\xi$ $(\xi =1,2,\ldots ,\tau )$ be the number of $q^{r}$OFNs. Their values combined by the $q^{r}$OFAAHA operator remain a $q^{r}$OFN, and

$$\begin{aligned}&q^{r}OFAAHA_{\gamma ,\wp }(\psi _1,\psi _2,\ldots ,\psi _{\tau }) \\ & \quad ={\mathop {\bigoplus }\limits _{\xi =1}^{\tau }}(\gamma _\xi \dot{\psi }_{\phi (\xi )})\\ & \quad = \Bigg \langle \root q \of {1-e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi \big (-\ln \big (1- \dot{\zeta }^{q}_{\psi _{\phi (\xi )}}\big )\big )^\eth \big )^{1/\eth }}}, \\ & \quad \root q \of {e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi \big (-\ln \dot{\varphi }^{q}_{\psi _{\phi (\xi )}}\big )^\eth \big )^{1/\eth }}}\Bigg \rangle. \end{aligned}$$

(6)

Proof

Similar to Theorem 2, Theorem 11 can be easily derived. $\square$

Theorem 12

The $q^{r}$OFAAWA and $q^{r}$OFAAOWA operators are special cases of the $q^{r}$OFAAHA operator.

Proof

(1) Let $\wp =(1/\tau ,1/\tau ,\ldots ,1/\tau )^T$. Then

$$\begin{aligned}&q^{r}OFAAHA_{\gamma ,\wp }(\psi _1, \psi _2, \ldots , \psi _{\tau })\\&\quad = \wp _1 \dot{\psi }_{\phi (1)} \bigoplus \wp _2 \dot{\psi }_{\phi (2)} \bigoplus \cdots \bigoplus \wp _{\tau } \dot{\psi }_{\phi (\tau )}\\&\quad =\frac{1}{\tau }\big (\dot{\psi }_{\phi (1)} \bigoplus \dot{\psi }_{\phi (2)} \bigoplus \cdots \bigoplus \dot{\psi }_{\phi (\tau )}\big )\\&\quad = \gamma _1 \psi _1 \bigoplus \gamma _2 \psi _2 \bigoplus \cdots \bigoplus \gamma _{\tau } \psi _{\tau } \\&\quad = q^{r}OFAAWA_{\gamma }(\psi _1, \psi _2, \ldots , \psi _{\tau }), \end{aligned}$$

(2) Let $\gamma =(1/\tau ,1/\tau ,\ldots ,1/\tau )^T$. Then $\dot{\psi }_\xi =\psi _\xi$ $(\xi =1,2,\ldots ,\tau )$ and

$$\begin{aligned}&q^{r}OFAAHA_{\gamma ,\wp }(\psi _1, \psi _2, \ldots , \psi _{\tau })\\&\quad = \wp _1 \dot{\psi }_{\phi (1)} \bigoplus \wp _2 \dot{\psi }_{\phi (2)} \bigoplus \cdots \bigoplus \wp _{\tau } \dot{\psi }_{\phi (\tau )}\\&\quad = \wp _1 \psi _{\phi (1)} \bigoplus \wp _2 \psi _{\phi (2)} \bigoplus \cdots \bigoplus \wp _{\tau } \psi _{\phi (\tau )}\\&\quad = q^{r}OFAAOWA_{\wp }(\psi _1, \psi _2, \ldots , \psi _{\tau }), \end{aligned}$$

which concludes the proof. $\square$

5 MADM Method Based on the $q^{r}$OFAAWA Operator

In the following part, we will apply the recommended operators to a MADM issue while operating in a $q^{r}$OF environment.

5.1 Mathematical Formulation of MADM Utilizing $q^{r}$OFNs

MADM issues are substantial in real-life choice circumstances [9, 15]. A MADM issue is to obtain the most attractive alternative from a lot of achievable alternatives based on the decision data about attribute values and attribute weights supplied by DMs. The estimation of the attribute values plays a significant role in MADM. In the technique of decision-making, the information about attribute values is normally fuzzy or uncertain because of the expanding intricacy of the financial and social condition and the ambiguity of intrinsic abstract nature of human reasoning. This reality has driven numerous authors to use FS hypothesis to demonstrate the vulnerability and ambiguity in decision procedures.

Here, we may recommend a MADM procedure controlling $q^{r}$OF Aczel–Alsina aggregation operators where attribute values are in terms of $q^{r}$OFNs and attribute weights are organized as real numbers. Assume that ${\mathcal {W}}=\{{\mathcal {W}}_1, {\mathcal {W}}_2,\ldots , {\mathcal {W}}_m\}$ are the discretely arrangements of alternatives, $\delta =\{\delta _1, \delta _2,$ $\ldots , \delta _{\tau }\}$ are the discretely arrangements of attributes and $\gamma =(\gamma _1,\gamma _2,\ldots ,\gamma _{\tau })$ are weight vector of the attribute $\delta _\xi$ $(\xi =1,2,\ldots ,\tau )$ such that $\gamma _\xi >0$ and ${\mathop {\sum } _{\xi =1}^{\tau }}\gamma _\xi =1$. Suppose that $R=(\psi _{s \xi })_{m\times \tau }=(\zeta _{\psi _{s \xi }}, \varphi _{\psi _{s \xi }})_{m\times \tau }$ is the $q^{r}$OF decision matrix, as appeared in Fig. 2, where $\zeta _{\psi _{s \xi }}$ denote MD by which alternative ${\mathcal {W}}_s$ satisfies the attribute $\delta _\xi$, and $\varphi _{\psi _{s \xi }}$ denote NMD by which alternative ${\mathcal {W}}_s$ does not satisfies the attribute $\delta _\xi$, where $\zeta _{\psi _{s \xi }} \subset [0,1]$, and $\varphi _{\psi _{s \xi }} \subset [0,1]$ permitting $0\le \zeta ^{q}_{\psi _{s \xi }}+\varphi ^{q}_{\psi _{s \xi }}\le 1$, $(s=1,2,\ldots ,m)$ and $(\xi =1,2,\ldots ,\tau )$.

Fig. 2

$q^{r}$OF decision matrix

5.2 Algorithmic Formulations of the Developed Model

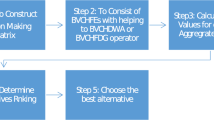
In the following algorithm, we develop a methodology for selecting the best alternative(s) for the MADM problem, taking into account the $q^{r}$OFAAWA operators. This method includes the steps listed below, and Fig. 3 shows a complete flowchart of the method:

• Step I The $q^{r}$OF decision matrix $R=(\psi _{s \xi })_{m\times \tau }$ is constructed for a MADM problem involving $q^{r}$OFNs, where the entries $\psi _{s \xi }$ $(s = 1, 2, \ldots , m$; $\xi =1,2,$ $\ldots ,\tau )$ represent the evaluations of the option ${\mathcal {W}}_m$ with respect to the criterion $\delta _{\tau }$.

• Step II The $q^{r}$OF decision matrix $R=(\psi _{s \xi })_{m\times \tau }$ is transformed into the normalised one ${\widetilde{R}}=\big ({\mathcal {G}}_{s \xi } \big )_{m \times \tau }$ when there are two types of criterion, such as benefit (B) and cost (C), by solving the following equation:

  $$\begin{aligned} {\mathcal {G}}_{s \xi }=\left\{ \begin{array}{ll} \psi _{s \xi }, & {} \xi \in B\\ \psi ^c_{s \xi }, & {} \xi \in C, \end{array}\right. \end{aligned}$$

  (7)

  where $\psi ^c_{s \xi }$ is the complement of $\psi _{s \xi }$.

• Step III Based on the decision matrix ${\widetilde{R}}$, which was found in step 2, the $q^{r}$OFAAWA operator is used to find the total aggregated value of the alternative ${\mathcal {W}}_s$ $(s=1, 2,\ldots , m)$ under the different criteria $\delta _\xi$. This gives the general decision values ${\mathcal {G}}_s$ $(s=1,2,\ldots ,m)$ for every alternative ${\mathcal {W}}_s$, that is, ${\mathcal {G}}_s=q^{r}OFAAWA({\mathcal {G}}_{s1},{\mathcal {G}}_{s2},\ldots ,{\mathcal {G}}_{s\tau })={\mathop {\bigoplus }\limits _{\xi =1}^{\tau }}(\gamma _\xi {\mathcal {G}}_{s \xi })$

  $$\begin{aligned} =\Bigg \langle \root q \of {1-e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln (1- \zeta ^{q}_{\psi _{s \xi }}))^\eth \big )^{1/\eth }}}, \root q \of {e^{-\big ({\mathop {\sum }\limits _{\xi =1}^{\tau }}\gamma _\xi (-\ln \varphi ^{q}_{\psi _{s \xi }})^\eth \big )^{1/\eth }}}\Bigg \rangle . \end{aligned}$$

  Step IV Based on the overall $q^{r}$OF data ${\mathcal {G}}_s$ $(s=1,2,\ldots ,m)$, we calculate the score values $\hat{Z}({\mathcal {G}}_s)$ $(s=1,2,\ldots , m)$ so that we can rate all possible ${\mathcal {W}}_s$ $(s=1,2,\ldots ,m)$ and select the best one. If the score functions $\hat{Z}({\mathcal {G}}_s)$ and $\hat{Z}({\mathcal {G}}_\xi )$ are the same, we keep going to start figuring out the accuracy degrees of $\hat{L}({\mathcal {G}}_s)$ and $\hat{L}({\mathcal {G}}_\xi )$ from the overall $q^{r}$OF data of ${\mathcal {G}}_s$ and ${\mathcal {G}}_\xi$, and we rank the choices ${\mathcal {W}}_s$ based on these accuracy degrees.

• Step V We order all of the potential alternatives ${\mathcal {W}}_s$ $(s=1,2,\ldots ,m)$ according to the descending value of their score values, and then we choose the one that comes out on top as the most viable option.

• Step VI End.

  Fig. 3

  

  Flow chart of the proposed MADM algorithm

6 Numerical Experiment

In this section, we will introduce a MADM issue to exhibit the implementation and adaptability of the suggested technique.

As globalization of the world economy makes companies face more complicated external and internal environment, finding a suitable partner is a significant way to steadfastly keep up its competitiveness, which can be influenced by numerous factors. With the intension of choosing an appropriate global partner, a company has chosen five candidate enterprises in the global scope. The arrangement of alternative enterprises is ${\mathcal {W}} =\{{\mathcal {W}}_1,{\mathcal {W}}_2,{\mathcal {W}}_3,{\mathcal {W}}_4,{\mathcal {W}}_5\}$, and four attributes are considered, namely, $\delta _1$: “research and technological development capability”; $\delta _2$: “business operation level” $\delta _3$: “international cooperation level”; and $\delta _4$: “credit level”. Note that all the attributes presented here are benefit type attributes. The attribute set $\delta =\{\delta _1,\delta _2,\delta _3,\delta _4\}$ is provided, and their relating weight vector is $\gamma =(0.30,0.20,0.15,0.35)^{T}$. On the basis of decision data, a decision matrix with the notation $\widetilde{R}=({\mathcal {G}}_{s \xi })_{5\times 4}$ is generated. The notation for this matrix may be found in Table 1.

Table 1 $q^{r}$OF decision matrix

We use the $q^{r}$OFAAWA operator to build a MADM approach with $q^{r}$OF data in order to find the appropriate global partner ${\mathcal {W}}_\xi$ (where $\xi =1,2,\ldots ,\tau$). This approach can be assessed in the following manner:

• Step 1 On the assumption that $\eth =1$ and $q=4$. Engaging the $q^{r}$OFAAWA operator to compute the perfect decision values ${\mathcal {G}}_s$ of each alternatives ${\mathcal {W}}_s$ $(s=1,2,\ldots ,5)$ ${\mathcal {G}}_1= (0.617508, 0.496757)$, ${\mathcal {G}}_2=(0.555684, 0.452754)$, ${\mathcal {G}}_3=(0.741877, 0.343146)$, ${\mathcal {G}}_4=(0.508392, 0.518331)$, ${\mathcal {G}}_5=(0.560468, 0.478098)$.

• Step 2 Calculate the score values $\hat{Z}( {\mathcal {G}}_s)$ $(s=1,2,\ldots ,$ 5) of the entire $q^{r}$OFNs ${\mathcal {G}}_s$ $(s=1,2,\ldots ,5)$ in the following way: $\hat{Z}({\mathcal {G}}_1)=0.084507$, $\hat{Z}({\mathcal {G}}_2)=0.053328$, $\hat{Z}({\mathcal {G}}_3)=0.289056$, $\hat{Z}({\mathcal {G}}_4)=-0.005379$, $\hat{Z}({\mathcal {G}}_5)=0.046426$.

• Step 3 Since $\hat{Z}({\mathcal {G}}_3)>\hat{Z}({\mathcal {G}}_1)>\hat{Z}({\mathcal {G}}_2)>\hat{Z}({\mathcal {G}}_5)>\hat{Z}({\mathcal {G}}_4)$ thus we have ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_2\succ {\mathcal {W}}_5\succ {\mathcal {W}}_4$. Hence, the suitable global partner is ${\mathcal {W}}_3$.

7 Analysis of the Influence of Parameters q and $\eth$ in Decision-Making Consequences

To explain the impact of the working parameters q and $\eth$ on MADM results, we will utilize various estimations of q and $\eth$ to rank the alternatives. Here we discuss three cases:

• Case I: (When only parameter $\eth$ changes) Suppose $q=4$. Table 2 illustrates the results of the score function as well as the preference ordering of the options ${\mathcal {W}}_\xi$ $(\xi =1,2,\ldots ,5)$ in the interim $1\le \eth \le 10$ based on the $q^{r}$OFAAWA operator.

  Table 2 Ordering of alternatives with varying parameter values $\eth$ executed by $q^{r}$OFAAWA operator

  It is observed that when the value of $\eth$ is varied for $q^{r}$OFAAWA operator, the order of preferences are different, and the relating best alternatives continue as before. When, $\eth =1,2$, order of preference is ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_2 \succ {\mathcal {W}}_5\succ {\mathcal {W}}_4$, and best choice are ${\mathcal {W}}_3$. When, $\eth =3,4$, order of preference is ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_2 \succ {\mathcal {W}}_4\succ {\mathcal {W}}_5$, and best choice are ${\mathcal {W}}_3$. When $5\le \eth \le 10$, corresponding ranking is ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_4\succ {\mathcal {W}}_2\succ {\mathcal {W}}_5$, but best one is ${\mathcal {W}}_3$.

• Case II: (When only parameter q changes) Suppose $\eth =4$. Then using $q^{r}$OFAAWA operator, the score values and preference order of the alternatives ${\mathcal {W}}_\xi$ $(\xi =1,2,\ldots ,5)$ in the interim of $1\le q \le 10$ are exhibited in Table 3.

  Table 3 Ordering of alternatives with varying parameter values q executed by $q^{r}$OFAAWA operator

  It has noted that when the value of q is varied for $q^{r}$OFAAWA operator, the preference orders are different, and the relating best alternatives continue as before. When, $q =1$, order of preference is ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_2 \succ {\mathcal {W}}_5\succ {\mathcal {W}}_4$, and best choice are ${\mathcal {W}}_3$. When, $2\le q \le 5$, order of preference is ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_2 \succ {\mathcal {W}}_4\succ {\mathcal {W}}_5$, and best choice are ${\mathcal {W}}_3$. When $6\le q \le 10$, corresponding ranking is ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_4\succ {\mathcal {W}}_2\succ {\mathcal {W}}_5$, but best one is ${\mathcal {W}}_3$.

• Case III: (When both parameter q and $\eth$ changes) We calculate score values and preference order of the alternatives ${\mathcal {W}}_\xi$ $(\xi =1,2,\ldots ,5)$ for arbitrary values of q and $\eth$ based on $q^{r}$OFAAWA operator. The results are exhibited in Table 4. From Table 4, we get different types of preference order, such as ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_2\succ {\mathcal {W}}_5\succ {\mathcal {W}}_4$, ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_4\succ {\mathcal {W}}_2\succ {\mathcal {W}}_5$, ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_2\succ {\mathcal {W}}_4\succ {\mathcal {W}}_5$ and ${\mathcal {W}}_3\succ {\mathcal {W}}_1\succ {\mathcal {W}}_4\succ {\mathcal {W}}_2\succ {\mathcal {W}}_5$ but in every type the corresponding best alternative is ${\mathcal {W}}_3$.

  Table 4 Order of preferences of the alternatives for separate values of parameter q and $\eth$ by $q^{r}$OFAAWA operator

8 Sensitivity Analysis (SA) of Criteria Weights

We suggest conducting a sensitivity analysis so as to investigate how the weighting of the criteria affects the final ranking. This is achieved using 24 distinct weight sets, specifically $S1, S2,\ldots , S24$ (Table 5), that are formed by assessing all conceivable configurations of the criteria weights $\psi _1=0.3$, $\psi _2=0.2$, $\psi _3=0.15$, and $\psi _4=0.35$. When determining the impact that the developed model has, this is an important step to take in order to obtain a wider variety of criterion weights. Figure 4 illustrates the total scores earned by each option, while Table 6 lists the choices in the order of their respective relative ranking. When the $q^{r}$OFAAWA operator (assuming $\wp =5$ and $q=3$) is used, it is clear from an examination of the sequence in which the alternatives are ranked that ${\mathcal {W}}_3$ is in first place in each and every one of the possible outcomes. Therefore, the credibility of the alternatives’ precedence that was achieved using our proposed technique may be proven.

Table 5 Various weight sets of criteria

Table 6 Priority order of alternatives for diverse weight sets

Fig. 4

Final utility values of alternatives for various criteria weight sets

9 Comparative Analysis

In this section, we evaluate our improved approaches to those of the “$q^{r}$OF weighted averaging ($q^{r}$OFWA) operator” [28], the “$q^{r}$OF weighted geometric ($q^{r}$OFWG) operator” [28], the “$q^{r}$OF Einstein weighted averaging ($q^{r}$OFEWA) operator” [39], the “$q^{r}$OF Einstein weighted geometric ($q^{r}$OFEWG) operator” [39], the “$q^{r}$OF Hamacher weighted averaging ($q^{r}$OFHWA) operator” [6], the “$q^{r}$OF Hamacher weighted geometric ($q^{r}$OFHWG) operator” [6], the “$q^{r}$OF Dombi weighted averaging ($q^{r}$OFDWA) operator” [16] and the “$q^{r}$OF Dombi weighted geometric ($q^{r}$OFDWG) operator” [8]. The results are displayed in Table 7, and represented graphically in Fig. 5.

These kinds of outcomes are conclusive evidence that the suggested operators and approach are effective. Also, unlike the operators and methods that other researchers use, our operators and methods have a number of important advantages, such as:

• (i) In the entirety of the study [28], the $q^{r}$OFWA operator is derived from “algebraic t-norm and t-conorm”. However, the $q^{r}$OFAAWA operator is derived from “AA t-norm and t-conorm” in this paper. The $q^{r}$OFWA operator that was established in the literary works [28] is a specific case of our recommended $q^{r}$OFAAWA operator, that happens when $\eth =1$, as shown in Tables 2 and 7. Because of this, the operators and methods suggested in this work are much more general and adaptable than those that have been shown before [28].

• (ii) The parameters $\eth$ and q reflect the preferences of the DMs, as indicated in Tables 2 and 3, and the DMs can pick the optimal values for $\eth$ and q depending on their preferences to choose the most suitable result. We are able to design a variety of scoring functions, and consequently a variety of ranks for the alternative, by adjusting the values of the parameters $\eth$ and q. When employed in conjunction with parameters, the developed aggregation operators concentrate on providing us with a greater number of possibilities and a greater degree of adaptability than the existing aggregation operators [6, 28, 39]. This is due to the fact that they provide us with the ability to have positive variants for the parameters that emphasis various real-life events. This is an intriguing issue that warrants further investigation.

• (iii) The key benefit of the optimization technique is that the $q^{r}$OFAAWA operator has two different characteristics, which outperform all the previous methods [6, 8, 16, 28, 39]. It increases monotonically in respect of the parameter $\eth$ and decreases monotonically in respect of the parameter q. This gives DMs the right value based on how they feel about risk. If the individual making the selection has a certain level of comfort with risk, we can adjust the parameters of $\eth$ to be as low as possible. If the person making the decision is concerned about taking risks, we can adjust the parameters of $\eth$ such that they are as large as possible. On the other hand, if the person making the decision has a predilection for risk, we have the option of making the parameters q as large as possible. If the person making the decision is concerned about taking risks, we can adjust the parameters q to be as low as reasonably practicable. So, the person in charge of making the choice is the one who can decide what the right parameter value is based on how much risk they are willing to take and what they need.

Based on evaluations and studies that have already been done, the method presented in this work is better than other methods that focus on the Hamacher operations, the Einstein operations, the algebraic operations, and the Dombi operations.

Table 7 Comparison with alternative methods that are already in use

Fig. 5

Comparative analysis employing a few prevalent methods

10 Conclusions

Information aggregation is one of the core issues of MADM problems. This paper suggests a few novel operational rules for $q^{r}$OFNs by virtue of Aczel–Alsina t-norm, and Aczel–Alsina t-conorm. Based on these new operational laws, we have produced number of new information aggregation operators, including $q^{r}$OFAAWA operator, $q^{r}$OFAAOWA operator, and $q^{r}$OFAAHA operator. The important features of these developed operators are studied. Next, we have proposed $q^{r}$OFAAWA operator-based method to address the MADM process with $q^{r}$OF information. A numerical instance is presented to demonstrate the developed techniques. By systematic comparison between the proposed methods in this paper with previously proposed $q^{r}$OF MADM methods, some advantages of the proposed $q^{r}$OF MCDM methods are shown. The developed approach consists of two general parameter q and $\eth$. The DMs can set the values of the parameters based on what they need in real-life. This requirement gives the suggested technique a lot of flexibility and reliability. In our ongoing investigation, we plan to develop these aggregation operators further so that they can be used to the “probabilistic uncertain linguistic term set” [41, 46, 56, 64], ELICIT information [22] and Consensus Reaching Processes [11, 21, 23, 40].