An Intelligent Fault Diagnosis Method Based on Extension Theory for DC–AC Converters

Abstract

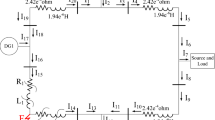
In this paper, an extension evaluation method was proposed to diagnose the fault of a DC–AC converter in a motor drive system. First, the PSIM software package was used to construct a three-level neutral point clamped (NPC) DC–AC converter for simulating the occurrence of the fault of any power transistor in the NPC DC–AC converter. Simultaneously, the fast Fourier transform was adopted to transcribe the waveform of phase voltage in time domain into the spectrum in frequency domain, looking for the corresponding characteristic spectrum during the fault of the power transistor in a DC–AC converter. Then, we establish the relationship between the fault type and the specific spectrum as the characteristics of the extension evaluation method, building up a fault diagnosis system for a DC–AC converter. Finally, the simulation results are made to demonstrate the feasibility of the proposed intelligent fault diagnosis system.

Appendix

1.1 Summary of Extension Theory

Extension theory was first proposed in 1983 by Professor Cai [22]. The major structure of this theory is comprised of the matter-element theory and extension mathematics. Therefore, the extension theory sets up the matter-element model of objects and uses the transforming characteristics as the transformation between the quality and quantity of a matter.

1.2 The Basic Concept of Extension Matter Elements

A matter element, represented here as “R”, is the basic element that delineates an object in the extension theory. Since “R” is composed of the N (name), c (characteristic) and the corresponding v (value) of the offered object, the mathematic form of the matter is as follows [22]:

$$R = \left( {N,c,v} \right)$$

(14)

In addition, in the extension theory, if one matter element has numerous traits, we can use c ₁, c ₂,…,c _m to represent each trait and v ₁,v ₂,…,v _m to represent their corresponding values. The mathematic form representing their mutual relationship is as follows [22]:

$${\text{R}} = \left[ {\begin{array}{*{20}c} {R_{1} } \\ {R_{2} } \\ \cdots \\ {R_{m} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {N,} & {c_{1} ,} & {v_{1} } \\ {} & {c_{2} ,} & {v_{2} } \\ {} & \cdots & \cdots \\ {} & {c_{m} ,} & {v_{m} } \\ \end{array} } \right]$$

(15)

From (15), we name R as the m-dimensioned matter element, and use R _k  = (N, c _k , v _k ) (k = 1, 2,…, m) to represent the dimension of each matter element. Consequently, we can rewrite (3) as R = (N, C, V), matrix C = [c ₁, c ₂,…, c _m ]^T and matrix V = [v ₁, v ₂,…, v _m ]^T. In this way, we can describe any object in our real life in the form of a multi-dimensional matter element. For instance, if we use the extension element form to represent the measured value of a DC–AC converter, we can get the mathematic form as follows:

$$R = \left[ \begin{aligned} Converter, \, Voltage ,\, {\text{ 110 V}} \hfill \\ \, Current , \quad{ 0} . 5 {\text{A}} \hfill \\ \quad Frequency ,\, {\text{ 60\,H}}z \hfill \\ \end{aligned} \right]$$

(16)

1.3 Extension Mathematics

In the Cantor set, an element either belongs to or does not belong to a set. Therefore, the range of the Cantor set {0, 1} can be used to solve a two-valued problem. In contrast to the standard set, the fuzzy set allows for describing concepts in which the boundary is not explicit. It concerns not only whether an element belongs to the set but also to what degree it belongs. The range of a fuzzy set is [0, 1]. However, the extension set extends the fuzzy set from [0, 1] to (–∞, +∞). As a result, it allows us to define a set including any data in the domain [22]. Extension theory tries to solve the incompatibility or contradiction problems by transformation of the matter element [22]. The matter-element theory includes extension theory of the matter element and the transformation theory of the matter element. Extension mathematics, based on the extension set, is the quantitative tool for solving problems. Comparisons of the standard sets, fuzzy sets and extension sets are shown in Table 6 [23].

Table 6 Three different sorts of mathematical sets

In extension mathematics, the way to define the extension set can be represented through the following mathematic form.

We assume that W is a universe of discourse, and for each element a, a $\in$ W, we obtain a real number corresponding with it.

$$K\left( a \right)\,\, \in \,\,\left( { - \infty , \, + \infty } \right)$$

(17)

If Ŝ is one extension set in the universe of discourse, W, the related mathematic form, can be represented as follows:

$$\hat{S} = \{ \left( {a,\gamma } \right) \, |a \in W,\,\gamma = K\left( a \right) \in \left( { - \infty , \, + \infty } \right)\}$$

(18)

In (18), the correlation function Ŝ is γ = K(a), and K(a) is the correlation degree to which a belongs to Ŝ. Therefore, we can classify the range of K(a) as follows:

$$P = \{ a|a \in W,K\left( a \right) \, \ge \, 0\}$$

(19)

$$\overline{P} = \{ a|a \in W,K\left( a \right) \le 0\}$$

(20)

$$J_{0} = \{ a|a \in W,K\left( a \right) = 0\}$$

(21)

(19) is the positive region of Ŝ; (20) is the negative region of Ŝ; (21) is the critical region of Ŝ.

Moreover, if a $\in$ J ₀ , then a $\in$ P, and simultaneously, a $\in$ $\overline{P}$. Figure 6 shows the ranges of each region in the extension set. From this figure, we can observe that if a $\in$ a ₁ (or a ₂), then element a can be classified into the positive region or the negative one.

Fig. 6

Each region of the extension set

1.4 Definition the Distance and Rank Value of Extension Theory

In real life, we have to face all kinds of problems and solve them. However, in the process, we often encounter contradictory problems while we are solving the original problems. The degree of the contradiction is represented in measured values according to the degree to which this problem meets certain properties. However, the values obtained can be divided into quantified values and unquantified values. The former is represented in numbers, such as 25 °C, 60 kg, 1.7 m and so on. The latter is described through words, such as deep and shallow, high and low, fat and thin, and so on. Among the values, the unquantified values need to be transformed so as to be represented in numbers by quantifying them. Then, the extension set is used to describe the degree of correlation between the measured values and the objects on the real axes. In the extension set, we use the correlation function as the solution to the contradictory problems. Consequently, to establish the relative function on the real axis, we must first introduce the concepts of “distance” and “rank value” [22].

• (1) Distance

This refers to the distance between the range and one point on the real domain in the extension set, and is defined as follows:

If we assume that a is one point in the real field of (–∞, +∞), and any range $A_{ 1} = \left\langle { va_{ 1} ,va_{ 2} } \right\rangle$ also belongs to the real field, the distance between a and A ₁ can be represented in (22).

$$\psi (a, \, A_{1} ) = \left| {a - \frac{{va_{1} + va_{2} }}{2}} \right| - \frac{{va_{2} - va_{1} }}{2}$$

(22)

• (2) Rank value

In addition, in real life, we not only consider the relativity between points and the range but also the relationship between the two ranges and among the points and the two ranges. Therefore, the relationship between one point and two ranges can be represented in rank value and defined as follows:

If we set $A_{ 1} = \left\langle {va_{ 1} ,va_{ 2} } \right\rangle ,\,A_{ 2} = \left\langle {va_{ 3} ,va_{ 4} } \right\rangle$ as the two ranges belonging to the real field and we put the range A ₁ within the range A ₂, then the rank values of a, the range A ₁ and the range A ₂ can be represented as follows:

$$D(a, \, A_{1} , \, A_{2} ) = \left\{ {\begin{array}{*{20}l} {\psi (a, \, A_{2} ) - \psi (a, \, A_{1} ),\quad\,a \notin A_{1} } \\ { - 1{ , }\quad a \in A_{1} } \\ \end{array} } \right.$$

(23)

1.5 The Basic Form of the Correlation Function

If we assume $A_{ 1} = \left\langle {va_{ 1} ,va_{ 2} } \right\rangle ,A_{ 2} = \left\langle {va_{ 3} ,va_{ 4} } \right\rangle$, $A_{1} \subset A_{2}$, and that they do not have a common connective point, then the correlation function of a and the two ranges, A ₁ and A ₂, can be represented as follows:

$$K(a) = \frac{{\psi (a,A_{1} )}}{{D(a,A_{1} ,A_{2} )}}$$

(24)

And this function has the following properties:

• (1) $a \in A_{1} , {\text{ and }}a \ne va_{1} , \, va_{2} \Leftrightarrow K(a) > 0$;

• (2) $a = va_{1} {\text{ or }}a = va_{2} \Leftrightarrow K(a) = 0$;

• (3) $a \notin A_{1} ,a \in A_{2} ,{\text{and }}a \ne va_{1} ,va_{2} ,va_{3} ,va_{4}$ $\Leftrightarrow - 1 < K(a) < 0$;

• (4) $a = va_{3} {\text{ or }}a = va_{4} \Leftrightarrow K(a) = - 1$;

• (5) $a \notin A_{2} ,{\text{ and }}a \ne va_{3} ,va_{4} \Leftrightarrow K(a) < - 1$.

If the correlation function can reach the maximum when a = 0.5(va ₁ + va ₂), then this function will be called the initial correlation function, as represented in Fig. 7. This figure shows that when K(a) < −1, it means that a is outside of the range $A_{ 2} \left( { = \left\langle {va_{3} ,va_{ 4} } \right\rangle } \right)$; when K(a) > 0, it means that a is within the range $A_{ 1} \left( { = \left\langle {va_{ 1} ,va_{ 2} } \right\rangle } \right)$; if −1 < K(a) < 0, it means that a is located within the extension domain. If we transform the conditions of a, we can classify a into the range A ₁.

Fig. 7

The diagram of the initial correlation function