Introduction

Artificial reservoirs are crucial infrastructure for providing drinking water, water for irrigation, flood protection, recreation, and hydroelectric power (Zarfl et al. 2015; Schleiss et al. 2016; Kim et al. 2020). However, reservoirs interrupt the longitudinal continuity of fluvial systems (Hinderer et al. 2013; Sun et al. 2021). For instance, low flow velocities lead to sediment deposition in reservoirs. The deposited sediment is missing in downstream reaches and reduces the active storage capacity of reservoirs (Kondolf 1997). To minimize sediment deposition and ensure sustainable reservoir operation, it is essential to quantify and accurately predict sedimentation processes. State-of-the-art tools for predicting reservoir sedimentation are two (2d) or three (3d) dimensional numerical models coupling hydrodynamics and sediment transport (Haun et al. 2013; Hanmaiahgari et al. 2018; Olsen and Hillebrand 2018; Khorrami and Banihashemi 2021).

Advances in numerical methods and computing power have led to remarkable improvements in the accuracy and speed of numerical models. Every numerical model requires calibration, which is a subjective and time-consuming process. Calibration is particularly important because the equations used in numerical models are based on simplified assumptions that are partly empirical. To calibrate a model, uncertain calibration parameters are adjusted within a physically reasonable range to achieve a good agreement between modeled and measured data with appropriate tolerance (Simons et al. 2000; Oberkampf et al. 2004; Paul and Negahban-Azar 2018). A common approach to calibrating numerical models is the iterative trial-and-error adaption of calibration parameters. However, this method is time-consuming, labor-intensive, and subjectively biased because it does not account for uncertainty in measured data, modeling errors, nor equifinality (Schmelter and Stevens 2013; Muehleisen and Bergerson 2016; Beckers et al. 2020). While Bayesian inference, a type of stochastic calibration, can address some limitations, it requires many iterations and is therefore not practical for use with computationally intensive models (e.g., hydro-morphodynamic models to simulate reservoir sedimentation). Mohammadi et al. (2018), Beckers et al. (2020), and Scheurer et al. (2021) overcame this challenge using metamodels (also known as surrogate models, response surface, reduced model, etc.) to replicate the full complexity of a deterministic numerical model. These studies employed metamodel updating to reduce the total number of evaluations of the original model required to train the metamodel.

Modeling reservoir sedimentation requires specific simplifying assumptions regarding hydrodynamics and morphodynamics. In comparison to the simulation of rivers, fluctuating water levels and outflow conditions due to reservoir operation, and the simultaneous simulation of very shallow shores and tributary deltas along with deep waters are particularly challenging in reservoir modeling. For instance, wetting and drying of mesh nodes at the shoreline of a reservoir require model simplifications (e.g., the definition of a minimum water depth for a cell). In addition, channel erosion and deltaic avulsion might occur at the head of the reservoir. These erosion and avulsion processes and their exact location are hard to predict and result from stochastic environmental forcing (Hajek and Wolinsky 2012; Chadwick et al. 2019). Furthermore, these processes are still an open research topic (e.g., Langendoen et al. 2016) and difficult to simulate accurately, much less with the same model simplifications as the deposition of fine sediments in deeper waters. As a result of global model assumptions, some regions of a reservoir model may not be accurately represented by the numerical model. This is because the model is generally calibrated to accurately represent either fine sediment deposition in deep waters or delta progression and erosion processes at the head of the reservoir, but not both. This is why we are investigating in this study how complex numerical models for reservoir sedimentation can be calibrated in light of competing model simplifications. To this end, we test the hypothesis (i) that Bayesian calibration only converges toward physically meaningful calibration parameter combinations when the model is well-conditioned (i.e., measured data are in the validity domain of model assumptions). The verification of this hypothesis aims to enrich the scientific baseline for modeling complex hydro-morphodynamic processes in reservoirs, which inherently require modeling regions that may be physically invalid. To test this hypothesis, we adapt a Bayesian calibration technique that uses surrogate-assisted Bayesian inversion with a metamodel in the form of a Gaussian Process Emulator (GPE) according to Oladyshkin et al. (2020). The metamodel and its updating build on Bayesian active learning (BAL), which we further improve through the cumulative consideration of measurement and metamodel errors. To test hypothesis (i), we introduce two spatially distinct measurement data scenarios for calibrating a 2d hydro-morphodynamic reservoir sedimentation model of the large Banja reservoir in Albania.

Bayesian calibration typically starts with the definition of calibration parameters and the corresponding physically meaningful parameter ranges (e.g., Kim and Park 2016; Beckers et al. 2020). Based on initial model tests, we selected the four most sensitive parameters in the form of dry-bulk density of deposited sediments \({\rho }_{b}\), critical shear stress for erosion \({\tau }_{cr}\), critical shear stress for deposition \({\tau }_{d}\), and a diameter multiplier \(\gamma\) that defines the grain size distribution. The large number of four calibration parameters presents a challenge for any calibration process and results in a four-dimensional parameter space with millions of combination options, leading to problems regarding maximum floating-point precision. Hence, we implemented optimization strategies for Bayesian calibration intending to bypass precision errors (arithmetic underflow) caused by the multidimensional space of possible calibration parameter combinations. Furthermore, these parameters carry a high degree of uncertainty that must be thoroughly considered during modeling (Schmelter et al. 2015; Villaret et al. 2016). The grain size distribution, the two critical bed shear stresses for cohesive sediments, and the dry-bulk density can only be determined with great effort by field sampling. Therefore, it is important to identify and prioritize the most important parameters when planning field data collection. This insight enables the development of optimized measurement concepts, to reduce costs and workload. Hence, we investigate whether our modified Bayesian calibration enables the identification of driving calibration parameters for modeling reservoir sedimentation even in a four-dimensional parameter space. By examining the importance of four potentially important parameters driving reservoir sedimentation, we test the hypothesis (ii) that at least one of the four calibration parameters plays a dominant role in the fluvial deposition of suspended load in reservoirs. Therefore, we aim to identify the most important calibration parameter that should be addressed in sampling campaigns at reservoirs.

Materials and methods

Study area

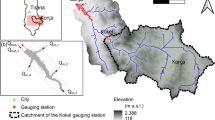
The Banja Reservoir

In this study, we numerically simulated hydro-morphodynamic processes in the Banja Reservoir at the Devoll River in central Albania. With a length of 196 km, the Devoll River is the third longest river in Albania and has its source in the Gramos Mountains near the Greek border. The river flows northwestward and is dammed after approximately 160 km, forming the Banja reservoir (see Fig. 1). The reservoir was commissioned in 2016 and has a length of 14 km, a maximum water depth of 60 m close to the dam, and a surface area of approximately 14 km², leading to a storage capacity of approximately 400 million m³. It is mainly fed by the Devoll River (89%, MQ \(\approx\) 33 m³ s-1), Holta River (9%), and two smaller tributaries (Zalli and Skebices River, 1% each). The catchment of the reservoir is characterized by dry and hot summers and wet winters, resulting in low summer, high winter, and high spring flows. Since snowfall is frequent in winter at high elevations, the flow regime is driven by precipitation and snowmelt. The sediment yield of the Banja catchment is particularly high due to high rainfall erosivity on steep terrains composed of loose soils (Walling and Webb 1996; Borrelli et al. 2020; Mouris et al. 2022).

Fig. 1
figure 1

Location of the study area; a European context, b national context, and c the bathymetry of the Banja reservoir with indication of the calibration nodes, major tributaries and turbine intake. The red calibration nodes are excluded in the VALDOME data scenario

Full size image

Measurement data

The initial bathymetry was interpolated onto a numerical mesh from a photogrammetry-based digital elevation model (DEM) from 2016, before filling the reservoir. In addition, the reservoir bathymetry was measured in 2019 with an acoustic Doppler current profiler (ADCP) boat providing approximately 632 × 103 bed level measurements.

The grain size distribution of the suspended sediment was determined based on suspended sediment measurements at the Devoll River upstream of the reservoir (Ardiclioglu et al. 2011) and reservoir bed samples. The per-sample median diameters of the deposited sediment ranged from 5.7 to 37.4 μm with a mean of 10.5 μm, emphasizing the cohesive nature of the deposits. Upstream of the reservoir, the extracted granulometric curve had cohesive characteristics, with 98% of the volume having grain diameters smaller than 60 μm. Neither cobble, gravel, nor coarse sand was present in the study area. Consequently, bedload was not considered in the numerical model. The available measurement data for this study are summarized in Table 1.

Table 1 Used input data for the Bayesian calibration of the Banja reservoir
Full size table

Numerical full-complexity model

General setup

In this study, we used Telemac-2D (Hervouet 2007) with its sediment transport and bed evolution module GAIA (Audouin et al. 2020) to simulate reservoir sedimentation processes. Telemac-2D abstracts river landscapes with unstructured grids. The here-used unstructured, triangular numerical mesh consisted of 24,241 elements and 12,600 nodes, resulting in element sizes of approximately 40 m. We defined two roughness coefficients to differentiate between the original river course (before filling) and the newly wetted areas. Due to the low flow velocities, the influence of boundary roughness on reservoir hydrodynamics was small and we applied Manning coefficients of 0.032 s m-1/3 (original cobble-gravel-bed river) and 0.06 s m-1/3 elsewhere (many trees and brushes were not removed before the impoundment of the reservoir).

Telemac-2D approximates the shallow water equations with a combined explicit-implicit solver to calculate the flow field. The hydrodynamic module passes the calculated hydrodynamic variables (water depth, depth-averaged flow velocity) and bed shear stress to the GAIA module. We set the numerical model parameters with the premise of maximizing computational and numeric stability while keeping computing time short. Therefore, we applied a finite element numerical scheme and treated tidal flats (or dry-wet elements) according to software recommendations to use only positive water depths (Hervouet et al. 2011). Furthermore, the method of characteristic solves the advective part of the hydrodynamic equations and improves stability (a result of preliminary model tests). The mixing length turbulence model serves to calculate the turbulent viscosity coefficient, which is similar to the k-ɛ model when the transverse shear stress is the main turbulence generator, as in the case of a reservoir, but requires 20% less computing time (Dorfmann and Zenz 2016).

To calculate the depth-averaged concentration \(C\left(x,y,t\right)\) of tracers (i.e., fine particles) in (g L-1), the 2d advection-diffusion-equation is solved.

$$\frac{\partial \left(hC\right)}{\partial t}+\frac{\partial \left(huC\right)}{\partial x}+\frac{\partial \left(hvC\right)}{\partial y}=\frac{\partial }{\partial x}\left(h\epsilon \frac{\partial C}{\partial x}\right)+\frac{\partial }{\partial y}\left(h\epsilon \frac{\partial C}{\partial y}\right)+\left(E-D\right)$$
(1)

where \(h\) is the water depth (m), \(u\) (m s-1) and \(v\) (m s-1) are the depth-averaged components of flow velocity, ε is the turbulent diffusivity of the sediment (m² s-1), and \(E\) and \(D\) are the erosion and deposition fluxes (kg m-2 s1), respectively. We applied the default treatment of the diffusion term in Eq. (1) to increase numerical stability. In addition, we chose the “Edge-based N-Scheme” to solve the advective term because it provides mass conservative results and treats tidal flats. The erosion and deposition fluxes for cohesive sediment are calculated as follows:

$$D={\omega }_{s}C\left(1-\frac{{\tau }_{b}}{{\tau }_{d}}\right)if{\tau }_{b}>{\tau }_{d}$$
(2)
$$E=M\left(\frac{{\tau }_{b}}{{\tau }_{ce}}-1\right)if{\tau }_{b}>{\tau }_{ce}$$
(3)

where \(M\) is the Krone-Partheniades erosion constant (kg m-2 s-1), \({\tau }_{b}\)is the bed shear stress (N m-2), \({\tau }_{ce}\) is the critical shear stress for erosion (N m-2), \({\tau }_{d}\) is the critical shear stress for deposition (N m-2), and \({\omega }_{s}\) is the settling velocity (m s-1). The settling velocity is a function of the mean sediment diameter, the ratio of the sediment and water densities, and the kinematic viscosity of the water. The measurement data (see above) had shown that the deposits predominantly consisted of cohesive sediment, and therefore, only suspended transport was considered in this study.

After determining the erosion and deposition fluxes and calculating the net transport flux per element, GAIA updates the bed level using the Exner equation (Paola and Voller 2005). For a detailed description of the free surface flow and sediment modeling algorithms used, the reader is referred to Hervouet (2007, 2020) and Audouin and Tassi (2020). The steering file for the Telemac-2D simulations is available at Acuna Espinoza et al. (2022).

The focus of the numerical model was on the time-efficient simulation of suspended sediment transport in a large reservoir to ease repetitive calibration runs. Therefore, bedload was not considered and a coarse mesh resolution was used. Due to these simplifying assumptions, but also because of the general limitation of numerical models, it is not possible to accurately predict channel avulsion and erosion through previously deposited cohesive sediments (Hajek and Wolinsky 2012; Liang et al. 2015). Furthermore, channel bank failure depends on the sediment type, moisture content, and seepage processes (Luppi et al. 2009; Rinaldi and Nardi 2013; Olsen and Haun 2020). Therefore, bank failure cannot be simulated with a numerical setup for reservoir sedimentation due to fine particle deposition. Since bank failure processes only occur at the head of the reservoir, the bed level changes in this domain cannot be predicted in a physically correct and stable manner. Still, the above-introduced model setup is valid in deep-water model domains outside of the shallow deposition delta of the Devoll River.

Boundary conditions

For the simulation of reservoir sedimentation over three years, between the two surveys from August 2016 and August 2019, we defined the reservoir inflow \({Q}_{in}\) (m³ s-1) as a function of measured water levels and measured outflow \({Q}_{out}\) (m³ s-1) based on a routing equation. More detailed information can be found in SI 1.

Since the suspended sediment concentrations at the tributaries were not known for the simulation period, we implemented a previously developed indirect calculation method (Mouris et al. 2022). The indirect method builds on a calibrated soil erosion and sediment transport model with a monthly resolution (tons month-1) to calculate the suspended sediment yield (SSY) of the catchment of the Banja reservoir. We divided the SSY from Mouris et al. (2022) at the Devoll River by the monthly inflow volume to prescribe suspended sediment concentrations (SSC) at the liquid model boundaries. Thus, SSC was constant for every month but varied from month to month. The mean SSC at the Devoll River for the calibration period was 1.36 kg m-3 with a maximum of 4.0 kg m-3 in September 2017.

Calibration parameters

This study optimized four calibration parameters in the form of dry-bulk density of deposited sediments \({\rho }_{b}\), critical shear stress for erosion \({\tau }_{cr}\), critical shear stress for deposition \({\tau }_{d}\), and a diameter multiplier \(\gamma\) for settling velocities. The calibration parameter values were to be adapted to yield a possibly best simulation of the measured bed level changes \(\varDelta {z}_{meas}\)between 2016 and 2019.

The dry-bulk density \({\rho }_{b}\) and consolidation processes of mud-sand mixtures strongly depend on the sand content (van Rijn and Barth 2019). Because more than 98% of the deposited sediment in the Banja reservoir is cohesive, we defined \({\rho }_{b}\) based on reported literature values for very low (< 10%) sand content. We considered the dry-bulk density a quasi-random variable with equally likely values (i.e., uniformly distributed) between 200 kg m-3 and 500 kg m-3 (van Rijn and Barth 2019; van Rijn 2020).

The critical shear stresses for erosion \({\tau }_{cr}\) and deposition \({\tau }_{d}\) control the exchange rate between suspended and deposited sediment. To define quasi-random, uniformly distributed value ranges for \({\tau }_{cr}\) and \({\tau }_{d}\), we referred to field and laboratory tests with sediment mixtures with similar characteristics (grain size distribution, bulk density) as in the Banja reservoir. To this end, we tested value ranges for \({\tau }_{cr}\) between 0.05 and 0.4 Pa (Kornman and Deckere 1998; Widdows et al. 1998; Houwing 1999; Lumborg 2005; Shi et al. 2012; van Rijn 2020), and for \({\tau }_{d}\) between 0.01 and 0.1 Pa (Krone 1962; Lumborg 2005; Shi et al. 2012).

The deposition pattern in the reservoir also depends on the particle size that drives the settling velocity \({\omega }_{s}\) (see Eq. (2)). We applied the granulometric curves of suspended sediment upstream of the reservoir, which were subjected to considerable variability (i.e., uncertainty) in the model domain. Figure 2 plots the granulometric curve defined by three diameters representing the lower, middle, and upper third of the total volume. To account for uncertainty, we multiplied every diameter by a factor \(\gamma\) that takes uniformly distributed values between 0.8 and 1.7. Thus, the upper limit of grain sizes was 41 μm, which was larger than 95% of the sediment sample volume. The lower limit of 1.8 μm (2.3 μm \(\bullet\) 0.8) was based on preliminary model runs, in which we tested the smallest possible sediment particles that remain in suspension and have an almost negligible influence on the deposition volume. Table 2 shows the resulting value ranges for the four calibration parameters considered in this study.

Fig. 2
figure 2

Granulometric curve with the minimum and maximum grain sizes defined by the \(\gamma\)-multiplier

Full size image
Table 2 Calibration parameters and their value ranges for uniform distributions U(min, max) considered in this study
Full size table

Bayesian calibration

Bayesian inference

To calibrate a numerical model using Bayesian inference, we inferred the posterior distribution \(p\left(\omega |{z}_{meas}\right)\) of the model calibration parameters (and hence the corresponding model responses) based on the measured bed levels \({z}_{meas}\) and defined initial ranges for the calibration parameters. The posterior distribution \(p\left(\omega |{z}_{meas}\right)\) is the result of evaluating Bayes’ theorem in the context of model updating:

$$p\left(\omega |{z}_{meas}\right)=\frac{p\left({z}_{meas}|\omega \right)\bullet p\left(\omega \right)}{p\left({z}_{meas}\right)}$$
(4)

where \(p\left(\omega \right)\) is the prior probability distribution that defines the initial probability of the calibration parameters before considering new or additional evidence (\({z}_{meas}\)). \(p\left({z}_{meas}|\omega \right)\) is the so-called likelihood function and indicates how well the metamodel reproduces the measured data \({z}_{meas}\) given a parameter combination \(\omega\). \(p\left(\omega |{z}_{meas}\right)\) is the posterior probability distribution (i.e., the updated probability of the calibration parameters \(\omega\) given measured data \({z}_{meas}\)), which is expected to be narrower than \(p\left(\omega \right)\) (Box and Tiao 1992; Oladyshkin and Nowak 2019). \(p\left({z}_{meas}\right)\) is a normalization factor, often referred to as Bayesian model evidence (BME), and is important when different posterior distributions are being compared with each other or several competing models are being evaluated (Mohammadi et al. 2018). Assuming that the deviations between the measured bed levels \({z}_{meas}\) and the modeled bed levels \({z}_{mod}\) are normally distributed and independent, the likelihood function \(p\left({z}_{meas}|\omega \right)\) is calculated proportionally to the sum of squared errors \({\delta }_{i}^{2}\) between measured and simulated bed levels \({z}_{meas}-{z}_{mod}\) weighted by the total error \({e}_{i}\), where \(i\) indicates the calibration node.

$$p\left({z}_{meas}|\omega \right)\propto \text{e}\text{x}\text{p}(-0.5\left[\frac{{\delta }_{1}^{2}}{{e}_{1}^{2}}+\frac{{\delta }_{2}^{2}}{{e}_{2}^{2}}+\dots +\frac{{\delta }_{n}^{2}}{{e}_{n}^{2}}\right])$$
(5)

This study provides additional novelty by improving BAL because of how we implement the measurement error \({e}_{meas}\) and the metamodel error \({e}_{meta}\). In particular, we calculated the total errors \({e}_{i}\) for each calibration node \(i\) as the sums of \({e}_{meas,i}\) and \({e}_{meta,i}\) according to the following descriptions.

The measurement errors \({e}_{meas}\) resulted from the interpolation of the bed level measurements at the calibration nodes of the numerical mesh and uncertainties of field measurements. We used an interpolation radius of 3 m around the calibration nodes to average the bed level. Thus, the number of measurements per calibration node varied from 1 to 35 (8 on average). The variable amount of measurements available for averaging affected the confidence in the averaged values because, for instance, 15 measurements are more representative than two. The mean measurement error \({e}_{meas}\) was approximately 0.4 m (measurement precision according to operator) where possible sources of errors were a high concentration of suspended sediment near the bottom, uncertainties in the water level of the reservoir, and the movement of the ADCP boat due to waves. Thus, to calculate the measurement errors \({e}_{meas,i}\) at every node, we introduce Eq. (6) where \({s}_{i}\) is the number of observation points within the 3-m radius:

$${e}_{meas,i}=\frac{adapted \, error}{1+ln\left({s}_{i}\right)}$$
(6)

where an \(adapted error\) of 1.02 m was computed iteratively to ensure that the average value of \({e}_{meas}\) for the total number of calibration nodes was 0.4 m. Thus, for example, \({e}_{meas,i}\) for a calibration node where the bed level was calculated based on 26 survey points is 0.24 m, while two survey points resulted in an \({e}_{meas,i}\) of 0.6 m.

In addition, we accounted for a metamodel error \({e}_{meta}\) in the likelihood function because the metamodel is just an approximation of the full-complexity numerical model. We calculated \({e}_{meta}\) through a leave-one-out cross-validation (LOO-CV), in which the model is repeatedly fitted on n-1 calibration nodes. Then, we calculated the LOO-CV error for each calibration node and training point. The LOO-CV error variance per calibration node was subsequently calculated and implemented as metamodel error \({e}_{meta,i}\). Finally, the total error \({e}_{i}\) included in the likelihood function is composed of the calibration node-specific measurement error \({e}_{meas,i}\) (6) and the metamodel error \({e}_{meta,i}\):

$${e}_{i}^{2}={e}_{meas,i}^{2}+{e}_{meta,i}^{2}$$
(7)

If the total errors \({e}_{i}\) (Eq. (7)) were significant, the influence of the difference between the measured and modeled bed level on the likelihood score decreased (Eq. (5)).

Metamodel construction

Equation (4) can be approximated through Monte Carlo sampling, which requires thousands of numerical model evaluations. However, models that simulate hydrodynamic and morphodynamic processes may require a long computing time, making it computationally impractical to perform thousands of trials. To circumvent unacceptably long computing time, we employed a surrogate-assisted (referring to the metamodel being a surrogate for a full-complexity model, Oladyshkin et al. 2020) Bayesian inversion technique, which replaces the full-complexity numerical model with a metamodel. In particular, a metamodel emulates the output trends of a complex model but requires orders of magnitude less computing time (Beckers et al. 2020; An et al. 2022). Here, we used a Gaussian process emulator (GPE) as metamodel, which is discussed in more detail by Rasmussen and Williams (2006). As the GPE requires the definition of a kernel, we used a radial basis (i.e., squared exponential covariance) function (RBF) kernel in this study. The RBF needs the definition of length scales and their boundaries. The resulting GPE metamodel can then be trained with numerical model responses resulting from various combinations of possible calibration parameter values. Thus, the GPE metamodel was fitted toward a multidimensional response surface where the number of dimensions corresponds to the number of calibration parameters. Note that the metamodel cannot generally replace the numerical model and only serves the purpose of accelerating model calibration.

Bayesian active learning through metamodel training

In this study, we used the GPE metamodel to approximate the prior \(p\left(\omega \right)\) through 106 random Monte Carlo samples. The quality of the surrogate-assisted Bayesian calibration depends on the ability of the metamodel to replicate the full-complexity model. The more training points used to train the metamodel, the better the predictions, since more information is provided to the metamodel with fewer gaps in the parameter space (i.e., fewer gaps need to be closed through stochastic interpolation). However, filling the entire parameter space with training points with a computationally expensive full-complexity model is practically not feasible because it requires several hours to compute one training point (sums up to more than 500 years of computing time in our case). To bypass long computing time, we applied BAL, which identifies optimal regions in the parameter space for calibrating parameters as a function of metamodel responses. BAL iteratively improves the metamodel in those regions of the parameter space that are most important for Bayesian inference (Oladyshkin and Nowak 2019; Oladyshkin et al. 2020).

Before starting the BAL process, a prior probability distribution \(p\left(\omega \right)\) was assigned to every calibration parameter. Initially, a uniform probability distribution between two limit values was assumed. The next step is to compute an initial metamodel, using \(m\) parameter realizations and the corresponding full-complexity numerical model runs to train the metamodel. BAL starts with iteratively updating the initial metamodel with new training points so that the metamodel predictions better represent the full-complexity model. For this purpose, we sampled \(q\) parameter realizations \({\omega }_{i}\) that compete to be the next training point (exploration).

The parameter realizations constitute the parameter space and each combination is evaluated in the metamodel to generate an output space. Here, we had n outputs, associated with the location of our calibration nodes. An advantage of Gaussian processes for generating the metamodel is that each prediction of the output space consists of a mean \({\mu }_{n}\) and a standard deviation \({\sigma }_{n}\). Therefore, one can explore the output space using a multivariate Gaussian distribution. Figure 3 shows the BAL workflow and exemplary features two random exploration samples (black and gray circles), which in our study, are not just two but 105 random exploration samples forming the output space prior. To yield the output space posterior distribution, we considered two options, notably rejection sampling and Bayesian reweighting. Due to the high dimensionality of the output space (142 calibration points), the rejection rate for the first case was too high, and we chose Bayesian reweighting. For this purpose, we renormalized each value of the prior´s likelihood by their total sum to generate the posterior distribution. Consequently, all realizations (i.e., Monte Carlo samples) of the prior contributed to the posterior statistics (i.e., length scales), proportional to their likelihood. Once the prior \(p\left(\omega \right)\) and posterior \(p\left(\omega |{z}_{meas}\right)\) distributions had been generated, we used Eq. (8) to evaluate the so-called relative entropy \({D}_{KL}\left(p\left(\omega |{z}_{meas}\right),p\left(\omega \right)\right)\) (also referred to as Kullback–Leibler divergence) between both distributions (Kullback and Leibler 1951; Oladyshkin et al. 2020).

$${D}_{KL}\left(p\left(\omega |{z}_{meas}\right),p\left(\omega \right)\right)=-ln\left[BME\right]+{E}_{p\left(\omega |{z}_{meas}\right)}\left(ln\left[p\left({z}_{meas}|\omega \right)\right]\right)$$
(8)

where \({E}_{p\left(\omega |{z}_{meas}\right)}\) is the average of the posterior sample’s likelihood (through the likelihood function, cf. Equation (5)). In this context, the relative entropy expresses the information gain from the prior to the posterior distribution.

Fig. 3
figure 3

Flow diagram explaining the Bayesian active learning method applied in this study

Full size image

To this end, every BAL iteration involves the calculation of \({D}_{KL}\left(p\left(\omega |{z}_{meas}\right),p\left(\omega \right)\right)\) for \(q\) samples from the parameter space. After evaluating \({D}_{KL}\left(p\left(\omega |{z}_{meas}\right),p\left(\omega \right)\right)\), we calculated the parameter combination \({\omega }_{max\left(DKL\right)}\) that produced the maximum value of relative entropy to select the stochastically best-performing values for the calibration parameters in this iteration step (exploitation). We used the set of calibration parameters with the highest relative entropy to re-run the numerical full-complexity model and prepared the next BAL iteration step. In particular, the results of the new full-complexity model run serve as new training points for the GPE at the beginning of the next BAL iteration step. The BAL iterations continue until a stop criterion is reached, which is typically the convergence of relative entropy and BME (Oladyshkin et al. 2020). In this study, we additionally considered the evolution of the root-mean-square error (RMSE) after every BAL iteration. The BAL workflow (Fig. 3) and creation of the initial metamodel are explained in detail in the supplemental material SI 2. The complete procedure is implemented in a Python code (Acuna Espinoza et al. 2022).

Selection of calibration nodes for model calibration

The numerical model of the Banja reservoir was calibrated toward measured bed levels at the end of the three-year simulation period from 2016 to 2019. However, we could not use the totality of the available 632 × 103 bed level measurements because we needed to meet two criteria. First, the measurements needed to comply with the computational mesh and we agglomerated multiple measurements into one at the calibration nodes of the mesh. Second, the number of BAL iterations depends on the number of calibration nodes, and a large number of nodes can result in the so-called curse of dimensionality (Bellman 1957), which we will discuss later in light of the results. For instance, if we used 3500 measurement points, the multivariate Gaussian density for calculating the prior output space would have 3500 dimensions of spatially explicit bed level change.

Therefore, we only used nodes located at a maximum distance of 1.5 m from a measured point for calibration, and we agglomerated all measurements in a 3-m radius at the resulting calibration nodes into one bed level value. Further, we did not consider measurements in the downstream section of the reservoir, as we are only interested in the upstream area, where most sediments deposit. These selection filters resulted in 142 calibration nodes at which we evaluated modeled bed levels in the calibration process (see also Fig. 1). For testing the hypothesis (i) that Bayesian calibration only converges toward physically meaningful model parameter combinations when the model is well-conditioned, we introduced two scenarios of measurement data available for the calibration process. First, we considered all 142 calibration nodes that define the MAXME (MAximum MEasurements) data scenario (black and red calibration nodes in Fig. 1). Second, we removed points in regions where deltaic avulsion and channel erosion occurred according to the observation from 2016 to 2019 to define a VALDOME (VAlid DOmain MEasurements) data scenario, where all calibration nodes are in the domain of validity of the numerical model. In particular, we removed points adjacent to dry areas (tidal flats) and all measurements where the model uncertainty from the MAXME data scenario was high, as indicated by LOO-CV error greater than 5.5 m based on an expert assessment. These two removal criteria essentially excluded model regions where avulsion and channel erosion occurred at the head of the reservoir, which the full-complexity model will not be able to simulate correctly. The application of these removal criteria left 109 calibration nodes that we used for the VALDOME scenario (black calibration nodes in Fig. 1).

Experimental procedure

Bayesian calibration stability

The proposed optimization of the Bayesian calibration scheme refers to the extension of the BAL framework, notably the adaptive implementation of errors in the likelihood function through LOO-CV, and its application to four calibration parameters. With these two novel aspects of BAL, we investigated the robustness of Bayesian calibration regarding the quality of the numerical model and in light of equifinality. Therefore, we applied Bayesian calibration to the two above-introduced data scenarios (MAXME and VALDOME).

To prepare the BAL iterations, we ran the full-complexity model with 15 calibration parameter combinations to train the initial metamodel. 13 of the parameter combinations stemmed from random sampling in the parameter space, and the remaining two corresponded to theoretically maximum and minimum sedimentation (i.e., high/low \({\tau }_{cr}\), low/high \({\tau }_{d}\), low/high \({\rho }_{b}\), high/low \(\gamma\), respectively). A minimum of one training point would be sufficient for the initial metamodel, but more initial training points for BAL can reduce the total time required to achieve convergence. We tracked BME, and RMSE to evaluate if the calibration reached convergence regarding uncertainty and error (see the above section on Bayesian active learning). However, convergence may not be achieved if multiple high-probability regions cause exploitation to jump between very different calibration parameter combinations in the BAL iterations. In these cases, BAL theoretically bounces back and forth eternally between nearly equally likely combinations of calibration parameters. This phenomenon, known as equifinality, poses a great challenge for model calibration (e.g., Franks et al. 1997).

To address equifinality, we analyzed the BAL convergence in the two measurement data scenarios (see above) with 55 iterations according to literature recommendations (Mohammadi et al. 2018; Beckers et al. 2020; Scheurer et al. 2021). We verified hypothesis (i) if the VALDOME scenario led to more unique and physically meaningful maximum likelihood regions than the MAXME data scenario, and less significant, later, or no convergence in the MAXME data scenario. To this end, we investigated the evolution of BME, RMSE, and the variability of the four calibration parameters in the last five BAL iteration steps. To assess the ability of the metamodel to reproduce the results of the full-complexity model, we compared the results predicted by the metamodel with those predicted by the numerical model. We present the global model accuracy after the Bayesian calibration by comparing the calculated and measured bed level changes after running the two data scenarios.

Importance of calibration parameters

The Bayesian calibration looks for the best-fit combination of the four calibration parameters \({\tau }_{cr}\), \({\tau }_{d}\), \({\rho }_{b}\), and \(\gamma\) to investigate optimization methods for multidimensional calibration parameter spaces and find the most relevant parameters driving reservoir sedimentation in this numerical model. The four calibration parameters are known to be relevant for hydro-morphodynamic processes in reservoirs (Haun et al. 2013; Dutta and Sen 2016; Hillebrand et al. 2016). However, to our best knowledge, the four parameters have never been directly compared with each other due to the limited capacities of subjective trial-and-error calibration. The adapted Bayesian framework and the VALDOME scenario enable us to perform such a comparison of the four calibration parameters. Thus, we aim to test hypothesis (ii) that at least one of the calibration parameters \({\tau }_{cr}\), \({\tau }_{d}\), \({\rho }_{b}\), or \(\gamma\) plays a governing role in the fluvial deposition of suspended sediments in reservoirs. To this end, we made use of a multi-parameter plot of the posterior distributions (Eq. (5)) of the four calibration parameters for both data scenarios. We will accept hypothesis (ii) if at least one of the four calibration parameters has a considerably narrower posterior distribution than the other parameters. This parameter will be more important than the other calibration parameters because it has the smallest uncertainty (i.e., narrowest posterior) of the maximum likelihoods.

Results

Convergence speed

In the VALDOME scenario, the BME began converging toward a value of approximately 10–31 after the 46th BAL iteration, and we ran in total 55 iterations to monitor the convergence trend (see Fig. 4). The BME for the MAXME scenario fluctuated around a value of 10–37 during the 55 BAL iterations, and no clear convergence trend was observed. In addition, Fig. 4 also shows the evolution of the RMSE between the metamodel and full-complexity model results for every tested parameter combination used as a training point in BAL. The plots reveal that the RMSE is higher for the MAXME scenario, and more importantly, there is no decreasing trend for this scenario. In contrast, the evolution of the RMSE for the VALDOME scenario decreased. Figure 5 shows the variability of the four calibration parameters in the last five BAL iterations for the VALDOME scenario in black and the MAXME scenario in gray. Comparing the two data scenarios shows that the MAXME scenario had significantly higher variability and no physical convergence for \({\tau }_{cr}\) and \({\tau }_{d}\). In contrast, there was hardly any variability of \({\rho }_{b}\) in both scenarios, whereas the variability in \(\gamma\) was slightly higher in the VALDOME scenario. The total computing time for the BAL iterations per scenario was approximately one month (on 12 Cores using AMD Ryzen 9 5950 × 16- (32) @ 3.4 GHz processor), which was only possible with the coarse mesh resolution.

Fig. 4
figure 4

BME (top) and RMSE evolution including linear trend lines (bottom) for the 55 BAL iterations and both data scenarios

Full size image
Fig. 5
figure 5

Variability of the four calibration parameters for the five last BAL iterations 50–55 and both data scenarios

Full size image

Posterior distributions and importance of calibration parameters

Maximum likelihoods

Table 3 shows the maximum likelihood of posterior distributions for the calibration parameters, which is the realization of the Monte Carlo sample with the highest likelihood and comparable to a deterministic best-fit solution. The maximum likelihood of \({\tau }_{cr}\) was 0.39 Pa, close to the upper limit considering all calibration nodes (MAXME). In the physically relevant-only (VALDOME) scenario, \({\tau }_{cr}\) was 0.25 Pa. The critical shear stress for deposition \({\tau }_{d}\) was close to the lower limit at 0.02 Pa and 0.01 Pa in the MAXME and VALDOME scenarios, respectively. The maximum likelihood of \({\rho }_{b}\) was close to 410 kg m-3 in both scenarios. The diameter multiplier \(\gamma\) was 0.82 in the MAXME scenario and 0.98 in the VALDOME scenario. A detailed analysis of the posterior parameter space is provided below.

Table 3 Calibrated parameters for the morphodynamic model of the Banja reservoir using BAL
Full size table

Posterior parameter distributions

The posterior distributions of the calibration parameters indicate the uncertainty in the maximum likelihoods listed in Table 3. Figure 6 shows the individual posterior histograms for each calibration parameter after the MAXME scenario at the top (433 posterior samples) and after the VALDOME scenario at the bottom (540 posterior samples).

Fig. 6
figure 6

Posterior distributions in the parameter space, and associated relative entropy (RE) at the end of the MAXME scenario in gray (top) and the VALDOME scenario in light gray (bottom). The dashed vertical lines indicate the maximum likelihood values of the calibration parameters

Full size image

As a standardized measure to identify driving calibration parameters and evaluate their uncertainty, we calculated the Kullback–Leibler divergence (Kullback and Leibler 1951), also known as relative entropy (RE), to measure the information gain between the initial (uniform) prior and the final posterior probability distribution for every calibration parameter. High RE characterizes a narrow distribution, which represents high information gain and low uncertainty in the maximum likelihoods.

Figure 6 shows that \({\rho }_{b}\) and \({\tau }_{d}\) have the narrowest posterior distribution in both calibration scenarios, which indicates that these parameters are the most restrictive and important in the calibration process. This finding is also supported by the high RE of 1.68 and 2.29 for \({\rho }_{b}\) and 2.01 and 1.77 for \({\tau }_{d}\). That is, only values close to the maximum likelihood value (dashed line) led to accurate results. However, the maximum likelihood for \({\tau }_{d}\) was close to the lower limit in both data scenarios. The histogram for \({\tau }_{cr}\) differs significantly between the two different scenarios. For the MAXME scenario, the distribution peaks close to the upper limit, and the RE was 1.23 whereas the histogram for the VALDOME scenario peaks at 0.25 Pa and gets wider, characterized by a lower RE of 0.89. The histogram of the diameter multiplier \(\gamma\) peaks in both scenarios close to the lower limit of the initial range and the RE slightly increased from 1.23 to 1.34 for the VALDOME scenario.

The meaningfulness and qualitative significance of the yielded maximum likelihoods can also be interpreted by examining data patterns and regions of high and distinguishable maximum likelihoods in the parameter space. For this purpose, Fig. 7 illustrates the likelihood of all possible calibration parameter combinations of \({\tau }_{d}\), \({\tau }_{cr}\), \(\gamma\), and \({\rho }_{b}\) at the end of the VALDOME scenario. Similar plots of the results for the MAXME scenario can be found in SI Fig. 2. Since a four-dimensional parameter space cannot be plotted graphically, we created six two-dimensional plots of the possible combinations. The three plots on the right of Fig. 7 clearly show that the likelihoods for \({\rho }_{b}\)< 300 kg m-3 are very small and quite small for \({\rho }_{b}\)> 450 kg m-3 (in line with Fig. 6). Thus, values of \({\rho }_{b}\) significantly lower or higher than the maximum likelihood did not lead to accurate results, and the data pattern of \({\rho }_{b}\) confirms its high relative importance compared to the other three calibration parameters. In contrast, the boundary between high and low probabilities in the data pattern for \({\tau }_{d}\) was less distinct, with the highest likelihoods occurring for \({\tau }_{d}\) < 0.05 Pa. \({\tau }_{cr}\) had the least pronounced data pattern, and high probabilities occurred almost throughout the entire range. In addition, the data pattern for \(\gamma\) showed high likelihoods over a wide range with \(\gamma\) < 1.2.

Fig. 7
figure 7

Likelihood values along the six possible parameter space combinations at the end of the VALDOME scenario

Full size image

Furthermore, there was no significant correlation between the calibration parameters (see SI Fig. 3), which indicates that the calibration parameters were well chosen and independent. If there were high correlations between the calibration parameters, they would contain redundant information and the variation in one parameter could be compensated by a change of another parameter. In such a case, calibration would be restricted to determining the ratios between the parameters.

Simulated bed level changes

Figure 8 shows the cumulative bed level changes and water depth in the Banja reservoir after the end of the three-year simulation period with the calibration parameters for the VALDOME scenario listed in Table 3. In the region near the Devoll River tributary, the water became shallow and several channels formed. The highest deposits of more than 4 m occurred in the upstream part of the reservoir. At low water levels, some of the deposited sediment in the upstream part of the reservoir was eroded, resulting in the formation of smaller channels. These channels did not occur in permanently impounded regions (shown in dark blue). The sediment deposit height decreased in flow direction because of the decreasing flow velocity and the continuous settling of sediment particles. In the reservoir, the deposition heights in flow direction were less than 4 m after 2.4 km, less than 1.5 m after 4.6 km, and less than 0.5 m after 8.0 km.

Fig. 8
figure 8

Cumulative bed level changes (left) and water depth (right) after the end of the simulation period of the VALDOME scenario

Full size image

Model accuracy

Agreement between GPE metamodel and numerical model

Since the final calibration parameters stem from the metamodel, we performed two analyses to evaluate the calibration quality. First, we compared the metamodel with the 2d hydro-morphodynamic model to quantify how well the metamodel mimics the full-complexity model results. Second, we compared the calibrated numerical model with the measurement data to evaluate the final model quality.

To evaluate the quality of the metamodel results, the numerical model was run with the optimal calibration parameter combinations shown in Table 3. The inclusion of all calibration nodes (MAXME) led to a Pearson’s correlation \(r\) of 0.92, an RMSE of 0.87 m, and a mean absolute error (MAE) of 0.45 m (Fig. 9). Hence, the metamodel reproduced the numerical model results with good accuracy. However, the metamodel significantly overestimated bed level changes for some calibration nodes in the upstream part near the Devoll River tributary. Excluding these upstream nodes (VALDOME) resulted in a significantly better \(r\) of 0.98, an RMSE of 0.32, and an MAE of only 0.13 m. Therefore, the trained metamodel accurately emulated the full-complexity numerical model results at the end of the simulation period.

Fig. 9
figure 9

Scatter plot of the computed bed level changes \(\varDelta z\) from the metamodel and the numerical model after the MAXME scenario at the left and VALDOME scenario at the right. The dashed line represents the hypothetic perfect metamodel accuracy

Full size image

To assess the regions of high uncertainty in the metamodel, we calculated the LOO-CV errors for the 142 calibration nodes and the 70 parameter combinations used as training points. We averaged the absolute values of the differences for each point to estimate the expected error between the metamodel and the full-complexity model. This analysis is important because a high model metamodel error causes decreased influence of the difference between the measured and modeled bed level on the likelihood (Eq. 5). Therefore, calibration nodes with a large LOO-CV error indicate high uncertainty in the metamodel and carry less weight in the final likelihood calculation. The LOO-CV mean errors for the MAXME scenario ranged from 0.04 to 4.04 m (0.8 m on average). The highest errors occurred near the upstream boundary, which is also shown in SI Fig. 4. In contrast, the LOO-CV errors for the VALDOME were significantly smaller and ranged from 0.03 to 1.76 m (0.35 m on average).

Modeled and measured agreement

To evaluate the quality of the calibrated hydro-morphodynamic numerical model, we calculated Pearson’s \(r\) and the RMSE for both scenarios. The MAXME scenario led to an \(r\) of 0.70, RMSE of 1.62 m, and MAE of 1.17 m. The VALDOME scenario yielded a similar \(r\) of 0.66, a smaller RMSE of 1.04, and a smaller MAE of 0.91 m. Thus, both scenarios yielded satisfactory agreement between the measured and modeled results according to global statistics indicating a good representation of the sedimentation patterns in the Banja reservoir (see Fig. 10). Still, the MAE and RSME were not negligible but significantly lower in the VALDOME scenario. In the MAXME scenario, there were 11 calibration nodes with bed level change errors greater than 2 m compared to only three such nodes in the VALDOME scenario (see SI Fig. 5). In addition, Fig. 10 indicated that the numerical model tends to underestimate small measured bed level changes by approximately 1 m in both scenarios.

Fig. 10
figure 10

Scatter plot of modeled and simulated bed level changes \(\varDelta z\) for the MAXME scenario at the left and VALDOME scenario at the right. The dashed line represents the hypothetic perfect model accuracy

Full size image

Discussion

Deposition patterns and model deviations

Figure 11 shows the results of the bed level evolution in the upstream part of the reservoir after three years and for two simulations with similar parameter combinations. The figure shows several channels with high topographic gradients at different locations. Thick sediment deposits occurred next to these channels, particularly at mesh nodes that were only temporarily wet in the simulation period. These nodes can be inside a channel (small sediment deposits) in one model run and outside the channel (thick sediment deposits) in the next model run. Although the physical model environment is similar, the patterns in Fig. 11a and b are very different, which indicates numerical instabilities that the metamodel attempted to emulate by drastically changing the calibration parameter values (see Fig. 5).

The coarse mesh used in this study (to reduce computing time) affected the accuracy of the results and numerical stability. In addition, the model only considered suspended sediment transport and was not able to reproduce shallow water regions experiencing channel erosion, deltaic avulsion, or bank failures. The simplification assumptions made the model physically not fully well defined for simulating morphological processes at the head of the reservoir. In the MAXME scenario, the BAL iterations attempted to overcome mismatches between measured and modeled erosion channels by prominent changes in the calibration parameter values, indicating equifinality. As a result, the BAL iterations were unstable and did not converge. This is reflected in the higher fluctuations of the calibration parameters (Fig. 5) and maximum likelihoods near the limit of the investigated range for three of the four calibration parameters in the MAXME scenario. In addition, the BME (Fig. 4) did not converge because every BAL iteration tried to explore numerical instability in the delta region. Yet, the adapted Bayesian calibration worked well in the model domain where suspended sediment deposition could be reproduced and the model was stable (VALDOME). The BAL converged toward a solution that is confirmed by a very low RMSE of 0.32 m and a high Pearson’s \(r\) of 0.98 between the full-complexity and the metamodel. However, the RMSE of 1.04 m of the numerical model regarding measured data was significantly smaller compared to the MAXME scenario but not negligible, which is due to the limitations of the modeling approach. For instance, complex three-dimensional hydrodynamics and stratified flow cannot be represented by a 2d model, which is expected to affect the deposition pattern in the reservoir. Also, we assumed a constant \({\rho }_{b}\) for the entire reservoir, while consolidation occurs over time and the density increases (Mehta et al. 1989; Winterwerp and Kesteren 2004; Lo et al. 2014; Hoffmann et al. 2017). Accordingly, the average bulk density in a reservoir is often heterogeneous and varies over time, which is not reflected in our model assumptions. In addition, some boundary conditions were not measured directly, and therefore, subject to additional uncertainty. For example, the inflow into the reservoir was calculated from measured outflow, reservoir water levels, and hydrological model outputs. Also, the sediment yields of the tributaries stem from a model with monthly resolution only (Mouris et al. 2022). Considering the uncertainty related to these model simplifications, as well as the mean measurement error of approximately 0.4 m, the final model quality is acceptable in the VALDOME scenario. In light of the instability of the MAXME scenario, we verify the hypothesis (i) that Bayesian calibration only converges toward physically meaningful model parameter combinations when the model is well-conditioned (i.e., measured data are in the validity domain of model assumptions).

Fig. 11
figure 11

Simulated bed level changes (2016–2019) in the upstream part of the reservoir for two different simulations with similar calibration parameters at the end of the simulation period

Full size image

Relevant calibration parameters

Since the Bayesian calibration only converges toward physically meaningful model parameter combinations when the calibration nodes are in the range of validity of the numerical model, we only used the VALDOME scenario to identify the calibration parameter importance for reservoir sedimentation modeling.

Figure 6 shows that the density \({\rho }_{b}\) was the most restrictive (i.e., constraining) calibration parameter due to its narrow-shaped posterior distribution, which was not imposed by the initial value ranges (Table 2). This is also evident in the clear data pattern of \({\rho }_{b}\) across the parameter space (Fig. 7), where high likelihoods occurred only in a very narrow range. Yet, many studies exclude \({\rho }_{b}\) from the calibration process and use fixed literature values or empirical equations to obtain a representative value (Foster and Charlesworth 1994; Verstraeten and Poesen 2001; Banasik et al. 2021). Our findings suggest that \({\rho }_{b}\) should be either calibrated or directly measured, rather than simply derived from the literature. This finding is important because, for instance, models for calculating the sediment yield are often calibrated against the volume change in lakes or reservoirs. Since the volume of the deposited sediments is directly related to the dry-bulk density of the sediments, an incorrect value for \({\rho }_{b}\) results in an incorrect calculation of sediment masses. For example, if the sediment inflow is underestimated, the error can be compensated for by a lower dry-bulk density for the deposited sediment. In this study, the Bayesian calibration led to a reasonable value of 403.6 kg m-3 in the VALDOME scenario (van Rijn and Barth 2019; van Rijn 2020).

According to the posterior distribution (see Fig. 6), \({\tau }_{d}\) was the second most restrictive (i.e., constraining) parameter with a small maximum likelihood of 0.01 Pa. Yet, the maximum likelihood was located at the lower limit of the investigated range, which suggests that the Bayesian calibration would have tried an even smaller \({\tau }_{d}\) if possible. Hence, the posterior distribution should be interpreted carefully, as a broader range may result in a wider distribution. A possible explanation for why the Bayesian calibration preferred small values of \({\tau }_{d}\) is the maximization of suspended load trajectories. Since fine particles are kept in suspension by turbulence even at low flow velocities, the BAL attempted to compensate for the insufficient model assumptions regarding 3d turbulence (mixing length model) by decreasing \({\tau }_{d}\). Furthermore, the actual shear stresses in a large reservoir are very small. Thus, only very small \({\tau }_{d}\) values affect the deposition process in the numerical model, especially since we disregarded measured data in the shallow delta region in the VALDOME scenario.

The calibrated diameter multiplier \(\gamma\) was 0.98, which falls into the lower half of the initial range. \(\gamma\) was not very restrictive and yielded high likelihoods for a comparatively wide range with \(\gamma\) < 1.2. These small \(\gamma\) values indicate that the observed particle size diameters and the corresponding settling velocities were rather too large and smaller particle sizes and settling velocities lead to better results. Generally, the grain size distribution of a suspended sediment load sample represents the present hydraulic conditions. Therefore, we recommend using grain sizes in a reasonable range for calibration or varying the grain size distributions as a function of discharge. The stochastic approach led to representative grain size ranges: d17 = 1.89 to 2.25 μm, d50 = 7.0 to 8.33 μm, and d83 = 19.76 to 23.62 μm. However, flocculation processes can alter the settling velocity of cohesive particles (Dyer and Manning 1999; Winterwerp and Kesteren 2004), and therefore, the actual grain sizes of individual particles can be even smaller.

The optimum \({\tau }_{cr}\) was 0.25 (VALDOME) and the corresponding likelihood pattern was not very pronounced and had little impact on the calibration process, because only the very upstream calibration nodes were affected by erosion and resuspension. In contrast to a free-flowing river, sedimentation dominates in the reservoir due to the large water depths and low flow velocities. Thus, there were significant differences between the two sets of calibration nodes, underlining that particularly the upstream delta section of the reservoir was controlled by \({\tau }_{cr}\). Hence, the RE further decreased with the exclusion of the calibration nodes in the upstream part (VALDOME), which emphasizes the diminishing importance and higher uncertainty of \({\tau }_{cr}\).

Ultimately, we verify hypothesis (ii) since the Bayesian calibration identified \({\rho }_{b}\) as the driving calibration parameter in the fluvial deposition of suspended sediments in reservoirs. In contrast, \(\gamma\) or \({\tau }_{cr}\) had significantly less influence on the final sedimentation pattern. Parameters with narrow posterior distributions and high relative entropy compared to a uniform distribution can be interpreted as driving and restrictive, while parameters with wide posterior distributions can be interpreted as less important and uncertain. The narrow posterior distribution for \({\tau }_{d}\) suggests a high information gain through BAL, with the maximum likelihood at the lower limit. Consequently, small \({\tau }_{d}\) lead to more accurate results, although the importance of \({\tau }_{d}\) cannot be objectively assessed.

The curse of dimensionality

The so-called curse of dimensionality (see also the methods section on Bayesian calibration) forced us to limit the number of calibration nodes. Even though we limited the number of calibration nodes, the dimensions of the response surface were still too high and both scenarios were subjected to the curse of dimensionality. This phenomenon occurred because of the exponential term of the likelihood function (Eq. (5)), which represents the (negative) weighted sum of the squared difference between the measured and modeled bed level change. The more calibration nodes we used, the larger the negative value of the sum becomes. In consequence, the exponential term became a number so close to zero that the precision of a computer is insufficient to express it. This problem, known as arithmetic underflow (e.g., Coonen 1980), caused the likelihood function to become zero, which does not allow for the calculation of convergence scores and selection of a next training point. To solve this problem, we artificially increased the total error in Eq. (7) by multiplying it by 5. The artificial error amplification was equally applied to all individual errors and represented the smallest integer amplification factor that avoided arithmetic underflow. Since the amplification factor was constant, the rank of the output realization remained unchanged.

The curse of dimensionality also affected the number of Monte Carlo (MC) samples that could be drawn to approximate the posterior distribution in Eq. (5). With increasing dimensionality, the required computing power for a representative sample increased exponentially. In consequence, the region with the highest density became more restrictive and the vast majority of the probability density function was concentrated in low-likelihood areas. To balance representativeness, the curse of dimensionality, and computing time, we limited the sample size to 105 MC realizations.

The curse of dimensionality also affects the generation of the posterior distribution through rejection sampling (Smith and Gelfand 1992) or the here-used Bayesian weighting strategy, as most of the samples were concentrated in low-likelihood areas. Thus, the weight of nearby all samples was close to zero or arithmetic underflow occurred. The above-introduced error multiplier helped to avoid these arithmetic underflow issues by increasing the width of the high-likelihood region and enabling a representative posterior.

Conclusion

The region where the model simplifications were not entirely valid caused stability issues in the upstream part of the reservoir, where small channels with low water depths led to high topographic gradients and large model uncertainty. Hence, the inclusion of all calibration nodes resulted in a degradation of model accuracy, fluctuating Bayesian model evidence, and higher variability of the four calibration parameters in the last five BAL iterations. In addition, the maximum likelihood values of the calibration parameters were located near the limit of the investigated range. Consequently, Bayesian calibration only converged toward physically meaningful parameter combinations when the model was well-conditioned (i.e., when the measurement data are in physically representative regions of the model domain). The final model quality was still affected by the limitations of the 2d numerical model, leading to a considerable mean absolute error of approx. 1 m regarding the modeled deposition height.

Bayesian calibration identified the dry-bulk density as the driving and most important parameter to simulate the fluvial deposition of suspended sediments in reservoirs. Thus, the dry-bulk density should be prioritized in data collection, already before setting up a reservoir sedimentation model. In contrast, the particle diameter multiplier and the critical shear stress for erosion had less influence on the deposition pattern as can be seen from the wider posterior distribution. The importance of the critical shear stress for deposition could not be objectively assessed because the maximum likelihood is located at the lower limit of the initial range. Yet, small values led to better results because the BAL tried to maximize suspended load trajectories to compensate for insufficient model assumptions about 3d turbulence that keeps fine particles in suspension.

Ultimately, this study shows that a robust Bayesian calibration can also be achieved when global model simplification hypotheses cannot be applied to the entire model domain, requiring that the measurement data for calibration must be from model domains where the simplifying assumptions are valid. Furthermore, our modified BAL approach accounted for both measurement and metamodel errors, enabling a multi-parametric comparison and identification of driving calibration parameters even in four-dimensional parameter space.