Stability analysis of periodic traveling waves in a model of vegetation patterns in semi-arid ecosystems

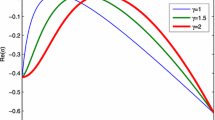
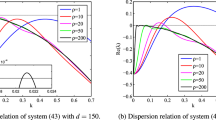
Abstract

Banded vegetation pattern is a striking feature of self-organized ecosystems. In particular, vegetation patterns in semi-arid ecosystems are typical on hillsides, orienting parallel to the contours. The present study concerns a system of coupled reaction–advection–diffusion equations model for this phenomenon and studies the existence and stability of periodic traveling waves in a one-parameter family of solutions. Specifically, we consider a parameter region in which vegetation patterns occur and subdivide into stable and unstable regions as solutions of the model equations. Our numerical results show that the periodic traveling wave changes their stability by Eckhaus (sideband) bifurcation. We discuss the variations of the wavelength, wave speed as well as the conditions of the rainfall parameter by using linear analysis. We also explore how the solution patterns grow when the bifurcation parameter is changing slowly. In order to compare this result with the spatiotemporal pattern in the direct simulation, we show that when it passes a critical value of rainfall parameter a stable pattern becomes unstable and finally disappear. In addition, we investigate the existence and stability of periodic traveling waves as a function of water transport parameter.

Appendix A

Mathematical review and methods of computation

Vegetation stripes that slowly migrate in the uphill direction mean that they are PTWs. We study PTWs via the ansatz $u(x, t) = U(z)$, $w(x, t) = W(z)$, where the traveling wave coordinate $z = x - {\mathbf {c}}t$, x and t are the one-dimensional space and time coordinates respectively and ${\mathbf {c}}$ represents the speed of the wave. Substituting these into Eq. (1), we obtain the second order Ordinary Differential Equations (ODEs) as follows:

$$\begin{aligned} \begin{aligned}&\frac{\text {d}^2U}{\text {d}z^2} + {\mathbf {c}} \frac{\text {d}U}{\text {d}z} + WU^2 - BU = 0,\\&d_w\frac{\text {d}^2W}{\text {d}z^2} + (\nu +{\mathbf {c}}) \frac{\text {d}W}{\text {d}z} + A - W - WU^2 = 0. \end{aligned} \end{aligned}$$

(2)

Reducing Eq. (2) to first order ODE system is given as follows:

$$\begin{aligned} \begin{aligned} \frac{\text {d}U}{\text {d}z}&= M, \\ \frac{\text {d}M}{\text {d}z}&= \frac{\text {d}^2U}{\text {d}z^2} = -{\mathbf {c}}M + BU - WU^2, \\ \frac{\text {d}W}{\text {d}}&= N, \\ \frac{\text {d}N}{\text {d}z}&= \frac{\text {d}^2W}{\text {d}z^2} = \frac{-({\mathbf {c}} + \nu )N -A + W + WU^2}{d_{w}}. \end{aligned} \end{aligned}$$

(3)

A PTW is a limit cycle (periodic) solution of Eq. (3). In general, the solution of Eq. (3) has a solution branch initiating from the point of Hopf bifurcation and also be a monotonic function of parameters. In addition, the limit cycle is typically unstable as an ODE solution in the both positive and negative z directions, meaning that it cannot be calculated by direct numerical integration of the ODEs. Using numerical calculation via solution branch, we calculate the PTW initiating from the Hopf bifurcation point (Sherratt 2012) and continue the branch of periodic orbit until the required value of control parameter is reached. Thus, extensions of this approach enables us to calculate the regions of parameter space in which PTWs exist. In order to study the PTWs that typically born from a Hopf bifurcation point of the traveling wave equations, we need a single formula to define a steady state solution for each traveling wave variable, which is to be valid for all values of the control parameter. The steady states can be found by solving R.H.S of Eq. (3) equal to zero. Corresponding to spatially homogeneous perturbations of the model (Eq. 1), the model has one or three steady sates. The steady states of the system are: (i) bare desert state, $U_b = 0, W_b = A$, which is linearly stable and always exits; (ii and iii) two nontrivial steady states arising from saddle-node bifurcation and these are given as follows:

$$\begin{aligned} U = U_{+}\equiv \frac{2B}{A+\sqrt{A^2 -4B^2}}, W = W_{+}\equiv \frac{A+\sqrt{A^2 -4B^2}}{2}, \end{aligned}$$

(4)

and

$$\begin{aligned} U = U_{-}\equiv \frac{2B}{A-\sqrt{A^2 -4B^2}}, W = W_{-}\equiv \frac{A-\sqrt{A^2 -4B^2}}{2}. \end{aligned}$$

(5)

We consider that $A > 2B$, the required condition for spatial pattering (Sherratt 2005), for the coexistence of $(U_{+}, W_{+})$ and $(U_{-}, W_{-})$. $(U_{+}, W_{+})$ is always unstable to spatially homogeneous perturbations and the other $(U_{-}, W_{-})$ is locally stable for ecologically relevant parameters (Klausmeier 1999; Sherratt 2005). For realistic assumption for semi-arid environments, we logically consider these restriction throughout this paper.

In general, investigating the existence of PTW solutions is not enough in application, we need to know the stability of the PTWs (Sherratt and Smith 2008; Deconinck and Kutz 2006). Correspondingly, we linearize about the traveling wave solution to investigate the stability of the PTWs. Therefore, neglecting the higher order terms, (Eq. 1) becomes

$$\begin{aligned} \begin{aligned} \frac{\partial u_{\text {lin}}}{\partial t}&= \frac{\partial ^2 u_{\text {lin}}}{\partial x^2} + u_{\text {lin}}(-B + 2WU) + w_{\text {lin}}U^2, \\ \frac{\partial w_{\text {lin}}}{\partial t}&= d_w \frac{\partial ^2 w_{\text {lin}}}{\partial x^2} + \nu \frac{\partial w_{\text {lin}}}{\partial x} + u_{\text {lin}}(-2UW) + w_{\text {lin}}(-1-U^2), \end{aligned} \end{aligned}$$

(6)

where $u_{\text {lin}} (x,t)=u(x,t) - U(z)$ and $w_{\text {lin}} (x,t) = w(x,t) - W(z)$. Now, substituting $u_{\text {lin}} (x,t)=e^{\lambda t} U_{\text {lin}} (z)$ and $w_{\text {lin}} (x,t) = e^{\lambda t} W_{\text {lin}} (z)$ in Eq. (6), we get the following eigenvalue problem:

$$\begin{aligned} \begin{aligned} \lambda U_{\text {lin}}&= \frac{\text {d}^2 U_{lin}}{\text {d} x^2} + {\mathbf {c}} \frac{\text {d} U_{\text {lin}}}{\text {d} x} + U_{\text {lin}}(-B + 2WU) + W_{\text {lin}}U^2,\\ \lambda W_{\text {lin}}&= d_w \frac{\text {d}^2 W_{\text {lin}}}{\text {d} x^2} + ({\mathbf {c}}+ \nu ) \frac{\text {d} W_{\text {lin}}}{\text {d} x}\\&\quad + U_{\text {lin}}(-2UW)+ W_{\text {lin}}(-1-U^2), \end{aligned} \end{aligned}$$

(7)

with the boundary conditions, using Floquet theory (Rademacher et al. 2007),

$$\begin{aligned} \begin{aligned} U_{\text {lin}}(L)&= U_{\text {lin}}(0) \exp {i \gamma }, \\ W_{\text {lin}}(L)&= W_{\text {lin}}(0) \exp {i \gamma }, \text {for some } \gamma \in {\mathbb {R}}, \end{aligned} \end{aligned}$$

(8)

where L is the period of the PTW, $\gamma$ denotes the phase shift across one period of the wave, ${\mathbf {U}_{\text {lin}}}$ represents the eigenfunction, and $\lambda$ is the eigenvalue. In order to make the boundary conditions regular and rescale L to unity, it is required to use a transformation, namely Bloch transformation (Rademacher et al. 2007). Then, one can solve the above problem numerically. Hence, the eigenvalue Eq. (7) can be reduced to the first order ODE system as follows:

$$\begin{aligned} \begin{aligned} \frac{\text {d}U_{\text {lin}}}{\text {d}z}&= M_{\text {lin}}, \\ \frac{\text {d}M_{\text {lin}}}{\text {d}z}&= \frac{\text {d}^2 U_{\text {lin}}}{\text {d}z^2} = \lambda U_{{\text {lin}}}-cM_{\text {lin}}\\&\quad -U_{\text {lin}} (-B+2UW)-W_{\text {lin}} U^2, \\ \frac{\text {d}W_{\text {lin}}}{\text {d}z}&= N_{\text {lin}}, \\ \frac{\text {d}N_{\text {lin}}}{\text {d}z}&= \frac{\text {d}^2 W_{\text {lin}}}{\text {d}z^2}\\&= \frac{\lambda W_{\text {lin}\text {lin}}-(c+\nu )N_{\text {lin}}-U_{\text {lin}} (-2UW)-W_{\text {lin}} (-1-U)^2)}{d_{w}}. \end{aligned} \end{aligned}$$

(9)

This implies,

$$\begin{aligned} \frac{\text {d}}{\text {d}z} \begin{bmatrix} U_{\text {lin}} \\ M_{\text {lin}} \\ W_{\text {lin}} \\ N_{\text {lin}} \\ \end{bmatrix} = (C(z) + \lambda D) \begin{bmatrix} U_{\text {lin}} \\ M_{\text {lin}} \\ W_{\text {lin}} \\ N_{\text {lin}} \\ \end{bmatrix}, \end{aligned}$$

where C and D are the $4\times 4$ matrices given by

$$\begin{aligned} C = \begin{bmatrix} 0 &{} 1&{} 0&{} 0 \\ B-2UW &{} -{\mathbf {c}} &{} -U^2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 2UW/d_w &{} 0 &{} (1+U^2 )/d_w &{} -({\mathbf {c}}+\nu )/d_w ) \end{bmatrix}, \end{aligned}$$

(10)

and

$$\begin{aligned} D = \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1/d_w &{}0 \end{bmatrix}. \end{aligned}$$

(11)

For $\gamma = 0$, one can solve Eqs. (7) and (8) using standard numerical method (De Boor and Swartz 1980; Chatelin 1981). However, for $\gamma \ne 0$, one cannot reduce (Eqs. 7 and 8) to matrix eigenvalue problem and can be solved by numerical continuation method for the difference phase of $\gamma$ (Sherratt 2012). To perform a continuous numerical calculation over $0< \gamma < 2 \pi$, one might calculate matrix eigenvalues and eigenfunction for $\gamma = 0$ as initial data. The continuation procedure of this implementation require some additional settings, e.g., set orthogonality conditions, ensuring the normalization of integral constraints in the eigenfunctions etc., full details are given in Rademacher et al. (2007). WAVETRAIN (Sherratt 2012; Rademacher et al. 2007; Sherratt 2013a), a package of numerical continuation, take care of this problem to solve (Eqs. (7), (8)). Moreover, for the direct PDE simulation, we restrict the numerical simulations in one dimension and use an implicit finite difference scheme with periodic boundary conditions