Introduction

Urmia Lake (UL) is one of the most significant lakes in Iran and the second largest salt lake in the world (Karbassi et al. 2010). Since 1967 it has been considered as a wetland protected region, in 1971 the Ramsar convention declared it as an important international wetland, and in 1976 it designated as a UNESCO biosphere reserve (Fathian et al. 2014a; Vaheddoost and Aksoy 2016). The region’s industrial and agricultural sectors have been jeopardized and the vibrant and vivid lake has experienced underwater buried salt exposure due to the water level decline in recent years (Eimanifar and Mohebbi 2007; Fathian et al. 2014b). The persistence of the declining trend of water level in UL due to various reasons allows the exposed salt to blow away, causing a serious threat to the health of the inhabitants of the region, and has reached the level of a national concern (Hassanzadeh et al. 2012).

Undoubtedly, studies on water level fluctuations are important for planning, design, construction and operation of lake shore structures, testing the impacts of the natural climate fluctuation or human induced climate changes on lake hydrology, and also in modeling water levels to use those for quantitative interpretation (Çimen and Kisi 2009; Kakahaji et al. 2013). Furthermore, various studies have been done in modeling and statistical analysis of water level fluctuations in different lakes over the world, specifically for UL of Iran (See Jones et al. 2001; Kebede et al. 2006; Çimen and Kisi 2009; Yin and Yang 2012; Kavehkar et al. 2011; Kakahaji et al. 2013). Modeling water level series of UL, as a continuing worry in water resources management and hydrological researches, can help in reducing the damages (Kebede et al. 2006; Fathian et al. 2014a). Therefore, it is necessary to build and develop a suitable model for simulating water level changes.

A direct method for calculating water level values is to build a complicated model involving the hydroclimatic variables; however, modeling water level series on the basis of past levels is an economically preferable technique. In this regard, time series analysis methods are applied and developed for finding out temporal pattern of water levels (Çimen and Kisi 2009; Aksoy et al. 2013). Application of linear time series models for simulation and forecasting hydrological time series, which were described by Box and Jenkins (1976) for the use of practicing engineers, has received many attentions during recent decades (Modarres and Ouarda 2012a, b). Among these linear models, the Seasonal Autoregressive Integrated Moving Average (SARIMA) linear model is a common applied model. However, linear models are not capable of capturing an important part of hydrologic fluctuation, e.g. nonlinear variation. In this case, the application of the Generalized Autoregressive Conditional Heteroscedasticity (GARCH) nonlinear approach has been recently growing in modeling time-dependent variance of hydrological time series. Several studies have been carried out to apply both linear and nonlinear models for hydrological and climatic variables such as temperature (Romilly 2005; Modarres and Ouarda 2014), rainfall (Modarres and Ouarda 2012a), streamflow (Wang et al. 2006; Chen et al. 2008; Modarres and Ouarda 2012b) and drought (Modarres and Ouarda 2014). Not only the application of GARCH model in hydrology is rare but also water level fluctuations of lake are a missing variable in nonlinear time series modeling.

This study is carried out to build and develop the linear and nonlinear time series models to capture monthly UL water level series during 1966–2012. In this regard, water level modeling in the existence of trend will be also developed. In addition, the linearity and nonlinearity of this series will be investigated. Therefore, the objectives of this study are (1) to identify the changes in the statistical characteristics in terms of trend, stationarity, linearity/nonlinearity and change point detection analyses; (2) develop linear and nonlinear models for the seasonal variations by considering mono- and multiple-time trend (Mono- and Multiple-TT) models to remove the trend behavior in that series; (3) present the useful/harmful effects of the GARCH model for modeling the UL water level series. As it is seen from the literature review, this is the first study of its kind investigating these statistical models for great lake water level, specifically for UL of Iran.

Study area and data

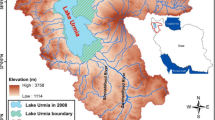
UL is located in the northwestern territory, inside the Urmia Lake Basin, of Iran, and extends as much as 140 km from north to south and is as wide as 85 km east to west during high water periods (Vaheddoost et al. 2015). Urmia Lake Basin is shared between three provinces of West Azerbaijan, East Azerbaijan, and Kurdistan of Iran. It is located between 44°07′ and 47°53′ North longitudes and 35°40′ and 38°30′ East latitudes and can be classified as a semi-arid (cold) climate region (Vaheddoost and Aksoy 2016). The lake’s surface area has been estimated to have been as large as 6100 km2, but since 1995 it has generally been declining; in August of 2011, it was estimated from satellite data to be only 2366 km2 (Eimanifar and Mohebbi 2007). The drainage area of the lake is 51,800 km2. The lake basin includes 14 main subbasins that surround the lake, and the ZarrinehRoud, SiminehRoud and Aji Chai (Fig. 1) are the most important rivers of the basin (Fathian et al. 2014b). These rivers are the source of the majority of the Lake’s expected annual water intake, and additional input comes from rainfall directly over the lake, floodwater from the immediate watershed and a very small fraction from groundwater flow (Eimanifar and Mohebbi 2007). For UL, the monthly average water level data during the period of 1966–2012 (47 years, i.e. 564 monthly levels) is used in this study.

Fig. 1
figure 1

Location of UL basin and hydroclimatic stations into basin

Full size image

The monthly water level series is illustrated in Fig. 2a. As it can be seen, the water level had a gradually upward trend in the late 1960 s, after which it maintained an almost constant level, and subsequently a gradual upward jump was observed in the 1990s to reach its maximum level. After that, at the end of the water level series, a sudden decline is recorded and this downward trend is continuously observed. Minimum and maximum observed values of water level series were 1270.98 and 1278.39 m during the period of 1966–2012, respectively. The mean and standard deviation (sd) behaviors of water level series for all months (Fig. 2b) display that the water level behavior increase in the early winter, continuously increases until spring, decrease in summer and then stay almost constant in autumn. Notably, when the mean water level increases, the standard deviation of the water level also increases from January to June. This can be due to the great deal of variability in hydroclimatic variables, such as precipitation, snowmelt and temperature fluctuations during this time period.

Fig. 2
figure 2

a Monthly average water level time series, b monthly distribution of UL water level mean and standard deviation for 1966–2012 period

Full size image

Methods

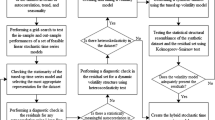
Testing procedures

Trend assessment and change point detection

The dependence of an observed value to the past observed values and the stationarity of the statistical moments through time are as two key assumptions of the SARIMA models. Therefore, it is unavoidable to examine monthly water level series in terms of a trend or nonstationarity behavior before applying the SARIMA model (Modarres et al. 2012). The nonparametric Mann–Kendall (MK) test is applied to explore the nonstationarity behavior in water level series. To find significant change point for the water level series, the nonparametric Pettitt’s test (Fathian et al. 2014a), which is less sensitive to outliers, as well as segmentation software called AUG-SEGMENTER (Gedikli et al. 2010; Aksoy et al. 2013), which introduced as a user-friendly tool for segmentation of long time series, have been used. A change point presents an abrupt change (or a sudden change) in the statistics of the trend. (Rybski and Neumann 2011).

Testing for equality

In the presence of trend in water level series, two nonparametric tests are applied to examine the change in the mean and the standard deviation values before and after the detected change point (Modarres et al. 2012). These tests are including the Wilcoxon rank sum test and the Levene’s test for the equality of the mean and the standard deviation, respectively (Levene 1960; McCuen 2003). The comparison of the water level statistical parameters before and after the change point will provide the opportunity to examine the temporal trend in the future and to apply this analysis before trend analysis in order to avoid misleading results (Villarini et al. 2009).

Testing for stationarity and nonlinearity

To test the change in stationarity and nonlinearity of the water levels and its heteroscedasticity, two tests are employed namely, the Augmented Dickey Fuller (ADF) test (Dickey and Fuller 1979) for stationarity and the Brock–Dechert–Scheinkman (BDS) test (Brock et al. 1996) for nonlinearity. The ADF test is to test the presence of a unit root in the series based on considering an autoregressive AR(1) model. If the autoregressive parameter is equal to one, the process is considered nonstationarity. Otherwise, the process is stationary. The BDS test is useful to detect deterministic chaos based on the correlation integral of the time series, and presents the time series dynamic by testing the serial independence and temporal correlation (Wang et al. 2006). These two tests are applied to compare the water levels before and after the change point. For details of the formulations of these tests see Wang (2006).

SARIMA model

The SARIMA model is used to build a model of seasonal time series, which the seasonality is as a general element of monthly variation of UL water level. The general multiplicative form of a SARIMA model is written as SARIMA (p,d,q) × (P,D,Q), where p, d and q are the order of nonseasonal and P, D and Q are the order of seasonal parameters (Modarres and Ouarda 2012a). The mathematical formulation of this model can be written as follows:

$$\phi_{p} (B)\varPhi_{P} (B^{S} )\nabla^{d} \nabla_{S}^{D} Y_{t} = \theta_{q} (B)\varTheta_{Q} (B^{S} )\omega_{t} ,$$
(1)

where \(\omega_{t}\) is the usual Gaussian white noise process. \(Y_{t}\) is the observed time series, the ordinary autoregressive and moving average components are represented by polynomials \(\phi_{p} (B)\) and \(\theta_{q} (B)\) of order p and q, respectively, and the seasonal autoregressive and moving average components by \(\varPhi_{P}\) and \(\varTheta_{Q}\) of orders P and Q, and ordinary and seasonal difference components by \(\nabla^{d}\) and \(\nabla_{S}^{D}\). B is the backward operator and S represents the number of seasons per year (Hipel and McLeod 1996).

For modeling the monthly water level series by SARIMA model, first step is to select the order value of the SARIMA model parameters with the help of the autocorrelation function (ACF) and Partial ACF (PACF) of the observed series. Then, the parameters of the selected model are estimated and should be significant at a specified significance level (Modarres et al. 2012). In order to check the acceptable fitted SARIMA model, the ACF of the obtained residual series by fitted model is first examined. The adequacy of the fitted SARIMA model is accepted if all coefficients of the ACF locate within the confidence intervals. In addition, the Ljung–Box test is also used to examine the ACF structure of the residual series (Modarres and Ouarda 2012a). This test calculates a statistics Q, which is distributed as Chi square with (L–p–q) degrees of freedom and as below form (Ljung and Box 1978):

$$Q = N(N + 2)\sum\limits_{k = 1}^{L} {(N - K)^{ - 1} r_{k}^{2} (\omega )} ,$$
(2)

where N is the sample size, L is the number of autocorrelation of the residuals between 15 and 25, and \(r_{k}\) is the ACF of the residuals, ω, at lag k. If the calculated Q-statistic is less than tabulated value at a significance level, it means that the residual series are uncorrelated, and then the fitted model is acceptable (Hipel and McLeod 1996).

Given the existence of a significant trend in a water level series, the trend behavior is first removed using two mono- and multiple-trend regression models between water level and time. Then, the SARIMA model is fitted to the residuals of two time trend models, which are now trend-free time series (Modarres et al. 2012). Therefore, it can be modeled the deterministic component of the monthly water level series using two Mono- and Multiple-TT models, and the stochastic component using a SARIMA model (Aksoy et al. 2013). The performances of the SARIMA and TT-SARIMA in comparison with observation water levels are then examines.

Nonlinear modeling approach

When a SARIMA model is fitted to a seasonal time series, the calculated residuals from the fitted model may show adequate fitting. However, the squared residual series may show the significant autocorrelation in ACF structure of residuals. Therefore, heteroscedasticity behavior or conditional time-variant variance may be observed in the residual series. This behavior can be modeled by a GARCH approach, which is named a SARIMA-GARCH model (Modarres and Ouarda 2012a). The GARCH model, introduced by Bollerslev (1986), is defined as follows:

$$\sigma_{t}^{2} = \gamma + \sum\limits_{i = 1}^{V} {\alpha_{i} \omega_{t - i}^{2} } + \sum\limits_{j = 1}^{M} {\beta_{j} \sigma_{t - j}^{2} } ,$$
(3)
$$\omega_{t} = \sigma_{t} e_{t} \,\,\,\,\,\,\,e_{t} \sim Normal(0,1),$$
(4)

where \(\sigma_{t}^{2}\) is the conditional time-variant variance of the residual series, γ is a constant, and \(\alpha_{1} , \ldots ,\alpha_{V}\) and \(\beta_{1} , \ldots ,\beta_{M}\) are the coefficients of the GARCH (V,M) approach where V and M are the order of the coefficients (Wei 2006). In order to identify and check the existence of the heteroscedasticity in the residual series, Bollerslev (1986) presented the testing ACF of the standardized squared residuals (SSRs, hereinafter) could be helpful technique. In identifying and checking GARCH behavior for SSRs, the Ljung–Box test if the time-dependent variance exists can be applied. Similar Eq. (2), the Ljung–Box Q-statistic is calculated for SSRs series (ω 2) instead of residual series. The assumption of no GARCH effect (as null hypothesis) for the residual series is approved if the calculated Q-statistic is less than tabulated value at a significance level (Modarres and Ouarda 2012a, b).

Comparison approach

The performance of the different modeling methods applied for this research is examined by means of evaluation metrics set (Modarres and Ouarda 2012a, b). The used evaluation metrics are given by:

  1. 1.

    Root mean squared error (RMSE)

    $$RMSE = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {(Q_{i} - \hat{Q}_{i} )^{2} } }}{n}} .$$
    (5)
  2. 2.

    Relative absolute error

    $$RAE = \frac{{\sum\limits_{i = 1}^{n} {\left| {Q_{i} - \hat{Q}_{i} } \right|} }}{{\sum\limits_{i = 1}^{n} {\left| {Q_{i} - \bar{Q}} \right|} }}.$$
    (6)
  3. 3.

    Mean error

    $$ME = \frac{1}{n}\sum\limits_{i = 1}^{n} {(\hat{Q}_{i} - Q_{i} )} .$$
    (7)
  4. 4.

    Coefficient of determination (R-squared)

    $$R^{2} = \left[ {\frac{{\sum\limits_{i = 1}^{n} {(Q_{i} - \bar{Q})(\hat{Q}_{i} - \tilde{Q})} }}{{\sqrt {\sum\limits_{i = 1}^{n} {(Q_{i} - \bar{Q})}^{2} \sum\limits_{i = 1}^{n} {(\hat{Q}_{i} - \tilde{Q})}^{2} } }}} \right].$$
    (8)

According to the above equations, \(Q_{i}\) and \(\hat{Q}_{i}\) are the observed and estimated data, and \(\bar{Q}\) and \(\tilde{Q}\) are the mean of the observed and the estimated data, respectively.

Results and discussion

Change point and trend analysis of lake levels

Using the Pettitt’s test as well as AUG-SEGMENTER method, a change point in the UL water level series in 1999 was detected. By partitioning the time series based on the detected change point and fitting a regression line to each segment (Fig. 3), the water levels are divided into two segments, 1966–1999 and 2000–2012. This change point indicates a shift (also called a “jump”) in the trend detection of the water level series during the study period. As shown in Fig. 3, the decreasing mono-trend fitted to the whole time series can have different behavior when the multiple inner trend lines are taken for each segment (the green solid lines). For 1966–2012, the MK test indicates a downward trend (the MK test statistic is −0.313) for the water level at 1% significance level (the brown dash line). The MK trend test was also applied for first (1966–1999) and second (2000–2012) segments. The results showed a significant upward (downward) trend for first (second) subseries and their MK test statistic value is 0.268 (−0.853) for the water level. According to Fathian et al. (2014b), the results of trend detection after the common change point (2000–2010) showed that water levels experienced significant downward trends, while there are upward trends but not significant in all subseries before the detected change point. Confirmation of these results is obviously observable.

Fig. 3
figure 3

Illustration of change point detection for the water level time series (1966–2012). The solid green lines show the trend line to each segment (Multiple-trend line) in the water level data before and after 1999. The dashed brown line shows the trend line to the whole time series (Mono-trend line)

Full size image

Statistical comparison of the UL water levels

When considering 1999 as a change point in the UL water level series, the change in the descriptive statistics of the water level is first examined. It can be seen in Table 1 that the mean (unconditional) variance, skewness, and kurtosis values show remarkable change after 1999. The mean changed from 1276.06 to 1272.94. The (unconditional) variance increased from 0.89 to 1.45. Moreover, the distribution of the water level series has become less skewed and peaked. According to the study of Aksoy et al. (2013), this statistical information may be helpful in many cases and it is important when the inner trends may behave differently than the trends taken over the whole time series.

Table 1 Descriptive statistics of the water level time series
Full size table

Figure 4 shows the explanatory data analysis of the water level series before and after 1999. The normal histograms (Fig. 4a) and quantile–quantile plots (Fig. 4b) demonstrate a change in the upper and lower tails after 1999, where a downward monotonic trend is observed for the second period. The Jarque–Bera test for normality (results not shown) indicates that the normality assumption (as null hypothesis) cannot be rejected for the first and second periods at 5% significance level. The normality for the 1999–2012 cannot be rejected (p value = 0.160) while the normality is violated for the 1966–1999 (p value = 0.053) period at 10% significant level. This suggests that monotonic negative trend has a significant effect on the symmetry, or normality, of the water level frequency distribution in the second period.

Fig. 4
figure 4

Exploratory data analysis plot for the water level series: a normal histogram, b quantile–quantile plot, c ACF for water level, d ACF for squared water level

Full size image

The ACFs of the lake level series (Fig. 4c) and its squared series (Fig. 4d) show an observable change in the second period in comparison with first period, while there is no difference between the two ACFs in two figures. Consequently, Fig. 4d shows that the autocorrelation coefficients at most lag times (k) are higher for the second period than for the first period. This suggests that the time-varying variance or the conditional variance became stronger after 1999.

The statistical changes in the lake level data during whole period (1966–2012) are also examined by the Wilcoxon rank sum and Levene’s methods to test the validity of the explanatory analysis for the statistical features. The results of the two nonparametric tests showed that the mean value of water level points out a strong difference (significant at the 1% level) before and after 1999, and the change in the standard deviation is also significant according to the Levene test at the 1% level. According to the some previous studies, the UL water level decline in the two most recent decades has been caused by many factors (such as changes in hydroclimatic variables, human activities, etc.), which have resulted in many socioeconomic and ecological problems (Fathian et al. 2014a). Accordingly, the timing of trends in the study factors began in the 1990s, and generally there is a significant relationship among them (Hassanzadeh et al. 2012). The results of the analyses as presented in this section confirm the conclusion of this paper.

The stationarity and nonlinearity of the water level series before and after the change point are evaluated using the ADF and BDS tests. The results are presented in Table 2. The ADF statistics indicate that the water level series before and after the change point are nonstationary and it cannot be accepted the stationarity at the 10% or lower significance level. The less negative ADF statistic indicates a stronger acceptance of the hypothesis of a unit root. Therefore, one can see that the nonstationarity of the water level series for 1999–2012 is greater than that for 1966–1999. In addition, the results of the BDS test also demonstrate increasing nonlinearity after 1999. For all dimensions (m2–m5), the nonlinearity is significant for both periods, but the test statistics are greater for the second period, which implies the existence of a higher degree of nonlinearity in the water level series after 1999. The results obtained from this section show that the water level series have nonstationarity and nonlinearity behaviors, which can be appropriated to the existence of these behaviors in the hydroclimatic variables of the UL basin. Consequently, fluctuations in these behaviors could have caused a change in the UL water level series during the two last decades. In inspecting the influence of various factors on UL fluctuations, Hassanzadeh et al. (2012) found that changes in hydroclimatic variables have been most influential.

Table 2 Stationarity and nonlinearity test results for the water level
Full size table

Time series modeling of the UL water level

For modeling section, the SARIMA, TT-SARIMA and TT-SARIMA-GARCH approaches are adopted for fitting these models to the water level data. For TT-SARIMA approach, a SARIMA model is fitted to the residuals of Mono- and Multiple-TT models separately, which is first applied for fitting to the water level data, which has a significant trend. In the case of the SARIMA model, the SARIMA(3,1,2)(2,1,3)12 model fitted to the water levels. This model is selected based on the minimum Akaike Information Criterion (AIC) and testing the residuals of the model for adequacy. Figure 5a shows the sample ACF of water level series, which shows an intense nonseasonal behavior. It should be noted that the unit of horizontal axis (lag time) in all figures is one month. The SARIMA(3,1,2)(2,1,3)12 model includes five nonseasonal autoregressive and moving average parameters of orders 3 and 2, and five seasonal autoregressive and moving average parameters of orders 2 and 3, respectively, that are significant at the 95% confidence level.

Fig. 5
figure 5

a ACF of monthly water level series, b ACF of the residuals of the SARIMA(3,1,2)(2,1,3)12 model, c p values of the Ljung–Box test of the residuals, and d p values of the Ljung–Box test for the SSRs of the SARIMA(3,1,2)(2,0,3)12 model

Full size image

The adequacy of this approach is confirmed using the Ljung–Box test and inspecting ACF behavior in residual series, as shown in Fig. 5b, c. The ACF behavior shows no significant autocorrelation structure in the residuals (Fig. 5b). Since the seasonality behavior is not significant for the residual series, thus, the sample autocorrelation values locate between two upper and lower confidence lines for lags k = 12, 24. The sufficiency of the fitted approach is also confirmed by Ljung–Box test (Fig. 5c), as the p values of this test is higher than the critical line at 1% significance level. For this purpose, it can be accepted that there is no significant autocorrelation values in the residual series structure (null hypothesis). However, in order to show the existence of the GARCH effect, the autocorrelation structure of the SSRs is examined. The extracted p values from Ljung–Box test are presented in Fig. 5d for inspecting the GARCH effect in the SSRs of the SARIMA(3,1,2)(2,1,3)12 model. The results demonstrate the existence of a GARCH effect (rejection of the null hypothesis) in the SSRs for all lags.

In the case of the Mono- and Multiple-TT-SARIMA models, the fitted models are selected based on the minimum (AIC) including Mono-TT-SARIMA(3,1,2)(2,1,3)12 and Multiple-TT-SARIMA(1,1,0)(1,0,1)12, respectively. Figure 6a1, a2 show the ACF of the residuals of the fitted Mono- and Multiple-TT models to the original water level series, respectively, which indicate high persistence and non-stationarity. The sample ACF structure in the residual series for two TT-SARIMA models (as mentioned above) (Fig. 6b1, b2) and the calculated p values from Ljung–Box test (Fig. 6c1, c2) indicate the adequacy of the fitted models. No autocorrelation structure is observed in the residual series, as all autocorrelation values are located between the lower and upper critical lines, however, two autocorrelation values for lags k = 12 and k = 22 intersect the upper critical line at 5% significance level (Fig. 6b1). It can be considered to be a random effect according to the study of Modarres and Ouarda (2012a); furthermore, there is no significant seasonality in the behavior of residual series. The Ljung–Box goodness-of-fit test indicates the adequacy of the fitted model (acceptance the null hypothesis as all probability values located above the significance line at 1% level).

Fig. 6
figure 6

a1, a2 ACF of mono- and multiple- time trend model residuals of the water level series, b1, b2 ACF of the residuals of the Mono- and Multiple-TT-SARIMA(3,1,2)(2,1,3)12 and (1,1,0)(1,0,1)12 models, c1, c2 p values of the Ljung–Box test of the residuals of the above models, respectively

Full size image

By investigating the ACF plot of SSRs series as well as the Ljung–Box test, it can be demonstrated the existence of a GARCH behavior in the SSRs of the fitted models. The sample ACF of SSRs (Fig. 7a1) indicates the existence of a conditional variance behavior or heteroscedasticity for residual series of the Mono-TT-SARIMA(3,1,2)(2,1,3)12 model. Figure 7a1 shows that the autocorrelation values cut off the critical line at the 5% significant level are significant for lags k = 1, 2, 11 and 12. Figure 7b1 shows the calculated p values from the Ljung–Box test for SSRs series. As seen, all probability values are located below the critical line at 5% significant level, and the existence of GARCH behavior is confirmed. However, for Multiple-TT-SARIMA(1,1,0)(1,0,1)12 model, the ACF of SSRs series did not illustrate the presence of heteroscedasticity in this model (Fig. 7a2). In other words, as shown in Fig. 7b2, the null hypothesis of no GARCH effect cannot be rejected for all lags at 5% level.

Fig. 7
figure 7

a1, a2 Autocorrelation function, b1, b2 p values of the Ljung–Box test for the SSRs of the Mono- and Multiple-TT-SARIMA(3,1,2)(2,1,3)12 and (1,1,0)(1,0,1)12 models, respectively

Full size image

It is necessary to apply a GARCH approach for the calculated residuals series from the SARIMA and Mono-TT-SARIMA models in order to capture the existence conditional time-dependent variance (or heteroscedasticity) in the residuals series. The GARCH(2,0) model is selected as the best fitted model to the extracted residuals from the SARIMA and Mono-TT-SARIMA (3,1,2)(2,1,3)12 models for the water level series. The estimated parameters of these two GARCH models are presented in Table 3. The GARCH models were selected based on the minimum AIC in favour of higher order models. It can be seen that the parameters of two GARCH models are statistically significant. This implies the existence of a heteroscedasticity in the residuals of the water level series during the study period. According to the Table 3, the intensity of the short-run persistence of the heteroscedasticity seems to be very strong (0.71–0.84) for two fitted GARCH models. Moreover, the short-run persistence characteristic for the SARIMA model is more than the Mono-TT-SARIMA model (α = 0.84 > 0.71).

Table 3 Parameters of the GARCH models fitted to SARIMA and Mono-TT-SARIMA models for the water level time series
Full size table

Figure 8a1, a2 demonstrates the sample autocorrelation structure of the SSRs series for SARIMA- and Mono-TT-SARIMA(3,1,2)(2,1,3)12–GARCH(2,0) combined models to examine the GARCH behavior for the water level series. The two ACF plots of the residuals do not indicate not only nonseasonal heteroscedasticity but also seasonal heteroscedasticity for these fitted models. Therefore, as the plots show, the autocorrelation values are insignificant at 5% significance level. However, two autocorrelation values for lags k = 11 and 22 cut off the upper critical line. According to the Modarres and Ouarda (2012a), these significant values are as random effects in conditional variance behavior of water level data. Based on the Ljung–Box test (Fig. 8b1, b2), no GARCH effect are also found out in the residuals series of the SARIMA- and Mono-TT-SARIMA(3,1,2)(2,1,3)12–GARCH(2,0) models. It is important to note that, as shown in Fig. 7a1, all significant autocorrelation coefficients of the residuals (except at lag k = 11) were eliminated. It can be concluded that the GARCH model is an appropriate approach for modeling the heteroscedasticity of water level series where it indicates irregular temporal (time trend) fluctuations and variations.

Fig. 8
figure 8

a1, a2 Autocorrelation function, b1, b2 p values of the Ljung–Box test for the SSRs of the SARIMA and Mono-TT-SARIMA(3,1,2)(2,1,3)12-GARCH(2,0) model for the water level data, respectively

Full size image

Model comparison

The performance of the applied SARIMA and GARCH models in this study for modeling the water level series of UL are evaluated using the multi-criteria approach listed in “Comparison approach”. Before illustrating the evaluation criteria, the scatter and time series plots of the observed against estimated water level series are shown for all five fitted models in Fig. 9a–e. It can be seen from the hydrographs that the SARIMA (Fig. 9a) and Mono-TT-SARIMA (Fig. 9b) are closer to the corresponding observed values than those of the rest of the fitted models especially for the peak values. In the form of scatter plots, it can be seen from the fit line equations that the line slope value for the SARIMA, Mono- and Multiple-TT-SARIMA models are closer to the 1 than those of the rest of the fitted models. The performance of these models is shown in Table 4. As seen, the SARIMA and Mono-TT-SARIMA models indicate slightly better performance than the SARIMA- and Mono-TT-SARIMA-GARCH models according to the applied criteria. It can also be seen that the first two models have the smallest RMSE (0.07), RAE (0.03) and ME (0.005), whereas the last two models have highest R 2 (0.999). For the Mono- and Multiple- time trend models, it is observed that the evaluated outcome for the Mono-TT-SARIMA model is better than the Multiple-TT-SARIMA model according to the error criteria and R-squared. The fitted SARIMA and Mono-TT-SARIMA models and their combination with the GARCH model have the same performance based on the error evaluation criteria for the water level series, which has significant trend. Therefore, the criteria in Table 4 suggest that the performance of the time trend and GARCH combined models do not become better than the SARIMA. It should be noted that the GARCH model can capture the conditional variance behavior (or heteroscedasticity) which exist in the residuals series of a SARIMA model. However, there is no guarantee to make better the performance by a GARCH approach (as was reported by Modarres and Ouarda 2012a), at least for this case study. Kakahaji et al. (2013) predicted the fluctuations of monthly UL water level by linear models such as AR with exogenous input (ARX), Box-Jenkins models and intelligent methods during the period of 1967–2006. Comparative results showed that the intelligent methods are superior to traditional models, and they are in agreement with the results of this study. Çimen and Kisi (2009) and Aksoy et al. (2013) used SVM, ANN and stochastic time series techniques in modeling monthly water level data of Lake Van in Turkey. The results showed that the estimated water level is found to be in agreement with the corresponding observed values. The modeling results of this paper confirm the explanation of these two studies.

Fig. 9
figure 9figure 9

Scatter and time series plots of observed and estimated water level for different fitted models. a SARIMA(3,1,2)(2,1,3)12, b Mono-TT-SARIMA(3,1,2)(2,1,3)12, c Multiple-TT-SARIMA(1,1,0)(1,0,1)12, d SARIMA(3,1,2)(2,1,3)12-GARCH(2,0), e Mono-TT-SARIMA(3,1,2)(2,1,3)12-GARCH(2,0) models

Full size image
Table 4 Model multi-criteria for the water level time series
Full size table

For verifying the powerfulness (the significance of differences between the observed and estimated values) of different fitted models, the results were also tested using one way analysis of variance (ANOVA) and t test methods. Table 5 shows the statistics of the two methods for UL water level at 5% significance level. If the p value was higher than 0.05, the differences between observed and estimated values were not considered significant. The SARIMA, Mono- and Multiple-TT_SARIMA models yield smaller testing values with higher p values for the ANOVA and t test than the last two models. It means that the (a), (b) and (c) models, which have not been combined with GARCH approach, seem to be more powerful in water level modeling than the (d) and (e) models. In other words, the similarity between the observed water levels and estimated values from (a), (b) and (c) models are significantly high. It can be found that the GARCH methodology is not appropriate to model water level fluctuations based on these results.

Table 5 Analysis of variance and t test for different fitted models to the water level
Full size table

Summary and conclusions

In this paper, a study of changes in the UL water level was performed incorporating the trend and change point detection approaches, assessment of the changes in mean and standard deviation, testing the changes in stationarity and nonlinearity, and applying the SARIMA, Mono- and Multiple-TT-SARIMA models. The results are summarized as follows.

In the case of the time trend models, it was observed that monthly water level series had a significant statistically decreasing trend in the mono time-trend case. However, in the multiple-time trend approach the linear model fitted to first and second subseries had significant increasing and decreasing trends, respectively. In the case of the change point detection method, a significant change point was detected in 1999. Comparison of the UL water level series before and after 1999 shows a remarkable change in descriptive statistics. In the case of testing for equality, the descriptive statistics showed a remarkable change after 1999. Because the continuous downward trend of the UL water level after 1999 has occurred in this unique ecosystem.

In the case of the stationarity and nonlinearity approaches, there is evidence of nonstationarity and nonlinearity behaviors in the UL water levels, so that, the statistic absolute values of these two approaches for the water level series after the change point in 1999 are more than those before 1999. These behaviors may be in the form of gradual (trend) or abrupt (shift) changes or a combination of both as evidence of nonstationarity. It has been shown that the (unconditional) variance of the water level series has increased, and that the distribution of this time series became normal and the coefficient of skewness has decreased after 1999. These behaviors in water level series can be due to the effect of both natural and human forces on the Lake’s water budget. A combination of the changes in inflow caused by climate change and diversion of surface water for upstream use, construction of dams, drought and mismanagement can be declined the water level in the recent decades.

After the time series was made trend-free, the SARIMA- and GARCH-type stochastic models were built and developed for both mono- and multiple-trend cases. These models are helpful statistical methods for modeling monthly variation of water level with a significant trend and the different fitted models were compared with each other. The SARIMA and Mono-TT-SARIMA models were found to be slightly better than that obtained using the Multiple-TT-SARIMA model. The heteroscedasticity was not significant in the residuals of the Multiple-TT-SARIMA models, but it was significant in the residuals of the SARIMA and Mono-TT-SARIMA models. The GARCH parameters presented the strong heteroscedasticity and the existence of the short-term persistence in the water level series. This existence in the heteroscedasticity may lead to existing frequency of extreme events, such as extreme hydroclimatic variables in relation to extreme water levels.

Possible future studies

In general, this study demonstrated the applications of two Mono- and Multiple-TT linear models, the GARCH modeling approach for both improving/not improving the efficiency of the model, and capturing the heteroscedasticity in the residuals of the linear time series model. In order to better understand the application of the GARCH modeling approach and Mono- and Multiple-TT models for water level of lakes, the use of water levels from different areas around the world is proposed for the future researches. Furthermore, the application of nonlinear, multivariate and multiple time series regression models with exogenous data such as climate variables is proposed for water level modeling. The application of multivariate GARCH models for modeling the effects of streamflow, climate changes and other factors such as land use/land cover change and dams on water level fluctuations is also an interesting topic for future research.