Introduction

The split Hopkinson pressure bar method (SHPB) is currently the most widely used material testing method for a high strain rate. Although many articles on the methodological aspects of SHPB testing have been published, some methodological issues have not yet been fully analysed.

For a valid SHPB test, the specimen is required to deform nearly uniformly at a constant strain rate under dynamically equilibrated stresses, and the propagation of elastic waves through the input and output bars is described by a one-dimensional wave theory [1]. The nearly uniform specimen deformation at a constant strain rate under dynamically equilibrated stresses is realized by application of a pulse shaping technique. This technique can be realized with the use of a small disk called a pulse shaper [2,3,4] or with a conical/tapered striker [5].

However, to satisfy the aforementioned methodical requirements, the SHPB test system should be properly aligned [6], and the material sample should be uniform and geometrically correct. Particularly, the parallelism of the sample faces and their flatness guarantee the reliability of the experimental results illustrating the mechanical response of the material to the dynamic load. Generally, the deviation of the parallelism and flatness of the sample surface should be as small as possible [1]. In the available literature, only in [7], it was stated that the flatness of the side surfaces of the sample should not be greater than 0.01 mm. There are no publications in which the geometrical imperfection of the sample is considered. Therefore, the authors of the present article have focused on determining the influence of sample geometry imperfections on the shape of wave pulses propagated in the bars and consequently, on the results of the split Hopkinson pressure bar experiments. The main problem of the paper was considered based on numerical analyses using a finite element method (FEM) and experimental research. The geometrical imperfection of the sample presented in Fig. 1 and marked with symbols from A to E was analysed.

Fig. 1
figure 1

Type of the specimen imperfections analysed in the paper with their character designation, α – angle specifying the size of the imperfection

Full size image

At this point, it should be noted that the geometrical imperfections of the samples shown in Fig. 1 may result in an incorrect position of the specimen relative to the longitudinal axis of the bars. Therefore, the influence of the non-axial position of the specimens on the character of the waves propagated in the bars was additionally investigated. Figure 2 shows the cases of the incorrect positions of the specimens that were analysed in this paper.

Fig. 2
figure 2

Non-axial positions of the specimens with their character designation

Full size image

The structure of the article is as follows: Second section presents the SHPB principle, and a numerical model and its validation. The obtained results of the numerical analyses are presented in third section. Fourth section presents the formulated conclusions.

SHPB Background and Numerical Modelling Approach

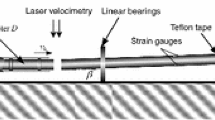
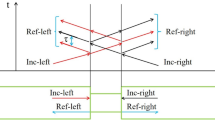
In the SHPB set-up, the material sample is loaded by a stress impulse generated by the striker impact on the front surface of the input bar (Fig. 3). The striker generates a trapezoidal stress impulse (incident wave) that travels through the impacted bar. When the elastic wave reaches the specimen, due to the mismatch of mechanical impedances between the bar and specimen material, part of the incident wave is reflected back (reflected wave) and the rest of the incident wave is transmitted through the specimen. The wave compresses the specimen with high rates, and the remainder of the wave travels to the output bar as a transmitted wave. The incident and reflected signals are recorded by the strain gauges, which are glued on the input bar, whereas the transmitted signals are sensed by the strain gauges located on the output bar. The recorded signals allow determination of the time-resolved engineering average stress, strain and strain rate in the specimen and are treated as pointwise valid material properties in accordance with equations (1)–(3) [1]:

$$ \sigma (t)=\frac{A}{2{A}_S}E\left[{\varepsilon}_I(t)+{\varepsilon}_R(t)+{\varepsilon}_T(t)\right], $$
(1)
$$ \dot{\varepsilon}(t)=\frac{c_0}{L_S}\left[{\varepsilon}_I(t)-{\varepsilon}_R(t)-{\varepsilon}_T(t)\right], $$
(2)
$$ \varepsilon (t)=\frac{c_0}{L_S}{\int}_0^t\left[{\varepsilon}_I\left(\tau \right)-{\varepsilon}_R\left(\tau \right)-{\varepsilon}_T\left(\tau \right)\right] d\tau, $$
(3)

where As and Ls are the initial cross-sectional area and length of the specimen, respectively, c0, E, and A are the sound velocity, Young’s modulus, and the initial cross section of the bars, respectively, ε(t) are the strain signals sensed by the strain gauges, and the subscripts I, R, and T denote the incident, reflected and transmitted pulses, respectively.

Fig. 3
figure 3

SHPB setup with strain gauge positions and recorded signals

Full size image

The SHPB technique allows for an investigation of materials with strain rates from 102 to 5 × 104 1/s. Different types of materials (metals and their alloys, ceramics, polymers and elastomers, composites, shape memory alloys, foams, and biological tissues) were tested under different load conditions (compression, tension, and torsion) [8,9,10,11,12].

For the purposes of present studies, it was developed the FEM of the SHPB setup, which contains all the main components of the arrangement (Fig. 4). In addition to the main part of the setup (bars, sample, and striker), the model included a pulse shaper, slide bearings and a barrel. In the simulation, the dimensions of all the elements of the SHPB were the same as in the experiments [13].

Fig. 4
figure 4

A schematic diagram of the SHPB setup used in numerical analysis

Full size image

Between the interacting surfaces, there was defined the contact based on a contact–impact algorithm, the parameters of which were established on the basis of authors’ previous works [14, 15]. Additionally, Coulomb’s law was used to predict the friction between the interacting surfaces. The friction coefficient was equal to 0.06, which corresponds to the greased surfaces [16]. The authors used a finite element method with a central difference time integration scheme implemented in commercial LS-Dyna code to carry out the numerical simulations [15].

The bars, striker, barrel and slide bearings were given elastic material properties of maraging steel: Young’s modulus EB = 190.6 GPa, Poisson’s ratio νB = 0.3, and density ρΒ = 8100 kg/m3.

The Johnson-Cook (JC) model [17, 18] and simplified Johnson-Cook [15] constitutive models were used in the numerical analysis to describe the material from which the samples were made. The JC constitutive relation was complemented with a hydrodynamic equation of state in the Gruneisen form [19].

The JC model and Gruneisen equation of state was used to describe the properties of a semi-hard copper pulse shaper. The material constants determining the behaviour of the copper were taken from the literature [18, 19] and are shown in Tables 1 and 2. The simplified JC model was used to describe steel sample. The material constants for this material are obtained on the basis of our own research and shown in Table 1.

Table 1 Material constants for steel and copper [18]
Full size table
Table 2 EOS for copper [19]
Full size table

A numerical model validation was performed on a C-type specimen (Fig. 2) with an angle of α = 0.6° and a striker hitting with a velocity, V0 = 12.4 m/s. The selection of a C-type specimen for the validation test resulted from the prediction that this type of the specimen geometric imperfection causes considerable disturbances in the waves profiles. Figure 5 presents experimental and numerical waveforms of both the reflected and transmitted pulses. A comparison of these curves with the results of the experimental research shows good compatibility of numerical modelling results, which confirms the correctness of the developed numerical model.

Fig. 5
figure 5

Finite element model validation; reflected (a) and transmitted (b) pulses for a C-type specimen, α = 0.6°, and striker velocity V0 = 12.4 m/s

Full size image

Results and Discussion

The results of the numerical analyses are presented in Figs. 6, 7, 8, and 9. The correlated curves not only reflect the influence of the specimen geometric imperfections and their position relative to the bars but also the magnitude of the geometric imperfections defined by angle α. The magnitude of this angle is assumed to be 0.3, 0.6 and 0.9°. All the analyses were carried out with the use of a 250-mm long striker hitting the input bar with velocity V0 = 12.5 m/s.

Fig. 6
figure 6

Reflected (left) and transmitted (right) pulses for A-type specimens and their different positions

Full size image
Fig. 7
figure 7

Reflected (left) and transmitted (right) pulses for B-type specimens and their different positions

Full size image
Fig. 8
figure 8

Reflected (left) and transmitted (right) pulses for C-type specimens and their different positions

Full size image
Fig. 9
figure 9

Reflected (left) and transmitted (right) pulses for D- and E-type specimens and their different positions

Full size image

In general, it can be concluded that the effect of the imperfection of the sample on the level of plastic flow stress is very low. However, this influence is relatively large on the value of the determined strains and depends on the type of imperfection and the location of the sample in relation to the axis of the bars. In the case of BB imperfections (Fig. 7(c) and (d)), the disturbances in the reflected and transmission wave profiles do not practically occur, whereas for B, C and CC (Figs. 7(a), (b) and 8), the disturbances are the greatest. Note that these disturbances are visible only at the beginning and end portions of the reflected and transmitted pulses. They are characterized by step changes in the wave profile on the rising edge and oscillations in the final part of the wave profile. The amplitude of these disturbances apparently increases with an increase in the imperfection (angle α) for angles of 0.6 and 0.9°, and the disturbances amplitude reaches the highest values (Fig. 8(c)). In particular, this finding applies to the reflected pulse on the basis of the specimen strain that is calculated. Hence, the results indicate that the greatest errors, due to the geometric imperfections of specimens, are committed during the determination of the specimen strain on the basis of the above SHPB experimental results.

In addition, it was found that the geometrical imperfections of the sample cause transmitted signal disturbances that significantly hinder the starting point of the signal determination (Fig. 7(b)). According to [1], incorrect evaluation/determination of the signal starting point results in an erroneous calculation of the force at the rear end of the specimen, which provides an incorrect assessment of the dynamic stress equilibrium. This incorrect assessment leads to invalid stress-strain curves (Fig. 10).

Fig. 10
figure 10

Stress – strain curves for the imperfect samples

Full size image

The results presented in Fig. 6 also prove that the orientation of the imperfection relative to the contact surfaces of the bars is also important. For example, the orientation of the specimen imperfection A evokes pronounced oscillations in the end portions of the reflected pulses (Fig. 6(a)). However, in the case of a specimen with the same imperfection A, but with the opposite orientation, i.e., the output bar directed to the contact surface of the output bar, the reflected signal is smoother in the part of the curve over 100 μs (Fig. 6(c)). A reverse dependence of the influence of the imperfection orientation can be observed in the case of the transmitted pulse. In this case, the orientation A causes less signal disturbance in its final phase compared to that of the orientation AA (Fig. 6(b) and (d)). A similar relationship was found for imperfection C and its orientation C-CC (Fig. 8).

The reflected and transmitted pulse disturbances caused by the imperfections and the influence of specimen orientation are obviously reflected in the stress-strain curve profile (Fig. 10). Generally, the analysed geometric imperfections introduce an error for small and large strains in the range of different strain values that correspond to the different stress values. This is particularly evident for imperfections B and C, for which the stress-strain curves are invalid, even for strains reaching 0.04 (Fig. 10(c)). It should be noted that the influence of angle α, which is a measure of the imperfection size, on the profiles of stress-strain curves obtained for specimens with imperfection D is relatively small. In this case, the geometry of the specimens with imperfections deviates slightly from the correct shape of the sample (cylinder).

Conclusion

It is widely known that the specimen geometrical imperfections and the specimen orientations relative to the bars adversely affect the results of the SHPB tests. This finding is particularly true for brittle materials. However, numerical analyses performed in this work proved that this also applies to ductile materials, whereas for some types of specimen geometrical imperfections and their values, the obtained results of the SHPB experiments can be considered reliable from a practical point of view. In the case of all analysed imperfections, it can be assumed that for angles α ≤ 0.3°, errors in the determination of the stress-strain curves can be omitted. This conclusion is of a great practical importance, as it is not necessary to meet high technological requirements related to the manufacturing accuracy of the specimen or the use of time-consuming and expensive manufacturing technologies.