Introduction

When the surface of a material is damaged with a dent or gouge, there is a significant impact on the life span of the structure, particularly in the case of metal alloys. The very first report, which dates back to 1950 [1], focussed on the concept of tribology, which indicates the problem imposed by the gouge/dent defects. The gouge and dent defects are significant challenges that cover the entire industrial sector, but particularly affect the pipe structures made of special steel and cast iron.

Since 1960, the transfer of fluids from industrial sites to the end-user was possible with a robust pipeline network made of stainless steel. The lifetime of these pipeline systems was approximately 40 years. Different fluids, as well as hydrogen, water, oil and gas (Fig. 1) circulate through this network that traverses the seas and soils. Due to pressure variation, these components were always vulnerable to mechanical damage, as well as by fluctuation of mechanical loading induced by external environmental action. It is noted that the majority of pipeline ruptures, located under soils or crossing the seas, is caused from external aggression. Indeed, this is confirmed by the European Gas Pipeline Incident Group [2]. From 1060 cases of pipeline ruptures, 49.6% are due to external aggression; other incidents represent corrosion attack (15.3%), design defects (16.5%), inadequate operation condition (4.6%), soil slippage (7.3%) and other causes (6.7%).

Fig. 1
figure 1

Graphical layout of a gas pipe and a failed welded joint of water pipeline

Full size image

The damage mechanism induced by the dent/gauge defect is very complex and often poorly estimated [3, 4]. It has been noted that these dents and gouges may act to accelerate the damage process. The literature describes the gouge or/and dent scenario as an extension of fracture mechanics principles [3, 4]. By using the fracture mechanics approach the following was achieved: a) accurate determination of the Stress Intensity Factor “K” (SIF) mode I of aluminium alloy (linked to the toughness of materials studied KIC), configured as cracked samples, by applying the mechanical loading on 3-point bending specimens; b) assessment of the influence of crack tip radius starting from experimental observations; c) comparison of relative performance of standard FEM and X-FEM; d) determination of the critical value of the SIFs.

This work presents a complete study combining experimental tests with traditional numerical approximation and innovative finite element method. The novel approach of X-FEM applied in this study allows to understand better crack propagation mechanisms when the structure is subject to extreme loading conditions. The numerical strategy was implemented in ABAQUS. In order to detect aluminium alloy (A1) pipeline structural behavior, a case study is proposed on a defective pipe to identify the occurrences following the application of mechanical loading. A typical configuration that presents a defect due to applied pressure is depicted in Fig. 2.

Fig. 2
figure 2

Rupture initiated from a gouge or/and dent

Full size image

Theory

The main cause of catastrophic metallic pipeline failure has been highlighted through industrial experience and recent literature as the presence of a few geometrical defects. The defects, perceived as external damage of the body, occur often by a crack or cracks that develop due to corrosion mechanisms and very often take the shape of a gouge and/or dent. It is noted that fracture mechanics deals with determining the crack history in a component with defects, such as a pipe containing a defect. The numerical approximation engaged under FEM/X-FEM becomes an independent technique to predict fracture processes. This strategy is appropriate for describing crack propagation under 3-point bending loading considered in this study.

Fracture Mechanics Crack Assessment

In order to ensure a good understanding of the crack mechanisms, fracture mechanics was introduced into a graphical diagram by Feddersen [5]. The critical stress is associated with the crack size. Figure 3 shows a case study of a plate having the width “W” containing a simple lateral crack. It appears that the crack extends to different length size “a” as a non-dimensional function of crack depth (a/W).

Fig. 3
figure 3

Feddersen diagram

Full size image

The Stress Intensity Factor “K” (SIF)

The so-called SIF parameter “K” is capable of generating details of the activity near to the crack tip. In general, a crack is defined by a tip radius and a specific angle. Once mechanical loading is applied, crack may propagate in the component. Irwin [6] proposed an analytical allowable stress distribution near to the crack front described as:

$$ {\sigma}_{ij}=\frac{K_I}{\sqrt{2\pi r}}{f}_{ij}\left(\theta \right) $$
(1)

where: KI is the so-called SIF. The parameters r and θ are defined in Fig. 4 and represent the polar coordinates from the measured zone, the zone surrounded by the front of the crack tip; and the function fij, depends on θ.

Fig. 4
figure 4

Typical stress state near crack extremities

Full size image

The value of KI parameter results from structure characteristics, component geometry, loading conditions, and, of course, crack configuration (size, shape and location). The KI parameter represents the magnitude of the stress singularity generated by the front of the crack tip in correspondence of the crack extension as per loading conditions, which allows crack propagation toward the edge of the component. When the stress load achieves critical values, the crack can extend all the way to the edge of the component generating a final fracture. Hence, fracture toughness indicates when the critical crack values are achieved.

Fracture toughness parameter assessment

The classical strength-based methods determine the existence of a continuum material configuration. Unfortunately, this theory is ineffective when considering any structures or materials that have cracks or voids. The energetic theory and the Stress Intensity approach work better to detect the mechanical behaviour of a component that presents defects.

Griffith [7] introduced an energy approach based on the strain energy release parameter G, known as the degree of variation in the potential energy reported to the crack location. For mode I, the strain energy release rate is obtained by \( G=\frac{\mathrm{\partial \Pi }}{\partial A} \). The potential energy (Π = U − V) represents a difference between the external work V required to propagate a crack and the amount of the elastic strain energy U stored in the body. This alternative approach permits an effective understanding of the material behaviour and/or structures that contain cracks. Here, the magnitude expressed by the elastic stress component of the crack-tip represents a finite scaling parameter K, known as the Stress Intensity Factor [8].

The toughness parameter of the opening mode load is detected by using standard procedures stated in ASTM and ISO standards [9, 10]. In the case of single edge notched samples, modified for bending procedure, the numerical values of the Stress Intensity Factor depend on the geometry samples and applied load F. The fracture regime of linear elastic parts can be calculated by applying the Stress Intensity Factor in the opening mode I using equations (2–3):

$$ {K}_I=\frac{F}{B\sqrt{W}}{f}_{ij}\left(\frac{a}{W}\right) $$
(2)

Where

$$ f\left(\frac{a}{W}\right)=6{\sqrt{\left(\frac{a}{W}\right)}}^{\ast}\left|\frac{\left(1.99-\left(\frac{a}{W}\right)\left[1-\left(\frac{a}{W}\right)\right]\ast \left[2.145-3.93\left(\frac{a}{W}\right)+2.7{\left(\frac{a}{W}\right)}^2\right]\right)}{\left[1-2\left(\frac{a}{W}\right)\right]{\left[1-\left(\frac{a}{W}\right)\right]}^{3/2}}\right| $$
(3)

represents the geometry shape factor and the components B and W are the specimen thickness and width, respectively. The initial value of the crack length, a, is determined by the sum of the V-notch depth and the length of pre-crack, and its numerical values vary between \( 0.45\le \frac{a}{W}\le 0.55 \).

The Numerical Methods

Standard finite element method (FEM)

Nowadays, a design strategy based on FEM represents a standard tool for industrial products. For effective numerical simulation, a powerful computer is required to guarantee adequate performance. With this, the parallel architecture permits the development of algorithms with a better resolution and a more sophisticated approach. This results in a very rapid calculation time. In FEM, material discontinuities can be modelled using proper boundary conditions. A surface discontinuity is generated by cutting its elements. Their “surfaces” grow over the time (i.e. crack propagation, hole expandability, propagating a solidification front) making the linking unavoidable, and sometimes causing the spraying of the solution that permits the creation of a new mesh structure in the affected area. This local re-meshing is necessary when a new surface is created into an existing mesh.

Generally, an industrial problem requires a convergence solution by multiple re-meshing. In addition to the geometric constraints on the mesh generation, the user sometimes imposes a specific element size in various areas, thereby, reducing the approximation errors. In the short term, networking and linking represents a stumbling block for the industrial calculations.

The presence of cracks or an interface between materials is modelled by introducing discontinuous functions [11] or discontinuous derivatives [12], while re-meshing is not required in the evolution of these surfaces [13]. The classical finite element modelling requires the mesh to match to the tip crack profile. Therefore, re-meshing is required for crack propagation. Rashid [14] and de Ingraffea et al. [15, 16] contributed to the simplification of the re-meshing processes, but they proposed a laborious 3D model. Unfortunately, this flexibility comes at a higher price. Trivial operations within finite elements, such as assessment of shape function at specified points, integration of linear and bilinear forms or taking into account conditions in the Dirichlet boundary condition, become difficult and even very costly. Additionally, clever meshing strategies, such as the ‘mesh free’ example, do not fully solve the issue.

Over past few years a new approach developed under mesh-free methods was introduced to handle these difficulties that appears in the linear elastic fracture mechanics problems under thermo-mechanical loads [17]. Besides, the symmetric Galerkin boundary element method (SGBEM) is an alternative solution that can be used as an effective method to analyse crack growth simulation for a surface crack and a short through-thickness crack [18].

This paper describes the alternative approach to reduce the difficulties related to the mesh. This is achieved by approaching the problem with the eXtended Finite Element algorithms known by the acronym X-FEM (eXtended Finite Element Method) or the Generalized method of finite elements (G-FEM).

Innovative method of X-FEM

An X-FEM formulation extends the performances of the classical finite element method without losing any of its benefits. Additional information on a particular configuration may be incorporated to improve the accuracy of the calculation. This strategy includes the use of asymptotic properties by defining a displacement field in the vicinity of the crack tip and releasing the enrichment, as described by Strouboulis, Babuška and Copps [19]. Belytschko et al. [20], and Oliver [21] proposed a discontinuous function to easily solve this problem.

The advantage of XFEM in simulating fracture behavior is demonstrated in literature. The sharp crack is a surface where the displacement field is considered discontinuous. The initial crack model simulated by the X-FEM was presented in [22] as a 2-D case, and later extended to the three-dimensional case [23]. Sukumar et al. [24] used the X-FEM strategy under the “Fast Marching Method” and resolved the problems of a plane cracking in 3D environments. A non-planar crack propagation situation in 3D environments was highlighted in [25].

The discontinuity surfaces modelled by the X-FEM method enhance element interpolation using a smart technique based on unity partition, described by Melenk and Babuška [26]. The technique is summarised below. The size of a finite element approximation reported to a given displacement field surrounded by an element Ωe is written:

$$ u(x)\kern0.24em \left|\;{\Omega}_e\right.\kern0.72em =\sum \limits_{i\in {N}_n(x)}\sum \limits_{\alpha }{u}_i^{\alpha}\;{\varphi}_i^{\alpha }(x) $$
(4)

Where Nn(x) represents the set of the nodes surrounded by the elements that contain the point x, \( {u}_i^{\alpha } \) is the size of the displacement at the node i for a direction α and \( {\phi}_i^{\alpha } \) corresponds to shape function.

The degrees of freedom determined for a single node should have similar value for all the elements connected to this node. The approximations for each item may be “assembled” providing a valid approximation to every point x bounded by a domain Ω:

$$ u(x)\kern0.48em =\sum \limits_{i\in {N}_n(x)}\sum \limits_{\alpha }{u}_i^{\alpha}\;{\varphi}_i^{\alpha }(x) $$
(5)

An area of influence generated by the interpolation function \( {\phi}_i^{\alpha } \) represents the numerical set of the elements linked to the node i. The whole Nn(x) covers a surrounding size of nodes connected to the point, x. The approximation of the enriched elements permits the representation of an amplitude shift F(x) which is accorded in any direction on the area ΩF ⊂  Ω, and is written:

(6)

There, NF denotes the set of the nodes that aid the build connexion of area ΩF. The evidence is detected when setting zero, the coefficients \( {b}_i^{\alpha } \) and the shape functions of the finite elements become capable of representing all the rigid nodes.

The modelling process of a crack by X-FEM includes two types of enrichment:

  • an enrichment for the front of the crack (the crack tip) using the function {F}i = 1, 4 and characterizing the asymptotic behaviour released by the displacement size near to the crack front [20, 27],

  • an enrichment of the internal crack part with a jump function H to a value of 1 to one side of the crack and − 1 for the other [20]. Whether or not a node gets upgraded depends on its relative position to the base and the crack position due to enhancement as shown in Fig. 5. The circled nodes can enrich the presence of a discontinuity and its surrounded nodes, which are associated to a square enriched by an asymptotic method at the crack front [28].

Fig. 5
figure 5

A crack surrounded by a uniform mesh (left) and a non-uniform one (right)

Full size image

The numerical approximation with finite elements that are enriched in the presence of a crack is written:

(7)

where:

I:

denotes the set of mesh nodes;

u i :

represents the degree of freedom (vector) classic to node i;

ϕ i :

represents a scalar shape function linked to the node i;

L ⊂ I:

represent a set of nodes that are enriched at the discontinuity. The coefficients airepresent the degrees of freedom (vector) correspondents. A node may belong to L if the medium is split by a crack that does not include any of its points (an example of these types of encircled nodes is present in Fig. 5 for a different case of a uniform and non-uniform mesh);

K1 ⊂ I and K2 ⊂ I:

represent the node-sets that are enriched when modelling the crack of front 1 and 2, respectively. The degrees of freedom for this structure are \( {b}_{i,1}^l \) and \( {b}_{i,2}^l \), l = 1, …, 4 . A single node may belong to K1 or K2 when the statement contains a first or a second crack tip, respectively; nodes are surrounded by a square in Fig. 5.

The functions (\( {F}_i^l(x),l=1,\dots, 4,\dots i=1,2 \)) that permit the modelling of the crack front are given in elasticity as:

$$ {F}_i^1=\sqrt{r\kern0.24em \sin \frac{\theta }{2}},\kern0.5em {F}_i^2=\sqrt{r\kern0.24em \cos \frac{\theta }{2}},\kern0.5em {F}_i^3=\sqrt{r\kern0.24em \sin \frac{\theta }{2}\cos \theta },\kern0.5em {F}_i^4=\sqrt{r\kern0.24em \cos \frac{\theta }{2}\cos \theta } $$
(8)

Where (r, θ) denote the polar coordinates as local axes in the front of the crack (see Fig. 6 for reference).

Fig. 6
figure 6

A sketch of the polar coordinates in front of crack

Full size image

Experimental Tests

This section describes the 3-point bending tests carried out on notched specimens including cracks of different sizes as well as the mechanical characterization process of the tested material.

Each notch test sample has the following dimensions: length of 140 mm, width of 20 mm and 10 mm thickness. Specimens were manufactured from an aluminium alloy A1. In each sample a pre-crack (notch), with different crack tip radius, was built after manufacturing. The notch was created by electrical discharge machining to produce the notch/radius with very narrow tolerances.

The chemical composition of the material studied was detected by a scanning electron microscope (SEM) measurement. The weight composition of the tested material is given in Table 1: listed values are consistent with those reported in literaure for the A1 aluminum alloy [29].

Table 1 Chemical composition of the aluminium alloy studied
Full size table

Some classical tensile tests were performed at room temperature, in order to obtain the mechanical properties of studied alloy. The configuration of the tests is based on the samples manufactured from the longitudinal direction of the pipe. Figure 7 represents a conventional experimental stress-strain curve for the studied material. The mechanical characteristics of this material display a ductile behaviour.

Fig. 7
figure 7

Mechanical constitutive law of the alloy investigated

Full size image

Table 2 summarizes the mechanical properties determined from tensile tests.

Table 2 Mechanical properties (room temperature) of aluminium alloy Alloy A1 (According to ASTM standard E8–95 [27])
Full size table

Setup of Mechanical Test

Experiments were carried out using the classical Instron 5585H machine. An electromechanically actuated action has been imposed during the three-point bending test. Figure 8 presents the details of the testing apparatus.

Fig. 8
figure 8

Tensile/compression machine (INSTRON 5585H) used for the 3-point bending test

Full size image

The parts shown in Fig. 8 are:

  • 1-a video extensometer, 2- the load cell, 3- jaws, 4- notched specimen, 5- upper jaw (mobile), 6- lower jaw (fixed).

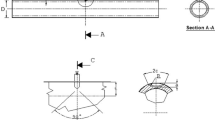
The main geometric dimensions of a typical specimen are shown in Fig. 9:

  • L: the length = 140 mm.

  • W: the width = 20 mm.

  • B: thickness = 10 mm.

  • l: the distance between the two jaws = 100 mm

  • a: the notch depth = 10 mm

  • Ri: the notch radius = 0.15, 0.3, 0.5, 0.8 and 1 mm

Fig. 9
figure 9

Schematic of a typical sample with indication of its main geometric dimensions

Full size image

Test Methodology and Results

In this survey, 15 specimens have been considered for the testing protocol. A minimum of three trials were performed for each configuration, which referred to a specific notch radius. A speed of 0.5 mm/min was considered during the tests. The sample was clamped on two points of the lower jaw (Fig. 8). During the tests, the load-displacement data were transmitted to a control unit, recording the test data as per force (F) vs. displacement variation.

Figure 10 shows the test pieces of different notch rays that were submitted to 3-point bending. The observation highlights that for all the tests, on different samples containing a diverse notch radius, the defect (notch) spreads over one of the sides at the end of the notch and not radial to the notch. This issue is caused by a flaw introduced during machining of the notch radius.

Fig. 10
figure 10

Schematic details of the samples after the 3-point bending

Full size image

Results of 3-point bending tests are summarized by the load displacement curves. Figure 11 presents the experimental load-displacement curves for the material investigated as a function of the notch radius.

Fig. 11
figure 11

Evolution of the load versus deformation for R = 0.15, 0.3, 0.5, 0.8 and 1 mm

Full size image

A peak (maximum) load characteristic of the critical load Fc was detected on the load-displacement curve. The rupture process that occurs on the sample may be decomposed into three parts:

  • The first part ① is almost linear, where the load remains low while moving around 0.37 mm. It is noted that the distance decreases by increasing the notch radius.

  • The second part ② is when the load increases to a maximum that corresponds to the material tensile strength Fc (load peak).

  • The third part ③ is itself divided into another two parts, one part where the load decreases abruptly while the second part shows a progressive decrease in the load.

The values of critical load may increase by increasing the notch radius, according to the results listed in Table 3. In fact, the notch radius has a great impact of starting the rupture process.

Table 3 Critical loads measured from experiments
Full size table

Calculation of the KIc and Interpretation of Results

The values of KIc were determined to understand the material fracture resistance within ambient environment on the samples containing a sharp crack submitted to critical tensile constraint. In the front of the crack, the stresses released produced a triaxial plane strain, whereas the crack-tip plastic region is considered small in respect to the crack size and the specimen dimensions. The numerical parameter KIc denotes the fracture toughness. This value helps by estimating the link between stress at failure and defect size of a material in service, while critical conditions are expected. To establish whether a valid KIc has been obtained, a conditional strategy based on the KQ parameter was described as follows: The consistency in the results was verified for the size and yield strength of the samples according to standard E8–95 [30]. The numerical value of load PQ was determined from instructions set in the standard and its impact to KI was also analysed. In order to determine the PQ, a straight line was drawn from the origin. The slope represents 95% of a linear part of a load–displacement curve (see Fig. 11 for reference).

The maximum admissible load represents the value taken for PQ (Table 4) in this algorithm. The relationship (Pmax/PQ) needs to be smaller than 1.10. as per Fig. 11 showing the steps of this criterion:

$$ \frac{P_{Max}}{P_Q}\le 1.1 $$
(9)
Table 4 The Stress Intensity Factor values in accordance with E 399
Full size table

The KI value for a compact sample may be calculated according to the following expression [9, 10]:

$$ {K}_I=\frac{P_Q}{B\sqrt{W}}f\left(\frac{a}{W}\right) $$
(10)

Where

PQ:

the load

B:

thickness of specimen

W:

width of specimen

a:

length of crack.

The configuration is surrounded by:

$$ 0.45\le \frac{a}{W}\le 0.55 $$
(11)

In order to compute KI, the values of \( f\left(\frac{a}{W}\right) \) were tabulated from the E 399 standard [31]. In the present case, the following values were found:

$$ f\left(\frac{a}{W}\right)=6{\sqrt{\left(\frac{a}{W}\right)}}^{\ast}\left|\frac{\left(1.99-\left(\frac{a}{W}\right)\left[1-\left(\frac{a}{W}\right)\right]\ast \left[2.145-3.93\left(\frac{a}{W}\right)+2.7{\left(\frac{a}{W}\right)}^2\right]\right)}{\left[1-2\left(\frac{a}{W}\right)\right]{\left[1-\left(\frac{a}{W}\right)\right]}^{3/2}}\right| $$
(12)

The computed values are listed in Table 4, that were identified in accordance with expression E399 [2].

Numerical Results of FEM and XFEM Strategies

FEM Vs XFEM Strategy

Schematic diagrams of three-point bending specimens (2D-FEM model and 3D-XFEM) that contain crack-like defects are depicted in Fig. 12. The indenter and its support of the three-point bending test were defined as analytical rigid parts. The loading inserted in the numerical simulation corresponds to a 100 N determinate from experimental assessment.

Fig. 12
figure 12

Geometry of the sample (a) 2D model simulated by FEM and (b) 3D model simulated by XFEM

Full size image

In the 2D-FEM model, a structured mesh was produced using the CPS4 (a 4-node bilinear plane stress quadrilateral) element (approx. 3000) and, in the X-FEM strategy, the bars were meshed with C3D8I (an 8-node linear brick, incompatible mode) element (approx. 3200); afterward, the size of the initial crack was embedded into the numerical model of FE. Meshed models are shown in Fig. 13. The mesh near to the crack tip was refined by highlighting the stress singularity, resulting in a very dense mesh for the sharp radius.

Fig. 13
figure 13

A typical mesh of the specimen (a) 2D FEM model with a1) crack tip radius of 0.15 mm a2) crack tip radius 1 mm and (b) 3D XFEM model with b1) crack tip radius 0.15 mm and b2) crack tip radius 1 mm

Full size image

FE simulations clarify crack propagation mechanisms and predict the conditions under which the material may fail under the action of loads. In Fig. 14, it was demonstrated by using the Von Mises criterion that the aluminium alloys A1 material withstand the critical load imposed, which makes this alloy capable of resisting crack propagation depending on the loading applied. Numerical determination confirms the absence of plastic behaviour near to the crack tip front that agrees with the experimental results.

Fig. 14
figure 14

Crack propagation for a specific radius of 0.5 mm (a) 2D FEM determination and (b) 3D XFEM evaluation

Full size image

The innovative technique of X-FEM allows accurate understanding of the process of crack propagation starting at the crack tip up to the end of the crack front. The simulated crack path on the X-FEM presents very good similarity with experimental tests, and allows the reproduction of the trajectory of the crack due to machining capabilities (for reference see Fig. 10). Instead, the FEM has a reduced performance that allows the production of only radial cracks on the notch radius.

Fracture toughness KIC of aluminium alloys A1 expose positive performances for a crack starting from a radius greater than 0.5 mm, while for a sharp crack tip radius, their mechanical properties in terms of crack allowance are critical. This fact is in agreement with most of the aluminium alloys [32,33,34]. Variation of the Stress Intensity Factor with respect to crack tip radius is plotted in Fig. 15. Consistency of experimental data and FE results confirm the validity of the proposed approach.

Fig. 15
figure 15

Variation of stress intensity factor with crack tip radius

Full size image

Conclusions

This work was conducted in order to identify the influence of notch radius on the Stress Intensity Factor in the components with defects. For that purpose, three-point bending tests were carried out. Fifteen tests were carried out (three trials for each notch radius). These tests have allowed us to determine the critical load for each notch radius. These critical loads were used for the numerical simulation of 3-point bending tests.

Fracture toughness KIC of aluminium alloys A1 determined under 3-point bending is higher when the initial crack tip radius is larger than 0.5 mm.