Abstract
The paper presents an experimental procedure based on micro-scratching to detect stresses in the ground layer of panel paintings. The method relies on the fact that cracking of the material during a micro-scratching test is the outcome of a combination of local force applied by an indenter and the stresses present in the material. The critical normal load at which damage appears during the test has a strong correlation with the stress in the material. The method, although not providing absolute values of stress, is sensitive to stress magnitude and direction, only micro-destructive, and attractive for monitoring stress changes caused by relaxation processes also in multi-layer materials. The presented tests were performed on artistic materials for which information on stress relaxation is particularly important when developing strategies for their storage and transportation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The analysis of mechanical response of artefacts to climate variations is one of the fundamental approaches to rational guidelines for the control of climate in museums and historic buildings. The formation of environmentally-induced cracks in panel paintings, one of the categories of cultural artefacts most susceptible to climate variations, has been extensively analysed for more than two decades, in order to establish the allowable ranges of climatic variations which the painted wood can endure without damage [1].
The moisture response of a multi-layer structure consisting of wood, animal glue, gesso (chalk bound with animal glue), and paints to variations of relative humidity (RH) in its environment is an outcome of complex interactions between the individual layers. The gesso (ground) layer was historically used to prepare a smooth, paintable surface on wood. The mismatch between high dimensional response of the wood substrate in the transverse direction to the tree trunk to humidity variations and negligible response of the dimensionally stable ground layer has been identified as the worst-case condition leading to increased stresses in the entire pictorial layer and ultimately its fracture [2]. Therefore, knowing stress levels in the ground layer - which is most prone to cracking in the system - is of crucial importance when looking for optimal conditions for protecting paintings from damage.
Gesso is a brittle, granular material composed of chalk grains connected by animal glue. The total stress generated in the ground layer is the result of external loading and drying shrinkage during material preparation as well as the history of RH variations the material experienced, especially excursions into very moist conditions [3]. Total stress is the main factor defining the performance of brittle materials. There is a large number of experimental methods that allow to measure stresses in solid bodies at macro and micro-level. The most commonly used are: mechanical, compliance, and diffraction. Other methods are described in [4]. These experimental methods have, however, only a limited applicability in the case of granular materials where distribution of inhomogeneous microscopic contact forces between particles is highly complex [5, 6]. The analysis of conditions leading to yielding and cracking of granular materials has been focus of many experimental studies implementing different measurement techniques to probe granular microscopic properties that provide structure and contact forces in three-dimensional packing (see for example a recent work utilizing the refractive index matching tomography [7]). It should be noted, however, that the general relationship between external forces applied at the system boundaries and the resulting microscopic force chains in its bulk represents a fundamental and still unsolved problem of granular mechanics.
This study describes a micro-scratching technique for evaluating stress exerted on the ground layer. The method relies on the fact that cracking of the material during a micro-scratching test is an outcome of a combination of a local force applied by the indenter and stress in the material which is in turn related to the external stress exerted on the material boundaries. During the test, an increasing normal load is applied to the indenter with a rounded tip as it is drawn over the material surface. The groove created can then be analysed microscopically to characterize the type of micro-damage created. The diversity of scratch damage created in most materials indicates that it occurs through multiple mechanisms [8, 9]. In brittle materials, it is possible to identify curved periodic cracks concave to the indenter wake. A systematic analysis of the influence of the surface friction coefficient on size and magnitude of stress zones can be found in [9]. The tensile stress field causing mode I of cracking is created right behind the indenter tip. It results from the force applied locally through the indenter as well as residual stress present in the material. Therefore, the critical load applied to the indenter at which cracking of the surface starts can be correlated with stress in the material and used as a stress indicator.
In this study, magnitude and distribution of stress in the ground layer created by externally applied force was evaluated. The analysis was performed despite the lack of a precise model describing the relationship between micro- and macro-stresses in the ground layer.
Material and Experimental Tests
Gesso analysed in this study was prepared using rabbit-skin glue and ground chalk. The ratio of the chalk (the pigment), to the glue is expressed as the pigment volume concentration (PVC):
where, P and B are volumes of the pigment and the dry glue binder, respectively. PVC value of 92% was selected to produce a ground layer of very good mechanical properties and, at the same time, accepted by a restorer as matching gessoes commonly used to restore panel paintings [10, 11].
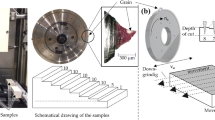
The Scanning Electron Microscope (SEM) image of the ground layer obtained using a Phenom ProX shows clearly the granular nature of the material (Fig. 1(a)). The chalk grain size distribution was calculated using ImageJ 1.49v software and procedure described in [12]. The size of grains ranges from 0.5 to 4.5 μm: an average diameter for the obtained asymmetric distribution is 1.0 ± 0.5 μm and a median diameter is 0.9 μm (Fig. 1(b)).
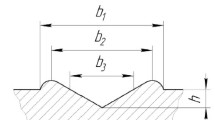
All micro-scratching tests were performed using a Micro-Combi Tester “(CSM Instruments, Switzerland) following the ISO 20502 standard [13]. In the tests, the speed of indenter sliding over the surface and the rate at which normal load was applied were 12 mm/min and 14 N/min, respectively. Micro-scratch length in most tests was 10 mm. The pre-scratch scan of the sample surface with a minimal force of 10 mN was performed before each measurement. The recorded shape of the surface was used to correctly evaluate the depth of the indenter during micro-scratching with increasing normal load. During the experiment, friction force was recorded in real time and the scratch groove was analysed using optical microscope at the end of each test. The geometry of scratching experiments is explained in Fig. 8.
Experimental Results
Ground Layer on a Metal Substrate
The initial test was designed to observe cracking in the ground layer caused by the scratching process, identify the cracking mode and determine the force leading to the damage. The test was performed on a 0.7 mm thick ground layer painted on 2.5 mm thick metal alloy support with the elastic modulus of 253 GPa. The metal support was selected for the calibration tests due to its well-known mechanical properties and high homogeneity (the elasticity modulus was determined experimentally in a 3-point bending test). Using such material allowed for precise control of stresses during the experimental procedure. It was determined experimentally that the beam can be bent elastically to the curvature radius of 0.25 m. In the scratch test, a Rockwell diamond indenter with a rounded tip was used. The radius of the tip was 200 μm. A typical fracture pattern created during the test is shown in Fig. 2.
The regularly spaced micro-cracks, perpendicular to the scratch direction (mode I cracks), were dominant features observed in the scratch track. In a brittle material, mode I crack initiates when stresses exceed tensile strength of the material. In order to evaluate the effect of ground layer stress on the initiation of cracking during the micro-scratching, the following test was performed. The metal substrate was bent to induce additional lateral stresses in the outer ground layer (Fig 3). Since the Poisson’s ratio of metal and gesso is similar, one component of stress, in the direction along which the specimen had been bent, was dominant.
The micro-scratching test was performed for four different deflections, namely −5, 0, 5 and 10 mm resulting in four different stresses of the ground layer of 25, 0,-25 and − 50 MPa. The results of typical micro-scratch measurements for different deformations of the sample are presented in Fig. 4.
The Fn-Ft curves are almost identical for small values of the normal force. On each graph, a value of the normal force at which first cracks on the ground layer surface were observed using an optical microscope was indicated by a vertical arrow and description “Opt”. The obtained results indicate that the onset of oscillations of the friction force correlates well with the value of the position at which the first crack in the ground layer appears. The observation indicates that both methods of determination of the critical load, i.e. optical and instrumental can be used for assessing stresses in a material.
Values of normal loads leading to cracking of the ground layer as a function of stress are presented in Fig. 5 for different deflections of the sample. The results clearly indicate that forces in the ground layer can be evaluated by measuring the critical load leading to cracking of the material in the micro-scratching test. ANOVA analysis showed that data points of Fig. 5 were statistically different with the confidence level of 99.99% in case of the optical observation and 99.92% for the instrumental measurements. Furthermore, the analysis based on friction force instability gave the same results as the optical analysis of the scratch groove but the detection of the onset of friction force instability was more easily automatized.
The influence of scratching speed, load rate, type of the tip and its radius in respect to coating hardness, roughness, and friction on micro-scratch test results has already been thoroughly investigated and discussed (see for example refs [14, 15]) for different substrates and coatings. In the case of gesso, the optimum tip radius turned out to be the most important factor to achieve unambiguous results. The results obtained for three different radii of Rockwell tip are presented in Fig. 6.
The most pronounced change in the friction force pattern is observed for tip radius of 200 μm (200 times bigger than the average size of particle grains in the analysed material). For bigger radii, the friction force is changing very smoothly and it is difficult to clearly recognize the normal load at which cracking starts, whereas for small radii, the friction force is unstable during the entire test. The 200 μm radius indenter has a contact area big enough for the interaction with individual grains to average out. For such indenter, the measurement is not influenced by the interaction with individual grains but still is able to detect microscopic cracks created during the scratching process.
Ground Layer on a Wooden Substrate
The tests presented above allowed us to verify a basic concept of evaluating stress in a granular material using the micro-scratching technique and to optimize the measurement procedure. Still, it was crucial to verify the method on a sample on a wooden substrate, which would better mimic the system in which the measurements of stresses are of interest. Moreover, gesso on a wooden substrate has a more complicated stress state than the one on a metal support. Due to anisotropic nature of wood, gesso is stressed not only in the direction across the grain but also along the grain. Therefore, measurements on wood were carried out to test if the measurement in any given direction of the wood substrate was affected by other components of the stress tensor.
To prepare such samples, 10 mm thick, radially-cut lime wood panels were covered by six layers of fresh gesso mixture and dried. Stresses in the gesso layer were annealed by submitting samples to 30 o C and 90% relative humidity (RH), which was verified using the layer removal technique [5] - no change in wood curvature was observed after removing the gesso layer. Three samples were prepared.
To perform micro-scratching tests, the samples were cut into 160x10x10 mm3 pieces which were installed in simple mechanical holders. Such a holder allows a sample to be flattened in a controlled way and, in consequence, to systematically increase compressive stress in the ground layer (Fig. 7).
Result of simulation of directional stress: perpendicular (left) and parallel (right) to the wood grain for a sample flattened using the holder shown in Fig. 7 with a deflection of 10 mm
To evaluate stresses in the gesso layer on a deformed anisotropic wooden support, computer-aided modeling was performed. The Comsol Multiphysics software [16] was used to do calculations using the Finite Element Method. It was assumed that at the initial state (before flattening), the ground layer stress in the longitudinal and radial directions of wood was zero. Mechanical properties of ground layer and lime wood from [17, 18] were used in the simulation. However, the simulation was simplified by assuming that both the wood and the ground layer were homogeneous and continuous media.
The simulation results presented in Fig. 9 show both components of stress: perpendicular and parallel to the wood grain, which appear during flattening of the sample. The source of stress parallel to the wood grain lays in restraining any movement of the gesso in the longitudinal direction of the wood. Wood has a very high modulus of elasticity in the longitudinal direction and unusually low transverse-longitudinal Poisson ratio. It means that the wood compressed in the transverse direction has almost no longitudinal expansion. This restrains the gesso layer movement, engendering the longitudinal stress.
A series of micro-scratching tests were then performed parallel and perpendicular to the wood grain direction on a sample with different compressive stresses in the ground layer to analyze critical loads leading to gesso cracking. The total stress field leading to cracking of the ground layer was a result of the scratching process (stress exerted by the moving indenter) as well as external force applied to the sample. It should be noted that only the external force changed in consecutive experiments and therefore it was possible to simplify stress analysis by correlating only stress resulting from the external force (simulated above) with critical load leading to cracking.
As shown in Fig. 9, flattening of the sample (by applying an external load) increased stress in the gesso layer in the direction perpendicular to the wood grain to a much greater extent than in the direction parallel to the grain. This effect is clearly visible in Fig. 10 indicating that the applied method is sensitive to the direction of stresses in the analysed material. The linear fitting of experimental data for perpendicular direction to wood grains gives R2 = 0.966. Figure 10 indicates that there may or may not be a systematic correlation (R2 drops to 0.54825) between critical force and stress along the wood grain. The plot serves to show potential cross talk between the two directions. Figure 11 presents data obtained for three different specimens in three deformation states. A strong correlation between the applied stress and the critical load as well as good agreement between the instrumental measurement of critical load and its optical assessment are evident.
The ratio of critical load for micro-scratch tests performed across the wood grain to its counterpart relative to tests performed along the wood grain for different deflection of the sample (Fig. 10) is 2.5 ± 1.1. However, the finite element simulations showed that the ratio of transverse-to-longitudinal compressive stresses was 6.6. This means that the increase in the critical load while scratching along the wood grain cannot be explained exclusively by the fact that the gesso is compressed in this direction. In other words, the statistical analysis showed that with 80% confidence level, the value of the critical load obtained in the test was influenced by stress perpendicular to the scratch direction. The obtained results clearly demonstrate that critical load leading to brittle cracking is proportional to the value of compressive stress. However, these data also showed that the method was not accurate enough to provide information about an absolute value of directional stress in the analysed material. Therefore, the method should be treated at this stage as a qualitative detection rather than a quantitative determination of stress.
Critical load standard deviation was assumed to be the uncertainty of the value and propagated using the exact differentiation of the linear relation from Fig 10. Assuming linear relation between critical load LC and stress σ: LC = a σ + b we obtain linear reverse relation. \( \sigma =\frac{L_C}{a}-\frac{L_C}{a} \) . To get stress uncertainty ϵσ: we use exact differentiation \( \epsilon \sigma =\frac{\partial\ \sigma }{\partial\ {L}_C}\ \epsilon {L}_C \) Taking average standard deviation of critical load ϵLC = 0.254 N and derivative of stress as a linear function of critical load by critical load \( \frac{\partial\ \sigma }{\partial\ {L}_C}=\frac{\partial\ \sigma }{\partial\ {L}_C}=50\ \mathrm{MPa}/\mathrm{N} \) we get the single measurement error ϵσ = 13 MPa.
Measurements of Residual Stress in Gesso on Wood
The motivation for this work was to test micro-scratching as a minimally invasive method for measuring residual stress in the ground layer on a wooden substrate. In order to verify the usefulness of the method, three samples (identical to those described in the previous section) were prepared. Two of the samples were subjected to a treatment in order to induce stress in the ground layer, whereas one was treated as a reference. The treatment consisted of placing samples at high humidity (90% RH) and subsequently transferring them to low humidity. In high humidity environment, wood is expanding and gesso is experiencing a dramatic loss of stiffness, due to the transition of the rabbit-skin glue from the brittle to the ductile (gel like) state taking place at approximately 75% RH [3]. Therefore, expanding wood easily deforms (stretches) the gesso layer. During drying, the ductile gesso mass is firstly hardening and then compressed by shrinking wooden substrate. As a result, compressive stress in gesso layer is induced. The value of this stress depends on properties of materials and parameters of treatment and is generally unknown before measuring.
Three samples were tested using the scratching technique described earlier. Five scratches were performed on each specimen, error bars in Fig. 10 show uncertainty of the single measurement (standard deviation). The value of stress determined on the basis of critical load (see Fig. 11 for relation between critical load and stress) was compared with the stress in the gesso obtained using the layer removal technique [5]. The comparison is presented in Fig. 12. Although there is the same tendency in results obtained using both techniques, agreement is not perfect. It confirms that the proposed micro-scratching technique is sensitive to stress level in the material, and therefore capable of monitoring stress alterations, but rather inaccurate when providing absolute values for this stress.
Conclusions
This study made it possible to measure differences in stress levels in the ground layer on two different substrates – a homogeneous metal plate and a wooden panel, both deformed with external forces. The method is sensitive to stress direction and detects predominately stress component parallel to the direction of scratching. The method is only micro-destructive and therefore attractive for monitoring stress changes caused by relaxation processes in multi-layer materials. It has to be noted that that stress field must be uniform in the scratching area of several mm2. Information on absolute values of forces present in the analysed ground layer is still limited due to lack of a proper calibration procedure based on analysing the relationship between stress field generated during micro-scratching and critical condition of brittle cracking of the material. Such a procedure needs to be integrated by comprehensive computer-aided modeling of micro-indentation process in granular media. Although in the present form the method is too invasive to be directly applied to real artworks, it can be used for analysing model samples to provide valuable information on stresses and relaxation processes in artistic (and especially historic) materials.
This may help to understand how changes in environmental conditions affect heritage objects and to manage indoor environments in museums and historic buildings in a rational and efficient manner.
References
Bratasz Ł (2013) Allowable microclimatic variations for painted wood. Stud Conserv 58(2):65–79
Łukomski M (2012) Painted wood. What makes the paint crack? J Cult Herit 13(3):S90–S93
Krzemień L, Łukomski M, Bratasz Ł, Kozłowski R, Mecklenburg MF (2016) Mechanism of craquelure pattern formation on panel paintings. Stud Conserv 61(6):324–330
Withers PJ, Bhadeshia HKDH (2001) Residual stress. Part 1--measurement techniques. Mater Sci Technol 17(4):355–365
Nedderman RM (2005) Statics and kinematics of granular materials. Cambridge University Press, New York
Wensrich CM, Kisi EH, Luzin V (2013) Non-contact stress measurement in granular materials via neutron and X-ray diffraction: Theoretical foundations. Granul Matter 15(3):275–286
Brodu N, Dijksman JA, Behringer RP (2015) Spanning the scales of granular materials through microscopic force imaging. Nat Commun 6:6361
Holmberg K, Laukkanen A, Ronkainen H, Wallin K, Varjus S, Koskinen J (2006) Tribological contact analysis of a rigid ball sliding on a hard coated surface: Part I: Modelling stresses and strains. Surf Coat Technol 200(12):3793–3809
Ghosh D, Subhash G, Radhakrishnan R, Sudarshan TS (2008) Scratch-induced microplasticity and microcracking in zirconium diboride--silicon carbide composite. Acta Mater 56(13):3011–3022
Mecklenburg MF (1991) Some mechanical and physical properties of gilding gesso. Foundation of the American Institute for Conservation of Historic and Artistic Works. Gilded wood: conservation and history. Sound View Press, Madison, pp 163–170
Michalski S (1991) Crack mechanisms in gilding. Foundation of the American Institute for Conservation of Historic and Artistic Works. Gilded Wood Conservation and History. Sound View Press, Madison, pp 171–181
Reinking L (2007) Examples of image analysis using image J. The Department of Biology, Millersville University. https://imagej.nih.gov/ij/docs/pdfs/examples.pdf
ISO 20502 (2005) Fine ceramics (advanced ceramics, advanced technical ceramics) — Determination of adhesion of ceramic coatings by scratch testing. https://www.iso.org/standard/34189.html
Steinmann PA, Tardy Y, Hintermann HE (1987) Adhesion testing by the scratch test method: The influence of intrinsic and extrinsic parameters on the critical load. Thin Solid Films 154(1):333–349
CSM Instruments Influence of tip size on the critical load during scratch testing with the Micro Scratch Tester. APPLICATIONS BULLETIN. [Online] 2000
Zimmerman WBJ (2006) Multiphysics modeling with finite element methods, series A, vol 18. World Scientific Publishing Co., Inc, Singapore
Rachwał B, Bratasz Ł, Łukomski M, Kozłowski R (2012) Response of wood supports in panel paintings subjected to changing climate conditions. Strain 48(5):366–374
Rachwał B, Bratasz Ł, Krzemień L, Łukomski M, Kozłowski R (2012) Fatigue damage of the gesso layer in panel paintings subjected to changing climate conditions. Strain 48(6):474–481
Acknowledgments
The authors would like to express their gratitude to the Getty Conservation Institute’s Managing Collection Environments Initiative as well as the Polish National Science Centre (grant no. UMO-2011/01/B/HS2/02586) for their support. The authors would also like to thank their colleagues Arkadiusz Kupczak and Agata Mleczkowska for the Comsol modelling and SEM images.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
L. Krzemień, M. Kot and M. Łukomski state that there are no conflicts of interest.
Electronic supplementary material
ESM 1
(DOCX 11 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Krzemień, L., Kot, M. & Łukomski, M. Stress Assessment in Artistic Materials Using a Micro-Scratching Technique. Exp Tech 42, 473–479 (2018). https://doi.org/10.1007/s40799-018-0245-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40799-018-0245-2