A Note on R&D Innovation with Socially Responsible Firms

Abstract

This work revisits the R&D duopoly à la (d’Aspremont and Jacquemin, Am Econ Rev 78:1133–1137, 1988, d’Aspremont and Jacquemin, Am Econ Rev 80:641–642, 1990) (AJ henceforth) considering an economy with firms engaged in corporate social responsibility (CSR). In the traditional AJ setting without spill-over effects, firms invest in R&D as a sub-game perfect Nash equilibrium (SPNE) strategy, but they are cast into a prisoner’s dilemma. Socially responsible firms can get the same SPNE result. Preliminarily, we show that the level of firms’ social concern has a positive effect on the R&D investment. Unlike the basic framework, however, if the consumer welfare weights enough in each firm’s objective, investing in R&D becomes a firm’s utility-enhancing strategy also without R&D spillovers: the prisoner’s dilemma vanishes, and the R&D investment-decision game with CSR turns out to be an anti-prisoner’s dilemma, in which investing in R&D is the firm’s Pareto-efficient choice. Then, if firms are CSR-oriented, investing in R&D becomes a Pareto-superior outcome for society (with or without R&D spillovers). The article also shows that R&D subsidies can be used as a welfare-maximising tool.

1 Introduction

In recent decades, engagement in corporate social responsibility (CSR) activities is a relevant worldwide phenomenon involving several firms. The presence of CSR firms is a dominant global business phenomenon, as the following figures released by KPMG (2020) reveal: (1) while in 1993 only 12 per cent of the top 100 companies surveyed in 45 countries reported the realisation of CSR activities, those figures have increased to 80 per cent in 2020 in 52 countries; (2) the 250 Global Fortune Index companies (the world’s 250 largest companies) reports that those figures have risen from 35 per cent in 1999 to 96 per cent in 2020. Furthermore, the European Union institutions believe that it is important to extend the phenomenon of the CSR firms, see e.g., the European Union Commission’s Green Paper (2001), “Promoting a European framework for corporate social responsibility”.

The rationales for a firm to become socially responsible are multiple and may regard aspects of economics, politics, social integration, and ethics (e.g., Garriga and Melè 2004). For instance, according to Bénabou and Tirole (2010), CSR is a pro-social behaviour produced by multiple interacting reasons (e.g., pure altruism, material motivation, social and self-esteem concerns). Moreover, looking closer at the economics approach, the economic aspects of CSR adoption may refer to the so-called stakeholder view of the firm (Freeman 1984): firms’ managers aim to satisfy a variety of stakeholders (such as shareholders, consumers, and workers), therefore departing from the standard pure profit maximisation objective.

Likewise, the firms’ R&D investments have received increasing attention in recent years. For instance, the promotion of private firms’ R&D investments is crucial for European institutions as well. Indeed, the European Commission (2020, pp. 11–13) lists among its current objectives “…strengthening knowledge and innovation as drivers of our future growth…. to re-focus R&D and innovation policy on the challenges facing our society…to prioritise knowledge expenditure….to promote greater private R&D investments”.

However, as known from the R&D literature, R&D investments produce knowledge and information, which have the nature of public goods, and consequently are subject to fundamental market failures. As Poyago-Theotoky (2007, p. 64) clarifies, if there are no leakages of R&D information (or, in other words, spillovers are absent due to an effective patent system), then choosing “their R&D strategically (in the sense that they choose R&D first, followed by output), firms tend to over-invest in R&D as they attempt to gain an advantage over their rivals. This is a strategic over-investment effect”. In terms of the pathbreaking d’Aspremont and Jacquemin (1988) model of cost-reducing R&D (AJ henceforth), the over-investment effect results from the Nash equilibrium of the game on the choice whether to invest, which is always a prisoner’s dilemma game: firms invest too much in R&D which is detrimental for their profits.

Which are the roles played by the spill-over parameter and the cost of R&D on the occurrence of the prisoner’s dilemma (e.g., Burr et al. 2013)? First, high spillovers are always expected to reduce firms’ incentives for R&D due to the well-known free riding effect of the public goods nature of the problem, and thus they also tend to reduce the prisoner’s dilemma loss of profitability. Second, higher costs of R&D always reduce the engagement in R&D, and thus indirectly reduce the prisoner’s dilemma loss of profitability.

On the other hand, when firms engage in non-cooperative R&D and are entrapped in a profit-worsening prisoner’s dilemma, consumers are better off; moreover, these benefits more than offset the negative impact on firms’ profits, and thus social welfare increases. The prisoner’s dilemma enhances social welfare as a whole; however, it is Pareto-inferior as consumers are better off but firms are worse off.

Therefore, the question addressed in this article relates to the effects of CSR on R&D investments. We question whether and how the presence of CSR affects the unpleasant (for firms) prisoner’s dilemma result. To make this point, we extend the AJ model of cost-reducing R&D considering CSR (instead of only profit-maximizing) firms. The main findings of this work go in the direction of solving the prisoner’s dilemma that emerge in the AJ literature (Bacchiega et al. 2010) also in the absence of R&D spillovers. This is because of the pro-social effects that CSR generates on output passing through the R&D investments. The article also offer a social welfare analysis finding that the well-known positive effect of CSR on societal welfare is magnified by R&D investment choices: not only CSR firms invest in R&D more than profit-maximising firms (already pinpointed by the receiving literature), but the positive effect of the private R&D effort contribute to increase societal welfare beyond the level that can be obtained in the absence of R&D investments. The higher is the firm’s social concern, the higher is the positive welfare effect of the R&D on the society. Finally, the article studies the role of R&D subsidies in an economy with CSR-oriented firms finding, unlike the related existing literature (e.g., Amir et al. 2019), that it is convenient to subsidise the R&D activity also in the absence of R&D spillovers, i.e., R&D subsidies can be used as a welfare-maximising tool with or without disclosure on the results of the R&D activity.

The rest of the paper is organised as follows. Section 2 describes the basic elements of the model. Section 3 analyses the game-theoretic setting studying the properties of the subgame-perfect Nash equilibrium (in which both firms invest). Section 4 concentrates on the social welfare analysis and introduces R&D subsidies in an environment with CSR firms. Section 5 offers some concluding remarks.

2 The Model

The model directly follows the seminal work of d’Aspremont and Jacquemin (1988, 1990), which introduces process (cost-reducing) innovation in a Cournot duopoly and considers–in the non-cooperative version–a two-stage game in which firms choose the extent of R&D investment in the first stage and the output in the second (market) stage. Unlike AJ and in line with Bacchiega et al. (2010) and Buccella et al. (2022a, b) the present article introduces an additional stage, the investment-decision stage, in which firms choose whether to invest in R&D. However, the decision of investing or non-investing in R&D is made by CSR firms, whose aim is the maximisation of a weighted sum of profits and consumer surplus, instead of the traditional selfish profit-maximising firms considered so far in the literature.

From a modelling perspective, we assume the following standard linear inverse market demand on the consumer side:

$$p=1-q_i-q_j,\;i,j=\left\{\text{1,2}\right\},\;i\neq j$$

(1)

where $p$ is the market price and ${q}_{i}$ and ${q}_{j}$ represent the production of firm $i$ and firm $j$, respectively. The following cost function describes firm $i$’s technology (d’Aspremont and Jacquemin 1988, 1990):

$$C_i=\left(w-x_i-\beta_jx_j\right)q_i,$$

(2)

where the variables ${x}_{i}$ and ${x}_{j}$ are the R&D investment efforts chosen by firm $i$ and firm $j$, $0<w<1$ represents the ex-ante unitary cost of production, i.e., it measures the unitary technology of production cost irrespective of R&D investments, and ${\beta }_{j}\in \left[\text{0,1}\right]$ captures the extent of R&D spillovers flowing from the R&D activity of firm $j$ as a cost-reducing device to firm $i$. The R&D technology displays decreasing returns to scale, and the cost associated with a reduction of ${x}_{i}$ in the unitary production cost $w-{x}_{i}-{\beta }_{j}{x}_{j}>0$ is $\frac{\gamma }{2}{x}_{i}^{2}$, in which $\gamma >0$ is a parameter measuring the extent of efficiency of the R&D technology (the lower $\gamma$, is the higher is the R&D efficiency). Thus, firm $i$’s profits in the symmetric sub-game in which both firms invest in R&D are:

$$\Pi_i=\left(1-q_i-q_j\right)q_i-\left(w-x_i-\beta_jx_j\right)q_i-\frac\gamma2x_i^2,$$

(3)

Following a recent established literature (e.g., Goering 2007, 2008; Kopel and Brandt 2012; Lambertini and Tampieri 2012, 2015; Fanti e Buccella 2017a, b; 2021), this model assumes that all the social concerns can be interpreted as part of the consumer surplus: the feature of a CSR firm is to be sensitive to it. Therefore, we suppose that firm $i$, in its objective, aims at maximising profits plus the consumer surplus that accrues to its stakeholders. We define $0\le {k}_{i}<1$ as the exogenous parameter weighting the relative importance that each firm puts on the consumer surplus. To simplify as much as possible the analysis, we assume henceforth: (1) a symmetric value of the weight ${k}_{i}$, so that ${k}_{i}={k}_{j}=k$; (2) a symmetric value of the intensity of the spill-over externality ${\beta }_{j}$, so that ${\beta }_{j}={\beta }_{i}=\beta$; and (3) the parameters $w$ and $\gamma$ are high enough to guarantee that the feasibility conditions (i.e., the second-order condition, the stability conditions, the R&D cost conditions, etc., see Buccella et al. 2022a) are fulfilled, as it will be clear later in this article.

Therefore, the CSR R&D-investing firm $i$’s objective function can be specified as a simple parameterised combination of profits and consumer surplus, which is the firm’s utility function ($W$) and given by:

$$W_i=\Pi_i+kCS,$$

(4)

where $CS=\frac{{\left({q}_{i}+{q}_{j}\right)}^{2}}{2}$ is the consumer surplus.

The main aim of the present work is to build a three-stage game with CSR firms instead of traditional firms, whose timing resembles Bacchiega et al. (2010) and Buccella et al. (2022a, b), which is as follows: at Stage 1, each firm decides to invest (I) or not to invest (NI). At Stage 2, firms non-cooperatively choose the extent of their R&D investment, or they do not invest at all. At Stage 3, firms compete in the output market in a Cournot setting. This timing implicitly assumes that the decisions of firms about their R&D investments precede those on the quantity (following AJ). The equilibrium concept considered is the sub-game perfect Nash equilibrium (SPNE) by backward induction. We now consider the outcome of each (symmetric and asymmetric) sub-game to get the equilibrium values of the utility function $W$, to be used by each firm at the decision stage 1, showing them in the simplest possible way, leaving the reference of the details to Buccella et al. (2022a, b), which analyse the investment-decision game with traditional profit-maximising firms considering horizontally differentiated products and consumption externalities (network effects), respectively.

The equilibrium at the third stage of each sub-game (the market game) must satisfy the first-order condition:

$$\frac{\partial W}{\partial q_i}=0,$$

(5)

for $i,j=\left\{\text{1,2}\right\}$, $i\ne j$. From (5), we obtain the output reaction functions

$$q_i(q_j,x_i,x_j)=\frac{1-w+x_i+\beta x_j-q_j(1-k)}{2-k},$$

(6)

for $i,j=\left\{\text{1,2}\right\}$, $i\ne j$. Equation (6) refers to the symmetric sub-game I/I, in which both firms invest in R&D. By setting ${x}_{i}={x}_{j}=0$ it can easily boil down to the symmetric sub-game NI/NI, in which both firms do not invest in R&D. By setting ${x}_{i}>0$ and ${x}_{j}=0$ (alternatively, ${x}_{i}=0$ and ${x}_{j}>0$), one gets the asymmetric sub-game I/NI (alternatively, NI/I), in which only one firm invests in R&D. In addition to the usual effects on the output reaction functions of the intensity of the R&D externality ($\beta$), Eq. (6) clearly tells us that an increase in the weight of the consumer surplus in the firm’s objective shifts outwards each reaction function by increasing production.

By using Eq. (6) and the counterpart for firm $j$, one gets the equilibrium output as a function of the R&D expenditure, i.e.:

$${q}_{i}({x}_{i},{x}_{j})=\frac{1-w+\left(2-\beta \right){x}_{i}-\left(1-2\beta \right){x}_{j}+k(1-\beta )({x}_{j}-{x}_{i})}{3-2k}$$

(7)

The existence of a parameter weighting the consumer surplus in the objective function of the firm negatively affects the output through its own R&D investment and positively affects the output through the R&D investment of the rival.

Now, by inserting (7) in the objective function (4) (and the same counterpart for firm $j$), and maximising it with respect to ${x}_{i}$ ($i,j=\left\{\text{1,2}\right\}$, $i\ne j$), we obtain the following reaction functions in the R&D investment space:

$${x}_{i}\left({x}_{j}\right)=\frac{2\left(2-\beta \right)\left[1-w-\left(1-2\beta \right){x}_{j}\right]+2\left(1-\beta \right){k}^{2}\left[1-w-\left(1-\beta \right){x}_{j}\right]-(1-\beta )k\left[5\left(1-w\right)-6\left(1-\beta \right){x}_{j}\right]}{{(3-2k)}^{2}\gamma -k\left(1-\beta \right)\left(\beta +4k-11\right)+2\beta (4-\beta )-8}$$

(8)

The condition $g>{g}_{SOC}(\beta ,k)$ that guarantees that the denominator of Eq. (8) is positive should be always fulfilled to guarantee that the firm’s maximisation problem is meaningful (this will be clear later, see Eq. (10), where the subscript $SOC$ denotes “Second Order Condition”. Of course, Eq. (8) holds for the symmetric sub-game I/I. In the asymmetric sub-game I/NI, in which ${x}_{j}=0$, Eq. (8) represents the equilibrium R&D effort of the investing firm.

Regarding the sub-game I/I, solving the system of the R&D reaction functions of firm $i$ and firm $j$ from (8) allows us to obtain the amount of equilibrium investment (denoted as usual with an asterisk) following the process innovation effort at the second stage of the game (and consequently the symmetrical firm $j$’s response), that is:

$${x}_{i}^{*I/I}=\frac{\left(1-w\right)[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]}{{(3-2k)}^{2}\gamma -(1+\beta )[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]}$$

(9)

The numerator of (9) is positive for any feasible value of $k$. Then, ${x}_{i}^{*I/I}>0$ if and only if the denominator is positive, that is $\gamma >{\gamma }_{SC}^{{\beta }_{high}}(\beta ,k)$, which is defined in Eq. (12) and the subscript $SC$ denotes “Stability Condition”.

The second-order condition for a maximum (concavity) requires that ${\left.\frac{{\partial }^{2}{W}_{i}({x}_{i},{x}_{j})}{\partial {x}_{i}^{2}}\right|}_{{x}_{i}={x}_{i}^{*I/I}}<0$. This implies that the inequality

$$\begin{aligned}& \gamma > \frac{{k\left( {1 - \beta } \right)\left( {\beta + 4k - 11} \right) - 2\beta \left( {4 - \beta } \right) + 8}}{{(3 - 2k)^{2} }}\\ &\quad = \gamma _{{SOC}} (\beta ,k)\left( {{\text{second-order}}\;{\text{condition}}} \right),\end{aligned} $$

(10)

must hold to guarantee that the solution to the firm’s maximisation problem is economically meaningful. This condition boils down to $\gamma>\gamma_{SOC}\left(\beta,\;0\right)=\frac29\left(2-\beta\right)^2$ if $k=0$, which replicates exactly the AJ’s result in our normalised setup. The R&D equilibrium characterised by the expression in (9) is stable (in the sense of Seade 1980) if and only if the reaction functions defined in the R&D space should cross (Henriques 1990). Indeed, Henriques (1990) and Bacchiega et al. (2010) find that the R&D reaction curves can be downward sloping or upward sloping depending on the relative size of $\beta$ (the R&D externality). If they are downward sloping (resp. upward-sloping), ${x}_{i}$ and ${x}_{j}$ are strategic substitutes (resp. complements). This holds when the R&D externality is small (resp. large). The stability conditions require that $\left|\frac{d{x}_{i}}{d{x}_{j}}\right|<1$ in both cases of strategic substitutability and complementarity and thus leads to a relationship only between $\gamma$ and $\beta$ in the traditional AJ setting. Differently, the R&D reaction curves in a CSR environment can be downward sloping or upward sloping depending on the relative size of $\beta$ and $k$ and consequently the stability conditions include three parameters ($\gamma$, $\beta$ and $k$). The stability condition is $\left|\frac{d{x}_{i}}{d{x}_{j}}\right|<1$ and requires that one should impose:

$$\begin{aligned} & \gamma>\frac{\left(1-\beta\right)\left[2\left(2-\beta\right)-k\left(3-\beta\right)\right]}{3-2k}=\gamma_{SC}^{\beta_{low}}\left(\beta,\;k\right)\;if\;\\ & 0 \leq\beta<\frac{1-k}{2-k},\;\left(x_i\;\mathrm{and}\;x_j\;\mathrm{are}\;\mathrm{strategic}\;\mathrm{substitutes}\right),\end{aligned} $$

(11)

and

$$\begin{aligned}& \gamma>\frac{\left(1+\beta\right)\left[2\left(2-\beta\right)-k\left(1-\beta\right)\left(5-2k\right)\right]}{{(3-2k)}^2}\\ & =\gamma_{SC}^{\beta_{high}}\left(\beta,\;k\right)\;if\;\frac{1-k}{2-k}<\beta\leq1,\;\left(x_i\;\mathrm{and}\;x_j\;\mathrm{are}\;\mathrm{strategic}\;\mathrm{complements}\right),\end{aligned} $$

(12)

where ${\gamma }_{SC}^{{\beta }_{low}}\left(\beta ,k\right)>{\gamma }_{SC}^{{\beta }_{high}}(\beta ,k)$ for any $0\le \beta \le \frac{1-k}{2-k}$ and ${\gamma }_{SC}^{{\beta }_{low}}\left(\beta ,k\right)<{\gamma }_{SC}^{{\beta }_{high}}(\beta ,k)$ for any $\frac{1-k}{2-k}\le \beta \le 1$, that is ${\gamma }_{SC}^{{\beta }_{low}}\left(\beta ,k\right)$ is binding for any $0\le \beta <\frac{1-k}{2-k}$, and ${\gamma }_{SC}^{{\beta }_{high}}(\beta ,k)$ is binding for any $\frac{1-k}{2-k}<\beta \le 1$. Therefore, the condition that guarantees positive R&D investments ($\gamma >{\gamma }_{SC}^{{\beta }_{high}}(\beta ,k)$) from Eq. (9) and the second-order condition ($\gamma >{\gamma }_{SOC}(\beta ,k)$) are fulfilled for any $0\le \beta \le 1$ if the stability conditions are satisfied. From (9), the following lemma holds.

Lemma 1

(i) The output and the R&D investment increase directly with the level of social concern. (ii) The level of social concern always increases output indirectly, via the increase in the R&D investment.

Proof

By inspection of the first-order derivatives with respect to of Eqs. (7) and (9) (Part (i)), and because $\frac{{{\partial ^2}{q_i}}}{{\partial {x_i}\partial k}}>0$ evaluated at the equilibrium (Part (ii)).

The analysis so far should be augmented with additional constraints on the side of the costs of production. The unitary production cost $w-{x}_{i}-\beta {x}_{j}$ must always be positive. Therefore, by considering the symmetric sub-game I/I and using Eq. (9), the inequality $w-{x}_{i}-\beta {x}_{j}>0$ is fulfilled if and only if:

$$\begin{aligned} & \gamma>\frac{\left(1+\beta\right)\left[2\left(2-\beta\right)-k\left(1-\beta\right)\left(5-2k\right)\right]}{{w\left(3-2k\right)}^2}\\ & =\gamma_T^{I/I}\left(\beta,\;k,\;w\;\right),\;\left(\mathrm R\&\mathrm D\;\mathrm{cost}\;\mathrm{condition}\right),\end{aligned} $$

(13)

where the subscript $T$ stands for “Threshold”. The inequality in (13) must hold as an additional threshold in determining meaningful Nash equilibrium outcomes of the investment-decision game with CSR. Comparison of (12) and (13) clearly reveals that ${{\gamma }_{T}^{I/I}(\beta ,k,w)>\gamma }_{SC}^{{\beta }_{high}}(\beta ,k)$ for any $w<1$ and ${{\gamma }_{T}^{I/I}(\beta ,k,1)\to \gamma }_{SC}^{{\beta }_{high}}(\beta ,k)$ from above for $w\to 1$.

Now, by using Eq. (9) one can compute the equilibrium values of production as well as profits and firm’s utility, which are respectively given by:

$${q}_{i}^{*I/I}=\frac{\gamma \left(1-w\right)(3-2k)}{{(3-2k)}^{2}\gamma -(1+\beta )[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]},$$

(14)

$${{\Pi }}_{i}^{*I/I}=\frac{\gamma {\left(1-w\right)}^{2}\left\{{2\left(3-2k\right)}^{2}\left(1-2k\right)\gamma -{[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]}^{2}\right\}}{{2\left\{{(3-2k)}^{2}\gamma -(1+\beta )[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]\right\}}^{2}}$$

(15)

and

$${W}_{i}^{*I/I}=\frac{\gamma {\left(1-w\right)}^{2}\left\{{2\left(3-2k\right)}^{2}\gamma -{[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]}^{2}\right\}}{{2\left\{{(3-2k)}^{2}\gamma -(1+\beta )[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]\right\}}^{2}}$$

(16)

From Eq. (14), ${q}_{i}^{*I/I}>0$ if and only if the denominator is positive, that is $\gamma >{\gamma }_{SC}^{{\beta }_{high}}(\beta ,k)$, and $k<2/3$. From Eq. (15), ${{\Pi }}_{i}^{*I/I}>0$ if and only if $\gamma >\frac{{[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]}^{2}}{{2\left(3-2k\right)}^{2}(1-2k)}={\gamma }_{{\Pi }}^{I/I}(\beta ,k)$, which requires $k<1/2$, a condition stricter than that related to the non-negativity of output. From Eq. (16), ${W}_{i}^{*I/I}>0$ if and only if $\gamma >\frac{{[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]}^{2}}{{2\left(3-2k\right)}^{2}}$, which is always fulfilled if the condition to get positive profits holds.

One can apply the backward induction analysis so far to obtain the equilibrium values of the relevant variables in the symmetric sub-game NI/NI and in the asymmetric sub-game I/NI, which are respectively given by:

$$q_i^{\ast NI/NI}=\frac{1-w}{3-2k},$$

(17)

$$\Pi_i^{\ast NI/NI}=\frac{\left(1-w\right)^2(1-2k)}{{(3-2k)}^2},$$

(18)

which requires $k<1/2$ to be positive, and

$${W}_{i}^{*NI/NI}=\frac{{\left(1-w\right)}^{2}}{{(3-2k)}^{2}}$$

(19)

and

$${x}_{i}^{*I/NI}=\frac{\left(1-w\right)[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]}{{(3-2k)}^{2}\gamma -2{\left(2-\beta \right)}^{2}+k(1-\beta )(\beta +4k-11)},$$

(20)

$${q}_{i}^{*I/NI}=\frac{\left(1-w\right)\left\{\left(3-2k\right)\gamma -k(1-\beta )[\left(1-\beta \right)\left(1-k\right)-\beta ]\right\}}{{(3-2k)}^{2}\gamma -2{\left(2-\beta \right)}^{2}+k(1-\beta )(\beta +4k-11)},$$

(21)

and

$${q}_{j}^{*I/NI}=\frac{\left(1-w\right)\left\{\left(3-2k\right)\gamma -(1-\beta )(2-k)[2-\beta -k(1-\beta \left)\right]\right\}}{{(3-2k)}^{2}\gamma -2{\left(2-\beta \right)}^{2}+k(1-\beta )(\beta +4k-11)}$$

(22)

From Eqs. (20, 21, 22), it is possible to compute the equilibrium values of ${{\Pi }}_{i}^{*I/NI}$, ${{\Pi }}_{j}^{*I/NI}$, ${W}_{i}^{*I/NI}$ and ${W}_{j}^{*I/NI}$. We do not report their values here as they are cumbersome. The additional relevant constraints useful to determine the feasible region and compute the SPNE of the investment-decision game with CSR firms are given by the inequalities $\gamma >{\gamma }_{T}^{I/NI}(\beta ,k,w)$, which represents the R&D cost condition of the investing firm $i$, that is the condition for which $w-{x}_{i}>0$ and $\gamma >{\gamma }_{{\Pi }}^{I/NI}(\beta ,k)$, which should be satisfied to get positive profits of the non-investing firm $j$.

3 The Game-Theoretic Analysis

This section examines the first stage of the game, in which CSR firms choose whether to invest in R&D in a non-cooperative quantity-setting AJ environment. Using the equilibrium values of the firm’s utility $W$ in each sub-game, we can build the payoff matrix summarised in Table 1 regarding the R&D-investment-decision game with CSR.

Table 1 The investment-decision game with CSR (payoff matrix)

To satisfy the technical restrictions and have well-defined equilibria in pure strategies for every strategic profile (one for each player), the analysis is restricted to the feasibility constraints discussed so far. To derive all of the possible equilibria of the game, one must study the sign of the utility differentials ${\Delta }{W}_{A}={W}_{i}^{*I/NI}-{W}_{i}^{*NI/NI}$, ${\Delta }{W}_{B}={W}_{i}^{*NI/I}-{W}_{i}^{*I/I}$ and ${\Delta }{W}_{C}={W}_{i}^{*NI/NI}-{W}_{i}^{*I/I}$ for $i=\left\{\text{1,2}\right\}, i\ne j$. The analysis of the utility differentials reveals that ${\Delta }{W}_{A}>0$ and ${\Delta }{W}_{B}<0,$ irrespective of the parameter scale, whereas the sign of

$${\Delta }{W}_{C}=\frac{{\left(1-w\right)}^{2}\left[2\left(2-\beta \right)-k(1-\beta )(5-2k)\right]\left\{{\left(3-2k\right)}^{2}\left[6\beta +k(1-\beta )(5-2k)\right]\gamma -2{\left(1+\beta \right)}^{2}\left[2\left(2-\beta \right)-k(1-\beta )(5-2k)\right]\right\}}{{2\left(3-2k\right)}^{2}{\left\{{\left(3-2k\right)}^{2}\gamma -\left(1+\beta \right)[2\left(2-\beta \right)-k(1-\beta \left)\right(5-2k\left)\right]\right\}}^{2}},$$

(23)

changes depending on the relative values of $\beta$, $\gamma$ and $k$ (the denominator of (23) is always positive as the condition $\gamma >{\gamma }_{SC}^{{\beta }_{high}}(\beta ,k)$ must hold). In this regard, let

$$\gamma_C\left(\beta,k\right)=\frac{2\left(1+\beta\right)^2\left[2\left(2-\beta\right)-k(1-\beta)(5-2k)\right]}{\left(3-2k\right)^2\left[6\beta+k(1-\beta)(5-2k)\right]},$$

(24)

be the threshold value of $\gamma$ as a function of the intensity of the R&D spill-over effects and the degree of the firm’s social concern such that ${\Delta }{W}_{C}=0$ (the numerator of which is positive for all the feasible values of $k$). If ${\gamma <\gamma }_{C}\left(\beta ,k\right)$ then ${\Delta }{W}_{C}>0$, and the firm’s utilities under the strategic profile NI/NI are higher than the firm’s utilities under the strategic profile I/I. If ${\gamma >\gamma }_{C}\left(\beta ,k\right),$ then ${\Delta }{W}_{C}<0$, and the firm’s utility under the strategic profile I/I are higher than the firm’s utilities under the strategic profile NI/NI.¹

Equation (24) highlights the most significant difference between the R&D investment-decision game with traditional profit-maximising firms (Bacchiega et al. 2010) and the R&D investment-decision game with CSR firms. The results of this non-cooperative game differ from those of the traditional model developed by Bacchiega et al. (2010) in one crucial respect: in their work, the prisoner’s dilemma vanishes if and only if the extent of technological spillovers ($\beta$) is positive and sufficiently high. This would require that firms disclose (or equivalently be unable to keep undisclosed) the information on the results of their R&D investment to a certain degree (perfect patenting). However, the non-disclosure of R&D-related results in the AJ setting is in the unilateral interest of each non-cooperative firm (Buccella et al. 2021). If firms are sufficiently CSR-oriented, the prisoner’s dilemma can vanish also in the absence of R&D spillovers ($\beta =0$), in turn, representing the robust outcome according to a game-theoretic approach. When $k=0,$ Eq. (24) boils down to $\gamma_C\left(\beta,0\right)=\frac{2\left(1+\beta\right)^2(2-\beta)}{27\beta}$, so that ${\gamma }_{C}\left(\text{0,0}\right)\to +\infty$ if $\beta \to 0$. Differently, if $k>0$ and $\beta =0$ we get $\gamma_C\left(0,k\right)=\frac{2\left[4-k\left(5-2k\right)\right]}{{k\left(3-2k\right)}^2\left(5-2k\right)}<+\infty$.

Therefore, in the traditional AJ setting (Bacchiega et al. 2010) $\gamma$ can be higher or lower than ${\gamma }_{C}\left(\beta ,1\right)$ if and only if $0<\beta \le 1$, implying that under no disclosure ($\beta =0$), it is not possible to find a finite value of $\gamma$ to solve the prisoner’s dilemma of the R&D game. Differently, if firms are CSR-oriented $\gamma_C\left(0,k\right)=\frac{2\left[4-k\left(5-2k\right)\right]}{{k\left(3-2k\right)}^2\left(5-2k\right)}>0$ if $\beta =0$. Therefore, $\gamma$ can be higher or lower than ${\gamma }_{C}\left(\beta ,k\right)$ for any $0\le \beta \le 1$ if $k>0$. This means that there exists a finite value of $\gamma$ that solves the prisoner’s dilemma of the R&D investment-decision game with CSR firms. This holds regardless of the extent of R&D spillovers, including the case of no disclosure, which is in the unilateral interest of each firm in the AJ setting.

The Nash equilibrium of the R&D investment-decision game with CSR is (I,I) irrespective of the parameter configuration. This is in line with Bacchiega et al. (2010) and Buccella et al. (2022a, b). However, this equilibrium can be Pareto inefficient, so that firms are entrapped in a prisoner’s dilemma (self-interest and mutual benefit of cost-reducing innovation conflict), i.e., investing in R&D is worse off for firms, or it can be Pareto efficient (self-interest and mutual benefit of cost-reducing innovation do not conflict), i.e., investing in R&D is better off for firms and the game turns to be an anti-prisoner’s dilemma (deadlock) also in the absence of R&D spill-over. Ceteris paribus, this outcome depends on the degree of social responsibility, i.e., how firms weight the consumer surplus in their objective function. In a traditional AJ setting (Bacchiega et al. 2010), the Nash equilibrium (I,I) is Pareto inefficient for any $\gamma$ if $\beta =0$ or it can be Pareto inefficient or efficient depending on the relative weight between $\gamma$ and $\beta$ if $\beta >0$. In the R&D investment-decision game with CSR firms, the Nash equilibrium (I,I) can be Pareto inefficient or Pareto efficient depending on the relative weight between $\gamma$ and $k$ for any $\beta \ge 0$. This means that (I,I) can be Pareto efficient also in the absence of R&D spillovers if $k$ is sufficiently high.²

Result 1 pinpoints the main equilibrium outcomes of the game for $\beta \ge 0$ within the feasible region bounded by the constraints discussed so far by assuming that $w$ is sufficiently high.

Result 1. The Nash equilibrium outcomes of the R&D investment-decision game with CSR are the following:

• 1. Let $0\le \beta <0.2$ hold. If $0\le k<0.1275$ then (1.1) for any ${\gamma <\gamma }_{C}\left(\beta ,k\right)$ (I,I) is the Pareto inefficient SPNE of the R&D investment-decision game with CSR (prisoner’s dilemma), and (1.2) for any ${\gamma >\gamma }_{C}\left(\beta ,k\right)$ (I,I) is the Pareto efficient SPNE of the R&D investment-decision game with CSR (anti-prisoner’s dilemma or deadlock). (1.3) If $0.1275\le k<0.5$ then (I,I) is the Pareto efficient SPNE of the R&D investment-decision game with CSR, so that the game is an anti-prisoner’s dilemma (deadlock) for any feasible value of $\gamma$.

• 2. Let $0.2\le \beta \le 1$ hold. Then, for any $0\le k<0.5$ (I,I) is the Pareto efficient SPNE of the R&D investment-decision game with CSR, so that the game is an anti-prisoner’s dilemma (deadlock) for any feasible value of $\gamma$.

Proof

By equating $\gamma _{C} \left( {\beta ,k} \right)=\gamma _{\prod }^{{I/NI}} \left( {\beta ,k} \right)$ and setting $\beta =0$ one can get $k=0.1275$. By equating, e.g., $\gamma _{{SC}}^{{\beta _{{low}} }} \left( {\beta ,k} \right) = \gamma _{C} \left( {\beta ,k} \right)$ and setting $k = 0$ one can get $\beta = 0.2$. If $\gamma < \gamma _{C} \left( {\beta ,k} \right)$ then $\Delta W_{A}>0$, $\Delta W_{B}<0$ and $\Delta W_{C}>0$, so that the SPNE (I,I) is Pareto inefficient. If $\gamma > \gamma _{C} \left( {\beta ,k} \right)$ then $\Delta W_{A}>0$, $\Delta W_{B}<0$ and $\Delta W_{C}>0$, so that the SPNE (I,I) is Pareto efficient. □

Result 1 pinpoints a relevant difference from Bacchiega et al. (2010): introducing a mechanism that favours a pro-social behaviour in an AJ setting allows to solve the (prisoner’s) dilemma embedded in the R&D game also in the absence of R&D spillovers (i.e., no disclosure). In fact, it is sufficient that the consumer surplus weights enough in the firm objective. Indeed, an increase in the weight of the consumer surplus in the firm’s objective favours the R&D investment for the investing firms but also the production in all sub-games. This, in turn, causes an increase in profits and consumer surplus; however, the increase in the R&D investment sustains the output of investing firms and this causes the utility of the investing firms to grow more than the utility of the non-investing firms. More specifically, the narrative following Lemma 1 reveals that the adoption of CSR behaviours always implies a more intense R&D investment and a larger output. There are, however, two counterbalancing effects of the level of social concern on the utility of the CSR firm. A larger social concern implies (1) a larger output as well as a larger R&D investment (direct effect); and (2) a further larger output due to the cost reduction induced by the larger R&D innovation (indirect effect). This expansive effect on output leads, on the one hand, to a price reduction which is profit-reducing (if ${\Delta }{W}_{C}>0$, the profit-reducing price effect overweighs the profit-enhancing output effect); on the other hand, to an increase in the consumers’ welfare (which enjoy the results of the lower price and higher quantity). The second effect becomes prevailing when the weight on the consumers’ welfare is sufficiently significant (${\Delta }{W}_{C}<0$). Also, workers enjoy the output expansion because employment increases.³ Hence, the main stakeholders–consumers and workers–enjoy the increase in the firms’ social concern and the corresponding increase in R&D innovation and output.

If for some technological reasons CSR firms can disclose the results of their R&D activity to a sufficiently high degree, they can be better off by investing in R&D also when there is no pro-social behaviour. Of course, the R&D spillovers deepen the investment effect through the usual channels and then favour the emergence of a Pareto efficient Nash equilibrium.

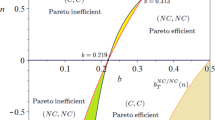
Figures 1 and 2 depict the utility differentials of CSR firms in the $(\gamma ,k)$ space for $\beta =0$ and $\beta =0.2$, respectively and are plotted for $w=0.8$. The figures also show the feasible (white) region and the unfeasible (sand-coloured) region. The feasible region is bounded by the relevant constraints discussed so far and shows the emergence of a Pareto inefficient or Pareto efficient Nash equilibrium. An increase in $\beta$ shifts downwards the black dotted line (${\gamma }_{C}\left(\beta ,k\right)$) shrinking the area of Pareto inefficiency and expanding the area of Pareto efficiency of (I,I) for the players. When the R&D spill-over is sufficiently high ($\beta \ge 0.2$), the Nash equilibrium is Pareto efficient for any $\gamma$ and $k$ in the feasible region.

Fig. 1

CSR firm-utility differential in the in the $(\gamma ,k)$ space for $\beta =0$ and $w=0.8$. The sand-coloured region represents the unfeasible parameter space. If ${\Delta }{W}_{C}>0$, the Nash equilibrium (I,I) is Pareto inefficient and the R&D game with CSR firms is a prisoner’s dilemma. If ${\Delta }{W}_{C}<0$, the Nash equilibrium (I,I) is Pareto efficient and the R&D game with CSR firms is an anti-prisoner’s dilemma (deadlock)

Fig. 2

CSR firm-utility differential in the in the $(\gamma ,k)$ space for $\beta =0.2$ and $w=0.8$. The sand-coloured region represents the unfeasible parameter space. The Nash equilibrium (I,I) is Pareto efficient and the R&D game with CSR firms is an anti-prisoner’s dilemma (deadlock) irrespective of $\gamma$ and $k$

The comparison between Figs. 1 and 2 clearly illustrates Result 1. Therefore, we note that also in the case of CSR-oriented firms the presence of R&D spillovers tends to make more likely–in line with the results of Bacchiega et al. (2010) and Buccella et al. (2022a, b)–the occurrence of a Pareto-efficient R&D investment choice by firms.

4 R&D Subsidies as a Welfare Maximising Tool in an Environment with CSR Firms

The analysis can also be extended by studying the behaviour of social welfare, defined as $SW=2{\Pi }+CS$, following the equilibrium outcomes of the game. Specifically, we stress, in line with the already established outcomes of the literature, equilibrium social welfare under I/I in this environment is larger than the corresponding level under NI/NI, i.e., ${SW}_{i}^{*I/I}>{SW}_{i}^{*NI/NI}$, and both are increasing functions of $k$. However, the social welfare differential ${SW}_{i}^{*I/I}-{SW}_{i}^{*NI/NI}$ increases more than proportionally with $k$. This means that not only R&D-investing firms favour a pro-social outcome more than non-investing firms, but the positive effect of the R&D effort exerted by each firm on the society is higher when firms are of CSR-oriented, and the higher is the firm’s social concern the higher is the increasing effect on the societal perspective of the R&D investments. We do not report here the analytical details of this study, but they are available on request.

This section aims also at complementing the analysis made so far with some policy prescriptions. The main result of the R&D game with CSR firms is related to the solution of the prisoner’s dilemma emerging in Bacchiega et al. (2010). In this regard, the pro-social behaviour allows CSR-R&D-investing firms to increase their payoffs more than CSR-non-investing firms. This allows to let the game become a deadlock instead of a prisoner’s dilemma. This result–together with that on social welfare–opens the route to policies that favour the CSR behaviour. A policy instrument that can be used in this environment is represented by the standard R&D subsidy aimed at incentivising the private R&D effort along the line of Hinloopen (1997), Hinloopen (2000) and Amir et al. (2019). In what follows, we briefly present the structure of the R&D incentive scheme in the subgame I/I and then compare the welfare outcomes.

The public policy to incentivise the firm’s R&D effort directly follows the model of Amir et al. (2019) and shows that $k$ has a relevant role at the optimum. Specifically, unlike Amir et al. (2019), when firms are CSR-oriented the optimal subsidy is positive also in the absence of R&D spillovers ($\beta =0$).

From a modelling perspective, we assume that the R&D subsidies towards firm $i$ (${{\Sigma }}_{i}>0$) and firm $j$ (${{\Sigma }}_{j}>0$) are financed at a balanced budget with a uniform non-distorting lump-sum tax ($T>0$) on the side of consumers (i.e., the tax does not cause additional violations of the conditions for social efficiency). The available post-tax exogenous nominal income of the representative consumer ($M-T>0$) is high enough to avoid corner solutions. Therefore, the government budget constraint reads as follows:

$$T=\Sigma_i+\Sigma_j,$$

(25)

where ${{\Sigma }}_{i}=\sigma \frac{\gamma }{2}{x}_{i}^{2}$, ${{\Sigma }}_{j}=\sigma \frac{\gamma }{2}{x}_{j}^{2}$ and $0\le \sigma \le 1$ is the subsidy rate. Definitively, the government first announces the policy, and then let firms be engaged in the R&D investment decision game with CSR discussed so far.

Firm $i$’s utility in the sub-game I/I becomes:

$${W}_{i}^{I/I}=\left(1-{q}_{i}-{q}_{j}\right){q}_{i}-\left(w-{x}_{i}-\beta {x}_{j}\right){q}_{i}-\frac{\gamma }{2}{x}_{i}^{2}\left(1-\sigma \right)+kCS$$

(26)

Equation (26) is used to compute the Nash equilibrium of the sub-game I/I following the choices at Stage 2 and Stage 3 described in Sect. 2. The decision of CSR firms at Stage 1 do not change in presence of R&D subsidies so that the SPNE continues to be (I,I). Then, social welfare at the equilibrium can be computed as ${SW}^{*I/I}\left(\sigma \right)={CS}^{*I/I}\left(\sigma \right)+{2{\Pi }}^{*I/I}\left(\sigma \right)-{T}^{*I/I}\left(\sigma \right)$. The analysis of ${SW}^{*I/I}\left(\sigma \right)$ leads to the following proposition.

Proposition 1

Introducing R&D subsidies in an environment with CSR-oriented firms is welfare improving, and there exists a welfare-maximising optimal policy if and only if:

$${\sigma=\sigma}^{OPT}\left(k\right)=\frac{6\beta+k\left[\left(1-\beta\right)\left(1-2k\right)-8\beta\right]}{4(1+\beta)(1-k)}<1,$$

(27)

for any $0\le \beta \le 1$ and $0\le k<1/2$, where (1) ${\sigma }^{OPT}\left(k\right)>0$ for any $0\le \beta \le 1$ if $0<k<1/2$, (2) $\sigma^{OPT}\left(0\right)=\frac{3\beta}{2\left(1+\beta\right)}>0$ for any $0<\beta \le 1$ if $k=0$ and ${\sigma }^{OPT}\left(0\right)=0$ if $\beta =0$ and $k=0$, and (3) ${SW}^{*I/I}\left(\sigma \right)$ is a monotonic decreasing function if $\beta =0$ and $k=0$.

Proof

Differentiating SW^*I/I for σ for one gets:

$$sgn\left\{{\left.\frac{{\partial SW}^{\ast I/I}\left(\sigma\right)}{\partial\sigma}\right|}_{\sigma=0}\right\}=sgn\left\{6\beta+k\left[\left(1-\beta\right)\left(1-2k\right)-8\beta\right]\right\}>0,$$

(28)

and

$$sgn\left\{\frac{{\partial SW}^{*I/I}\left(\sigma \right)}{\partial \sigma }\right\}=sgn\left\{4\left(1+\beta \right)\left(1-k\right)\sigma -6\beta -k\left[\left(1-\beta \right)\left(1-2k\right)-8\beta \right]\right\}$$

(29)

Then, $\frac{{\partial SW}^{*I/I}\left(\sigma \right)}{\partial \sigma }=0$ if and only if $\sigma ={\sigma }^{OPT}\left(k\right)$. Therefore, $\frac{{\partial SW}^{*I/I}\left(\sigma \right)}{\partial \sigma }>0$ if $\sigma <{\sigma }^{OPT}\left(k\right)$ and $\frac{{\partial SW}^{*I/I}\left(\sigma \right)}{\partial \sigma }<0$ if $\sigma >{\sigma }^{OPT}\left(k\right)$. Point 1 immediately follows from (27). Point 2 follows from (27) by setting either $\beta >0$ and $k=0$ or $\beta =0$ and $k=0$. Point 3 follows from the sign of $\frac{{\partial SW}^{*I/I}\left(\sigma \right)}{\partial \sigma }$ by setting $\beta =0$ and $k=0$, that is $\frac{{\partial W}^{*I/I}\left(\sigma \right)}{\partial \sigma }=\frac{-288{\gamma }^{2}{\left(1-w\right)}^{2}\sigma }{{\left[9 g\left(1-\sigma \right)-4\right]}^{3}}<0$. □

Proposition 1 resembles and complements Amir et al. (2019) with CSR-oriented firms. The policy implications are interesting as–unlike Amir et al. (2019)–R&D subsidies can be applied also in the absence of R&D spillovers as a welfare-improving fiscal tool. Indeed, the benefits of introducing this kind of fiscal tool are intensified by the pro-social behaviour of firms. This result is in line with Buccella et al. (2022a), who introduced this kind of instrument in a traditional AJ setting with horizontal product differentiation, i.e., CSR-oriented firms always under-invest in R&D in the market so there is the need to incentivise their R&D activity.

5 Conclusion

By revisiting the R&D duopoly à la d’Aspremont and Jacquemin (1988, 1990) to include socially responsible firms (CSR), this article shows that the adoption of CSR rules implies a more intense R&D investment and a larger output. If the social concern in the firm’s objective function is low, the R&D innovation reduces the utility of the CSR firm: that is, firms are cast into a classical prisoner’s dilemma. This fact is exacerbated by a low cost of investment because in such a case firms tend to over-invest. However, if the social concern is not too low, the prisoner’s dilemma vanishes, and firms increase their utility by increasing their R&D innovation. Importantly, this result holds also in the absence of R&D spillovers, i.e., in the case of no disclosure of the R&D-related results. This result arises because the firm’s utility function increases the weight of consumers; thus, the profit-reducing effect is more than counterbalanced by the consumers’ welfare-enhancing effect. Our outcome has a win-win effect: the larger the social concern, the larger the R&D innovation, and the higher both firms’ utility and the utility of the other agents, i.e., consumers and workers. Indeed, social welfare is also higher than in the absence of R&D investments, in turn, representing therefore a win-win outcome from a societal perspective. If firms adopt a pro-social behaviour, there is no need to disclose to get a Pareto efficient result in the game and a Pareto superior outcome for the society: it is sufficient weighting enough the consumer surplus in the firm’s objective. The work also pinpointed the role of R&D subsidies in the AJ setting with CSR-oriented firms.