1 Introduction

Today, network goods, whose utility increases with the number of users who consume the goods, are of extreme relevance. The massive expansion of mobile devices such as smartphones and tablets, and their relative software and apps provide an effective example.Footnote 1

In several cases, network industries are characterised by an oligopolistic market structure whose labour force can be unionised. On the one hand, tech corporations such as Silicon Valley giants Apple and Facebook are not unionised, and their attitude towards organised work has fluctuated between aversion and clear hostility (Quartz 2017).

On the other hand, in other network industries, a different unionisation path can be recognised, for example, as seen in the US wireless career provider industry. According to the Bureau of Labour Statistics data, after the deregulation in the sector and the shrinking workforce at Baby Bells, the percentage of unionised workers declined from 42.4 percent in 1983 to 21.8 percent in 2002 (The New York Times 2006). Large operators such as Verizon Wireless have discouraged unionisation. In their view, organised labour hinders their ability to move workers, cut costs, and make the necessary changes to compete in a high-tech industry. The management of Cingular Wireless, now called AT&T Mobility, made an opposite move with respect to its rivals. In 2004, the company acquired AT&T Wireless. Since July 2005, the Communications Workers of America, the largest union operating in the US telecommunication sector, recruited 16,500 former AT&T workers at retail stores and call centres nationwide as union members, sending the message that organised labour can serve as a management ally. Indeed, the AT&T Mobility market shares increased from 26.6 percent in 2011 (CNNmoney 2011) to 34.07 percent in 2018 (Statista.com 2019).

Furthermore, in recent years, other several large companies in network industries have become unionised. For instance, in September 2015, 38 full-time bug testers employed to review apps for Microsoft voted to create a union, the Temporary Workers of America (BloombergBusinessweek 2015). On January 4, 2021, hundreds of employees at Google and its parent company, Alphabet, launched a union (open to full-time workers as well as contractors at the tech giant), called The Alphabet Workers' Union, in which 226 of the group's members signed union cards with the Communications Workers of America (CNN.com 2021).

Because a vast body of literature in industrial organisations has acknowledged the unions’ crucial role in oligopolies (see, inter alia, Dowrick 1989, 1990; Horn and Wolinsky 1988; Correa-López and Naylor 2004), it is appropriate to study the effect of unionisation in those industries.

In addition, several large unionised companies in network industries also engage in corporate social responsibility (CSR) activities, one of the most worldwide attention-catching phenomena during recent decades. In fact, according to KPMG, CSR engagement is currently a dominant global business practice. In 2002, only 23 percent of the top 100 companies surveyed in 45 countries have reported the realisation of CSR activities. Those figures have increased to 75 percent in 2017. Closer examination of the 250 Global Fortune Index companies (the world’s 250 largest companies) reveals that those figures have risen from 45 to 93 percent. Network industries are in a leading position among the sectors that have witnessed a striking development pace with regard to CSR activities. Indeed, according to recent KPMG reports, among the surveyed industries, the technology, media, and telecommunications sector demonstrate the highest percentage, with 79 percent of the companies reporting CSR activities (KPMG 2005, 2017). In detail, the telecommunication subsector has the largest share of firms reporting CSR activities, with 87 percent of the companies (KPMG 2016a, b). Moreover, the Reputation Institute global CSR survey reveals that companies in network industries have established a major presence in the world’s top ranking with regard to the companies with the best CSR reputations: Microsoft ranks 5th, Sony 6th, Intel 11th, Google 14th, and Philips 18th (Reputation Institute 2019).

Empirical studies have determined that labour unions can take different positions with regard to CSR, especially if CSR can affect bargaining issues (Colombo et al. 2019). Empirical evidence exists that unions have a proactive role in advancing social responsibility, particularly concerning the broader social and environmental issues; their involvement seems to improve the possibility that companies positively counteract such demands (e.g. Brammer 2011). On the other hand, other contributions have revealed that unions can play an antagonistic role with respect to CSR, mostly when those activities give the impression of (1) weakening the unions’ main objectives to raise employment and wages (e.g. Fredriksson and Gaston 1999) and (2) providing a new strategy for union avoidance (e.g. Marens 2010). Indeed, unions are commonly believed to perceive CSR activities to threaten employees when companies spontaneously develop precise social and environmental conduct which generates a trade-off with employees’ interests or when unions believe companies consider them not to be specific stakeholders but in the same vein of other internal or external actors (Greenwood and Anderson 2009; Preuss 2008; Van Buren and Greenwood 2011).

Because of the relevance of network industries in contemporary economies, and given that the joint presence of network externalities, unionisation, and CSR activities within a firm are widespread observed facts, a comprehensive analysis of the interconnections between network externalities, unionisation, and CSR is well timed. In fact, the interplay of these elements can affect the standard outcomes of strategic oligopolistic contexts.

In fact, on the one hand, by altering production (labour) costs, unionisation can influence the consumers’ expectations with regard to total sales and the final prices of the products, with consequent impact on the commercial/business strategies of the operating companies. On the other hand, the presence of CSR can impact the union wage setting for companies and their profitability: network externalities are an exogenous market feature; however, CSR activities can be a firm’s choice variable strategically used to enhance its performance.

Furthermore, other plausible rationales for the network firms to assume involvement in CSR can be: (1) to create a signal effect: in fact, having relevant lock-in effects, the companies’ engagement in CSR represents a clear signal to influence buyers' expectations and demand. Therefore, not adopting CSR behaviours and losing one client from the installed base generates a double penalty for the company: one is the product unit lost, and the other is the lower consumer utility. Consequently, the lower willingness to buy/demand among those who will evaluate the purchase in the future. Another point of plausible rationale is (2) the size of their markets imply large budgets for communication strategies and corporate identity, and CSR is amongst the recent trends.

According to Garriga and Melè (2004), the concept of CSR can be interpreted in several ways. The most relevant approaches concentrate on one of the following aspects of social reality: economics, politics, social integration, and ethics. CSR can be broadly defined as a “company’s verifiable commitment to operating in an economically, socially, and environmentally sustainable manner that is transparent and increasingly satisfying to its stakeholders” (Katsoulakos et al. 2004). For instance, CSR cover activities ranging from the adoption of codes of conduct and customer relationship management (economic aspects) to environmental actions, labour practice indicators, standards for suppliers, and philanthropy (social aspects).

Looking closer at the economics’ approach, which is relevant to this paper, a corporation is a tool to create wealth and whose unique social responsibility is to maximize shareholders’ value. As Nobel Prize-winning Milton Friedman (1970) clearly states, “the only one responsibility of business towards society is the maximisation of profits to the shareholders within the legal framework and the ethical custom of the country”.

In detail, this paper focuses on one of the economic aspects of CSR adoption, that is consumer friendliness (consumer satisfaction) and implicitly, it is hypothesised as a stakeholder view of the firm (Freeman 1984). That is, managers aim to satisfy a variety of stakeholders, therefore departing from the standard objective of the pure profit maximisation, thereby influencing firms’ outcomes.

In the standard industrial organisation literature (e.g. Cournot competition), to maximize the shareholders’ value coincides with firms’ short-term profit orientation. Therefore, in the framework of the basic Cournot model, it seems that there would be no room to engage in CSR activities in an industry at equilibrium: in fact, from the perspective of profit-seeking shareholders, an excessive amount of output is produced. Thus, such over-production would be unprofitable, unless CSR activities have a positive (direct or indirect) impact on a firm’s economic costs.Footnote 2 However, engagement in CSR can become relevant if firms start considering CSR as a strategic variable that can be used in oligopolistic markets. In fact, shareholders can see CSR engagements as a commitment device for their strategic choices in an oligopolistic framework aimed at maximising their profits by increasing its own market share in a manner similar to the managers’ incentives towards sales the managerial delegation literature analyses.

Up to the current stage, a broad and expanding body of literature has disjointedly investigated the impact of CSR activities and network externalities on firms’ market behaviour. This paper addresses the following research questions: (i) Does the presence of unions modify the profit-enhancing role played by the choice of firms’ owners to be socially interested in network industry?; (ii) How does the choice of firms’ owners to become socially interested affect the welfare of workers and consumers and of the overall society?; (iii) Is the choice of CSR levels prior to or after the renewal of wage contracts better for owners (and the other agents)?

To answer those questions, we use two three-stage games in which owners can cooperate in the choice regarding the CSR level structure. However, once the level of CSR engagement is fixed, companies compete in the product market. In other words, with regard to the choice of CSR, firms act in a semi-collusive way.Footnote 3 This is an aspect that the industrial organisation literature has broadly investigated in other fields in which firms compete in a dimension, generally price or quantity, because the competition policy prevents companies from colluding (explicitly) in the market for final products and services. Nonetheless, prior to the market stage, firms might collude on other dimensions such as investments on product quality (e.g. Foros et al. 2002), advertising (e.g. Dewenter et al. 2011), and R&D activities (e.g. Brod and Shivakumar 1999), because semi-collusion can turn out to be advantageous for them.

We define two games by distinguishing the case in which wage contracts are stipulated prior to/after the decision of whether to engage in CSR.Footnote 4 We show that, when unions set wages prior to owners’ choice of the CSR levels (game A), CSR raises wages and employment, and therefore, workers in CSR-type firms achieve greater welfare. At the same time, the output expansion induced by the social responsibility—to the extent that the intensity of network effect is so great that prices are reduced less than the extent to which quantities are increased—enhances the firms’ profitability despite the induced wages raise. As a consequence, to be a CSR-type firm, increasing the welfare of owners, consumers, and workers, is a Pareto-superior choice.

On the other hand, when owners choose the CSR levels prior to the unions’ wage-setting stage (game B), they tend to reduce the CSR level because, as first movers, they can observe that by selecting a high CSR level, they also induce an increase in wages, notably when unions are wage-aggressive. In comparison to the case in which unions set wages at the beginning of the game, this crucial effect on the wage costs side allows firms, on the one hand, to achieve higher profits. However, on the other hand, the CSR levels are always lower in such a case, and the choice to engage in CSR is less likely the more wage-aggressive unions are. Also, in this case, the owners’ engagement in social responsibility raises the welfare of owners, consumers, and workers, which leads again to a Pareto-superior outcome. Moreover, the comparison of the results under the two different timings with respect to the decisions on wages and CSR shows that, on the one hand, wages and profits are always higher, while on the other hand, the welfare of workers, consumers, and thus society as a whole are always lower in game B than in game A, despite the higher profits. This implies that: (i) firm owners should prefer to be a leader of their own unions in determining the sequence of decisions on CSR and wage contracts and (ii) the timing of the decision about CSR relative to that about the wage setting generates an unsolvable conflict of interest with regard to the economic agents’ welfare between the firms’ owners on the one side and consumers, unions (workers), and the overall society, on the other side.

In conclusion, the noteworthy finding is that, in a network industry, also under unionisation, and regardless of whether the wage setting occurs prior to or after the choice of the CSR levels, being a CSR-type firm can lead to larger profits and thus higher welfare for their owners/stakeholders. In other words, the findings of this paper clearly indicate that the engagement in consumer-friendly CSR activities can be motivated by the selfish behaviour of the firms’ owners, revealing that the Friedman’s exhortation (that the firm must pursue only the owners’ interests) is satisfied.

In the next section, we survey the relevant related literature. Then, in Sect. 3, we introduce the basic game model with unions and the endogenous choice of CSR activities by owners, under the two above-described sequences of moves. For comparative purposes, in Sects. 4 and 5, the results under each sequence of moves are (analytically and numerically) compared to equilibrium outcomes of the standard model without CSR. On the other hand, Sect. 6 compares the outcomes of the models under the two different sequences of moves and derives the main results. The last section sums up our findings and outlines areas for future research.

2 Literature review

The literature has followed different approaches to focus on the issue relative to a firm’s decision to become of CSR type. On the one hand, a substantial part of the literature attributes the firms’ CSR engagement to the fact that consumers price it (e.g. Manasakis et al. 2013, 2014; Graf and Wirl 2014), shareholders exhibit social concerns (e.g. Baron 2008), and other social actors encourage firms to engage in CSR (e.g. Baron 2001; Baron and Diermeier 2007). For example, Manasakis et al. (2013, 2014) and Graf and Wirl (2014) assume that consumers are willing to pay a higher price for the goods a CSR firm produces. Baron (2008) assumes that firms will adopt CSR either because consumers reward social activities or because shareholders and management value them (or both). The analysis of Baron (2001) and Baron and Diermeier (2007) considers the role of political and social activists (frequently motivated by social or ethical concerns) as one of the business environment’s central factors that place pressure on firms for social involvement. In fact, the activism’s aim is often to influence firms’ behaviours and industry practices. Scholars such as Becchetti et al. (2016) assume that employees are unique corporate stakeholders, and CSR-employment contracts exist to prevent a company from laying off workers, even if subsequent negative shocks affect the accumulation of capital.

On the other hand, other papers assume either that CSR engagement can be rationalised for its strategic role, even if neither consumers nor shareholders evaluate social activities (Goering 2012; Brand and Grothe 2013, 2015; García et al. 2018), or that CSR is exogenously given (e.g. Goering 2007; Lambertini and Tampieri 2012, 2015; Fanti and Buccella 2017a, b) or endogenously chosen by only one firm (Kopel and Brand 2012) or all firms in the market (Hino and Zennyo 2017; Nakamura 2018; Planer-Friedrich and Sahm 2018, 2020). In those works, CSR is modelled as consumer-friendly activities, i.e. firms also consider the consumers’ welfare in their objective function.

For instance, Goering (2012) studies a bilateral monopoly in which either the manufacturer or the retailer is socially concerned. A share of the consumers’ surplus which is added to the firm's profit in the objective function, represents the firm's social concern. The findings reveal that the optimal two-part tariff depends on the firms’ objective function, and CSR decreases a firm's profit. Brand and Grothe (2013) further develop the analysis of the case in which both the manufacturer and the retailer have social concerns and investigate the impact of CSR on a perfectly coordinated marketing channel. The authors reveal that the equilibrium outcomes are independent of the retailer's level of CSR. In an extension of their previous work, Brand and Grothe (2015) find that a firm’s social concern increase profits for both the manufacturer and retailer, essentially because CSR activities mitigate the double marginalisation problem. García et al. (2018) investigate CSR in a linear bilateral monopoly with cost-reducing R&D investment and the endogenous timing game.

In a managerial delegation game under Cournot–Stackelberg competition, Hino and Zennyo (2017) study the endogenous decision-making behaviour regarding the CSR level. The authors show that, when firms sequentially select the CSR level, the follower can reach its maximal profit, which is also larger than that of the leader. Extending the work of Hino and Zennyo (2017), Nakamura (2018) analyses the endogenous choice of strategic contracts in an asymmetric duopoly, with substitute goods in which a managerial firm offers a standard sales delegation contract, and a CSR firm offers a managerial scheme based on a linear combination of social welfare and quantity. Planer-Friedrich and Sahm (2018, 2020) consider symmetric Cournot competition and show that the endogenous level of CSR is positive, but such positive CSR levels imply smaller equilibrium profits.

Goering (2007) creates a managerial delegation model in which managerial incentives are divergent from the firm’s true objective. Only one firm adds to profits a share of the consumer surplus in its objective function. The author finds that managerial incentives decrease as the share of the consumer surplus in the CSR-type firm’s objective function increases. This is because the CSR-type firm moves closer to a social planner’s objective function. Likewise, Kopel and Brand (2012) consider a duopoly in which firms can choose to hire managers; however, only one firm can engage in socially responsible activities. The main result is that CSR can be beneficial, provided that it is not broadly used.

Fanti and Buccella (2017a) study the firms’ strategic choice to adopt CSR using a Cournot duopoly model with differentiated products. Making use of a game-theoretic approach, the authors show that, depending on the degree of product differentiation and firms’ level of social concern, several equilibria can emerge. In fact, either all firms engage in CSR or are profit-maximising, or asymmetric and multiple symmetric equilibria can arise in the industry. As expected, all contributing studies reveal that CSR activities (also when endogenously determined) reduce profits at the Nash equilibrium. Nonetheless, in a duopoly with managerial firms, Fanti and Buccella (2017b) find that undertaking CSR is the sub-game-perfect Nash equilibrium, and this engagement increases the firms’ profitability, while it is detrimental for the welfare of consumers and society, a result in contrast to the conventional one obtained with non-managerial firms.

With regard to the interaction of CSR and labour market institution, in particular trade unions, the subject has not received much attention in the literature. However, Fanti and Buccella (2019a, b) and Goerke (2020) have introduced this interaction in their analysis. Fanti and Buccella (2019a, b) move from an industrial organisation perspective and consider a unionised oligopoly in which firms show decreasing returns to scale technology, and a monopoly union fixes the wage at the industry level. Despite the different frameworks, both papers show that the owners’ choice of engaging in consumer-friendly CSR activities is motivated by the firms’ purely selfish interest: in fact, profits under CSR are higher than those under the standard profit-maximising rule. The reason for this result is that the distortion created by the CSR objective curbs the union wage demand. Nonetheless, the union, consumers, and social welfare on the whole with CSR are higher than without CSR: the firms’ owners social concern leads to a Pareto-superior outcome.

Goerke (2020) analyses the impact of CSR activities on firm-union’s bargaining outcomes. The embeddedness of CSR objectives leads firms to expand output, and the effects on bargaining outcomes are different depending on the institutional arrangement: ambiguous wage and employment consequences arise under wage negotiations only and an increase in employment under efficient bargaining, in which wages and employment are negotiated. From a normative perspective, CSR objectives make a welfare‐enhancing role of unions more likely in the presence of wage negotiations, while the reverse holds true in the case of efficient bargaining.

With regard to network industries, an increasing number of scholars have started studying how the presence of positive consumption externalities/network effects can alter the results of the standard models of imperfect competition. Hoernig (2012), Chirco and Scrimitore (2013), Battacharjee and Pal (2014), and Fanti and Buccella (2016a), among others, have analysed network models mainly focusing on the role of strategic managerial delegation or the role of bargaining agenda in a unionised monopoly (e.g. Fanti and Buccella 2016b) following the simple mechanism describing the network effects established by Katz and Shapiro (1985), as also assumed in this work, in which the surplus a consumer obtains directly increases with the number of other consumers of the goods. To the best of the authors’ knowledge, the only papers dealing with CSR in network industries are Fanti and Buccella (2016c, 2018). Fanti and Buccella (2016c) analyse a duopoly in a network industry in which firms engage in CSR. They show that the presence of network effects can improve firms' profitability, in contrast to the conventional result that the higher the weight on CSR, the lower the firms’ profitability.

It has to be remarked that, in the standard IO models’ framework, whenever firms are consumer-friendly socially concerned, profits decrease and, consequently, the shareholders’ value does as well. Such a negative impact on profits occurs even if the strategic effect of CSR is taken into account, exactly as in the case of the managerial delegation. In fact, the adoption of CSR increases the profits of the firm that engages in social activities that its rival does not; thus, all firms have an incentive to engage in CSR, and in equilibrium, this leads profits of all firms to decrease. However, Fanti and Buccella (2018) recently show the rather surprising result that, in network industries, owners can find advantageous to consider—cooperatively as well as non-cooperatively—engaging in CSR activities in the form of caring also for the consumers’ welfare when they decide the quantities in the market competition. In such a paper, those authors assume a competitive labour market (i.e. without unions). However, given the diffusion of unionised labour in network industries in Europe and the rise of unions in leading US companies, the present paper includes in the analysis the presence of organised work to investigate the role that unionisation can have in affecting wage and employment (and, consequently, CSR) levels as well as the overall welfare.

3 The model

We assume a duopoly industry in which firms produce homogeneous network goods. The inverse linear demand function (see Fanti and Buccella 2016b) is

$$p = a - q_{i} - q_{j} + n(y_{i} + y_{j} ),$$
(1)

where \(p\) denotes the price of the goods, \(q_{i}\) and \(q_{j}\) are the quantities the two firms (i.e. \(i,j = 1,2;\;i \ne j\)) produce, \(y_{i}\) and \(y_{j}\) are the consumers' rational expectations about the firms’ sales (see Katz and Shapiro 1985), the parameter \(n \in [0,1)\) denotes the strength of network effects (i.e. the higher the value of n is, the stronger the network effects are), and \(a > 0\) is the intercept of the demand function.

It is assumed standard constant returns to scale production function in the sole input, labour, identical for both firms:

$$q_{i} = AL_{i}$$
(2)

where \(L_{i}\) is the labour force firm i employs, and A is an index of the labour productivity fixed for analytical convenience, and without loss of generality, to the unity. The wage rate per unit of labour of the i-th firm is \(w_{i}\). Thus, the firm i’s linear cost function is represented by:

$$C_{i} \left( {q_{i} } \right) = w_{i} L_{i} = w_{i} q_{i} .$$
(3)

The firm i’s profit function is:

$$\pi_{i} = (a - q_{i} - q_{j} + n(y_{1} + y_{j} )) - w_{i} \,q_{i}$$
(4)

In line with the recent established literature (e.g. Goering 2007, 2008; Lambertini and Tampieri 2012), the model considers that social concerns can be interpreted as taking care of the consumers; therefore, the characteristic of a CSR firm is to be responsive to them. As a consequence, each firm is supposed, in its objective, to maximize profits plus a fraction \(k_{i}\) of the consumer surplus, which represents the firm’s ‘‘social concern’’ or care for consumers. Thus, the CSR-type firm’s objective function is a parameterised combination of profits and consumer surplus. In the present context, the consumer surplus is \({\text{CS}} = \frac{{(q_{i} + q_{j} )^{2} - n(y_{i} + y_{j} )^{2} }}{2}\), and therefore, the CSR-type firm objective function (\(W_{i}\)) becomes

$$W_{i} = \pi_{i} + k_{i} {\text{CS}} = \left[ {a - q_{i} - q_{j} + n(y_{i} + y_{j} ) - w_{i} } \right]q_{i} + k_{i} \left[ {\frac{{(q_{i} + q_{j} )^{2} - n(y_{i} + y_{j} )^{2} }}{2}} \right].$$
(5)

The timing of the game reflects the assumptions on which strategic decision is more or less frequently adjusted with respect to the others. While it is common to consider the decisions on the market sub-game as the more frequently revised (generally, always assumed at the last stage of the game), the decisions on wages as well as on the CSR level have not a well-defined relative timing. Indeed, on the one hand, we may note that a sequence of decisions reflecting the fact that the stipulation of wage contracts (assumed at stage 1) occurs less frequently than the adjustment about the decision to make CSR activities (assumed at stage 2) can be realistic when we consider that the duration of the wage contracts is about two or three years, as it is in general in Europe. On the other hand, a reversed sequence of moves between the wages and CSR choices can be also postulated because this option can be considered likewise realistic when the length of the wage contracts is short, for instance less than one year, as in many North-American cases. Thus, it is also worth to investigate how the timing of the game affects the owners’ choice whether to be socially interested.

The game has a three-stage structure. We define the games A and B by distinguishing the case in which wage contracts are stipulated prior to (resp. after) the decision whether to engage in CSR. In game A, at stage one (resp. at stage two in the game B), firm specific monopoly unions independently, and non-cooperatively, choose the workers’ wages.

At stage two (resp. at stage one in the game B), owners cooperatively decide the weight k of consumer surplus to include in the objective function through the maximisation of the joint profits. In both games, at stage three, firms choose output maximising their CSR objective functions. As usual, the game is solved by backward induction. Figure 1 shows the specific sequence of moves for these games.

Fig. 1
figure 1

Sequence of moves in games A and B

Full size image

3.1 Game A

Consider first the game specification A. At the third stage (the market game), firms decide simultaneously on their output levels, \(q_{i} \ge 0\), to maximize their objective functions \(W_{i}\). The usual maximisation of the objective function in (5) leads to the firms’ reaction functions and, imposing the “rational expectations” conditions, that is \(y_{i} = q_{i}\) for \(i = 1,\,2\), one obtains the firms’ output as function of the wages of each firm (which will be set by competing unions at the second stage) and the CSR level (which is common to both firms and will be set cooperatively by firms’ owners at the first stage):

$$q_{i} (w_{i} ,w_{j} ,k) = \frac{{a - \left[ {(k + n)(w_{j} - w_{i} ) - w_{j} + 2w_{i} } \right]}}{3 - 2(k + n)}$$
(6)

We assume that the firms’ choice of the level of “social concern”, i.e. the level of k, is totally under the control of the firms' owners and does not depend on the stakeholders. In particular, we assume that owners choose cooperatively to undertake the same level of CSR, that is, the level of k which maximises the firms’ joint profits (while, of course, the firms compete on the product market).

At the second stage, the optimal value of the parameter k is obtained maximising the sum of firms’ profits (i.e. Eq. (4) plus its counterpart for the firm j). Substitution of Eq. (6) (and its counterpart for the firm j) into (4) and its counterpart for the firm j, obtains each firm’s profits as

$$\pi_{i} = - \frac{{[2a(2k - 1) + [n(w_{j} - w_{i} ) - w_{j} + 2w_{i} ] - 2kw_{i} ][a - (k + n)(w_{j} - w_{i} ) + w_{j} - 2w_{i} ]}}{{\left[ {3 - 2(k + n) - 3} \right]^{2} }}.$$
(7)

The joint profits equation as a function of k and the wage of each firm is given by:

$$(\pi_{i} + \pi_{j} ) = - \frac{{2a^{2} (2k - 1) - 2a(w_{j} + w_{i} )(2k - 1) - \left[ \begin{gathered} 2k^{2} (w_{j} - w_{i} )^{2} + \hfill \\ k\left[ {4n(w_{j} - w_{i} )^{2} - (7w_{j}^{2} - 10w_{i} w_{j} + 7w^{2} )} \right] \hfill \\ + 2n^{2} (w_{j} - w_{i} )^{2} - 6n(w_{j} - w_{i} )^{2} \hfill \\ + 5w{}_{j}^{2} - 8w_{i} w_{j} + 5w_{i}^{2} \hfill \\ \end{gathered} \right]}}{{\left[ {3 - 2(k + n)} \right]^{2} }}.$$
(8)

Maximisation of (8) with respect to k yields \(\frac{{\partial (\pi_{i} + \pi_{j} )}}{\partial k} = \frac{{(1 + 2k - 2n)(w_{i} + w_{j} - 2a)^{2} }}{(2k + 2n - 3)}\). Assuming that \(2k + 2n - 3 < 0 \Rightarrow k < {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2} - n\), the above derivative is positive \({\text{iff}}\;k < n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\). It can be easily checked that the second-order conditions are satisfied. This implies that the optimal CSR level chosen by owners is

$$k = n - \frac{1}{2}$$
(9)

provided that the network externality is \(n > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\). The latter result seems to suggest that network externalities need to be adequately high in order to sustain the price of the goods, which may fall because of the indirect effect of output on firms’ revenues.

Substituting backwards Eq. (9) in Eq. (6), we get the employment level as a function of the wages:

$$q_{i} (w_{j} ,w_{i} ) = \frac{{[2a - 4n(w_{i} - w_{j} ) - 5w_{j} + 3w_{i} ]}}{8(1 - n)}.$$
(10)

We assume that wages are no longer exogenously given for firms, but they are the outcome of a strategic game previously played between “monopolistic” firm-level unions which maximise the following utility functionFootnote 5:

$$V_{i} = (w_{i} - w^\circ )^{\theta } (L_{i} )^{1 - \theta } = (w_{i} - w^\circ )^{\theta } (q_{i} )^{1 - \theta }$$
(11)

where \(w^\circ\) denotes the reservation wage, i.e. the wage workers can earn in the competitive sector of the economy, and the parameter \(\theta \in [0,1]\) represents the union’s wage sensitivity (or wage orientation): values of \(\theta < ( > )0.5\) indicate that the union is less (more) focused on wages and more (less) focused on jobs. Note that, when \(\theta = 0.5\), this functional form corresponds to a rent-maximizing union (i.e. the union aims at maximizing the total rent); in the special case of \(w^\circ = 0\), it represents a total wage-bill maximizing union. Given that the assumption \(w^\circ = 0\) does not produce any qualitative change on our final results, for algebraic simplicity, we consider total wage bill maximising unions.

With regard to the role played by the parameter \(\theta\), a three-fold consideration is here in order: (1) when \(\theta = 0.5\) (and \(w^\circ = 0\)), the union’s maximisation problem is equivalent to the issue faced by a profit maximizing upstream monopoly that is allowed to set the price of a common input it supplies to downstream firms. This implies that the model of this paper also represents a vertical industry with a common monopoly manufacturer, and thus all the results hold true also for such a case; (2) the parameter \(\theta\) can also indirectly describe the “insiders’” power: the more relevant is the insiders’ role in unions, the stronger is the union's preference for wages (all else equal) (e.g. Lommerud and Straume 2012); (3) although the model considers a monopoly union, another interpretation of the parameter \(\theta\) can be that of a rough measure of the union’s bargaining strength in a conventional firm-union Nash bargaining over wage, in the sense that a higher value of \(\theta\) approximates a higher union’s strength in wage bargaining.Footnote 6

At the first stage, after substitution of Eq. (10) into Eq. (11), unions’ choices take simultaneously place across firms, with each union taking the wage of the other firm as given. Each union i maximises its utility function with respect to \(w_{i}\), which straightforwardly leads to the following equations defining (for the union–firm pair i) the sub-game perfect best-reply function in relation to the wage:

$$w_{i} (w_{j} ) = \frac{{\theta [2a + w_{j} (3 - 4n)]}}{5 - 4n}$$
(12)

In the symmetric sub-game perfect equilibrium, we have that \(w_{i} = w_{j} = w\); hence, from (12), the equilibrium wage is:

$$w^{*} = \frac{2a\theta }{{5 - 3\theta - 4n(1 - \theta )}}.$$
(13)

Therefore, substitution of (13) into (10) yields the equilibrium quantity:

$$q^{*} = \frac{a(1 - \theta )(5 - 4n)}{{4(1 - n)\left[ {5 - 3\theta - 4n(1 - \theta )} \right]}}.$$
(14)

Substituting backwards (13) and (14), and considering that, in the Cournot equilibrium, the overall welfare is generically given by\(SW = CS + 2\pi + 2V^{^\circ }\), where \(V^{^\circ }\) is the wage bill,Footnote 7 we obtain the equilibrium outcomes of all the variables of the model (the upper script A defines the game):

$$k^{*A} = n - \frac{1}{2}$$
(15)
$$\pi^{*A} = \frac{{a^{2} (1 - \theta )^{2} (5 - 4n)^{2} }}{{8(1 - n)\left[ {5 - 3\theta - 4n(1 - \theta )} \right]^{2} }}$$
(16)
$$V^{^\circ *A} = \frac{{\theta a^{2} (1 - \theta )(5 - 4n)}}{{2(1 - n)\left[ {5 - 3\theta - 4n(1 - \theta )} \right]^{2} }}$$
(17)
$${\text{CS}}^{*A} = 2\left[ {\frac{a(1 - \theta )(5 - 4n)}{{4(1 - n)\left[ {5 - 3\theta - 4n(1 - \theta )} \right]}}} \right]^{2}$$
(18)
$${\text{SW}}^{*A} = \frac{{a^{2} (1 - \theta )(5 - 4n)\left[ {15 + 2n(7\theta - 11) + 8n^{2} (1 - \theta ) - 7\theta } \right]}}{{8(1 - n)^{2} \left[ {5 - 3\theta - 4n(1 - \theta )} \right]^{2} }}.$$
(19)

3.2 Game B

Let us now consider the game specification B. Taking into account the equilibrium output at the third stage in (6), at the second stage unions competitively choose their wages by maximizing their utility functions in (11), obtaining the sub-game perfect best-reply function in relation to the wage:

$$w_{i} (w_{j} ) = \frac{{\theta [a + w_{j} (1 - k - n)]}}{2 - k - n}$$
(20)

In the symmetric sub-game perfect equilibrium, it holds that \(w_{i} = w_{j} = w\). Hence, from (20), the equilibrium wage is:

$$w = \frac{a\theta }{{2 - \theta - (k + n)(1 - \theta )}}.$$
(21)

At the first stage, the optimal value of the parameter k is obtained maximising the sum of firms’ profits (i.e. Eq. (4) plus its counterpart for the firm j). By exploiting (21), the joint profits equation as a function of k is:

$$(\pi_{i} + \pi_{j} ) = 2\frac{{[a^{2} (1 - \theta )^{2} (2 - n - k)(1 - 2k)]}}{{[3 - 2(k + n)]^{2} [2 - \theta - (k + n)(1 - \theta )]^{2} }}$$
(22)

The maximisation of (22) with respect to k yields the following first-order condition

$$\frac{{\partial (\pi_{i} + \pi_{j} )}}{\partial k} = \frac{{\left[ {4a^{2} (1 - \theta )^{2} (2 - n - k)} \right]\left[ \begin{gathered} 2k^{3} (\theta - 1) + k^{2} \left[ {2n(\theta - 1) + 7 - 9\theta } \right] - \hfill \\ k\left[ {2n^{2} (\theta - 1) + 2n(\theta + 1) + 4 - 9\theta } \right] - \hfill \\ \left[ {2n^{3} (\theta - 1) + n^{2} (9 - 7\theta ) + n(5\theta - 12) + \theta + 4} \right] \hfill \\ \end{gathered} \right]}}{{\left[ {3 - 2(k + n)} \right]^{3} \left[ {2 - \theta - (k + n)(1 - \theta )} \right]^{3} }} = 0$$
(23)

Equation (23) is a polynomial of fourth order in k, with only one real solution \(k^{*B}\) as a function of the sole parameters n and \(\theta\), which is, unfortunately, algebraically intractable. However, exhaustive numerical simulations allow for an analysis of the conditions for the existence of a positive optimal CSR level \(k^{*B} (n,\theta )\), and its dependence on the network effect as well as unions’ preferences (see Table 2 below, Sect. 4).

Substituting backwards \(k^{*B}\), we obtain the game B’s equilibrium outcomes:

$$w^{*B} = \frac{a\theta }{{2 - \theta - (k^{*B} + n)(1 - \theta )}}$$
(24)
$$q^{*B} = \frac{{a(1 - \theta )(2 - k^{*B} - n)}}{{\left[ {3 - 2(k^{*B} + n)} \right]\left[ {2 - \theta - (k^{*B} + n)(1 - \theta )} \right]}}$$
(25)
$$\pi^{*B} = \frac{{\left[ {a^{2} (1 - \theta )^{2} (2 - n - k^{*B} )^{2} (1 - 2k^{*B} )} \right]}}{{\left[ {3 - 2(k^{*B} + n)} \right]^{2} \left[ {2 - \theta - (k^{*B} + n)(1 - \theta )} \right]^{2} }}$$
(26)
$$V^{^\circ *B} = \frac{{\left[ {\theta a^{2} (1 - \theta )(2 - n - k^{*B} )} \right]}}{{\left[ {3 - 2(k^{*B} + n)} \right]\left[ {2 - \theta - (k^{*B} + n)(1 - \theta )} \right]^{2} }}$$
(27)
$${\text{CS}}^{*B} = \frac{{(1 - n)\left[ {2a^{2} (1 - \theta )^{2} (2 - n - k^{*B} )^{2} } \right]}}{{\left[ {3 - 2(k^{*B} + n)} \right]^{2} \left[ {2 - \theta - (k^{*B} + n)(1 - \theta )} \right]^{2} }}$$
(28)
$$SW^{*B} = - \frac{{\left[ {2a^{2} (1 - \theta )(n + k^{*B} - 2)} \right]\left[ \begin{gathered} 2k^{*B2} (\theta - 1) + k^{*B} \left[ {3n(\theta - 1) - 2(2\theta - 3)} \right] + \hfill \\ n^{2} (\theta - 1) - 2n(\theta - 2) + \theta - 4 \hfill \\ \end{gathered} \right]}}{{\left[ {3 - 2(k^{*B} + n)} \right]^{2} \left[ {2 - \theta - (k^{*B} + n)(1 - \theta )} \right]^{2} }}.$$
(29)

3.3 The standard case of profit-seeking firms

For comparison purposes, we report here the equilibrium outcomes when firms are traditionally profit-seeking (denoted with the apex PS). These expressions are straightforwardly obtained by applying standard calculations to the model of the previous sections under the assumption \(k = 0\).

$$w^{{{\text{PS}}}} = \frac{a\theta }{{\left[ {2 - \theta - n(1 - \theta )} \right]}}$$
(30)
$$q^{{{\text{PS}}}} = \frac{a(1 - \theta )(2 - n)}{{(3 - 2n)\left[ {2 - \theta - n(1 - \theta )} \right]}}$$
(31)
$$\pi^{{{\text{PS}}}} = \frac{{a^{2} (1 - \theta )^{2} (2 - n)^{2} }}{{(2n - 3)^{2} \left[ {2 - \theta - n(1 - \theta )} \right]^{2} }}$$
(32)
$$V^{{^\circ {\text{PS}}}} = \frac{{\theta a^{2} (1 - \theta )(2 - n)}}{{(3 - 2n)\left[ {2 - \theta - n(1 - \theta )} \right]^{2} }}$$
(33)
$${\text{CS}}^{{{\text{PS}}}} = \frac{{2(1 - n)a^{2} (1 - \theta )^{2} (2 - n)^{2} }}{{(3 - 2n)^{2} \left[ {2 - \theta - n(1 - \theta )} \right]^{2} }}$$
(34)
$${\text{SW}}^{{{\text{PS}}}} = - \frac{{a^{2} (1 - \theta )(2 - n)[n^{2} (\theta - 1) + 2n(2 - \theta ) + \theta - 4]}}{{(3 - 2n)^{2} [2 - \theta - n(1 - \theta )]^{2} }}.$$
(35)

4 Profit-seeking versus CSR firms in Game A: analysis and discussion

Preliminarily, we recall that if \(n > ( < ){1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\) firms choose to be (not to be) socially concerned. Therefore, for any level of network externalities higher than \(n = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\), the comparison between the outcomes of profit-seeking and CSR-type firms is meaningful and the following holds.

Lemma 1

In comparison with profit-seeking firms (i) wages are always higher with CSR-type firms; (ii) the employment is always higher with CSR-type firms.

Proof

(i) By simple inspection of (13) and (30); (ii) \((q^{*} - q^{{{\text{PS}}}} ) > 0\).

The intuition behind Lemma 1 is as follows. Since the choice of a positive CSR level raises the level of output and employment, then at the beginning of the game unions anticipate a higher employment and thus set a higher wage.

From Lemma 1, the following results may be straightforwardly derived. Because the firms’ social concern raises unions’ wages, then the profit-enhancing effect of a cooperative choice of the CSR level might be undermined by the presence of unions. However, we will show that this is not the case and the unexpected positive effect of CSR on the shareholders’ welfare may still hold true despite the induced increase in wage costs. In particular, this always occurs when the network effect is very intense, independently of the presence of unions. On the other hand, if the network effects are less intense, this occurs provided that unions are not too much wage-aggressive.

Result 1

When firms’ owners choose to be of CSR-type, profits are (i) always enhanced when \(n > n^{o} = .945\), regardless the union’s preference; (ii) enhanced provided that unions are not too much wage-oriented, i.e. \(\theta < \theta^{o}\).

Proof

$$(\pi^{*} - \pi^{PS} ) = \frac{{a^{2} (1 - \theta )^{2} (2n - 1)\Psi }}{{8(3 - 2n)^{2} (1 - n)\left[ {4n(\theta - 1) + 5 - 3\theta } \right]^{2} \left[ {2 - \theta - n(1 - \theta )} \right]^{2} }}$$

where \(\Psi = \left[ \begin{gathered} 32n^{5} (1 - \theta )^{{^{2} }} - 32n^{4} (1 - \theta )(7 - 5\theta ) + 2n^{3} (125\theta^{2}- 410\theta + 301) - n^{2} (77\theta^{2} - 702 + 769 \hfill \\ - 2n(54\theta^{2} + 71\theta - 230) + 63\theta^{2} - 60\theta - 100 \hfill \\ \end{gathered} \right]\)

Therefore,

\((\pi^{*} - \pi^{PS} )\frac{ > }{ < }0\; \Leftrightarrow \;\Psi \frac{ > }{ < }0\; \Leftrightarrow \theta \frac{ < }{ > }\theta^\circ = \frac{{(2 - n)(5 - 4n)\left[ {2(8n^{2} - 14n - 3)\sqrt {1 - n} + 12\sqrt 2 - 8\sqrt 2 n} \right]}}{{2\sqrt {1 - n} \left( {32n^{4} - 128n^{3} + 122n^{2} + 45n - 63} \right)}}\)

Moreover, \(\theta^{o} > 1\) when \(n > .945\) and thus, in such a case, profits are always higher under CSR.

The content of Result 1 is also illustrated in Fig. 2. Given that the CSR activities raise the wage levels (i.e. the costs side), the possibility of a positive effect of the former on profits will depend crucially on the effects on the demand side, that is on prices and quantities.

Fig. 2
figure 2

Plot of the curve \(\theta^{o}\). Below (resp. beyond) the curve, \((\pi^{*} - \pi^{{{\text{PS}}}} ) > ({\text{resp}}. < )0\)

Full size image

The basic mechanism behind the result is the following. First, there are two counterbalancing effect of CSR activities on profits: on the one hand, the raised production for caring consumers’ welfare reduces prices, and thus profits; however, on the other hand, expanded production enlarges the network size and then increases the consumers’ willingness to pay, so increasing profits. Second, the intensity of the network effect (n) impacts on the relationship between the CSR level and prices in an opposite way with respect to that on the relationship between the CSR level and output: for increasing levels of n, an increase in the CSR level tends to reduce prices less than the increase of quantities,Footnote 8 and then it occurs that, for sufficiently high levels of n, engaging in CSR activities becomes profit-enhancing and the higher n is, the higher the optimal level of CSR is.

Therefore, provided that unions are not excessive wage-oriented (thus, they do not increase too much wages), the positive effects induced by the CSR activities on the demand side overweighs the negative effects induced on the costs side. The former effect prevails even if the unions were oriented only to wage when the network effect is strong.

As Lemma 1 shows, the firms’ social concern increases both wages and employment; hence, it is straightforward to show the following:

Result 2

The workers’ welfare is always higher when firms choose to be of CSR-type.

Proof

\((V^{^\circ *} - V^{^\circ PS} ) > 0\).

Since, from Lemma 1, quantities are higher with CSR, so the consumer surplus does.

Result 3

The consumers’ welfare is always higher when firms choose to be of CSR-type.

Proof

\((CS^{*} - CS^{PS} ) > 0\).

Finally, given the positive effect on workers and consumers’ welfare, and despite the ambiguity of the effect with respect to profits, social welfare as a whole also benefits from the choice of CSR.

Result 4

The social welfare as a whole is always higher when firms choose to be of CSR-type.

Proof

\((SW^{*} - SW^{PS} ) > 0\).

Corollary 1

From Results 1–4, it follows that the firms’ engagement in CSR behaviours leads to a Pareto-superior outcome, provided that \(n > n^{o}\) or \(\theta < \theta^{o}\).

5 Profit-seeking versus CSR firms in Game B: analysis and discussion

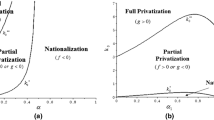
When the owners’ choice of CSR levels is prior to the unions’ choice of wages, we may observe that the optimal parameter \(k^{B}\) depends on the network effect intensity and union’s preferences, and it is positive only if n is sufficiently high and \(\theta\) sufficiently low, as clearly displayed in Fig. 3. Since the solid curve indicates the optimal level of CSR in the case of the absence of unions as well as the case of the game A (in which the choice of unions is prior to that of owners and the optimal CSR levels depend only on n), then it is easy to argue that, in the game B, the existence of an optimal CSR level (which always lies on the right of the solid line in Fig. 3) is less likely, and its level is always lower than in the case of game A. Moreover, when the union is sizably wage-oriented, the relationship between profits and CSR level is bimodal, in the sense that for an increasing CSR level when the latter is introduced or is low, profits are reducing until to a minimum level: for instance, in Fig. 4, it is shown that when \(n = .93\) and \(\theta = .85\), the introduction of CSR reduces profits until a minimum value reached at \(k = .11\) and then, for further increases of the CSR parameter, profits are increasing to the maximum CSR value, about \(k^{B} = .34\).

Fig. 3
figure 3

Optimal values of the CSR level kB as a function of the network effect parameter, n, for the cases of the absence of unions (\(\theta = 0\), solid line), employment-oriented unions (\(\theta = .2\), dotted line), wage bill maximiser unions (\(\theta = .5\), dashed line), wage-oriented unions (\(\theta = .85\), dashed–dotted line)

Full size image
Fig. 4
figure 4

Profits as a function of the level of CSR, k, when \(n = .93\) and \(\theta = .85\)

Full size image

This means that, under conditions of strong consumption externalities and strong union’s wage orientation, owners have to pay much attention to how much being careful of the consumer’s welfare, because being careful but not too much can be worse than being totally selfish. However, also in the game B, being of CSR-type may be welfare-enhancing for the owners. As shown by the comparison of the values of the different equilibrium outcomes under profit-seeking (PS) firms and under CSR in the game A and B reported in Tables 1 and 2, respectively, the following Lemma and Result hold.

Table 1 Equilibrium outcomes in the standard case of profit-seeking firms for three values of the network parameter and five values of the unions’ preference parameter
Full size table
Table 2 CSR parameter equilibrium values and corresponding outcomes for three values of the network parameter and five values of the unions’ preference parameter, for both games A and B
Full size table

Lemma 2

Owners’ CSR engagement increases the wages unions fix, and such an increase is larger the higher is the union’s preference for wages.

Proof

From the analysis of (21), we easily see that \(\frac{\partial w}{{\partial k}} > 0\) and \(\frac{\partial w}{{\partial k\partial \theta }} > 0\).

The wage resulting at the second stage equilibrium increases if owners choose a positive value of k, especially when unions are wage-aggressive: this means that, at the first stage, owners have to pay attention in the choice of undertaking CSR, which, however, may also be used as a device to control wage claims. For instance (applying simple numerical calculations to (21)), for a given \(n = .75\), an introduction—starting from the profit-seeking behaviour (i.e. \(k = 0\))—of a level of CSR of about \(k = .1\) brings upon a wage increase of about 0.0065 when \(\theta = .1\) but of about 0.012 when \(\theta = .85\), illustrating that introducing a CSR behaviour is more wage-increasing the more wage-aggressive is the union.

However, despite the induced increase in wages, the effect of being CSR will be still profit-enhancing, provided that the union is not too much wage-aggressive and the network effect parameter is sufficiently high such that the basic mechanism leading to a profit-enhancement by making CSR activities discussed in the previous section (see, for instance, footnote 6) is still working.

Result 5

In the case of game B, Results 1 to 4 still hold true, that is profits, workers’ and consumers’ welfare and social welfare as a whole are larger under the endogenous choice of CSR by owners.

It is easy to see, as an exhaustive numerical illustration of Result 5, that wages, profits, wage bill, consumer surplus and social welfare under CSR-type firms in the game B (in Table 2) are always higher than under PS firms (in Table 1).

Therefore, we have shown that, also in the game B, selfish owners find optimal to be careful of the welfare of consumers, so leading to a Pareto-improvement. Moreover, it is of interest to investigate—in the next section—which game, that is, which “timing” of the decisions about CSR and wage setting, may be preferred by firms’ owners and by the other agents—workers and consumers—and finally by the society as a whole.

6 A comparison between game A and B

In both games, owners find optimal the engagement in CSR activities when the network effect is sufficiently high: the necessary condition is \(n > n^{o} = .5\), but the threshold \(n^{o}\) is increasing with the unions’ parameter \(\theta\), that is, the presence of unions at the intermediate stage of the game reduces the likelihood to make CSR and its size, as shown by Table 2 (e.g. as shown by comparing the values of \(k^{A}\) and \(k^{B}\) in the third and fourth column in Table 2).

In particular, the more wage-aggressive the union, (i) the less likely owners choose to make CSR, (ii) the smaller the chosen CSR level, especially if the network effect is not large (for instance, when \(n\) is high, e.g. \(n = .9\), a positive level of CSR is chosen until the union is not too much wage-aggressive, i.e. until \(\theta < .75\), while when \(n\) is relatively low, e.g. \(n = .6\), owners do not make CSR even if unions are very employment-oriented, i.e. \(k = 0\) for \(\theta > .18\)).

Moreover, while the optimal \(k\) in the game A remains the same for any level of the union’s preference, in the game B it is always smaller than in the game A and rapidly decreases with the union’s wage orientation, especially when \(n\) is not too large: for instance, when \(n = .6\), even a minimal union’s wage interest, e.g. \(\theta = .05\), drastically reduces the CSR parameter which is, for such a value of \(\theta\), of about \(k^{A} = .4\) in the game A and becomes of about \(k^{B} = .08\) in the game B.

The intuition behind the smaller presence of CSR activities is that, in this case, in addition to the basic mechanism on the demand side analysed in the previous section, there is also a crucial effect on the wage costs side, as Lemma 2 shows, that is, owners at the beginning of the game anticipate that if they choose a higher CSR levels, then they also cause higher wages.

Therefore, to dampen wage claims, owners tend to reduce the CSR level (while in the game A wages are set prior to the CSR levels). This is the main reason for the fact that CSR levels are always lower, and the choice to engage in CSR less likely than in the game A. The above discussion can be resumed in the following results.

Result 6

The engagement in CSR activities is always lower in the game B than in the game A.

Result 7

Wages and profits are always higher in the game B than in the game A.

This result shows the preference of firms’ owners for a “leader” role with respect to their own unions in determining the sequence of decisions on CSR and wage contracts. Given Result 6, a lower CSR level also means lower quantities and consequently a lower consumer surplus.

Result 8

The consumer surplus is always lower in the game B than in the game A.

As regards the workers’ welfare, Results 7 and 8 indicate that wages are higher in the game B, but the employment is higher in the game A; however, the net result of these two counterbalancing effects is always such that the following Result holds.

Result 9

The workers’ welfare (i.e. wage bill) is always lower in the game B than in the game A.

As regards the social welfare as a whole, it is always lower in the game B because the lower welfare of workers and consumers in the game B more than counterbalances the higher profits the owners achieve in such a game.

Result 10

The social welfare is always lower in the game B than in the game A.

Therefore, the welfare analysis has shown that (1) the engagement of CSR activities always improves the societal well-being, and (2) however, there is always conflict of interests between the firms’ owners, on the one side, and consumers, unions (workers) and the society, on the other side, with respect to the “timing” of the decision about CSR relatively to that about the wage setting.

These results lead to the following policy insights. First, a government whose objective is to maximize the society’s well-being, should promote and encourage CSR activities.

Second, when wage contracts are of medium-term duration (game A), the achievement of a Pareto-superior outcome occurs in the presence of strong network externalities: in that case, the government’s role should be to facilitate customers the access to the network of compatible products (e.g. in the case of telecommunications, installing repeaters in areas with weak signal).

Third, social welfare under medium-term wage contract duration is larger than that under short-term one. This seems to suggest that the government has room to intervene in the labour market general regulatory framework, for instance, to modify the part concerning the (maximal) duration of the parties’ bargaining agreements within specific sectors. Nonetheless, the Pareto-superior outcomes under medium-term wage contract duration are achieved when the unions’ preference over wage are not too high. Therefore, to keep the unions’ sensitivity to wage low, besides regulatory revisions, the government should simultaneously devise alternative (non-wages) compensation measures to sustain workers’ income.

Finally, the results also show that far-reaching welfare implications arises if one considers a regulatory framework in which owners can freely decide the “timing” of their move, e.g. deciding whether and how to make CSR activities before or after the workers’ wage determination stage.

7 Conclusions

In a Cournot duopoly industry characterised by firms producing homogeneous network goods and with a decentralised union wage setting, this paper has investigated the effect of the firms’ adoption of consumer-friendly CSR activities on wages, profitability, the welfare of each component of society, and the overall social welfare. It has been shown that, regardless of whether the unions’ wage setting takes place prior to or after the firms’ cooperative choice of the CSR levels, being a CSR-type firm rather than following the standard profit-maximizing in such semi-collusive framework can lead to larger profits and thus higher welfare for their owners/stakeholders. Nonetheless, the analysis of the welfare of each component has revealed that a permanent conflict of interest among the economic agents arises with respect to the timing of the decision about CSR relative to that about the wage setting. In fact, on the one side, firms’ owners prefer to choose CSR prior to the wage setting, and on the other side, consumers, unions (workers), and society prefer wage setting prior to firms’ common choice of CSR activities.

The basic framework here proposed absolutely calls for further extensions to check the robustness of the paper’s findings. First, it would be suitable to investigate the presence of horizontally differentiated products, both under the Cournot conjecture and under other forms of market competition, notably price (Bertrand) competition. Vertical differentiation can represent another suitable research option. Second, it would be valuable to consider the introduction of consumption externalities. Third, it can be of interest to develop a model which considers the possibility that firms engage in cost-reducing R&D activities. Another promising line of research is the analysis of forms of CSR that differ from consumer friendliness; for instance, environmental CSR and green innovation. Finally, because the organisational form of numerous (especially large) companies in contemporary economies is characterised by the separation of management and control, it would be worthwhile to extend the analysis to managerial delegation in which owners delegate sales and CSR level decisions to managers. Those extensions are left for future research.