1 Introduction

Risk aversion can be elicited experimentally through a variety of methods (for a review, see Harrison and Rutström 2008; Charness et al. 2013). Typically, elicitation methods present the decision maker with a menu of monetary lotteries with varying risk and ask her to choose the lotteries she prefers. Well-known examples of such elicitation methods are the ‘ordered list selection’ (Binswanger 1980; Eckel and Grossman 2002) and the ‘multiple price list’ (Holt and Laury 2002).

In these elicitation tasks, lotteries can be presented through a verbal description stating the outcomes and their likelihood (e.g., “Win $5 with probability 10%”, “1/10 chance to win $5”). The numeric risk information may be accompanied by a pictorial display, such as a pie chart or bar graph (for a review of pictorial displays in risk elicitation tasks, see Harrison and Rutström 2008, especially Appendix A).

Although alternative numeric formats and alternative pictorial displays may fundamentally convey the same risk information (e.g., “10%” vs “1/10”), the literature on risk communication shows that each format and each display may frame it in a way that alters the perception of risk (e.g., Halpern et al. 1989; Schapira et al. 2001; Ancker et al. 2006; Lipkus 2007). For example, in a qualitative study on alternative formats to convey the risk of a disease, Schapira et al. (2001) find that the figure “1 out of 10” leads individuals to declare a lower concern for risk than the equivalent figure of “10%”. A similar but opposite effect is found in pictorial displays: risk information presented through discrete graphs (e.g., human stick figures) elicits a higher concern for risk than risk information presented through continuous graphs (e.g., a bar chart) (Schapira et al. 2001; Ancker et al. 2006).

If alternative numeric and pictorial formats can frame risk differently, then their use in risk elicitation tasks might give rise to framing effects in the elicitation of risk aversion. In this paper, I test for numeric and pictorial framing effects in a lottery choice experiment. Specifically, I administer a multiple price list (MPL) to 95 University students in a 2 × 2 between-subject design, where risk information is presented either as percentages (“10%”) or ratios (“1 out of 10”) and is accompanied by a pie chart sliced either in two or ten slices.

In the MPL task, participants are confronted with a menu of ten pairs of lotteries. In each of the ten pairs, lottery A and lottery B have two fixed outcomes each and the same probabilities for the high and low outcomes. For example, lottery A and lottery B in the first pair are, respectively, A1 = (100, 0.1; 75, 0.9) and B1 = (150, 0.1; 25, 0.9). The remaining pairs are constructed by increasing the probability of the high outcome by 0.1 and commensurably reducing that of the low outcome, so that the two probabilities are 0.2 and 0.8 in the second pair, 0.3 and 0.7 in third, and so on to the last pair, in which they are 1 and 0.

Framings were applied with respect to either numeric risk information or pictorial risk information or both. Taking as an example lottery A4, the description was either “Win 100 tokens with probability 40%, win 75 tokens with probability 60%” or “Win 100 tokens with probability 4 out of 10, win 75 tokens with probability 6 out of 10”. Pictorially, lottery A4 was accompanied by either a standard pie chart with one blue slice covering 40% of the pie and one orange slice covering the remaining 60%, or a ‘sliced’ pie chart with 4 blue slices and 6 orange slices.

Risk aversion was elicited under the two (numeric) × two (pictorial) framings. It was measured as the number of the menu row where lottery B, the riskier lottery of the pair, is first selected by the participant. A weighted linear regression shows that the numeric framing (using ratios) and the pictorial framing (slicing pies) reduce the switching row, respectively, by 0.27 (p = 0.621) and 0.84 (p = 0.255). This implies that, on average, the two numeric and pictorial framings do not significantly change the number of the row where participants switch their selection from the safer lottery A to the riskier lottery B. These results remain not significant when controlling for potential confounders, such as the tendency to mentally convert a numeric format to an equivalent one (e.g., percentages in ratios) and the degree of perceived inconsistency of the numeric information with the pictorial display (e.g., the use of ratios with standard pies, respectively conveying risk information as units and proportions).

The experiment found, however, an interaction effect between the two framings and the probability which draws the most attention: participants who declare to have focused more on the probability of the high outcome when making decisions exhibit a lower switching row when presented with ratios (− 3.7; p = 0.075) and when presented with sliced pies (− 8.17; p = 0.001).

Ultimately, the findings of the present experiment suggest that, in MPLs and similar lottery-based tasks, the elicitation of risk aversion may be robust to both numeric formats (i.e., percentages and ratios), but the impact of the pictorial framing may depend on which probability draws the most attention.

The rest of the paper is structured as follows. Section 2 reviews the literature on numeric and pictorial framings and formulates the related hypotheses. Section 3 illustrates the MPL task and the experiment design. Section 4 reports the estimation of treatment effects and potential confounding factors, and Sect. 5 concludes.

2 Related Literature and Hypotheses

2.1 Numeric Presentation of Risk

Typically, numeric information in MPLs is conveyed either as percentages (e.g., Lévy-Garboua et al. 2012; Maart-Noelck and Mußhoff 2014; Gamba et al. 2017; Bauermeister and Mußhoff 2019) or as ratios in base 10 (e.g., Holt and Laury 2002, 2005; Crosetto and Filippin 2016; Drichoutis and Lusk 2016). Thus, MPLs elicit risk aversion by employing relatively ‘simple’ numbers, that is, integers from 1 to 10 and multiples of 10. No contribution on MPLs has assessed the impact on the elicited risk aversion of adopting either numeric format.

In the literature on risk communication, the qualitative study of Schapira et al. (2001) tests numeric figures similar to those used in MPLs (i.e., “1 out of 10” and “10%”), and finds that ratios elicit lower estimates of risk because the information conveyed may be interpreted ‘optimistically’. In fact, when provided with information of the type “1 individual out of 10 is affected by X”, participants tended to identify themselves with one of the nine cases not affected by X, thus declaring a lower concern for risk than when they were provided with the equivalent figure of “10%”. A possible explanation is that decision makers focus more on the absolute value of the ‘foreground’ number (the “1” in “1 out of 10” and the “10” in “10%”) and less on the ‘background’ number (the “10” in “1 out of 10” and the “percent” in “10%”), and judge the figure with the higher foreground to entail a higher risk. In effect, Yamagishi (1997) finds that individuals judge the information “1286 out of 10,000” to imply a higher risk than the information “24.14 out of 100”, while no sensible decision maker would consider the equivalent figures of 12.86% to be higher than 24.14%. Relatedly, Siegrist (1997) shows that decision makers are more risk averse when exposed to high risk if presented with ratios (e.g., 600 out of 1,000,000) rather than a ‘probability’, that is, decimals between 0 and 1 (e.g., 0.0006).

We now attempt to draw some considerations for the present experiment. First, we cannot anticipate whether the findings of the reviewed literature carry over to the setting of the present experiment. In fact, while Schapira et al. (2001) test numeric figures that are typically adopted in an MPL, they do so on the participants’ stated concern for risk rather than on their risk aversion. Similarly, Siegrist (1997) and Yamagishi (1997) find numeric framing effects, respectively, on risk aversion and perception, but they rely on much more complicated figures than those of the MPL task. Besides, the experiment by Siegrist (1997) measures risk aversion in terms of stated willingness to pay to reduce risk, while MPLs measure risk aversion based on observed choices between lottery pairs. These differences might hinder the occurrence of numeric framing effects in the present setting.

Second, if decision makers truly focus more on the absolute value of the foreground, it means that “10%” will be judged to imply a higher likelihood than “1 out of 10”. However, in an MPL both the likelihood of the high outcome and that of the low outcome are explicitly stated (e.g., lottery A1 states, “Win 100 tokens with probability 10%, win 75 tokens with probability 90%”). If percentages lead to an overestimation of risk with respect to ratios, it means that both probabilities will be overestimated. Hence, risk aversion may depend on which probability draws the most attention, if any. In fact, if a decision maker focuses more on the probability of the high outcome, she will overestimate her probability to win the most desirable outcome of the lottery and may be tempted to risk more, while if she focuses more on the probability of the low outcome, she will overestimate her probability to win the least desirable outcome of the lottery, and may be tempted to risk less. Finally, if the decision maker focuses equally on both probabilities, it might be that her risk aversion does not change considerably across the two numeric formats.Footnote 1

2.2 Pictorial Presentation of Risk

Only a few contributions have represented probabilities pictorially in the MPL task (Drichoutis and Lusk 2016; Gamba et al. 2017; Zhou and Hey 2018; Bauermeister and Mußhoff 2019). When a pictorial display is included, it is typically a pie chart (e.g., Drichoutis and Lusk 2016; Gamba et al. 2017); still, other formats have been used, such as bar charts (Zhou and Hey 2018) and colored marbles (Bauermeister and Mußhoff 2019). No contribution on MPLs has yet assessed the impact of manipulating the pictorial display on risk aversion. A partial exception to this is the study by Bauermeister and Mußhoff (2019), who compare an MPL where lotteries were either framed in words (e.g., “10% winning €60, 90% winning €48”) or uniquely via pictorial representation (a bag of marbles). The authors find that the pictorial display reduces multiple switching behavior (see Sect. 3.1), but do not test the effect of the pictorial display on the elicited risk aversion.

The literature on the communication of risk reports several interesting mechanisms that distort risk perception depending on the adopted pictorial representation (see, e.g., Stone et al. 1997, 2003; Schapira et al. 2001; for a review, see Lipkus and Hollands 1999; Ancker et al. 2006; Lipkus 2007). At any rate, the only mechanism that is relevant for the present experiment concerns the different perception of risk deriving from discrete graphs as compared to continuous graphs. To the best of my knowledge, only the study by Schapira et al. (2001) tests the impact of the two types of graphs on the stated risk aversion. Specifically, in their qualitative study, a sample of middle-aged American women was presented with two graphs depicting a lifetime risk of breast cancer of 9%. One graph involved a set of 10 feminine stick figures on a white background, with the first colored in red for 9/10 of its area. The alternative graph was a white horizontal bar with 9% of its area colored in red. When presented with the stick figures, participants declared a higher understanding and higher concern for the risk involved (i.e., higher stated risk aversion) than when presented with the bar graph.

Again, we now attempt to draw some considerations for the present experiment. First, although Schapira et al. (2001) have found that discrete units elicit higher risk estimates than continuous formats, this is true for specific shapes of discrete units, that is, stylized women, which further increases emotional involvement (see Ancker et al. 2006).

Second, stick figures do not form a unique, continuous area. By contrast, in our setting we consider a pictorial display where units are part of the same whole area and the impact of these units is related precisely to how visually obvious they are with respect to the whole area. While no contribution has yet shown that contiguity of units has any effect on risk perception or aversion, it remains difficult to draw firm hypotheses for our experiment from the study by Schapira et al. (2001).

In light of the insufficient evidence, we will assume that the pictorial framing has the same effect on risk aversion as the numeric framing (if not enhanced), because it allows the decision maker to visualize more effectively the areas and units representing probabilities. Hence, as compared to non-sliced pies, when confronted with sliced pies the decision maker exhibits higher risk aversion if she focuses on the probability of the high outcome, because she underestimates the probability of winning the most desirable outcome of the lottery, and exhibits lower risk aversion if she focuses on the probability of the low outcome, because she overestimates the probability of winning the least desirable outcome of the lottery.

3 The Experiment

3.1 Task

This experiment employs an adapted version of the multiple price list (MPL) method put forward by Holt and Laury (2002). The MPL task presents subjects with a list of ten pairs of lotteries. Table 1 reports outcomes and probabilities of our lotteries as adapted for the experiment. In our adaptation, lottery A has outcomes 100 and 75 tokens, while lottery B has outcomes 150 and 25 tokens. In each pair, the lotteries have the same probability distribution. This means that the low outcome of lottery A (75) is as equally likely as the low outcome of lottery B (25), and that the high outcome of lottery A (100) is as equally likely as the high outcome of lottery B (150). Hence, since lottery A has the same probabilities but less dispersed outcomes than lottery B, lottery A is safer than lottery B.

Table 1 The MPL administered in the experiment
Full size table

Table 1 shows the MPL administered in the experiment. It is based on the version proposed by Holt and Laury (2002), although it employs different lottery outcomes: 25, 75, 100, and 150 tokens. In each row, the participant must choose one of the two lotteries. Risk aversion is measured as the number of the row where lottery B is first chosen. Note that this table is not shown to participants.

A sensible decision pattern in the MPL task is to choose lottery A for the first rows, switch to lottery B at some intermediate row, and stick with lottery B for the remaining rows. In fact, once the decision maker switches to the riskier lottery for a given probability of winning the high outcome (say, 0.6), there is no reason to switch back to the safer lottery when the probability of winning the high outcome is even higher (say, 0.8). However, in the MPL task it is common to observe multiple switching behavior—that is, selecting A for some rows, then B for some others, and then A again for some or all the remaining ones (Holt and Laury 2002; Lévy-Garboua et al. 2012; Bauermeister and Mußhoff 2019). Thus, in accordance with the methodological literature on the MPL task (notably, Andersen et al. 2006), the present experiment implemented an ‘autocompletion feature’ to enforce a unique switching point. The effect of this feature was that, once the participant selected her first lottery B, all lottery Bs in the subsequent pairs were automatically selected. For example, if lottery B was selected at row 6, then lottery B was automatically selected also for rows 7–10. Similarly, once the participant selected a lottery A, all lottery As in the preceding pairs were automatically selected. For instance, if lottery A was selected at row 6, then lottery A was also automatically selected for rows 1–5. This implies that the measurement of risk aversion can be based on the ‘switching row’, that is, the number of the row where the decision maker switches her lottery selection from the safer lottery A to the riskier lottery B.Footnote 2

3.2 Treatments

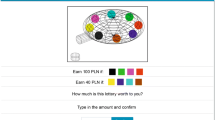
The participants were not presented with lotteries in the form shown in Table 1. Rather, as anticipated, these lotteries featured a verbal description and a pictorial representation, and framings at both dimensions were performed (Fig. 1).

Fig. 1
figure 1

An illustration of lottery pair 4 in the four treatments

Full size image

Taking as an example lottery A4, the numeric risk information was either framed as percentages (“Win 100 tokens with probability 40%, win 75 tokens with probability 60%”) or as ratios in base 10 (“Win 100 tokens with probability 4 out of 10, win 75 tokens with probability 6 out of 10”). As concerns the pictorial framing, one version employed a standard pie chart, representing risk information by means of proportions between slices. I chose the pie chart since it is a widely adopted display and participants were assumed to have familiarity with it. Since in our task lotteries have only two outcomes, the pie has only two slices—the blue slice represents the probability of the high outcome; the orange slice represents the probability of the low outcome.

The alternative framing was to ‘slice’ the standard pie into ten equal slices. Taking again as example lottery A4, the pie had 4 blue slices representing the high outcome and 6 orange slices representing the low outcome. For the remainder of this paper, the ten-slice pie will be termed ‘sliced’, while the standard pie will be termed ‘non-sliced’.

The experiment employed four treatments, given by the combination of the framings: a treatment with non-sliced pies and percentages (NSP), a treatment with non-sliced pies and ratios (NSR), a treatment with sliced pies and percentages (SP), and a treatment with sliced pies and ratios (SR).

3.3 Procedure

The experiment was programmed and conducted with oTree (Chen et al. 2016; Holzmeister 2017). It was run in May and June 2019 in three sessions at the Department of Economics of the University of Insubria, Varese (Italy). Participants were students enrolled at the University of Insubria—mostly undergraduates—randomly recruited through advertising on campus and social media. The experiment was conducted in Italian. The final sample counted 95 observations.Footnote 3

Upon arrival, participants were randomly assigned to computer terminals separated by dividers. Each participant was then randomly assigned to one and only one treatment. Instructions for the MPL task were displayed on each participant’s screen and read aloud by the experimenter (see Appendix A).

In the task, the participant had to select, for each row, the lottery she preferred by clicking on the corresponding radio button below the lottery description. After all selections were performed, the participant could press the confirmation button. Only at this point were her answers considered definitive. Then, the program selected one row at random, played the lottery chosen at that row, and displayed results on a separate screen. The conversion rate between token and euro was 25:1, meaning that 25, 75, 100, and 150 tokens were worth, respectively, €1, €3, €4, and €6.

At the end of the task, participants were confronted with a computer-based questionnaire (available in Appendix B) about sociodemographic characteristics and potential confounders for treatment effects (selected descriptive statistics reported below).

Finally, participants were confronted with an adapted, non-incentivized version of the Raven’s progressive matrices test (Appendix C). The test aimed at collecting a measure of the participant’s cognitive ability, since the related literature suggests a relationship between this trait and risk aversion (e.g., Taylor 2013). In our adaptation, the test consisted of six matrices to be filled in within a total time of six minutes.

Participants were told that, for the completion of both the questionnaire and the test, they would be rewarded with 25 tokens (€2), irrespective of the answers provided. At the end of the experiment, each participant received her final prize—consisting of the prize from the MPL task plus the prize from questionnaire and test completion—in a sealed envelope, marked with the participant code used for identification purposes (while guaranteeing anonymity). The average prize amounted to €6.32, for a commitment of no more than thirty minutes. All monetary prizes were delivered through Amazon gift cards of equivalent value.

3.4 Sample

Participants’ mean age was 22.35 (SD = 2.09), within a range of 19–30 years. Fifty participants were male (52.63%) and nine (9.5%) were non-Italian natives (but spoke Italian). The majority were bachelor’s students (79; 83.15%), twenty-three (24.21%) were from fields other than economics (e.g., computer science) and only eighteen (18.95%) had previously taken a course on decision making under risk. Descriptive statistics for demographics in each treatment are reported in Table 2.

Table 2 Descriptive statistics for socio-demographic variablesa
Full size table

A one-way ANOVA test on the age means and Fisher’s exact tests on the frequencies of the remaining demographics show that differences across treatments are not statistically significant.

4 Results

4.1 Treatment Effects

Our variable of interest is the switching row, that is, the row where the participant switches selection to lottery B. As already discussed, higher values for the switching row denote higher risk aversion. Overall, the average switching row is 6.05 (SD = 2.11), meaning that on average the participant switched to the risky lottery at row 6, where the expected values of lotteries A and B are equal. Descriptive statistics for the switching row variable across the four treatments are graphed in Fig. 2; histograms with the frequency of each switching row across treatments can be found in Appendix D. As Fig. 2 show, the distributions of the switching row in the two treatments with ratios (NSR and SR) are very similar to each other, as they have a very close mean (6.1 vs. 6.07) and standard deviation (1.84 vs. 1.74). The difference is more accentuated between treatments NSP and SP, with considerably different means (6.37 vs. 5.53) and standard deviations (2.02 vs. 2.93). Also, these two treatments differ considerably from their respective counterparts with ratios. Notably, treatment SP has the lowest mean (5.53) and highest standard deviation (2.93).

Fig. 2
figure 2

Distribution of the switching row variable across treatments. The figure shows a bar graph with the mean value of the switching row across treatments (left); segments denote standard errors. On the right, the figure shows a boxplot with the switching row’s standard deviation, mean (dotted line) and median (thick line) across treatments. The switching row value ranges from 1 (lottery B is first selected at row 1) to 10 (lottery B is first selected at row 10)

Full size image

To estimate the effects of the numeric and pictorial framings on the switching row (i.e., treatment effects), three alternative model specifications were compared:

$$\begin{aligned} {\text{SW}}_{{\text{i}}} &= \,\beta_{0} \, + \,\beta_{{1}} {\text{Ratio Format}}_{{\text{i}}} \, + \,\beta_{{2}} {\text{Sliced Pie}}_{{\text{i}}} \, + \,\beta_{{3}} {\text{Ratio Format}}_{{\text{i}}} \\ &\quad\times \,{\text{Sliced Pie}}_{{\text{i}}} \, + \,\varepsilon_{{\text{i}}} ,\end{aligned} $$
(1)
$$\begin{aligned} {\text{SW}}_{{\text{i}}} &= \,\beta_{0} \, + \,\beta_{{1}} {\text{Ratio Format}}_{{\text{i}}} \, + \,\beta_{{2}} {\text{Sliced Pie}}_{{\text{i}}} \, + \,\beta_{{3}} {\text{Ratio Format}}_{{\text{i}}} \,\\ &\quad\times \,{\text{Sliced Pie}}_{{\text{i}}} \, + \,{\mathbf{D}}_{{\text{i}}} \, + \,\varepsilon_{{\text{i}}} ,\end{aligned} $$
(2)
$$ \begin{aligned}{\text{SW}}_{{\text{i}}} &= \,\beta_{0} \, + \,\beta_{{1}} {\text{Ratio Format}}_{{\text{i}}} \, + \,\beta_{{2}} {\text{Sliced Pie}}_{{\text{i}}} \, + \,\beta_{{3}} {\text{Ratio Format}}_{{\text{i}}} \\ &\quad\times \,{\text{Sliced Pie}}_{{\text{i}}} \, + \,{\mathbf{D}}_{{\text{i}}} \, + {\mathbf{X}}_{{\text{i}}} \, + \,\varepsilon_{{\text{i}}} ,\end{aligned} $$
(3)

where Di = β4 Agei + β5 Malei + β6 Italiani and Xi = β7 Decision Familiari + β8 Raven Matricesi.

Model 1 includes only treatment variables, that is, dummy variables indicating whether probabilities are expressed as ratios (Ratio Format) and pies are sliced (Sliced Pie), as well as the interaction between the two (Ratio Format × Sliced Pie).

Model 2 includes a vector of demographic controls (Di) related to the subject’s age, sex (Male), and nationality (Italian). Model 3 includes a vector (Xi) which captures whether the participant had previously taken a course in decision making under risk (Decision Familiar, dummy) and the number of Raven’s test matrices filled in correctly by the subject (Raven Matrices, which takes a value from 0 to 6).Footnote 4

Estimation results for the three specifications are reported in Table 3. Model 1 tests the effect of treatment variables on the switching row. Results show that both framings reduce the switching row value, but their effect is not statistically significant. Specifically, the numeric framing reduced the switching row by 0.27 (p = 0.621), suggesting that, with respect to participants exposed to percentages, those exposed to ratios anticipate their selection of lottery B, on average, by considerably less than one row. By contrast, the pictorial framing reduced the switching row by 0.84 (p = 0.255), implying that, on average, participants exposed to sliced pies anticipated the selection of lottery B by about one row compared to participants exposed to non-sliced pies. These effects remain nonetheless not statistically significant. The interaction effect between the two variables increases the switching row by about one unit (0.82), but again it is not statistically significant (p = 0.391). These results remain not statistically significant also when estimating the three specifications with pooled data, that is, using as grouping variable the numeric format irrespective of the pictorial display and, conversely, the pictorial display irrespective of the numeric format (see Tables 8 and 9 in Appendix E). Similar results are found when performing non-parametric exact tests on both non-pooled and pooled data. In fact, a Kruskal–Wallis rank test fails to reject the null hypothesis of equality of populations with a p-value of 0.753 when performed on non-pooled data, and with a p-value of 0.988 and 0.376 when performed on data pooled, respectively, by numeric format and by pictorial display.

Table 3 Estimation of treatment effects
Full size table

Model 2 controls for demographic variables and Model 3 for familiarity with decision making under risk and for cognitive ability. Among demographic controls, age, sex, and nationality reduce the switching row, respectively, by approximately 0.2 (p = 0.017; p = 0.034), 0.8 (p = 0.073; p = 0.071) and 1.8 (p = 0.025; p = 0.029) in both models. Finally, familiarity with decision making under risk and cognitive ability slightly decrease the switching row as well, but their effect is not statistically significant (p = 0.694 and p = 0.746, respectively).

4.2 Heterogeneous Treatment Effects

As argued in Sect. 2, there is reason to conjecture that the elicitation of risk aversion could depend on which probability between that of the high outcome and that of the low outcome draws the most attention. Table 4 reports the proportion of participants that deemed the probability of the high outcome less, equally, or more relevant for decision than that of the low outcome. Table 4 also reports the proportion of participants who declared that the pie chart was less, equally, or more relevant for decision than the numeric information. Fisher’s exact tests show that differences across treatments are not statistically significant.

Table 4 Descriptive statistics for the relevance of probability of high outcome (lottery’s upside) and relevance of the pie for decision with respect to that of the numeric informationa
Full size table

To estimate heterogeneous treatment effects, the treatment variables in the three models specified in Sect. 4.1 were interacted with the stated relevance of the probability of the high outcome for decision. Specifically, the regressor Upside Relevant captures whether the participant declared that the probability of the high outcome was less relevant (0), equally relevant (1), or more relevant (2) for decision than the probability of the low outcome. The additional specifications were estimated also controlling for the relevance of the pictorial display with respect to that of the numeric information: Pie Relevant is a dummy variable which takes the value of 1 if the participant declared paying at least equal attention to the pie chart as to the numeric information.

Estimations are reported in Table 5. Results show an interaction effect between the two framings and the relevance of the lottery’s upside for decision. Specifically, when the participant declares to have focused more on the lottery’s upside than the lottery’s downside, her switching row is reduced by around 4 points when exposed to ratios (p = 0.075) and by around 8 points when exposed to sliced pies (p = 0.001). Estimating the three models of Sect. 4.1 on the three subgroups of Upside Relevant yields consistent results (see Appendix E, Table 10). However, these results are not confirmed by non-parametric exact tests: a Kruskal–Wallis rank test performed on the three Upside Relevant subgroups fails to reject the null hypothesis of equality of populations with p-value of 0.218, 0.264 and 0.056, respectively, for the first, second and third subgroups.

Table 5 Estimation of treatment effects interacted with relevance of lottery’s upside
Full size table

4.3 Confounding Effects

In the questionnaire I also collected data on potential confounders for the two framing effects. Beginning with the numeric framing, I asked participants whether they converted a probability in another format in their mind, such as a ratio in the equivalent percentage format, or vice versa, or whether they stuck with the given format. As reported in Table 6, while most participants reasoned with the probability format they were provided with (66; 69.47%), some participants did convert one format into the other, and the conversion was more frequent for participants in ratio treatments (19 out of 49; 39%) than for participants in percentage treatments (5 out of 46; 11%). A chi-squared test shows that this difference is statistically significant (p = 0.003).Footnote 5 Nonetheless, it is difficult to argue whether such format conversion did actually hinder the numeric framing effect. In fact, converting a format in one’s mind does not ‘cancel’ the starting format from one’s view, implying that the effect of the ratio format might still be in place despite the mental conversion. In partial support of this conjecture, a set of linear regressions controlling for whether participants have reasoned in ratios show no impact on the ratio format coefficient.Footnote 6

Table 6 Frequencies and proportions of participants who converted probabilitiesa
Full size table

A second, potential confounder for the two framing effects is related to the perceived consistency between the numeric and the pictorial information provided. In fact, the use of a continuous graph to represent discrete data, such as a standard pie to represent ratios (or the use of a discrete graph to represent continuous data, such as a sliced pie to represent percentages) might give rise to an additional cognitive burden and increase the perceived complexity of the task. Thus, in the questionnaire I attempted to assess the degree to which the participant considered the numeric framing to be consistent with the pictorial one. Framings in treatments NSP and SR are consistent with one another because, in each treatment respectively, they both highlight either the proportion of favorable and unfavorable cases, or the number of favorable and unfavorable cases. By contrast, in treatments NSR and SP the two framings are of the opposite type. Therefore, I asked the participants whether in their opinion the two pieces of information were mutually consistent, not consistent, or whether they had no opinion on this.

The proportion of participants who deemed a combination consistent across treatment is reported in Table 7. To some limited extent, it seems that participants judged the two framings to be consistent more frequently in treatments NSP and SR than in NSR and SP, in accordance with our assumption about consistency. However, the difference is not particularly dramatic, since one would have expected a much lower proportion of consistency in treatments NSR and SP. And in fact, a Fisher-exact test fails to reject the null hypothesis of equal distribution across treatments (p = 0.278). Thus, participants seem not to judge framings of the opposite type as inconsistent. A set of linear regressions controlling for the participant’s perceived inconsistency shows no impact on the ratio format and sliced pie coefficients (again, see fn. 6).

Table 7 Frequencies and proportion of participants who deemed the two framings consistent, not consistent, and that did not have an opinion in merit
Full size table

In sum, there is reason to believe that the two potential confounders analyzed here—mental conversion of numeric format and perceived inconsistency of the two framings—did not significantly hinder the occurrence of the framing effects.

5 Discussion

The findings of the present experiment contribute to the question of determining which framings of risk information alter the decision maker’s risk perception and aversion (and which do not). Specifically, the present experiment tested whether framing effects previously documented in the literature on risk communication carried over to the experimental elicitation of risk aversion by means of lottery-based tasks.

Results show that, overall, the elicitation of risk aversion proved robust to both the numeric and the pictorial framings. Robustness to the numeric framing could be explained by the fact that MPLs typically employ easily interpretable figures (integers from 1 to 10 and multiples of 10), while the contributions in the literature on risk communication that report numeric framing effects employ figures that are much more complicated and that differ considerably from one another (e.g., “600 out of 1,000,000” vs “0.0006”). Thus, numeric framing effects might be limited to those settings in which the numeric information is difficult to process or compare.

Another aspect that was suspected to hinder the numeric framing is that almost half of participants exposed to the ratio format mentally converted it to a percentage. Nonetheless, considering that the mental conversion does not cancel the format one is exposed to, and considering the limited impact of mental conversion on the ratio format coefficient, this hardly explains the lack of a framing effect. Along with the finding that the opposite behavior (converting percentages to ratios) was considerably less frequent, this gives us reason to believe that participants were more at ease with risk information stated in percentages rather than ratios. Further research might corroborate this conjecture.

With respect to the pictorial framing, the literature on health risk communication has compared graphs that differ considerably in terms of how they provide risk information. For example, Schapira et al. (2001) test continuous graphs (bar charts) in comparison with discrete graphs where units are not contiguous (stick figures). Our pictorial framing involved the subdivision of a whole area into contiguous units (slicing a pie), which still allows the decision maker to reconstruct the underlying areas. Thus, it might be that the difference between a sliced and a non-sliced pie is not sufficient to trigger a framing effect.

It was also argued that the perceived inconsistency of the numeric and pictorial information could ameliorate the two framing effects. However, results show that participants did not deem framings in treatments NSR and SP to be significantly less consistent than those in NSP and SR. Thus, it seems that participants did not perceive framings of the opposite type as inconsistent. While this cannot rule out that the effect of the inconsistency was in place, at the same time participants also declared to have focused more on the numeric figures than on the pictorial display, and this might have severely hindered the potential impact of the inconsistency.

The numeric and pictorial framing effects were estimated controlling for sociodemographic variables such as the decision maker’s age, gender, nationality, and cognitive ability. In general, the inclusion of these regressors did not significantly alter the estimation of framing effects. However, some regressors altered the estimation of the switching row. For example, the switching row was lower in older participants, males and Italians, although, in accordance with the literature on MPLs, the effect of gender was barely significant (Crosetto and Filippin 2016; Filippin and Crosetto 2016). Finally, cognitive ability did not significantly impact the switching row. Even interacting treatment variables with the Raven test scores does not result in statistically significant differences either in the elicitation of risk aversion or in the impact of the two framing effects (see Appendix E, Table 13).Footnote 7 Nonetheless, the effect of cognitive ability on risk aversion is still the subject of debate (see, e.g., Taylor 2013; Pedroni et al. 2017).

Notably, it seems that the framing effects might be related to how much the decision maker focuses on the lottery’s upside. In fact, when the participant declares to have focused more on the lottery’s upside than on the downside, her switching row is significantly lower when presented with sliced pies. This suggests that the elicitation of risk aversion may be sensitive to the pictorial framing conditional on the relevance of the lottery’s upside for the participant. At any rate, it should be noted that the numeric and pictorial framings per se did not have any impact on the salience of the lottery’s upside, meaning that the relevance of this element for decision was primarily related to the participant’s personal characteristics. It should also be noted that the findings of the present experiment might suffer from the limited sample size. Further research with a richer sample may strengthen the validity of these results.

In conclusion, the findings of the present experiment suggest that the elicitation of risk aversion in MPLs and similar lottery-based tasks may be robust to numeric framings of risk information. Thus, experimenters interested in the elicitation of risk aversion can ‘safely’ employ both percentages and ratios. However, given that participants tended to mentally convert ratios to percentages, this gives us reason to conjecture that resorting to percentages might aid participants in undertaking the MPL task. By contrast, the impact of the pictorial framing seems to be related to the relevance of the lottery’s upside for the participant. While the pictorial display adopted here did not alter the salience of the lottery’s upside, experimenters should consider avoiding the use of pictorial displays which might give prominence to this element of the decisional context.