Asset Specificity and the Secondary Market for Productive Assets

Abstract

The aim of this paper is to explore how debt contracts are affected by investment in asset specialization and by the dynamics of the secondary market for collateralized productive assets. Before applying for a loan, financially constrained firms face a specificity trade-off: asset specialization increases firms’ project returns, but decreases the liquidation value of assets in the secondary market if the firm is in financial distress. To study this trade-off, the paper uses a theoretical model in which the choice of asset specificity and the outcome of the secondary market for distressed firms’ assets are endogenous. High redeployability costs and a small number of participants in the secondary market are associated to low recovery values and to a high cost of debt. The paper shows the conditions under which financial constraints reduce firms’ incentive to invest in asset specificity.

1 Introduction

The ability to pledge collateral significantly raises the firms’ financial capacity. When a borrower cannot repay its debt obligations, the creditor has the opportunity to seize and liquidate collateralized assets in order to recover a partial amount of the original credit. Liquidation values depend on the degree of specificity and on the presence of a secondary market (Shleifer and Vishny 1992).

Asset specificity is the ability to reuse a productive asset by alternative users and/or to alternative uses with the least sacrifice in terms of productivity (Williamson 1988, 1991). Therefore, the degree of specificity is a key determinant of the resale value of an asset in the secondary market: if it can be redeployed at a small cost, then its resale value is high. Hence, assets with different degree of asset specificity are associated to different resale values. The recent empirical literature has highlighted how firms that use more redeployable assets obtain better financing conditions (e.g., Benmelech et al. 2005; Benmelech and Bergman 2008, 2009).

Even if the concept of asset specificity could seem abstract, it can be applied to any financial contract in which a borrower pledges collateral. Assets that are most frequently used in this type of contract are real estates, inventories and standardized machines and equipment, which are easily redeployable. By contrast, examples of less redeployable assets are firm-specific machinery and patents. Moreover, while pledging collateral can help any firm to raise external finance, pledging assets with low redeployability could be difficult for small, informationally opaque and shallow-pocket firms, which usually rely on banks and trade creditors (Norden and van Kampen 2013). This paper builds on the fact that borrowers have the possibility to choose (at least to some extent) the specificity of their productive assets. A classical example is the airline industry, in which the redeployability of aircrafts used by airlines affects the cost of external financing (Benmelech and Bergman 2008, 2009). Since airlines tend to use a limited number of aircraft types, the secondary market for an aircraft is mainly populated by companies already operating with that model. Suppose that a firm operates with an aircraft model that is not commonly used in the industry. If the firm goes bankrupt, the resale value of its aircrafts might be low for two reasons. First, the number of potential buyer that can efficiently redeploy those assets is very low. Second, a firm which is not using that type of aircraft has to pay large redeployability costs in order to include that model in its activities (e.g., pilot and staff training). Here, the choice of the degree of specialization is determined by which aircrafts and how many different models to use, and it might give rise to the redeployability problem.

In this paper I study the relation between the secondary market for productive assets and firms’ financing conditions by focusing on the ex-ante choice of asset specificity. I develop a theoretical model in which an entrepreneur¹ may run a risky project, and may invest in asset specialization before applying for a loan.² In a first-best scenario, where the entrepreneur is not financially constrained, she will choose the maximum degree of asset specificity (provided that the marginal benefit of the investment overcomes the marginal cost). However, when she is financially constrained, she has to pledge her productive asset as collateral in order to get funds to run the project. Here, the degree of asset specificity affects the repayment to lenders through the secondary market, i.e. the auction that takes place when a creditor seizes an asset from a borrower in financial distress. In this auction, the main determinant of liquidation values is the degree of asset specificity: on one hand, asset specialization increases productivity and the return of the project when the firm is active; on the other hand, it reduces the asset’s redeployability and hence its recovery value when the firm is in financial distress. I will refer to this statement as the specialization trade-off. In addition, there is substitutability between investing in asset specificity and the amount invested in the project: if the borrower does not invest in asset specificity, she devotes her initial cash in the project, lowering the amount of debt needed from the capital market. If instead she invests in asset specificity, then she needs additional capital in order to cover the cost of the project. I will refer to this trade-off as the substitutability trade-off.

The paper explains how the substitutability trade-off and the specialization trade-off play a crucial role in the determination of specific investments. I show that the number of potential buyers in the secondary market and redeployability costs are the main determinants of firms’ ex-ante choice of asset specificity: if the number of potential buyers is small, then liquidation values are low and credit constrained firms do not invest in asset specificity. If the number of potential buyers is large, then liquidation values are high, allowing firms to specialize their assets since they find better financial conditions. Moreover, redeployability costs have a direct effect on the resale value of the asset: the higher the redeployability costs, the lower the asset’s resale value. If redeployability costs are low, then by investing in asset specificity, firms face both favourable credit conditions and higher project returns in the non-distress case. If instead redeployability costs are high, then the investment in asset specificity deteriorates firms’ financing conditions. In this case a firm does not invest in asset specificity when the increase in the cost of credit overcomes the increment in the expected return of the project.

This paper contributes to the existing theoretical literature on financial contracting by providing a simple and elastic model in which investments in asset specificity, financial conditions and the dynamics of the secondary market for productive assets are interconnected and endogenously determined in equilibrium. The paper derives the conditions under which asset specialization becomes optimal, and shows that, overall, financially constraints reduce firms’ incentive to invest in asset specificity. Those findings may provide some guidance in assessing the collateral channel, particularly in those industries where specific investments are used to build competitive advantage.

The remainder of the paper is organized as follows. Section 2 provides an overview of the main related literature. Section 3 introduces the theoretical model (the benchmark, the secondary market and the financial contract). Section 4 provides the results (for both self-financing and financially constrained firms). Section 5 discusses the analysis and the main hypothesis behind the theoretical framework. Section 6 concludes. All proofs for the theoretical model are in Appendix B.

2 Related Literature

There is a body of theoretical and empirical literature on the importance of liquidation values on financial contracts. The two milestones of this literature are the contributions from Williamson (1988) and Shleifer and Vishny (1992). Williamson (1988) argues that more redeployable assets should involve the use of debt, while non-redeployable assets should be financed by equity. Shleifer and Vishny (1992) discuss the problem of financially distressed firms and argue that when a firm is distressed, the resale value of its assets will depend on the number of potential healthy buyers on the market. As a matter of fact, productive assets are most valuable for firms already operating in the same industry, and with the same typology of assets. In addition, Hart and Moore (1994) develop a theoretical model where an entrepreneur has to finance a project but cannot commit to withdraw the human capital and renegotiation is possible. They show that the optimal repayment schedule is directly affected by the durability and the specificity of productive assets.

The main contribution of this paper to the literature is that both the ex-ante choice of asset specificity and the outcome of the secondary market are endogenous. In order to do this, the model departs from Cerasi et al. (2017), where firms competing á la Cournot are financed through collateralized debt contract. In their theoretical model, they introduce a probability of default and investigate the secondary market for financially distressed firms’ assets, where both healthy competitors and outsiders are willing to acquire them. They focus on the number of rivals and its effect on financial contracts, taking the degree of specificity as given, while the core of this paper is the specialization choice.

This work is close to Habib and Johnsen (1999) and to Marquez and Yavuz (2013), in which the investment in asset specificity is non-contractible. Habib and Johnsen (1999) provide a model of state-specific asset value in which the entrepreneur can use efficiently the asset in the good state of the world, while she lacks the skill to efficiently use it if the bad state occurs. Therefore, the entrepreneur contracts directly with an asset redeployer who is able to use better the general asset in the bad state. In my model each firm contracts with a lender who has no skill in redeploying the asset, and therefore resells it in the secondary market. Marquez and Yavuz (2013) consider a model of endogenous choice of asset specificity with financially constrained firms where asset specialization improves performance in the long run, but decreases the liquidation value of the asset. They show that the need of outside financing and the resulting investors’ liquidation threat lead to a lower level of specificity compared to the self-financing case. However, a proper secondary market for distressed firms’ assets is not considered.

This paper is also close to Flor and Hirth (2013), where the liquidity and the redeployability of existing assets affect firms corporate investments. They show that the investment level is less sensitive to liquid funds for firms which assets have a higher degree of redeployability. This happens because a low level of redeployability costs allow financially constrained firms to achieve investment level closer to the first-best. This result goes in a different direction with respect to the discussion of the investment sensitivity in Almeida and Campello (2007). In particular, Almeida and Campello (2007) show that, while asset tangibility has no effect on cash-flows sensitivities of financially unconstrained firms, a constrained firm’s investment level is more sensitive if its assets are more tangible. This difference in the results is due to the set-up and the environment of the theoretical models: Flor and Hirth (2013) assume risky debt and allow borrowing against existing assets, while Almeida and Campello (2007) consider risk-free debt and do not allow for borrowing against existing assets. My approach goes beyond those two papers, since in my model the initial investment asset specificity reduces the level of internal liquid funds of the firm (the substitutability trade-off). Therefore, by choosing high degree of asset specificity, a firm increases the amount of resources needed from the capital market and decreases the asset redeployability.

Salgado et al. (2017) consider a model where firms operate in a specialized industry with an aggregate shock. They argue that if firms can anticipate costly foreclosures, then they can also reduce the cost of financial distress by searching for potential buyers of their asset before being in financial distress. As a consequence, firms can find potential buyers who have a higher valuation of their assets compared to their lenders’. In this paper, instead, firms are not allowed to search for the best redeployer and the price of the asset will be determined in a bankruptcy auction.

Bernardo et al. (2020) links the capital structure choice to endogenous asset liquidation values. They show that the liquidation value of productive assets might be a direct consequences of firms capital structure policies, taking asset redeployability as an exogenous parameter. By contrast, I consider redeployability costs as a direct consequence of the initial choice of asset specificity faced by entrepreneurs. In this way it is possible to show the effect of the specificity trade-off on the financial contract.

In my model there are no source of asymmetric information between lenders and firms. A large stream of literature has focused on the effect on the role of collateral in financial markets with imperfect or incomplete information (e.g., Bester 1987; Besanko and Thakor 1987; Boot and Thakor 1994). Vilasuso and Minkler (2001) consider both agency costs and asset specificity in a model of capital structure in an imperfect capital market setting. They find that, following the transaction cost economy, firms with a high level of asset specificity tend to use equity instead of debt. This implies that, over time, bondholders could become less vulnerable to excessive risk taking by shareholders. The objective of my paper is to provide a simple model in which asset specificity and the dynamic of the secondary market are endogenously determined in equilibrium. Thus, considering asymmetric information is not required to the scope of the paper.

The empirical literature upholds the idea that firms with highly redeployable assets (low-specificity assets) find better financial condition (longer maturities, lower cost of external financing). Benmelech et al. (2005) support this result using commercial property loans. They approach redeployability using Williamson (1988) definition: zoning regulation defines the uses which a property can be devoted to. If a property can be used in several ways, then the number of potential buyers is high, meaning that it has a high value in the case of liquidation. Therefore, they use as a redeployability measure the property’s zoning possible designations from the zoning regulation.

Benmelech and Bergman (2009, 2011), use an U.S. airlines industry dataset which contains information on assets pledged as collateral in debt contracts. In the first paper, they construct three measures of redeployability which are proxies for the ease at which lenders will be able to liquidate their position. Their conclusions confirm the general view that more redeployable collateral is associated to better credit conditions (lower credit spreads, higher credit ratings and higher loan-to-value ratios). In the second paper, they focus on the collateral channel, defined as the (negative) effect of bankrupt firms on their healthy competitors’ collateral values. Furthermore, Gavazza (2010) focuses on leasing contracts in the same industry and shows that more liquid assets (which are more redeployable) make leasing more likely and, in operating leasing, are associated to lower lease rates.

Norden and van Kampen (2013) find that properties, plants and equipments (highly redeployable assets) are important drivers of the collateral channel. They also show that the collateral channel is more important for firms that cannot access public debt markets but have to rely on bank or trade creditors to raise funds. In the agricultural industry, Mondelli and Klein (2014) shows that physical asset specificity plays a key role in explaining the use of external equity finance by firms. They find that companies in farming activities involving highly-specific assets are more likely to receive external equity investments. Acharya et al. (2007) provide evidences on the link between asset specificity and recovery values. They show that if assets in the industry are more specific,³ then industry distress implies very low creditors’ recoveries. Campello and Giambona (2011) show that asset tangibility and redeployability are the main determinant of firms’ leverage. In particular, they show that the use of tangible assets enables firms to sustain high borrowing capacity, but only to the extent that those asset are redeployable. Kim and Kung (2017) build an industry measure of asset redeployability based on Williamson (1988): an asset is highly redeployable if it can be used in a large number of industries. They show that low asset redeployability combined with economic uncertainty can dampen capital accumulation and economic growth.

3 The Model

3.1 The Benchmark

I consider an economy with $n>2$ risk-neutral firms. Each firm may invest in a risky project, with a fixed cost I, and owns a productive asset and some initial liquid cash M (lower than I for financially constrained firms). Before going to the capital market, each entrepreneur may invest a constant amount $s<M$ in asset specificity in order to increase the return of the project. I indicate with $\lambda \in \{0,1\}$ the degree of asset specificity: if she chooses to invest ($\lambda =1$), the final return is R(1), while if she chooses not to invest ($\lambda =0$), the return is $R(0)<R(1)$. The value $\varDelta R=R(1)-R(0)$ represents the increment in the return of the project from specialization. Notice that returns are not interdependent, that is the choice of each firm does not have an impact on the returns of rivals (it is as if each firm was producing as a local monopolist). This choice is common knowledge.

When firms are financially constrained, they need to pledge their productive assets as collateral, in order to raise the needed amount to run the project (either $I-M$ if $\lambda =0$ or $I-(M-s)$ if $\lambda =1$). It is assumed that the capital market is under perfect competition and that each lender may only lend to one entrepreneur. Each lender sets a future repayment for each firm, $r_i(\lambda _i)$. Each firm seeks a lender who provides the initial investment cost. There is no discounting factor.

After being financed, each firm may be hit by a negative shock (i.i.d. across firms) with probability $1-p$. Lenders receive a perfect signal about the realization of the shock: if the shock occurs, then they anticipate that the firm will not be able to repay the debt: this is what I define as financial distress. In this case, the lender seizes the firm’s asset and sells it in the secondary market, i.e. a first price auction in which all healthy firms may participate and bid.⁴ Since healthy firms are financially constrained, they must be granted additional funds from their original lenders in order to be able to participate in the auction.⁵ Bids for all assets on sale are contemporaneously submitted by all participating firms. The firm that places the highest bid will win the asset and it must pay redeployability cost d if the asset is specific ($\lambda =1$) in order to run the new project. Here, it is important to highlight that s and d are two different costs: the first one is the cost associated to the specialization of a general asset, while the latter is the cost of re-utilization of a specific asset. After the reallocation of financially-distressed firms’ assets, returns are realized and payments to lenders occur.

Summing up, the timing is the following:

$t=-1$:

Each firm owns an asset and M (cash) dollars. Firms have to decide whether to invest in asset specificity, paying the cost $s<M$. At the end of this period, any firm i owns either $M-s$ dollars if $\lambda _i=1$, or M dollars if $\lambda _i=0$.

$t=0$:

Firms go to the capital market. Each lender sets the future repayment $r_i(\lambda _i)$ that the firm i will pay at the end of the game if it will not be hit by the negative shock. Firm i is matched to a lender and pledges its productive asset as collateral. The lender of firm i provides either $I-M$ if $\lambda _i=0$ or $I-(M-s)$ if $\lambda _i=1$.

$t=1$:

With probability $1-p$ each borrower may be hit by a negative shock (i.i.d.) and the return of her project at the end of the game will be zero, otherwise $R(\lambda _i)$. The lender perfectly observes the future realization of the project. If a negative signal is observed, then the lender seizes the productive asset and sells it in the secondary market.

$t=2$:

The secondary market takes place. Healthy firms may bid in the auction. Lenders cash the resale value. When an asset is reallocated to a healthy firm, its lender finances the bid and the redeployability cost d (if the purchased asset is specific).

$t=3$:

Realization of project returns and payments to lenders are made.

The generic firm i takes action at $t=-1$, when it chooses the degree of asset specificity, and at $t=2$, in the case it is healthy and participates to the secondary market. Lenders take action at $t=0$, when they set the future repayment for each firm. It is assumed that the degree of asset specificity is public information for all firms and all lenders.

I define the specialization outcome ${\varvec{\varLambda }}$ the vector of all choices of asset specificity in the economy after $t=-1$, namely: ${{{\varvec{\varLambda }}}}=(\lambda _1, \lambda _2, \ldots \lambda _n)$. A strategy for firm i is a pair $(\lambda _i, B_i({{{\varvec{\varLambda }}}}))$, where $\lambda _i$ is the initial choice of asset specificity, while $B_i({{\varvec{\varLambda }}})$ is the vector of bids for other firms’ assets in the secondary market. A strategy for a lender is represented by the vector ${{{\varvec{r}}}}=(r_1(\lambda _1), r_2(\lambda _2),\ldots , r_n(\lambda _n)$), which contains all the final repayment proposed by each lender to all firms. Since there are not source of asymmetry, in equilibrium all firms choose the same degree of asset specificity and all lenders offer the same contract to all firms. The analysis proceeds by backward induction starting from the secondary market. I use the Subgame-Perfect Nash Equilibrium (SPNE) as the equilibrium concept throughout the paper.

3.2 The Secondary Market

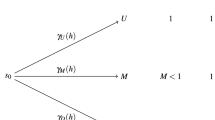
I indicate with h the number of healthy firms participating to the secondary market at $t=2$. If $h=n$ or $h=0$, then the auction will not take place: in the first case, there are no assets on sale, while in the second one there are no bidders. If instead $1<h<n$, the auction takes place and it is assumed that, for each asset on sale, each firm cannot bid more than its maximum willingness to pay for that asset.⁶

When $1<h<n$ two possible scenarios arise.

• If $h=1$, then there is only one healthy firm. Hence, it wins all the assets in the auction by bidding the smallest amount $\epsilon$ greater than zero.⁷

• If $1< h< n$, then all healthy firms compete for each asset on sale. Each firm will bid its maximum willingness to pay, which is $R(1)-d$ if $\lambda =1$ or R(0) if $\lambda =0$. Therefore, in equilibrium, a tie always happens, and the asset is randomly allocated to one of the bidding firms.⁸

Let me indicate with $\nu _i(\lambda _j)$ the maximum willingness to pay of firm i for an asset with degree of asset specificity $\lambda _j$. The price of an asset in the secondary market depends on the number of healthy firms that participate in the auction:

• When $h=1$ (with probability $p(1-p)^{n-1}$), all assets are sold to one firm that bids the smallest amount $\epsilon$ for all assets, independently of their degree of asset specificity.

• When $1<h<n$ (with probability $p^h(1-p)^{n-h}$), the price of an asset with specificity $\lambda =0$ ($\lambda =1$) is $\nu (0)=R(0)$ ($\nu (1)=R(1)-d$).

Now it is possible to define the expected liquidation value (at $t=0$) of an asset with degree of asset specificity $\lambda$.

Lemma 1

The expected liquidation value of an asset for any degree of asset specificity $\lambda$ at $t=0$ is

$$\begin{aligned} E_{t=0}(LV(\lambda ,d)) =p(1-p)^{n-1}\epsilon + \left[ \sum _{h=2}^{n-1} p^{h}(1-p)^{n-h} \right] \nu (\lambda ) \end{aligned}$$

Moreover, this value is increasing in n for any $n>2$.

When an asset is in liquidation, there are two possible cases: if there is only one healthy firm in the market, it gets all the assets by bidding the smallest amount $\epsilon$; if the number of potential buyers is greater than one, all active firms compete for any assets on sale and the price will be $\nu (\lambda )$. The expected liquidation value described in Lemma 1 is increasing in n: since shocks are i.i.d. and only two healthy firms are needed to have a price greater than zero, the higher the number of firms in the market, the higher the number of potential healthy buyers after the realization of the negative shock. Moreover, since $\nu (1)$ is decreasing in the level of redeployability costs, then the expected liquidation value is decreasing in d as well.

3.3 The Financial Contract

At $t=0$ each lender anticipates all the possible outcomes of the secondary market and computes the optimal future repayment. Given the assumption of perfectly competitive capital markets, then $r_i(\lambda _i)$ is obtained from the expected zero-profit condition for lenders, where

• Lenders’ revenues are the expected future repayment when the firm is healthy plus the expected recovery value of the firm’s asset in the secondary market when it is in distress.

• Lenders’ costs are the initial loan plus the expected loan to the firm when it is healthy and gets an asset in the auction at $t=2$.

Lemma 2

If the capital market is perfectly competitive, and then the financial contract for any firm i takes the following form

$$\begin{aligned} pr_i(\lambda _i)=I(\lambda _i)-E_{t=0}(LV(\lambda _i,d)-L({{\varvec{\varLambda }}})) \end{aligned}$$

Where $pr_i(\lambda _i)$ is the expected future repayment to the lender, $I(\lambda _i)$ is the initial loan to the firm, $E_{t=0}[LV(\lambda _i,d)]$ is the expected liquidation value of the firm’s asset when it is in distress and $E_{t=0}[L({{{\varvec{\varLambda }}}})]$ is the additional loan to the firm when it gets an asset in the secondary market.

The zero-profit condition implies that the expected future repayment to the lender is equal to the difference between the lender’s costs (the initial loan plus the additional loan to the firm at $t=2$) and the expected recovery value of the firm’s asset. If this value is larger than $pR(\lambda _i)$, at $t=0$ the firm does not sign the contract, because the expected future repayment to the lender is higher than the expected return of the project. In other words, $pR(\lambda _i)$ is the upper bound of the expected future repayment to the lender. However, when $pr(\lambda _i)=pR(\lambda _i)<I(\lambda _i)-E_{t=0}(LV(\lambda _i,d)-L({{{\varvec{\varLambda }}}}))$, lenders are losing money in expectation, so they will never lend to the firm. This no-lending area is different between assets with different degree of specificity (this issue will be discussed in Sect. 4.3).

Lemma 2 shows both the substitutability trade-off and the specificity trade-off. If a firm invests in asset specificity, it will need a higher loan from the capital market. As $I(\lambda _i)$ increases, the expected future repayment $pr_i(\lambda _i)$ increases. Moreover, redeployability costs will affect the expected future repayment through the liquidation value $LV(\lambda _i,d)$: if redeployability costs are low, then firms will find favorable financial conditions even when they invest in asset specificity. Lastly, the financial condition of a firm is affected by the choice of all other firms in the market, through the expected loan to the firm when it is healthy and purchases one or more assets in the secondary market.

4 Equilibrium

4.1 First Best: Self-Financing Firms

As a first-best case, I solve the problem considering financially unconstrained firms, namely $M>I+s$. In this case firms do not raise funds from the capital market, and they invest in asset specificity if and only if the expected benefit due to specialization $p\varDelta R=p(R(1)-R(0))$ is greater than its cost s. Since there is no source of heterogeneity, in equilibrium firms will choose the same level of asset specificity.

Proposition 1

When firms are not financially constrained, if $\varDelta R \ge \frac{s}{p}$, then the outcome of the SPNE in pure strategies is $\lambda _i=1$ for any firm i. If $\varDelta R < \frac{s}{p}$, then the outcome of the SPNE in pure strategies is $\lambda _i=0$ for any firm i.

Let me define the threshold $\varDelta R^* \equiv \frac{s}{p}$. Figure 1 represents the threshold $\varDelta R^*$ and shows the equilibrium choice of the firm: $\lambda =1$ if $\varDelta R \ge \varDelta R^*$, otherwise $\lambda =0$.

The first best threshold $\varDelta R^* (p)$ is always decreasing in p for any $p \in (0,1)$. When the probability of success is low, firms need a very high increment in the return of the project in order to specialize the asset. Instead, as the probability of success increases, the marginal benefit from specialization needed is lower. At the maximum, when the project is successful (when $p=1$), it is sufficient that $\varDelta R$ is greater than the specialization cost s.

4.2 Second Best: Financially Constrained Firms

When firms are financially constrained, they need to pledge their assets as collateral. Lenders take into account the degree of asset specificity and have access to the secondary market if the financed firm is in distress.

Proposition 2

If $\varDelta R \ge \varDelta R^{SB*}$, where $\varDelta R^{SB*} \equiv \frac{s+d[\sum _{i=2}^{n-1} p^{i}(1-p)^{n-i}] }{p+\sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} }$ then the outcome of the SPNE in pure strategies is $\lambda _i=1$ for any firm i. If $\varDelta R < \varDelta R^{SB*}$, then the outcome of the SPNE in pure strategies is $\lambda _i=0$ for any firm i.

The strategies supporting the equilibrium described in Proposition 2 are the following: the representative firm i at $t=-1$ chooses $\lambda _i=1$ if and only if $\varDelta R \ge \varDelta R^{SB*}$, otherwise $\lambda _i=0$; if at $t=1$ firm i is not hit by the negative shock, then at $t=2$ it bids the smallest $\epsilon >0$ to all assets on sale if it is the only one participating to the auction, while if there is at least another healthy competitor, it bids its maximum willingness to pay for all assets in sale. At $t=0$, lenders offer the contract described in Lemma 2.

The new threshold $\varDelta R^{SB*}$ is increasing in the level of redeployability costs d for any probability of success p. The relationship between the two threshold depends on the probability of success of the project: if $pd>s$, then $\varDelta R^{SB*} > \varDelta R^*$, otherwise $\varDelta R^* > \varDelta R^{SB*}$. For $n=3$ the relationship between the thresholds is depicted in Fig. 2.

The panel a of Fig. 2 shows that if redeployability costs are lower than the specialization cost s then $\varDelta R^* > \varDelta R^{SB*}$: the region in which firms choose $\lambda =1$ is bigger than the one in the first best scenario. In this case, they require less $\varDelta R$ in order to specialize the asset. This scenario should not be seen as over-investment: the collateral channel is helping firms to invest in asset specificity and earn additional rents, because the liquidation value of specific assets is high, even though they still require positive redeployability costs when re-used. Hence, firms receive overall better financial conditions. Panel b shows that when $d>s$, there is a level of probability ${\tilde{p}}$ such that if $p<{\tilde{p}}$ then $\varDelta R^* > \varDelta R^{SB*}$, while if $p>{\tilde{p}}$ then $\varDelta R^{SB*} > \varDelta R^*$. If the probability of success is low, provided that the no-lending scenario is avoided, investing in asset specificity is like a bet, since firms expect to be hit by the negative shock. However, any healthy firm can acquire a large number of assets from the secondary market. The combination of these two effects makes the threshold of financially constrained firms lower than the first-best one. This scenario could be seen as over-investment, since firms find it easy to invest in asset specificity, even though redeployability costs are high and the probability of success of the project is relatively low. If redeployability costs are high and the probability of success is higher than ${\tilde{p}}$, then $\varDelta R^* < \varDelta R^{SB*}$: investors care about the recovery value and set a higher repayment to borrowers that specialize the asset. Therefore, the $\varDelta R$ required for specialization is higher. The secondary market effect can be defined as the difference between $\varDelta R^*$ and $\varDelta R^{SB*}$. When redeployability costs are low, the difference is positive, meaning that the secondary market is actually helping firms to specialize their assets, through the financial contract. When redeployability costs are high, the difference is negative and firms find it difficult to invest in asset specificity, since the secondary market has a severe impact on the financial contract.

Now it is useful to understand the impact of the number of firms n on the equilibrium threshold $\varDelta R^{SB*}$ .

Lemma 3

When $d>s/p$, $\varDelta R^{SB*}(n+1) \le \varDelta R^{SB*}(n)$.

If redeployability costs are low, then the investment in asset specificity is easier because the liquidation value of a specific asset is high. Instead, as d increases, the second-best threshold moves upward, and the number of firms n plays a key role in dampening this effect. In this case, an increase in the number of active firms in the market will move downward the specialization threshold, because there will be an increase in the number of potential healthy buyers in the secondary market. Therefore, the model predicts that markets populated by a large number of firms should be associated to larger investment in asset specialization. In other words, the effect of the specificity trade-off is severe in markets with few companies, because it is difficult to re-allocate specific assets from distressed firms.

In the next subsection the number of firms is fixed and equal to three (which is the minimum number of firms in order to have a secondary market worth to be considered), in order to focus on the effect of redeployability costs on the equilibrium threshold.

4.3 A Scenario with Three Firms

When there are only 3 firms in the market, the secondary market takes place when $h=2$. If there is only one healthy firm, then it wins all the assets in the auction, by bidding the lowest amount $\epsilon >0$. If $h=2$, then both healthy firms bid their maximum willingness to pay for the asset on sale. Whenever a tie occurs, the asset is randomly allocated (thus, each firm may obtain the asset with probability 0.5).

The outcome of the secondary market is anticipated in the financial contract. Lemma 4 states the future repayment set by the lender at $t=0$.

Lemma 4

When $n=3$, then:

• if all firms choose $\lambda =0$, then $r(0)=\frac{1}{p}( I-M-p^2(1-p)\nu (0)+E_{t=0}L({{{\varvec{\varLambda }}}}))$

• if all firms choose $\lambda =1$, then $r(1)=\frac{1}{p}(I-(M-s)-p^2(1-p)\nu (1) +E_{t=0}L({{{\varvec{\varLambda }}}}))$

Lemma 4 shows the substitutability effect and the effect of redeployability costs on the future repayment when $n=3$. When firms choose to invest in asset specificity, they pay the specialization cost s. This increases the loan asked to the lender by the amount s and the future repayment by s/p. Secondly, redeployability costs increase the future repayment to the lender since they decrease the asset liquidation value and increase the additional loan granted to the firm at $t=2$. Figure 3 plots the repayment in both scenarios and shows that r(1) is always greater than r(0). Moreover, the future repayment to lenders is increasing in the level of redeployability costs d, and is decreasing in p, since the higher the probability of success, the lower the risk. When $p=1$, the future repayment is equal to the initial loan: since all firms are always healthy, they can certainly repay the lender at $t=2$, and given that the capital market is perfectly competitive, the repayment must not exceed the initial loan. The dotted lines represent the no-lending areas, in which $pr(\lambda _i)>pR(\lambda _i)$. These scenarios happen when the probability of success is very low, that is, when the expected future repayment required by lenders is higher then the expected return of the project. Lemma 5 describes the conditions under which the no-lending area for specific assets is larger than the one of non-specialized asset.

Lemma 5

For non-specific asset ($\lambda =0$), the probability under which no-lending occurs, $p_{nl}(0)$, is the solution to the following problem:

$$\begin{aligned} p+p^2(1-p)=\frac{I-M}{R(0)} \end{aligned}$$

The cut-off for specific assets, $p_{nl}(1)$, is larger than $p_{nl}(0)$ if and only if

$$\begin{aligned} p_{nl}(0)R(1)< & {} I-M+s-\frac{1}{2}p_{nl}(0)^2(1-p_{nl}(0))(R(1)-d)\\&+\,d\left( \frac{1}{2}p_{nl}(0)^2(1-p_{nl}(0))+ p_{nl}(0)(1-p_{nl}(0))^2\right) \end{aligned}$$

When $n=3$, the threshold above which specialization becomes optimal is the following:

$$\begin{aligned} \varDelta R^{SB*}(3) = \frac{s+dp^2(1-p) }{p+p^2(1-p) } \end{aligned}$$

The panel a of Fig. 4, shows the equilibrium areas, while panel b shows the effect of a rise in d on the threshold.

For very low level of the probability of success, the future repayment asked by lenders is very high (provided that the no-lending scenario is avoided). If the firm is in financial distress, then its asset is reallocated with difficulty since the number of potential healthy buyers is small. Hence, recovery values are very low for both specialized and generic assets. Lenders set high future repayments, since both the recovery value of the asset and the probability of success of the project is low. Firms need a very high $\varDelta R$ in order to specialize the asset.

For intermediate/low level of the probability of success, the secondary market effect is severe for high level of redeployability costs. In this scenario, the liquidation value of a specific asset is very low for two reason: first the maximum willingness to pay for that asset is low; second, since p is relatively small, the number of healthy firms that participate in the secondary market is small. If $\varDelta R < \varDelta R^{SB*}$ (in other words, in the region under the second best threshold), lenders punish firms that choose to specialize the asset because the recovery value of a specific asset is low, inducing them to choose $\lambda =0$.

For medium/high level of the probability of success, lenders expect that the firm will be able to meet the repayment (even if it deviates from the equilibrium). In other words, lenders do not expect the firm to be in distress. However, if the firm is hit by the negative shock, then there is a high probability that both the other firms will be healthy and hence the expected recovery values for both specific and general assets are high.

The panel b of Fig. 4 shows that redeployability costs have a direct effect on the shape of the equilibrium threshold. If redeployability costs increase, then the threshold moves upward and firms have less incentives to invest in asset specificity. Moreover, if d is very large, then the threshold could become non-monotone in p.

4.4 A Scenario with Two Regions

Until now the model has focused on a market in which healthy firms are the only ones allowed to participate in the secondary market. However, following the intuition provided by Shleifer and Vishny (1992), firms that run similar projects but in other regions may be willing to enter the market by acquiring distressed firms’ assets. Hence, the previous model can be extended by considering the presence of those firms (outsiders) which can interact with firms already present in the market (incumbents) in the bankruptcy auction.

I consider a context of two regions, H for Home and F for Foreign. At the beginning of the game two firms are active in region H and two firms are active in region F (the outsiders, from the point of view of the home region). The only difference between the two regions is the cost of specialization, $s^H < s^F$: without loss of generality, I assume that firms in the home region face a lower cost of specialization, i.e. they are more efficient in specializing the asset.⁹ Further assumptions are: (i) as before, in order to re-use a general asset ($\lambda =0$), any firm faces no additional costs other than the price of the asset; (ii) if a firm buys a specific asset ($\lambda =1$) from a firm in its region, it pays redeployability costs d, while if the specific asset is purchased from a firm in the other region, the buyer has to pay ${\hat{d}}>d$ in order to re-use the asset (in other words, the best redeployer of a specific asset is a firm located in the same region of the seller); (iii) I assume that a firm that buys an asset from another region has to pay constant transportation cost $t>0$; (iv) any firm prefers to buy a general asset from the other region rather than a specific one (${\hat{d}}>\varDelta R$); (v) firms are active only in one market.¹⁰

Given the set up described above, I denote with $\nu _r(\lambda ,z)$ the region-r firms’ maximum willingness to pay for an asset in region z with specificity $\lambda$. Therefore, firms’ maximum willingness to pay for any asset is:

• $\nu _H(0,H)=\nu _F(0,F)=R(0)$;

• $\nu _H(0,F)=\nu _F(0,H)=R(0)-t$;

• $\nu _H(1,H)=\nu _F(1,F)=R(1)-d$;

• $\nu _H(1,F)=\nu _F(1,H)=R(1)-{\hat{d}}-t$.

This framework implies that when a firm with a specific asset is in financial distress, the other firm in that region has an advantage in the auction with respect to outsiders.

Since there are two different specialization costs, there will be two equilibrium thresholds, one for firms located in region H and one for firms located in region F. Let me define the following value.

$$\begin{aligned} \varDelta R^o(s^r)^*=\frac{s^r+{\hat{d}}p^2(1-p)(3-2p)}{p+p^2(1-p)(3-2p)} \end{aligned}$$

Therefore, since $s^H < s^F$, $\varDelta R^o(s^H)^*<\varDelta R^o(s^F)^*$. Now it is possible to solve the model and find when firms invest in asset specificity.

Proposition 3

If $\varDelta R \ge \varDelta R^o(s^F)^*$, then the outcome of the SPNE in pure strategies is $\lambda _i=1$ for any firm i in any region. If $\varDelta R < \varDelta R^o(s^H)^*$, then the outcome of the SPNE in pure strategies is $\lambda _i=0$ for any firm i in any region.

As in the previous case with only one region, two symmetric equilibriums arise:

• If the benefit $\varDelta R$ is lower than $\varDelta R^o(s^H)^*$ , then all firms choose not to specialize their assets.

• If the benefit $\varDelta R$ is higher than $\varDelta R^o(s^F)^*$, then all firms choose to specialize their assets.

In this framework also an asymmetric equilibrium may arise, where firms in region H choose to specialize their assets while firms in region F choose $\lambda =0$.

Proposition 4

If $\varDelta R^o(s^H)^* \le \varDelta R < \varDelta R^o(s^F)^*$, then the outcome of the SPNE in pure strategies is $\lambda _i=1$ for any firm i in region H and $\lambda _j=0$ for any firm j in region F.

Figure 5 represents the locus of the equilibriums described by Propositions 3 and 4. Above the threshold $\varDelta R^o(s^F)^*$, all firms in all regions choose to specialize the asset, while below the threshold $\varDelta R^o(s^H)^*$ all firms choose $\lambda =0$. Instead, in the shaded area between the two thresholds, the asymmetric equilibrium arises: in region H, firms specialize their assets, while firms in region F do not. This happens because the specialization cost is lower in region H. It is also possible to show that in the asymmetric equilibrium, firms in region H, which specialize the asset, will pay a higher repayment to their lenders with respect to firms in region F. This is due to both the substitutability effect and to the secondary market effect, since firms in region H need a higher loan at $t=0$ from the capital market, and the liquidation value of their assets is low because firms in the other region incur in high costs in redeploying those specific assets.

5 Discussion

The paper provides a simple and elastic theoretical model in which asset specificity, financial constraints and the secondary market are interconnected. The model shows that low redeployability costs are associated to high liquidation values and thus induce firms to choose high degrees of asset specificity. Instead, when redeployability costs are high, then firms choose low level of asset specificity due to the substitutability trade-off and to the specificity trade-off. Furthermore, the number of firms in the market plays a key role in dampening the specificity trade-off by increasing the number of potential healthy buyers in the secondary market and the connected expected liquidation values.

The value added by the paper consists of the analysis of the substitutability trade-off and the specificity trade-off, which are the main determinant of firms’ investment decisions, in a model where the ex-ante choice of asset specificity and the liquidation value of a distressed firm’s asset are endogenously determined in equilibrium. Marquez and Yavuz (2013) consider an endogenous investment in asset specificity that decreases the liquidation value of the asset when the lender has liquidation rights over the firm’s assets, and they find that financial constraints lead to a low level of specialization compared to the level achieved under self-financing. In this paper, I take a wider approach, by taking into account the dynamics of the secondary market in the determination of the liquidation value. Moreover, I also consider the direct effect of the number of firms in the market, as in Cerasi et al. (2017).

While Almeida and Campello (2007) and Flor and Hirth (2013) focus on the investment sensitivity to liquid funds, and its change with respect to redeployability costs, in this paper I focus on the investment sensitivity to redeployability costs. I show that the investment in asset specificity is most sensible to the redeployability costs when the probability of success of the project is medium-low. Instead, when the probability of success is very low or approaches the unit, investment levels are close to the first best.

The previous analysis is built on three main assumptions: first, firms invest in asset specificity before going to the capital market. Second I assume that the number of potential buyers is fixed - it does not depend on the degree of specificity of the asset on sale. Moreover also the potential buyer’s asset specificity may play a crucial role in the secondary market. Third, the capital market is under perfect competition.

Two reasons motivate the timing assumption. First, empirical evidence (e.g., Benmelech et al. 2005; Campello and Giambona 2011) asserts that capital providers, such as banks, in general prefer to lend to entrepreneurs with tangible and highly redeployable assets, that in case of failure can be easily liquidated. Thus, it will be difficult for firms to undertake specific investments (in a similar way as R&D investments) by accessing external finance. This implies that firms have to rely on internal funds when investing in asset specificity.

Second, there is a vocational attitude of firms such that the degree of asset specificity is chosen before going to the capital market. Firms need to set up a business plan when they seek funds for a project, in which the firm declares the final characteristics of the product and the productive assets planned to be used in the production. This is crucial in industries where firms are required to produce a prototype of the final product to show to potential lenders. In this example, firms have to decide the specificity of productive assets, as well as the characteristics of the final product before asking funds.

But what would happen in a model in which firms ask funds before investing in asset specificity? With respect to the standard model, the role of lenders changes. If firms want to invest a positive amount in asset specificity, they need to ask for a higher loan to the capital market. In this case, lenders might want to reduce the initial loan in order to prevent firms to over-invest in asset specificity. Specifically, they want to neglect this over-investment when the outcome of the secondary market is particularly hostile, i.e. when the redeployability of specific asset is low. Marquez and Yavuz (2013) show that under- or over-investments could be the outcome of the inability of the borrower to credibly commit to a given level of specialization. In particular, when she cannot commit to a certain level of asset specificity, she will over-invest in asset specificity when specialization has a large impact on liquidation values, while she will under-invest if the larger impact is on the long-term return of the project.

The second main assumption is that in the secondary market both incumbents and outsiders are always willing to bid, independently from their degree of asset specificity. However, since less-specialized equipment can be used for a wider set of uses, the number of potential buyers for general assets may be higher than the one of specific assets. In addition, redeployability costs might be affected not only by the specificity of the asset on sale, but also from the specificity of the buyer’s assets. For instance, suppose that redeployability costs are:

$$\begin{aligned} d(\lambda _b;\lambda _s)=\lambda _s + |\lambda _b-\lambda _s| \end{aligned}$$

where $\lambda _b$ is the buyer’s asset specificity, while $\lambda _s$ is the degree of asset specificity of the asset on sale. This formulation represents a case in which redeployability costs are a function of the two asset specificities: the higher the distance between the asset specificity chosen by the seller and the buyer, the higher the redeployability costs. In this case there might be coordination between firms because they may try to choose similar level of asset specificity in order to reduce those costs.

The last assumption that I discuss is relative to the capital market. In the analysis it is assumed that capital markets are under perfect competition. This means that lenders are breaking-even in expectation and thus there is no transfer of surplus between any firm and its lender. Even in this simple case, the model is able to show both the substitutability trade-off and the specificity trade-off. By relaxing this assumption it is possible to introduce bargaining power between lenders and borrowers. When lenders are able to extract some surplus from the borrower, they are able to design incentive-compatible contracts, in order to induce firms to choose a desired level of asset specificity, but only when that choice is after the settlement of the financial contract.

The main limitation of the model is that I do not consider competition between firms. In the model, firms interact strategically only through the secondary market, in which they compete for distressed firms’ assets and their choice of asset specificity is relevant for rivals. Indeed, asset specialization might affect product market competition. For instance, investments in asset specialization might increase product differentiation, so that when firms invest in asset specificity, they can reduce the degree of competition in the product market.

The analysis uses a binomial framework, but it could be extended to a continuous production function, or to consider the investment in asset specificity as a continuous variable. As a consequence, the return of the project $R(\lambda )$, the specialization cost $s(\lambda )$ and redeployability cost $d(\lambda )$ become continuous as well. Here, the first-best case could be found by setting the first order condition of the firm’s maximization problem, which is:

$$\begin{aligned} R(\lambda )=s(\lambda ) \end{aligned}$$

Instead, a firm’s maximum willingness to pay for an asset in the secondary market is

$$\begin{aligned} R(\lambda )-d(\lambda ) \end{aligned}$$

This framework allows for a deeper analysis on the implication of different degree of specificity on liquidation values and firm’s financial constraints. In particular, the different sensitivities of redeployability costs and specialization costs to changes in the level of $\lambda$ could bring new information concerning the collateral channel. Marquez and Yavuz (2013) show that when $s(\lambda )$ is pecuniary and the firm can choose the size of both the investment I and $\lambda$ after the stage of the financial contract, firms’ choose lower level of specialization with respect to the non-pecuniary case. However, they do not consider the role of redeployability costs in the secondary market.

Lastly, the analysis provides several empirical implications that could be tested.

Prediction 1

Asset specificity and market structure: Markets with a high number of active firms observe high investments in asset specialization.

The model shows that the liquidation value of a firm’s asset is positively associated to the number of companies in the market. Therefore, the empirical research that links firms financial constraints and the environment in which they operate (e.g. product market competition) should focus on the effect of the collateral channel in firms investment decisions.

Prediction 2

Redeployability costs and firms financial constraints: When redeployability costs are high, firms that use more redeployable assets will face better financing conditions with respect to firms that undertake specific investments.

There is a body of empirical evidence asserting that firms with highly redeployable assets find better financing condition. The empirical challenge is to find a measure for redeployability costs, which are difficult to observe from an external point of view. For instance, Benmelech and Bergman (2009) construct three redeployability measures by using the diffusion of aircraft types, the number of operators per type and the number of operators who operate at least five aircraft per type. Hence, the empirical research should focus on considering direct redeployability costs, in order to relate the liquidation value of the collateral to firms financing conditions.

6 Conclusions

This paper analysed the effect of the secondary market for productive assets used as collateral in financial contracts and the ex-ante choice of specificity faced by firms. If companies are financially constrained, they care about the ex-ante choice of asset specificity since it will affect the cost of debt through the collateral channel.

The analysis shows that the number of potential buyers and the degree of asset specialization directly affect the firms’ cost of debt. When the number of potential buyers is high, assets have a high expected resale value, and therefore firms find better financial condition. In the model, asset specificity influences both the return of firms’ project and redeployability costs. When redeployability costs are high, financially constrained firms do not invest in asset specialization since they want to reduce the cost of debt by pledging non-specific assets as collateral. Overall, financially constrained firms invest less in asset specialization compared to self-financing firms.

Appendices

Appendix A: Figures

See Figs. 1, 2, 3, 4 and 5.

Fig. 1

The first-best threshold $\varDelta R^*$, above the which firms invest in asset specificity, since the expected increment in the gross surplus $p\varDelta R$ is greater than the specialization cost s. When $p=1$, the increment in the project return required for the investment in asset specificity is equal to s. ($n=3$; $s=5$)

Fig. 2

The first best threshold, $\varDelta R^*$ (black) and the second best one, $\varDelta R^{SB*}$ (red), for $n=3$. If redeployability costs are low, $d<s$, (a), then the second-best threshold is lower than the first-best one. If redeployability costs are high, $d>s$ (b), then the second-best threshold is greater than the first-best one if $p>{\tilde{p}}$. ($n=3$; $s=5$; a $d=2$; b $d=20$)

Fig. 3

The figure plots the future repayment to the lender r as a function of the probability of success. In red, the future repayment to lenders when all firm choose $\lambda =0$. When instead firms choose $\lambda =1$, blue (black) line represent the case with high (low) redeployability costs. Dotted lines represent the no-lending area, in which the expected repayment required by lenders is above the return of the project. ($n=3$; $R(0)=30$; $R(1)=40$; $s=2$; low redeployability cost: $d=2$; high redeployability cost $d=10$) (color figure online)

Fig. 4

The threshold $\varDelta R^{SB*}$ (when $n=3$), above the which firms invest in asset specificity (a), and the effect of redeployability costs on the equilibrium threshold (b). Notice that for high level of d, the threshold might become non-monotone in p ($s=5$; a $d=15$; b $d_1=15$; $d_2=45$; $d_3=75$)

Fig. 5

The two-region model thresholds. The Home threshold $\varDelta R^o(s^H)^*$ (blue) and the Foreign threshold $\varDelta R^o(s^F)^*$ (red). In the region below $\varDelta R^o(s^H)^*$ , all firms choose not to specialize their assets; in the region above $\varDelta R^o(s^F)^*$, all firms specialize their assets; in the region between those two thresholds, shaded in red, only firms in the home region specialize their assets. ($s^H=5$; $s^F=10$; ${\hat{d}}=15$) (color figure online)

Appendix B: Proofs

Lemma 1

With probability p the firm is active at $t=3$, and thus the liquidation value is zero. With probability $1-p$ the firm is not active, and liquidation values are:

• When $h=1$ (with probability $p(1-p)^{n-1})$, all assets are sold to one firm that bids the smallest amount $\epsilon$ for all assets, independently of their degree of asset specificity.

• When $1<h<n$ (with probability $p^h(1-p)^{n-h})$, the price of an asset with $\lambda =0$ $(\lambda =1)$ is $\nu (0)=R(0)$ ($\nu (1)=R(1)-d$).

By computing the first derivative of $E_{t=0}(LV(\lambda ,d))$ with respect to n, it is possible to find that $\frac{\partial E_{t=0}(LV(\lambda ,d))}{\partial n}=(n-1)p(1-p)^{n-1}\ln {(n-1)}\epsilon + \left[ \sum _{h=2}^{n-1} (n-h)p^{h}(1-p)^{n-h}\ln {(n-h)} \right] \nu (\lambda )$, which is always positive for any $n>2$.

Lemma 2

The break-even condition is: $pr_i(\lambda _i)+E_{t=0}(LV(\lambda _i,d))=I(\lambda _i)++E_{t=0}(L({\varvec{\varLambda }},d))$. It follows that $pr_i(\lambda _i)=I(\lambda _i)-E_{t=0}(LV(\lambda _i,d)-L({\varvec{\varLambda }},d))$. However, if the right-hand side is larger than $pR(\lambda _i)$, then it means that at t=0 the firm will not sign the contract, since the expected future repayment to the lender is higher than the expected return of the project. Thus, $pR(\lambda _i)$ is the upper bound of the expected future repayment to the lender. But, at that threshold, lenders earn negative profits, so they will never lend to the firm.

Proposition 1

When the firm specialize the asset, its profits are $pR(1)-I-s$, while if it choose not to, it gets $pR(0)-I$. $pR(1)-I-s \ge pR(0)-I \Rightarrow \varDelta R \ge \frac{s}{p}$

Proposition 2

First, we can rewrite the financial contract for firm i as follows

$$\begin{aligned} pr_i^{\lambda _i}=I_0(\lambda _i)- \left[ p(1-p)^{n-1}\epsilon +\left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] \nu (\lambda _i) \right] +E_{t=0}[L_{t=2}(\varLambda )] \end{aligned}$$

Where $\nu (\lambda _i)$ represent other firms’ maximum willingness to pay for firm i’s asset (which is either R(0) if $\lambda _i=0$ or $R(1)-d$ if $\lambda _i=1)$.

Let us consider the specialization outcome $\lambda _i=1$ $\forall i \in \{1, \ldots , n\}$. In this case, the financial contract for the generic firm i is (we let $\epsilon \rightarrow 0$)

$$\begin{aligned} pr_i^{1}=I-(M-s)- \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] (R(1)-d) +E_{t=0}[L_{t=2}(1)] \end{aligned}$$

If firm i deviates and choose $\lambda _i^d=0$, then its financial contract will be

$$\begin{aligned} pr_i^{0,d}=I-M- \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] R(0) +E_{t=0}[L_{t=2}(1)] \end{aligned}$$

Now we can write the equilibrium profits and the deviation profits:

$$\begin{aligned} E_{t=-1}(\varPi _i(1))= & {} pR(1)-\left[ I-(M-s)- \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] \right. \\&\left. \quad \times \, (R(1)-d) +E_{t=0}[L_{t=2}(1)] \right] +E_{t=-1}[G_i(1)]\\ E_{t=-1}(\varPi _i^d(0))= & {} pR(0)-\left[ I-M- \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] \right. \\&\left. \quad \times \, R(0) +E_{t=0}[L_{t=2}(1)] \right] +E_{t=-1}[G_i(1)] \end{aligned}$$

Where $E_{t=-1}[G_i(1)]$ is the firm’s expected gain from the secondary market. Now, $E_{t=-1}(\varPi _i(1)) \ge E_{t=-1}(\varPi _i^d(0))$ if and only if :

$$\begin{aligned}&pR(1)-\left[ s- \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] (R(1)-d)\right] \\&\quad \ge pR(0)-\left[ - \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] R(0) \right] \\&\qquad \times \,\varDelta R \left( p+\sum _{i=2}^{n-1} p^{i}(1-p)^{n-i}\right) \ge s+d \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \end{aligned}$$

Therefore the specialization outcome $\lambda _i=1$ $\forall i \in \{1,\ldots , n\}$ is the outcome of the SPNE if and only if

$$\begin{aligned} \varDelta R \ge \varDelta R^* = \frac{s+d \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i}}{p+\sum _{i=2}^{n-1} p^{i}(1-p)^{n-i}} \end{aligned}$$

The proof for the specialization outcome $\lambda _i=0$ $\forall i \in \{1,\ldots , n\}$ follows the same path. In equilibrium, financial contract and expected profits are as follows

$$\begin{aligned} pr_i^{0}= & {} I-M- \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] R(0) +E_{t=0}[L_{t=2}(0)]\\ E_{t=-1}(\varPi _i(0))= & {} pR(0)-\left[ I-M- \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] R(0) +E_{t=0}[L_{t=2}(0)] \right] \\&+\,E_{t=-1}[G_i(0)] \end{aligned}$$

If the generic firm i deviates and choose $\lambda _i^d=1$, then:

$$\begin{aligned} pr_i^{1,d}= & {} I-(M-s)- \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] (R(1)-d) +E_{t=0}[L_{t=2}(0)] \\ E_{t=-1}(\varPi _i^d(1))= & {} pR(1)-\left[ I-(M-s)- \left[ \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i} \right] \right. \\&\left. \quad (R(1)-d) +E_{t=0}[L_{t=2}(0)] \right] +\\&\quad +\,E_{t=-1}[G_i(0)] \end{aligned}$$

Therefore, firm i will not deviate if and only if

$$\begin{aligned} E_{t=-1}(\varPi _i(0)) \ge E_{t=-1}(\varPi _i^d(1)) \Longleftrightarrow \varDelta R \le \varDelta R^* = \frac{s+d \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i}}{p+\sum _{i=2}^{n-1} p^{i}(1-p)^{n-i}} \end{aligned}$$

Lemma 3

Define $\gamma (n,p)=\gamma (n) \equiv \sum _{i=2}^{n-1} p^{i}(1-p)^{n-i}$. Therefore, $\gamma (n+1)= \sum _{i=2}^{n} p^{i}(1-p)^{n+1-i}=$

$(1-p)\gamma (n)+p^n(1-p)$. Moreover, $\gamma (n)-\gamma (n+1)=\gamma (n)-((1-p)\gamma (n)+p^n(1-p))=p(\gamma (n)-p^{n-1}(1-p))=p(1-p)\gamma (n-1)$. Finally notice that $\gamma (2)=0$.

Now we compute the difference $\varDelta R^*(n+1)-\varDelta R^*(n)$.

$$\begin{aligned} \varDelta R^*(n+1)-\varDelta R^*(n)= & {} \frac{s+d\gamma (n+1)}{p+\gamma (n+1)}-\frac{s+d\gamma (n)}{p+\gamma (n)}\\= & {} \frac{(s-dp)(p(1-p)\gamma (n-1))}{(p+\gamma (n))(p+\gamma (n+1))} \end{aligned}$$

Which is not positive if and only if $d>\frac{s}{p}$. Moreover, $\varDelta R^*(n+1)-\varDelta R^*(n)$ is strictly negative for $n >3$.

Lemma 4

It directly follows from Lemma 2.

Lemma 5

From Lemma 2:

$pr(0)= I-M-\frac{1}{2}p^2(1-p)R(0)$

$pr(1)= I-M+s-\frac{1}{2}p^2(1-p)(R(1)-d)+d(\frac{1}{2}p^2(1-p)+2p(1-p)^2)$

The no-lending scenario occurs when

$pR(0)\le I-M-\frac{1}{2}p^2(1-p)R(0)$

$pR(1)\le I-M+s-\frac{1}{2}p^2(1-p)(R(1)-d)+d(\frac{1}{2}p^2(1-p)+2p(1-p)^2)$

We can solve the first equation with respect to p and find the threshold $p_nl(0)$. By re-writing the condition, we find that $p_{nl}(0)$ is the solution of the following equation

$$\begin{aligned} p+p^2(1-p)=\frac{I-M}{R(0)} \end{aligned}$$

For any level of $\frac{I-M}{R(0)}<1$, and since $p \in [0,1]$ the condition above has one solution ($p_{nl}(0)$).

Then, by substitution, we find the condition under the which $p_{nl}(0)$ is lower than the cutoff for specific asset, $p_{nl}(1)$:

$p_{nl}(0)R(1)< I-M+s-\frac{1}{2}p_{nl}(0)^2(1-p_{nl}(0))(R(1)-d)+d(\frac{1}{2}p_{nl}(0)^2(1-p_{nl}(0))+2p_{nl}(0)(1-p_{nl}(0))^2$

Proposition 3

Let us consider the specialization outcome $\lambda _i=0$ $\forall i$ in all regions. Then, by solving the secondary market we find that

$$\begin{aligned}&E_{t=0}(L_{t=2}({\varLambda }))=[3p^2(1-p)^2+p^3(1-p)](R(0)-t)\\&E_{t=0}(LV_{t=2}(0))=[3p^2(1-p)^2+p^3(1-p)](R(0)-t) \end{aligned}$$

Therefore, the financial contract in equilibrium is $pr(0)=I-M$. If any firm deviates, then

$$\begin{aligned} E^d_{t=0}(LV_{t=2}(1))=[3p^2(1-p)^2+p^3(1-p)](R(1)-{\hat{d}}-t) \end{aligned}$$

And therefore the deviating financial contract is

$$\begin{aligned} pr^d(1)=I-(M-s^r)+p^2(1-p)(3-2p)[{\hat{d}}-\varDelta R] \end{aligned}$$

Firm i will not deviate if and only if

$$\begin{aligned} E_{t=-1}(\varPi _i(0)) \ge E_{t=-1}(\varPi _i^d(1)) \Longleftrightarrow pR(0)-pr(0)\ge pR(1)-pr^d(1) \end{aligned}$$

Which implies

$$\begin{aligned} \varDelta R \le \varDelta R_o^* (s^r) = \frac{s^r+{\hat{d}}p^2(1-p)(3-2p)}{p+p^2(1-p)(3-2p)} \end{aligned}$$

Therefore, if $\varDelta R \le \varDelta R^0(s^H)^*$, then $\lambda _{i}=0$ $\forall i$ and for all regions is the outcome of the SPNE in pure strategies.

Let us now consider the specialization outcome $\lambda _{i}=1$ $\forall i$ and in all regions. In this case

$$\begin{aligned}&E_{t=0}(L_{t=2}({\varLambda }))=[3p^2(1-p)^2+p^3(1-p)](R(1)-{\hat{d}}-t)+\psi ^r_o(p,d,{\hat{d}})\\&E_{t=0}(LV_{t=2}(1))=[3p^2(1-p)^2+p^3(1-p)](R(1)-{\hat{d}}-t) \end{aligned}$$

Therefore, the financial contract in equilibrium is $pr(1)=I-(M-s)+\psi _o(p,d,{\hat{d}})$, where $\psi _o(p,d,{\hat{d}})$ is the difference between $E_{t=0}(L_{t=2}({\varLambda }))$ and $E_{t=0}(LV_{t=2}(1))$ If any firm deviates, then

$$\begin{aligned} E^d_{t=0}(LV_{t=2}(0))=[3p^2(1-p)^2+p^3(1-p)](R(0)-t) \end{aligned}$$

And therefore the deviating financial contract is

$$\begin{aligned} pr^d(0)=I-M-p^2(1-p)(3-2p)[{\hat{d}}-\varDelta R]+\psi (p,d,{\hat{d}}) \end{aligned}$$

Firm i will not deviate if and only if

$$\begin{aligned} E_{t=-1}(\varPi _i(1)) \ge E_{t=-1}(\varPi _i^d(0)) \Longleftrightarrow pR(1)-pr(1)\ge pR(0)-pr^d(0) \end{aligned}$$

Which implies:

$$\begin{aligned} \varDelta R \ge \varDelta R_o^* (s^r) = \frac{s^r+{\hat{d}}p^2(1-p)(3-2p)}{p+p^2(1-p)(3-2p)} \end{aligned}$$

Therefore, if $\varDelta R \ge \varDelta R_o^*(s^F)$, then $\lambda ^{i,r}=1$ $\forall i,r$ is the outcome of the SPNE in pure strategies.

Proposition 4

In region H, $\lambda ^{i}=1$ $\forall i$. Therefore

$$\begin{aligned} E_{t=0}(L_{t=2}({\varLambda }))= & {} [2p^2(1-p)^2+p^3(1-p)](R(1)-{\hat{d}}-t)\\&+p^2(1-p)^2[R(0)-t]+\psi (p,d)\\ E_{t=0}(LV_{t=2}(1))= & {} [3p^2(1-p)^2+p^3(1-p)](R(1)-{\hat{d}}-t) \end{aligned}$$

Where psi(p, d) is the expected additional grant to the firm when it has to pay redeployability cos d. The equilibrium financial contract in region H is

$$\begin{aligned} pr_H(1)=I-(M-s^H)+p^2(1-p)^2[{\hat{d}}-\varDelta R]+\psi (p,d) \end{aligned}$$

If the generic firm i in H deviates, then

$$\begin{aligned} E^d_{t=0}(LV_{t=2}(0))=[3p^2(1-p)^2+p^3(1-p)](R(0)-t) \end{aligned}$$

And the deviating financial contract is

$$\begin{aligned} pr^d(0)=I-M-p^2(1-p)(2-p)[{\hat{d}}-\varDelta R] +\psi (p,d) \end{aligned}$$

Firm i in H will not deviate if and only if

$$\begin{aligned} E_{t=-1}(\varPi _i(1)) \ge E_{t=-1}(\varPi _i^d(0)) \Longleftrightarrow pR(1)-pr_H(1)\ge pR(0)-pr^d(0) \end{aligned}$$

Which is the case when:

$$\begin{aligned} \varDelta R \ge \varDelta R_o^*(s^H)= \frac{s^H+{\hat{d}}p^2(1-p)(3-2p)}{p+p^2(1-p)(3-2p)} \end{aligned}$$

In region F, $\lambda _i=0$ $\forall i$. Therefore

$$\begin{aligned} E_{t=0}(L_{t=2}({\varLambda }))= & {} [2p^2(1-p)^2+p^3(1-p)](R(0)-t)\\&+\,p^2(1-p)^2[R(1)-{\hat{d}}-t]+\psi (p,{\hat{d}})\\ E_{t=0}(LV_{t=2}(0))= & {} [3p^2(1-p)^2+p^3(1-p)](R(0)-t) \end{aligned}$$

The equilibrium financial contract in region F is

$$\begin{aligned} pr_F(0)=I-M-p^2(1-p)^2[{\hat{d}}-\varDelta R]+\psi (p,{\hat{d}}) \end{aligned}$$

If the generic firm i in F deviates, then

$$\begin{aligned} E^d_{t=0}(LV_{t=2}(1))=[3p^2(1-p)^2+p^3(1-p)](R(1)-{\hat{d}}-t) \end{aligned}$$

And the deviating financial contract is

$$\begin{aligned} pr^d(1)=I-(M-s^F)+p^2(1-p)(2-p)[{\hat{d}}-\varDelta R] +\psi (p,{\hat{d}}) \end{aligned}$$

Firm i in F will not deviate if and only if

$$\begin{aligned} E_{t=-1}(\varPi _i(0)) \ge E_{t=-1}(\varPi _i^d(1)) \Longleftrightarrow pR(1)-pr_F(0)\ge pR(0)-pr^d(1) \end{aligned}$$

Which implies:

$$\begin{aligned} \varDelta R \le \varDelta R_o^*(s^F)= \frac{s^F+{\hat{d}}p^2(1-p)(3-2p)}{p+p^2(1-p)(3-2p)} \end{aligned}$$

Therefore, if $\frac{s^H+{\hat{d}}p^2(1-p)(3-2p)}{p+p^2(1-p)(3-2p)} \le \varDelta R \le \frac{s^F+{\hat{d}}p^2(1-p)(3-2p)}{p+p^2(1-p)(3-2p)}$, then $\lambda _i=1$ for all firms in region H and $\lambda _j=0$ for all firms in region F is the specialization outcome of the SPNE.