1 Introduction

In most rock engineering cases, there are a large number of discontinuities (such as fissures, joints, and weak surfaces) in rocks because of geological movement and the tectonic stress field (Jiang et al. 2016; Cao et al. 2016). Especially for soft rocks such as coal, which are affected by sedimentary effects, the surrounding rock mass of underground coal mines is generally soft and rich in joints and cracks (Kong et al. 2019; Gao et al. 2021). These discontinuities, joints, or cracks in the rock are widely believed to have a significant influence on the stability of the rock mass, particularly with regard to the following two aspects: (1) they decrease the strength and stiffness of the rock, and (2) they are a source of initiation of new discontinuities, which in turn may propagate and link with other cracks and further decrease the strength and stiffness of the rock (Wong and Einstein 2009; Bobet and Einstein 1998; Sagong and Bobet 2002). Therefore, understanding the relationship between crack geometric parameters and rock mechanical properties is important in coal engineering.

Numerous rock laboratory tests and numerical simulation studies have been reported on the effects of crack geometric parameters on rock mechanical properties. For example, via numerical simulations, Cui et al. (2020) tested a particle model based on flat-joint and smooth-joint contacts to explore the effect of joint dip angle and joint spacing on the strength characteristics of rock under uniaxial compression with a set of nonpersistent open joints. Zhao et al. (2022) used a particle flow model to represent rock materials to investigate the relationship between the main microparameters (joint angle, length, density, and aperture) and uniaxial tensile strength; and Patel and Martin (2020) used a flat-jointed contact model to investigate the role of initial crack volume on the crack initiation stress of rock. By using laboratory tests, Li et al. (2019) produced preexisting joints in white marble by a high-pressure water cutting method to study the effect of the dip angles of joints on the rock dynamic mechanical properties, fracturing behavior, and energy evolution characteristics. In addition, 3D printing was used by Zhao et al. (2023) as a tool to examine the mechanical behavior of rock with discontinuities, and a control variable test was performed to investigate the effect of jointed geometric parameters (joint angle, length, and aperture) on the UCS and failure pattern. These studies indicate that the crack geometric parameters (joint angle, length, density, volume, aperture, etc.) have a very significant impact on rock mechanics properties. However, to date, few studies have been conducted to quantitatively analyze the correlation between crack geometric parameters and rock mechanics properties, even though a clear and deep understanding of this relationship in cracked rock is of great importance to the design of engineering rock mass structures.

Additionally, a large body of research has shown that the sampling interval, or sampling threshold, will greatly affect the crack morphology parameters (Xie et al. 1997; Xu et al. 2022). Furthermore, it will also undoubtedly have an impact on the correlation between crack geometric parameters and rock mechanics properties. Some researchers have shown that when the sampling interval of a crack surface meets a certain condition, the calculation results of the morphology parameters are very stable, and much research has been carried out to explore a reasonable sampling interval (Bao et al. 2020; Ge et al. 2021). However, there have been few reports about the effect of the sampling threshold on the correlation between crack geometric parameters and rock mechanics properties, which limits mechanical experimental investigations on complex crack rocks to a certain extent.

In this study, CT scanning was used to extract the internal crack network of coal specimens. Based on the crack size and dominant crack number, the parameters of crack area, volume, length, width, and angle were statistically analyzed by different sampling thresholds. In addition, the Pearson correlation coefficients between the crack parameters and uniaxial compression rock mechanics properties (uniaxial compressive strength UCS, elasticity modulus E) were calculated to quantitatively analyze the impact of each parameter. Furthermore, the Pearson correlation coefficients were compared under different sampling thresholds, and the key parameters and the optimal threshold value were obtained. The results of this study will facilitate further research on the mechanical properties of rocks with complex cracks.

2 Extraction and analysis of crack network information based on CT scanning

2.1 The extraction of cracks

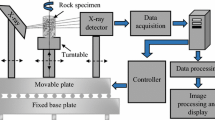
The Liangbaosi coal mine is located in Jining city, Shandong Province. The presence of softness and weak discontinuities (such as faults, joints or fractures) is consistent with the research objectives of this project (Zhu et al. 2021). Therefore, borehole core logging was conducted in the roof of the Liangbaosi coal mine, and specimens were obtained for the CT scanning tests. When X-rays emitted from an emission source pass through an object, the intensity of the X-rays is attenuated to some extent; the attenuation is influenced by the thickness and internal structure of the specimen. The attenuation characteristics follow the Lambert‒Beer law, which is expressed as follows (Salamon et al. 2019; Zhou et al. 2016):

$$I = I_{0} \exp ( - \mu x)$$
(1)

where I is the intensity of X-rays after passing through the object, I0 is the intensity of X-rays before passing through the object, μ is the attenuation coefficient of the sample being detected, and x is the penetration length of the incident X-rays.

The original grayscale CT image was binarized based on Otsu’s method (Otsu et al. 1979). The black areas represent pores, and cracks can be easily identified and segmented from the solid matrix. In addition, the pores and cracks were assigned a value of 0, and the solid matrix was assigned a value of 1 (Huang et al. 2021; Omori et al. 2023). The pores and cracks can be divided from the scan slice one by one.

The X-ray 3D microscope nanoVoxel-4000 system of Tianjin Sanying Technology Company was used for the CT scanning measurements, and the CT device and the process of crack network reconstruction are shown in Fig. 1. The main parameters for the CT scanning tests include the following: the voltage = 150 kV, the current = 150 μA, the exposure time = 0.8 s, the magnification = 4.6, the spatial separation rate = 0.127 mm, and the frame number = 1400/360°. The CT scanning data were first processed layer by layer to extract cracks. After the cracks were extracted, the slices were stacked layer by layer to form a three-dimensional structure. A total of 1000 16-bit grayscale images with 850 × 850 pixels were obtained by CT scanning of the entire standard coal specimen. At this time, the cracks were further identified, information about each fracture (length, area, volume, width, angle, etc.) was extracted in three dimensions, and finally, the crack network of the entire specimen was reconstructed (Wu et al. 2021; Yang et al. 2021).

Fig. 1
figure 1

CT device and crack network reconstruction process

Full size image

2.2 The analysis of correlations

To establish a quantitative relationship between the mechanical properties (UCS and E) and crack data of the CT image, the coal specimens were scanned using X-ray CT. Then, eight typical specimens were selected to conduct uniaxial compression tests to obtain the UCS and E. The stress–strain curves of the coal specimens are shown in Fig. 2, and the typical four stages (i.e., compaction, elastic stage, yielding and postpeak stage) and brittle failure is evident in each curve (Liu et al. 2018; Wang et al. 2020). Due to the presence of a large number of micropores and cracks, all the specimens showed notable compaction characteristics during initial loading, and then the stress gradually reached the peak value as the strain increased (Liu et al. 2019; Zhao et al. 2023). However, the UCS and E of the specimens were different due to the varied internal crack structures of the specimens.

Fig. 2
figure 2

Comparison of the stress–strain curves of the coal specimens

Full size image

Table 1 shows the results of the uniaxial compression tests and CT scans. Through the CT scanning image, it can be seen that the interior of the coal specimen is teeming with a large number of randomly distributed cracks. These cracks with different sizes and characteristics greatly affect the stress structure of the specimens, resulting in different mechanical properties, such as UCS and E (Liu et al. 2019; Zhao et al. 2023). However, it is difficult to directly analyze the relationship between crack characteristics and rock mechanical properties only from the data in Table 1.

Table 1 Results of the uniaxial compression test and CT scan
Full size table

The Pearson correlation coefficient (R) is a widely used statistical tool that measures the strength of the relationship between variables (Abubakar et al. 2023; Aladejare et al. 2022). Therefore, this coefficient is introduced here to analyze the correlation between rock mechanical properties and crack characteristics and is calculated as follows (Cai et al. 2020):

$$R = \frac{{\sum\limits_{i = 1}^{n} {(X_{i} - \overline{X})(Y_{i} - \overline{Y})} }}{{\sqrt {\sum\limits_{i = 1}^{n} {(X_{i} - \overline{X})^{2} } } \sqrt {\sum\limits_{i = 1}^{n} {(Y_{i} - \overline{Y})^{2} } } }}$$
(2)

where R is the Pearson correlation coefficient between parameters X and Y, n is the number of samples of parameters X and Y, Xi and Yi are the individual sample points indexed with i, \(\overline{X}\) is the sample mean of Xi, and \(\overline{Y}\) is the sample mean of Yi.

The value range of R is between − 1 and + 1. When R > 0, the two parameters are positively correlated. Otherwise, they are negatively correlated. Conventionally, the absolute values of R from 0.8 to 1.0 indicate an extremely strong correlation, values ranging from 0.6 to 0.8 indicate a strong correlation, values from 0.4 to 0.6 indicate a moderate correlation, values from 0.2 to 0.4 indicate a weak correlation, and values ranging from 0 to 0.2 indicate a very weak correlation or no correlation (Chen et al. 2022; Su et al. 2020; Zhao et al. 2021).

Correlations between the number of cracks, porosity, and different mechanical parameters (UCS, E) of the coals, calculated according to Eq. (2), are shown in Table 2. It can be seen that the porosity is weakly correlated with UCS and E, reflecting the porosity weakening effect on the strength and stiffness at a lower level. In addition, the number of cracks has almost no effect on UCS but has a relatively strong effect on E, reflecting the weakening effect of the number of cracks on the stiffness. More factors affecting the rock mechanics properties will be analyzed in the following sections.

Table 2 Correlations between the number of cracks, porosity, and different mechanical parameters of the coals
Full size table

Numerous studies have shown that the mechanical properties of rocks are significantly affected by porosity and crack geometric parameters (such as crack angle, and length) (Patel and Martin 2020; He et al. 2022; Zhao et al. 2023). Specifically, porosity is closely related to the total number, volume, and area of cracks. Based on the fractal concept, a selection of crack parameters, such as the area, volume, length, and width of the cracks within the specimen, were statistically calculated as variables about the crack parameters (the statistical results are shown in “Appendix A”), and Pearson coefficients R were calculated between the variables and the mechanical parameters of the coal specimens (UCS, E), as shown in Table 3.

Table 3 Correlations between different crack parameters and different mechanical parameters of the coals
Full size table

With regard to the variables related to area, the variable Smax had the strongest correlation with the UCS (R = − 0.60), showing a strong negative correlation. The variable Sta had the weakest correlation with the UCS (R = − 0.35), showing a weak negative correlation. Additionally, it was discovered that as the statistical threshold was increased, the correlation between the variables associated with area and the UCS also increased, indicating that the dominant crack played a role in weakening strength. Regarding the mechanical parameter E, Smax also had a strong correlation (R = − 0.45), showing a moderate positive correlation. This indicates that the dominant crack also played an important role in weakening stiffness. Notably, the correlation between E and the area variables decreased as the statistical threshold was increased, until the threshold reached 10 mm2, at which point the correlation changed from moderate to weak, which is different from the UCS. These results indicated that small cracks can also weaken stiffness.

Among the volume-related variables, the variable Smax also showed the strongest negative correlation with the UCS (R = − 0.62), and the correlation between the volume-related variables and the UCS also increased as the statistical threshold increased, which further indicated that the dominant crack played a role in weakening strength. For the mechanical parameter E, Smax displays the strongest correlation (R = − 0.37) among the volume-related variables but shows a weak correlation. In addition, Vta also showed a weak correlation (R = − 0.37), while V1, V5 and V10 indicated a very weak correlation or no correlation with E.

In terms of length, the variable Lmax retained the strongest negative correlation with the UCS (R = − 0.57), but the absolute values of R between UCS and other length-related variables were below 0.2 and demonstrated a very weak correlation or no correlation. For the mechanical parameter E, Lta displayed the strongest correlation (R = − 0.53) with the length-related variables, and the correlation between E and the variables related to length decreased as the statistical threshold increased. L10 exhibited a very weak correlation or no correlation with E.

For the variables related to width, the variable Wmax has the strongest negative correlation with the UCS (R = − 0.58), and the correlation between other variables about width and UCS varies with the statistical threshold in a pattern consistent with that of area-related variables. For the mechanical parameter E, Wta displays the strongest correlation (R = − 0.55) among the width-related variables, and the variable Wmax also has a relatively strong correlation with E (R = − 0.48). Notably, the correlation between E and the width-related variables increased as the statistical threshold increased, which is different from the area.

Previous studies have indicated that the crack angle has a significant effect on the mechanical properties of the specimen (Aliha et al. 2010; Tahmasebinia et al. 2018; Zhao et al. 2023). Therefore, the correlations between the maximum crack angle (βmax), area-weighted average angle (βs), volume-weighted average angle (βv), and different mechanical parameters (UCS, E) of the coals can be calculated as shown in Table 4. The calculation of the weighted average angle is as follows:

$$\beta_{\text{s}} = \frac{{\sum\limits_{i = 1}^{m} {\beta_{\text{i}} } *S_{\text{i}} }}{{\sum\limits_{i = 1}^{m} {S_{\text{i}} } }}$$
(3)
$$\beta_{\text{v}} = \frac{{\sum\limits_{i = 1}^{m} {\beta_{\text{i}} } *V_{\text{i}} }}{{\sum\limits_{i = 1}^{m} {V_{\text{i}} } }}$$
(4)

where m is the number of cracks taken and βi, Si and Vi are the individual crack angle, area and volume, respectively.

Table 4 Correlations between the crack angle and different mechanical parameters of the coals
Full size table

According to Table 4, βmax shows the strongest negative correlation with the ultimate compressive strength (UCS) (R = 0.54), followed by βs (R = 0.44), which both exhibit a moderate correlation. For the mechanical parameter E, although βmax also shows a moderate correlation (R = 0.47), its correlation is weaker than βs (R = 0.60) and βv (R = 0.61). These analyses all indicate that increasing the crack angle weakens the weakening effect of cracks on the strength and stiffness of the specimen.

The correlations between different weighted average angle and mechanical parameters of the coal specimens (UCS, E) were counted for further analysis, as shown in Table 5. It can be seen that as the statistical threshold increased, there was a noticeable increase in the correlation between mechanical parameters and area-weighted variables. This correlation continued to be enhanced until the threshold reached 5 mm2, at which point it became remarkably close to the βmax. For volume-weighted variables, the correlation between UCS and the variables increased as the statistical threshold was increased, until the threshold reached 10 mm3, at which point it became remarkably close to the βmax.

Table 5 Correlations between different weighted average angle and different mechanical parameters of the coals
Full size table

According to the above analysis of the correlation between crack characteristics and rock mechanical properties, it was discovered that as the statistical threshold is increased, the correlation between the variables and the UCS also increases. All the aforementioned analyses indicate that the dominant crack played an important role in weakening both the strength and stiffness. Furthermore, an analysis of Tables 3, 4, and 5 reveals that when the statistical threshold for crack area is set to 5 mm2, there is a high level of correlation between various parameters of the crack and mechanical parameters, meaning that cracks larger than 5 mm2 have a significant impact on the mechanical parameters.

3 Crack selection and validation of the triaxial test

3.1 The selection of cracks

The internal cracks in the specimens were sorted in order of size, and then, based on the fractal concept, the sorted cracks were statistically analyzed separately according to single, four, eight, sixteen, and thirty-two cracks. The statistical results are shown in “Appendix B”. Subsequently, the correlation between each crack parameter obtained from each statistical method and the rock mechanical properties was calculated separately, as shown in Table 6.

Table 6 Correlations between different crack parameters and different mechanical parameters of the coals
Full size table

When studying the correlation, to reduce the impact of error and chance, the top three parameters that were most correlated with each of the two rock mechanics properties were selected for marking (three positive and three negative correlations were chosen for each parameter). During the marking process, the correlation level was considered based on the classification of correlation coefficients in Sect. 2.2, and the parameters with lower correlation levels were removed. The parameters that showed a positive correlation with UCS were βs (R = 0.58) for eight cracks, βs (R = 0.54) for single cracks, βv (R = 0.54) for sixteen cracks, and βs (R = 0.54) for thirty-two cracks, and they all showed moderate correlations. The parameters that showed a negative correlation with UCS were Vta (R = − 0.62), Sta (R = − 0.60), and Wta (R = − 0.58), which all showed a strong correlation. Wta showed a moderate correlation and should be removed during marking. The parameters that showed a positive correlation with E were βs (R = 0.59) for thirty-two cracks, βs (R = 0.58) for sixteen cracks, and βv (R = 0.56) for sixteen and thirty-two cracks. The parameters that showed a negative correlation with E were Wta (R = − 0.48), Sta (R = − 0.45), and Vta (R = − 0.37), which all showed moderate correlations. Vta showed a weak correlation with E and should be removed during marking.

Finally, a statistical analysis was conducted on the parameters marked, and it was found that the parameters marked the most were Sta for single cracks and βs for 16-fold and thirty-twofold cracks, which were marked twice each. This indicates that these parameters have a strong impact on both UCS and E. Additionally, we found that the β and βv parameters for all statistical methods had correlation coefficients of over 0.4 with the rock mechanics properties, which is not the case for other parameters. This indicates that the angle has a strong impact on the rock mechanics properties, which is consistent with the research of Tahmasebinia et al. (2018) and Zhao et al. (2023). When comparing the number of parameters marked under different statistical methods, the parameters were marked the most when the statistical methods were single cracks. This further indicates that dominant cracks play a crucial role in affecting the rock mechanics properties. Additionally, sixteen and thirty-two cracks were also marked three times each, indicating that using these statistical methods can also significantly improve the correlation between each parameter of cracks and the rock mechanics properties. This may imply that in future studies on rock masses with complex cracks, in addition to analyzing the parameters of the largest cracks in focus, the geometric parameters of at least 16 cracks should be used as statistics for further analysis or physical reproduction using 3D printing.

3.2 Validation of the triaxial test

To further verify the effectiveness of the conclusions obtained from the abovementioned research in triaxial tests that are closer to the conditions of real coal masses, two specimens were selected from the Liangbaosi coal mine and numbered TC-1 and TC-2 for subsequent triaxial tests. Referring to the ultimate strengths of the specimens in Sect. 2.2 that were determined from uniaxial tests, the confining pressure in the triaxial test was set at 5.0 MPa. The confining pressure increases to the expected value at a constant rate of 0.025 MPa/s. The displacement loading mode with a speed of 0.01 mm/s was used in the axial direction (Chen et al. 2021; Mishra and Vermaet 2015; Pang et al. 2014).

According to the conclusion of the previous section, CT scans were performed on the specimens before and after the triaxial test, and the largest 16 cracks were extracted for statistics (“Appendix C”), which were then analyzed in conjunction with the test results. Finally, the CT scanning images before and after testing (Fig. 3), the statistical results of cracks before and after the test (Table 7), and the stress‒strain curves of TC-1 and TC-2 were obtained (Fig. 4).

Fig. 3
figure 3

Changes in the internal cracks in specimens before and after the triaxial compression test

Full size image
Table 7 Results of the triaxial compression test and statistical crack parameters
Full size table
Fig. 4
figure 4

Stress‒strain curves of triaxial compression

Full size image

In the previous section, it was found that Smax and βs had a large correlation with rock mechanics properties (UCS, E). Therefore, in this section a statistical analysis is performed on these two parameters, as shown in Table 7, and UCS and E are also added for comparison. By comparing the Smax and βs of TC-1 and TC-2 before testing, it was found that the Smax of TC-1 was 3.41 times that of TC-2, and the βs values of TC-1 were significantly smaller than those of TC-2. By comparing the rock mechanics properties, it was determined that the UCS and E of TC-1 were significantly smaller than those of TC-2. These comparisons indicate that there is also a negative correlation between Smax and UCS and E in triaxial testing and a positive correlation between βs and UCS and E, which is completely consistent with the rules discovered in the uniaxial test.

Table 7 also statistically analyzes the porosity changes before and after the triaxial tests, as well as the two key parameters (Smax and βs). The βs values of TC-1 did not change greatly before and after the test, while those of TC-2 changed significantly (i.e., the βs of TC-2 decreased from 82.84° to 51.94°). Additionally, the Smax of TC-1 after testing is larger than that of TC-2, which is 3.4 times that of TC-2. These analyses indicate that the failure of TC-1 is mainly due to instability and failure after the propagation of cracks, and TC-2 exhibits more damage than TC-1 after the test, which can also be seen from the CT scanning images (Fig. 3). Further analysis will be conducted based on the stress‒strain curves and electron microscopy scanning images.

It is observed that the damage to coal specimens occurs in four different stages following loading. These four stages have different deformation characteristics, and the specific results of the analysis are as follows:

Stage I: The compaction stage. Stage I begins from the start point of the stress to point A. As the load continues to increase, the axial and volumetric strains show positive growth, which means that the specimens are axially compressed while their volume decreases. However, it can be seen from the radial strain‒stress curve that the radial strain is continuously decreasing, but the magnitude is relatively small. This indicates that during Stage I, the pores and cracks inside the specimen are compacted, and no significant damage is caused. The larger porosity of TC-1 results in a longer duration for this stage compared to TC-2.

Stage II: The crack initiation and steady expansion stage. This stage starts from stress point A, goes to point B1, and then reaches point B2. The axial strain continues to increase, but the volumetric strain starts to decrease continuously. The decrease in radial strain starts to increase, which indicates that the specimen is starting to crack and experience steady expansion. During the loading process, the specimen is subjected to both strain hardening and strain softening, and these two mechanisms compete with each other (Carpinteri et al. 2006; Zhao et al. 2023). It is noteworthy that TC-2 exhibits a longer duration during this stage and has a smoother ascent of the stress‒strain curve compared to TC-1. According to “Appendix C”, the angles of the four largest cracks in the TC-2 specimen are 86.89°, 87.49°, 88.03°, and 89.92°, which are very close to the direction of primary cracks in rock materials during compression (primary cracks, as tensile cracks, usually propagate in a stable manner toward the direction of maximum compression) (Bobet and Einstein 1998; Sagong and Bobet 2002). The similarity in direction facilitates the smooth expansion of cracks.

Stage III: The accelerated destruction stage. This stage starts from stress point B2, goes to point C1, and then reaches point C2. The stress‒strain curves begin to depart from the linear behavior, and the volumetric strain and radial strain start to accelerate. This indicates that the specimen enters the stage of accelerated destruction, in which dilatancy deformation and rupture become dominant (Sondergeld and Estey. 1981). Due to the stable propagation of the cracks in the CT-2 specimen toward the direction of maximum compression, this stage lasts for a shorter duration compared to CT-1.

Stage IV: The postpeak stage. This stage starts from stress point B2 and lasts until the stress drops. CT-1 experienced multiple small stress releases in Stage II and Stage III, so its stress‒strain curve slumped slowly. However, significant decreases in volumetric strain and radial strain indicate that the specimen has undergone instability and failure due to the propagation of the cracks, which can also be seen in the CT scanning images after the CT-1 test (Fig. 3a). In contrast, CT-2 experienced no significant stress releases in the early stage, and large stress releases only occurred after the stress reached its peak. As a result, the stress‒strain curve of CT-2 dropped more quickly, and CT scanning images after its destruction (Fig. 3b) show that specimen CT-2 is more broken than CT-1 inside.

Samples were taken near the main crack of specimens TC-1 and TC-2 after testing to study the micromorphology characteristics of the fracture surface. The samples were analyzed with an APREO electron microscopy scanning system from the FEI Corporation to obtain the micromorphology images of the coal samples, and an accelerating voltage of 2 kV was used in this study.

The typical micromorphology images of TC-1 and TC-2 near the main fractures are shown in Fig. 5. The typical features of the coal samples near the TC-1 main fracture show that most cracks are deflected along the grain boundaries, resulting in a sharp angular edge, and the overall fracture surface appears to be rougher, which is referred to as a typical intergranular (IG) fracture (Mendhe et al. 2018; Wang et al. 2023). In contrast, the typical features of the coal samples near the TC-2 main fracture show that the overall fracture surface is relatively smoother. Locally, the boundaries of mineral grains are incomplete, and the surfaces have scratches sliding along the fracture surface, which is referred to as a typical transgranular (TG) fracture (Mahanta et al. 2017; Zhu et al. 2023). IG fractures and TG fractures are related to the energy stored before the sample breaks. IG fractures are caused by less energy consumption during the fracture process, while TG fractures are caused by more energy consumption during the fracture process (Abdollahi et al. 2012; Zhang et al. 2023; Zhou et al. 2022). TC-2 experienced no significant stress releases in the early stage, and large stress releases only occurred after the stress reached its peak, resulting in more energy consumption during the fracture process, which caused more TG fractures to occur, which is completely consistent with the trend of the stress‒strain curves.

Fig. 5
figure 5

Microstructure of coal after triaxial compression failure

Full size image

4 Discussion

It is clear that a deep understanding of the relationship of crack geometric parameters and rock mechanics properties in cracked rock is of great importance to the design of engineering rock mass structures. Currently, 3D printing has been proven to be a powerful technique for simulating rocks and has advantages in replicating complex cracks (Ge et al. 2021; Niu et al. 2023). However, due to the limitations of machine accuracy, 3D printing still has some limitations in replicating small defects, such as microcracks and micropores, which will be a challenge for mechanical experimental research on complex crack rocks. Determining the optimal threshold value will provide a scope for 3D printing to determine the cracks that need to be reproduced during the process of reproducing complex crack rocks. This is so that the rocks reproduced can preserve the impact of cracks on rock mechanics properties to the greatest extent, thereby making the 3D printing specimens more similar to real rocks.

Although the Pearson coefficient was calculated using only 8 test specimens, a significant number of scholars maintain the belief that it can still yield an accurate correlation in similar scenarios (Chen et al. 2022; Abubakar et al. 2023). Furthermore, the results have been corroborated through triaxial compression tests. However, the previous studies indicate that significant correlations exist between the parameters, meaning that the effect of one crack geometric parameter on UCS is significantly correlated with other crack geometric parameters (Zhao et al. 2023), which is not taken into account by the Pearson correlation coefficients. Therefore, the findings of this study merely represent an initial exploration into the influence of crack geometric parameters on mechanical properties. To obtain more precise data and establish an accurate functional relationship, additional experimental data are needed, which will be a crucial undertaking.

5 Conclusions

In this paper, CT scanning was used to extract the internal crack network of coal specimens. Based on the crack size and dominant crack number, the parameters of crack area, volume, length, width, and angle were statistically analyzed. The Pearson correlation coefficients between the crack parameters and uniaxial compression rock mechanics properties (UCS, E) were calculated to analyze the impact of each parameter, and the results were further verified through triaxial testing. Based on the study results, the following conclusions can be made:

  1. (1)

    The UCS and E of the specimens changed with the varied internal crack structures of the specimens, porosity was weakly negatively correlated with UCS and E, and the number of cracks had almost no effect on UCS but had a relatively strong negative correlation with E.

  2. (2)

    The crack parameters of area, volume, length and width were all negatively correlated with UCS and E. The correlation between the variables and the UCS increased as the statistical threshold increased, and the dominant crack played an important role in weakening strength and stiffness. More specifically, there is a high level of correlation between various parameters of the crack and mechanical parameters when the statistical threshold for crack area is set to 5 mm2. Hence, the statistics of geometric parameters of the cracks with an area larger than 5 mm2 are suggested for analyzing complex cracked rock mass.

  3. (3)

    A method based on Pearson coefficients was used to grade the correlation between crack geometric parameters and rock mechanical properties to determine threshold values. The results indicated a positive correlation between angle-related variables and both UCS and E. Increasing the quantity of crack statistics significantly improved this correlation. However, the improvement became insignificant when the number of crack statistics reached 16. Therefore, the statistics of geometric parameters of at least 16 cracks are suggested for analyzing complex cracked rock mass or physical reproduction using 3D printing.

  4. (4)

    Smax and βs showed a larger correlation with rock mechanics properties (UCS, E), and the two key parameters were also proven to have a significant impact on the mechanics parameters of the specimens under triaxial testing, and this impact was largely consistent with that observed during uniaxial testing.

The results of this study can facilitate further targeted research on mechanical properties of rocks with complex cracks, especially how to accurately and efficiently select a few cracks that may have a significant influence on rock mechanical properties from complex and numerous cracks. Furthermore, additional studies may determine that the results may not be limited to soft rock.