1 Introduction

The rock uniaxial compressive strength (UCS) is an indispensable parameter in rock mass stability analysis, underground chamber excavation, and support design for transportation, mines, and hydraulic projects. Accurate acquisition of the UCS is a precondition for engineering construction. In particular, the rock UCS should be obtained rapidly for underground engineering with complex geological conditions, such as soft rock, fracture areas, and high stress (Cao et al. 2016; Wang et al. 2017b, 2018, 2019, 2020a, b; Yang et al. 2017) to adjust the excavation and support plan and ensure construction safety. The conventional rock uniaxial compression test is a common method to measure the rock UCS (Chen et al. 2017; Liu et al. 2018; Meng et al. 2016; Xu and Dai 2017). However, on-site core drilling and laboratory testing is required, which is a cumbersome process with long measurement periods. Thus, the surrounding rock UCS at a construction site cannot be obtained in real-time, and effectively obtaining rock core specimens for UCS measurements from the fractured surrounding rock is difficult. Therefore, an in situ test method to measure the surrounding rock UCS in engineering sites in real-time is needed.

The point load method (Heidari et al. 2012; Kaya and Karaman 2016; Ozturk and Altinpinar 2017) and Schmidt hammer testing (Goktan and Gunes 2005; Wang et al. 2017a) are commonly used in situ methods to measure rock strength. However, the surrounding rock needs to be core drilled to obtain the rock strength for these methods. Some researchers have investigated in situ rock UCS forecasting based on regression analysis or artificial neural networks (Dehghan et al. 2010; Moradian and Behnia 2009; Sharma et al. 2017; Tiryaki 2008; Torabi-Kaveh et al. 2015; Yesiloglu-Gultekin et al. 2013). The majority of previous in situ rock strength testing methods only support measurements of the rock UCS at a limited number of points. The UCS from a chamber surface to the surrounding rock at a considerable depth does not enable continuous measurements. Therefore, developing a continuous and quick test method for the rock strength parameters in situ has become the key focus of geotechnical test technology research.

This analysis reveals that drilling is required in the majority of surrounding rock strength parameter testing methods. Quick in situ measurements of rock strength will be achieved if the rock UCS is obtained during drilling. Digital drilling test technology (Ersoy 2003; Gui et al. 2002; Munoz et al. 2016; Sugawara et al. 2003; Yue et al. 2004) provides an effective means to support real-time monitoring of drilling parameters, including the rate, thrust, rotating speed, and torque. Studies by several researchers have indicated that the digital drilling parameters and rock UCS are correlated (Aalizad and Rashidinejad 2012; Ataei et al. 2015; Fattahi and Bazdar 2017; Kumar et al. 2011; Li and Itakura 2012; Yaşar et al. 2011).

The drilling parameters and rock core at the corresponding positions can be obtained during digital core drilling of the surrounding rock. The rock UCS from laboratory testing is compared with the forecasted value from the drilling parameters. A quantitative relationship model for the drilling parameters and rock UCS is continuously modified to form the rock UCS digital core drilling real-time acquisition method. Therefore, this surrounding rock digital core drilling test provides a new approach for the continuous and real-time acquisition of rock UCS on site. The key to this approach is establishing a quantitative relationship between the digital core drilling parameters and the rock UCS.

To achieve real-time acquisition of the rock UCS, digital core drilling tests and uniaxial compression tests are conducted on cement mortar specimens of varying strengths and sandstone specimens to determine the drilling parameters and UCS. These tests are based on the rock mass digital drilling test system and a specially developed digital core bit. The mechanical analysis of rock cutting is performed to obtain the digital core drilling strength (DCS). A quantitative relationship model (CDP-UCS model) between the digital core drilling parameters and rock UCS is generated for the proposed digital core drilling-based rock UCS forecast method.

2 Digital core drilling test

2.1 Test equipment

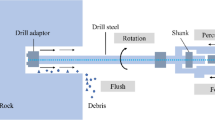
The rock digital core drilling test is based on a rock mass digital drilling system that was developed by the authors, as shown in Fig. 1. This test equipmement includes the drilling system, the loading system, the pressure chamber, and the monitoring and control system with a maximum drilling thrust and rotating speed of 50 kN and 400 r/min, respectively. The overall dimensions of the main device are 1750 mm × 2350 mm × 4335 mm. During drilling, the system supports real-time monitoring and control of the drilling parameters, including the drilling rate V (mm/min), rotating speed N (r/min), drilling thrust F (kN), and drilling torque M (N m). Thus, four control modes of constant V–N, constant V–M, constant F–N, and constant F–M are formed, and rock digital drilling tests under multiple control modes are realized.

Fig. 1
figure 1

Rock mass digital drilling system

Full size image

A specially designed PDC (Polycrystalline Diamond Compact) bit for digital core drilling is used, which consists of the rectangular PDC and matrix, as shown in Fig. 2. The rock cutting mechanical analysis of the drill bit conforms to the theoretical hypothesis, and the rectangular compact design ensures that the shape and stress characteristics remain unchanged to reduce the impact of compact wear on the test data, even if the compact wears during drilling.

Fig. 2
figure 2

Special PDC bit for digital core drilling

Full size image

2.2 Test plan design

The specimens in the digital drilling test include cement mortar specimens with various strengths and sandstone specimens. The sandstone specimens are made from relatively intact natural rock, and the cement mortar specimens are prepared based on seven mix ratios to simulate intact rock of different strengths, as listed in Table 1. Three groups are prepared for each type of test specimen, giving a total of 24 groups. The specimen dimensions are as follows: length × width × height = 150 mm × 150 mm × 200 mm.

Table 1 Material consumption of making cement mortar specimens with various strength grades per m3
Full size table

The digital core drilling test controls the drilling rate V and rotating speed N while monitoring the thrust F and torque M. The V and N are set to one of two levels: 60 or 85 mm/min and 50 or 100 r/min, respectively. The cement mortar specimens with seven strength grades are numbered as S1–S7, and the sandstone specimen is numbered as S8. The core drilling depth of the test specimen is 150 mm. After the drilling tests, the rock core is collected, cut, and polished to prepare the conventional specimens for the UCS measurements, which is based on the “Standard Test Methods for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures” (ASTM Standard Designation: D7012–14). The dimensions of the prepared rock core specimens are diameter × height = 50 mm × 100 mm. The detailed test plan is given in Table 2.

Table 2 Digital core drilling test plan
Full size table

3 Statistics and analysis of test results

3.1 Statistics of drilling parameter results

The rock digital core drilling tests are performed based on the test plan in Table 2. The specimens before and after the tests are shown in Fig. 3. During the digital core drilling test, the V, N, M, and F are monitored in real-time. Typical test data from specimen S53 are taken as an example, and the drilling parameter curves are shown in Figs. 4 and 5, where V = h/t, h is the drilling depth and t is the drilling time.

Fig. 3
figure 3

Partial digital core drilling test specimens

Full size image
Fig. 4
figure 4

Analysis curves of controlled drilling parameters

Full size image
Fig. 5
figure 5

Analysis curves of monitored drilling parameters

Full size image

As shown in Fig. 4, the V and N for drilling specimen S53 stabilize at the predefined values of 85 mm/min and 100 r/min, respectively, which give the desired control results. As shown in Fig. 5 for the drilling specimen S53, the trends of F and M with h are similar. As the drilling depth increases, F and M rapidly increase at the initial stage and then stabilize and fluctuate over a small range.

The F and M test values are the averages of the stable segment minus their initial values. The M measurement results from specimen S53 are taken as an example. The average value in the stable segment is Ma = 33.99 N m with an initial value of Mi = 17.0 N m. Then, the test value of this specimen becomes M = Ma-Mi = 16.99 N m The monitoring results of V, N, F, and M for all specimens are counted, and the standard rock UCS of the test specimen is measured. The detailed results are given in Table 3.

Table 3 Statistics of digital core drilling test and uniaxial compression test results for test specimens
Full size table

3.2 Analysis of responses for M and F to rock UCS

Based on the test data in Table 3, a V of 60 mm/min and N of 100 r/min are taken as an example, the response laws for M and F to the rock UCS are analyzed, as shown in Figs. 6 and 7.

Fig. 6
figure 6

Analysis of response of drilling torque M to rock UCS

Full size image
Fig. 7
figure 7

Analysis of response of drilling thrust F to rock UCS

Full size image

The analysis of Figs. 6 and 7 shows that the variation laws for M and the F to the rock UCS are consistent. Both laws demonstrate an overall increasing trend for a larger rock UCS. Therefore, intuitively analyzing the response degrees of the drilling parameters to the rock UCS allows using the drilling torque M as an example to generate λ, which is the response evaluation index of M to the rock UCS.

$$\lambda = \frac{{\left| {\Delta M} \right|}}{{\left| {\Delta {\text{UCS}}} \right|}}$$
(1)

where, ΔM is the difference between monitored drilling torques M in two plans, N m; ΔUCS is the difference between measured rock UCS in two plans, MPa.

Taking specimens S12 and S22 with small strength differences and specimens S72 and S82 with significant strength differences as examples, the λ between specimens S12 and S22 is 1.15 N m/MPa, while that between specimens S72 and S82 is 1.26 N m/MPa. The difference value in the responses of M to the UCS is relatively small for plans with significant or small strength differences. Therefore, the monitored drilling parameters during rock drilling are highly responsive to the UCS.

4 Quantitative relationships between drilling parameters and rock UCS

4.1 Mechanical analysis of rock cutting

The aforementioned response laws of the core drilling parameters to the UCS indicate that rock UCS forecasting is feasible based on the digital core drilling parameters. To establish a quantitative relationship between the core drilling parameters and the UCS, the monitored drilling parameters V, N, M, and F are comprehensively applied to reduce the discreteness of using a single type of drilling parameter. Additionally, to reveal the in-depth rock cutting mechanism of the special digital core bit, a rock cutting mechanical analysis model is created based on the rock cutting failure characteristics, as shown in Fig. 8. As the length of each row of cutting edges greatly exceeds the rock cutting depth over one rotation by a single row of cutting edges (i.e., instantaneous cutting depth H), the cutting edge is treated as linear motion over each rock cutting cycle, and the rock cutting problem is simplified to a planar strain problem.

Fig. 8
figure 8

Rock cutting mechanical analysis model for digital core drilling

Full size image

The rock cutting mechanical model in Fig. 8 is used to calculate the required torque M for the drill bit to cut rock. This torque contains the cutting torque Mc as generated by the horizontal component force of the resistance Fc from the front rock on the cutting edge and the friction torque Mf generated by the horizontal component of the force Ff from the rock at the bottom of the hole on the cutting edges.

As shown in Fig. 9, the radius of the special digital core drilling bit in the test is R = 37.5 mm. The bit contains n = 5 rows of cutting edges, and the length of each row of the cutting edges is l = 9 mm. The torque generated by the force on an arbitrary microsegment dr of the cutting edge is:

$${\text{d}}M = {\text{d}}M_{c} + {\text{d}}M_{f} = F_{c} r\cos (\theta + \alpha ){\text{d}}r + F_{f} r\sin \beta {\text{d}}r$$
(2)
Fig. 9
figure 9

Special digital core bit and a row of cutting edges

Full size image

where, α is the angle between the force Fc and the normal direction of the cutting edge surface, θ is the inclination angle of the cutting edge in the special digital core drilling bit (θ = 15°), and β is the angle between the force Ff and the vertical direction, which is also the friction angle between the cutting edge and the rock. Based on the research results of Huang et al. (2013) and Yahiaoui et al. (2016), α and β are set to 12°.

The moments for all the cutting edges of the special digital core bit are superimposed to obtain the drilling torque M as:

$$\begin{aligned} M & = n\int_{R - l}^{R} {\left[ {F_{c} \cos (\theta { + }\alpha ) + F_{f} \sin \beta )} \right]} r{\text{d}}r \\ & { = nl(R - \frac{l}{2})\left[ {F_{c} \cos (\theta { + }\alpha ) + F_{f} \sin \beta } \right]} \\ \end{aligned}$$
(3)

The drilling thrust F is equal to the sum of the vertical components of the forces Fc and Ff, as shown in Fig. 8. As shown in Fig. 9, the vertical force dF on an arbitrary microsegment dr of the cutting edges is:

$${\text{d}}F = {\text{d}}N_{c} + {\text{d}}N_{f} = F_{c} \sin (\theta + \alpha ){\text{d}}r + F_{f} \cos \beta {\text{d}}r$$
(4)

The vertical forces for all rows of cutting edges in the special digital core bit are superimposed to obtain the drilling thrust F as:

$$\begin{aligned} F & = n\int_{R - l}^{R} {\left[ {F_{c} \sin (\theta + \alpha ) + F_{f} \cos \beta } \right]} {\text{d}}r \\ & = nl\left[ {F_{c} \sin (\theta + \alpha ) + F_{f} \cos \beta } \right] \\ \end{aligned}$$
(5)

Equations (3) and (5) are combined to eliminate the unknown force Ff:

$$M = nl(R - \frac{l}{2})\left[ {F_{c} \cos (\theta + \alpha ) - F_{c} \sin (\theta + \alpha )\tan \beta + \frac{F\tan \beta }{{nl}}} \right]$$
(6)

Then, the cutting force Fc′ from the cutting edge on the front rock is:

$$F_{c}^{^{\prime}} = F_{c} = \frac{2M - F(2R - l)\tan \beta }{{nl(2R - l)\left[ {\cos (\theta + \alpha ) - \sin (\theta + \alpha )\tan \beta } \right]}}$$
(7)

The digital core drilling strength (DCS), whose physical significance is the cutting force of the special digital core drilling bit when cutting a unit area of rock, is obtained as:

$$DCS = \frac{{F_{c}^{^{\prime}} }}{S} = \frac{{N\left[ {2M - F(2R - l)\tan \beta } \right]}}{{Vl(2R - l)\left[ {\cos (\theta + \alpha ) - \sin (\theta + \alpha )\tan \beta } \right]}}$$
(8)

where, the rock cutting area corresponding to the cutting force Fc′ is S = H × 1 under the assumption of a planar strain problem. The instantaneous cutting depth of rock is H = V/nN. Based on the rock cutting mechanical analysis, the obtained drilling parameters V, N, M, and F for each specimen are substituted into Eq. (8) to obtain the rock DCS. The average values of the DCS and UCS in the three plans for the mortar specimen and the sandstone specimen of the same grade are the average DCS and the average UCS for this grade. The detailed results are given in Table 4.

Table 4 Statistics of the average DCS and average UCS results for test specimens
Full size table

4.2 Established relational model for drilling parameters and rock UCS

A scatter plot from the relationship analysis of the rock DCS and UCS is shown in Fig. 10 based on the average values of the DCS and UCS for the test specimens in Table 4.

Fig. 10
figure 10

Scatter diagram of relational analysis for rock DCS and UCS

Full size image

The analysis of Fig. 10 indicates that the rock DCS obtained from the core drilling tests increases with the rock UCS, and the two have a high degree of linear response correlation. Based on the digital core drilling test results for the sandstone and cement mortar specimens with a strength range of 1.56–55.68 MPa, the quantitative relationship formula for the rock DCS and UCS is obtained via linear regression, as shown in Eq. (9). The linear goodness of fit R2 is 0.9784, which indicates that the rock DCS and UCS have a high degree of fit.

$$UCS = 0.268DCS + 2.075$$
(9)

Based on this established linear quantitative relational formula for the rock DCS and rock UCS, Eq. (8) is substituted into (9) to obtain a quantitative relationship model (CDP-UCS model) for the digital core drilling parameters and UCS, as shown in Eq. (10).

$$UCS = 0.268\frac{{N\left[ {2M - F(2R - l)\tan \beta } \right]}}{{Vl(2R - l)\left[ {\cos (\theta + \alpha ) - \sin (\theta + \alpha )\tan \beta } \right]}}{ + 2}{\text{.075}}$$
(10)

4.3 Establishment of real-time in situ forecast method for rock UCS

The research results for the relationship between the drilling parameters and the rock UCS provide a promising concept for rock UCS forecasting. Based on the established CDP-UCS model, a digital core drilling parameter-based rock UCS forecast method is proposed. Its procedure is given as follows:

  1. (1)

    The surrounding rock digital core drilling test is performed based on a digital drilling test system for underground engineering. The drilling parameters V, N, M, and F over the entire drilling range are obtained.

  2. (2)

    The surrounding rock UCS distribution law over the entire drilling range is obtained based on the CDP-UCS model in Eq. (10).

During the application of the rock UCS forecast method, the UCS values of the rock core samples obtained from laboratory tests are compared with the forecasted values from the CDP-UCS model for verification. The CDP-UCS model is continuously modified to ensure accurate forecasts. The continuous and real-time acquisition of the surrounding rock UCS during construction can guide the design and prompt optimization of support plans based on the geological conditions to ensure construction safety.

5 Conclusions

  1. (1)

    The digital core drilling test and the uniaxial compression test are conducted on 24 groups of cement mortar specimens and sandstone specimens with various strength grades to determine the drilling parameters V, N, M, and F, which are monitored during drilling, as well as the rock UCS based on the rock mass digital drilling system and the special digital core drilling bit developed by the authors.

  2. (2)

    The response laws of the drilling torque M and the drilling thrust F to the rock UCS are analyzed. The results indicate that the variation laws for M and F to the rock UCS are consistent, and both demonstrate an overall increasing trend for a larger rock UCS. Thus, M and F are highly responsive to the rock UCS.

  3. (3)

    Based on the rock cutting fracture characteristics of the core drilling, the mechanical analysis of rock cutting is performed to obtain the calculation model for the digital core drilling strength. The average rock DCS of the cement mortar specimens and sandstone specimens for various grades is obtained based on the drilling parameters measured in the digital core drilling tests.

  4. (4)

    A quantitative relationship model (CDP-UCS model) for the digital core drilling parameters and rock UCS is established based on the digital core drilling testing results for sandstone and cement mortar specimens with a strength range of 1.56–55.68 MPa. Thus, a digital core drilling-based rock UCS forecast method is proposed. Digital core drilling tests for intact rock with a wide strength range and weak fractured rock mass will be performed to propose a rock UCS forecast method with a wide application range. This method provides a technical solution for continuous and quick acquisitions of the surrounding rock UCS.