Habitat quality assessment of mining cities based on InVEST model—a case study of Yanshan County, Jiangxi Province

Abstract

The assessment of the spatiotemporal evolution of habitat quality caused by land use changes can provide a scientific basis for the ecological protection and green development of mining cities. Taking Yanshan County as an example of a typical mining city, this article discussed the spatial pattern and evolution characteristics of habitat quality in 2000 and 2018 based on the ArcGIS platform and the InVEST model. The conclusions are as below: from 2000 to 2018, the area of farmland and construction land changed the most in the study area. Among them, the area of farmland decreased by 3.48%, and the area of industrial and mining land and construction land increased by 53.25%. Areas of low, relatively low and high habitat quality expanded, and areas of medium and relatively high habitat quality shrank, which is closely related to the distribution of land use. The areas with high habitat degradation degrees appear around cities, mining areas and watersheds, while the areas with low habitat degradation degrees are mainly distributed in the southern woodland. The distribution of cold and hot spots in the habitat quality distribution of Yanshan County presents a pattern of “hot in the south and cold in the north”. The results are of great significance to the precise implementation of ecosystem management decisions in mining cities and the creation of a landscape pattern of “beautiful countrysides, green cities, and green mines”.

Introduction

Habitat quality is the ability of an ecosystem to provide the conditions necessary for the continued survival and reproduction of individual species, populations, communities, and humans (Hall et al. 1997). It can be used to characterize the ecological suitability of regional landscape patches, and its numerical value can reflect the fragmentation degree of regional habitat patches and the resistance of each landscape patch to habitat degradation (Swades et al. 2020). Habitat quality assessment is a hot spot and difficult area in current ecological assessment. Conducting habitat quality assessment can not only clarify the changes in ecological environment and its driving forces, but also provide a scientific basis for habitat quality improvement.

In the early stage, scholars focused on static analysis and generally evaluated habitat quality by establishing a habitat evaluation index system. For example, Valero took the riparian vegetation index (QBR), riparian quality index (RQI) and river habitat index (IHF) as indicators of river habitat ecological status and studied their application in ecological restoration and reconstruction (Valero et al. 2015). In recent years, dynamic analysis methods, including the SolVES model (Wang et al. 2016), MIMES model (Roelof et al. 2015), HSI model and InVEST model (Goldstein et al. 2012), have been used for quantitative analysis. Among them, the InVEST model developed by Stanford University and the World Nature Wide Fund has the characteristics of quantitative accuracy, visualization of results, and low cost of use and is widely used in ecosystem service function evaluation research (Terrado et al. 2016). Nelson et al. used this model to study different land use situations in the Willamette watershed in Oregon, North America, and explored the value and distribution of ecosystem services in the entire landscape under different situations (Nelson et al. 2009). Leh, Mansoor et al. discussed the evolution of habitat quality under different stages of land use changes and conducted an overall assessment of the level of habitat quality in two countries of West Africa (Leh et al. 2013). Gao et al. discussed the impact of land use changes in mountainous areas in Dali Prefecture on the quality of habitats, and the results showed that the degradation of habitats is inseparable from the urban expansion of low-slope areas, and the development of returning farmland to forests, fruit industry and tourism improved the habitat quality in this area (Gao et al. 2021).

Although habitat quality research has achieved some preliminary results, the research area is mainly concentrated in nature reserves, watershed areas and metropolitan areas, and less research has been conducted on mining areas rich in mineral resources and where mining geological hazards are frequent. Yanshan County, located in northeastern Jiangxi Province, is rich in mineral resources and has the second largest copper mine, the Yongping Copper Mine, in Asia. As a “forest city of Jiangxi Province”, it is also an important ecological functional area in Jiangxi Province. In recent years, with the economic development of Yanshan County, open-pit mining will lead to habitat damage, degradation and disappearance (Hu 2019; Hu et al. 2020; Li 2021; Zhao et al. 2021). Land is the carrier of all kinds of surface ecosystems, and land use change is the direct embodiment of human activities on the ecological environment, and also an important factor causing the change of regional habitat quality. Therefore, from the perspective of land use evolution, Yanshan County of Jiangxi Province, where mineral resource development is the leading industry and natural and human disturbance is obvious, was selected as the research area. Based on ArcGIS platform and InVEST model, the spatial–temporal evolution and differentiation characteristics of habitat quality in Yanshan County in recent 20 years were analyzed. To explore the impact of human engineering activities such as mining, industrial and mining land expansion on the ecosystem, and put forward countermeasures and suggestions for restoring the habitat quality in the study area. This study not only sets a scientific baseline for exploring the complex dynamic evolution mechanism of habitats in the mining area, but also provides a reference guide and application demonstration for the ecological restoration practice and land use planning of similar mining areas.

Materials and methods

Study area

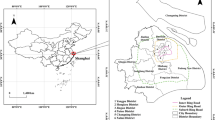
Yanshan County belongs to Shangrao city in northeastern Jiangxi Province, located between east longitude 117° 26′–118° 00′ and north latitude 27° 48′–28° 24′. It connects Guangxin District in the east, Yiyang County and Guixi City in the west, Hengfeng County in the north, Wuyishan City and Guangze County in Fujian Province in the south. The county has a total area of 2178 square kilometers and a resident population of more than 380,000. The forest coverage rate in the region is more than 70%, and the ecological environment is excellent. However, Yanshan County is rich in mineral resources. There are 52 mining areas listed in the resource reserve table, and 44 mining areas have been developed and utilized. The development and utilization of mineral resources greatly promotes economic development, inevitably brings mine environmental problems and leads to the deterioration of the ecological environment (Fig. 1).

Fig. 1

Geographic location of the study area

Data sources and processing

The land-use data in this study were mainly obtained by Landsat TM/ETM+ image interpretation with remote sensing images from the United States Geological Survey with a resolution of 30 m for the time period including 2000 and 2018, and the months were from July to August. ENVI software was applied to preprocess the 3-phase remote sensing images with radiation calibration, atmospheric correction, declouding, image stitching and cropping to obtain remote sensing images of the study area. According to the actual situation of land resource utilization in Yanshan County, the combination of supervised classification and manual visual interpretation was used to decode and extract the land-use categories of the study area for two periods of 2000 and 2018, and the categories included five major categories, namely, farmland, woodland, grassland, water area and construction land; additionally, the accuracy of interpretation data was verified, and 200 sample points were selected for each of the five land use types. The overall accuracy of classification in the two phases reached over 85%. According to Eike's research conclusion (Eike and Andeas 2008), the interpretation accuracy can meet the needs of this study. Elevation and slope maps extracted and generated from the 30 m resolution digital elevation model data were downloaded from the China Geospatial Data Cloud Platform (http://www.gscloud.cn/). The population density, GDP per capita data at a 1 km resolution and other road traffic data for the corresponding years were obtained from the Chinese Academy of Sciences in Resource and Environmental Sciences data (http://www.resdc.cn/).

Methodology

Habitat quality module of the InVEST model

The InVEST (Integrated Valuation of Environmental Services and Tradeoffs) model was developed by Stanford University, the World Wildlife Fund and the Nature Conservancy to quantitatively assess habitat quality from a biodiversity perspective (Xu et al. 2019). The analysis of habitat quality is carried out by using the habitat quality module in the InVEST model. The module assumes that areas with better habitat quality have higher biodiversity and analyzes the impact of ecological threats related to human activities on land use, leading to an overall assessment of habitat degradation, habitat quality, and habitat scarcity. The main idea of this analysis method is that different land use types may damage habitat quality as a threat source, and habitat quality is linked to the threat source to study the impact of the threat source on habitat quality. Combined with related literature (Li et al. 2018; Chen et al. 2021), we selected farmland, rural resident land, urban land, and industrial and mining land that have a large impact on the ecological landscape to define as threat sources and show them on the threat factor layer (Fig. 2). Then we assigned impact weights and maximum impact distances to these four types of threat sources (Table 1).

Fig. 2

Ecological threat factor types in 2000 and 2018

Table 1 Attributes of threat data

In addition, each land use type as a habitat type is also related to its own habitat suitability and its sensitivity to threat sources. The higher the suitability of the habitat type, the better its habitat quality performance. The stronger the sensitivity of the habitat type to threat sources, the lower its anti-interference ability, and the worse the habitat quality. The habitat suitability of the habitat types and their sensitivity to threat sources were determined by referring to the recommended values of the model, synthesizing the relevant literature (Chu et al. 2018) and the opinions of relevant experts (Table 2).

Table 2 Landscape types and sensitivity of landscape types to each threat

Principles of habitat quality assessment

Habitat quality is the environmental level that the ecological environment provides for the survival of individual organisms and populations. It is a continuous variable with a numerical range from low to high. The higher the quality of the habitat, the more stable the ecological structure and function of the patch. The way and intensity of human land use determines the quality of the habitat, and the more intense the land use, the more pronounced the decline in habitat quality (Almpanidou et al. 2014). Habitat quality was calculated based on the degree of habitat degradation, and the habitat quality score decreased with increasing habitat degradation score. The calculation formula of habitat quality is as follows:

$$Q_{xj} = H_{j} \left[ {1 - \left( {\frac{{D_{xj}^{z} }}{{D_{xj}^{z} + k^{z} }}} \right)} \right]$$

(1)

where, $Q_{xj}$ is the habitat quality of grid cell $x$ in land cover type $j$; $H_{j}$ is the habitat suitability of land cover type $j$; $D_{xj}^{z}$ is the level of habitat threat for grid cell $x$ in land cover type $j$; $k$ is the half-saturation factor, which is generally taken as half of the maximum value of $D_{xj}^{z}$; and $x$ is a constant.

Principles of habitat degradation assessment

The degree of habitat degradation represents the degree of influence of threat factors on the habitat structure, and its calculation is based on the following assumption: the higher the sensitivity of a certain type of land use in the ecosystem to threat factors is, the greater the degree of degradation of the land type (Nakanishi et al. 2021). The degree of habitat degradation is closely related to factors such as the distance between each category in the habitat and the threat factor, the sensitivity of the land category to threat factors, and the number of threat factors. The calculation formula of habitat degradation $Q_{xj}$ is as follows:

$$D_{xj} = \sum\limits_{r = 1}^{R} {\sum\limits_{y = 1}^{{Y_{r} }} {\left( {\frac{{w_{r} }}{{\sum\nolimits_{r = 1}^{R} {w_{r} } }}} \right)} } r_{y} i_{rxy} \beta_{x} S_{jr}$$

(2)

where, $R$ is the number of threat factors; $y$ is all grid cells with threat factor $r$; $Y_{r}$ is the total number of grid cells occupied by threat factor $r$; $r_{y}$ is the threat factor $r$ in grid cell $y$; and $i_{rxy}$ is the threat effect of the threat factor $r\left( {r_{y} } \right)$ in grid cell $y$ on habitat grid cell x, $w_{r}$ is the weight of threat factor $r$; $\beta_{x}$ indicates the level of accessibility in grid cell $x$, where 1 indicates complete accessibility; and $S_{jr}$ is the sensitivity of habitat type $j$ to threat $r$, where values closer to 1 indicate greater sensitivity.

Principles of habitat scarcity assessment

Habitat scarcity is a relative concept that can reveal the impact of land use changes on habitats. It is evaluated with reference to the benchmark land use, that is, the scarcity of land types relative to the reference state (Ansari and Golabi 2019). Based on this, we infer the threats faced by the widely distributed land types in the past. The scarcity of habitats in areas where land use types have changed drastically and legal protection is not in place has increased, and the stability of ecosystems has deteriorated. Ecosystems in areas of gentle change also have more balanced internal material cycles and energy flows and are more stable. The change index R is first calculated for each land use type $j$.

$$R_{j} = 1 - \frac{{N_{j} }}{{N_{j\text{baseline}} }}$$

(3)

where $N_{j}$ is the number of grids for class $j$ in the current land use map and $N_{j\text{baseline}}$ is similar to $N_{j}$ for the reference land use map. If there are no class $j$, $R_{j}$ equals 0.

Based on $R_{j}$, the total habitat scarcity index $R_{x}$ of grid $x$ can be calculated as:

$$R_{x} = \sum\limits_{x = 1}^{x} {\sigma_{xj} } R_{j}$$

(4)

where $\sigma_{xj}$ is used to determine whether the current type of grid is $j$ (the value of 1 indicates yes, and 0 indicates the opposite).

Cold and hot spot analysis and spatial autocorrelation analysis of habitat quality

Cold and hot spot analysis can obtain the spatial clustering of high- or low-value elements, of which the Getis-Ord Gi* index is often used as an important indicator whose value reflects the degree of intraregional linkage (Li et al. 2017), expressed as follows:

$${\text{Gi*}} = \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{ij} x_{j} - \overline{X} \sum\nolimits_{j = 1}^{n} {\omega_{ij} } } }}{{\sqrt[{{}_{s}}]{{\frac{{\left[n\sum\nolimits_{j = 1}^{n} {\omega_{ij}^{2} - \left(\sum\nolimits_{j = 1}^{n} {\omega_{ij} } \right)} \right]^{2} }}{n - 1}}}}}$$

(5)

where $x_{j}$ is the eigenvalue of raster $j$, $w_{ij}$ is the indicator of spatial distribution of weights between raster $i$ and raster $j$, and $n$ is the total number of rasters. When the Gi* value is significantly positive, the habitat quality is clustered with high values, the area is a hot spot. When the Gi* value is significantly negative, the habitat quality is clustered with low values, the area is a cold spot.

Spatial autocorrelation refers to the correlation degree of a certain attribute of geographical things in different spatial locations, which is divided into global autocorrelation and local autocorrelation. Global autocorrelation can be used to describe whether there is a clustering effect of habitat quality in the whole region. In this paper, we used the global Moran's I index for estimation, whose value range is [− 1, 1]. A value greater than 0 indicates a positive correlation, a value closer to 1 indicates a higher degree of agglomeration, a value less than 0 indicates a negative correlation, and a value equal to 0 indicates a random distribution (Moran 1950).

Results

Land use and its transfer changes in the study area

Woodland and farmland are the main land types in the study area, accounting for 95% of the total area, of which 75% is farmland (Fig. 3). The land-use pattern of the study area changed considerably between 2000 and 2018, with the greatest changes occurring in farmland and construction land. The area change of each land type was mainly reflected in the decreases in farmland, woodland and grassland each year. Among them, the area of cultivated land has decreased by 3.48% in 20 years, with a total reduction of 1532 hm², and the pressure of farmland has been increasing. Woodland and grassland also showed shrinkage, but the change was not obvious. Construction land had been expanding year by year, with an increase of 53.25% in 20 years, with an area of 1369 hm², indicating that the demand for construction land expansion had been increasing under the realistic environment of expanding urbanization and improving economic level. The rate of shrinkage of unused land was more moderate. It is noteworthy that the watershed area had increased by 26.38% in 20 years (Fig. 4).

Fig. 3

Spatial distribution maps of land use in 2000 and 2018

Fig. 4

Area of each land-use type in 2000 and 2018

Table 3 shows that from 2000 to 2018 woodland was the most transferred out land use category in the study area, with a net transfer out of 14,755 hm², mainly to cultivated land (30,643 hm²) and construction land (2937 hm²). Deforestation and land expansion for urban construction are the main reasons for the transfer out of woodland. The most transferred land use type in the study area is cultivated land, with a net transfer of 11,655 hm², which has a significant mutual transformation with woodland. The construction land is transferred into 1231 hm², and the expanded area mainly comes from woodland (2937 hm²) and cultivated land (960 hm²). The water area is 1209 hm², mainly from woodland and cultivated land, and the grassland area fluctuated slightly.

Table 3 Land use transfer matrix in the study area (hm²)

The result of habitat quality assessment

The habitat quality index refers to the capacity of the environment to provide conditions and resources for the sustainable survival and reproduction of species and populations. In the grid layer, the habitat quality index changes continuously from 0 to 1. The closer the value is to 1, the better the habitat quality and the more favorable the maintenance of biodiversity. To further investigate the impact of land-use change on habitat quality in the study area, the results of the habitat quality index calculations for the two periods were classified into five levels: low (0–0.2), relatively low (0.2–0.3), medium (0.3–0.4), relatively high (0.4–0.8) and high (0.8–1.0) (Table 4), and the habitat quality area and its percentage of each level in the two periods were calculated (Table 5, Fig. 5). The results showed the following:

Table 4 Classification value of habitat quality in the study area

Table 5 Area and percentage of habitat quality at all grades

Fig. 5

Spatial distribution pattern of habitat quality in 2000 and 2018

• (1) From the perspective of time change, the proportion of low-grade and lower-grade habitats had been increasing in 18 years; the proportion of medium-grade habitats decreased by 1.04%. The proportion of higher-grade habitats also showed a slightly decreasing trend, and the proportion of high-grade habitats increased slightly. The increase in the proportion of low-grade and lower-grade habitats is mainly due to the expansion of industrial and mining construction land, increased interference with the surrounding ecological environment and habitat degradation.

• (2) From the perspective of spatial pattern, the overall habitat quality of the ecosystem in Yanshan County is good. The high-value area has a wide distribution area, mainly in the southern part of the area. This area is dominated by woodland, with rich biodiversity, few human activities, and a high degree of ecological protection. The low value areas mainly appear in Hufang town and Shitang town, and the low habitat quality areas are concentrated and contiguously distributed in Hekou town and Yongping town. These areas are dominated by industrial and mining construction land and arable land, with rapid economic development, expansion of industrial and mining construction land, concentrated settlements, single biodiversity, and human activities causing more disturbances and ecological destruction.

Habitat degradation in the study area

The degree of habitat degradation expresses the degree to which the land type is affected by the stress factors under the current supervision level and thus reflects the probability of habitat degradation and habitat quality reduction. The value range of the habitat degradation index is 0–1, which represents the relative habitat degradation level of current land use, in which 1 is high degradation and 0 is low degradation.

Figure 6 shows the spatial distribution of habitat degradation. The maximum values of the Habitat Degradation Index in 2000 and 2018 were 0.1418 and 0.1454, respectively, showing an increasing trend year by year. In terms of spatial pattern, areas with high habitat degradation appear in the surrounding areas of Hekou Town and Yongping Town and in various watersheds. With low-quality habitats such as central urban areas as the center, the degradation of habitats gradually decreases. This is because the ecological environment near the watershed is relatively fragile, and it is easily destroyed after being disturbed by the outside world. Then, the expansion of industrial and mining land in Hekou town and Yongping town caused other surrounding land use types to become construction land, and the ecological environment was seriously disturbed by human activities. In addition, in the southern part of the region, the land use type is mainly woodland, which is less subject to human disturbance, and the degradation of habitat quality is not significant.

Fig. 6

Spatial distribution pattern of the habitat degradation index in 2000 and 2018

Habitat scarcity in the study area

Habitat scarcity can be used to characterize the stability level of a regional ecosystem. The greater the scarcity value of the habitat is, the more frequent the evolution of the land use pattern in the region, the more unstable the ecosystem and the more vulnerable it is to external disturbances.

According to the analysis of the land use types in Fig. 7, the red area indicates that the habitat scarcity score is the highest, and the land use category is mainly cultivated land. Due to the expansion of industrial and mining construction land, the possibility of occupying cultivated land increases, the landscape integrity of cultivated land is broken, and the stability is reduced. The woodland landscape (orange) in the western and southeastern parts of the study area had a high habitat scarcity, which may be due to the influence of the surrounding construction land as well as human factors. The land use categories with low habitat scarcity (blue) are mainly construction land and water areas.

Fig. 7

Spatial distribution pattern of habitat scarcity index in 2000–2018

Coldspots and hotspots of habitat quality in the study area

Before the cold and hot spot analysis, spatial autocorrelation analysis was applied to determine whether the habitat quality in Leadville County had spatial aggregation characteristics, and the results are shown in Table 6. Among them, the Moran's I of habitat quality in the study area in both 2000 and 2018 was greater than 0, indicating that the data in both periods were spatially correlated, while the Z scores were both greater than 2.58 and the P values were less than 0.05, indicating that the spatial distribution of habitat quality in the study area was not a random state but an aggregated state. Based on this, cold and hot spot analysis of habitat quality in Yanshan County was carried out, and the results are shown in Fig. 8.

Table 6 Global autocorrelation analysis of habitat quality change in Yanshan County

Fig. 8

Hotspots and coldpots of habitat quality in the study area (2000–2018)

During 2000–2018, the spatial distribution patterns of cold and hot spots of habitat quality in the study area were similar, showing a pattern of “hot in the south and cold in the north” (Fig. 8). The hotspot area is mainly located in the south, including Tianzhushan Township, Wuyishan Township, Taiyuan Township and Yingjiang Township. The land use type is mainly woodland, and the forest coverage rate is 71.4%. Due to little interference from human activities, the habitat quality is generally high (average habitat quality is above 0.8); thus, areas of high habitat quality cluster to form hotspots. Cold spots are mainly distributed in the north and middle of the study area, mainly in Hekou town, Wanger town, Yongping town, Hufang town and Gexianshan township, which are rich in mineral resources, and a large number of mining enterprises gather here. However, mining development inevitably brings mine environmental problems, which leads to a series of geological environmental problems, such as landform and landscape damage, land resource damage, geological disasters, aquifer damage, and water and soil pollution, resulting in sparse vegetation and broken terrain, so the habitat quality is generally low, leading to the clustering of low habitat quality areas to form coldspots.

In terms of temporal changes, Moran's I increased from 0.680755 in 2000 to 0.696159 in 2018, indicating an increase in spatial clustering of habitat quality. From 2000 to 2018, the area of cold spots changed little. Cold spots are mainly distributed in the economic development center and population concentration area of the study area. Over the years, the urbanization process has promoted the expansion of farmland and industrial and mining land in the area, and the corresponding reduced land types are farmland and a small amount of woodland. Based on the threat factor weight setting of the INVEST model and the actual local situation, the contribution of woodland to maintaining high habitat quality is higher than that of farmland, so the slight reduction of woodland causes the overall habitat quality in Yanshan County to decrease, which is reflected in the reduction of hotspot areas in the south.

Discussion

Analysis of the causes of changes in habitat quality

The reasons for changes in habitat quality differed between study area types. For large cities with high human activity, rapid urbanization have led to increased fragmentation of habitat patches, resulting in reduced habitat quality (Qiu et al. 2021). For watersheds and nature reserves with rich biological diversity, over-exploitation and irrational use of natural resources have led to a yearly decline in natural vegetation, decreasing populations of wildlife and habitat degradation. For ecologically fragile areas with little rainfall and sparse vegetation, ecological degradation, soil salinization, and frequent sand and dust attacks have posed a greater threat to habitat quality and even ecological sustainability in the area. As for the mining areas rich in mineral resources, the expansion of industrial and mining land and a series of ecological and environmental problems caused by mining activities are the main causes of habitat loss and fragmentation (Xie et al. 2019; Zhao et al. 2020), which can be discussed from the following three aspects.

In terms of land use, the evolutionary law of the study area is reflected in the sharp reduction of woodland with high habitat suitability and the rapid expansion of construction land with high habitat suitability. As a threat source of habitat quality, industrial and mining construction land expanded significantly from 2000 to 2018, especially Hekou town in the north and Yongping town in the middle of the study area. Then, the areas continued to invade the land with better habitat suitability, resulting in the continuous expansion of the scale and scope of threat sources and an increase in the proportion of low-grade habitats in the area.

In terms of mineral resource development, Yanshan County is rich in mineral resources, and a large number of mining enterprises and pillar industries gather here. However, mining development inevitably brings mine environmental problems, especially historical development issues, which leads to a series of geological environmental problems, such as landform and landscape damage, land resource damage, geological disasters, aquifer damage, and water and soil pollution (Xiao et al. 2018; Chen and Hu 2018), resulting in habitat loss and fragmentation and an increase in the low habitat quality areas in the region.

From the perspective of the spatial distribution of habitat quality, the areas with a habitat quality index above 0.8 were mainly distributed in the southern part of the region. This zone is dominated by woodland, with rich biodiversity, few human activities, and a high degree of ecological protection. It is worth noting that the construction of the Luntan Reservoir in Tianzhu township, located in the northwestern part of Yanshan County, in 2008 increased the water area, which led to a slight increase in the proportion of high-grade habitats. Therefore, it is necessary to formulate corresponding adjustment and optimization strategies according to the habitat characteristics and differences of different regions within the region.

In summary, analyzing the problems of ecological safety in mining cities and exploring the causes of habitat degradation are not only of theoretical guidance for habitat assessment in mining areas, but also provide methods and application demonstrations for ecological restoration practices and land use planning in similar mining areas.

Countermeasures and recommendations

Assessing the habitat quality of Yanshan County is crucial to optimizing landscape patterns and maintaining regional ecological security. To prevent regional ecological deterioration, measures should be taken to balance the contradiction between economic development and ecological protection and create a landscape pattern of “beautiful countryside, green city and green mine”.

The expansion of industrial and mining construction land is the primary reason for the decline in habitat quality. The scale of construction land should be controlled through scientific planning (He et al. 2021; Yang et al. 2019). On the principle of meeting the requirements of land and space planning, we should strictly control the supply of industrial and mining construction land to prevent the abnormal expansion of industrial and mining construction land.

Although the forest resources in Yanshan County are rich and the overall habitat quality is high, the expansion of industrial and mining construction land promotes the expansion of the scope of human activities and the increase in the intensity of land use, causing certain damage to the habitat. The ecological red line can be delineated to improve the resource responsibility system of the ecological barrier area, focusing on monitoring the junction area between high and low habitat quality, controlling the threats to habitat quality from the expansion of industrial and mining construction land and human activities, and providing guidance for future ecological environmental protection and sustainable development of the protected area.

From the perspective of habitat degradation, the degradation degree of habitats near cities and river basins is not optimistic. On the basis of strict management and control of the scale of urban construction land, it is also necessary to strengthen watershed protection and establish a sound watershed green development mechanism. Then, the goal of ecological balance and sustainable development can be achieved by realizing the development of the social economy and biodiversity protection in the basin.

Conclusions

Based on the ArcGIS platform and the InVEST model, the Yanshan County’s habitat quality spatial pattern and its evolution characteristics in 2000 and 2018 were discussed, and the following conclusions were drawn:

• (1) From 2000 to 2018, the cultivated land, woodland and grassland in the study area showed a trend of shrinking year by year, and the reduction rate of cultivated land was relatively large. The growth rate of construction land is the fastest, with a growth rate of 53.25% in 20 years, indicating that mining cities take industry and mining as the pillar industry, and there is a great demand for industrial and mining construction land.

• (2) The proportion of low-grade and lower-grade habitats has been increasing in the past 18 years, the proportion of medium-grade habitats has decreased, and the proportion of high-grade habitats has increased slightly. The spatial distribution of habitat quality is closely related to the distribution of land use and is greatly affected by human activities, indicating that the overall development and utilization of Yanshan County is relatively low.

• (3) Areas with a high degree of habitat degradation appear around the city and various watersheds in Yanshan County, while areas with a low degree of habitat degradation are mainly distributed in the southern area, where woodland is the main landscape type. The land use types with high habitat scarcity are mainly woodland and cultivated land. Due to the influence of the surrounding unnatural landscape and human management factors, the degree of fragmentation increases, and the stability worsens.

• (4) The distribution of cold and hot spots in the habitat quality space of Yanshan County presents a pattern of “hot in the south and cold in the north”. The hot spots are mainly located in the southern part of the rich biodiversity, and the cold spots are mainly distributed in the northern and central parts of the study area where industrial and mining construction land and cultivated land are concentrated.

Since the evolution of land use patterns is a complex process that is affected not only by the geographical conditions of the region but also by human intervention, such as land use policy, it is necessary to explore the role of policy intervention on land pattern evolution in the future to improve the prediction accuracy. In addition, the InVEST model only considers the impact of stress factors within the study area on the habitat, while the habitat at the edge is also affected by other stress factors outside the boundary of this study area, which may make the evaluation results have some errors. Attention should be given to collecting threat factor data at the edge of the study area in the future. Nevertheless, this study provides a scientific reference for improving the current mine ecological environment and promoting the landscape pattern of “beautiful countrysides, green cities and green mines” in the Yanshan area.