Abstract
Rock burst is a catastrophic dynamic disaster caused by sudden failure and instability of coal, loading paths play an important role in the failure of coal, the coal failure process is associated with charge exception information. Hence, violent coal failure mechanics and time–frequency domain distribution of charge signal such as rock burst under different loading paths should be studied in-depth. In this paper, grade and cyclic loading test were carried out for coal with impact tendency samples produced by blocks cored from 800 depth in Xiaoqing coal mine of the Tiefa coal group in northeast China. Theory discussion was carried out for the result of stress and strain, frequency-spectra analysis was conducted for the wavelet charge data, figures showing the evolution mechanism of mechanical properties and the relationship of time–frequency domain amplitude of charge signals in coal with different loading paths and stage were obtained. The failure process and characteristics of coal under different loading paths were summarized. It found that the loading path changed the manner of energy accelerate–release, there were more plastic strain generation in coal under cyclic loading than that under grade loading, the former was more likely to cause greater damage and failure, then the strength of coal under cyclic loading is generally lower than that under grade loading, an energy conversion mechanical model of stress, damage and deformation was developed and explained the effect of the loading path. Charge signal was primarily distributed in the strengthening and peak stages, where there was a high amplitude pulse at each stress drop. The charge pulse was a type of low frequency signal with a primary frequency distribution range of 1 –100 Hz. Discussion on the charge generating mechanism from the perspective of friction slip, it demonstrated that the charge obtained during the coal failure process directly to stress loaded on and damage, the result verified it better. We propose that the research results in this study could be efficiently applied to daily mining activities, to provide an early warning and effectively avoid rock burst disaster.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Rock burst is a dynamic disaster that causes spontaneous, violent fracture of coal in underground mines, which primarily occurs in roadways and working faces. It can cause instantaneous failure of the coal mine and release elastic deformation energy spraying shattered coal into the mining space, inflicting injury and destroying equipment. Rock burst has caused serious problems for underground mining in the past century (Alber et al. 2009; Mark 2016; Lannacchione and Tadolini 2016), especially in China (Pan et al. 2003; Jiang et al. 2014). By the end of 2016, there were over 140 mines experiencing this problem. Along with deep coal mining, the frequency and scale of rock burst is increasing, posing a serious threat to daily production and the safety of the miners’ lives. Thus, the prediction and minimization of rock burst is a critical problem to be resolved.
The main aim of this study was to investigate the cause and mechanical mechanism of coal failure. Since coal is the main part of rock burst, describing its mechanical behavior, energy acceleration, and the relationships between them correctly was the first step in this investigation. Coal as a special type of rock, whose mechanical properties are similar to rock. However, its pore–crack structure contributes to its properties of discontinuity, heterogeneity, and anisotropy. From a macroscopic view, influence of external loading on the failure and deformation behaviors, induced by a mining stress field, become substantially evident and it causes the rock burst hazard evaluation to become considerably more difficult. Understanding the connection between the loading path and the mechanical behavior of coal accurately is of substantial significance in forecasting the occurrence probability of a disaster.
A considerable number of scholars had paid attention to coal mechanics, the mechanism of rock burst and the relationships between them (Aubertin et al. 1994; Hoek and Brown 1998; Bobet and Einstein 1998; Pan et al. 2009; Wang et al. 2011; Jaeger et al. 2007), they observed that the maximum loading capacity improved with the increase in confining pressure, in a non-linear pattern. The energy dissipation and release play an important role in deformation and failure, it’s the key to control the catastrophe (Salamon 1984; Boler et al. 1997; Peng et al. 2015; Jiang et al. 2011). Medhurst and Brown (1998) investigated the effects of scale on the mechanical behavior of coal, strength data was observed to be related to the degree of cleating or brightness of the coal samples. Lawson et al. (2016) analyzed 306 coal records from the Pennsylvania State coal sample database, and observed that both inherent susceptibility and appropriate stress conditions are necessary to facilitate a dynamic failure. Aguado and González (2009) conducted studies in tow mines and observed that sublevel caving is one of the methods primarily influencing the stress state, thus the condition of sublevel caving is an extremely important parameter to prevent disaster in mines. Zhang et al. (2016) considered that if the width of the isolated coal pillar is not sufficiently large, the shallow coal seam would be damaged at first, and, subsequently, the high abutment pressure would be transferred to the deep coal seam that might cause an overall burst- instability accident. Pan et al. (2009) considered that the crack is primarily a tear-type crack under quasi-static loading, and could be analyzed with the mode I crack theory using the three-point bending experiment.
The failure of coal is an evolutionary process from mesoscopic to macroscopic damage, and it includes crack propagation and bearing structure interaction. During this process, faint charge would appear at the crack tip and fracture surface, which combines the action of the friction effect, piezoelectric effect, and other mechanisms. Volarovich and Parkhomenko (1954) detected micro electric signals for the first time in the rock failure experiment. Kuksenko (1997a, b) explored the effect of mechanical loading on electric field variation in natural dielectrics. Frid et al. (2003); Bahat et al. (2004); Rabinovitch et al. (2005) obtained a relationship between the width of a fracture and the wavelength, frequency, time duration, and rise–fall time of the emitted electromagnetic radiation (EMR) pulse. Song et al. (2012, 2016) analyzed the EMR and dissipated energy, and a relationship between them was established using the voltage amplitude of the EMR signal during the coal failure process. Pan et al. (2013); Xiao et al. (2015) explored charge signal law under different loading rates of coal, granite, and sand rock, and explained the charge generation mechanism from a microscopic viewpoint.
Investigating the law of energy dissipation–release during the coal failure process, and the time–frequency distribution of charge signal, handing the relationship between them, using it to invert the stress and damage, to achieve the objective of early disaster warning and finally reduce disaster accident rates.
2 Experimental system and methods
The coal specimens were obtained from a depth of 800 m in the Xiaoqing mine of the Tiefa Coal Group in northeast China, see in Fig. 1. In the long coal-forming process, the coal seams may not always extend in the horizontal direction, due to geological structure, then there had a certain angle between the coalbed bedding and the principal stress direction. On the one hand, in order to eliminate the influence of the bedding on the test results as much as possible, on the other hand, it’s also intended to explore the influence of bedding on the mechanical properties of coal. The core drill was drilled vertical and parallel to the bedding of coal block, the cylindrical specimens measuring Φ 50 mm × 100 mm were prepared and divided into two groups, namely, I and II, which the group. I had a load direction parallel to the bedding, group. II had a load direction perpendicular to the bedding in the experiment, both ends of each specimen were polished to ensure that the flatness error was less than ± 0.02 mm, the samples is shown in Fig. 2.
Tests were conducted at the Liaoning Key Laboratory of mine environment and disaster mechanics, Liaoning Technical University, Fuxin. An MTS digital hydraulic servo testing machine was used for the uniaxial compression test, the load and displacement data was used to automatically obtain the measurements. The machine had a compression capacity of 600 kN with a resolution of 5‰, show in Fig. 3a.
The charge exception information generated for the coal failure process was obtained by the self- developed charge signal monitoring system, which was included a micro electro sensitive alloy sheet, preamplifier, acquisition instrument, and computer, the devices is shown in Fig. 4.
The cyclic and grade loading were conducted to investigating the effect of loading path on mechanical properties, energy dissipation and release characteristics, charge signal time- frequency domain evolution of coal in deformation and fracture process. The test was carried out according to the following scheme. (1) Placed the coal specimen in the shield pressure cylinder, shown in Fig. 3b. (2) Set the axial displacement control mode with a loading/unloading rate of 0.2 mm/min, input the displacement point of loading and unloading to the control system, the data was automatically recorded by the computer six times per second, and the loading path set by programming, shown in Fig. 5. (3) Turn on the testing machine and charge signal monitoring system simultaneously, applied axial loading until coal destroyed completely. (4) Stored the test data and recorded the fracture characteristics of coal. It should be pointed out that, the evidence for the selection of displacement points was the strength of coal, which were the result of 10 samples under uniaxial compression.
3 Experimental result and discussions
3.1 Uniaxial mechanical properties of coal with different loading paths and analysis
In Fig. 6a, b illustrated the typical stress–strain relationship of coal specimens at cyclic and grade loading, the results demonstrated that the loading path had a significant effect on the mechanical characteristics of coal.
The observation that the stress–strain curve of cyclic loading had certain differences compared with previous studies was unexpected, shown in Fig. 6a, b. For each loading and unloading cycle, the curve formed an “opening” instead of a “loop” (Jaeger et al. 2007), and the size of “opening” increased with the cycle time. It also could be observed that the stress–strain curve of coal by the grade loading was considerably smoother than that by the cyclic loading, this phenomenon was more pronounced in the results of the group. II. We divided evolution of stress into two parts: pre- peak and post-peak. At the pre-peak stage, when the specimen was under a cyclic loading path, the slope of the curve reduced with increased in the number of cycles. Notably, there was a distinct yield segment before reached the peak stress. When the specimen under grade loading, the slope of the curve was approximately constant and the yield segment hardly existed. At the post-peak stage, the stress drop was slow when coal under cyclic loading, and the drop was sudden under grade loading.
Failure of coal was a complex mechanical evolution process, which included not only elastic deformation, but also plastic deformation caused by damage. The mechanics of coal failure cannot be fully explained by only elastic or plastic deformation. Further, the failure process, owing to energy accumulation and release, which was a result of elastic and plastic deformation, thus, the phenomenon could be explained from the point of view of energy.
The test was conducted by the testing machine. We proposed a function to describe the strain energy from machine work as follows:
where px, py, pz are the stress of x, y, z. u, v, w are the strain of x, y, z. W is the strain energy. s is the stressed area elements.
In the uniaxial compression test px = py = 0, then the strain energy is given by:
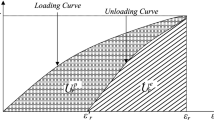
Based on elastic theory, the strain energy contained in the coal was the area under the stress–strain curve. In Fig. 7, under external loading, the total strain of a pure elastomer was caused by elastic deformation, which expressed as the red dash line in the figure, the actual situation was express as the dark blue solid line. Therefore, the strain energy (W′) was equal to the area under stress–strain curve, which was the area enclosed by ted dash and could be described as:
where E is the elastic modulus, W′ is the strain energy, εe is the ideal elastic deformation.
Coal is an elastoplastic material, under the external loading, the strain not only included elastic strain, but also plastic strain. At the same times, we provided a definition that the plastic part was no carrying capacity and the elastic part is load-bearing structure. In Fig. 7, the coal actual energy contained was the blue dash enclosed and the relationship describes actual energy with elastic and plastic strain:
where σ′ is the actual stress, ε′e is actual elastic strain, ε′p is plastic strain.
Based on the damage theory, under uniaxial stress, Broberg defined the damage variable as the ratio of nondestructive load area to actual destructive load area (Li 2002), expressed as:
The relationship between coal damage effective elastic modulus and elastic modulus is given by
where D is the damage variable, A and \(\tilde{A}\) are the loaded area and effective loaded area, respectively, \(\tilde{E}\) is the effective elastic modulus, in the analysis of Eq. (10), the actual elastic modulus became progressively smaller with increased in coal damage, subsequently Eq. (9) introduced the elastic modulus containing damage variables. We proposed the following function to describe the variation of energy with the elastic modulus and the damage variables:
where U is dissipated energy, defined it caused damage:
For the Eq. (14) can be used to determine the dissipated energy and damage variables. The relational expression demonstrates that total energy is equal to external work during the loading process, which was proportional to the actual elastic–plastic strain combination “ε ′ e + ε ′ p ”, the elastic part of which was converted to elastic strain energy, the other is converted to surface energy of cracks and promoted they development causing plastic failure at last, as the green area shown in Fig. 7a, b. We observed that when all strain was elastic and no dissipation this behaved like a perfect elastomer, conversely, when it was plastic the energy dissipation as to forming damage caused the failed of coal. Thus, we concluded that when the total energy was constant, the more energy dissipation caused damage, the less elastic energy of coal, and vice versa. Once damage caused by plastic strain appeared, the dissipated energy increased and promoting further cracks source expansion, then the coal destruction was accelerated, as illustrated in Eq. (14). As shown in Fig. 8, we could observed that the broken fragment of coal under grade loading was more complete than the one under cyclic loading. Further, it was evident that cyclic loading caused substantial damage when specimens had the same dependent variables.
In addition, we thought that the result of “opening” in each loading–unloading cycle was mainly due to the relationship of elastic and plastic strain. With the loading increased the elastic and plastic strain emerged inside of coal, unloading for the stress reach a certain value the stress–strain curve given an expression of the elastic part rebound. When loading again, there was the elastic deformation of elastic part and new damage to caused plastic strain, then the curve of loading can’t along that of unloading before, that’s why, there had an “opening” in each loading and unloading cycle. It worth notice that the size of “opening” improved during multiple cycles, because the elastic part was much more than the plastic at initial phase, the damage accumulation gradually increases as the number of cycles and more plastic strain formed, which promoted more energy release and caused damage further, based on the Eq. (14), as the result, the difference between elastic strain amount of recovery during the unloading and that of compression during the loading was increased in each cycle, then the elastic the curves of loading can’t along that of unloading before and the larger “opening” between two lines. As is known to all, the strength of coal bedding is much less than that of matrix (Jaeger et al. 2007), and it’s more likely damaged the latter. The bedding in the samples of group. I were compressed, but that of group. II were tension under external stress. Cracks produced in the bedding firstly and expansion easier, then the size of “opening” in group. II was larger than that in group. I, for the result shown in Fig. 8. It also verified the rationality of the previous analysis.
Counted the test results of all specimens treated separately accorded groups (I and II), the peak value of stress and its corresponding strain was investigated. As shown in Fig. 9a, b, the results illustrated that the loading path had a significant effect on the strength. In general, the strength of coal under grade loading was higher than that under cyclic loading for both groups I and II. The relationship between the peak stress and its corresponding strain was an approximately linear function, which could be expressed as:
where σMax is the peak stress, εMax is the strain of peak stress, we defined “a” as stress correction factor and “b” as failure stress–strain ratio. Combined with the fitting results, both “a” and “b” were affected by the loading path, the angle of loading direction and the bedding, the smaller the angle, the smaller value of failure stress–strain ratio.
According to the aforementioned analysis, the loading path changed the phase of the energy release. In case of coal under grade loading, the external work converted into elastic energy of coal and the dissipated energy little. Shown in Fig. 7a, after attaining peak strength, where the smaller the curve enveloping area, the less coal rupture was consumed, that the major energy was released concentrically at the post peak phase. When under cyclic loading, the elastic strain and plastic damage caused by repeated stress initiated cracking by fatigue. With the increased damage of coal, the elastic modulus became progressively smaller, as illustrated in Eq. (14). Then the dissipated energy further promoted cracks source expansion and caused energy to dissipate considerably. In Fig. 7b, the external work converted into elastic and plastic energy. Further, the dissipated energy caused gradual energy release before peak stress. During to the energy release effect on coal failure, the cracks propagation promoted and the damage of coal was increased, the macroscopic manifestation of this was the energy release under grade loading was comparatively less than that for cyclic loading at pre-peak, the damage occurred in “advance” for the latter, as a result there had a lower peak stress of specimens under cyclic loading. The difference in energy release phase is the reason behind the effect of the loading path on the mechanical characteristics variation in coal.
3.2 Charge signal time–frequency characteristics during coal failure
In this section we discussed the distribution of the signal in time and frequency domain, a set of typical data was selected for regular elaboration, as shown in Fig. 10, it demonstrated the charge time-domain signal at different loading stages for coal under uniaxial loading, it worth notice that the charge signal pulse demonstrated a satisfactory relationship with stress.
From Fig. 10, it was evident that the high amplitude charge time-domain signal distribution had a satisfactory inversion of stress phases. At the compaction and elastic phase, few signal pulses appeared, until the later stages of the elastic phase, where low amplitude pulses occurred discretely. Owing to loading in the strengthening phase, the amplitude of signal pulse converted from low to high, and the distribution transformed from discrete to intensive as the stress increased. At the time of peak strength, there existed a distinct high amplitude signal, and subsequently at the post-peak phase, near ultimate destruction, the high amplitude signal became intensive. In particular, at each stress drop there was a high amplitude signal occurrence.
The set of typical frequencies obtained by Fourier transformation(FFT) to the charge waveform recorded for the samples, analysis of the spectrum of charge pulse production at different stages based on Nyquist sampling theorem, the characteristics of charge time-domain signal at different stress states was investigated, as shown in Fig. 11, it illustrated the signal spectrum result, where the yellow line is time signal and the blue line is the corresponding frequency distribution. In Fig. 11a, the signal was a regular sine wave, which was mainly the white noise of the laboratory power-line interference, and its frequency composition was fixed. During the coal was loaded from the elastic to the post peak phase, shown in Fig. 11b–d, the time-domain signal converted from a small fluctuation to a high amplitude pulse. Further, some flat phenomenon existed and the amplitude of frequency distribution increased considerably as the time- domain signal pulse improved, which is the ranging between 1 and 100 Hz. Thus, it can be inferred that the charge is a type of low-frequency signal with primary frequency distribution from 1 to 100 Hz, the feature of frequency is the most significant difference between charge induction and electromagnetic radiation (Frid et al. 2003, 2004, 2005; Song et al. 2012, 2016).
3.3 The charge tribological mechanism during coal failure process
Previous studies demonstrated that the charge appearing in rock or coal failure processes was directly related to the cracks under the influence of a complicated mechanism, and the coal failure at uniaxial compression as a result of tension creak owing to micro shear slip (Xiao et al. 2015). In this section we had provided a discussion on the charge induction mechanism from the perspective of tribology, which was caused by shear slip between both sides of the crack faces.
Owing to the loading on the coal, the primary and new fractures developed gradually. Both sides of the crack face contacted and compressed each other under the action of the stress, and there was a relative displacement between them during the process of shear slip. Therefore, numbers of electrons formed on both sides, creating a charge effect that we monitored (Fig. 12).
For a crack, we assumed there was an angle θ with the horizontal, under the action of force σ, there was a relative slip, and concluded that the friction on the crack face was expressed as follows.
where \(\tilde{\sigma }\) is the effective stress.
According to Amontons’ first law, the stress loading on the crack face is represented as σx and σy, as illustrated by Eqs. (17) and (18).
where σx and σy are stresses parallel and perpendicular to the crack face, respectively, θ is the angle between crack extension direction and the horizontal, and μ is the sliding friction coefficient.
Research illustrated that the charge created by the sliding friction was directly related to the positive pressure and the relative velocity (Budakian and Putterman 2000; Zeghloul et al. 2017).
where nq is magnitude of charge and vx is relative velocity along the fractured surface.
For one side of the crack, there was a relative displacement u to the other side, and the relative velocity was as shown in Eq. (23). During the coal failure process, the stress and the creak development controlled the charge affecting factors. The higher the stress loaded on and fragment, the higher is the charge signal monitored.
where ax is acceleration along the fractured surface and ρ is density of coal.
3.4 Charge signal time–frequency characteristics during coal failure at different loading paths
Based on the aforementioned analysis, the energy accumulated–released law was affected by loading path. It had a direct impact on the mechanical properties. Simultaneously, the bearing of charge was affected by the mechanical properties of coal. The result of charge signal during coal failure at different loading paths is obtained. The Fig. 13 illustrated the two typical charge time-domain signals at grade and cyclic loading paths, and the Fig. 14 demonstrated their spectrum.
The result indicated that the charge pulse was affected by the loading path, as shown in Fig. 13. Under grade loading, it first emerged at the strengthening phase at approximately 60% strength. Subsequently, a high amplitude signal was generated at each stress drop. By comparison, under cyclic loading, the first pulse emerged at the strengthening phase at approximately 51% strength, it worth notice that there was a high amplitude pulse at each point of loading turn to unloading, high amplitude signals are generated after loading in the strengthening phase, and the signal continuity is evidently stronger than the grading load. In Fig. 14, it demonstrated the signal feature point waveform and spectrum, where the main frequency distribution primarily focuses on 1–100 Hz, and the amplitude of the main frequency band under grade loading was comparatively higher than that under cyclic loading.
This result demonstrated that the loading path affected the mechanical properties of coal, further, it affected the features of charge time–frequency domain signal distribution and amplitude during the failure process. Based on the aforementioned point of view, in case of coal under cyclic loading, energy was released and the cracks propagation was accelerated, promoting further damage, therefor, the damage of former was comparatively higher than that under grade loading, particularly, the cracks inside of coal were abundant compared with the coal under the action of grade loading. The movement of fractures was more severe and produced further charges during the failure process of coal, as a result, the amplitude and continuity of the charge signal produced by the coal under cyclic loading were evidently stronger than those under the grade loading. Simultaneously, the frequency domain analysis demonstrates that the amplitude of the main frequency band was higher than that under cyclic load.
4 Conclusion
During the coal failure process, the loading path changed the manner of energy accelerate–release, which was the reason that with different mechanical responses of coal for loading paths. Experimental and theoretical analysis results shown that under cyclic loading, the energy released before the peak promoted the development of cracks in coal, hence, it was easier to attain peak stress and instability, which the strain softening was evident at the post peak stage. When under grade loading, relatively less energy was released before the peak, and the development of internal fracture was concentrated on strengthening and peak value before and after, the brittleness characteristics were evident. Macroscopically, the strength of coal under cyclic loading is evidently lower than that under grade loading, and the integrity after destruction was relatively poor. The parameters of stress correction factor a and failure stress–strain ratio b are proposed to describe the effect of the loading path on the failure mode of coal.
Experiment results indicated that the charge signal measure up to the stress and damage during coal deformation and failure process, charge pulse appears concentrated in the strengthening and post-peak phases, a high amplitude signal response was produced with the sudden drop of stress. Frequency domain analysis by Fourier transformation (FFT) to the charge waveform recorded for the samples indicated that the charge pulse was a type of low-frequency signal with primary frequency distribution of 1 Hz–100 Hz, and the amplitude of the frequency components reflected the stress and damage. Analysis of electricity generation mechanism from the perspective of tribology, it demonstrated that the charge was proportional to the damage factor and the stress loading on the coal, which produced by the shear slip between both sides of crack face.
Based on the law of the charge generation for coal failure, and the evolution of damage and stress of coal under different loading paths. The damage of coal increased on the pre-peak phase, which was under cyclic loading, then the first high amplitude signal appears ahead of time. The amplitude of the signal in the frequency domain is significantly affected by the stress, which was improved with stress increased, and this shown a better verification of the charge friction slip mechanism.
Abbreviations
- p :
-
Stress
- s :
-
Stressed area elements
- W′ :
-
Strain energy
- σ′ :
-
Actual stress
- ε′ p :
-
Plastic strain
- D :
-
Damage variable
- \(\tilde{A}\) :
-
Effective loaded area
- σ Max :
-
Peak strength
- a :
-
Stress correction factor
- \(\tilde{\sigma }\) :
-
Effective stress
- σ y :
-
Stress perpendicular to crack face
- μ :
-
Sliding friction coefficient
- n q :
-
Magnitude of charge
- W :
-
External work
- E :
-
Elastic modulus
- ε e :
-
Elastic deformation ideally
- ε′ e :
-
Actual elastic strain
- U :
-
Dissipated energy
- A :
-
Loaded area
- \(\tilde{E}\) :
-
Effective elastic module
- ε Max :
-
Strain of peak strength
- b :
-
Failure stress–strain ratio
- σ x :
-
Stress parallel to crack face
- θ :
-
Angel between crack extended direction and horizontal
- a x :
-
Acceleration alone the fractured surface
- ρ :
-
Density of coal
References
Aguado MBD, González C (2009) Influence of the stress state in a coal bump-prone deep coalbed: a case study. Int J Rock Mech Min Sci 46:333–345
Alber M, Fristschen R, Bischoff M, Meier T (2009) Rock mechanical investigation of seismic events in a deep longwall coal mine. Int J Rock Mech Min Sci 46(2):408–420
Aubertin M, Gill DE, Simon R (1994) On the use of the brittleness index modified (BIM) to estimate the post-peak behavior of rocks. In: Nelson PP, Laubach SE (eds) Rock mechanics models and measurement challenges from industry. A. A. Balkema, Rotterdam, pp 945–952
Bahat D, Frid V, Rabinovitch A, Palchik V (2004) Exploration via electromagnetic radiation and fractographic methods of fracture properties induced by compression in glass-ceramic. Int J Fract 116(2):179–194
Bobet A, Einstein HH (1998) Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int J Rock Mech Min Sci 35(7):863–888
Boler FM, Billington S, Zipf RK (1997) Seismoligical and energy balance constraints on the mechanism of a catastrophic bump in the book cliffs coal mining district, Utah, USA. Int J Rock Mech Min Sci 34(1):27–43
Budakian R, Putterman SJ (2000) Correlation between charge transfer and stick-slip friction at a metal-insulator interface. Phys Rev Lett 85(5):1000–1003
Frid V, Rabinovitch A, Bahat D (2003) Fracture induced electromagnetic radiation. J Phys D Appl Phys 36:1620–1628
Hoek E, Brown ET (1998) Practical estimates of rock mass strength. Int J Rock Mech Min Sci 34:1165–1186
Jaeger JC, Cook NGW, Zimmerman RW (2007) Fundamentals of rock mechanics (fourth edition chapman and hall). Blackwell, London
Jiang Y, Wang H, Zhao Y, Zhu J, Pang X (2011) The influence of roadway back fill on bursting liability and strength of coal pillar by numerical investigation. Procedia Eng 26:1125–1143
Jiang Y, Pan Y, Jiang F, Dou L, Ju Y (2014) State of the art review on mechanism and prevention of coal bumps in China. J China Coal Soc 39(2):205–213
Kuksenko VS, Makhmudov KhF (1997) Mechanically-induced electrical effects in natural dielectrics. Tech Phys Lett 23(2):126–130
Kuksenko VS, Makhmudov KhF, Ponomarev AV (1997) Relaxation of electric fields induced by mechanical loading in natural dielectrics. Phys Solid State 39(7):1065–1070
Lannacchione AT, Tadolini SC (2016) Occurrence, predication, and control of coal burst events in the US. Int J Min Sci Technol 26:39–46
Lawson H, v A, Miller A (2016) Dynamic failure in coal seams: implications of coal composition for bump susceptibility. Int J Min Sci Technol 26:3–8
Mark C (2016) Coal bursts in the deep longwall mines of the Unite States. Int J Coal Sci Technol 3(1):1–9
Medhurst TP, Brown ET (1998) A study of the mechanical behavior of coal for pillar design. Int J Rock Mech Min Sci 35(8):1087–1105
Pan Y, Li Z, Zhang M (2003) Distribution, type, mechanism and prevention of rockbrust in China. Chin J Rock Mech Eng 22(11):1844–1851
Pan PZ, Feng XT, Hudson JohnA (2009) Study of failure and scale effects in rocks under uniaxial compression using 3D cellular automata. Int J Rock Mech Min Sci 46:674–685
Pan Y, Tang Z, Li Z, Zhu L, Li G (2013) Research on the charge inducing regularity of coal rock at different loading rate in uniaxial compression tests. Chin J Geophys 56(3):1043–1048
Peng R, Ju Y, Wang JG, Xie H, Gao F, Mao L (2015) Energy dissipation and release during coal failure under conventional triaxial compression. Rock Mech Rock Eng 48:509–526
Rabinovitch A, Shay A, Liraz R, Frid V, Bahat D (2005) Electromagnetic radiation emitted during friction process. Int J Fract 131(2):L21–L27
Salamon MDG (1984) Energy consideration in rock mechanics fundamental results. Int J S Afr Inst Min Metall 84:237–246
Song DZ, Wang EY, Liu J (2012) Relationship between EMR and dissipated energy of coal rock mass during cyclic loading process. Saf Sci 50:751–760
Song DZ, Wang EY, Song XY (2016) Changes in frequency of electromagnetic radiation from loaded coal rock. Rock Mech Rock Eng 49:219
Volarovich MP, Parkhomenko EI (1954) Piezoelectric effect in rocks. Dokl Akad Nauk SSSR 2:99
Wang H, Poulsen BA, Shen B, Xue S, Jiang Y (2011) The influence of roadway backfill on the coal pillar strength by numerical investigation. Int J Rock Mech Min Sci 48(3):443–450
Xiao X, Ding X, Pan Y, Wang X, Jun X, Luo H, Zhao X (2015) Experiment of acoustic emission and charge induction in granular coal rock failure. J China Coal Soc 40(8):1796–1804
Zeghloul T, Neagoe MB, Prawatya YE, Dascalescu L (2017). Triboelectrical charge generated by frictional sliding contact between polymeric materials. In: IOP conference series: materials science and engineering, vol. 174, no. 1, 012002
Zhang J, Jiang F, Zhu S, Zhang L (2016) Width design for gobs and isolated coal pillars based on overall burst- instability prevention in coal mines. Int J Rock Mech Geotech Eng 8:551–558
Zhaoxia L (2002) Damage mechanics and application. Science Press, Beijing
Acknowledgements
This study was finally supported by the National Key Research & Development Program of China (2017YFC0804208); the National Nature Science Foundation of China (Grant Nos. 51774122, 51774048, 51504122); Scientific Research Foundation of State Key Lab. of Coal Mine Disaster Dynamics and Control (2011DA105287-FW 201605).
Author information
Authors and Affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ding, X., Xiao, Xc., Wu, D. et al. Mechanical properties and charge signal characteristics in coal material failure under different loading paths. Int J Coal Sci Technol 6, 138–149 (2019). https://doi.org/10.1007/s40789-019-0239-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40789-019-0239-4