1 Introduction

Rock burst is one of the common disasters in coal mining. As coal mining enters the stage of deep mining, the risk of rock burst becomes more and more serious and often induces other accidents such as coal and gas outbursts, water damage and more (Cai et al. 2016; Mark 2016; Xu et al. 2019). The mechanical characteristics of deep rock mass determine the obvious difference between deep mining and shallow mining (Wu et al. 2019, 2021). In addition to high static loading, coal and rock masses also receive dynamic loading disturbance due to mining disturbance, roof collapse, fault slip and so on (Du et al. 2016; Kong et al. 2020; Yin et al. 2020). Therefore, studying the mechanical response of coal and rock mass under dynamic and static loading conditions is significant to prevent and control rock bursts (Xiang et al. 2022).

Rock burst can be classified into three categories: strain rock burst, fault-slip rock burst, and roof fracture rock burst. Among them, the strain rock burst occurs mostly within highly stressed hard rock and coal mass with high strain energy (Li et al. 2022). The accumulation of strain energy of coal rock mass is related to strain rate of loading (Jangara and Ozturk 2021; Zou et al. 2022a, b). Strain rate is also an important parameter to characterize the distinction between static loading and dynamic loading (Liu et al. 2022; Zou et al. 2022a, b). In recent years, many scholars have researched strain rate effect on rock from strength characteristics, energy characteristics, failure characteristics and other aspects (Bazant et al. 1993; Chen et al. 2019; Dong et al. 2021). This provides a basis for studying the mechanical response of coal and rock under dynamic and static loading conditions and the control and prevention of strain rock burst (Huang et al. 2021a, b; Xie et al. 2022).

Strain rates can be divided into low strain rate (10−5–10−1 s−1), medium strain rate (10−1–102 s−1) and high strain rate (101–104 s−1) (Campbell 1973). In the initial study on the influence of strain rate effect, scholars mainly focused on the creep characteristics of rock under strain rates lower than 10−5 s−1 s−1. However, in recent years, with the increasingly severe dynamic disasters, the research focus has gradually shifted to high strain rates, especially under the widespread use of drop hammer impact test machine and Hopkinson pressure bar (Ramesh et al. 2015). As early as 1981, Britain (Blanton 1981) studied the uniaxial compressive strength of granodiorite, sandstone and limestone under a certain confining pressure within 10−2 s−1–10 s−1. It was concluded that the peak stress of the three rocks increased significantly with the increase in strain rate, and it was believed that this phenomenon was caused by machine inertia. It does not reflect the nature of the material itself. Chong et al. (1990) studied the elastic modulus characteristics of shale in the range of 10−5 s−1–100 s−1 and concluded that the elastic modulus of rock was significantly affected by strain rate. Mahmutoglu (2006) studied the mechanical properties of marble in the range of 5 × 10−7 s−1–2 × 10−5 s−1. Peak stress increased linearly with strain rate increasing. Zhao et al. (2014) studied the mechanical properties of brittle coal within 10−3 s−1–10−2 s−1 through laboratory experiments and numerical simulation. The UCS of coal increases with strain rate increasing, while elastic modulus remains a constant value. The above studies are all carried out under low strain rates. With the rise of Hopkinson pressure bar in recent years, more and more scholars have used it to test the dynamic mechanical properties of rock (Li et al. 2017; Zhou et al. 2020). Cheng et al. (2020; Feng et al. 2021; Huang et al. 2021a, b) respectively studied the mechanical properties of gas-bearing coal, granite and sandstone with cross fractures under dynamic impact, finding that peak stress was highly correlated with strain rate and showed an increasing trend. The results show that strain rate has a positive effect on these mechanical parameters. However, some researches show that these mechanical parameters do not always increase with strain rate increaseing. Instead, there is a strain rate region. When strain rate increases, these mechanical parameters will appear a lower value (Li et al. 2014).

In addition, the strain rate effect on energy dissipation and particle size distribution of rock have also been studied. Liang et al. (Liang et al. 2016) researched size effect on the energy dissipation characteristics and fractured forms of granite under low strain rates. They pointed out that elastic energy determines the amount of energy released at the moment of rock failure. Hong et al. (Hong et al. 2009) researched the energy dissipation and fractured characteristics of rocks within the range of 40–150 s−1. They found that the dissipated energy density has a linear relationship with total incident energy, and the higher the dissipated energy density is, the more serious the fracture degree is Yan et al. (2020) studied the energy dissipation of fractured sandstone with strain rates ranging from 38–175 s−1. Energy dissipation increases when strain rate increasing. The degree of rocks’ breakage and uniformity was also characterized by fractal dimension in the study. Mahanta et al. (2017) carried out experiments on semicircular curved shale specimens and proposed that the change in energy release rate was not obvious at a lower strain rate, while it was very different at a higher strain rate. Li et al. (2014) studied the energy evolution and failure characteristics of grey coarsely crystallized marble. Elastic and plastic energy increase with strain rate increasing. The above studies have studied the energy and failure characteristics of rock under different strain rates, providing many research methods and interesting new findings.

In conclusion, there are extensive studies on mechanical response characteristics, such as UCS of different rocks with different strain rates. However, there are only a few related studies on the mechanical response and failure characteristics of coal under quasi-static loading. In particular, the mechanical response characteristics of elastic-brittle coal within the range of quasi-static strain rates need to be further studied. This is of great significance for preventing coal bursts under high static loading. Therefore, this paper intends to study the mechanical properties and failure characteristics of coal under quasi-static loading from five aspects of mechanical properties, acoustic emission characteristic parameters, deformation characteristics, energy evolution and failure characteristics, to provide a basis for the prevention of strain rock burst induced by high static loading.

2 Sample preparation and experimental procedures

2.1 Sample preparation

The coals were taken from Ximengou Coal Mine, Shaanxi Province, China. The sampling direction was perpendicular to bedding. The length of the coal sample is 100 mm, the diameter is 50 mm, and the height-diameter ratio is 2:1, as shown in Fig. 1. After polishing the upper and lower ends of coal, the unevenness is less than 0.05 mm, meeting the requirements of ISRM. Finally, six coal samples with similar quality were selected with a similar quality and wave velocity.

Fig. 1
figure 1

Schematic diagram of standard raw coal sample

Full size image

2.2 Experimental procedures

The uniaxial compression experiment device adopts a microcomputer controlled electronic universal test machine (Fig. 2), which can test the elastic modulus, uniaxial compressive strength of coal.

Fig. 2
figure 2

Schematic diagram of microcomputer electronic universal testing machine

Full size image

In this experiment, the displacement loading method was adopted, and different loading rates were selected to realize the loading of different strain rates under quasi-static range. Strain rate can be calculated according to the following formula:

$$\dot {\varepsilon }={{{v_{lr}}} \mathord{\left/ {\vphantom {{{v_{lr}}} L}} \right. \kern-0pt} L}$$
(1)

where, \(\dot {\varepsilon }\) is strain rate, s−1; vlr is the loading rate of the experimental machine, mm/min; L is the length of coal, mm.

Different coal samples were subjected to compression at different displacement loading rates until the samples failed. Furthermore, a DS5 acoustic emission system (AE) was used in the experiment, and two AE sensors were installed on each sample to monitor the acoustic signals during the loading process. The experimental scheme is shown in Table 1.

Table 1 Experiment scheme of uniaxial compression with different strain rates
Full size table

After the samples failed, 16 sample screens with different diameters were used to screen the samples, and the particle mass in each size range was recorded. The aperture of the 16 sample screen is 12.5 mm, 8 mm, 6 mm, 5 mm, 4 mm, 3 mm, 2 mm, 1.6 mm, 1.43 mm, 1.25 mm, 1 mm, 0.9 mm, 0.8 mm, 0.6 mm, 0.45 mm, 0.355 mm, respectively.

3 Results and discussion

3.1 Stress-strain characteristics

The uniaxial compression stress-strain curves of coal samples with different strain rates mainly show four stages: pore compaction, elastic, stable development of micro-cracks and post-peak stage (Fig. 4).

In the pore compaction stage, the stress-strain curves show a consistent growth trend, and the pores inside the coal sample are compressed, which shows that strain increases slowly with the increase of stress. All coal samples show elasticity in the elastic stage, accounting for more than 80% of all stress-strain curves. However, the stable development stage of micro-cracks is not significant, which may be related to the vertical bedding angle and sampling direction of coal samples and displacement loading mode. All coal samples show brittle failure characteristics. The elastic deformation and elastic energy of coal increase continuously, and the stress concentration degree also increases, with micro-cracks developing accordingly. When the stress reaches the peak stress, the coal fails instantly due to the high degree of development of internal micro-cracks. The macroscopic manifestation is that the fragments of the coal sample are ejected with high kinetic energy, which results from the instant release after accumulating of elastic energy (Liang et al. 2016). After peak stress, the stress-strain curve generally shows a downward trend. Figure 3 clearly illustrates the stress drop phenomenon as the strain is almost constant, while the stress drops rapidly to zero.

Fig. 3
figure 3

Stress-axial strain curves of coal

Full size image

The uniaxial compressive strength (UCS) of coal ranges from 35.97 to 53.58 MPa, which shows an increasing trend with Lg\(\dot {\varepsilon }\) increasing (Mahmutoglu 2006; Zhao et al. 2014), as shown in Fig. 4a. However, a valley value appears at 10−2 s−1, which may be caused by the complex internal structure of coal. The elastic modulus (E) decreases first and then increases and the minimum value appears in a particular range (Li et al. 2014). This is a unique strain rate range in which some rock parameters, including elastic modulus, show a low value. Judging from previous research experience, the mechanical parameters of coal increase with \(\dot {\varepsilon }\) increasing, but there still exists a range where strain rate effect is not significant. In this paper, this strain rate range is named as strain rate effect invisible area. This indicates that the mechanical response of coal is subject to the combined effect of strain rate and complex microscopic structure of coal. When strain rate exceeds a certain value, E increases significantly, as shown in Fig. 4b.

Fig. 4
figure 4

UCS and E of coal: a UCS, b E

Full size image

Since displacement loading method is adopted, the strain-time curves of coal are all straight lines. As shown in Fig. 5a, strain-time curves of coal show reasonable regularity. With Lg\(\dot {\varepsilon }\) increasing, the loading time decreases exponentially (Fig. 5b). Maximum strain \({\varepsilon _m}\) (the maximum strain of coal after failure) and peak strain \({\varepsilon _p}\) (the strain when appliedstress reaches peak stress) are primarily over 3%. \({\varepsilon _m}\) increases exponentially with Lg\(\dot {\varepsilon }\) increasing, while \({\varepsilon _p}\) increases slowly and tends to be linear. When strain rate is at a low value, \({\varepsilon _m}\) is close to \({\varepsilon _p}\). When \(\dot {\varepsilon }\) increases to 1 × 103 s−1, \({\varepsilon _m}\) is larger than \({\varepsilon _p}\), and the difference increases with Lg\(\dot {\varepsilon }\) increasing. On one hand, the internal cracks of coal develop slowly and fully under lower strain rate loading, and the strain at coal failure is small. Under higher strain rate, \(\dot {\varepsilon }\) increases rapidly, the elastic energy accumulates rapidly, and \({\varepsilon _p}\) is also more considerable. On the other hand, When \(\dot {\varepsilon }\) increases to a certain value, the difference between the maximum strain and peak strain becomes more prominent due to the gradual emergence of the strain rate effect.

Fig. 5
figure 5

Deformation characteristics of coal: a Strain time curve, b Deformation characteristics

Full size image

3.2 Energy evolution

According to the study of Xie et al. (2005), energy dissipation reflects rock failure by the continuous development of micro-defects and the continuous reduction of strength. The relationship between input energy, elastic energy and dissipated energy is as follows.

$$U={U_d}+{U_e}$$
(2)

where, U is input energy, MJ/m3; Ud is dissipated strain energy, MJ/m3; Ue is elastic strain energy, MJ/m3.

Furthermore, Ue can be calculated by the following formula:

$${U_e}=\frac{{{\sigma ^2}}}{{2E}}$$
(3)

where, σ is the stress during uniaxial compression, MPa; E is elastic modulus of coal, GPa.

According to Eqs. (2) and (3), the evolution curves of Ue and Ud of coal during uniaxial compression can be obtained (Fig. 6). The energy evolution of coal under different strain rates shows similar characteristics. Ue always accounts for a high proportion of coal samples before failure and reaches more than 90% at failure, while the proportion of Ud is very small. This indicates that most of input energy is used for the accumulation of elastic energy. If coal dislocates in the loading process, Ue will decrease partly, and Ud will increase suddenly. This dislocation is more likely to occur at lower strain rates. At the moment of coal failure, accumulated elastic energy is released instantly to destroy coal. The difference is that Ue decreases sharply to 0 at lower strain rates, while the stress drop phenomenon gradually slows down at higher strain rates, and stress peak point gradually moves forward. In addition, the proportion of Ue increases with Lg\(\dot {\varepsilon }\) increasing during coal failure, as shown in Fig. 7. This is because, at a lower strain rate, more energy dissipation occurs during fracture development, expansion and connection, while at a higher strain rate, more input energy will be used for elastic energy accumulation due to a higher loading rate, thus showing higher strength at a higher strain rate (Liang et al. 2016).

Fig. 6
figure 6

Energy evolution characteristics of coal

Full size image
Fig. 7
figure 7

Proportion of Ue and Ud of coal

Full size image

3.3 Failure characteristics

The particle size distribution results show no large fragments of the whole block (Fig. 8). Overall fragmentation degree is large, and the number of small fragments is large. The fracture surface is rough, without an obvious slip surface. Therefore, Tensile failure is the primary failure mode of specimens. When applied stress reaches the peak stress, accumulated elastic strain energy is suddenly released, and the cracks are connected. As a result, the coal sample immediately failed into numerous fragments of different sizes, which are catapulted out with high kinetic energy (Mahmutoglu 2006; Zhao et al. 2014), as shown in Fig. 8. Overall, the grain size distribution curve of coal gradually moves from the lower right to the upper left with Lg\(\dot {\varepsilon }\) increasing. This is the manifestation of the increased degree of crushing. The cumulative mass ratio curve of logarithmic particle size shows that the coal particle size distribution is relatively uniform, as shown in Fig. 9a.

According to the study by Mandelbrot(Mandelbrot 1985) on fractal dimension D of rock fragmentation, The relationship among mass, particle size and D of rock fragments after fragmentation is shown in Eq. (4).

$$M(X{\text{)/}}{M_{\text{T}}}={(X/{X_{\text{m}}})^{3 - D}}$$
(4)

where, X is particle size, mm; Xm is the maximum particle size of rock after crushing, mm; M(X) is the accumulated mass of fragments under a certain particle size, g; MT is the total mass of rock after crushing, g; D is the fractal dimension representing rock fragmentation and uniformity, which is referred to as the fractal dimension of fragmentation.

Equation (5) can be obtained by taking the logarithms of both sides of Eq. (4):

$$Lg\left[ {M(X{\text{)/}}{M_{\text{T}}}} \right]=\left( {3 - D} \right)L{\text{g}}(X/{X_{\text{m}}})$$
(5)

According to the relevant results of the fractal curve (as shown in Fig. 9(b)), the fractal dimension of fragmentation under different strain rates can be calculated. D shows an exponential growth trend as Lg\(\dot {\varepsilon }\) increases. This indicates that the fragmentation and uniformity of coal increase with \(\dot {\varepsilon }\) increasing, but the increase slows down. It is worth noting that the fractal dimension of 4 × 10−4 s−1 shows a valley value, which is consistent with the changing trend of elastic modulus and the proportion of elastic energy mentioned above. This may be related to the microstructure of coal samples (Li et al. 2014).

Fig. 8
figure 8

Failure mode of coal: a 5 × 10−5 s−1, b 10−4 s−1, c 5 × 10−4 s−1, d 10−3 s−1, e 10−2 s−1, f 4 × 10−2 s−1

Full size image
Fig. 9
figure 9

Particle size distribution and fractal characteristics of coal: a Particle size distribution, b Fractal curve, c D

Full size image

3.4 Acoustic emission (AE) ringing counts, amplitude and energy characteristics

The variation of AE parameters such as ringing count, amplitude and energy can reflect the fracture development behavior of coal samples during loading (Kao et al. 2011; Lockner 1993; Sagar and Prasad 2012). As shown in Fig. 10, AE count and energy are not significant at the initial stage of loading. In this stage, low-amplitude signals often appear, indicating that cracks are compressed. At the moment of coal failure, the cumulative AE count and energy rise significantly, and signals of different amplitude gather, especially those with large amplitudes (Liu et al. 2020). However, at lower strain rates, obvious precursor AE signals can be observed, and the ringing count and energy signals will significantly change before the coal fails. While at higher strain rates, this phenomenon is not obvious, and the intensity of amplitude signals also decreases, which may bring difficulties in identifying precursor information under higher strain rates loading.

Fig. 10
figure 10

AE characteristic curves of coal. (stress curve, AE energy, cumulative ringing curve, amplitude)

Full size image

To some extent, AF and RA values can represent the failure mode of coal in the process of uniaxial compression (Wang et al. 2016). AF is the ratio of AE count to time of duration, and RA is the ratio of rising time to amplitude, as shown in Fig. 11. When the data points are more distributed in the upper left, the failure mode of coal is more inclined to tensile failure. When the data points are more distributed in the lower right, the failure mode of coal is more inclined to shear failure (Ohno and Ohtsu 2010; Rodriguez and Celestino 2019). As shown in Fig. 11, more data points are distributed in the upper left region. Combined with the analysis in Sect. 3.3, within the range of experimental strain rates, coal failure presents a combined failure mode of stretch-shear under the dominance of tensile failure. However, the contribution of the shear failure to coal failure also increases with \(\dot {\varepsilon }\) increasing. The proportion of Ue is relatively small, and the final fracture degree is relatively small. While at higher strain rates, stress concentration will occur at the weak plane, resulting in a higher degree of elastic energy accumulation and stress concentration, leading to a more prominent contribution of the shear failure to coal failure. However, for the data of sample 10−4 s−1, the contribution of tensile failure increases more, which is consistent with the fractal dimension of fragmentation and the proportion of elastic energy mentioned above.

Fig. 11
figure 11

AF and RA characteristics

Full size image

3.5 Discussion on the relationship between parameters

From the above analysis, UCS, E, the proportion of Ue and D all show increasing trends with \(\dot {\varepsilon }\) increasing. However, whether there is a link between them remains to be seen. E, the proportion of Ue and D all show a trend of decreasing first and then increasing (Fig. 12). In this study, the region of this decline is named as strain rate effect invisible area. Wasantha et al. (2015) suggested that this behavior could be explained by the grain size related mechanism and was related to stress redistribution caused by internal grain rupture. The above three parameters have a certain correlation, but the lowest point of E is different from the other two parameters. The proportion of Ue is more closely related to D of fragmentation. UCS and strain parameters are different from the above three parameters. The strain parameters show reasonable regularity. \({\varepsilon _p}\) shows a specific linear growth trend with Lg\(\dot {\varepsilon }\) increasing, while \({\varepsilon _m}\) shows an exponential growth trend with good regularity. By contrast, UCS presents more complex. On one hand, it has no apparent correlation with other parameters. On the other hand, a valley value appears at a higher strain rate (10−2 s−1), which has rarely been reported in the literature. Yet, this does not affect the overall upward trend.

Fig. 12
figure 12

The relationship between the parameters

Full size image

In the history of strain rate effect research, UCS and E are the most frequent parameters which many scholars have discussed. Figure 13 lists the data from several previous studies for comparison with the data in this paper. Zhao et al. ( 2021), Cao et al. (2019), and Meng et al. (2016) studied the variation of UCS of yellow sandstone, gray sandstone and red sandstone in the quasi-static range, respectively. Feng et al. (2018) researched the evolution law of peak strength of rock materials with cross fractures. Alam et al. (2015) studied the characteristics of the peak strength of porphyry-bearing sandstone, adopting the method of regression analysis. In terms of E, Rybacki et al. (2015) studied the effects of different temperatures, confining pressures and \(\dot {\varepsilon }\) on E of black shale. Mahanta et al. (2018) studied the influence of \(\dot {\varepsilon }\) on peak strength, tensile strength, E, fracture toughness and brittleness index in the quasi-static range. Schuster et al. (2021) studied the elastic modulus characteristics of sandstone under different confining pressures, temperatures and sampling directions, including those parallel to bedding directions. Singh et al. (2015) took granite as the research object and discussed the thermodynamic behavior of granite under different strain rates and temperatures. Although the above studies differ in research methods, sample types and research focus, UCS and E generally increase with Lg\(\dot {\varepsilon }\) increasing (Fig. 13), which is consistent with the research results in this paper, even if there are some anomalies in the figure. This may be related to the strain rate effect invisible area.

Fig. 13
figure 13

Comparison with previous research: a UCS, b E

Full size image

3.6 Guiding significance for rock burst control

In the engineering practice of rock burst prevention, the possibility of a rock burst is often represented by the bursting energy index, which means that coal and rock mass have the property of accumulating deformation energy and producing impact damage. It includes UCS, elastic energy index, dynamic failure time and bursting energy index (KE). Among them, KE is calculated as follows formula (Xu et al. 2020):

$${K_E}{\text{=}}{K_{\text{b}}}/{K_{\text{a}}}$$
(6)

where, Kb is the strain energy accumulated before the peak during the uniaxial compression test, MJ/m3; Ka is strain energy accumulated after the peak, MJ/m3.

Figure 14 shows the data diagram of UCS at different strain rates, the proportion of Ue and KE of coal failure. Generally, when \(\dot {\varepsilon }\) is low, UCS is relatively low, and KE is high. The coal under this loading is more prone to impact damage, but because of the small energy accumulation and elastic energy accumulation, the damage and risk are relatively small. On the contrary, when \(\dot {\varepsilon }\) is high, UCS is relatively high, and KE is low. Due to the high degree of elastic energy accumulation, although the coal mass under such loading is less prone to impact, it will be more destructive and dangerous once impact damage occurs.

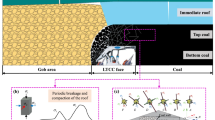
Figure 15 shows the situation of coal mass at the front of the working face under high static loading. In addition, it also includes the condition of isolated coal pillars and other coal mass subjected to approximate uniaxial compression. Therefore, to reduce the risk of rock burst, on the one hand, the static loading stress level should be reduced; that is, the stress concentration should be reduced. On the other hand, the direct action of high strain rate loading should be avoided. The research achievements deepen the understanding of the strain rock burst to support the control and prevention of strain rock burst induced by high static loading.

Fig. 14
figure 14

Rockburst tendency and risk analysis

Full size image
Fig. 15
figure 15

The mechanism of rock burst induced by high static loading

Full size image

4 Conclusions

In this paper, the mechanical response characteristics of coal are analyzed from the view of strain rate by laboratory experiments. The results show that:

(1) The UCS of coal generally shows an increasing trend with Lg\(\dot {\varepsilon }\) increasing, while E exhibits a nonlinear characteristic of first decreasing and then increasing as Lg\(\dot {\varepsilon }\) increases. \({\varepsilon _m}\) increases exponentially with Lg\(\dot {\varepsilon }\) increasing, while \({\varepsilon _p}\) increases slowly, which is closer to a linear growth trend. When \(\dot {\varepsilon }\) increases to 1 × 103 s−1, \({\varepsilon _m}\) is larger than \({\varepsilon _p}\), and the difference increases with Lg\(\dot {\varepsilon }\) increasing.

(2) The Ue of coal always accounts for a high proportion before failure and reaches more than 90% of the total strain energy at failure, while the proportion of Ud is minimal. As \(\dot {\varepsilon }\) increases, the stress drop phenomenon gradually slows down, and the peak point gradually moves forward. The proportion of Ue at coal failure increases with Lg\(\dot {\varepsilon }\) increasing.

(3) The coal fragmentation and uniformity after uniaxial compression increases with \(\dot {\varepsilon }\) increasing, but the increase slows down. Furthermore, the failure mode of coal presents a combined failure mode of tensile and shear under the dominance of tensile failure. with Lg\(\dot {\varepsilon }\) increasing, the contribution of the shear failure to coal failure increases correspondingly.

(4) Under quasi-static loading, There is a range where the strain rate effect does not appear, named as strain rate effect invisible area. This results from the combined effect of \(\dot {\varepsilon }\), grain size and the development of primary cracks. The proportion of Ue is closer to D. To reduce the risk of strain rock burst, on the one hand, the static loading stress level should be reduced, that is, the stress concentration should be reduced; on the other hand, the direct action of high strain rate loading should be avoided.