Earth’s gradients as the engine of plate tectonics and earthquakes

Abstract

The processes occurring on the Earth are controlled by several gradients. The surface of the Planet is featured by complex geological patterns produced by both endogenous and exogenous phenomena. The lack of direct investigations still makes Earth interior poorly understood and prevents complete clarification of the mechanisms ruling geodynamics and tectonics. Nowadays, slab-pull is considered the force with the greatest impact on plate motions, but also ridge-push, trench suction and physico-chemical heterogeneities are thought to play an important role. However, several counterarguments suggest that these mechanisms are insufficient to explain plate tectonics. While large part of the scientific community agreed that either bottom-up or top-down driven mantle convection is the cause of lithospheric displacements, geodetic observations and geodynamic models also support an astronomical contribution to plate motions. Moreover, several evidences indicate that tectonic plates follow a mainstream and how the lithosphere has a roughly westerly drift with respect to the asthenospheric mantle. An even more wide-open debate rises for the occurrence of earthquakes, which should be framed within the different tectonic setting, which affects the spatial and temporal properties of seismicity. In extensional regions, the dominant source of energy is given by gravitational potential, whereas in strike-slip faults and thrusts, earthquakes mainly dissipate elastic potential energy indeed. In the present article, a review is given of the most significant results of the last years in the field of geodynamics and earthquake geology following the common thread of gradients, which ultimately shape our planet.

1 Introduction

A gradient indicates a variation of any parameter, such as the degree of inclination of a plane; in physics, the rate at which, for example, pressure or temperature vary in space or time; in mathematics, a gradient is a vector having components the partial derivatives of a function with respect to its variables; in chemistry, a gradient can be identified as the variation of electro-chemical potential differences between two bodies; in biology, a gradient can be considered as the progressively increasing or decreasing differences in the growth rate, metabolism, physiological activity of a cell, organ or organism, in the distribution across membranes of ions with different concentrations and valences. Several gradients of parameters acting together with different times and rates on systems with a large number of degree of freedom can determine non-linearity, chaos and self-organization that can ultimately evolve into catastrophic collective behaviors [1, 2]. A gradient generates forces producing or being the expression of a difference of a certain physical observable in time or space. The gradient of electric potential between the two poles of a battery allows to start a car. Lightning is the release of energy due to the breaking of materials when electric potential gradient overcomes their dielectric resistance. Earth hosts Life because of the mobility of its mantle, thermal gradients inducing volcanic eruptions and velocity differences among crustal volumes provoking faulting, mountain growth and ocean spreading. What is the nature of these planetary gradients? How can we study them and how do they punctuate Earth dynamics? Each gust of wind is determined by atmospheric pressure gradient: areas where atmospheric pressure is greater push air toward areas of lower pressure. The greater the gradient, the faster the winds. Cyclones, tornadoes, rain and snow are controlled by those gradients. For analogous reasons, in the two hemispheres, the Coriolis force plays opposite and the linear velocity gradient induces clockwise or counterclockwise atmospheric circulation. Rivers flow downstream because of a topographic gradient and therefore a gravitational one: gravity never stops working. Atmospheric disturbances determine heavy rains, which in turn lower the friction in the soil and rocks, causing landslides: it is a succession of gradients that shape the Earth’s surface, with a tendency to decrease or eliminate morphological irregularities. Volcanoes erupt violently because inside the magma chambers, where the lava accumulates and melts the embedded rocks, pressure gradients are created that break through the overlying Earth’s crust. The density gradient that is generated for the thermal expansion of molten rocks contributes to the ascent of magma together with gas bubble coalescence that, as soon as reaches the surface, finds an opposite gradient producing lava flows on the sides of the volcanic apparatus, or disperses with pyroclastic clouds. The higher is the viscosity of magmas, the greater is the pressure gradient that manages to accumulate, and the viscosity generally tends to increase with the silica content of the magma. The higher the magma viscosity, the greater the explosiveness and the episodic nature of volcanism: this is an example of chemical gradient affecting geophysical dynamics. Therefore, the processes acting on the Earth are controlled by the gradients of the potential energy field according to the formula

$$\begin{aligned} \vec {F} = - \vec {\nabla }U \end{aligned}$$

(1)

if the force is conservative, while non-conservative forces act to reduce the free energy of a system increasing its entropy and moving it towards a more stable internal state. Gradients are determined by variations in pressure, temperature, chemical and mineralogical composition, friction, rigidity, viscosity, electromagnetic field, etc. The greatest the gradient, the largest the energy involved, yielding a wide range of manifestations at different spatial and temporal scales. The surface of the Earth is featured by complex geological patterns produced by both endogenous and exogenous events playing as a mirror of phenomena acting since the dawn of our planet. The lack of direct investigations still makes Earth interior poorly understood and also prevents complete clarification of peculiar mechanisms ruling geodynamics and related phenomena [3, 4]. For the same reason, the effective roles of the different forces contributing to plate tectonics remain elusive [5,6,7,8,9]. While large part of the scientific community has agreed that mantle convection is the cause of crustal displacements for fifty years [10, 11], geodetic observations and geodynamic models have been proposed since the last quarter of the past century highlighted exogenous local contributions to plate motions. Nowadays, slab-pull is considered the force with the greatest impact on plate motions by a large part of geodynamists [12, 13], but also ridge-push, trench suction, local crustal interactions and physico-chemical heterogeneities are thought to play a key role in affecting crustal dynamics at both regional and global spatial scales [14,15,16,17,18,19]. Moreover, a number of evidences suggest that a certain degree of polarization in global geodynamics exists [20]. The Earth layers move relative to each other, being the energy sourced by the internal heat dissipation, local gradients and tidal forces, acting on the whole planet. According to a part of the scientific community, also the latter one has a role in geodynamics, which is made more relevant since it is the only intrinsically asymmetric force acting on the Earth, like on other terrestrial and gaseous celestial bodies, whose internal dynamics are proven to be modulated by their gravitational interaction with others [21, 22]. In this view, lithospheric plates are proposed to be pushed westerly relatively to the underlying mantle by the low-frequency horizontal components of solid Earth tides and their angular speed correlates with the viscosity gradient at their base in the low-velocity zone. Whatever the model, it is clear that a great part of the effort needed for dispelling incongruities, providing better evidences and fine-tuning geophysical and geological constraints so that an appropriate, comprehensive theory of Earth dynamics can be achieved is still ahead. In the last decennials, research pointed out a deep differentiation and complexity of the planet internal structure far beyond the classical view suggested by the pioneering works of the early modern geophysicists. Enhanced investigation techniques and empowered computational tools and simulations are nowadays changing our idea of how the Earth works underlying unnoticed effects and also bringing previously discarded hypotheses back up. An even more conflicting and wide open debate rises for the most impacting consequence of plate motion: the occurrence of earthquakes. Seismicity represents the dissipation of a part of the energy concentrated in the brittle cold layers of the lithosphere. In fact, the energy supplied for moving fault planes comes from the velocity gradients at plate boundaries, determining mechanical gradients. Depending on the tectonic settings and other geological features, faults are activated under slightly different conditions: a cascade of gradients generating seismic activity. Moreover, in the case of seismicity, a further degree of complexity must be added to the discussion: while most of the processes that occur on Earth can be described in the light of classical physics, others, such as earthquakes, landslides and volcanic eruptions, exhibit behaviors that are difficult to predict, which alternate long periods of quiescence to violent activity [23]. This peculiarity is a direct consequence of the strong non-linearity of the physics of these systems, which allows them to generate emerging properties, i.e., they cannot be traced directly to the simplest components that make up the geological structure. As a consequence, it is not possible to predict the evolution of the system by studying the fundamental laws ruling its components. Instead, it is necessary to understand how the system works as a whole. This objective requires a higher physical-mathematical effort. In this view, the essence of phenomena featured by completely different behaviors depending on the spatial and temporal scale at which they are observed from cannot be abridged into a single formula, and even devising a comprehensive framework to describe them can be extraordinarily difficult or almost impossible [24]. The same physical system can appear different according to the scale at which it is investigated [25]. In the case of earthquakes, a clear split exists among theoretical and statistical seismology and tectonics. Even though they investigate the same subject, differences are so deep that they can be put in relation with each other not without a significant effort [26, 27]. Classical seismology explains what happens during a few seconds of fault slip following rock breakdown, with the consequent radiation of seismic waves, while statistical seismology describes how seismicity occurs in space and time. On the other hand, seismic sequences follow the rules of statistical seismology, mainly grounded on two fundamental mathematical power–law frequency-size distributions, the so-called Gutenberg–Richter and Omori–Utsu laws, respectively describing the frequency of seismic events as a function of their magnitudes and the temporal attenuation of seismic activity with time after a mainshock [28,29,30,31]. In our article, we review some significant results in geodynamics and earthquake geology following the thread of gradients shaping our planet; a wide discussion is realized to compare models and observations, describing successes, but also underlying inconsistencies, paying great attention to open questions and lively scientific debates. The final picture outlined by our path in Earth dynamics is still confused, riddled with several unsolved issues and puzzling brain-teasers soliciting scientific community to persevere in doing research all-round.

2 Observing the Earth

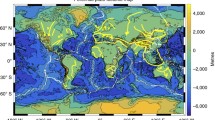
In recent decades, planetary observation techniques have made incredible strides. Since the first satellite navigation system, Transit, set up by the American army in the Sixties, several facilities have been developed for civil and scientific applications. At first, regional monitoring systems were realized; later in time some of them have been gradually enlarged to achieve a global coverage. They are referred as Global Navigation Satellite Systems (GNSS). Nowadays, four global navigation networks are at work: the U.S. Global Positioning System (GPS) satellite constellation now joined by the European monitoring network Galileo, the Russian GLONASS and the Chinese BDS. Satellite data allow horizontal ground motions to be resolved with millimeter accuracy. The thousands of stations scattered on the planet allow to have a clear definition of the speed with which Earth plates move with respect to each other [32], reaching 15 cm per year of opening of the Southern Pacific Oceanic Ridge. For instance, in Italy, convergence movements in the Alps are about 2 mm/year, while in the Apennines, the ridge is extending about 4–5 mm/year, with a convergence sector on the Po-Adriatic-Ionian side of about 2–3 mm/year [33]. Vertical movements are also recorded, but error-bars are larger than for horizontal displacements, usually in the order of centimeters for rapid motions, while positions averaged over longer time intervals can be resolved with accuracy comparable to the horizontal ones, even though stress sources affecting vertical land motion, e.g. anthropic, thermal, tidal and hydrological loading, make it intrinsically noisier (e.g., [34, 35]). Based on the GNSS network, time series are also used for realizing strain rate maps that show regional variations controlled by variable crustal coupling and the time-dependent seismic cycles [36]. High resolution observations can also be achieved using Very Long Baseline Interferometry (VLBI), using the differences in arrival of radio signals from quasars at different telescopes located on the Earth surface. VLBI has been fundamental in the development of models for relative plate motions [37]. The InSAR (Interferometric synthetic-aperture radar) technology is also now well established. Thanks to the electromagnetic pulses sent to earth by satellites of space agencies around the world (Alos, Sentinel, Cosmo-Skymed, etc.) it allows to calculate the vertical movements of the ground with the precision of millimeters. This technique allows to evaluate subsidence or ground uplift in seismically active areas, the swelling of volcanoes, the activation of landslides, the extraction of water or hydrocarbons from the subsoil. It is now a technique with endless applications that provides extremely precise monitoring of ground movements. Persistent Scatterer Interferometry (PSI), a specific class of the Differential Interferometric Synthetic Aperture Radar (DInSAR) techniques, is featured by a resolution with the order of millimeters also for the monitoring of slow deformation processes (its uncertainty ranges in $\sigma _{vel} \sim$ 0.5 mm/year for deformation velocity and $\sigma _{dis} \sim$ 1–4 mm for displacements [38]). Because of its outstanding accuracy, PSI-InSAR is broadly applied to several different issues such as urban growth monitoring [39], hydro-geological risk evaluation (e.g., [40, 41]), volcano deformation measures [42] and reservoir analysis [43]. These techniques are essential for studying of the Earth’s shape and movements of the crust in order to better understand geodynamics and tectonic processes. Gravimetric data collected by Grace (Gravity Recovery and Climate Experiment) and Goce (Gravity Field and Steady-state Ocean Circulation Explorer) satellites [44,45,46], as well as continuous superconducting gravimeter time series [47] and Lidar (Light Detection and Ranging) techniques that use light in the form of laser pulses in the ultraviolet, visible and infrared spectra to determine shape of the Earth and surface motions (e.g., [48,49,50]) are key for monitoring Earth surface evolution. Despite the large number of techniques available for direct observation of the Earth, great part of the aspects of surface dynamics are not directly attributable to exogenous phenomena. Therefore, it is necessary to understand what are the chemical and physical conditions acting inside the planet. Thermal anomaly investigations made using IR-satellite sensors allow the detection of minimal variations in soil temperature with multiple applications ranging from geothermal monitoring to the detection of temperature variations linked to seismic and volcanic processes [51,52,53]. The study of orientation and intensity of the Earth’s magnetic field in space and time has for decades offered valuable information about the physico-chemical properties of the Earth interior also furnishing chronological constraints to geological processes. Iron content, chemical composition, electrical conductivity, magnetic permeability and the mobility of masses at depth are examples of properties which can be investigated on the light of geomagnetism. The detection of magnetic anomalies at mid-ocean ridges was the first geophysical proof of active plate tectonic on the Earth. More recently, the anomalies of the electromagnetic field have been investigated as possible precursors to seismic events of moderate and large magnitude (e.g., [54, 55]), even if contrasting results have been achieved [56], this field of research is still very active and it is likely that with the enhancement of observation techniques, processing and analysis of electromagnetic signals, results of great interest will be obtained in the next future [57]. However, these are precursors identified a posteriori and not supported by statistical validations. This drawback affects not only the electromagnetic precursors, but many other precursors, always identified a posteriori and never before an event of specified location, size and occurrence time. The most important sources of information about the internal layers of the Earth are seismic waves. Reflection and refraction seismology is the base of seismic interpretation. It allows reservoir identification, discontinuity localization and also fosters our understanding of the geological history of crustal volumes grounding on seismic sections. Since the seminal paper published by Aki and Lee in 1976 [58], seismic tomography has been a fundamental tool for sketching the internal physical conditions of our planet. It also suggested several ideas and allowed to set up a certain number of models now milestones in the history of Earth Sciences (e.g., fully convecting mantle and mantle plumes [59]). Seismic tomography also allowed numerous hypotheses and geodynamic models to thrive (e.g., [60,61,62,63]), although often accompanied by a lively debate within the scientific community [64, 65]. Sources of doubt and contrasting results stem directly from the nature itself of this physical and computational tool: seismic tomography is a technique of imaging applied for the solution of a large class of inverse problems and too often it is presented as grounded on reliable data, whereas relative tomography is a 1D model dependent adopted by the author’s choice. This is a serious bias which can partially be removed using absolute rather relative mantle tomography (e.g., [66]). While we can predict the outcome of some measurements with a certain degree of belief that our solution is correct once we had got a satisfactory knowledge of our physical system using a model, i.e., addressing a forward problem, inverse problems retrieve some parameters of interest via statistical inference applied to available measures. The crux of the matter is that while forward problems have unique solutions, inverse problems do not and both prior knowledge and likelihood play a key role [67]. Moreover, few parameters such as shear modulus, viscosity etc. may show non-linear behavior ([68,69,70,71] and references therein). Given the output of measurements collected via seismic ray-paths acquisition

$$\begin{aligned} {{\textbf {D}}} = \{D_{1}, D_{2}, \ldots , D_{n}\} \end{aligned}$$

(2)

the probability that a certain set of parameters ${{\textbf {A}}} = \{a_{1}, a_{2}, \ldots , a_{m}\}$ describing the physical conditions of the internal Earth (e.g., density, temperature, shear modulus etc.) associated with a certain combination of prior information $\rho _{{{\textbf {m}}}}$, acquired data $\rho _{{{\textbf {D}}}}$ and theoretical modeling density function $\rho _{T}$ with respect to a homogeneous state of knowledge $\mu ({{\textbf {D}}})$ reads

$$\begin{aligned} P(A) = \int _{A} dm ~k ~\rho _{m}(m) \int _{{{\textbf {D}}}} d{{\textbf {D}}} ~\frac{\rho _{D}({{\textbf {D}}})\rho _{T}({{\textbf {D}}}\arrowvert m)}{\mu ({{\textbf {D}}})} \end{aligned}$$

(3)

where k is a constant; so that, repeating measures until a sufficiently dense data array is available, the most probable spatial distribution of the wave-attenuation coefficient within the investigated volume is obtained through minimization of the least-squared misfit function

$$\begin{aligned} S(m) = dist(m; D, D_{O}, m_{prior}) \sim \arrowvert \arrowvert D-D_{O}\arrowvert \arrowvert ^{2} + \arrowvert \arrowvert m-m_{prior}\arrowvert \arrowvert ^{2} \end{aligned}$$

(4)

evaluating the distance in the space of probability between observations and what is expected by the model via parameters estimation. Since no direct access to the inner layers of Earth is possible and models must be based on simplified hypotheses and limited observations, it is not surprising that different and sometimes conflicting interpretations can be given starting from the same dataset [71]. Even though powerful, seismic tomography suffers from sparse seismic ray coverage strongly limiting spatial resolution and affecting large-scale interpretation of cross-sections [72]; moreover, the role of data visualization is really crucial producing different interpretations according to the scale and cut-off used for representation. In addiction, inversion methods cannot be completely corrected for some effects such as seismic anisotropy and seismic wave velocity changes produced by local lithological and mineralogical variations, partial melting [73] and temperature anomalies. Tomographic images cannot be interpreted but assuming simple correlations among density, temperature and velocity of seismic waves indeed

$$\begin{aligned} {\left\{ \begin{array}{ll} v_{p} = \sqrt{\frac{\lambda (T,P) + 2\mu (T,P)}{\rho (T,P)}} \\ v_{s} = \sqrt{\frac{\mu (T,P)}{\rho (T,P)}} \end{array}\right. } \end{aligned}$$

(5)

where $\rho$ is the density of the medium, $\mu$ is the shear modulus and $\lambda$ is the first Lame’s coefficient, with the linearized dependence of the elastic moduli on temperature and pressure that can be written as [74]

$$\begin{aligned} \mu (T,P) = \mu _{0}\left[ 1-\left( \frac{T-T_{0}}{\mu _{0}}\right) \frac{\partial \mu }{\partial T} + \left( \frac{P-P_{0}}{\mu _{0}}\right) \frac{\partial \mu }{\partial P}\right] \end{aligned}$$

(6)

for instance in the case of the shear modulus, while the density dependence on temperature and pressure reads

$$\begin{aligned} \rho (T,P) = \rho _{0} e^{(\beta (P-P_{0} ) - \alpha (T - T_{0}))} \end{aligned}$$

(7)

where $\alpha$ and $\beta$, representing the thermal and pressure expansion coefficients respectively, are assumed to be approximately constant. Of course, the latter assumption is not realistic since great part of minerals and rocks exhibit significant changes of expansions coefficients as physical conditions vary [75]. Hence, elevated wave velocity is usually attributed to denser and colder rocks, while slower ray paths are ascribed to hotter, relatively buoyant material. However, the complex patterns of physical and geo-chemical properties at work inside the Earth and the huge variability of results as a function of data density acquisition, processing and analysis strongly suggest to correlate each result provided by seismic tomography with other investigations and techniques [76]. Recently, artificial intelligence has burst into the world of Earth sciences with dramatic improvement of seismic data acquisition [77] and geodetic signal resolution [78], while its effective power to push forward our comprehension and ability to predict still poorly understood phenomena such as earthquake remains uncertain [79, 80] with contrasting and sometimes indefensible results [81, 82], even though successful and promising outcomes were obtained in laboratory experiments [83] and in peculiar tectonic settings [84]. Some average physical properties derived from seismic waves velocity as a function of depth are shown in Fig. 1. These are clearly 1D average values and significant deviations can be expected.

Fig. 1

Average physical properties derived from seismic waves velocity as a function of depth in the crust and in the mantle. Seismic waves velocity data from [85], STW105 reference model (2008)

3 An overview on the structure and dynamics of the shallow Earth

The lithosphere is the outer shell of the Earth with an average thickness of about 100 km (varying between 30–250 km) and consists of the Earth’s crust and the lithospheric mantle. The crust represents the lightest chemical differentiate of the Earth and can be continental or oceanic, with average thicknesses of 30–40 km and 3–10 km respectively. The thickness of continental crust is larger in orogenic tectonic provinces (43 km on average, but it can be up to 80 km) and basins (44 km), while lower values are observed in forearcs (29 km), arcs (33 km) and large igneous provinces (35 km) [86]. Continental and oceanic crust also differ from each other in their chemical and physical properties. Oceanic crust is formed by unconsolidated or partially consolidated sediments ($\rho \sim$ 1.1–2.7 g/cm$^{3}$) in the upper layer 0.2–0.8 km thick on average, they are almost absent at ocean ridges; below them there are basalts ($\rho \sim$ 2.8–2.9 g/cm$^3$), gabbro ($\rho \sim$ 2.9 g/cm$^{3}$) and ultramafic rocks at the interface with the upper mantle (e.g., peridotites $\rho \sim$ 3.3–3.4 g/cm$^{3}$), so that the average density of the oceanic crust is $\rho \sim$ 3.0 g/cm$^{3}$. On the other hand, continental crust is rich in silicates (about 57$\%$ by weight) and aluminium (about 16$\%$) [87] organized in felsic rocks, e.g., granite, granodiorite and diorite, with a density $\rho \sim$ 2.6–2.9 g/cm$^{3}$). The crust has an average thermal gradient of about 30$^{\circ }$C/km in the first about 10 km, then decreases to 15$^{\circ }$C/km and 8$^{\circ }$C/km in the upper and lower crust respectively. The Moho, i.e., the boundary between crust and mantle, has an estimated temperature ranging from 450$^{\circ }$C to 700$^{\circ }$C [88]. The lithosphere has a temperature of about 1300$^{\circ }$C at its base and rests on what is called the asthenosphere (weak sphere, because of its low viscosity due to rocks with weak plastic rheology). The lithospheric mantle mainly consists of harzburgites and lherzolites, ultrafemic rocks composed of olivine (about 51$\%$), pyroxenes (about 26$\%$ orthopyroxene and 11$\%$ clinopyroxene) and other minor components such as garnet ($\sim$ 9$\%$) [89]. In the underlying mantle up to 2890 km, the thermal gradient is less than 1$^{\circ }$C/km. At the center of the Earth, the estimated maximum temperature is about 6000$^{\circ }$C. The asthenosphere ranges from about 100 to 410 km in depth and between 100–180 km, it is characterized by a relative lowering of seismic wave velocity [90] because of partial melting of the hosted material. For this reason, this layer is called the “low velocity channel” or “low velocity zone” (LVZ). The same stratification just described for crustal layers also occurs in the mantle according to the intrinsic density of minerals and rocks. Of course, mass transfer continuously homogenizes the mantle; however, effective homogeneity can be reached only if the variations of intrinsic density are not too large ($\le$ 3$\%$), but it is not the case: in between the free surface and the bottom of the upper mantle, located about 650 km at depth, density ranges in between 2.7 and 4.1 g/cm$^{3}$ [91] (Fig. 2).

Fig. 2

Schematic stratigraphy of the upper mantle, showing the density increase moving downward. Therefore, the lithosphere is lighter than the underlying mantle, preventing the slab pull as a possible mechanism of subduction activation. Therefore, the hypothesis of the slab pull as being the driving mechanism of plate motions cannot be valid [92]

Mantle stratification is clearly proven also by multiple discontinuities identified via seismic reflection. Systematic researches yielded to localize the most important phase changes in the mantle at about 220, 260, 410, 520, 660 and 800 km [93], while low-velocity zones and ultra-low velocity zones have been highlighted during regional campaigns at 180, 380, 450, 580 and 720 km at depth [94, 95]. The latter are due to partial melting, temperature increasing or rock hydration. However, the largest and most spread changes in density also producing seismic waves velocity variations are due to chemical and physical transitions within the mantle and not to temperature swings, which accounts for significant lateral heterogeneities in the mantle.

Physico-chemical changes are also responsible for the large variability of several physical parameters within the crust and the upper mantle. Among them, viscosity $\eta$ plays a key role for geodynamics and tectonic processes mainly controlling the timescale transition between elastic and viscous rheology through the relation with the Maxwell’s time $\tau _{M}$ and rigidity $\mu$

$$\begin{aligned} \tau _{M} = \frac{\eta }{\mu }. \end{aligned}$$

(8)

Classical estimation of viscosity values gives $\eta \approx$ 10$^{23-24}$ Pa s for the upper crust, $\eta \approx$ 10$^{18-19}$ Pa s for dry-harzburgitic and upper oceanic mantle [18], $\eta \approx$ 10$^{16-18}$ Pa s for melt or water weakened interfaces, $\eta \approx$ 10$^{15-18}$ Pa s for LVZ [96, 97] and $\eta \approx$ 10$^{19-20}$ Pa s for olivine-rich mantle in between 220 and 410 km at depth [98]. Compare with Fig. 3.

Fig. 3

Main nomenclature and parameters of the Earth’s upper 450 km after [99] and references therein. Azimuthal data are the root mean square of relative azimuthal anisotropy amplitude of elastic parameters. Gray bands tentatively indicate the potential variability. The lithosphere and the seismic lid are underlain by aligned melt accumulations (LLAMA), a low-velocity anisotropic layer (LVZ) that extends from the Gutenberg (G) to the Lehmann discontinuity (L). The amount of melt in the global LVZ is too small to explain seismic wave speeds and anisotropy unless the temperature is $\sim$200 K in excess of mid-ocean ridge basalt (MORB) temperatures, about the same excess as required to explain Hawaiian tholeiites and oceanic heat flow. This suggests that within-plate volcanoes are sampling ambient (local) boundary-layer mantle. The lowest wavespeeds and the highest-temperature magmas are associated with the well-known thermal overshoot. The most likely place to find magmas hotter than MORB is at this depth under mature plates, rather than in the subadiabatic interior. Most of the delay and lateral variability of teleseismic travel times occur in the upper 220 km. If this plus anisotropy is ignored, the result in relative tomography can be a plume-like artifact in the deep mantle. M Moho, OIB ocean-island basalt, LID lithospheric mantle

However, a large variability exists; moreover, a majority of viscosity measures are made using the mechanical response to vertical loading [100] or inversion techniques affected by the same troubles of seismic tomography, therefore their outputs must be taken with a grain of salt. Shear viscosity has been recently estimated by post-seismic relaxation geodetic time series, e.g., [101]. Even though promising, several phenomena cannot be included yet in the inversion algorithms in order to get a reliable estimation of viscosity, e.g., friction between subducting slabs and eclogitic crust, time dependent rheology due to temperature variation induced by seismic slip, melted fraction etc [102,103,104,105]. The role of melting is crucial because of its link with magmatism. Magmas are like windows into the lithosphere and mantle indeed, able to provide fundamental information about their formation, e.g., depth, and evolution processes. Various kinds of magma exist:

• Mid-ocean ridge basalts (MORB) are the most voluminous. They are homogeneous and fluid because of their basic chemical composition;

• Ocean-island basalts (OIB) are similar to MORBs except from their isotope ratios (e.g., (Rb/Sr)$_{MORB} \approx$ 0.007, (K/Rb)$_{MORB} \approx$ 1500, (Sm/Nd)$_{MORB} \approx$ 0.5, while (Rb/Sr)$_{OIB} \approx$ 0.04, (K/Rb)$_{OIB} \approx$ 500, (Sm/Nd)$_{OIB} \approx$ 0.25 [106]);

• Rhyolites are common on the continents and continental margins and also associated with the so-called large igneous provinces (LIP). Silicic magmatism is strongly affected by water content and on the composition of the crust besides the melted fraction of material;

• BB basin magmas, e.g., back-arc basin basalts (BABB);

• Island-arc basalt (IAB) are common in hot spots.

The spatial organization of depleted and enriched mantle zones, e.g., EMORBs and DMORBs, plays a key role in mass transfer within the mantle and the upper lithosphere. Materials move according to the buoyancy principle; therefore, deep masses can climb up because of melting formation due to a strong thermal gradient or adiabatic conditions, convective transport or via heat transfer by conduction. At last, Earth surface is riddled with dozens of regions featured by an excess of volcanism and anomalously thick crust. These areas, also associated with islands are usually called hot-spots. About fifty regions have been suggested to be hot spots, although with different likelihoods [107]; they are clustered around Africa [108], in Southern Pacific Ocean and along the Western American coasts, while other sparse hot spots are located in Iceland [109], Hawaii, Reunion [110] and off the eastern coast of Australia. Investigations via seismic tomography allow to localize low velocity zones below hot spots down to 250–350 km, while deeper magma sources are not certain and contrasting results have been published [111,112,113,114]. Geochemical magma analyses suggest that almost all the mass transfer stems from intra-asthenospheric wells [115, 116]. In this regard, two opposite models have been proposed so far: mantle plume hypothesis [117] suggests that diapirs rising from the lower mantle reach the surface because of a strong thermal anomaly; conversely, plate hypothesis of hot spot volcanism [118] claims that a combination of crustal weakness and geochemical anomalies produce passive magma rising starting from shallower depths. The latter model is strongly supported by geothermal analyses suggesting no significant temperature difference between normal mid-ocean ridges and hot spots; moreover, water-richer mantle domains have been positively correlated with hot spot locations, e.g., [119]. Therefore, lower melting temperature of the mantle was suggested to reconcile the higher degree of melting at hot spots (wet spots) with the lack of temperature anomaly [120].

4 Paths in large-scale geodynamics: observations and evidences

4.1 Mantle motions

The classical paradigm of mantle homogeneity is grounded on geo-chemical and geophysical observations and on a few assumptions belonging to the framework of thermal driven plate tectonics. The common assumption is that large part of the upper mantle can be approximately described on the light of a homogeneous depleted olivine-rich lithology similar to pyrolite [121]. In such models, absolute temperature gradients are claimed to induce the largest density variations controlling geochemical transitions and geodynamics [122]. Therefore, no lithologic diversity is supposed at a first step. According to this viewpoint, mantle homogeneity is a satisfactory approximation of reality thanks to permanently active convection involving both upper and lower mantle at both relatively small and large spatial scales; the effect of material circulation due to thermal-driven buoyancy is suggested to be sufficient to remove mantle vertical stratification. Uniform chemical composition of MORBS has been advocated as a proof of mantle homogeneity [123] and also the square-root-like trend of bathymetric profiles, d(t) , as a function of time t from basalt ejection at mid-ocean ridges [124]

$$\begin{aligned} d(t) \sim d(0) + \frac{2\alpha \rho T_{m}}{\sqrt{\pi }(\rho _{m} -\rho _{w})}\sqrt{\kappa t} \end{aligned}$$

(9)

is thought to be coherent with a dominant role of temperature gradient in outlining spatial density variations within the mantle. In the previous formula $\kappa$ is the thermal conductivity of the ocean crust, $\rho _{m}$ is the density of the upper mantle, $\rho _{w}$ is the density of sea water and $\alpha$ is the thermal expansion coefficient of the oceanic lithosphere. Nevertheless, reflection and refraction seismology, seismic tomography and other geo-chemical analyses tell an other story: the mantle is affected by strong lateral heterogeneity [125,126,127,128], which is proven by the different composition of magma sources, for instance, in terms of fertility [129, 130], i.e., basalt-eclogite and plagioclase content, and enrichment, i.e., isotope ratio values [131] (compare with the previous paragraph). Vertical physical and chemical mantle stratification is even more considerable at large scales: lherzolites and harzburgites accumulate just below the oceanic crust because of buoyancy. A monotonic, although not uniform density increase is observed going downward into both the upper and lower mantle, except for a thin layer located at the level of the low-velocity zone. Seismic reflectors and high-resolution seismic tomography, despite of their limitations, clearly show heterogeneities occurring at all spatial scales; seismic reflectors and ultra-low velocity zones highlight structural solid-solid or physical transitions within the mantle occurring all over the planet, even though at slightly different depth, depending on local crustal properties and on the geological history of the tectonic setting [132]. Mantle heterogeneity has played a key role in the history of the Earth, with extraordinary impact on geodynamics and planetary evolution [133]. Of course, thermal condition deeply affects mechanical stability, but its role should not be considered dominant on physical and chemical variations neither at local scales nor at global ones. It is now beneficial going a little deeper into the relationship between thermal and mechanical gradients to better understand mantle motions. Convection is enhanced by inverse density gradients in a gravitational field; if temperature is mainly responsible for compaction or expansion of materials, then a temperature gradient exists at which mechanical instability is produced. Such thermal gradient is the so-called adiabatic profile of the system. Along the adiabatic transformation path, energy is transferred without heat flow, so that the entire balance is due to mechanical work, e.g., volumetric expansion. During transportation in locally adiabatic conditions a mass sample undergoes a density change approximately equal to

$$\begin{aligned} \Delta \rho \approx \frac{d< P({{\textbf {x}}},t)>}{dx}\delta x \left( \left( \frac{\partial \rho }{\partial P}\right) _{S(t=0)} - \frac{d}{d< P({{\textbf {x}}},t)>}< \rho ({{\textbf {x}}},t)>\right) \end{aligned}$$

(10)

where $\delta x$ is taken positive as the displacement is directed along the increasing pressure gradient, otherwise it is negative. This result is due to the combined effect of local and average density gradients represented by the first and second term in the formula respectively. If $\Delta \rho$ has the same sign of $\delta x$, then the system is locally stable; conversely, it is not, and convection may occur. Local instability is not enough to allow convection, also rheological properties matter: elevated viscosity and thermal diffusivity suppress flow. The adimensional quantity marking the transition between convection and conduction dominant heat transfer is the celebrated Rayleigh number [134]. It depends on the size of the system, their thermal and mechanical properties and also on the source of density gradient. In the mantle, there are several sources of density gradients, i.e., heating from inner hotter layers, heating from radionuclide activity and geochemical structural transitions among the most important. Rayleigh numbers can be explicitly calculated assuming geochemical mantle homogeneity. For the first and the second contributions they read [122]

$$\begin{aligned} Ra_{ihl} = \frac{< \rho ({{\textbf {x}}})> g \alpha \Delta T d^{3}}{\nu \kappa } \end{aligned}$$

(11)

in the first case and

$$\begin{aligned} Ra_{r} = \frac{< \rho ^{2}({{\textbf {x}}})> g \alpha {\mathcal {P}}\Delta T d^{5}}{\nu \kappa } \end{aligned}$$

(12)

in the second, where d is the vertical distance between the boundaries kept at a thermal gradient $\Delta T$; ${\mathcal {P}}$ is the density of heat generation by internal radioactivity and $< \rho >$ is the average mantle density. The critical values of the Rayleigh numbers are $\approx$ 10$^{3}$, while the estimated values for the mantle range in between 10$^{6}$ and 10$^{8}$ [135]. Based on these results, forceful convection should be observed inside a completely homogenized mantle. However, mantle stratification is a matter of fact and the day has yet to come that a comfortable theory can prove reality is wrong. Fact-checking is key in science. The obvious contradiction between layered mantle and huge estimated Rayleigh numbers can be solved by performing a critical review of the assumptions [122] applied in the calculations. Equations 11 and 12 are obtained under the Boussinesq approximation for horizontal flow components, i.e., no lateral heterogeneity is considered, a perturbative expansion is performed along the vertical ones ($\Delta \rho \ll < \rho >$), geochemical transitions and geophysical ones (e.g., partial melting) are ignored, so that the whole mantle can be included within the same convective framework. Not one of the previous approximation can be considered valid. Lateral homogeneity is disproved by common seismic tomography investigation (e.g., [136]), while perturbative analysis requires $\frac{\Delta \rho }{< \rho >} \le 10^{-3}$ while it is of the same order of magnitude of the average mantle density ($< \rho > \simeq$ 4 g/cm$^{3}$ and $\Delta \rho \approx$ 2 g/cm$^{3}$). Moreover, reflection seismology clearly highlights seismic reflectors associated with vertical density increase with depth whose gradient is larger than the thermal one by far [137]. Since the Rayleigh numbers strongly depend on the thickness of the system, d, through a power relationship with exponent three or five according to the thermal source, intrinsic stratification greatly affects thermal stability of the mantle. At last, further objections could be added to the effective meaning of the Rayleigh number in a system such as Earth’s mantle (e.g., [138]). More realistic calculations of the Rayleigh numbers give $\sim 10^{3}$ [91]. However, analytical calculations are not very reliable, therefore other independent investigations must be considered. Nowadays, numerical simulations based on real geophysical and geochemical data allow to realize a plot of the average radial trend of the potential temperature inside the mantle. Results are in good agreement with the realistic estimations of the aforementioned Rayleigh numbers: the potential temperature profile turns out to be sub-adiabatic or adiabatic almost everywhere in the mantle [139,140,141,142,143]. Marked sub-adiabaticity is found in the lower layers, while the upper ones are slightly sub-adiabatic between 450 and 800 km of depth; only asthenosphere is clearly super-adiabatic. Hence, the upper mantle undergoes layered thermal convection, while it is likely the lower mantle does not. So far the effectiveness of thermal convection has been discussed; nonetheless, not a word was written about how convection happens. The Reynolds number, Re, represents the relationship of strength between inertial and viscous forces. For the mantle $Re \ll 1$; therefore, turbulence is not expected to occur and the mantle flow can be considered laminar [122]. At last, the Richardson number defined as the ratio between the buoyancy forces at work and the plastic shear

$$\begin{aligned} Ri = \frac{g\alpha \Delta T d}{v^{2}} \end{aligned}$$

(13)

marks the transition between free ($Ri > 1$) and forced ($Ri < 1$) convection. v represents the typical velocity of mass flow. In the case of Earth’s mantle, $Ri \gg 1$; therefore, where it takes place, convection occurs spontaneously. Based on considerations similar to those briefly discussed above, a flurry of models for mantle motions have been proposed so far. A rough classification can be done according to two main assumptions, i.e., degree and impact of heterogeneity on mantle dynamics and spatial extension of convection [144]. If mantle heterogeneity is assumed to be negligible because of intense mass flow due to the action of thermal gradients, then full-mantle convection is possible with huge transfer of material from the top to bottom and other way round, with significant implications on plate tectonics with slab subduction extended down to the core-mantle boundary. Mantle plume geodynamic models and single-convective-cell simulations are grounded on the previous hypotheses [59, 145, 146]. However, both the aforementioned classical and recent observations partially contradict them. Conversely, if mantle heterogeneity is considered, only layered convection is possible in the upper mantle, while at larger depths heat conduction is dominant [147, 148] and convection plays a minor role. In this view, thin vertical plumes should exist, even though debate on this issue is still open [149, 150], and the geodynamic impact of thermal gradient is rather reduced with respect to other models [151]. The thermal component of slab-pull forces acting on lithosphere is also radically abated (compare with paragraph 6.2), so that solid-solid transitions turn out to have a relevant rule. Consequently, two types of convection are attached to this model, namely that in which convection is due to the upwelling of the hot mantle [152] (henceforth, bottom up) or that with mantle motions dictated by the gravitational fall downward of cold lithosphere slabs [153] (top down). In summary, several convective models present inconsistencies with surface observables: the most important is that the mantle is strongly stratified with an increase in density and viscosity downward, inhibiting or slowing down convection in the lower mantle which is moreover estimated to have a sub-adiabatic potential temperature, inhibiting convection. Convection in the mantle must exist regardless, in the sense that material goes up along the ridges and lithospheric mantle goes down along the subduction zones, but mantle dynamics and kinematics are still to be deciphered. The super-adiabaticity of the asthenosphere lead to the assumption that this is the level of maximum convection, particularly in its upper part (LVZ), which should represent the plane of detachment of the overlying lithosphere.

4.2 Plate motions

Plate motions modeling and dynamics are evergreen subjects in Earth sciences. Recently, remote sensing techniques available for geodynamic observations have dramatically improved their resolution and precision with outstanding implications for the comprehension of those mechanisms driving the dynamics of lithosphere (compare with Sect. 2). Plate motions can be conveyed using different reference frames according to the purpose of our investigation. Relative plate motion describes how different crustal elements move with respect to each other assuming a zero average velocity with respect to the hypothetical center of mass of the Earth, i.e., assuming the sum of all the available displacement rate vectors is identically zero at each time. This hypothesis is the so-called no-net-rotation (NNR): it is at the base of the International Terrestrial Reference Frame [154]. GPS technology, VLBI and SLR (satellite laser ranging) also work grounded on it. Earth’s surface is divided into several plates. Each plate represents a portion of lithosphere rigidly shifting on the asthenosphere so that internal displacements are considered to be residual and not connected to separation, e.g., orogenic processes, volcano deformations. Since a precise definition of plate boundaries is missing, the number, area and features of tectonic plates have changed in time and no unique model exists so far. In our discussions, we refer to [155]. The surface A of plates is power law distributed [156] according to the relation [155]

$$\begin{aligned} N(\ge A) \approx cA^{-1/3} \end{aligned}$$

(14)

where $c \sim$ 7 and $N(\ge A)$ represents the cumulative number of plates with an area A expressed in steradians. It suggests that a self-organized process drives stress accommodation inside the lithosphere and crustal fragmentation [157]. Such a distribution also implies that no external cause, e.g., drag by mantle convection, is needed to explain the observed spatial subdivision of the Earth’s crust [29, 158]. Therefore, no direct connection exists between endogenous processes and spatial organization of the crust, mainly controlled by plate-plate interaction and other local phenomena due to lateral variations of physical and chemical properties of the shallow Earth. The largest is the Pacific plate. It is surrounded by a westerly-directed subduction zone recycling 30–90 mm/year of oceanic crust for more than one half of the Pacific perimeter separating it from the Eurasian, Philippine, Australian and North American plates, while the East Pacific Ridge spreads on the eastern borders at variable velocities ranging from about 55 mm/year in the southern part along the Antarctic plate up to 160 mm/year near the Easter Island hot spot besides the Nazca plate. The Pacific plate is made up of 5–15 km thick oceanic crust riddled with NW-SE oriented volcanic archipelagos and rests of basalt floods in the south-western area (Micronesia and Polynesia archipelagos, Ontong-Java plateau). Transcurrent seismogenic zones, such as the San Andreas fault, accommodate stress in the westernmost part of the plate at about 30$^{\circ }$ N. The North and South American plates are delimited by the West Pacific Subduction converging at about 60 mm/year below Mexico and 77–85 mm/year along the Peru-Chile Trench, while the Cocos plate undergoes subduction below the Caribbean plate with a relative velocity of 90 mm/year, and the Mid-Atlantic Ridge. Its spreading rate ranges in between 12 and 36 mm/year increasing from the Poles to the Equator Line. The Eurasian plate strongly interacts with the Australian one along a convergent border (subduction speed 65–80 mm/year) and the Indian plate that moves to north causing the elevation of the Himalayan belt. The average slip rate of the Himalayan Thrust is about 46 mm/year. At last, the African plate is actually undergoing complex interactions between different lithospheric regions moving at non-negligible relative velocity such as the Arabian, Madacascar, Nubia, Somali and Victoria plates which are involved in the spreading of the East African Ridge [159]. According to simulations and modeling, the past plate movements roughly coincide with present-day directions of motion just described above, at least for the last 45 millions of years [160,161,162]. However, relative plate motions provide poor information for understanding geodynamics. Absolute plate motion is the attempt to overcome the NNR-hypothesis, which ultimately means modeling how the lithosphere moves with respect to the underlying mantle. The lack of fixed reference frameworks with respect to the deep Earth allowed a series of different models to thrive basing on different hypotheses. Hot-spot reference frames assume stationary and vertical rising of magma from the bottom of the mantle so that its surface manifestations can be considered as a good candidate for referencing. Even though with slightly differences, hot spot models show that almost all the plates move westward. The highest velocity is reached by the Pacific plate (in HS3-NUVEL1A (1.06 ± 0.04)$^{\circ }$/Myr) followed by the Australian and Indian plates; slower displacement rates are observed for the African, Eurasian and American plates while Nazca and Cocos move eastward. The average west-ward drift defined as [163]

$$\begin{aligned} \omega = \frac{3}{8 \pi r^{4}}\sum _{i}^{}\int _{S_{i}}[(\omega _{i} \times r)\times r] dS_{i} \end{aligned}$$

(15)

where the sum is made over all the plates and the integral is applied to the surface of each plate, $\omega _{i}$ is the angular velocity of the i-th plate with respect to its rotation poles and r is the position vector ranges in between $\omega =$ (0.14 ± 0.03)$^{\circ }$/Myr [163] and $\omega =$ (0.44 ± 0.05)$^{\circ }$/Myr [164], which means an average westward drift of about 1–3 cm/year. Therefore, when measuring plate motions relative to the hot spots or even relative to Antarctica, plates have a mean “westerly” directed component [165] with only a few crustal elements showing significant eastward motions, i.e., Nazca and Cocos plates. However, hot spot reference frames are not absolute at all. The main proof of this is that hot spots are not fixed with respect to each other [166, 167]; moreover, geochemical and seismological analyses show their raising magma is of intra-asthenospheric origin in several cases [116, 118, 168,169,170,171]. Such evidences fostered researchers to modify the previous assumption of hot spots fixity using other geophysical observations. The seismic anisotropy in the upper mantle [172] indicates seismic waves travel faster along the trend of motion of plates because of the statistical alignment of crystals which tend to be oriented along the shearing direction. The measure of the seismic anisotropy is obviously affected by some uncertainties like any other indirect physical quantification. The seismic anisotropy can be interpreted in the light of partial decoupling occurring between the lithosphere and the underlying asthenospheric mantle between the upper mantle and the crust principally through the LVZ, atop the astenosphere, featured by weak rheology. The decoupling at the lithosphere-asthenosphere boundary (LAB) is inferred to occur between 100–180 km deep, where the shear waves are slower and the viscosity can be lower [173]. This layer can also be considered as the source location of magma pouring the surface hotspots [99], being the bases of the so-called shallow hot spots reference frame [174, 175] which proposes to add a further angular velocity to those of the “deep” hotspot reference frame in order to take into account of the relative motions of hot spots mainly depending on their magma source depth. The additional velocity vector is oriented along the principal direction of the upper mantle seismic anisotropy and westerly directed, so that the total drift of the lithosphere may be even larger than in the classical hot spots reference frame, up to $\sim$ 1.49$^{\circ }$/Myr. In this reference frame, the whole crust moves to west with respect to the underlying mantle, the Nazca plate also has its velocity coherently oriented with others with $\omega _{N} =$ 0.78$^{\circ }$/Myr [175] (Fig. 4).

Fig. 4

Plate kinematics computed assuming a hot spot reference frame “anchored” in the asthenosphere, i.e., within the decoupling zone. Note that the faster decoupling and “westward” drift of the lithosphere ($\ge$1$^{\circ }$/My.) occurs if the volcanic tracks are fed from a depth of $\sim$150 km (A), within the low-velocity zone (LVZ), because the superficial age-progressive volcanic track does not record the entire decoupling between lithosphere and the mantle beneath the LVZ. The two deeper depths of magmatic sources at 200 and 225 km (B, C respectively) would provide a slower westward drift. An even deeper source (2800 km) would make the net rotation very slow, in the order of 0.2$^{\circ }$/My–0.4$^{\circ }$/My. Slightly modified after [20]. BL boundary layer, TZ transition zone, VL velocity of the lithosphere, VO velocity observed at the surface, VX unrecorded velocity of the asthenosphere being below the magmatic source, VM velocity of the sub-asthenospheric mantle

However, the net westward rotation of the lithosphere relative to the underlying mantle is still a controversial effect. Even though incredibly interesting in view of its possible geodynamic implications, it has received scarce attention since its discovery and no unique explanation for its occurrence has been provided. Also concerning its effective size and duration some observations have been formulated suggesting it could be understood in the light of transient processes connected to lateral variations of viscosity in the asthenosphere [176]; nevertheless, geological observations, e.g., [177, 178], and simulations proved that the kinematic asymmetry has persisted for the last 150 Myr [163], even though with different intensity. Therefore, a transient nature of the westward drift should be excluded. Regarding the physical origin of the westward drift of the lithosphere, at least three causes have been suggested. Tidal forces act on the whole planet producing a decelerating torque whose intensity is not uniformly distributed as a function of depth because of the different values of viscosity and physical state of matter inside the Earth. In this view, significant radial differential rotation is localized at the core-mantle boundary and at the level of asthenosphere. In the first case, tidal drag could also contribute to explain the observed differential rotation between the inner core and the mantle together with electromagnetic and mechanical torques [179]. According to [180], the effect of tidal torque is dominant. Even though its effective value is still source of debate, recently published papers conclude the core-mantle differential angular velocity be $\Delta \omega _{CM} \sim$ 0.1–1.0$^{\circ }$/year [181,182,183], lower than the early estimations which found $\Delta \omega _{CM} \sim$ 1–3$^{\circ }$/year [184, 185]. A second mechanism for explaining the westward drift of the lithosphere is the downwelling of denser slabs in the lower the mantle which slightly decreases the moment of inertia of the Earth; however, this effect is really minor; at last, thin layers of ultra low viscosity hydrate zones located within the asthenosphere may play a key role in allowing crustal decoupling from the inner layers. The latter phenomenon could be enhanced by shear heating and mechanical fatigue [68]. The tendency to asymmetry is not exclusive of plate kinematic. The crustal structure of conjugate passive margins [186, 187], continental transform basins [188], ocean ridges [178, 189,190,191] were found to be asymmetric and also orogenesis has been suggested to be influenced by the orientation of mountain belts and subductions with respect to the direction of the underlying mantle, e.g., [192,193,194,195]. Plate motions locally betray the topography for both direct and indirect reasons: horizontal forces are generated by lateral gravitational gradients due to bathymetry at mid-ocean ridges [196], while gradients in the viscosity distribution in the lower lithosphere influenced by the local thickness of the crust slow down plates during continental collisions, e.g., it is the case of the Indian plate, which has undergone a significant deceleration with the relative rate of convergence between India and Asia dropping from 170 to about 40 mm/year during the last 50 Myr [197, 198]. At last, subductions are crucial for geodynamics because of the more than 50 000 km of convergent margins on the Earth’s surface; nonetheless, their role has not been completely clarified [199]. A significant correlation has been found between the fraction of plate boundary involved in subduction processes and the speed of the plate itself [12, 200]. The force driving slab downwelling is proportional to the density gradient between the subducting oceanic crust and the surrounding mantle [201]. The latter was proposed to be mainly controlled by the progressive cooling of the crust with time as it moves away from the mid-ocean ridge [202], so that, the older the slab, the higher the density gradient, the fastest should be the subduction dynamics, with evident implications for plate motions. However, no clear correlation has been found between slab dip angle and age of the subducting lithosphere with results largely depending on selection criteria [7], nor between length of the seismic zone and age of the oceanic crust and convergence rate, while a role is likely played by the thickness of the subducting slab influencing both bending and friction forces [203]. Moreover, a direct correlation has been highlighted between plate surface and their velocity in the shallow hot spots reference frame [204] but not in other ones. In addiction, 42 among the 52 plates of [155] are slab-less; nonetheless, they show absolute velocities comparable to those of plates bounded by subduction zones [205]. So, plates can move without slabs, e.g., Africa, Anatolia, Antarctica, North America, Eurasia, South America, Somalia etc. Subduction dynamics is also affected by asymmetry [199, 206,207,208] (Fig. 5).

Fig. 5

This picture shows our two models (in green), compared with a compilation of the slab dip measured along cross-sections perpendicular to the trench of most subduction zones (after [209]). Each line represents the mean trace of the seismicity along every subduction. Some E- or NE-subduction zones present a deeper scattered cluster of hypocentres between 550–670 km; a seismic gap occurs between about 300–550 km depth. Dominant down-dip compression occurs in the W-directed intra-slab seismicity, whereas down-dip extension prevails along the opposed E- or NE-directed slabs. The W-directed slabs are, on average, dipping 65.6$^{\circ }$, whereas the average dip of the E- or NE-directed slabs, to the right, is 27.1$^{\circ }$. In our models the dip of the slab fits within this average by assuming a minimum intensity of the horizontal mantle flow of 3 cm/year, but it could be even faster. In this figure the differences in topography and state of stress between the upper plates of both models can be seen

In this regard, the behavior of subduction hinges has been shown to be fundamental in convergent boundary dynamics [210,211,212]. Hinges migrating away from the upper plate, i.e. accompanying the slab retreat or rollback, are associated with back-arc spreading [213, 214], steep dip of Wadati–Benioff zone, deep trench and mantle partial melt. It is the case of the western side of the Pacific subduction zones. Conversely, back-arc compression is observed in Chilean-like subduction zones, with shallow-dip Wadati–Benioff zone, shallow trenches and crustal melting [215]. The first kind of subductions are mainly oriented to west, while the second kind to east [207, 216,217,218,219]. When comparing westerly versus easterly directed subduction zones, other differences also arise. Morphology, structural elevation, gravity anomalies, heat flow, metamorphic evolution, subsidence and uplift rates, depth of the decollement planes, mantle wedge thickness, magmatism etc. The to-west-dipping-class is featured by a much lower topography with respect to the eastern margins [187]. As an example the profile across the Pacific ocean shows low topography along the west-directed subduction zones of the western Pacific when compared to the eastern counterpart. Maxima and minima gravity anomalies are relatively more pronounced along the west-directed subduction zones and the negative gravity anomaly does not coincide with the lowest bathymetry along the trenches of the W-class. Such an asymmetry is ubiquitous along all subduction zones. In summary, boundary forces are able to deform significantly interacting plates producing local impact on plate motions, as highlighted in [220], while their effective ability to enhance large scale rigid displacement of plates with respect to the underlying mantle is still under debate [92, 205], although large part of scientific community supports subduction-driven models of tectonics. More important, a comprehensive view of geodynamic processes is still missing because of poor and arbitrarily selected data, limited analyses of their uncertainties estimate, and oversimplified physical models grounded on hypotheses now disregarded by geophysical and geochemical observations.

5 Gradients and earthquakes

5.1 The effect of relative plate motions

The plates have their own velocity as a function of the lateral viscosity gradient at the interface with the asthenosphere [221]. Consequently, the velocity variations between plates produced at their margins build up pressure gradients growing over time so that, in the shallow, cold and brittle layers of the lithosphere, once the critical loading is reached, earthquakes occur. Therefore, seismicity is the final output of a “cascade” of gradients acting on different properties such as geochemical composition, temperature, mechanical behavior, velocity and different components of stress. Earthquakes happen when the stability conditions for fault interfaces are not satisfied any more. At local scales, friction keeps faults locked; therefore, rheological anisotropies control fault activation on a simple interface. As a consequence, adjacent rock volumes slide with respect to each other generating stress perturbations which propagate as seismic waves because of the elastic properties of the surrounding media. Fault slip allows stress drop via potential energy dissipation E [222]

$$\begin{aligned} E = E_{S} + E_{W} + E_{H} \sim \int _{t_{0}}^{t_{f}}\frac{1}{S}\int _{S}\sigma (\xi ,t) {\dot{u}}(\xi ,t) ~dS dt \end{aligned}$$

(16)

through fresh surface generation ($E_{S}$), seismic waves radiation ($E_{W}$) and heat and rock fracturing ($E_{H}$). $\sigma (\xi ,t)$ is the instantaneous shear stress within the fault patch identified by $\xi$ and ${\dot{u}}(\xi ,t)$ is the local slip velocity at the time t during the seismic event. Only a little fraction of the dissipated energy is converted into seismic waves after the activation of an ideal fault according to

$$\begin{aligned} E_{S} \sim \int _{t_{0}}^{\infty }v_{s}\rho {\dot{u}}^{2}(t) ~dt \approx E_{R} + (\sigma _{R} - \sigma _{f})Su \end{aligned}$$

(17)

where $E_{R}$ and $\sigma _{R}$ are the residual potential energy and stress respectively survived to the fault slip u and $\sigma _{f}$ is so-called frictional stress fixing the activation condition. This quite simplistic view, in which a fault is a planar discontinuity featured by friction, is routinely and successfully applied in seismology for seismic wave detection and for the characterization of the seismic source. Slight changes are added in order to simulate weakening processes during fault slip assuming that the friction coefficient of the fault is not constant over time, but logarithmically depends on the contact duration of locked interfaced called asperities, i.e., rate-and-state friction laws [223,224,225]. Laboratory experiments are in complete agreement with this model [226]. Hence, at coseismic time-scales and under laboratory conditions, simple fractures behave in a simple almost predictable way being featured by a small set of physical parameters, e.g., fault friction, confinement stress, pore-pressure, differential stress and temperature, and driven by mounting stress that can be hold up to a critical value before breaking. Almost elastic deformations and energy gradients completely describe the life of laboratory faults according to a few simple experimental laws [227]. Unfortunately, real faults are more complicated and such a simple model as the previous cannot be applied in order to understand the physics of seismicity, nor a guarantee exists that the same framework be meaningful outside the subject of conception. No rigorous evidence has ever been provided that large-scale fault systems behave according to the aforementioned outline yet [228]. Of course, a series of similarity suggest that some features can be the same in both laboratory and tectonic fault settings [229, 230]. Without considering scaling arguments, other differences are the stress boundary conditions and the complex organization pattern of fractures inside the crust. In fact, real faults are featured by irregularities that cannot be described on the light of friction like man-made interfaces characterized by limited inhomogeneities [231]. Conversely, real faults systems are fractals with virtually infinite fault interfaces capable to nucleate earthquakes [232]. In this case, being fractal means that fractures are self-similar over a wide range of spatial scales. No friction must be advocated nor should be appropriate to introduce it to address the issue of mechanical conditions for real seismogenic zone activation. Fault complexities, i.e., the topology of the fault system, and potential energy stored in the volumes besides the interfaces drive seismic activity at global scales [233]. Since contact surfaces are fractals, associated stress fields are also fractals with extreme variability and localization around asperities. Hence, brittle failures depend on tiny details of the faulting that can be summarized by the local probability of failure under differential stress load $p(\sigma )$, so that the cumulative probability of breaking for the entire system ${\mathcal {S}}$ is $\mathbf {P}(\sigma , {\mathcal {S}})$ is EVT-distributed (e.g., Weibull-distributed) [234]

$$\begin{aligned} \mathbf {P}(\sigma , {\mathcal {S}}) = 1- \prod _{j=1}^{{\mathcal {S}}}\left( 1-p_{j}(\sigma )\right) \approx 1-e^{-\sum _{1}^{{\mathcal {S}}}p_{j}(\sigma )} {\mathop {\sim }\limits ^{{\tiny W}}} 1-e^{- f({\mathcal {S}})\sigma ^{W}} \end{aligned}$$

(18)

So, the weakest part of the interfaces determines the dynamic behavior of the whole system in real faulting. Average mechanical properties of rocks and stress fields do not play a crucial role in outlining spatial and temporal organization of seismicity, even though they may deeply affect coseismic processes, i.e., single earthquakes. This is one of the main reasons producing the differences observed between dynamics of laboratory seismicity with respect to real one: a few moments of the statistical distributions of physical properties, or even only the average value itself, are enough for the characterization of a simple stick-and-slip dynamic evolution. Moreover, boundary effects and constraints are well controlled in the laboratory implying that self-organization can arise only at tiny, negligible spatial scales with respect to those of the specimen [235,236,237]. Comparable results are found via computational simulations such as the classic result by Burridge and Knopoff [26]. In their celebrated model, a fault is simply represented as a series of blocks sticking on a rigid plate because of friction, connected to each other thanks to elastic springs and attached to leaf springs glued to a slowly sliding upper plate representing mounting tectonic stress, so that each block undergoes a net force given by the sum of three elastic contributions and a frictional one. When the elastic gradient overcomes the maximum friction, a block slides modifying the surrounding stress distribution. The Burridge-Knopoff model was the first attempt to understand the relationship between catastrophic failures and gradients acting inside the crust. As already stated, it is not but a simple framework useful for having the flavor of what happens during seismic events, but reality is still far even for the most advanced simulations realized so far. Seismology needs more complicated models able to catch the role of geometric complexities, i.e., asperities and barriers, and remote boundary conditions. Among the consequences of the widespread idea, albeit unsophisticated, of elastic stress accumulation as the driver of seismic processes are the concept of “seismic cycle” [238, 239], “typical earthquake” [240, 241] and the seismic gap hypothesis [242, 243]. For an alternative critical evaluation of these concepts, see [244]. The first one is an appealing framework concerning temporal distribution of seismicity within sufficiently localized bounded regions in which earthquakes are expected to occur after a period of stress increase due to tectonic forces, once the stress drop has happened, weakening processes are also responsible of a post-seismic phase in which minor events, i.e., aftershocks, are recorded before reaching a new state of mechanical stability. Essentially, the basic idea of seismic cycles within the brittle crust is almost completely accepted by the members of scientific community, while its implication of rough periodicity of similar magnitude events is still strongly debated. It is suggested that a set of faults, behaving as a close physical system may exhibit recurrent dynamical patterns, i.e., earthquakes with similar features such as magnitude, focal mechanism and aftershocks, even though not periodically, as a function of almost stationary energy accumulation [245,246,247,248]. However, no theoretical foundation has ever been provided in support of this hypothesis, conversely, chaos theory, self-organized criticality, turbulence theory and models, e.g., fiber-bundle model, applied to seismic dynamics disproved earthquake typicality [249,250,251,252]. Geological and geophysical observations also suggest large variability of occurrence, e.g., [253]. Possible explanations have been suggested on the light of temporal evolution of faulting, maturity stage and response to additional stress perturbations. At last, the seismic gap hypothesis, i.e., large earthquakes are not clustered in space and time, in both its original and updated versions, has been the base of several models and prediction attempts, e.g., [254]; nonetheless, it failed spectacularly both statistical tests and single cases of application [255,256,257]. Seismic gap hypothesis assumes that, while small earthquakes are clustered in space and time, large events have the opposite behavior, so that a new physics should be required for explaining “system-sized” earthquakes. However, analogue systems physics proves it is not true. For instance, the surface of a sand pile can slide even if it is below the critical slope locally, because slope failures can propagate remotely. Therefore, the idea that a region might be safe from major earthquake occurrences because of recent failure is completely unfounded [258]. A further step towards our understanding of the occurrence of large earthquakes came from the models of rheology and complexity on the fault interface. Stress arises from progressive deformation of rocks on large spatial scale; elevated stress values can result in a wide range of possible dynamic evolutions along weak interfaces, the so-called asperities. It is quite intuitive that the most unstable segments of the fault may coincide with those featured by low resistance to mechanical fatigue, according to Eq. 18. Depending on local physical properties, faults show different levels of locking. Interseismic coupling is usually observed to occur in spatial heterogeneous patches surrounded by partially unlocked creeping surfaces. High temperature and pore-pressure values as well as the abundance of rocks with low friction coefficients promote aseismic creep. On the other hand, fast strain changes and low normal stress encourage faulting. Nowadays, space geodesy and remote sensing allow accurate monitoring of fault zones: thanks to large amounts of information provided from recording, the partitioning of stress dissipation over long-term time scale can be inferred. Interseismic coupling is a key property for facing with this issue; it is defined as the ratio between the deficit of slip in the interseismic period and the long-term slip ${{\textbf {u}}}$

$$\begin{aligned} \chi = \frac{{{\textbf {u}}}_{s}+{{\textbf {u}}}_{a}}{{{\textbf {u}}}} \end{aligned}$$

(19)

where ${{\textbf {u}}}_{s}$ represents the coseismic cumulative displacement and ${{\textbf {u}}}_{a}$ is the cumulative aseismic displacement occurred during transients such as slow slip events (SSE) and afterslip. $0 \le \chi \le 1$ by definition. If $\chi \sim$ 1, almost all the displacement occurs as a consequence of faulting, on the contrary, if $\chi \sim$ 0, then aseismic creep dominates stress dissipation. As time goes, a deficit of seismic moment M mounts at a rate equal to [259]

$$\begin{aligned} {\dot{M}} \sim \int _{S} \chi (\xi )\mu {\dot{u}}(\xi )dS \end{aligned}$$

(20)

which has to be dissipated through earthquake nucleation. The interseismic coupling shows wide spatial variability also within the same fault system, so that locked and creeping areas are distributed as a function of fault system complexity. Creeping interfaces are usually featured by low stress activation. For this reason, they are often sensitive to seasonal and tidal loading, e.g., [260, 261], and featured by silent earthquakes. On the other hand, locked areas are characterized by elevated activation energy, so that they are almost unresponsive to additional stress perturbations far below the critical loading level [262]. However, considerations about stress, fault complexity, rock physics and structural properties of deformation regions, although useful for understanding tectonics, long-term regional seismicity and coseismic processes, cannot be applied for improving our comprehension of how earthquakes occur in space and time. Earthquakes belong to a set of phenomena showing self-organization, long-lasting memory and emerging critical features. Seismic clusters obey well-studied “empirical” laws: the Gutenberg–Richter law [263]

$$\begin{aligned} \log (N(\ge M_{w})) = a - bM_{w} \end{aligned}$$

(21)

where N is the number of events with magnitude larger than $M_{w}$, while a represents local seismicity and $b \sim 1$ and Omori–Utsu law [264]

$$\begin{aligned} n(t) = \frac{k}{(c + t)^{p}} \end{aligned}$$

(22)

which means that each event can induce a perturbation on unbroken fault segments provoking a series of power-law distributed avalanches. Both the Gutenberg–Richter and the Omori–Utsu laws are not valid in general, but only under precise conditions to be fulfilled. In fact, only ensembles of events occurring in regions smaller compared with the size of seismotectonic structures can be described by a simple power-law frequency-size scaling [28]; moreover, large events usually deviate from the above predicted trend because of the finite-size of the seismogenetic sources, so that the best fitting distribution is a tapered Gutenberg–Richter law [265,266,267]. Analogously, the Omori–Utsu temporal scaling is valid only for few days after the mainshock, while stretched exponentials have been found to more appropriately fit the decrease of recorded seismic events over longer time intervals (e.g., [268,269,270]). Due to the epidemic behavior of the occurrence of seismic events, it is often necessary to understand whether an earthquake was directly induced by an external disturbance or it was generated by spontaneous failure. Once declustering, i.e., the procedure thanks to which straight induced events are removed from the catalog, is performed, aftershocks in seismic time series are taken away. On this basis, it is clear that earthquakes involve not only different time and spatial scales [28], but also wide-ranging behaviors and phenomena, mainly referred to two non-interacting fields, i.e., physics of earthquakes (a.k.a. “classical” theoretical seismology) and statistical seismology, whose subject of investigation is the same (earthquakes), but formalized in such a way that, actually, it is split into two virtually separate observables: coseismic processes and seismic sequences. Clustering is a crucial property of earthquakes, which allow to roughly classify seismicity into four stages: the interseismic phase, featured by relatively weak and diffuse seismic activity, the pre-seismic phase (if any) should be characterized by anomalous patterns (usually either mounting energy release and grouping $-$ foreshocks $-$ or quiescence), the coseismic phase, i.e., the major earthquake, called “mainshock” and the post-seismic period (the seismic sequence), dominated by the Omori’s relaxation made up of aftershocks, whose frequencies and magnitudes scale as time goes. Together, these stages form a “cycle” according to the description we gave above, which iterates with wild variability in time, space and size, then difficult to predict; so complicated that, according to a part of scientific community, prediction is presently impossible [271]. In an ideal world, earthquakes are thought to occur periodically (the average period is called “recurrence time”) with similar features. Nevertheless, the real world is quite different and strong time and space clustering are routinely detected; moreover, single seismic sources and also fault systems can interact to generate giant unprecedented quakes [272], like is also highlighted by paleoseismological discovery (e.g., [273]). Therefore, self-organization is a key property of seismic activity and a major effort is still required in order to better understand how internal self-organized processes happen. What is certain is that earthquake dynamics evolves such that crustal volumes can be displaced, in order to improve the state of mechanical stability of fault interfaces, by optimizing the total energy gain produced via fault segment breaking constrained by dynamic conditions. Hence, given the seismic moment acting as a dislocation constraint, M, which depends on the deformation rates of local geodynamics, seismicity optimizes the triggering power of crack propagation, so that both seismic sequences and single earthquakes are ultimately driven by fault disorder (spatial distribution of barriers and asperities) [31]. In this view, the maturity level of fault damage zones may play an important role in featuring seismicity. Computational simulations show that immature fault systems tend to nucleate small and moderate earthquakes with irregular occurrence intervals and slow-slip events. On the other hand, more mature fault zones produce ruptures that can propagate throughout the seismogenic layers, resulting in complete “typical” ruptures with more regular recurrence intervals [274]. At last, earthquakes are liberation of energy which may be stored in different ways: the common paradigm is that faults, which are the source of seismicity, completely characterize seismic events they host. However, earthquakes are rather the result of dissipation of energy previously stored into the upper crustal volumes adjacent to the rupture interfaces [275]. For instance, during the interseismic period, along normal faults the hanging-wall volumes accumulate gravitational energy [276] (Fig. 6).

Fig. 6

The energy accumulated during the interseismic period above the BDT differs as a function of the tectonic setting. Along a normal fault, it is mostly gravitational potential energy. In contractional and strike-slip settings, it is rather elastic potential energy. In all settings, the available energy is dissipated in elastic seismic waves, friction, internal strain. The dip of the faults (q) also controls how the energy (E) is released. Legend: m represents the mass of the hanging wall; g is the gravity acceleration; h the hanging wall volume thickness; $\mu _{s}$, static friction, $\theta$ stands for the fault dip; d, displacement; K the Young’s elastic modulus; V, hanging-wall volume; $\rho$ is the average density of rocks (after [276])

Conversely, along strike-slip and thrust faults, the energy stored stems from progressive deformation of rocks. Therefore, faults dissipate different types of energy and in different ratios, which may also imply peculiar phenomenology depending on the tectonic style [277,278,279]. Faults are only the final mechanical guides along which the energy accumulated in the volumes is transformed into elastic waves. The computation of the amount of energy stored in a given volume of tectonically active zones may provide a first-order, approximate estimate of the maximum potential magnitude that can develop in a given area, even if no earthquakes were previously recorded. This technique, grounded on geological observations, may be useful to better characterize the hazard scenarios in earthquake prone areas providing complementary information with respect to historically developed deterministic (e.g., Maximum Credible Earthquake (MCE) [280]) and probabilistic, catalog-based approaches [281, 282].

5.2 The effect of terrestrial gradients on the features of earthquakes

In nature there are different types of tectonic settings (extension, strike-slip and contraction). The deformation affects a crust with a brittle behavior in its shallow layer (e.g., from 0 to 10–20 km deep), whereas it deforms in a ductile manner in the lower layer (from 10–20 to 30–40 km deep). The upper crust deformation is controlled by pressure and tectonic stress, whereas the lower crust by temperature and the transition among the two layers is defined as the brittle-ductile transition (henceforth, BDT), being the layer where the larger differential stress is required to deform rocks. Therefore, the two layers react differently to deformation, being the lower crust flattening or thickening in a steady state regime, whereas the upper crust undergoes dilatancy or overpressure during the interseismic period, releasing accumulated deformation during the episodic movements, i.e., the earthquakes. Along normal faults in extensional tectonic settings, a dilatant wedge is inferred to form during the interseismic period. This wedge will expand becoming less and less sustaining the hangingwall volume, which will eventually fall. On the other hand, in contractional areas, in the hangingwall above a thrust, an over-pressured volume will deform during the interseismic period. When the elastic energy will override the frictional resistance and the opposite gravitational load, the hangingwall will rebound elastically. Therefore, the tectonic setting determines the type of energy dissipated by earthquakes, and fault complexities govern the amount of slip partitioning during the interseismic and coseismic periods. The tectonic settings control the magnitude of earthquakes; in fact, normal faults did not generate known earthquakes much larger than M$_{w}$ 7.5 in continental settings. Strike-slip settings may rather provide M$_{w}$ 8.5, whereas contractional plate boundaries along subduction zones may determine $\ge$M$_{w}$ 9.5 [283]. The depth of the seismogenic zone, z, and the maximum length, L, of the activated volume show relative ratio that varies as a function of the tectonic setting, i.e., $L _{max} \approx 3z$ for extensional settings, $L_{max}\approx 10z$ for strike-slip settings and $L_{max} \ge 25z$ for contractional settings. Therefore, the maximum volume mobilized during an earthquake also depends on the tectonic setting. Unlike the standard seismological models that suggest the dimension of the fault plane is the unique controlling factor, the earthquake magnitude is also affected by the rheological properties of the surrounding volumes and stress patterns (Fig. 7).

Fig. 7

In extensional tectonic settings, the minimum stress tensor ($\sigma _{3}$) generates horizontal traction only above 1 km of depth, where it is negative. Below that depth it becomes positive, i.e., the crust is in compressive state even in rifting areas due to the increase of the confining pressure generated by the vertical, lithostatic load. Here an average density of 2.5 g/cm$^{3}$ and an increase of the lithostatic load of 25 MPa/km is assumed. The area between the lithostatic load and the minimum horizontal stress represents the deviatoric stress and contains the stress data measured in wells. To the right, the compressional tectonic setting in which contraction in the crust occurs also at shallow depth (after [284])

The depth of BDT is determined by the competition of frictional differential stress $\Delta \sigma _{f}$ at depth [285]

$$\begin{aligned} \Delta \sigma _{f} = \beta \rho gz(1-\lambda ) \end{aligned}$$

(23)

where $\lambda$ is a pore fluid factor and $\beta$ depends on the tectonic setting, being 3, 1.2 and 0.7 respectively in reverse, strike-slip and normal faulting, and viscous stress

$$\begin{aligned} \Delta \sigma _{v} \sim \left( \frac{{\dot{\varepsilon }}}{A}\right) ^{0.4} e^{\frac{Q}{nRT}} \end{aligned}$$

(24)

controlled by temperature T, strain rate ${\dot{\varepsilon }}$; Q, A and R are constants. In extensional tectonic settings, the increase of the BDT depth determines larger brittle volumes. For example, increasing three times the BDT depth from 7 to 21 km, the mass increases about thirty times, the gravitational energy is more than one hundred times larger, and the seismic energy becomes thousand times bigger. This is confirmed when plotting the maximum magnitude recorded in the extensional areas of the Italian area, where it is evident the correlation with the thickness of the brittle crust. Using different angles of the normal fault plane (e.g., 45$^{\circ }$ and 60$^{\circ }$) it is then possible to compute the maximum crustal volume can be mobilized during an earthquake of any given area, regardless the seismic catalog and the faults known. Therefore, crustal normal fault-related earthquakes also dissipate gravitational potential energy according to the dip angle and their magnitude increases with the involved volume and fault slip. Fault dip has been suggested to be controlled by the static friction of the involved crustal layers [286]. The depth of the brittle-ductile transition also depends on geothermal gradients, strain rates and fluids [287,288,289]. The difference among tectonic settings also affect the b-value of the Gutenberg–Richter law, i.e., 1.1–1.2 for extensional tectonic settings, $\sim$1.0 for strike-slip environments, and 0.7–0.9 for contractional earthquakes [290]. Even though this variability has been hypothesized to be spurious [291], a flurry of evidences and models have been provided in the last twenty years so that almost all the scientific community support the conclusion above. The variability of maximum magnitude has been also attributed to geological features, e.g., the lower strength of the continental lithosphere [292] or to the different mechanisms playing a relevant role at tectonic and geodynamic timescales [276]. However, regardless the tectonic style, at the local scale, the b-value can be extremely variable due to regional tectonics, rheology and strain rate and what really matters for seismic hazard assessment is the regional b-value. The most popular model inversely relates the value of b to the tectonic stress in the rock volume surrounding the fault plane [293]. The b-value is inversely related to the equilibrium state of differential stress $\Delta \sigma$ according to [294]

$$\begin{aligned} b= 1.23 \pm 0.06 - (0.0012\pm 0.0003)\Delta \sigma \end{aligned}$$

(25)

so that deep earthquakes tend to be featured by lower values of the scaling parameter of the frequency-size distribution. In the previous formula, $\Delta \sigma$ is expressed in MPa. In the last years, increasing attention has been paid to the variability of the b-value looking for seismic precursors, in particular, concerning the classification of large events as mainshocks or foreshocks [295, 296]. According to this approach, differential stress gradients over time highlight fault interfaces close to failure. A lively debate is ongoing and even though results have been suggested to suffer from data selection bias [297] and procedures employed in statistical analysis [298], b-value variability is among the most active research paths in the field of earthquake prediction [299]. Some concerns also arise about the physical interpretation of the variations of b: after a major seismic event, it undergoes a swift drop, followed by a progressive increase due to aftershocks. According to the mainstream approach, i.e., the scaling exponent is negatively correlated to the differential stress, the peak of stress and instability within the fault system should be reached just after the mainshock; conversely, the largest event is thought to produce a stress drop after the critical stress had been overcome moving the system towards stability. In addition, b is a global property of seismicity depending on the previous seismic time series, while differential stress is a local one and it is not affected by its history. Moreover, b becomes senseless if well-defined conditions are not satisfied, i.e., the frequency-size distribution of seismic events must be a power-law, stationarity of seismic dynamics and spatio-temporal long-range correlated earthquakes must be included in the analysis. Therefore, spatially detailed maps of the b-value should not be used for reliable hazard assessment. Different b-values are also correlated with distinct fracturing regimes occurring as a function of tectonic settings which change the rheological profile, steeper in compressive regions and flatter in extensional deforming areas [300]. Earthquakes occur in multifractal clusters [301, 302]; fractures are not planar [303]. A measure of the fractal dimension of the earthquake sequence at the resolution scale s behaves like if the dislocated surface $\Sigma _{c}(s) \sim s^{-D_{f}}$, where $D_{f}$ is the fractal dimension [304]. Taking as a reference an ideal planar faulting, if $\Sigma _{0}$ is the surface produced to dissipate a certain amount of energy stored in the crust, then, for a real fault

$$\begin{aligned} \Sigma _{c}(s) \propto \Sigma _{0}s^{(D_{f}(0)-D_{f})} \end{aligned}$$

(26)

To date, the generally accepted value for large-scale faulting is $D_{f} = 2.20 \pm 0.05$ [305]. However, a wide variability has been found, partially due to the unmodeled heterogeneity of the data. Nevertheless, it seems clear that a substantial difference exists in fractal dimensions between compressive and extensional faults [306]

$$\begin{aligned} D_{f} \approx 2b \end{aligned}$$

(27)

Fig. 8

Analysis of 47 fault systems in Italy, ITHACA database [308]. Top, Left: Scatter plot of the maximum recorded magnitude versus the annual slip rate. Extensional faulting (green dots) and compressive tectonic settings (blue circles) are prone to extreme events with similar magnitudes where the deformation rates are the same. This picture benefited of the data contained in the CPTI15 catalog of historical seismic events occurred in Italy since the XI century [309]. Top, Right: Length of faulting versus the annual slip rate in different tectonic settings in Italy. Extensional faults (green circles) are featured by lower length along strike with respect to compressive faulting (blue dots) once the average modulus of the slip rate is fixed. Strike-slip faults are highlighted in red. Bottom, Right: Annual rate of earthquakes versus the slip rate during the interseismic phase. Background normal faults-related events are more frequent than reverse ones analyzing areas with similar annual deforming rate. The variable represented at the ordinate axes is calculated by counting the events recorded in the volume surrounding the considered fault. A normalization is then performed with respect to a surface of 1000 km$^{2}$. Only earthquakes occurred during the interseismic phase with magnitudes above M$_{wc}$ are taken; data from the INGV earthquake catalog between 1990 and 2021 are used. Bottom, Left: Annual seismic energy rate versus average slip rate. Compressive and extensional faults in Italy nucleate equivalent seismic energy expressed in moment magnitude with the same slip rate during interseismic periods. The annual energy rates are calculated by adding the seismic moments of the events occurred within a volume embedding the considered fault system. Further explanations are given in the supplementary material

Normal faulting is featured by $D_{f} \sim$ 2.2 - 2.7, strike-slip faulting has $D_{f} \sim$ 1.9 - 2.3, while $D_{f} \sim$ 1.5 - 2.0 in reverse faulting. This means that various fracturing regimes occur because of different tectonic settings, which change the critical stress required for rupture propagation. Unlike contractional and strike-slip tectonic settings, extensional tectonic regimes determine a more diffuse interseismic dilatance within the brittle crust, resulting in widespread fracturing. Extensional tectonic settings have, on average, lower maximum magnitude, shorter fault length and smaller coseismic slip with respect to other tectonic settings. Fixed the seismic moment M, the average slip $u_{ext} < u_{0}$ and the fractured fault length $L_{ext} < L_{0}$ in extensional tectonic settings. On the contrary, subduction zones and thrust-associated faulting show surface fractures $\Sigma _{compr} < \Sigma _{0}$, which implies larger slips $u_{compr} > u_{0}$ and larger lengths along strike $L_{compr} > L_{0}$. These consequences follow immediately from the classical structural relationships between properties of earthquakes scaling and faulting [276, 307]. For instance, in Fig. 8 the scatter plot of the lengths of faulting versus the annual slip rate in different tectonic settings is represented. In this picture clearly emerges that extensional faults in Italy are characterized by lower length along strike $L_{ext}$ with respect to that of compressive faulting $L_{compr}$ once the average modulus of the slip rate is fixed, as expected. In the same figure, the annual rate of earthquakes versus the slip rate during the interseismic phase is also shown. This proves that the interseismic annual rate of seismic events is higher for extensional tectonic settings in Italy with respect to compressive ones, so that the same geodetic deformation is the reason of different spectra of magnitudes.

The role of stress is important for shaping seismicity. Several studies proved a strong sensitivity of seismicity to stress changes, e.g., [310], although minimal. For this reason, the variation of Coulomb failure stress [311, 312]

$$\begin{aligned} \Delta CFS = \Delta \sigma _{s} + \mu (\Delta \sigma _{n} + \Delta P_{pore}) \end{aligned}$$

(28)

where $\sigma _{s}$ is the shear stress, $\mu$ is the average shear modulus, $\Delta P_{pore}$ is the change of pore pressure and $\sigma _{n}$ is the normal stress, has been applied to correlate its variations with changes in aftershocks productivity [313,314,315,316]. Recently, some concerns have been advanced about the real effectiveness of this parameter to chart the spatial distributions of stress gradients in the crust, while others have been proposed [317, 318]. A difference between static and dynamic Coulomb stress is conventionally done: when loading is slow, so that its increasing/decreasing rate is negligible with respect to the compared time interval, then the static Coulomb stress is at work, on the contrary, if loading occurs suddenly (i.e., fluid injection, coseismic slip), then the dynamic Coulomb failure stress plays a relevant role. In general, the strain produced by earthquakes induces dynamic Coulomb stress swings that, at long distances, can be even an order of magnitude larger than the static stress changes. Stress variations are also classified into permanent and transient ones (e.g., some seismological and geodetic effects induced by the Great Kaikoura earthquake, New Zealand, 13/11/2016, M$_{w}$ 7.8, are illustrated in Figs. 9 and 10).

Fig. 9

Map of seismicity in Manawatu, North Island, New Zealand, GeoNet Catalog, 2000–2021, M$_{L}$ $\ge$ 2.5. Each earthquake is represented as a point whose color depends on the value of the tidal shear stress at which it occurred, according to the color bar. Black points are tremors. Seven GNSS stations located along dip with respect to the Hikurangi subduction zone are plotted on the map with the local vector velocity (red arrows) provided by NGL (MIDAS components). Red triangles represents volcanoes, while orange contours highlight regions shaken by large earthquakes

Fig. 10

Spectrograms and residual horizontal geodetic time series of seven GNSS stations in Manawatu. From the top to bottom: HAST, KERE, BSHT, VGMO, VGMT, VGPK and NYPT. SSEs are observed, moreover, the spectral amplitudes are noticed to increase before the Giant Kaikoura Earthquake (13/11/2016, M$_{w}$ 7.8) downline of the Manawatu ETS zone in the recordings of NYPT, VGPK and VGMT. The red lines stand for large earthquakes which caused a measurable displacement of the GNSS stations, while the orange dashed lines represent slow slip events. The green arrows highlight afterslip

There is a nonlinear dependence of the time to instability on stress variations [319]; this not only means that seismic rate is a direct effect of loading, but also implies that even a tiny additional stress can result in highly unpredictable states of crustal instability. From a mathematical viewpoint, these properties are summarized by the seismicity rate R(t) equation, which, in the simplest form, reads [312]

$$\begin{aligned} R(t) = \frac{R_{0}}{1+e^{-\frac{t}{T}} \left( e^{-\frac{\Delta CFS}{{\mathcal {K}} \sigma _{n}}}-1\right) } \end{aligned}$$

(29)

where $R_{0}$ is initial seismic rate, ${\mathcal {K}}$ is a constitutive parameter, and T is the duration of the loading. Observations suggest that the seismicity rate can be influenced by both static and dynamic perturbations. Solid [320,321,322], liquid [323] and polar tides [324], seasonal stress patterns [325,326,327,328], and anthropogenic actions such as fluid-injection [329,330,331] can affect seismicity. The case of tides is really interesting because of the tiny size of tidal shear stress $\Delta \sigma _{s} \sim$ 0.1$-$1 kPa with respect to the typical stress drop during earthquakes $\Delta \sigma \sim$ 1–10 MPa. Nevertheless, tidal perturbations are able to modulate seismic activity, above all at small magnitudes [332]. Once more, this effect highlights the critical component of seismic phenomena and their intrinsic non-linearity. Perturbation analysis also provided evidence that locked faults tend to become more and more sensitive to stress perturbations as they reach the breaking point [333]. The response of seismicity to perturbations also depends on the tectonic setting because of the different rheological profile, according to Eq. 23. Compressive faulting is less sensitive to additional perturbations with respect to transcurrent and normal-faulting regions because its rheological profile is steeper; therefore, the ratio between perturbation and differential stress is lower. Tectonic settings also seem to affect the temporal dynamics of seismicity. Different and sometimes contrasting results exist. For instance, in [334], a negative correlation between b and p value is found for a selection of about fifty major earthquakes, while [335] asserted a direct correlation between b and p by analyzing a set of about thirty seismic events. That result was in good agreement with the theory provided by Utsu in 1961, according to which $p \approx 4/3 b$. In [336] is instead showed that, using bifurcation theory, the Omori scaling exponent can be written in the form $p = 1 + \theta$, where $\theta$ is a small parameter which can also be negative. A recent research, [31], based on updated results suggests a slightly different empirical relation

$$\begin{aligned} p \approx \frac{2}{3}(b+1), \end{aligned}$$

(30)

in good agreement with the previous ones. This result has a pure statistical meaning only emerging by analyzing several seismic sequences (Fig. 11).

Fig. 11

Scatter plot of p versus b after [31]. p value and b value are positively correlated according to the result of the linear fit plotted above. A selection of one hundred seismic sequences among the most investigated in the last decades is given. Each circle represents a seismic sequence, and its color allows to recognize the tectonic setting where it occurred: extensional faulting is painted in green, blue is used for subduction and thrust events, red for strike-slip ones, while fluid injection-induced sequences are in yellow and volcanic-tectonic sequences are cyan dyed. As expected, all the dots are out of the forbidden half-plane bounded below by the line of equation $p=1+2/3 b$. The best weighted linear fit returns $p=0.60+0.65 b$

Even though a flurry of evidences has been collected about preseismic and coseismic processes with also compelling physical explanations, seismic prediction remains far, although there are ongoing algorithms and machine learning applications deserving attention [337,338,339,340]. Since the physics of faulting is still poorly understood and at least two possible mechanisms for nucleation were proven to exist, e.g., preslip and cascade models [341,342,343], universal seismic precursors are not expected to exist. Recently, artificial intelligence has been applied for enriching seismic catalogs via automatic phase-picking procedures [344]. Preliminary analyses of those empowered databases suggest the a large part of seismic events is forerun by foreshocks of small magnitude, $\sim 70 \%$ according to [345] and [346]; nonetheless, the final outputs may be biased by the applied statistical approach [347]. Moreover, no correlation has been found between duration and intensity of the swarm and the magnitude of the impending earthquake. Moreover, almost 90$\%$ of analogous seismic activity does not produce moderate or large events. Also physical considerations suggest that ultimate seismic prediction, i.e., prediction of time, hypocenter and magnitude of seismic events, may be intrinsically impossible. “Intrinsically” means that the fault system itself does not know whether it will undergo a major event or not. Wild non-linearity hardly suppresses the prediction horizon ${\mathcal {T}}_{p}^{event}$ of seismic events down to a fraction of the noise ${\mathbb {W}}$ timescale

$$\begin{aligned} {\mathcal {T}}_{p}^{event} \sim \frac{1}{\lambda _{max}} \log \left( \frac{\Delta }{\delta }\right) \sim {\mathcal {T}}_{{\mathbb {W}}}~~~~ \delta ,\Delta \longrightarrow 0 \end{aligned}$$

(31)

where $\Delta$ is the required accuracy of prediction and $\delta$ is the starting error and $\lambda _{max}$ is the maximum Lyapunov exponent of the dynamics [348]. However, it was proven that fault systems change their mechanical response during the different phases of seismic activity [23, 349,350,351,352], which is certainly not sufficient for forecasting or prediction, but it can be used to understand whether fault systems are evolving towards instability. New advances achieved in this research field are significant, with a potential impact on seismic hazards. In addition, they might provide new insights for the comprehension of the relationship between stress perturbations, earthquake nucleation and seismic sequences, which are still to be fully investigated. Brittle crust is an extremely complicated system because of the huge number of variables to consider, non-linearity and strong correlations acting therein. Slight local changes in composition of the rock can have significant influences on where the stress builds up causing earthquakes because of the non-self-averaging property of mechanical strength. Moreover, after each earthquake, a part of the “memory” of the system gets reshuffled, so the next one might be completely different even though the local stress situation is the same.This is the reason why often there are several small earthquakes before a big one, which could happen hours, days, weeks or months before it and sometimes a large earthquake happens without any warning at all (creeping failure): no unique mechanism exists for nucleation because of the strongly chaotic behavior of such a turbulent system. Even though seismic prediction has been considered impossible [271], no theoretical reason prevents it on the condition that one is interested in predicting, with some tolerance, large-scale seismic processes and not single seismic events. This positive viewpoint is grounded on several observations collected during the history of earthquake prediction. Even though seismic precursors (i.e., phenomena whose intensity is somewhat correlated with the magnitude of incoming earthquakes and occurring in regions and time intervals clearly connected to impending seismicity) have not been found yet and it is possible they do not exist at all, a certain number of geophysical processes clearly prove that preparatory phases to large earthquakes are a matter of fact. Among them, the variation of the ratio $v_{p}/v_{s}$ of the P-waves and S-waves velocities [353, 354] has been clearly identified both in real [355] and laboratory faults [356], spring, groundwater and well levels are observed to change before moderate and large earthquakes. Monitoring hydrogeochemical anomalies in springs selected around epicentral areas has also provided results. The concentrations of some elements such as Cr, V, U, Fe and As and molecules as carbon dioxide seem to undergo variations during the occurrence of seismic sequences, e.g., [357,358,359] (Fig. 12).

Fig. 12

Time series (January 1st, 2016–March 31st, 2017) of element concentration, pH (Sulmona test site springs), and earthquake magnitude during the 2016–2017 seismic sequence in central Italy (after [357]). Three mainshocks are shown by the vertical red lines. Concentration of elements is shown as box-and-whisker plots representing inter-quartile ranges (25th–75th quartiles). Each plot includes geochemical data from the Sulmona test site springs. Seismic data are from the INGV database (available online at http://cnt.rm.ingv.it/). (a) Iron, Fe, concentration. (b) Chrome, Cr, concentration. (c) Vanadium, V, concentration. (d) Arsenic, As, concentration. (e) Potential of hydrogen, pH. (f) Magnitude (M$_{w}$) of earthquakes belonging to the 2016–2017 central Apennines sequence. The concentrations of Fe, V, and As increase before the M$_{w}$ 6, August 24th 2016 mainshock

Fig. 13

In extensional tectonic settings, the ratio between the seismogenic layer depth and the hanging wall length appears to be, in average, three ($\sigma$1). As the thickness increases, the volume enlarges, the fault becomes longer, and the hanging wall instability is correlated with a greater fault slip and a consequent higher earthquake magnitude. BDT stands for brittle-ductile transition. The red wedges in the section above suggest the inferred dilated crustal volume permeated by thousands of microfractures (after [284])

All the previous observations are based on the hypothesis that the presence of micro-fractures (compare with Fig. 13) determines the possibility of accommodating fluids and therefore a possibility is given of recognizing anomalous bands because they must be characterized by a lower gradient of resistivity due to the presence of fluids, becoming potential indicators of where the next earthquakes will occur. Before and during the earthquake, fluids are ejected or migrate differently according to the tectonic environment, representing possible future seismic precursors [360, 361] (Fig. 14).

Fig. 14

Assuming a simplified two-layer crustal rheology, the ductile lower crust is characterized by a constant strain rate whereas the brittle upper crust displays episodic locking-unlocking behavior. Tensional and compressional faults generate opposite kinematics and mechanical evolutions. In the tensional tectonic environment a dilated area is formed during the interseismic period. Fluids may enter the fractured volume. Once shear stress along the locked part of the fault becomes larger than fault strength, the hangingwall will begin to collapse, increasing the fluid pressure into the fault gouge. This mechanism is self-supporting because it decreases fault strength, facilitating the final fall of the hangingwall generating the mainshock. Conversely, during the interseismic period, along a thrust plane an over-compressed band separates the ductile shear from the overlying locked fault segment. The hangingwall is eventually expelled during the coseismic period. Fluids discharge behaves differently as a function of the tectonic field (after [360])

Moreover, the responsiveness to stress perturbations such as tidal stress was found to increase in critically stressed fault systems [362, 363] (Fig. 15).

Fig. 15

A $\Delta$CFS map for seismicity in Southern California, SCEDC Catalog, 1985−2021, M$_{L} \ge$ 1.0. Seismicity occurs, on average, at slightly positive $\Delta CFS$ values. B Correlation $\rho$ between $\Delta$CFS and seismicity in the Ridgecrest District, California, between 1985 and 2021. The scatter plot is realized by taking into account earthquakes happened at latitude 35.2$^{\circ } -$36.4$^{\circ }$ N, longitude 117.0$^{\circ }$–118.2$^{\circ }$ W and $-2-20$ km deep, M$_{L}$ $\ge$ 1.0. A preseismic phase featured by an increase of the correlation is detected before the Ridgecrest seismic sequence, mainshock 6/7/2019, M$_{w}$ 7.1. The red line is a weighted smoothing spline. Two horizontal color bars above the scatter-plot show nested “seismic cycles" whose phases are highlighted by different colors (green for the post-seismic phase, the interseismic one is in yellow and the coseismic phase is in red). C Histogram of energy nucleated by earthquakes with M$_{L} \ge$ 1.0 (blue bars) and plot of the number of recorded seismic events (red line). After [333]

At last, an increasing number of evidences has been reported of geomagnetic and geoelectric anomalies correlated with the occurrence of major seismic events [364, 365].

5.3 Relationships between seismicity and global geodynamics

Earthquakes occur because of relative plate motions, local deformations and physical gradients produced by spatial heterogeneity inside the lithosphere. The strain rate is positively correlated with the frequency of earthquakes, as straightforwardly proven by probabilistic seismic hazard maps that highlight fast-paced seismic activity above all at plate boundaries, where diffuse crustal deformations are measured. However, the occurrence intervals of large earthquakes are affected by a lot of parameters in addition to the average slip. Equation 20 states that the seismic rate also depends on the interseismic coupling, the interface area and the rheological properties of rocks. Therefore, the larger the active fault surface, the larger the average seismic rate. The size of faulting is controlled by the depth of the BDT and by the longitudinal development of geologic structures. In compressive settings, e.g., subduction zones, rupture fronts can be thousand kilometers and the depth of the seismogenic layer can reach the bottom of the upper mantle, i.e., $\sim$ 650 km. Transcurrent regions may also be featured by elevated longitudinal size. Oceanic transform faults are among the longest seismogenic sources on our planet, however, great part of seismic activity is concentrated in the most shallow layers of the crust. Conversely, continental normal faulting is usually featured by extremely developed and densely segmented fracturing so that the maximum concurrently viable length along strike is limited, while ocean ridges do not abide by this rule (Fig. 16).

Fig. 16

A recapitulatory diagram of the results discussed in our article. (a) Left panel, the b-value of the Gutenberg–Richter law differs as a function of the tectonic setting, being higher in extensional tectonic settings. Therefore, normal faults have a steeper alignment, which means more low magnitude events and lower maximum magnitude earthquakes with respect to strike-slip (SS) and thrust faults; right panel, being the p-value of the Omori law correlated to the b-value, it shows different aftershocks evolution in time depending on the tectonic settings. On the base of theoretical considerations and statistical analysis of one hundred seismic sequences, the most reliable relationship between them reads $p \approx 2/3 (b+1)$. Larger p-values mean that seismic dynamics moves more rapidly towards stability, which also implies relatively higher probability of secondary ruptures and more numerous aftershocks than the average reference. (b) A geological interpretation of different scaling behaviors can be given in the light of different contributions to energy balance in the long-term rock volumes mobilization. (c) L$_{max}$ is the average maximum length of the volume and the related adjacent active fault in the different tectonic regimes; z, is the seismogenic thickness containing the hypocenter and the aftershocks. The aspect ratio between the two values increases moving from extensional to contractional tectonic settings (modified after [276]). This is consistent with the larger involved volumes of the great thrust-related earthquakes. The most important tectonic implication of our results provides a possible explanation of the variable length along strike of faults in different dynamic regimes. In extensional tectonic settings the seismogenic volumes are smaller, producing lower maximum magnitudes with respect to the other tectonic settings. Contractional settings require more energy in order to move against gravity and they may involve much larger volumes before reaching the threshold to slip, i.e., producing much larger magnitude events and a lower b-value and p-value

High interseismic coupling promotes stress accumulation at the interface making the clock of the seismic activity ticking faster. Since the expression “large earthquake” is often used in this section, it is better to clarify its meaning. We refer to a seismic event as “large” if its magnitude is almost the maximum observed or possible to be nucleated within a fault system according to the concept of “soft cut-off” of the Gutenberg–Richter law introduced in [266]. However, the Gaussian-like roll-off introduces an additional degree of freedom in the frequency-size distribution, or, if the width of the filter is assumed on a priori grounds, such a choice cannot be rigorously justified and a more general framework should be invoked (e.g., [28]). For this reason, our definition of “large earthquake” provided above should also be taken with a grain of salt. Therefore, the highest frequency of large earthquakes is observed along the fast subducting slabs, e.g., the Japanese Trench and the Mexican subduction zone, while the longest recurrence intervals are in the slowly deforming continental regions (henceforth SDCR) such as Mongolia, Brazil, North America, Australia, Tien Sahn and Fennoscandia. Different frequencies of large events do not automatically mean that also small and moderate magnitude earthquakes obey the same rule. A significant variability of the b-value is observed in the distinct tectonic settings; therefore, normal faulting are likely featured by more frequent back-ground seismicity with respect to compressive regions at fixed corner magnitude, seismic coupling and strain rate because of their statistically higher b-value (Fig. 17).

Fig. 17

The b-value of the Gutenberg–Richter law determines the dip of the correlation between the frequency of earthquakes and their magnitude. Normal faults have in average a higher b-value (1.1) according to their lower maximum magnitude (e.g., M$_{w}$ 7.5, in continental regions) with respect to thrusts that may have a lower b-value (0.9) and a much higher magnitude (e.g., M$_{w}$ 9.5). Therefore, in extensional settings there are more low magnitude earthquakes. In these settings the volume moves down in favor of gravity; vice versa, in contractional tectonic settings, the volume moves against gravity and the number of low magnitude earthquakes is smaller, accumulating more energy in order to move up the hanging-wall volume. In extensional settings, the maximum magnitude is controlled by the size of the volume, which depends on the thickness of the brittle upper crust, being less sensitive to the strain rate which, in turn, appears to affect the frequency of seismicity. In contractional settings the frequency of large magnitudes rather increases with the speed of convergence, which determines a thicker brittle layer and a larger brittle volume

Since relative plate motions is mainly directed almost parallel to the equator with increasing velocities approaching low latitudes, seismicity is also concentrated at low and middle latitudes [366, 367]. Observations indicate that in tectonic areas with similar strain rate, the number of earthquakes is higher for normal faults with respect to thrust faults. However, continental normal faults have lower maximum magnitude (M$_{w}$ about 7.5) with respect to thrusts (M$_{w}$ about 9.5). This is in agreement with the higher b-value ($\sim$1.1) of the Gutenberg–Richter of extensional tectonic settings [290] with respect to the world contractional settings where b-value is on average lower ($\sim$0.9). This difference can be explained because of different fracturing regimes and structural properties of fault systems; moreover, at tectonic timescales, rock volumes undergo different energy balance conditions as a function of the dip angle and relative motions of rock volumes along the fault interface. A rough approximation for critical stress in the case of shear cracks can be calculated by balancing the elastic energy released during the propagation of the rupture for a length L, involving the crust for a thickness D, $E_{e} = -D\mu \sigma ^{2} L^{2}$ [222], the variation of gravitational energy $E_{g}= \pm DR \rho gu \sin \xi$ ($-$ is chosen in normal faulting and $+$ in reverse faults), the surface energy $E_{S}= -2\gamma DL$, where $\gamma$ is the amount of energy released when a unit of surface is produced, and $E_{d}=-\mu DLu$, the total amount of energy loss due to friction at fault interface, where u$_{max} \sim cL$ [368] is the average fault slip and $c \approx 0.001-0.01$ [369]. Under the previous assumptions, the critical stress reads

$$\begin{aligned} \sigma (L,u) \approx \sqrt{\frac{\mu (2\gamma + \mu u \pm R\rho gu \sin \xi )}{2 \pi (1-\nu )L}} \end{aligned}$$

(32)

where $\rho$ is the average value of density of the rocks of the failure volume and $\nu$ is the Poisson’s modulus. However, the relevant error bars in geodetic analysis and still poor seismic catalogs are often not sufficient to provide a clear proof of this effect, hence the debate is open [370]. So far, we have dealt with the relationship between strain rate and frequency of seismic events, neglecting magnitudes. Several ideas have been proposed during the last decades. A positive correlation between relative plate velocity and maximum potential magnitude was suggested, e.g., in the case of subduction zones also was speculated that the younger the crust, the larger the events [371, 372], but this hypothesis has been disproved by the most important earthquakes occurred in the last twenty years, e.g., the Giant Tohoku-Oki megathrust earthquake (M$_{w}$ 9.0, $\sim$ 8 cm/year of convergence rate and 130 Myr old sea floor), the Sumatran Giant event (M$_{w}$ 9.2, $\sim$ 3 cm/year of convergence rate and 80 Myr old subducting crust) and the Maule earthquake (M$_{w}$ 8.8, $\sim$ 6 cm/year of convergence rate and $\sim$30–40 Myr old sea floor). Analogously, few analyses of selected background strain rate datasets in comparison with local seismicity have suggested that large magnitude earthquakes might be nucleated within regions of relatively low strain rate, e.g., [36]. The hypothesis below this kind of approach is that lateral gradients of horizontal strain induce elastic stress accumulation where faults are more locked with respect to the surroundings. Even this model did not survive the seismic events happened after its setting-up. For instance, the seismic sequence in Central Italy started in 2016 and still ongoing has taken place in a region of relatively elevated strain rate. It is now clear that the possibility of large events is mainly controlled by the size and complexity of fault systems rather than by strain rate and stress accumulation. The case of SDCR is really significant from this viewpoint. Slow slipping faults showcase a wide range of behaviors varying from almost absent background seismicity to devastating clustered seismic activity (M$_{w}>$ 8) [373]. Such a property poses a serious challenge to seismic hazard assessment because only a limited number of paleoseismological recordings are available. [374] highlighted strong clustering of seismicity in SDCR producing long-lasting memory of previous events. Seismic sequences are predicted to be significantly longer than those observed along plate boundaries. It is also coherent with the positive correlation between b-value and p-value. Data seem to support the hypothesis of long recurrence intervals of bursting seismicity in SDCR. For instance, the New Madrid earthquakes (M$_{w}$ 7.0–7.4), Missouri, USA, that occurred from December 1811 and February 1812 produced a seismic sequence has been still lasting today. Great part of worldwide seismicity occurs in the shallower 50 km of the lithosphere; nevertheless, a not negligible part of the nucleated energy is radiated by deep earthquakes [375]. Although similar to shallow events, deep ones have different rupture behaviors, statistics and aftershocks activity depending on the large-scale structure of subduction zones, local stress conditions, phase changes, geochemical heterogeneity, complexities and rheology. Phase transformations and chemical heterogeneity are thought to be crucial mechanisms for their generation [376].

6 The rules of global geodynamics

What moves the lithosphere? Where does the force that generates plate tectonics come from? The energy is generally interpreted as the dissipation of mantle convection, due to the thermal gradients between the surface and the bottom of the Earth’s mantle. However, several observations collected during the last decades tell another and more complicated story. Both exogenous and endogenous contributions have been highlighted acting in different ways over distinct or superimposed spatial and temporal scales, making the estimation of impact of each effect extremely difficult. In this section, we review the most important results in the field of global geodynamics on the light of the gradients acting on the Earth.

6.1 The role of topography

Topography reflects physical and chemical variations occurring in the lower layers of the Earth. The elevation at surface is proportional to the intensity of forces at work, but it is not a good estimator of the strength of the inner processes because exogenous phenomena ceaselessly shape the shallow Earth, while the characteristic length of the topographic signal is positively correlated to the source depth. Thermal cooling of the oceanic crust and lateral heterogeneity of the upper mantle produce horizontal pressure gradients driving the plate away from mid-ocean ridges. The force causing this effect, called, although improperly, ridge push [377], results from the balance of the hydrostatic pressure due to the upper water column, the lithostatic pressure produced by the weight of the crust and lithospheric mantle laying on the asthenospheric mantle and the lateral stress induced by the mantle at the ridge because of the difference of height according to Eq. 9. The classical derivation [122]

$$\begin{aligned} F_{rp} \approx g \rho _{m} \alpha \Delta T \kappa t \left( 1+\frac{2 \rho _{m} \alpha \Delta T }{\pi (\rho _{m}-\rho _{w})}\right) \end{aligned}$$

(33)

is obtained assuming that the gradient of density is mainly controlled by thermal cooling and other effects are negligible. More sophisticated models also include the contribution of upcoming mantle materials which exaggerate vertical development at ocean ridges. According to Eq. 33, the strength of ridge push is linearly proportional to the crustal age t and the thermal gradient between the lithosphere and the mantle $\Delta T$. Taking the average sizes and properties of the crust and mantle at ocean ridge, $F_{rp} \sim$10$^{12}$ N/m. The basal friction between plates rigidly moving with respect to the underlying layers with velocity ${\dot{u}}$ and the upper mantle balances ridge push by a distance, say L, of a few thousand kilometers. In fact, if we suppose, for the sake of simplicity, that a viscous dissipation occurs across a top-driven interface of thickness Z with the asthenosphere, then

$$\begin{aligned} F_{v} = \frac{1}{Z^{2}}\int _{0}^{L} \int _{0}^{Z}\eta (x,z) {\dot{u}}(x) dzdx \approx \frac{< \eta {\dot{u}} > L }{Z} \end{aligned}$$

(34)

gives $F_{v} \sim 10^{12}$ N/m if $Z \sim 10 -100$ km, $L\sim 10^{4}$ km, ${\dot{u}} \sim 10$ cm/year and $< \eta > \sim 10^{18}$ Pa s. Frictional forces are rather difficult to estimate especially under dynamic transient because of a wide range of possible rheological behaviors and the viscous term is just one of a more complicated pattern; therefore, the previous calculation must be taken with a grain of salt. In particular, if mantle motions due to convection in the asthenosphere are considered and their typical velocity is hypothesized to be of the same order of magnitude of the absolute crustal ones, then, the spatial action range of ridge push may be significantly shortened. In addition, the friction force of transform oceanic faults should be included. The previous estimation is enough to show that viscous force can easily stabilize the effect of ridge push with distance. Ridge push is mainly effective around the ridge crest, where mantle viscosity is lower and a significant melted fraction is present in the shallow lithosphere ($< \eta > \le 10^{16}$ Pa s. It is also shown, consistently with crustal stress patterns observations, that the elevation of ocean ridges propagates horizontal stress far enough that its contribution affects the whole ocean plate internal stress except for convergent plate boundaries. The analysis of long-term surface displacement are in good agreement with this; moreover, several studies pointed out that a significant correlation exists between the direction of the torque produced by ridge push and absolute plate motion for the North American, South American, Southern Pacific and Cocos plates [15]. Nevertheless, correlation does not mean causation; in this case, more than one reason can be advocated to justify this observation: ocean spreading is nearly orthogonal to subduction margins; therefore, the orientation of plate motions can be due to a combination of effects produced by both the boundary forces, continental plates also move almost in the same direction, e.g., with the largest component of velocity parallel to the Equator line and westerly directed with respect to the classical hotspot reference frame, with few exceptions, even if they are ridge-less. Ridge push is a local force acting along the direction of the topographic gradient; significant variations of local direction of crustal displacements result from transform faults friction and lateral heterogeneity of basal viscosity so that, partial melting, hydration and low viscosity material enhance local plate motion. Viscosity is observed to increase up to three orders of magnitude starting from the ridge towards the boundaries of the plates ($< \eta > \approx 10^{18}$ Pa s), e.g., [18]. This result reinforces the idea that ridge push cannot control the motion of the whole plates, above all the largest oceanic ones, and elevated values of basal viscosity ($< \eta > \ge 10^{19}$ Pa s) completely suppress ridge push in a few hundred kilometers close to the ridge. For this reason, it is unlikely that ridge push can promote subduction processes, at least on the base of the estimated values of viscosity. This conclusion seems to be supported by the measures of misfit between the direction of ridge push and absolute plate motions of the most important plates, also taking into account of other traditionally included contributions such as slab pull [98]. However, the debate about the geodynamic implications of ridge push is still open. For instance, the relative velocity between Indian and Eurasian plates has been going down progressively since 50 Myr ago, with an abrupt drop between 45 and 35 Myr followed by a slow decrease [197]. Nowadays, India-Eurasia collision goes forward at about 35 mm/year, while at the end of the Cenozoic Era, at its peak, the rate was $\approx$ 160 mm/year. More than one hypothesis has been formulated for explaining the fall of the convergence rate. Balancing pre-collision and post-collision forces, it turns out that the local ridge-push term approximately amounts at the same order of magnitude of the hypothesized slab pull force (10$^{12}$ N/m) and significantly smaller than the force produced by the continental collision. Therefore, basal traction from the mantle should be required to overcome the resisting force at Eurasia-India boundary. The viscosity of the lithosphere-asthenosphere interface is a crucial property for understanding the role of topography on plate motions. Ocean plates rest on low-viscosity material, on the contrary, the continental lithosphere makes the width of asthenosphere thinner, with higher minimal viscosity value. For this reason, the effective role of topography is still debated, above all regarding the evolution of continental margins where viscosity is likely too high to allow the horizontal compression of adjacent lithosphere to enhance plate motion. Returning to the previous example of the India-Asia collision, it has been suggested that the slowing of convergence usually attributed to the development of the Himalaya may be caused by the deformation of the continental lithosphere producing viscous resistance against the slab [198]. Topography has rates of variability dictated by the erosion rate, sediment supply, tectonic uplift/subsidence, climate and eustacy. However, tectonics is always winning, i.e., it is faster in generating topography than the erosion to remove the morphological gradients. Topography determines gradients in the lithostatic load, which acts in opposite way as a function of the tectonic setting. In fact, it represents the $\sigma _{1}$ in extensional settings, whereas it is $\sigma _{3}$ in contractional tectonic settings. Therefore, the increase of topography favors normal faulting, whereas a decrease in the lithostatic load enhances thrust faulting [378].

6.2 Mantle drag

The idea of plate motions driven by mantle circulation predates the dawn of plate tectonics. The fundamental idea is that mantle convection is able to produce coherent crustal displacements over large spatial scales. The crucial hypothesis is that the mechanical coupling between the top of the convection cells and the base of the oceanic and continental crust due to the viscosity of the asthenospheric mantle is sufficient for allowing the drag of lithosphere. In its original formulation, mantle drag was introduced to explain why stress drops occur during earthquakes and to provide a reason for the peculiar trend of surface displacement as a function of the distance from the fault plane [379]. While the upper crust is rigid, elastic and featured by extremely elevated viscosity, the lower layers are hotter, weaker by a rheological viewpoint, hence they can accommodate differential stress progressively inducing a gradient of velocity between the shallow crust and the basal lithosphere. Then, lateral variations of viscosity and complex patterns of mantle convection are suggested to be among the main energy sources of plate motions. The basal shear stress exerted by the the mantle flow dragging the lithosphere can be estimated as

$$\begin{aligned} \sigma _{md}(\xi ) = \frac{1}{Z^{2}}\int _{0}^{Z}\eta (\xi ,z) ~\delta v(\xi ) ~dz \end{aligned}$$

(35)

where Z represents the width of the dragging mantle, $\eta$ is the effective viscosity and $\delta v(\xi )$ is the gradient velocity between the crust and the underlying mantle. The force per unit length normal to the direction of motion is given by

$$\begin{aligned} F_{md} = \frac{1}{Z^{2}}\int _{0}^{L} \left( \delta v(x)~\int _{0}^{Z}\eta (x, z) ~dz \right) dx. \end{aligned}$$

(36)

L is the size of the plate. Following the usual assumptions, i.e., $Z \sim 10^{2}$ km, the average dimension of the plates is $L\sim 10^{3}-10^{4}$ km, the gradient velocity is of the same order of magnitude of absolute plate velocity $\delta v \sim 1-10$ cm/year and the effective viscosity is dominated by the values of the weakest layers $< \eta > \sim 10^{16}-10^{18}$ Pa s according to the kind of plate and the thickness of the crust [18, 380, 381]), which are similar to the values used for the calculation of the ridge push contribution, $F_{md} \sim 10^{10}-10^{11}$ N/m. Therefore, under reasonable, classical hypothesis for parameters assignment, the local force provided by mantle drag may be significant for plate motions [382]. Even though it is about two orders of magnitude smaller than boundary forces, it acts below the whole Earth’s surface; therefore, its effect can be more widespread and potentially even dominant for slab-less plates or far from hot spots and ocean ridges. There are some evidences in favor of an active role of mantle convection on plate motions. Among them, it was noticed that the basal shear stress and the average crustal earthquake stress drop are compatible with each other [379]. Moreover, a significant correlation exists between the strain release by earthquakes at boundaries and plate margins slip rates, e.g., [383] (compare with Paragraph 5.3). In addition, the basal shear traction of the largest slab-less plates for which the bars of error is well estimated and limited, such as Africa (0.2 MPa), North America (0.6 MPa); Eurasia (1.0 MPa) and South America (1.0 MPa) according to [205], is almost parallel to their absolute plate velocity. It is suggestive of a causal relationship between mantle drag and plate motion. On the contrary, significant torques have been estimated for plates with slabs and ridges. Therefore, the role of mantle drag has been suggested to be important for large continental plates without slabs. For instance, it is the case of North-America, which moves to west with respect to the underlying mantle without the effect of significant boundary forces [384]. Mantle drag has been also advocated for explaining the Cenozoic evolution of the India-Asia collision, but its effective role is still debated [385, 386]. Computational simulations taking into account of local rheology, geodetic data, mantle seismic anomalies and other observables proved that the mean basal strength traction is, in turn, statistically larger for smaller plates [205]; nevertheless, small plates are more sensitive to boundary effects with respect to the larger ones. Mantle drag may also have played a role in the lateral variation of crustal thickness, cratonic evolution [387] and seismic anisotropy in ocean basins [381]. However, several concerns have been formulated about the effective power of drag of large scale plate surfaces; we list the most important. Mantle convection occurs in stratified mass transfer cells according to the Rayleigh-Benard model. The ratio between lateral and top-bottom sizes of the Rayleigh-Benard cells is nearly one with few exceptions. Since the vertical width of the cells is limited to the thickness of the upper mantle (about 600 km) the same cell cannot drive plates for more than about one thousand kilometers, which is far below the average size of crustal plates [144, 388]. To be a little bit more rigorous, in Paragraph 4.1 was proven that mantle convection is stratified, as proved by seismic reflectors, geo-chemical data and ultra-low velocity zones; hence, the previous is a clear overestimation of the largest possible size of elementary convective cells in the upper mantle. Grounded on this observation, it is unlikely that mantle can drag effectively average-sized plates unless coherent convection occurs over large spatial scales, which is almost impossible without external forcing. It is also the conclusion of recent works aiming at understanding the relative impact of different forces on geodynamics, e.g., [389]. The frequency-size distribution of plate area is a power-law distribution with an upper cut-off due to the finite Earth [155]. This observation suggests that self-organization in plate fragmentation due to boundary interaction is likely the cause of crustal breaking and not opposite mantle tractions [158]. Another inconsistency regards the distribution of absolute plate velocity as a function of the upper-asthenospheric mantle viscosity. The fastest plates are those with lower basal viscosity, which contradicts Eq. 36. For instance, the basal effective viscosity for the Pacific plate, moving at about $\sim$ 1.06$^{\circ }/Myr$ [164], is about $< \eta _{Pac} > \sim 10^{15}-10^{17}$ Pa s, e.g., [18, 390], while the North American plate is featured by $< \eta _{Pac} > \sim 10^{19}-10^{20}$ Pa s and $\omega \sim$ 0.39$^{\circ }/Myr$ in HS3-NUVEL1A. At last, since the characteristic size of convective cells in the mantle is $\sim 10^{3}$ km or smaller (compare with the discussion above), then $\sim 10^{3}$ cells or more interact with the lithosphere. If no external forces act, the spin of each cell is randomly oriented except for a correlation with its first neighbors. Then, the total sum of the contributions to displacement at surface is almost zero because of trivial odds and the central limit theorem. This result is not compatible with the observed westward drift of the lithosphere in the absolute reference frames. In summary, mantle drag can be effective in enhancing small plate motions with elevated basal viscosity, i.e., continental plates, without intense boundary forces and local crustal interactions. Even though acting below the whole Earth’s surface, its potential is suppressed by the maximum possible size of convective cells, mantle stratification and lateral changes of viscosity.

6.3 Subductions

Subductions are fundamental geological structures for geodynamics. Although their length amounts at about 50,000 km, so just 20$\%$ of the total extent of plate boundaries, they allow the mass balance of the shallow Earth being responsible for more than 80$\%$ of destruction of oceanic and part of continental lithosphere. This apparent asymmetry stems from the elevated mean subduction velocity ($\sim$ 6.2 cm/year), which is twice as much the collective rate of other plate margins ($\sim$ 3 cm/year) [155]. These observations suggested that boundary forces may act on downgoing slabs due to thermal negative buoyancy with respect to the mantle, e.g., [12]. In its original formulation [377, 391], slab pull was suggested to be produced by a temperature gradient between the thermal structure of the subduing slab and a homogenized perpetually convecting mantle. Its temperature was also supposed to be homogeneous. So, a first estimation of the slab-pull force was given by [122]

$$\begin{aligned} F_{nsp} = \alpha \rho g \int _{S} \Delta T(\xi ) ~dS \approx \alpha \rho g L \int _{0}^{Z} \Delta T(z) ~dz \sim 2\alpha \rho g L T_{m} \sqrt{\frac{\kappa t}{\pi }} \end{aligned}$$

(37)

where $\Delta T(\xi )$ is the difference of temperature between the inner slab and the average thermal condition of the upper mantle, $T_{m}$, in the position described by the coordinate $\xi$, $\kappa$ is the thermal diffusivity, $\alpha \sim 3 \times 10^{-5}$ K$^{-1}$ is the coefficient of thermal expansion, Z is the maximum depth reached by the slab tip, L represents the length of the trench and S is the area of the slab. Taking usual values for the parameters, the naive-slab pull force is $F_{nsp} \sim 10^{13}$ N/m. This result compelled many geoscientists that slab pull is the principal force acting on plates and hence the main cause of plate tectonics. However, $F_{sp}$ given above is obtained by rough and unreliable approximations and even fake assumptions, also concerning the choice of the parameters, e.g. using the same density $\rho _{s}$ = 3.3 g/cm$^{3}$ for modeling both the density of the upper mantle and the slab is not reliable, compare with [122]. Equation 37 does not take into account of the contribution of progressive heating of the slab due to friction, while only the thermal diffusion term $T(z,t) \sim T_{m} erf \left( \frac{z}{2\kappa t}\right)$ is hypothesized to drive the suction of the oceanic lithosphere at depth. What is more important is that Eq. 37 assumes complete homogeneity of the upper mantle, which is resoundingly disproved by physical petrology, seismic investigations of the Earth interiors and also by classical one dimensional models of density and temperature profiles [88]. A significant stratification with increasing density and temperature at depth must be taken into account for a reliable estimate of slab pull forces, which can be roughly modeled as follows

$$\begin{aligned} F_{tsp} = \alpha g L \int _{0}^{Z} \left[ \rho _{m}(z) T_{m}(z) - \rho _{s}(z) T_{s}(z) \right] ~dz \end{aligned}$$

(38)

and solved numerically as a function of the slab length. $\rho _{s}(z)$ and $\rho _{m}(z)$ stand for the density of the slab and the surrounding mantle at depth z respectively, L is the length of the subduction zone. They are written explicitly because the largest variations of density are not due to thermal expansion, structural transitions have a major impact on it. Moreover, the effect of friction and dissipation should be introduced in order to calculate the net contribution of slab pull to geodynamics. Numerical simulations show that slab stagnation is likely without external forces pushing the slab downwards. Therefore, the role of phase transition is crucial, e.g., [98]. The most important ones, the 410 km discontinuity, due to the transition from $\alpha$-olivine to $\beta$-wadsleyite, and the 660 km passage from $\gamma$-spinel and perovskite, have been thought to control slab sinking. The first one is an exothermic transition, while the second is an endothermic one. This means that the 410 km discontinuity is associated to $dp/dT > 0$, hence to lower pressure, then to shallower depth inside the slightly colder slab. It causes a downward force acting on the slab. This force can be written as

$$\begin{aligned} F_{dsp} = g \Delta \rho _{\alpha -\beta } \int _{0}^{L} \delta h(x) ~dx \end{aligned}$$

(39)

where h(x) is the elevation of transition produced by the thermal gradient. Then, a theoretical estimation of pure slab pull contributions is dominated by the effect of the 410-km structural transition and gives $F_{sp} = F_{tsp} + F_{dsp} \sim 10^{12}$ N/m, which is comparable to the ridge push force, once the olivine-spinel discontinuity is reached. This result is compatible with the outputs of analogous-subduction laboratory experiments [13]. On the contrary, the 660 km discontinuity is endothermic, so it produces a lowering of the transition point rendering the plate locally buoyant with respect to the surrounding mantle. Therefore, slab penetration in the lower mantle is inhibited. However, a common viewpoint does not exists about the possibility of slabs to pass across this transition, above all without external forces to push them down. Moreover, what is described above requires that the slab can reach the 410 km transition, which is not trivial without external forces acting on the subduction zone. A flurry of geological evidences mine the effectiveness of the slab pull forces:

Fig. 18

Age vs slab dip plots for five different depth ranges, with data measured along sections perpendicular to the trench. These diagrams do not support an age-dependent negative buoyancy of slabs and the consequent supposed slab pull. After [7]

• The analysis of slab dip versus the age of the subducting oceanic lithosphere lacks of correlation [7] (Fig. 18).

  This is not in agreement with the idea of dominant slab pull contribution to subduction dynamics because the negative buoyancy of slabs should determine the pull of plates [392], but the dip of the subduction zones is not correlated with the age and the thermal state of the downgoing plates.

• a positive correlation exists between the area of plates vs their absolute angular velocities in the shallow hot spot reference frame, regardless the fraction of subduing boundary.

• The oceanic lithosphere is nothing but frozen shallow asthenosphere, previously depleted beneath a mid-oceanic ridge. Therefore, it is lighter than the deeper undepleted asthenosphere [393].

• The assumption that the lithosphere is heavier only because it is cooler is not necessarily true because of the vertical stratification of mantle density. Taking $\alpha \sim 3 \times 10^{-5}$ K$^{-1}$, then a thermal gradient of $\Delta T =$ 1000$^{\circ }$ C produces $\Delta \rho \approx$ 0.09 g/cm$^{3}$. Oceanic crust is formed by sediments ($\rho \sim$ 1.1–2.7 g/cm$^{3}$) in the upper layer 0.2–0.8 km thick; below them basalts ($\rho \sim$ 2.8–2.9), gabbro ($\rho \sim$ 2.9 g/cm$^{3}$) and ultramafic rocks (e.g., peridotites $\rho \sim$ 3.3–3.4 g/cm$^{3}$) are layered, so that its density is about 3.0–3.1 g/cm$^{3}$. On the other hand the density inside the upper mantle increases from 3.3–3.4 g/cm$^{3}$ at about 50–100 km in depth to 4.0 g/cm$^{3}$ at 650 km. This density contrast should require a thermal gradient larger than 3000$^{\circ }$ C for allowing thermal slab pull. Therefore, thermal slab pull could be overestimated if not negative [66, 151, 394, 395].

• A density anomaly that is suggested to contribute to slab pull comes from eclogitization of the subducting oceanic crust. This process involves only a thin layer ($\sim$ 5 km thick) and not the whole lithosphere; therefore, only a small portion of the crust, about 10$\%$, may take part to additional negative buoyancy, not enough to make the whole lithosphere denser than the mantle [396]. Nevertheless, the eclogites reach densities of about 3.4–3.5 g/cm$^{3}$ at depths of about 100 km [397], while the density of the ambient mantle at comparable depths is 3.4 g/cm$^{3}$. Therefore, even exaggerating this, the effect of eclogitization to the entire subduction lithosphere, thermal slab pull is not enough to reach the 410 km deep transition zone at density 3.7 g/cm$^{3}$ ( [88]) without an external force.

• Subduction processes also involve continental lithosphere descending down to 200 km, e.g., [398, 399], although the average continental crust is probably positively buoyant with respect to mantle rocks. Alps, Apennines, Dinaric Alps, Zagros, Himalayan, Caucasus Mountains are associated with continental subduction zones.

• The slab pull force is zero by definition at the initiation of the process; therefore, subductions cannot be produced by boundary forces, e.g., [400,401,402,403,404].

• Down-dip compression affects most of the slabs, this effect is complete below 300 km [405]. In fact, the intra-slab focal mechanisms of the westerly-directed slabs show dominant down-dip compression, whereas the opposite easterly-directed subductions are rather characterized by down-dip extension [396]. This peculiar asymmetry suggests that the W-slabs are forced to sink by top-driven compressive push and not by pull acting from the bottom, and viceversa.

• In hot spot reference frames a significant westward drift of the lithosphere is observed. Slab pull does not explain this phenomenon. Absolute plate velocities are inversely proportional to the basal viscosity. No significant correlation has been found between the length of the subduction zones and the age of the downgoing lithosphere, e.g., [92] and references therein.

• The oceanic lithosphere has low strength under extension ($\sim$ 10$^{12}$ N/m, [406, 407]) and it cannot resist the naive-slab pull force derived in [122], which should be considered completely unreliable. Mantle drag and viscous traction acting on the plates induced by slab sinking can contribute to solve this problem if added to a lower effective slab pull [408].

On the base of these observations, it is unlikely that the slab-pull force can be sufficient to explain the dynamics of subduction zones (Fig. 19) as listed in [92].

Fig. 19

Left panel, basic kinematics of subduction zones, assuming fixed the upper plate U, a converging lower plate L, and a transient subduction hinge, H. The subduction rate S is given by $V_{S}=V_{H}-V_{L}$. Values are only as an example. S increases when H diverges relative to the upper plate (a), whereas S decreases if H converges (b). The movements diverging from the upper plate are positive, whereas they are negative when converging. The case (a) is accompanied by backarc spreading, a low prism and is typical of W-directed subduction zones, whereas in case (b) double verging and elevated orogens form and is more frequent along E- to NNE-directed subduction zones. Note that in both W- and E–NE-directed subduction zones, the hinge migrates eastward relative to the upper plate, suggesting a global tuning in subduction processes. Right upper panel, the Tonga subduction zone. Note that the subduction rate is the sum of convergence between U and L, plus the motion of H. This is the fastest subduction in the world, where more than 700 km of lithosphere should sink in about 3 Ma. Right lower panel, the convergence between Nazca and South America plates is faster than the shortening in the Andes. The upper plate shortening decreases the subduction rate. The convergence/shortening ratio is about 1.88. After [396]

On this regard, also another evidence should be taken into account: different kinds of subductions have been highlighted. Differences in subduction styles have been explained as due to variations in convergence velocity, stress, plate thickness and age [409,410,411,412,413]. However, there are several cases where the same plate is subducting with opposite directions (west versus east or northeast) and angles, generating different orogens, e.g., the Adriatic continental plate sinking both westward beneath the Apennines and eastward beneath the Dinarides, or the northwestern Australia subducting both beneath the Banda Arc to the west and Papua-New Guinea to the northeast (Figs. 20 and 21).

Fig. 20

Schematic section showing that in the Alpine setting, the subduction rate is decreased by the migration of the hinge, H, toward the upper plate, U, and the orogen in the final collisional stage is composed both by the upper and lower plate, L, rocks. In the converse Apenninic setting, the subduction rate is rather increased by the migration of H away from U, and shallow rocks of L form the accretionary prism. The relatively shallower asthenosphere in the hanging wall is typical of W-directed subduction zones. This is coherent with the relatively higher heat flow in the hanging wall of the W-directed subduction zone along the backarc basin (after [92])

Fig. 21

Comparison of two end-members of orogens associated to opposite subduction zones, i.e., the Alps above and the Apennines below (after [414]) associated respectively to a subduction following and opposing the “eastward” mantle flow. The Alps have the subduction hinge converging relative to the upper plate, hence they have a double verging orogen, two shallow foreland basins, deep rocks involved and outcropping, high topography and no backarc basin. On the other hand, the Apennines are single verging, they are mainly composed of shallow crust rocks scraped off from the accretion of the lower Adriatic plate, they have low elevation and they are cross-cut by diffuse normal faulting generated by the slab hinge retreating from the upper plate and producing backarc extension

In addition, slabs with the same age and similar thickness can show completely different dip angles and behavior at depth. This proves that age, thickness and origin of the down-going lithosphere may not be a crucial feature for subduction dynamics.

6.4 The global tectonic pattern

Several pieces of evidence have been found highlighting a degree of polarization of global geodynamics. For instance, average topography and free-air gravity profiles across subduction zones show different signatures according to the polarity of the slab, i.e., according to its direction, if it is westerly or easterly directed. As an example, the profile across the Pacific ocean is featured by low topography along the W-directed subduction zones of the western Pacific when compared to the eastern counterpart. This geographic property is also accompanied by coherent gravity anomalies, i.e., more pronounced along the west-directed subduction zones and the negative gravity [187]. Another classical asymmetry concerns the subduction zones, which are steeper if westerly directed than those with opposite polarity [366] (Fig. 22).

Fig. 22

Subduction asymmetries and related global mantle flow. Topography and earthquakes hypocenters at convergent boundaries that point to their asymmetries, due to the kinematics of the subduction hinge and the geographical polarity. Here the asymmetry in volumes of the subducted lithosphere is striking. Since $\sim$214 km$^{3}$/year of lithosphere are currently subducting below slabs with mainly W-directed slabs whereas only $\sim$88 km$^{3}$/year are subducting below subduction zones with mainly E to NE-directed slabs, we would expect that about 120 km$^{3}$/year of material moves from W to E within the mantle, compensating the gradient in slab recycling. This leads to a global “eastward” mantle flow (after [219])

Moreover, also accretionary prisms are suggested to be affected by their spatial orientation, e.g., [415]. The orogens associated with easterly-directed subduction zones are about 5–10 times larger than the accretionary prisms related to westerly-directed subduction zones. This property implies that the decollements are deeper and exhume larger volumes along easterly-oriented subduction zones than those with opposite polarity. Not only subductions and accretionary prisms: asymmetries have been also discovered in back-arc basins with concave geometry at the western margin of the backarc basin opposed to the convexity of the external arc. However, the most important asymmetric feature in global geodynamics is the already cited west-ward drift of the lithosphere. Lithospheric plates move along a mainstream that is westerly polarized, being their tectonic equator at about 30$^{\circ }$ relative to the geographic equator (Fig. 23).

Fig. 23

Left, the mainstream of plate motions in the shallow hot spots reference frame (after [416]). The red dots are earthquakes $M \ge$ 6 which disappear in the polar areas. The flow of plates and its tectonic equator have an inclination that is close to the ecliptic plane plus the Moon revolution plane (about 29$^{\circ }$) and it mimics the angle of the Moon projection on the Earth. Right, the tectonic equator represents the bisector of the present geographic equator and the equator inclination in 13,000 yr due to the Earth’s axis precession. The Earth lithosphere has a Maxwell time (viscosity $\eta /\mu$ rigidity) compatible with the precession time (26,000 yr), explaining a visco-plastic behavior of the lithosphere at that timescale and the inclination of the tectonic versus the geographic equator (after [390])

This pattern can be interpreted as the result of the Earth’s secular cooling and the astronomical torques that govern the speed of plates and the distribution of seismicity decreasing toward the polar areas. In this level, the asthenosphere exhibits a lowering of viscosity that allows the lithosphere to “slip” over the asthenosphere (Fig. 24).

Fig. 24

Shear-wave absolute tomography after [178] along the tectonic equator, on which are inferred and schematized the westerly polarized vectors of the lithosphere (black arrows) and the mantle “eastward” relative motion (gray arrows). Notice the concentrated larger volumes of lithospheric recycling along the western Pacific slabs. The mantle compensates the lithospheric loss with a diffuse relatively easterly directed upwelling up to the sheared low-velocity zone (LVZ), where the lithosphere is decoupled and shifting to the west. Numbers above the tomographic section indicate the age of the oceanic crust (in Ma). EPR East Pacific Rise, MAR Mid-Atlantic Ridge, IR Indian Ridge, VS Shear-wave velocity. Numbers at the bottom are longitude (after [20])

Thus, the lithosphere is slightly decoupled from the underlying mantle, being able to move a few centimeters per year. Among other things, this movement is polarized westward, or rather along a flow exemplified by the “tectonic equator”, which is a maximum circle forming an angle of about 30$^{\circ }$ with the geographic equator. A simple explanation is that there are viscosity variations in the low-velocity channel that constrain the degree of decoupling between the individual plate and mantle. That is, lateral viscosity gradients in the plane of uncoupling control the velocity gradients between the plates and thus the seismicity that is due to pressure gradients that develop at the margins between the plates, whether they are approaching, receding, or sliding sideways. The fastest-moving plate in the world, as already mentioned, is the Pacific plate, which moves west-northwestward relative to the mantle by more than 10 cm per year and is the plate that has below it a low-velocity channel with the lowest known viscosity (10$^{17}$ Pa s), supporting the hypothesis that the velocity of the plates with respect to the mantle, and thus also to each other, is a function of the viscosity gradients at their base. A key factor in the control of plate tectonics is thus the influence of lateral variations in thickness, density, and composition in both the lithosphere and asthenospheric mantle. These contrasts control the amount of relative motion between the lithosphere and asthenosphere, in essence the speed of plates. If there were a perfectly uniform global mechanical coupling between lithosphere and mantle, then, ideally, the lithosphere would behave as a single, coherent shell with no internal relative velocities: that is, there would be no plate tectonics. This is perhaps the situation on other planets, where the continental lithosphere has probably grown to cover the entire globe, which is slowly happening on Earth as well. With a thick and uniform continental lithosphere of 150–200 km covering the entire planet, there would be no plate tectonics because being a condition of equilibrium there would be no possibility to compress or stretch the lithosphere. This is likely one of the reasons why there is no plate tectonics, as we know it, on other planets. Instead, the limited presence of continental lithosphere on the Earth’s surface and the contrast with the thinner and denser oceanic lithosphere, induce a pattern of differential velocities and therefore of relative movements among lithospheric plates, because each of them is characterized at its base by different viscosity values of the asthenosphere. Viscosity and other gradients ultimately control the magnitude of the lithosphere detachment and its “absolute” velocity. The polarization of the lithosphere towards the west is able to explain the greater inclination of the westerly-oriented subductions, compared to those opposite, as well as the difference between the associated mountain ranges: paradigmatic examples are the comparison between the western Pacific with its eastern side or simply the comparison between the characteristics of the Apennines compared to the Alps. A key readout is the kinematics of the subduction zone hinge, which generally moves away from the canopy plate in “westward” directed subductions, while approaching the canopy plate in opposite subductions. Based on the velocities of the GPS stations and the hinge behavior of the subduction zones, it is possible to calculate the volumes of lithosphere wedged into the Earth’s mantle: they are about 302±30 km$^{3}$/year [219]. However, there is an asymmetry, i.e., the volumes of subductions that submerge towards the west is more than 214±21 km$^{3}$/year, the remainder is for the opposite subductions towards the east (American cordilleras) or northeast (Alpine-Himalayan system). Therefore, a difference in recycling between the two systems implies an unbalance of mass. It must be compensated, so the Earth’s mantle must relatively migrate from west to east to replenish the mass gradient. This is consistent with a polarized plate tectonics, with the lithosphere moving westward relatively to the mantle. This asymmetry is also compatible with the difference between mountain ranges associated with subduction zones: low, with a deep fore-arc basin and the presence of a back-arc basin for westward-directed subductions, whereas they are high and composed of large outcrops of deep, crystalline rocks, with a shallow fore-arc and the absence of a back-arc basin for eastward- or northeastward-directed slabs. Examples of this asymmetry are the west versus east Pacific subductions, or the Apennines versus the Alps. However, no one of the forces we described in the previous paragraphs of this section can produce the asymmetries observed worldwide. This suggests that the effect of an additional force may be important for solving the puzzle of global geodynamics. What is the force that drives the lithosphere westward? Based on some of the observations that we have mentioned at the beginning of the paragraph, as early as the Seventies of the last century, the hypothesis was advanced that geodynamics could be affected by the lunar and solar tides. Despite some initial consensus and numerous confirmations, it was shelved as tidal forces were estimated too weak to generate a sufficient torque needed for moving the lithosphere westward with respect to the underlying mantle. Now, if the evidence described so far is not a coincidence, which is likely to say the least, and since not other torques act on the Earth to generate a polarized dynamics, one is forced to admit that, in some way, the tides should have some influence on geodynamics [417]. Therefore, it is convenient to briefly analyze the contribution of tidal forces on plate tectonics, focusing, as in the cases previously considered, on both their limits and strengths. The Earth undergoes significant gravitational forces generated by the Moon and Sun. In each place of the planet, a total force is given by the sum of the gravitational and centripetal one

$$\begin{aligned} \vec {F}_{{\mathcal {M}}}(P) = \vec {F}_{G}(P) + \vec {F}_{C}(P) \end{aligned}$$

(40)

from which the tidal acceleration can be immediately obtained

$$\begin{aligned} a = \frac{GM}{(R - r)^{2}} - \frac{GM}{R^{2}} \simeq \frac{2MGr}{R^{3}} \end{aligned}$$

(41)

in the last step, the distance of the celestial bodies, R, is assumed to be larger than the radius of the Earth $R_{T}$. The gravitational potential due to celestial body, e.g., Sun or Moon, with mass M, at a point P at a distance r from the center of the planet, can be expanded in a series of Legendre polynomials

$$\begin{aligned} W(R,\Psi ) = \frac{GM}{R} \sum _{n=2}^{\infty } \left( \frac{r}{R}\right) ^{n} P_{n}(cos\Psi ) \end{aligned}$$

(42)

From the ratios of masses and their mean distances, it follows that the solar tidal perturbation is $\sim$ 0.46 times the lunar tides. So, we can write that the total tidal potential is approximately given by the sum of lunar and solar dominant perturbations

$$\begin{aligned} W(R, \Psi ) \simeq \frac{GM}{R} \bigg (\frac{r}{R}\bigg )^{2} P_{2}(cos\Psi ) \end{aligned}$$

(43)

where $\Psi$ is the zenith of the body with respect to P and $P_{2}$ is the second degree Legendre polynomial, $cos\Psi = \cos \theta \cos \delta + \sin \theta \sin \delta \cos (\phi - \alpha )$, $\theta$ is the colatitude and $\phi$ is the easterly longitude of P, $\delta$ is the codeclination and $\alpha$ is the right-ascension of the body. The three terms represent the zonal, tesseral, and sectoral tides respectively [418]. We can write the potential so that three different contributions are highlighted

$$\begin{aligned} W(R, \Psi _{1}, \Psi _{2}, \Psi _{3}) = \frac{3GMr^{2}}{4R^{3}}[\Psi _{1} + \Psi _{2} + \Psi _{3}] \end{aligned}$$

(44)

where $\Psi _{1}$, $\Psi _{2}$ and $\Psi _{3}$ are functions of $\delta$, $\theta$ and $\phi$. Then, the displacement is given by

$$\begin{aligned} \delta {\mathcal {H}}(R,\Psi _{1}, \Psi _{2}, \Psi _{3}) = \frac{W(R,\Psi _{1}, \Psi _{2}, \Psi _{3})}{g} = \frac{3GMr^{2}}{4gR^{3}}\bigg (\Psi _{1} + \Psi _{2} + \Psi _{3}\bigg )\nonumber \\ \end{aligned}$$

(45)

The largest tidal harmonics are listed in Table 1 [419].

Table 1 Largest long-period tidal frequencies

The elastic deformation of the Earth has two modes: spheroidal and toroidal, but tidal forces excite only the spheroidal modes ( [320]). Displacements can be written in spherical coordinates [420]

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{r}=\frac{h_{2}(r)}{g(r)} W(r,\theta ,\phi ) \\ u_{\theta }= \frac{l_{2}(r)}{g(r)} \frac{\partial W(r,\theta ,\phi )}{\partial \theta }\\ u_{\phi }= \frac{l_{2}(r)}{g(r)\sin \theta } \frac{\partial W(r,\theta ,\phi )}{\partial \phi }\\ \end{array}\right. } \end{aligned}$$

(46)

$h_{2}$ and $l_{2}$ are the so-called Love and Shida numbers. So far, we have considered a perfectly spherical non-rotating elastic Earth. However, the Earth is not completely elastic at all. The anelasticity of the Earth has a practical effect. When the Moon or the Sun are at their own zenith, the surface protrudes with a few minutes delay, resulting in a misaligned bulge with respect to the line of maximum Earth–Moon gravitational attraction [421]. The tidal lag is given by [422]

$$\begin{aligned} \epsilon = \arctan {\left[ \frac{1}{4 \pi E} \oint \left( -\frac{dE}{dt} \right) dt \right] } \end{aligned}$$

(47)

where E is the maximum potential energy accumulated during by the tidal strain, while the quantity $-\frac{dE}{dt}$ represents the loss rate of energy dissipated during a tidal cycle. The larger the tidal lag, the larger the dissipated energy. In the case of the Earth, $\epsilon \sim$ 0.3–2.4$^{\circ }$ (Fig. 25).

Fig. 25

The tidal bulge should ideally form instantaneously along the Earth–Moon gravitational alignment. However, the anelastic component of the Earth determines a small delay in the Earth’s reaction to the Moon’s attraction. The greater the anelasticity, the larger the angle (0.3$^{\circ }$–2$^{\circ }$) This should generate a westerly oriented torque that could explain the westward drift of the lithosphere relative to the mantle

The tidal torque on the Earth produced by the Sun and the Moon reads

$$\begin{aligned} N_{tide} \sim \frac{9Gr_{e}^{5}}{4}\left[ \frac{m_{m}^{2} }{R_{m}^{6}\left( 1+\frac{19 \mu _{m}}{2g \rho _{m}r_{e}}\right) } + \frac{m_{s}^{2} }{R_{s}^{6}\left( 1+\frac{19 \mu _{s}}{2g \rho _{s}r_{e}}\right) }\right] \sin (2\epsilon ) \approx 4.5 \times 10^{16} N\cdot m.\nonumber \\ \end{aligned}$$

(48)

$R_{m}$ and $R_{s}$, $m_{m}$ and $m_{s}$, $\mu _{m}$ and $\mu _{s}$ are respectively the distance from our planet, the mass and the average rigidity of the Moon and the Sun, $r_{e}$ is the Earth’s radius and G is the universal gravitational constant. A significant portion of the torque above is dissipated within the upper mantle (a straightforward calculation gives $\Delta N \sim 0.66 N$). Therefore, the bulge produces a westward oriented momentum (Fig. 26).

Fig. 26

Lunisolar tidal drag on the Earth. The Earth viewed from above the North pole rotates eastward about 28 times faster than the Moon and the tidal bulge is misaligned ($\approx$0.1$^{\circ }$-0.3$^{\circ }$) relative to the gravitational alignment among the two celestial bodies, due to the delay generated by the anelastic component of our planet. The misplaced excess of mass and the faster rotation determine a westerly-directed torque on the lithosphere that is tuned by the tidal harmonics, which leave a nonzero horizontal component of the tidal drag, controlling plate velocities. Notice the longer “westerly” vector of the horizontal displacement which determines the residual (after [390])

This was suggested to be the reason of the westward drift of the lithosphere. This represents a small brake on the Earth’s rotation, which slows down by about 2 ms per century, explaining why 400 million years ago the year was made up of about 400 days and a day lasted about 20 hours (Fig. 27).

Fig. 27

The decoupling of the lithosphere from the asthenosphere is suggested to be allowed by the low viscosity in the low-velocity zone (LVZ). The combination of convection allowing descent of lithosphere into the mantle and upwelling of asthenosphere along ridge zones and the torque exerted by tidal drag produce the westward drift of the lithosphere

The variation of the length of day has been the object of several investigations in the field of seismology, tectonics and geodynamics (Fig. 28). The conservation of the angular momentum also implies that the Moon moves away from the Earth by about 3.8 cm per year.

Fig. 28

Top: Variation of the length of day ($\Delta$LOD) from 1962 to 2022. Blue points are the data, the pink shaded areas represents the 2$\sigma$ error-range, while the red line stands for the harmonic fit containing the annual and 18.6-years-long period tides. Bottom: FFT of $\Delta$LOD. Tidal frequencies dominate the spectrum. Tides are responsible of great part of $\Delta$LOD. Minor contributions at higher frequencies are due to recurrent ocean currents, megaquakes and atmospheric circulation

Tidal forces are also responsible for the differential rotation of the inner core with respect to the more external layers of the Earth [180]. The amount of yearly dissipated energy in the upper mantle is

$$\begin{aligned} E = - \int _{0}^{2\pi \times n_{days}} \Delta N ~d\theta \approx 2 \times 10^{20} ~J \end{aligned}$$

(49)

which is about two orders of magnitude larger than the energy dissipated by seismic events all over the Earth each year [423]. This result, suggesting the energetic feasibility of tidal drag in moving the lithosphere with respect to the underlying mantle, contributed to compel some researchers that solid Earth tides could drive plate tectonics, e.g., [424,425,426,427,428]. However, assuming a homogeneous upper mantle of viscosity $\eta$ and density $\rho$ at rest in between of a rigid internal spherical core and a thin crustal layer, the torque needed for keeping a differential rotation of angular velocity $\omega$ is given by [429]

$$\begin{aligned} N_{drag} = \frac{8 \pi \eta \omega }{(r_{up}^{-3} - r_{e}^{-3})}. \end{aligned}$$

(50)

Taking $\eta =$ 10$^{21}$ Pa s, $\omega \sim$ 10 cm/year, $r_{e} = 6371$ km and $r_{up} = 6000$ km, we get $N_{drag} \sim 10^{25}$ N$\cdot$m. This value is about nine orders of magnitude larger than the torque provided by tides. Therefore, according to this calculation, tides could be able to speed up plate motions only if $\eta \sim$ 10$^{12}$ Pa s, which is not compatible with observations. Moreover, it has been proved that mantle drag cannot result from differences in angular velocity between concentric shells rotating at different angular velocities [176]. In fact, even though the strength of drag resulting from the net westward rotation of the lithosphere is large enough for allowing a net rotation of about 0.2$^{\circ }$/Myr or more, the period of the largest tides, about twelve and twenty-four hours, is too short for enhance mechanical decoupling of the lithosphere because of the viscosity of the LVZ, which is featured by a Maxwell time of about $\tau \sim 10^{9}$ s [122]. On the base of these results, although based on simplistic hypotheses, the interest about tidal forces and their effect on geodynamics had a complete setback. More detailed analysis has been realized considering the heterogeneity in the mantle and the presence of low velocity zones. Carcaterra and Doglioni [97] showed that the average value of viscosity of the upper mantle is not a crucial quantity for geodynamic purposes. The dominant term affecting the west-ward drift of the lithosphere hypothetically produced to tidal drag depends on the minimal value of viscosity. In literature the minimum values of the asthenospheric viscosity are usually assumed to be in the order of $\eta _{min} \sim 10^{18}$ Pa s [430] or even lower as a consequence of post-seismic transients [101, 431] or below the oceanic crust featured by $\eta _{min} \sim 10^{17}$ Pa s, e.g., [18, 432]. However, these results are not compatible with the tidal torque as well. $\eta _{min} \le 10^{15}$ Pa s is required to permit a tectonic plate drift speed of about some centimeters per year. Even though there are some hints that the viscosity of the upper mantle and LVZ may be overestimated, e.g., [433], it is unlikely that this can ever justify the effectiveness of tidal forces in affecting plate tectonics. Nevertheless, other aspects have been neglected so far. In the previous calculations, the upper mantle is considered to be at rest and the whole effort needed to make its layers slide one upon an other is supposed to be completely furnished by tidal forces. It is obviously not true. Even though stratified, convection certainly occurs in the upper mantle. It has been demonstrated both analytically and via computational simulations that thermal convection between rigid, concentric, axisymmetric, differentially rotating spheres is affected by the kinematic configuration. In fact, heating a fluid at rest from below gives rise to convective cell if the thermal gradient allows it. At the same time, differential rotation also fosters convection with transfer of angular momentum. When both effects happen simultaneously, fluids tend to flow such that they maximize the transfer of angular momentum and heat [434]. Similar configurations studied in several different scientific fields also highlight complex, large-scale organized fluid circulation patterns [435, 436]. Laboratory experiments also support previous conclusions, [437, 438]. This means that the differential rotation is able to polarize mantle convection. There are also some proofs in this sense. Seismic anisotropy in the shallower layers of the upper convecting mantle proves that crystals of olivine and other materials are oriented along the direction of stress produced by the differential velocity between the lithosphere and the base of the astenosphere. So, the tidal drag of the lithosphere may be allowed by a combination of stratified and polarized mantle circulation in the upper mantle, providing part of the lacking torque, and the direct tidal drag of the lithosphere. Regarding the conclusions in [176], according to which tides should not affect plate motions because of their too high frequency with respect to the Maxwell time of the asthenosphere, more than a comment is needed. Of course the semi-diurnal and diurnal tides are the largest of the entire tide spectrum, however, also some significant long-period tides exist, e.g., the 13.66-days and monthly tides, the semi-annual and annual harmonics, polar contributions and the 18.6-years-long period tide, that are not negligible at all. Tides with longer periods are known, for instance, the Solar perigee tide $p_{s}$ (20,941 years) [419] and also large-scale, non-wavelike equilibrium tide should be considered in order to better understand long-lasting geological processes. They are one order of magnitude smaller than the most important tidal harmonic, i.e., the lunar semi-diurnal M$_{2}$ component (Fig. 29).

Fig. 29

The high-frequency tidal oscillations are buffered by the high viscosity of the lithosphere and upper mantle. However, the low-frequency tidal modulations are less attenuated by the upper mantle and therefore they may be effective in allowing decoupling between the lithosphere and the mantle. Although the average viscosity value of the upper mantle, the presence of the low-velocity zone (LVZ) at 100–200 Km depth, makes it possible the lithosphere slide over the underlying mantle under the action of low frequency lunisolar tidal forces. This can be due to the lower viscosity and shorter Maxwell time of the LVZ. The low-velocity zone behaves like a low-pass filter attenuating the high-frequency harmonics (for instance M$_{2}$, S$_{2}$, S$_{1}$, M$_{f}$, M$_{m}$, S$_{Sa}$, S$_{a}$), being its viscosity value too elevated; hence the LVZ has an almost fully elastic behavior. Decreasing the frequency, the elastic response is progressively replaced by a visco-plastic response (4.4, 8.8, 18.6, 25,772 years-long tides), (after [390])

Therefore, tiny modulations of plate motions due to plastic displacements induced by horizontal Solid earth tides should be observed [390] at least with periods comparable with or longer than the asthenospheric Maxwell time $\tau \sim 10^{9}$ s [122], i.e., 18.6- and 20,941-years long periods (Figs. 30 and 31).

Fig. 30

Tidal modulation of plate velocity between central Canada and Germany. (A) GNSS data showing the extension between the DUBO in Canada and Wettzell in Germany (WTZR) stations in from 1997 until 2018. (B) Plot of the residuals of the distance between the two sites. The plot was obtained by subtracting a slope of about 17.4 mm/year. The blue points represent the experimental data while the red curve corresponds to the expected theoretical trend. The residuals of the fit have a $\sigma \approx$ 4.5 mm. (C) The FFT analysis shows the meaningful presence of the harmonics selected to perform the non-linear fit. Also, in this case, there is a strong periodicity of 18.6 year, with an amplitude of $\approx$10 mm. Experimental data show some gaps due to seismic events or to failure of geolocation devices. The frequency is expressed in number of cycles. (D) Table of the data and tidal harmonics. The high quality of this time series is mainly because it is longer than the tidal term of 18.6 years. The C.I. at the level of 95%, i.e. 2$\sigma$ level of the amplitudes estimated by the fit, confirm the tidal signatures

Fig. 31

Detrended displacement of the Hawaiian GNSS station KOK5 (blue) with re-plotted 60-days moving-average data (red line). The FFT spectrum is obtained by the de-trended and filtered KOK5 data. A large peak at 0.05379 cycles/year (18.60 years) is observed, then 6.21 (1/3 of the lunar mode), 4.4 and 3.6 years-long period signals and the solar annual tidal harmonic. Modified from [390]

Short period tides can instead modulate plate motions along over-stressed boundary through modulation of moderate seismicity, e.g., [261, 439, 440], according to the mechanism described in Fig. 32. Even though the mechanisms of tidal triggering of earthquakes are complex and tides may hardly trigger the world’s largest earthquakes of M$_{w} \ge$ 7.5, a significant percentage of $M_{w} \ge 6$ earthquakes could be associated with tidal forcing [417].

Fig. 32

During their passage, tidal waves determine very small variations of gravity. However, these slight variations of the lithostatic load, acting on a lithosphere, which is slowly but persistently pumped westward, could determine the increase, or decrease of $\sigma$1 in extensional environments, or $\sigma$3 in compressional tectonic settings. Therefore, the same variation of the lithostatic load acts in an opposite way in the two different tectonic settings. In this model, the horizontal component of the solid Earth tide slowly accumulates the stress, whereas the vertical component could allow the downloading of the stress as a function of the tectonic setting and the orientation of the faults relative to the tidal waves (modified after [366])

The lack of long-lasting geodetic time series makes this kind of analyses extremely difficult and their reliability debated. These considerations suggest that Solid Earth tides can affect plate tectonics. Tidal forces are also suggested to play a key role in initiation of plate tectonics and, in particular, of subductions on Earth-like planets, e.g., [441]. This is also more likely if one takes into consideration of by far stronger tides and lower mantle viscosity at the dawn of plate tectonics. In summary, tidal drag explains the ubiquitous asymmetry of tectonic settings (Fig. 33) [427] allowing a more complete comprehension of large-scale geodynamics and shedding new light on still poorly understood phenomena.

Fig. 33

The swinging body tides release a permanent residual accounting for the relative motion among tectonic plates as shown in the previous figures. Since the entire lithosphere (LIT) has a net westerly directed rotation, moving along the tectonic equator, the different velocity of plates can be inferred as related to the variable decoupling at the lithosphere base, dictated by the viscosity in the low-velocity zone (LVZ). The faster westerly motion of plates occurs where the underlying LVZ has the lowest viscosity ($\eta _{1}$), and the slower has the higher viscosity ($\eta _{3}$) (after [390])

7 Conclusion

The Earth is an incredibly complex system on which a large number of forces act generating a flurry of geological and geophysical phenomena occurring over a wide range of spatial and temporal scales. In turn, they interact with each other, generating unprecedented events, whose dynamics is affected by several contributions by physical and compositional gradients. The action of even tiny processes lasting for a long time, as well as events with large potential concentrated in a few seconds, can contribute to the dynamics of a geologically active planet, although in a different way. In this article, we review the motions featuring the surface of the Earth giving it an ever-new shape. To do this, we focused on the forces acting on rocks, paying attention to presenting several different points of view proposed in recent years in the field of global geodynamics, tectonics and earthquake seismology. They are indeed the three fundamental research fields for the study of Earth dynamics. In the light of this, it is clear that a multidisciplinary approach is increasingly required to better understand geophysical events and geologic processes. Starting from the smallest scales, earthquakes are produced by the accumulation of elastic and gravitational potential energy in the rock volumes. Stress drops happen when the weakest segments of faults break. Seismic dynamics mainly depends on the topological properties and complexity of fault systems. The relative velocity of crustal volumes stems from compositional gradients that produce lateral variations of viscosity at the base of the crust. Plate tectonics is the result of several different contributions: boundary forces, i.e., ridge push, slab pull and trench suction, although considered dominant by the majority of geo-scientists, are not sufficient to explain key aspects of absolute plate motions, geological observations and also geophysical ones. Moreover, they act locally and they are partially buffered by frictional forces. In addition, mantle heterogeneity, physical and chemical stratification cast a shadow on the effective intensity of the slab pull force. Nowadays, it is accepted that mantle drag plays a less relevant role than previously thought, which is suggested by several considerations such as the power-law frequency-size distribution of the plate surface giving a propensity for self-organized fragmentation due to local interaction, by the observation that the fastest plates are those with lower basal viscosity and also the rigid body rotation of large plates which is not compatible with the dimension of convective cells. At last, the effect of tidal forces is reconsidered on the base of recent results. Although they are too weak to directly speed up plate motions, an interaction between stratified mantle convection, low viscosity zones in the upper mantle and horizontal solid Earth tides has likely given a fundamental contribution to plate tectonics. Tidal drag allows to explain why absolute plate motions, regardless the reference frame, show a significant westward drift of the lithosphere with respect to the underlying mantle and it also provides a reason for a lot of evidence of polarization, which otherwise should be attributed to chance. In summary, global geodynamics is affected by several forces generated by internal and external gradients whose actual contributions should be a primary future goal of research.