Trends in particle and nuclei identification techniques in nuclear physics experiments

Abstract

Particle identification techniques are fundamental tools in nuclear physics experiments. Discriminating particles or nuclei produced in nuclear interactions allows to better understand the underlying physics mechanisms. The energy interval of these reactions is very broad, from sub-eV up to TeV. For this reason, many different identification approaches have been developed, often combining two or more observables. This paper reviews several of these techniques with emphasis on the expertise gained within the current nuclear physics scientific program of the Italian Istituto Nazionale di Fisica Nucleare (INFN).

1 Introduction

To achieve their physics goals, nuclear physics experiments often need to identify particles or nuclei produced in the studied reactions. To this purpose, several techniques and detectors have been developed and improved over time. In recent years, the classical techniques based on $\varDelta E-E$, pulse shape analysis, gamma detection, time of flight, calorimetry and Cherenkov light have been adapted to the new possibilities offered by the use of solid-state sensors, new developments in the detector technologies and new scintillator materials. New readout solutions offer the possibility to extract more information from the signals and at a faster rate. Sophisticated software approaches, based on a combination of different techniques, are demonstrating their validity in several analyses.

The third scientific Committee of the Istituto Nazionale di Fisica Nucleare (INFN), CSN3, deals with experiments covering different aspects of nuclear physics reactions [1]. Twenty five experiments are followed by the Committee and are located in several national and international laboratories. The nuclear reactions studied cover a huge interval of center of mass energies, from sub-eV up to TeV at high energy colliders. As a consequence, each experiment developed specific and challenging solutions for its particle identification needs, adapting the techniques to the interval of energies to be covered, from eV particles produced in low energy machines up to GeV ones produced at colliders. These needs allowed the INFN groups to gain a huge expertise in the development and operation of detectors for Particle IDentification (PID).

The present paper will review the acquired knowledge, explaining the different technical solutions and the achieved performances and results. The main emphasis will be on the techniques used, the specific performances depending on the needs of the experiments and being not directly comparable. As it will become clear in the present review, PID is not only a way to identify particles or nuclear states and study their properties, but also offers a strategy to distinguish the type of reaction on the basis of the final products. The review will focus on active projects and will concentrate on the contributions of the Italian groups. A description of the state of the art is particularly timely in view of the new experimental scenarios connected to the upgrade programs of the accelerator facilities in the INFN National Laboratories of Legnaro (LNL) [2], Catania (LNS) [3,4,5], L’Aquila (LNGS) [6] and the new physics possibilities offered by CERN-LHC and BNL-EIC colliders [7].

The review is organized as follows: after a brief introduction of the different experiments, the various PID analyses are grouped according to the used technique and they are described in detail by means of specific applications.

2 Nuclear physics experiments in CSN3 implementing PID techniques

In this section, the experiments contributing to the present review are briefly described with their main physics goals and the developed PID techniques. The experiments in CSN3 are organized into six different research lines that match the NUPECC ones (Nuclear Physics European Collaboration Committee [8]): (i) Quark and hadron dynamics studying the hadron internal structure and the strong force among quarks, (ii) Phase transition of nuclear and hadronic matter concentrating on high energy ion collisions and Quark–Gluon Plasma (QGP) studies, (iii) Nuclear structure and reaction dynamics with a variety of measurements along the chart of nuclides to understand the characteristics of each element and the fundamental laws that govern the chart, (iv) Nuclear astrophysics pointing at low-energy reactions of interest for stellar evolution and nuclear species abundance studies, (v) Symmetries and fundamental interactions studying basic physics quantities like the nucleon radius or matter/anti-matter symmetry, (vi) Applications and societal benefits performing measurements useful in hadrotherapy or protection in space or for time metrology.

Although every experiment has its own specific goals and studies various reactions at different energies, there are many cross-connections among them. A clear example of this synergy among the different experiments in CSN3 can be found in the field of Nuclear Astrophysics [9].

In the following, each experiment is identified by the name of the corresponding international collaboration or by the acronym used within the INFN CSN3. The experiments are mostly performed inside INFN National Laboratories in Frascati (LNF), Legnaro (LNL), Catania (LNS) and Gran Sasso (LNGS), but also in several international laboratories like CERN, Jefferson Lab, GANIL, GSI, RIKEN.

2.1 Quark and hadron dynamics

2.1.1 EIC: electron ion collider at Brookhaven National Laboratory (BNL)

In spite of undoubted successes of QCD and its continuous progress, important aspects are still eluding our understanding. Among them, the emergence of the global nucleon properties, like mass and spin, from the dynamics of quarks and gluons inside the finite size nucleons; the full 3-D description of the nucleons; the properties of dense gluonic systems [10,11,12,13,14]. A complete picture can emerge only from a wide and deep systematic exploration, where the use of lepton probes has been demonstrated as the most successful approach. This is the mission of the electron ion collider (EIC), currently an approved project in USA [7, 15, 16].

The EIC will be hosted at the BNL and will be the first electron-ion collider capable of accelerating a wide variety of ions, from hydrogen to uranium, and providing highly polarized ($\sim$ 80%) electron and light nuclei beams. The center-of-mass energy will span a wide range from 20 to 141 GeV with peak luminosity above 10$^{34}$ cm$^{-2}$ s$^{-1}$. The collider opportunities have to be exploited by detectors with full 4$\pi$ coverage, to ensure a complete exploration of the interaction products. The first collider operation is scheduled in 2031.

Several key elements of the EIC physics program require excellent identification of the produced hadrons [17,18,19,20,21], and demand for improved and novel PID techniques. INFN groups are preparing their participation in the EIC experimental program largely contributing to the R&D studies in this sector. A particular development is being pursued on Ring Imaging CHerenkov (RICH) detectors, with different technical solutions allowing particle separation in the momentum range from few hundred MeV up to 60 GeV/c (see Sect. 8.2).

2.1.2 JLAB: studies on hadron structure at Jefferson Lab

The JLAB Collaboration groups researchers working at Jefferson Lab (USA) at the Continuous Electron Beam Accelerator Facility (CEBAF), recently upgraded to 12 GeV energy. The main physics goal is a deeper understanding of the structure of the hadrons, their parton content and the different contributions to their spin, also by means of polarized beams and targets. The collaboration contributes to several experiments in the two main halls of the facility.

In particular, the CLAS12 detector [22] has been designed to carry an extensive physics research program  [23], with two main aims. First, an innovative study of the 3D nucleon structure and of the underlying parton dynamics is planned in the valence quark region. This requires an excellent hadron identification to access flavor separation, and such a goal is achieved with an Aerogel RICH counter, able to identify pions, kaons and protons in the energy range 3–8 GeV [24] (see Sect. 8.3). Second, search for exotic states of the matter, like rare q$\bar{\mathrm {q}}$ states and unconventional mesons with exotic quantum numbers [25]. This is pursued in CLAS12 by tagging events of quasi photo-production with a small-angle lead-tungstate calorimeter, complemented by tracking and pre-shower systems and covering an electron energy interval 0.5–4.5 GeV (see Sect. 7.2).

2.1.3 KAONNIS: studies of Kaonic atoms at $DA\varPhi NE$ LNF

The KAONNIS collaboration includes a series of projects focusing on the Kaonic atoms that represent a unique opportunity to study low-energy (almost zero) QCD in the strangeness sector [26, 27]. The nature of the strong interaction between strange mesons and nucleons at threshold (almost zero relative kinetic energy ), where a perturbative approach is not anymore valid, is indeed an important brick of the Standard Model to be still fully understood. A kaonic atom is formed when a low momentum K$^-$ is stopped in a target and is captured in an atomic orbit, replacing an electron: due to its much heavier mass, the kaonic atom is formed in a highly excited state. The subsequent radiative transitions of the K$^-$ towards the fundamental level, where QCD effects overlap with the QED ones, represent a signature of the kaonic atom formation and can be used to retrieve information on the kaon–nucleon (KN) interaction. Typical energies of these transitions lay in the X-ray range: high-resolution spectroscopic detectors, like silicon drift detectors (SDDs) [28, 29], represent the ideal tool for their precision measurements.

Within the collaboration, in 2009, the SIDDHARTA experiment at the DA$\varPhi$NE collider at LNF [30, 31] performed a data taking campaign resulting in the highest precision measurement of KH, the first measurement of K$^4$He in a gaseous target and the first measurement ever of K$^3$He [32,33,34,35].

To achieve these results, the combined spectroscopic and timing capabilities of a scintillator pair (see Sect. 6.1.2) and a set of 1 cm$^2$ SDDs have been used (see Sect. 5.2). Background reduction is mandatory to perform a successful measurement: this is achieved combining SDDs and time of flight information to trigger the DAQ.

In 2021–2022, the SIDDHARTA-2 experiment should perform the first measurement ever of kaonic deuterium [36].

2.1.4 MAMBO: meson photoproduction on nucleon in the BGOOD experiment

The INFN-MAMBO Collaboration studies hadron photoproduction with and without polarization at different accelerators: ELSA (ELectron Stretcher Accelerator), delivering (un)polarized electrons in the 0.5–3.5 GeV energy range, in Bonn and MAMI (the Mainz Microtron). The BGOOD experiment, working at ELSA, is designed to investigate the hadron structure, studying exclusive channels of meson photoproduction on the nucleon [37,38,39]. It consists of two main parts: (1) a central detector with a Bismuth Germanium Oxide (BGO) crystal calorimeter, a plastic scintillator barrel and two Multi Wire Proportional Chambers (MWPCs); (2) a forward large aperture magnetic spectrometer. The photon beam (with energies in the interval 0.5–3.2 GeV), linearly polarized and tagged in energy, impinges on a liquid H$_2/$D$_2$ target. The detector is designed to measure charged particles, neutrons and gammas. In Sect. 7.3, the identification of neutrons and gammas in the BGO detector, necessary for the reconstruction of neutral meson decay, is described.

2.2 Phase transition of nuclear and hadronic matter

2.2.1 ALICE: QCD studies in extreme conditions with heavy-ion collisions at the CERN LHC

The ALICE experiment [40, 41] is dedicated to the study of pp, p–Pb and Pb–Pb collisions provided by CERN LHC and investigates the properties of the strongly interacting matter at extremely high temperatures and densities. In such conditions, the nuclear matter undergoes a phase transition, creating a new state of matter where quarks and gluons are not confined into hadrons, known as the quark–gluon plasma (QGP). Moreover the experiment, by studying the dependence of the particle production with respect to the multiplicity of tracks in the event, has demonstrated the presence of QGP-like effects also in small collision systems (pp) and a smooth connection of the production mechanisms in different interactions (pp, p–Pb and Pb–Pb), opening important windows towards a unified QCD description of these different size colliding systems. In addition, a series of studies on light (anti)nuclei production and annihilation gave precise measurements that allow a better understanding of nuclei formation and constrain the search for dark matter. Results from the RUN1 data taking period are summarized in [42], while more recent results can be found in [43].

To accomplish the physics goals, it is fundamental to have identification of particles produced in a wide momentum range. ALICE has unique particle identification capabilities among the LHC experiments; it exploits different PID techniques in the central barrel region, i.e., energy loss (see Sect. 3.3), time of flight measurements (see Sect. 6.1.1), Cherenkov and transition radiation detection (see Sect. 8.1), calorimetry (see Sect. 7.1.1) and topological ID (see Sect. 9.2.1). At forward rapidity, ALICE is equipped with a dedicated muon spectrometer to accomplish quarkonia states study (see Sect. 7.1.2).

2.3 Nuclear structure and reaction dynamics

2.3.1 CHIRONE: heavy-ion nuclear reactions in a wide range of energies

The CHIRONE experiment operates in the field of nuclear reactions, covering a wide energy range, from few MeV/nucleon to the Fermi energy (around 40 MeV/nucleon), and using stable and unstable ion beams. In this framework, many physics cases have been studied, such as: isospin effects on formation and decay mechanisms of compound nuclei, dynamical and thermodynamical effects on nuclear reactions, structure of weakly bound light nuclei, collective behaviour of nuclei, symmetry energy term of equation of state (EoS) and clustering of light nuclei with also nuclear astrophysics implications [44,45,46,47,48].

The complete nuclei identification from light to heavy ones and the determination of their direction of emission in momentum space are the basis to construct observables needed for the analyses. The CHIRONE experimental group operates mainly using the multidetector CHIMERA [44] and the FARCOS array [49] at LNS, where various identification techniques are applied. The $\varDelta E-E$ method is used to get the charge and mass of ions punching through the first stage of CHIMERA and FARCOS telescopes (see Sect. 3.2.1), the pulse shape analysis (PSA) in silicon detectors is used to obtain the charge of ions stopped in the first stage of CHIMERA telescopes (see Sect. 4.2.1), the PSA in scintillators is used to get charge and mass of Light Charged Particles ($Z<$ 5) stopped in the CsI(Tl) and for the $\gamma$ identification (see Sects. 4.1.1, 4.3.1 and 5.1). Moreover, time of flight is used for measurements of velocity and mass determination of ions stopped in the first stage of telescopes (see Sect. 6.2.2) and, in the case of reactions with few emitted particles, the use of kinematic methods allows to extrapolate energy and angular distributions with an improved accuracy, allowing a better identification (see Sect. 9.1.2). Combining these methods, the collaboration gets an almost complete event characterization, i.e., charge/mass, energy and velocity of all the charged particles and $\gamma$-rays.

2.3.2 FORTE: dynamics of fission and shell effects in super-heavy elements

The FORTE collaboration aims at studying the role of shell effects in reactions between heavy ions finalized to the search of Super Heavy Elements, and the production of nuclei very rich in neutrons populating the so called Terra Incognita. Shell effects embrace the entire chart of nuclides. To study their importance on the heavy and superheavy mass region, the following processes are the main focus of the collaboration: (1) fission, quasi-fission and ternary fission of intermediate mass, heavy and superheavy nuclei; (2) production mechanisms (multinucleon transfer and surrogate reactions) and properties of exotic neutron-rich species in the unknown nuclear chart regions, including those of astrophysical interest. The collaboration operates in several laboratories like LNL, ISOLDE and GSI.

The research program is implemented mainly using a time of flight spectrometer (TOF) coupled, whenever required by the experimental aim, with charged particles, neutrons and gamma-ray detectors. The TOF spectrometer measures masses and total kinetic energies of fragments in binary reactions (see Sect. 6.2.4). As an example, these quantities, measured in coincidence with the light charged particles detected by the 250 bi-telescopes of 8$\pi$LP at LNL in the fusion-evaporation and other channels [50,51,52,53], allow to estimate the reaction cross sections, to obtain a better understanding of the dynamics of processes occurring in heavy-ion induced reactions. This TOF spectrometer is well suited for both stable beams, presently available at LNL and future radioactive ion beams [54] produced by SPES [55]. Typical studies explore fission-dynamics  [56, 57] or the separation of the binary products of fast reactions (e.g. deep-inelastic and quasi-fission) from those of fission [58, 59], to get insight on the scission point configuration, e.g., deformation, mass asymmetry and dissipated energy. The compact size, light weight and easy-to-handle design of the TOF spectrometer makes it a portable solution and has recently been an important component of the experimental campaign performed at JYFL laboratory (Finland) focusing on the study of the ternary fission in heavy-ion-induced reactions and the fission modes in mercury isotopes.

2.3.3 GAMMA: study of the nuclear structure using $\gamma$ spectroscopy

The GAMMA collaboration aims at performing high precision $\gamma$ spectroscopy to make several studies covering, for example, the nuclear structure in regions far from stability, critical points and phase transitions between different nuclear shapes, collective modes of nuclei (vibration and rotation), resonances and particle/phonon coupled states, also of interest for astrophysics. To achieve this rich program the collaboration is involved in several experiments at different laboratories (like LNL, GANIL, GSI, IJC...), with specific devices for $\gamma$ and particle measurements, such as high-purity Germanium detectors (HPGe), silicon detectors and organic/inorganic scintillators.

Silicon detectors are widely used to perform X-ray and particle spectrometry. Due to the natural higher defect and contaminants density in silicon with respect to germanium, their thickness is limited to few mm. In such detectors, the position sensitivity is generally given by the electrode segmentation and the eventual evaluation of the charge sharing between neighbouring segments. In GAMMA the application of PSA to signals coming from silicon detectors is used to discriminate the impinging particles in charge and mass (see Sect. 4.2.2).

With the same approach, PSA is applied to organic and inorganic scintillators to discriminate incoming radiation resulting from mixed-field sources. In particular, it is possible to combine different scintillating materials with different signal shapes to obtain advantages in terms of efficiency, resolution and availability (see Sect. 4.3.2 ).

HPGe arrays are characterized by high-energy resolution that is however degraded when measuring in-flight emitted $\gamma$-rays, because of the indetermination in the measurement of the associated recoiling nucleus momentum. Many solutions adopted to overcome this limitation have undesired effects, like reduced acceptance or need for complementary detectors. An optimal strategy has been found in the PSA and $\gamma$-ray tracking techniques (see Sect. 4.4.1), adopted in their most advanced implementation by the AGATA detector array [60].

The upcoming facilities for radioactive beams, like SPES [55] at LNL, will open up new and challenging research lines for the GAMMA collaboration [61] probing clusterization, shape coexistence, high-order deformation and other interesting nuclear structure phenomena far from the valley of stability.

2.3.4 NUCLEX: nuclear dynamics and thermodynamics with heavy ions

The NUCLEX collaboration studies the behaviour of nuclear matter in a wide range of beam energies (5–100 MeV/nucleon) using different setups and particle identification techniques. This diversification is needed to better investigate phenomena typical of different energy regimes: compound nucleus formation and decay [62], $\alpha$-clustering [63], charged particle spectroscopy [64], isospin transport mechanisms [65,66,67] and neck emissions [68]. Various setups have been developed and used at LNS, LNL and GANIL: FAZIA [69, 70], GARFIELD [71], OSCAR [72] and the ACTAR demonstrator [73]. PID makes use of detectors based on combinations of sensors into telescopes (see Sect. 3). A particle, depending on its energy, may pass through one or more layers of the telescope: if it stops in the first layer it is possible to use PSA, Bragg spectroscopy (see Sects. 4.1.2, 4.2.3, 4.3.5) or time of flight techniques (see Sect. 6.2.5) to identify it, else the $\varDelta E - E$ correlation is adopted (see Sect. 3.2.2). Kinematic methods are also extensively used (see Sect. 9.1.3) to identify nuclei at relevant excitation energies.

2.3.5 NUMEN: nuclear matrix elements of neutrinoless double beta decays

The NUMEN project [74] proposes an innovative technique to access the nuclear matrix elements entering the expression of the lifetime of the double beta decay. It is based on accurate cross section measurements of heavy-ion induced double charge exchange (DCE) reactions at energies of 15–60 MeV/nucleon [75,76,77,78]. The NUMEN experiments are performed at LNS using the K800 Superconducting Cyclotron (SC) and MAGNEX large acceptance magnetic spectrometer to detect the emitted ions [79, 80]. MAGNEX is a powerful and versatile device that has been successfully used in a variety of nuclear physics researches [81,82,83,84,85,86]. The explored DCE reactions are induced by $^{18}$O and $^{20}$Ne beams, which imply the identification of $^{18}$Ne and $^{20}$O ejectiles, respectively. In addition, NUMEN proposes to measure also the complete set of competing reactions, i.e. single charge exchange, multi-nucleon transfers [87], elastic and inelastic scattering [88]. The corresponding ejectiles are typically in the mass region 18 $\le ~{A}~\le$ 22 and atomic number 8$~\le ~{Z}~\le$ 10. Different charge states are distributed at the focal plane for each isotope species, due to the interaction with the target [89], making the ion identification more challenging. The MAGNEX PID technique is based on a combination of measurements of energy loss, residual energy and magnetic rigidity (see Sect. 3.2.3) and guarantees a clear selection of the ions of interest among the whole range of A and Z produced in the collision.

2.3.6 PRISMA: heavy-ions dynamics with a large angle magnetic spectrometer at LNL

Binary reactions involving heavy ions allow to study the dynamics and the structure of nuclei in a wide range of angular momenta and excitation energies. In particular, with multi-nucleon transfer reactions it is possible to study the residual interaction in nuclei, especially the components responsible for nucleon coupling and correlations. Magnetic spectrometers equipped with proper detectors are well suited to analyze and interpret such reactions because they allow measuring at the same time mass and charge of reaction products, differential and total cross sections, and total kinetic energy.

In the experiment PRISMA at LNL [90], the development of a magnetic spectrometers covering large solid angles, coupled with precise ion tracking and an efficient time of flight measurement (see Sect. 6.2.6), allowed the improvement of the detection efficiency and mass resolution for very heavy ions, with important results in the field of nuclear structure and nuclear reaction dynamics. As an example, measurements of transfer probabilities in multi-nucleon transfer reactions at energies around the Coulomb barrier [91] or far below the Coulomb barrier [92] shed light on the nucleon pairing interaction [93]. When coupled to large $\gamma$ detector array like CLARA, the PRISMA spectrometer has allowed studies of particle–particle and particle–core couplings, thanks to the ability to detect individual transitions and study their population pattern and decay modes [94, 95]. For example, the analysis of particle-$\gamma$ coincidences resulted in a substantial suppression of $\gamma$-ray background and therefore provided improved sensitivity [96, 97].

The forthcoming new collaboration with the AGATA (see Sect. 2.3.3) array and the availability of radioactive ion beams provided by SPES will allow to unveil the structure and reaction dynamics of exotic nuclei even further away from the stability valley [2].

2.4 Nuclear astrophysics

2.4.1 ASFIN: nuclear astrophysics studies at very low energy

Stellar evolution is strictly related to the energy production due to nuclear reactions, which are also responsible for the synthesis of the elements. Owing to the presence of the Coulomb barrier at kinetic energies relevant for astrophysics, it is very difficult, or sometimes impossible, to measure astrophysical reaction rates in the laboratory. Consequently, trying to avoid extrapolations, alternative methods for determining bare nucleus cross sections of astrophysical interest are necessary [98], such as the Trojan-Horse Method (THM).

The method has been applied to nuclear structure and interaction problems, but mostly to hotly debated nuclear astrophysics issues (see [99] for the latest review). Recently, the method has been extended to the indirect study of neutron-induced reactions [100] and to reactions of astrophysical interest induced by radioactive ion beams [101], opening a new field of research overcoming the experimental difficulties related to the direct measurements of neutron-induced reactions with unstable beams [102].

The peculiarity of the method and the typical low energy range of a nuclear astrophysics experiment requires a non-trivial application of the standard particle identification techniques. Indeed, the needs of low-energy threshold detection triggered the realization of monolithic $\varDelta E-E$ detectors (see Sect. 3.1.2), while the necessity to measure reactions with three bodies in the final state inspired a kinematic method to determine the mass number of an undetected particle (see Sect. 9.1.1). To identify a specific reaction mechanism, a time of flight measurement can be applied (see Sect. 6.2.1). All these techniques were largely applied in the nuclear astrophysical research of the ASFIN group at the principal Italian national laboratories (LNS and LNL) and international ones (TRIUMF, RIKEN, GANIL...) using advanced experimental setup (CLAD [103], TECSA [104] and many others).

2.4.2 ERNA: direct measurements for C burning in stars

The main goals of the ERNA collaboration are cross section measurements of astrophysical interest with a mass recoil separator, performing charged particles spectroscopy, and the determination in meteoritic samples of the isotopic mass composition through mass spectrometry. For charged particle spectroscopy the collaboration designed a large scattering chamber where either a solid or a gas jet targets can be located, in combination with different detection setups.

A special case to illustrate the experimental challenges is the $^{12}$C + $^{12}$C reaction, playing a key role in the evolution of massive stars and in explosive scenarios such as type-Ia supernovae and super-bursts in binary stars. Carbon burning takes place at typical temperatures of $5\times 10^8$ K [105, 106], corresponding to an energy range of interest, the Gamow window [107], equal to $E_{\mathrm{c.m.}}~=~1.5\pm 0.3$ MeV [108]. Cross sections are very small ($\ll 10^{-9}$ b) and extremely difficult to measure in the laboratory due to critically low counting rates [109, 110], making it necessary to increase as much as possible the signal-to-noise ratio. At these energies, the $^{12}$C + $^{12}$C reactions proceed mainly through the $^{23}$Na + p, $^{20}$Ne + $\alpha$, so that $\alpha$ and p channels identification plays a crucial role for channel selection and background suppression.

The ERNA collaboration at CIRCE laboratory in Caserta aims to study these reactions that require: (a) great stability to allow for long measurement campaigns, (b) low intrinsic background and (c) heat resistance to withstand the intense beams necessary to optimise the counting rate. PID at such low energies (few MeV/nucleon) and in such experimental conditions requires challenging detectors and ERNA developed a dedicated $\varDelta E-E$ gas–silicon detector array, described in Sect. 3.1.1.

2.4.3 LUNA: study of nuclear reactions for astrophysics at LNGS

The LUNA collaboration operates inside the LNGS under the Gran Sasso massif between the cities of L’Aquila and Teramo in Italy. This unique facility takes advantage of the environmental background reduction (for instance, a neutron background reduction by three orders of magnitude has been observed [111]) and of the intense beam provided by the LUNA accelerator to measure low-energy nuclear fusion reactions responsible for the synthesis of the elements in the Universe (see [112] and references therein). The main goal is to lower the minimum energy ever achieved with a direct measurement targeting the Gamow windows [107], therefore, reaching typical astrophysical temperatures. As an example, LUNA has measured the neutron source for the main s-process¹: the $^{13}$C($\alpha$,n)$^{16}$O reaction. In this case a yield of about 1 neutron per Coulomb beam charge is expected. For this reason, the background must be minimized to have a signal-to-background ratio as high as possible and to limit the overall uncertainty to 10% as requested by model calculations [113].

Besides the naturally low-noise environment, further solutions were used to minimize background, for which PID plays a pivotal role. The background reduction was achieved in three steps:

• the production and characterization of pure 99% enriched $^{13}$C solid targets minimized beam induced background [114]

• the selection of materials and the usage of counters with stainless steel case (instead of typical aluminium case) reduced the intrinsic $\alpha$ background by one order of magnitude [115]

• an improved PSA analysis method allowed to distinguish signals from neutron capture in the $^{3}$He gas from residual $\alpha$ signals of the intrinsic background [116] (see Sect. 4.3.3).

2.4.4 n_TOF: neutron time of flight facility at CERN

The neutron time of flight facility n_TOF at CERN is a white neutron source based on the CERN Proton Synchrotron (PS). A high-intensity neutron beam is produced every 1.2 s (or multiples) from a pulse of 7$\times$10$^{12}$ protons of 20 GeV/c momentum accelerated by the PS, and impinging on a massive lead target, surrounded by 5 cm of water. At a distance of about 185 and 20 m from the spallation source the two experimental areas, EAR-1 and EAR-2 [117, 118], are placed. The characteristic experimental conditions of n_TOF ensure a high instantaneous neutron flux, which covers a wide energy range, from thermal energy to a few GeV. The neutron-induced reactions studied so far are radiative capture (n, $\gamma$), fission (n, f), charged particle emission (n, c.p.) and inelastic scattering (n, n$'$), of interest to fundamental nuclear physics, stellar nucleosynthesis or applications in nuclear technology and nuclear medicine [119]. Cross section studies require the simultaneous measurement of the products of the reaction and of the neutron flux impinging on the sample.

PID techniques are mainly applied to experimental data collected for (n, $\gamma$) cross section measurements, which typically involve neutrons with energy from thermal to few hundreds keV. The purpose of the applied PID techniques is twofold: to identify $\gamma$ rays from the radiative capture reaction and other background particles, i.e. neutrons or $\alpha$ particles, and to monitor the stability of detector gains (see Sect. 4.3.4). In the near future the collaboration is going to start a measurement campaign of (n, c.p.) reactions of interest to fusion technology, where PID represents a basic requirement. In addition, new counter telescopes developed by the collaboration make extensive use of the $\varDelta E-E$ technique combined with time of flight method to measure the neutron flux in the high-energy region, from 10 MeV to approximately 1 GeV (see Sect. 6.1.3).

2.4.5 PANDORA: plasma for astrophysics, nuclear decays observation and radiation for archaeometry

The PANDORA project [120, 121] proposes a new approach to measure, for the first time, in-plasma nuclear $\beta$-decays of isotopes of astrophysical interest (e.g. relevant for r- and s-process nucleosynthesis chain), covering different plasma densities $n_e$ and temperatures $T_e$ [122]. Theoretical predictions and former experiments on fully stripped ions have shown that the ionization state can modify, even of several orders of magnitudes, the isotopes lifetimes [123,124,125,126]. In the high-performance PANDORA plasma trap, the radionuclides can be trapped in a dynamic equilibrium, living for days or even weeks at almost constant local density and temperature. The plasma may reach $n_e\sim 10^{11}\div 10^{13}$ cm$^{-3}, T_e \sim 0.1\div 100$ keV and mimic some stellar-like environments concerning, mainly, the charge state distribution (CSD) conditions.

The experiment studies the $\beta$ decays of the radionuclides in the plasma trap via the identification and measurement of the $\gamma$ rays emitted from the excited states of the daughter nuclei and distinguishes the background coming from the plasma itself. This is obtained by means of a multi-diagnostic setup and HPGe detectors, as described in Sect. 5.3.

2.5 Applications and societal benefits

2.5.1 FOOT: nuclear cross section measurements for hadron therapy

The goal of the FOOT (FragmentatiOn Of Target) experiment [127] is to perform cross section measurements of nuclear fragmentation of projectiles and targets that are relevant for particle therapy and radiation protection in space. Specifically, FOOT will measure double differential (with respect to fragment kinetic energy and production angle) cross sections, using thin tissue-like (C, O, H) targets and light ($\mathrm{Z} \le 8$) projectiles with energies in the range 100–800 MeV/nucleon. Data of this kind are scarcely available. New measurements will provide important reference data sets for model benchmark, allowing a better understanding of the physical and biological effects of secondary particles produced in the human body during tumor irradiation in particle therapy and during exposure to space radiation in long-term space missions.

While projectile fragmentation can be studied directly, for target fragmentation studies involving very short range and low-energy fragments, FOOT applies an ’inverse kinematics approach’. To have a clear separation of the isotopes needed for the cross section measurements, the identification capabilities of the fragments in terms of charge Z and mass A should reach a level of precision of about 3 and 5%, respectively. Other constraints come from the fact that the experiment should be movable since the data taking periods are foreseen at different facilities. Based on the expected kinematic ranges of the fragments to be studied, two distinct experimental setups have been developed for FOOT:

• a setup optimized for fragments with $Z\ge$ 3, including a magnetic spectrometer, coupled with a tracking region, time-of-flight and calorimeter, covering up to about 20$^\circ$ (see Sect. 6.2.3).

• a setup optimized for fragments with $Z\le$ 2, consisting of an emulsion spectrometer placed behind the beam monitor, with acceptance of up to about 70$^\circ$ (see Sect. 3.4).

3 The $\varDelta E-E$ technique

In the case of non relativistic charged particles, a commonly adopted approach to their identification is the measurement of their energy loss in a material with a thickness insufficient to stop the particle. Indeed, when a charged particle traverses matter it undergoes a number of interactions, mainly inelastic collisions with the atomic electrons of the material and elastic scattering of atomic nuclei. Most frequently, collisions cause very small energy losses in comparison with the impinging energies (for 90% of all collisions the energy losses are less than 100 eV [128]). The cumulative effect of the many interactions is a sizable energy loss of the impinging particle and a deflection with respect to the original trajectory. Though the nature of these interactions is definitely stochastic, if the distance across the material is macroscopic then the number of collisions is very high and fluctuations are small, so an average energy loss can be unequivocally determined. The problem was already tackled at the very beginning of nuclear physics (Bohr’s formula dates back to 1913 [129]), and the energy loss per unit path (the so-called stopping power) is accurately described by the Bethe-Bloch formula (see [128] for a detailed discussion). The stopping power $\left\langle -\mathrm{d}E/\mathrm{d}x \right\rangle$ decreases with $\sim ~1/\beta ^2$ until about $\beta \gamma ~\sim ~3$, then a broad minimum is reached (minimum ionizing particles—MIPs in the following) and a weak increase is finally observed for relativistic energies. A general feature that makes stopping power very attractive for particle identification is the apparent dependence on $Z^2$, where Z is the charge of the incident particle, while a minor dependence on the particle mass M is present, which is easily predicted in the non-relativistic limit:

$$\begin{aligned} \left\langle -\frac{\mathrm{d}E}{\mathrm{d}x} \right\rangle \sim \frac{Z^2\,M}{E} \,. \end{aligned}$$

(1)

The linear dependence on the incident particle mass makes it possible to perform identification of different isotopes in the case of heavy ions, provided that high resolution in the measurement of the energy loss is attained. Since sufficient energy resolution to discriminate in mass is seldom reached, the measurement of the energy loss $\varDelta E$ is often coupled to other techniques. In the following subsections, we will discuss how the experiments use the $\varDelta E - E$ approach for particle identification. Such technique is based on the construction of 2D spectra where the energy loss in a thin detector ($\varDelta E$ stage) is drawn as a function of the residual energy measured in a thicker detector where the particle is stopped (the combination of the two—or more—detectors is often referred to as a telescope).

3.1 The low-energy limit: research in nuclear astrophysics

As discussed in 2.4, nuclear astrophysics experiments are characterized by very low (from keV to MeV) beam energies and cross sections. PID is therefore a challenge in terms of energy thresholds in detectors and signal-to-noise ratios.

3.1.1 ERNA: advanced ionization chamber as $\varDelta E$ detectors

The very low energies involved in the study of nuclear reactions of astrophysical interest require to push the standard detection technique of $\varDelta E$ to its limits. On one hand, a detector as thin as possible is necessary to measure the energy loss without introducing a significant threshold; on the other hand, energy loss cannot be too low to maintain good particle separation.

As an example, at low beam energies (6–8 MeV/nucleon), measurements of the $^{12}$C + $^{12}$C fusion reaction, proceeding through p and ${\alpha }$ channels, have proved that the $\varDelta E-E$ technique can successfully identify the emitted protons [130]. However, even the most energetic $\alpha$ particles are not visible if a sufficiently thin $\varDelta E$ stage is not used. Such phenomenon is especially true when the reaction channels involve excited states of ejectiles.

To overcome the threshold problem, within the ERNA collaboration a two-stage detector array called GASTLY (GAs Silicon Two-Layer sYstem) was specifically designed to fulfill the requirements of charge-particle measurements at low energies. The GASTLY array can accommodate up to eight $\varDelta E-E$ modules, each including an ionisation chamber (IC, $\varDelta E$ stage) and a silicon strip detector (SSD, $E_{\mathrm{rest}}$ stage) [131], spanning an angular range of about $70^{\circ }$ with a resolution $<1.3^{\circ }$. Each module consists of an aluminium pyramidal structure with square base. The IC is operated with CF$_4$ maintained at a constant pressure that can be adjusted from 0 to 250 mbar (limit imposed by the entrance window) to fit specific needs of different energy ranges or reactions [131], obtaining in this way a $\varDelta E$ stage as thin as needed. The second stage of each GASTLY module consists of a large (58$\times$58 mm$^2$ active area, $300 \pm 15$ $\upmu$m thick) SSD [132]. A typical $\varDelta E -E$ matrix is shown in Fig. 1.

Fig. 1

ERNA. Typical energy calibrated $\varDelta E-E_{\mathrm{rest}}$ scatter plot showing the $\alpha$ particles and protons loci. The figure is taken from [133]

Using four modules of the GASTLY array and the SSD as a whole [133], it was possible to identify the $^2$H contamination in the target allowing to perform a detailed study for beam-induced background reduction (see Ref. [134]). In addition, it was possible to test the optimum stability of the GASTLY system (2-week-long measurements), its great heat resistance (up to 40 $\upmu$A on target and $1400\,^{\circ }\hbox {C}$) and extremely low intrinsic background ($10^{-2}$ counts/h).

Currently, GASTLY is being tested at the LNGS to further investigate intrinsic background, with the aim of measuring the $^{12}$C + $^{12}$C reactions directly in the Gamow window.

3.1.2 ASFIN: pushing the low-thickness limit of solid-state devices

The use of ionization chambers as $\varDelta E$ stage of a conventional $\varDelta E - E$ telescope ensures low detection thresholds and has been largely and successfully applied in THM experiments (see Sect. 2.4.1) and in the study of nuclear structure close to the particle emission thresholds [135]. Typical drawbacks are the impossibility to reach compact dimensions and the difficulty of setting up $4\pi$ array for applications to radioactive ion beams. Si detectors allow one to build compact detection systems but such detectors are commercially available only down to about 5 $\upmu$m thickness, and such thin detectors are fragile and extremely expensive. Moreover, the high capacitance makes their performance unsuitable for nuclear astrophysics experiments.

Fig. 2

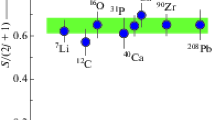
ASFIN. a Sketch (not to scale) of the monolithic telescope structure. Particles enter the detector from the top. b $\varDelta E-E$ spectrum for $^{40}$Ca + $^{48}$Ca collision at E = 400 MeV. Both pictures are from [137]

To overcome these difficulties, some prototypes of monolithic silicon telescopes were tested at LNS, where the $\varDelta E$ and E stages are integrated in the same silicon chip, following a fundamental work of Kemmer and other groups [136]. Basically, a monolithic telescope is a $\varDelta E-E$ detector with the structure of a double vertical diode built on a unique silicon bulk. A schematic view of the detector is reported in Fig. 2a. The p+ region acts as common ground electrode for the $\varDelta E$ and residual energy stages. Details on the sensor manufacturing can be found in [138]. Several devices were realized, manufactured by STMicroelectronics (Catania, Italy) in the framework of a collaboration with LNS, by combining photolithographic and ion implantation techniques. In this way, it was possible to obtain telescopes with a very thin (down to 2 $\upmu$m) first stage, leading to a $\varDelta Z/Z\sim ~10\%$.

Monolithic strip detectors were extensively used in several experiments at low and intermediate energies, both with stable and radioactive beams [139], showing their powerful features: modular structure with possibility to build very compact and versatile configurations; charge identification thresholds of the order of hundreds keV/nucleon for ions up to $Z=20$; good granularity; excellent $\beta$ background suppression in reactions induced by radioactive beams and possibility to enhance the position sensitivity [140]. Figure 2b shows a $\varDelta E-E$ spectrum obtained in the study of the collision $^{40}$Ca $+^{48}$Ca at a beam energy of 10 MeV/nucleon.

Recently, a cooperation between LNS and IMM-CNR (Institute for Microelectronic and Microsystems of the Italian National Research Council) has lead to the development of a new generation of detectors made of Silicon Carbide (SiC) [141]. Since SiC devices present a wider bandgap than traditional silicon detectors, they are very robust against radiation damage and also present a better signal-to-noise ratio at high temperature. In view of those potential applications, the SiCILIA (Silicon Carbide Detectors for Intense Luminosity Investigations and Applications) project established a new era for SiC devices regarding thicknesses, dimensions (detection area), and manufacturing technologies [141].

Among these advanced attributes, a brand new invention patent was recently deposited showing the possibility of building a monolithic multilayer SiC device [142]. This new telescopic detector will open new perspectives for studying reaction cross sections under plasma environment of fundamental importance for nuclear astrophysics [143].

3.2 Nuclear structure and dynamics experiments at intermediate energies

In heavy-ion collisions in the range of the Fermi energy, new challenges arise for PID due to the large number of emitted particles, making it necessary to develop detectors with high granularity and good resolution in charge and mass.

Fig. 3

CHIRONE. a $\varDelta E-E$ plot obtained in the reactions $^{124}$Xe + $^{64}$Ni,$^{64}$Zn at 20 MeV/nucleon using a FARCOS telescope. The inset shows a zoom of the $\varDelta E-E$ plot for small $\varDelta E$ values. b Uncalibrated $\varDelta E-E$ plot obtained in the reaction $^{68}$Ni +$^{12}$C at 28 MeV/nucleon considering two subsequently crossed strips of a FARCOS telescope (adapted from [144])

3.2.1 CHIRONE: energy loss in large acceptance arrays

The $\varDelta E-E$ method is largely applied, in both CHIMERA multidetector and FARCOS array (see Sect. 2.3.1). CHIMERA consists of 1192 telescopes and covers about the 94% of 4$\pi$. Each telescope consists of a 300 $\upmu$m Si detector followed by a CsI(Tl) from 3 to 12 cm thick [44]. The forward part of CHIMERA consists of 688 telescopes, distributed on 18 rings from 1$^\circ$ to 30$^\circ$. The backward part consists of 504 telescopes, distributed on a sphere from 30$^\circ$ to 176$^\circ$, with the target placed in the center. FARCOS is a modular array of telescopes, each of them consisting of two Double-Sided Silicon Strip Detectors (DSSSD), 300 and 1500 $\upmu$m thick, respectively, followed by a last stage including four CsI(Tl), 6 cm thick [49]. The final configuration of FARCOS consists of 20 telescopes.

The $\varDelta E-E$ method in the CHIMERA multidetector uses the signals coming from Silicon detectors and CsI(Tl) scintillators to identify in charge all the fragments passing through the Si stage, and in mass the ones with Z up to 10 (since $\varDelta Z/Z\sim ~2\%$ and $\varDelta$A/A $\sim ~5\%$). The same method is used to obtain particle identification with the FARCOS array; in this case signals coming from both the two silicon stages and second silicon stage-CsI(Tl) scintillator of a FARCOS telescope are used. Figure 3a shows a $\varDelta E-E$ plot obtained using a telescope of the FARCOS array in the reactions $^{124}$Xe + $^{64}$Zn,$^{64}$Ni at 20 MeV/nucleon. Here the energy scale was optimized to detect Intermediate Mass Fragments. Figure 3b shows a $\varDelta E-E$ plot obtained in the reaction $^{68}$Ni + $^{12}$C at 28 MeV/nucleon. The $\varDelta E-E$ plot was obtained considering a strip of the 300 $\upmu$m stage and the corresponding strip of the 1500 $\upmu$m detector, for a FARCOS telescope [144]. This figure shows the excellent performance of the FARCOS array allowing to identify in mass also nickel isotopes.

As it will be discussed in later sections, for the telescopes used in CHIRONE the $\varDelta E-E$ technique, suitable for particles punching through the first detection layer, is complemented by other methods. In particular, the Pulse Shape Analysis in silicon, described in Sect. 4.2.1, and in CsI(Tl), see 4.1.1, is used for particles stopped in the first layer and for light and fast particles, respectively. For particles stopped in the first layer also the E-TOF identification approach is adopted, as described in Sect. 6.2.2. Finally, the kinematic methods (see Sect. 9.1.2) are also used to improve the quality of the identification.

3.2.2 NUCLEX: tailored $\varDelta E - E$ solutions

Different compositions of sensors within a telescope lead to different identification capabilities. Therefore, the $\varDelta E - E$ combination has to be tailored to the physical problem under investigation. The NUCLEX collaboration has developed solutions incorporating solid-state devices only, such as FAZIA and OSCAR, and combination of gas and solid-state devices, as GARFIELD and ACTAR (see Sect. 2.3.4).

Regarding the former, FAZIA is made up of two silicon pads (300 and 500 $\upmu$m thick) followed by 10 cm CsI(Tl) scintillators and it is designed for beam energies above 20 MeV/nucleon, while OSCAR is devoted to the detection of low-energy (few MeV/nucleon) light charged particles, with a 20 $\upmu$m silicon strip detector followed by a 300 $\upmu$m Si pad wall.

GARFIELD is made up of two drift chambers surrounded by 180 4-cm-thick CsI(Tl) scintillators; it is frequently coupled (towards forward polar angles) with an ancillary Ring Counter (RCo), which features ionization chambers followed by 300-$\upmu$m-thick silicon strip pads and CsI(Tl) scintillators (third layer). The ACTAR demonstrator is a 64$\times$128$\times$170 mm$^3$ active target and time projection chamber followed by ancillary detectors as a second layer (e.g. it has been recently coupled with OSCAR). GARFIELD is more suited for higher energies, in the 5–25 MeV/nucleon range while the ACTAR demonstrator is meant for beam energies up to $\sim$ 10 MeV/nucleon (and detected particles of similar energies).

Fig. 4

NUCLEX. $\varDelta E - E$ correlation in a typical FAZIA telescope (first vs second silicon layer). Data come from $^{48}$Ca + $^{12}$C reactions at 25 MeV/nucleon. The insets show the mass discrimination performances at low ($Z=3$) and relatively high ($Z=20$) atomic number, the ridges corresponding to the different masses being still well separated

The advantage of the initial gas volume as in GARFIELD + RCo, transparent for fragments with at least 2 MeV/nucleon, is the very low charge identification threshold, making it possible to measure at relatively low beam energies. However, the energy resolution of gas chambers does not permit the isotopic discrimination of fragments. For particles of energy high enough to reach the CsI(Tl) third layer in RCo, the $\varDelta E - E$ technique could be exploited also correlating the energy lost in the Si layer with the residual energy loss inside the CsI(Tl) scintillators: in this case the determination of the mass number A is possible for particles up to $Z\sim$ 15, due to the better energy resolution of the $\varDelta E$ sensor ($\varDelta$A/A $\sim ~2.5\%$, $\varDelta Z/Z <~2\%$).

In contrast, in a system like FAZIA with solid-state detectors as first layers, 10 to 20 MeV/nucleon particle energies (depending on their charge) are necessary to punch through and thus allow for the use of $\varDelta E - E$ method. In this case isotopic discrimination is achieved for ions up to $Z\sim$ 25 ($\varDelta$A/A $\sim ~2\%$, $\varDelta$Z/Z$~<~ 2\%$), see Fig. 4. Moreover, the use of 10 cm CsI(Tl) crystals permits the identification of very fast particles (e.g. protons up to $\sim$ 195 MeV).

Exploiting the Bethe–Bloch formula it is also possible to carry out Bragg spectroscopy in TPCs (Time Projection Chambers) such as ACTAR demonstrator [73]. In TPCs, it is possible to independently measure the energy released in small regions of the active gas volume, so the energy loss profile (Bragg curve) of the detected particles can be reconstructed and thus they can be identified by a direct comparison to simulated curves. If the particles escape from the gas volume they can be still identified via $\varDelta E - E$ method, using ancillary detectors as a second layer. In the case of the ACTAR demonstrator, the energy loss is sampled in about 80 points (depending on the trajectory of the ions inside the chamber and on their energy).

Also for the telescopes of the NUCLEX Collaboration many different identification techniques are used to identify the particles hitting the detectors besides the $\varDelta E-E$ method. Taking as an example the FAZIA setup, the $\varDelta E-E$ technique is used when particles punch-through the first silicon layer. Otherwise, the PSA in silicon (see Sect. 4.2.3) is applied. Fast light particles are identified thanks to PSA in CsI(Tl) (see Sect. 4.1.2), while slow light particles can be identified also thanks to the E-TOF approach (see Sect. 6.2.5). Kinematic methods (see Sect. 9.1.3) can help to associate specific reaction channels. The combination of all these techniques makes these detectors powerful devices able to identify nuclei over a very wide interval of energies and species.

3.2.3 NUMEN: combining $\varDelta E$ and magnetic rigidity measurement

The PID procedure adopted in MAGNEX (see Sect. 2.3.5) is based on the combination of two techniques, the $\varDelta E-E$ technique and the correlation between the residual energy and the magnetic rigidity [145, 146]. The 3D tracking of the ion trajectory is performed by the focal plane detector (FPD). The energy loss and the residual energy are based on a gas tracker (filled with 99.95% isobutane at pressure ranging from few mbar up to several tenths of mbar) sensitive to the energy loss of the crossing ions and a silicon wall for the measurements of their residual energy. The atomic number of the ions can be therefore identified by the standard $\varDelta E-E$ technique. A typical $\varDelta E-E$ correlation plot is shown in Fig. 5a together with a graphical contour selecting the neon ions. The plotted parameters are the residual energy ($E_{\mathrm{resid}}$), measured by the silicon detectors wall, and the total energy loss in the FPD gas section ($\varDelta E_{\mathrm{tot}}$). The latter is corrected for the different path lengths in the gas thanks to the tracking capabilities, consequence of the wide range of horizontal angles at the focus (40$^{\circ }~\le ~\theta _{\mathrm{foc}}~\le ~72^{\circ }$)  [147]. For the mass reconstruction (A), an innovative particle identification technique for large acceptance spectrometers, which exploits the properties of the Lorentz force, was introduced in Ref. [148]. In the experimental conditions of NUMEN interest, in which oxygen, fluorine and neon ions should be detected, the identification procedure is successfully performed using the $X_{\mathrm{foc}}-E_{\mathrm{resid}}$ correlation, in which $X_{\mathrm{foc}}$ is the horizontal position measured at the focal plane. The relationship between the two quantities is approximately quadratic with a factor depending on the ratio $\sqrt{m}/q$

$$\begin{aligned} X_{\mathrm{foc}}\propto \frac{\sqrt{m}}{q}\sqrt{E_{\mathrm{resid}}}. \end{aligned}$$

(2)

In Fig. 5b, the correlation plot $X_{\mathrm{foc}}-E_{\mathrm{resid}}$ is shown for the data selected with the graphical condition on the $\varDelta E_{\mathrm{tot}}-E_{\mathrm{resid}}$ one (see Fig. 5a). The separation between the different neon isotopes, which allows for a clear selection of the $^{18}$Ne$^{10+}$ ejectile, as indicated by the graphical contour in Fig. 5b, is evident. The achieved resolution in this case is $\varDelta$A/A $\approx$ 1/300, better than the value already reported in Ref. [148], in which straggling effects on the $E_{\mathrm{resid}}$ parameter were more important.

Fig. 5

NUMEN. PID technique developed for experiments performed with the MAGNEX spectrometer. a Typical $\varDelta E_{\mathrm {tot}}$ vs. $E_{\mathrm {resid}}$ plot for unselected events in a single silicon detector measured in the $^{18}$O + $^{76}$Se reaction at 275 MeV and 0$^{\circ }~\le ~\theta _{\mathrm {lab}}~\le$ 8$^{\circ }$. The different atomic species and a graphical contour on the neon region are indicated (red line). b Typical X$_{\mathrm {foc}}$ vs. $E_{\mathrm {resid}}$ plot for the selected neon events on the $\varDelta E_{\mathrm {tot}}$ vs. $E_{\mathrm {resid}}$ for the same silicon detector (a) zoomed in the region of the 10$^+$ charge state. The different neon isotopes and a graphical contour (red line) selecting the $^{18}$Ne$^{10+}$ are indicated

In some cases, the $X_{\mathrm{foc}}-E_{\mathrm{resid}}$ representation is not enough to separate ions characterized by very similar $\sqrt{m}/q$ ratio, as for example the $^{22}$Ne$^{10+}$ and $^{18}$Ne$^{9+}$ ions ($\sqrt{m}/q~=$ 0.469 and 0.471, respectively). In these cases, a third step in the PID procedure can be performed using the time difference between the CS (superconductive cyclotron) radiofrequency periodic signal (STOP) and the timing signal coming from the silicon detectors of the FPD (START). This signal has a relative meaning connected to the different flight time of the two ions in the spectrometer. The technique allows to clearly identify the $^{22}$Ne$^{10+}$ and $^{18}$Ne$^{9+}$ ions, as demonstrated in Ref. [149].

An important feature of the MAGNEX PID technique is that it does not require absolute energy calibrations of the $E_{\mathrm {resid}}$ and $\varDelta E_{\mathrm {tot}}$ measurements, since they are used only for particle identification purposes. Usually, the loci in the PID plots are identified through supplementary elastic scattering runs. The capability of the PID in terms of the minimum cross-section significantly measurable by the MAGNEX spectrometer was investigated [150], demonstrating that it is suitable for accurate measurements of very rare processes like double charge exchange reactions, characterized by cross sections as low as tens of nbarn.

3.3 ALICE: the high-energy limit for particles and light nuclei at the GeV scale

In the ALICE experiment, most of the detected particles by means of energy loss measurement like baryons, mesons and nuclei are MIP’s. In this framework, PID is performed by the Inner Tracking System (ITS) and the Time Projection Chamber (TPC) correlating the energy loss with the momentum measured thanks to the magnetic field of ALICE. The ITS consists of six cylindrical layers of silicon detectors. It covers the pseudorapidity range $|\eta |~\le ~$0.9 and it is the central barrel detector closest to the beam axis. The distance from the nominal beam line ranges from 3.9 cm for the innermost layer up to 43 cm for the outermost. The two innermost layers are made of silicon pixel detectors (SPD), the two central layers of silicon drift detectors (SDD) and the two outermost layers of double-sided silicon strip detectors (SSD).

A detailed description of the three sub-systems can be found in [40]. The ITS has the main purposes of providing both primary and secondary vertices reconstruction and of improving the ALICE barrel tracking capabilities in the vicinity of the interaction point. The four outer layers (SDD and SSD) have analogue readout and therefore can be used for particle identification via dE/dx measurement in the non-relativistic region. The analogue readout has a dynamic range large enough to provide the dE/dx measurement for low-momentum ionising particles, down to the lowest momentum at which tracks can still be reconstructed. This feature gives the ITS stand-alone capability as a low-$p_{\mathrm{T}}$ particle spectrometer.

The ALICE SDDs were produced from very homogeneous high-resistivity (3 k$\Omega$cm) 300-$\upmu$m-thick Neutron Transmutation Doped (NTD) silicon, with a sensitive area of 70.17($r\phi$) $\times$ 75.26(z) mm$^2$ and a total area of 72.50$\times$87.59 mm$^2$. The sensitive area is split into two drift regions by the central cathode strip to which a HV bias of $-2.4$ kV is applied. In each drift region, and on both detector surfaces, 291 p$^+$ cathode strips, with 120 $\upmu$m pitch, fully deplete the detector volume and generate a drift field parallel to the wafer surface. A SDD module consists of one silicon drift detector and two front-end hybrids, each connected to the corresponding end-ladder low-voltage board. The two layers of SSD are crucial for the matching of tracks from the TPC to the ITS. Minimization of the material budget of the mechanical support for the detection modules is achieved using linear Carbon Fibre Composite (CFC) material for all support structures in the active volume. The sensors have 768 strips on each side with a pitch of 95 $\upmu$m. The stereo angle is 35 mrad which is a compromise between stereo view and reduction of ambiguities resulting from high particle densities. The stereo angle is obtained by defining strips with an angle of 7.5 mrad with respect to the sensor short edge on the p-side and with an angle of 27.5 mrad on the n-side.

Fig. 6

ALICE. a Distribution of the energy-loss signal in the ITS as a function of momentum in Pb–Pb collisions at $\sqrt{s_{\mathrm{NN}}}~=~2.76$ TeV (from [41]). Curves represent the Bethe–Bloch parameterisation. b distribution of specific energy loss dE/dx in the TPC as a function of the rigidity (p/ |Z|) for negative particles in Pb–Pb collisions at $\sqrt{s_{\mathrm{NN}}}~=~2.76$ TeV. The dashed lines are parameterisations of the Bethe–Bloch formula for the different particle species (from [152])

The stand-alone tracking in the ITS favors a momentum range wider towards lower $p_{\mathrm{T}}$ values, while the combined tracking with TPC provides a better momentum resolution. The energy loss measurement in each layer of the ITS is corrected for the track length in the sensitive volume using tracking information. In the case of SDD clusters, a linear correction for the dependence of the reconstructed raw charge as a function of drift time due to the combined effect of charge diffusion and zero suppression is also applied [151]. For each track, the energy loss is evaluated using a truncated mean. The average of the lowest two points in case four points are measured, or a weighted sum of the lowest (weight 1) and the second lowest point (weight 1/2), in case only three points are measured, is done. The final dE/dx resolution is about 10$\%$.

An example distribution of measured truncated mean energy loss values as a function of momentum in the ITS is shown in Fig. 6a. By means of this technique it is possible to identify $\pi ^{\pm }$, K$^{\pm }$, and ($\bar{\mathrm{p}}$)p in Pb–Pb (pp) collisions in the $p_{\mathrm{T}}$ intervals 0.1$-$ 0.7 GeV/c, 0.2$-$ 0.5 (0.6) GeV/c, and 0.3$-$ 0.6 (0.65) GeV/c, respectively.

In ALICE, identification via energy loss is completed by the TPC detector [153] which has a gas drift volume of 90 m$^3$ and allows identification of positive and negative pions, kaons and protons within the transverse momentum intervals 0.25$-$ 0.70 GeV/c, 0.25$-$ 0.45 GeV/c, and 0.45$-$ 0.90 GeV/c, respectively, and from $p_{\mathrm{T}}~\approx$ 2–3 GeV/c up to $p_{\mathrm{T}}$ = 20 GeV/c exploiting the dE/dx signal in the relativistic rise region (3 < $\beta \gamma$ $<<$ 1000). An example of the distribution of energy loss values as a function of momentum in the TPC is shown in Fig. 6b. Nuclei like deuteron, tritium and $^3$He are clearly identified in the $p_{\mathrm{T}}$ range 0.7$-$1.4 GeV/c, $0.6 - 2$ GeV/c, 2$-$7 GeV/c, respectively. Identification of $^4$He is possible exploiting also the time of flight information (see Sect. 6.1.1). Both the ITS and TPC are being upgraded for the 2022 data taking [154].

3.4 FOOT: particle identification for light fragment cross section measurements with emulsions

As mentioned in Sect. 2.5.1, in the FOOT experiment an emulsion spectrometer was developed for the identification of light fragments. It is divided into three parts:

• vertex and tracking detector, which is made of elementary cells of carbon or C$_2$H$_4$ layers, acting as target, alternated with emulsion film (300 $\upmu$m) to track the secondary fragments and reconstruct the vertex position.

• ionization detector for charge identification, composed of elementary cells, containing three emulsion films. After data taking, they are treated at different temperatures to separate low Z fragments (H, He, Li).

• tracking detector for momentum measurements, using 300 $\upmu$m thick emulsion films interleaved with 1-mm-thick lead plates as passive material. The mass and momentum can be obtained using two independent measurements (range and multiple Coulomb scattering).

The emulsion setup has been built and tested during various test beams, demonstrating an excellent performance in charge identification [155]. An example of the performance can be seen in Fig. 7, where the separation between two different populations of ions ($^4$He in red and $^{12}$C in green) can be seen [156]. The Volume Refreshing (VR) parameters on the axes are an estimate of the ionization (V) produced in the nuclear emulsions after two different thermal treatments (VR1 and VR2). The resolution on the charge measurement for $^4$He and $^{12}$C ions was about 8%.

Fig. 7

FOOT. Scatter plot showing two different populations of ions ($^4$He in red and $^{12}$C in green), separated according to their ionization produced in the nuclear emulsions. VR1 and VR2 are the track volumes normalized with respect to the emulsion thickness for two different thermal treatments (from [156])

4 Pulse shape analysis (PSA) for charged particles, neutrons and $\gamma$-rays

In this section PID techniques based on the PSA are presented. In these methods the particle identification is achieved from the correlation between two parameters related to the shape, i.e. to the evolution as a function of time of the signal induced by the detection of a particle, exploiting the fact that fragments with different Z, A and equal incident energy E produce signals of different profiles in the detector. The main advantage of this technique is the need of only one detector layer to obtain the particle identification, thus allowing a significant reduction of the detection thresholds with respect to the case of the $\varDelta E-E$ technique. Since many years the method is widely used for scintillators to identify light charged particles but also to discriminate neutrons and $\gamma$; more recently the technique has been applied also to silicon detectors to identify in charge (up to heavy ions, $Z\sim$ 50) and mass (up to medium size ions, $Z\le$ 20) the reaction ejectiles. The identification threshold depends on the range of the ion in silicon and it increases with the charge of the ion (for example, the minimum range is around 40 $\upmu$m for B and around 60 $\upmu$m for Ne). The charge being the same, the isotopic identification is more demanding and the minimum required range increases (for example, the charge identification for Carbon has a range threshold of 40 $\upmu$m, while its isotopic identification requires a minimum range greater than 100 $\upmu$m).

A different kind of PSA is that related to the $\gamma$-ray tracking in segmented HPGe detectors. In this case, the goal is to improve the energy resolution of the array by reconstructing the interaction positions of the $\gamma$ rays inside the crystals. This can be achieved by comparing the acquired signals with a library of shapes obtained once and for all illuminating the detector with collimated sources of known position.

4.1 PSA technique in CsI(Tl) scintillators

Thallium-doped cesium iodide scintillators are commonly used as the last stage detectors in telescopes because of their high stopping power, the good energy resolution and the ease of machining and operation.

A big advantage of CsI(Tl) detectors is the possibility to perform PSA for detected particles. This possibility comes from the fact that the scintillation of the CsI(Tl) crystal is well described by the sum of two exponentials with different time constants: a short one ($\tau _{\mathrm s}~\sim ~0.75~\upmu$s) and a long one ($\tau _{\mathrm l}~\sim ~5~\upmu$s). If we call $Q_{\mathrm s}$ and $Q_{\mathrm l}$ the charges induced in the photodiode/photomultiplier by short and long components of scintillation, respectively, particle identification capability comes from the different ionization density dependence of $Q_{\mathrm s}$ and $Q_{\mathrm l}$ components on Z and A of the ejectiles (i.e. of the reaction products). In particular, with the same total energy, the short scintillation component (commonly called “fast” component) is more intense for highly ionizing particles, i.e. with greater Z and A. On the other side, the long component (commonly called “slow” component) is more intense for $\gamma$ and cosmic rays, because they produce small ionization densities.² By means of two shapers with different shaping constants (sometimes applied via software on the digitized signal) it is possible to determine the intensity of the two components and so to perform PSA, identifying in charge and mass light charged particles stopped inside the crystal, thanks to the correlation between the fast and the slow components.

4.1.1 CHIRONE

Both CHIMERA and FARCOS multidetectors (see Sect. 2.3.1) are equipped with CsI(Tl) scintillators. For FARCOS the CsI(Tl) have a thickness of 6 cm and their area is 3.2 $\times$ 3.2 cm$^2$, while for CHIMERA the thickness ranges from 10–12 cm in the forward part to 8–3 cm in the backward part, with an area of 5$\times$5 cm$^2$.

For the CHIMERA multidetector the pulse shape discrimination, based on the two gates method [157], is used to identify the light charged particles stopped in CsI(Tl) scintillators. This method permits an isotopic separation for particles with $Z<$ 5. The same method is used with CsI(Tl) scintillators of the FARCOS array. Recently, also a digital electronics (GET) can be used, that allows the digitization of the total shape of signals [158, 159].

Fig. 8

CHIRONE. Fast–slow correlation obtained with a CsI(Tl) of FARCOS array, for the reaction $^{124}$Xe + $^{64}$Ni at 35 MeV/nucleon. The inset shows the yield as a function of the PID. For $\alpha$ particles the FWHM is 0.26

Figure 8 shows a fast–slow correlation obtained in the reaction $^{124}$Xe + $^{64}$Ni at 35 MeV/nucleon in a FARCOS CsI(Tl) module. The inset shows the PID spectrum, obtained tracing lines on each ridge corresponding to a different particle species, where H, He and Li isotopes are easily distinguished.

4.1.2 NUCLEX

GARFIELD, RCo and FAZIA setups (see Sects. 2.3.4 and 3.2.2) are equipped with CsI(Tl) detectors; the thickness of the CsI crystal has been chosen to stop even the most energetic light charged particles in the typical reactions investigated by NUCLEX, i.e. protons up to 105 MeV in GARFIELD + RCo and up to 195 MeV in FAZIA. In GARFIELD, RCo and in FAZIA these different shaping operations have been implemented directly on the digital electronics card purposely designed for these setups [70, 160]. By correlating the ratio between fast and slow shaped energy values versus the slow one it is possible to discriminate $\gamma$ rays and all the hydrogen, helium and lithium (in some cases even Be) isotopes (Fig. 9). Unfortunately, heavier fragments tend to overlap to the same ridge in the correlation, but they can be easily discriminated with $\varDelta E - E$ technique using the CsI(Tl) layer as the stopping layer (residual energy $E_\mathrm {res}$ detector).

Fig. 9

NUCLEX. Fast/slow vs slow correlation in a typical FAZIA CsI(Tl) crystal. Hydrogen, helium and lithium isotopes are well discriminated. Data come from $^{48}$Ca + $^{12}$C reactions at 25 MeV/nucleon

There are some limits of the PSA technique in CsI(Tl) scintillators: first, neutrons may interact with the crystal via (n,p) or (n,$\alpha$) reactions and thus they appear overlapped to protons or $\alpha$ particles in the correlation; second, protons (especially with energy above 100 MeV) can experience interactions (Coulomb or nuclear elastic scattering and reactions) which, in some cases, produce events characterized by an incomplete energy deposition (IED). In this kind of events, protons deviate off the $Z=1$ region, moving to the $\gamma$-like ridge in the correlation [161]. This is due to the fact that protons, in IED, react or escape from the crystal volume before reaching the Bragg peak, and thus they produce a track with moderate ionization density in the crystal, mainly stimulating the long scintillating component.

The experiments performed by NUCLEX collaboration are focused on charged particles, thus it is important to distinguish and possibly reject $\gamma$ particles and neutrons. Silicon layers in front of CsI(Tl) crystals have an almost zero detection efficiency for chargeless radiation, thus $\varDelta E - E$ correlations involving Si pads automatically reject $\gamma$ rays and neutrons. Si pads are used also as a veto to reject those kinds of particles from PSA in CsI(Tl) scintillators. As a general rule, since many identification mismatches (due to neutrons interacting with CsI(Tl) and producing n or $\alpha$) are possible with PSA in scintillators, the PID priority should be given to the $\varDelta E - E$ method. Instead, the case of IED is much more complex to handle, because usually fast protons release very little energy in Si layers and sometimes it is impossible to identify them via $\varDelta E - E$ technique.

4.2 PSA in silicon detectors

The PSA in Si detector has been studied and developed during the last thirty years [162,163,164,165,166]. In these detectors, the different shapes of the signals associated with different ions, being equal their energy, are due to the variation with Z, A and E of the penetration depth and of the ionization density profile along the particle track, which in turn affect the plasma erosion time [167, 168] and the collection time of the electron-hole pairs. The technique is able to identify in charge up to heavy ions ($Z\sim$ 50) and in mass up to medium size ions ($Z\sim$ 20).

4.2.1 CHIRONE

The collaboration has proven the capabilities of CHIMERA multidetector to provide accurate results in the Fermi energy regime, characterized by final states with a large number of charged products that populate a broad energy range. However, the possibility to employ the pulse shape analysis in Si detectors expanded the energy regime towards lower energy ($E~\le$ 10 MeV/nucleon) [169]. In CHIMERA, the PSA in Si is based on the analysis of the rise time of Si signals, and it allows the identification in charge of slow-moving particles, stopped in Si detectors (with a thickness of 300 $\upmu$m), having 3 $\le$ Z$~\le$ 18 [46, 170]. With the CHIMERA multidetector this technique is applied in Si direct configuration (i.e. entrance from the high electric field side), not to spoil time of flight measurements. In fact, a good time of flight requires fast signals and this can be achieved if the particles experience a high electric field at the entrance in the detector. The energy threshold for the charge identification ranges from 4 to 9 MeV/nucleon, as a function of increasing detected charge. The first experiment performed using the PSA in Si in a low-energy regime was ISODEC [169], studying the isospin influence on compound nucleus decay modes in the reactions $^{78}$Kr + $^{40}$Ca and $^{86}$Kr + $^{48}$Ca at 10 MeV/nucleon. Figure 10a shows an energy-rise time correlation obtained in the first reaction: the inset shows the Z distribution determined using the energy vs. rise-time plot. However, this method is also extensively used at higher energy, as we can see in Fig. 10b that shows an energy vs. rise-time plot obtained in the reaction $^{124}$Xe + $^{64}$Zn at 35 MeV/nucleon [46]. The energy threshold for the charge identification depends on Z; for example, it corresponds to 5.6 MeV/nucleon for $Z=6$ and it increases to 9 MeV/nucleon for $Z=16$.

Fig. 10

CHIRONE. a Energy of particles stopped in silicon detectors as a function of the signal rise time, at around 42$^\circ$, for $^{78}$Kr + $^{40}$Ca reaction at 10 MeV/nucleon. The inset shows the Z distribution determined using the energy-rise time plot, after excluding the region with short rise time where charge identification is not achieved. b The same as in a but at around 15.25$^\circ$, for $^{124}$Xe + $^{64}$Zn reaction at 35 MeV/nucleon. The inset shows the Z distribution determined using the energy-rise time plot, after excluding the region with short rise time where charge identification is not achieved

4.2.2 GAMMA

GAMMA exploits the PSA in silicon detectors in the GRIT (Granularity Resolution Identification Transparency) array [171, 172] and in the GALTRACE (GALILEO TRacking Array for Charged Ejectiles) prototype to identify light particles in charge and mass.

GRIT is an array of segmented silicon detectors developed within an international collaboration with the aim of performing particle spectroscopy and discrimination. It is designed to work as a standalone device or combined to large $\gamma$ spectrometers. It consists of 48 detectors in telescopic $\varDelta$E-E configuration arranged in a sphere-like geometry. For each telescope, the first ($\varDelta E$) layer is a 500-$\upmu$m-thick nTD (neutron-transmutation doped) detector while the second layer (E) is $1.5 \hbox {mm}$ thick. The detectors are segmented in 128 strips on both sides.

A small prototype detector array, GALTRACE, was recently developed to optimize the electronics. The detector readout is performed with custom ASIC (Application-Specific Integrated Circuit) pre-amplifiers [173,174,175,176]. The energy information is obtained with trapezoid filters using MWD (moving window deconvolution) implemented on the acquisition FPGAs (Field-Programmable Gate Arrays).

By analyzing the characteristics of the pre-amplifier signal leading edge, it is possible to gain information about the particles impinging on the detector. Clear PID can be obtained plotting the rise time or the maximum of the signal derivative (Imax) versus the deposited energy of the particles (see Fig. 11). This technique, complementary to the $\varDelta E-E$ one, allows to extend the particle discrimination capabilities of the detectors to particles stopping in the first silicon layer [177], thus allowing to cover the low-energy region, down to $\sim$ 1 MeV/nucleon for the main light particles [178, 179].

Fig. 11

GAMMA. Maximum signal derivative versus total amplitude, performed on one GRIT detector’s p-side strip (a) and one n-side strip (b). From [179]

Further developments of an integrated front-end electronics with reduced power consumption and the inclusion of the analog on-line signal are in progress. An analog memory [180, 181] is currently under development within the GRIT collaboration. Its aim is to work as an efficient, low-noise, low-power multiplexing system for the analog signals inside the reaction chamber.

4.2.3 NUCLEX

FAZIA collaboration widely studied PSA in silicon detectors, also developing a microscopic [182] and a phenomenological [165] model, which consider the progressive extraction of the electrons and holes from the high carrier density zone along the ionizing particle track. See [69] for a comprehensive report of all the work on PSA carried out by the collaboration.

There are two ways to analyze the pulse shape: it is possible to measure the rise time of the charge signal or the maximum value of the current pulse; then the correlation of the chosen variable to the energy released inside the sensor is built. In this way, ridges corresponding to different atomic species can be obtained, and, in optimized detectors, also isotopes for the lightest and most energetic fragments can be discriminated. The PSA performance is adversely affected by various factors like channeling effects, range straggling, non-uniformity of doping, residual sheet resistance and instability of the applied bias (see [69] for more details). For this reason, during FAZIA R&D phase, much effort has been devoted to the optimization of the silicon sensors:

• wafers are obtained from ingots with excellent declared doping homogeneity, usually but not uniquely guaranteed by the use of nTD technique;

• wafers are cut from ingots with an angle of $\sim$ 7$^\circ$ with respect to the main crystal axis to reduce channeling effects;

• pads are covered with a thin metallization layer to reduce the sheet resistance;

• bias voltage is kept under control and adjusted in real time to compensate for the drop due to the increasing (usually with radiation) reverse current circulating through the bias resistors.

With such treatments it is possible to distinguish isotopes for ions up to $Z\sim$ 20 with a threshold of around 10 MeV/nucleon (mass resolution about 5%), while charge identification is possible from 2–5 MeV/nucleon depending on the fragment atomic number (Fig. 12), with charge resolution about 2%.

Fig. 12

NUCLEX. $E - I_\mathrm {max}$ correlation in a typical FAZIA first silicon layer. Isotope discrimination is achieved up to $Z=20$. In the upper inset the PID spectrum in the region $Z=8{-}12$, restricted to the zone of the correlation in which the isotopic separation is achieved, is shown. In the bottom inset the region around $Z=18$ is expanded. Data come from $^{48}$Ca + $^{12}$C reactions at 25 MeV/nucleon

Of course, there are limits in the applicability of PSA in detectors when the particle tracks are modestly penetrating in the active volume (i.e. towards low deposited energies). For example, according to studies of the FAZIA group [183] charge identification for light ions in silicon is prevented for ion range below 30 $\upmu$m. In the same paper the quality of PSA is compared between front mounted (i.e. particles entering through the high electric field side) and rear-mounted detectors (i.e. particles entering through the low electric field side): the study shows that the identification threshold is much lower in the latter case, while there is no impact on energy resolution (and thus on the complementary $\varDelta E - E$ technique). For this reason, RCo (see Sect. 3.2.2) and FAZIA (see Sect. 3.2.2) adopt rear mounting.

PSA strongly benefits of digital processing: all the achievements obtained with RCo and FAZIA in lowering identification thresholds were possible also thanks to the digital electronics these detectors are equipped with. In fact, both in GARFIELD + RCo and in FAZIA, after a low-noise analogue stage including preamplifier and antialiasing filter, signals are immediately sampled with fast and high-resolution ADCs (14-bit, 250 MHz in FAZIA). As shown in [184], a proper digital processing of the sampled signals permits to improve the PSA quality.

4.3 n-$\gamma$-Charged particles and/or n-$\gamma$ discrimination

The discrimination among neutrons and $\gamma$ and/or charged particles is generally achieved by means of the PSA in various kinds of scintillators (liquid, solid, organic, inorganic), mainly correlating the fast vs. slow component as in the case of CsI(Tl) crystals (see Sect. 4.1). In nuclear astrophysics experiments the n-$\gamma$-charged particle discrimination is necessary to reject the background, for example that due to the intrinsic radioactivity of the detector. Neutron detection and discrimination from $\gamma$-ray is a common issue for nuclear safety and security, nuclear medicine, fundamental nuclear physics. For the latter, the neutrons can be used for the identification of the reaction products during fusion-evaporation reactions producing neutron-deficient species. On the other side of the nuclear chart, neutron emission is an important part of the decay process with $\beta$-delayed neutron emission. The two aforementioned cases required different types of detectors: for the in-beam data, fast detectors with high detection efficiency are more suitable, while for the decay studies, since neutron energy gives access to key spectroscopic information, good neutron energy measurement is the key to reconstruct the precise level scheme.

4.3.1 CHIRONE

In experiments with nuclear reactions induced by stable and exotic heavy-ion beams the discrimination of neutrons and light charged particles is of paramount importance. In this framework, the collaboration is carrying out a study to investigate performances of EJ 299-33 scintillator in discriminating charged particles, neutrons and $\gamma$-rays [185,186,187]. The used method is based on the pulse shape discrimination, using the fast and slow components of the scintillator light output. The discrimination properties of the scintillator have been investigated by selecting different parts of the digitized pulse and comparing the areas under such time windows. A clear separation of neutrons from $\gamma$-rays is observed in Fig. 13a. This can be better appreciated looking at the inset, where the projection on the Slow Component axis for events belonging to the region between the two dashed lines on the Fast Component axis is shown. In Fig. 13b the discrimination between $\alpha$ particles and neutrons is shown. In this case, a $^{228}$Th $\alpha$ source and an AmBe neutron source were used. The collaboration performed also a further study employing stable beams, delivered by the Cyclotron at INFN-LNS, to investigate the performance of EJ 299-33 scintillator in experiments with heavy ions, i.e. under high background conditions [186]. The results obtained with both radioactive sources and beams are very promising and show the good capability of the EJ 299-33 to discriminate neutrons, charged particles and $\gamma$-rays.

Fig. 13

CHIRONE. a The slow vs fast components plot shows neutron-$\gamma$ discrimination, in EJ 299-33 scintillator irradiated with AmBe and $^{60}$Co sources. The inset shows the Figure of Merit (FOM) for neutron-$\gamma$ separation relative to the slice in the fast component (1100–1200 keVee) displayed with dashed lines. Figure adapted from Ref. [185]. b The plot shows $\alpha$, neutron and $\gamma$-ray discrimination obtained using $^{228}$Th and AmBe sources. The unit keVee is for keV electron equivalent  [185]

4.3.2 GAMMA

GAMMA exploits the n-$\gamma$ discrimination both for spectroscopy (using inorganic scintillators in the PARIS setup [188] and investigating modern materials as the “CLYC”: Cs$_{2}$LiYCl$_6$:Ce) and for in-beam experiments (using organic scintillators in the NEDA array).

Scintillators designed to detect neutrons in in-beam experiments, such as the NEDA array [189], must present the largest possible detection efficiency for fast neutrons. NEDA consists of detection modules of organic liquid scintillator (EJ-301). Designed to be coupled with the AGATA array, NEDA makes use of a digital electronics developed within the collaboration. Because of the large counting rate in the liquid scintillators, due to the large $\gamma$ background in fusion-evaporation experiment ($\sim$ 80 kHz / NEDA cell), a first level of neutron-$\gamma$ discrimination needs to be performed online. For this purpose, two pieces of information can be combined at the FPGA level: a standard charge-comparison (CC) algorithm and a time-of-flight measurement using an external reference signal. Charge-comparison algorithms rely on the comparison between two integration windows of the signal, generally one short ($\sim$ 20–50 ns) and one long ($\sim$ 250 ns). This is effective, since signals generated by neutron events have a longer tail respect to the ones induced by $\gamma$-rays. Neutron selection can be configured on a detector-by-detector basis. Typical neutron-$\gamma$ discrimination figure are presented in Fig. 14, where the CC algorithm result is correlated to the total charge (panel a) and the TOF (panel b) for in-beam data obtained during the AGATA-NEDA campaign of 2018. The FPGA selection allows to reduce the $\gamma$ background, thus allowing large beam intensity resulting in very high counting rates.

Fig. 14

GAMMA. Neutron identification in the NEDA array. a Corresponds to the charge comparison algorithm, while b shows the correlation between the time of flight obtained using the delayed RF of the beam as a stop and the individual signal as start and the CC

On the other hand, scintillators designed to provide spectroscopic information should measure, with the highest possible precision, (i) the energy of the incident radiation, (ii) the interaction instant, and (iii) the nature of the radiation (e.g., $\gamma$-rays or neutrons). In this context, inorganic scintillator materials are more suitable, since the performance in terms of energy resolution of the organic liquid scintillators, such as the EJ-301 used by NEDA (also due to the quenching effect), is quite limited. Moreover, the xylene-based liquid are quite difficult to manage in terms of safety and durability of the detectors since xylene is a powerful solvent. An inorganic scintillator is often constituted by an artificially grown crystal, with a volume that can vary from a few tenth of mm$^3$ to a several dm$^3$. The works of Refs. [190, 191] discuss the performances of various inorganic scintillators, developed in recent years, with good neutron-$\gamma$ discrimination.

Modern materials such as the CLYC presents the advantage of combining a good energy resolution for $\gamma$-rays, slightly larger than the one of LaBr$_3$ (4.5–5% at 661 keV) with a good neutron-$\gamma$ discrimination using PSA techniques. By applying a CC algorithm to the signals from the CLYC scintillator, one can obtain the separation of signals induced by $\gamma$ radiation and neutrons, as shown on panel b of Fig. 15 [192, 193]. The red box highlights the contributions from thermal neutrons and $\gamma$-rays (depositing the same energy), which are located at PSA values around 0.8 and 0.7, respectively (see [192] for more details on the identification mechanisms).

Fig. 15

GAMMA. a Correlation between the maximum amplitude (Q$_{\mathrm {S}}$) and the total integral (Q$_{\mathrm {L}}$) of the signal, plotted on the y- and x-axes, respectively, for a phoswich detector of the PARIS array. Adapted from Ref. [188]. b Neutron-$\gamma$ discrimination matrix obtained using a $^6$Li enriched CLYC scintillator, with the charge comparison plotted against the total energy deposited. Figure adapted from [192]. The red box highlights the contributions from thermal neutrons and $\gamma$-rays (depositing the same energy), which are located at CC values around 0.8 and 0.7, respectively [192]

Scintillator materials are characterized by one or more scintillation-light decay constants. This feature uniquely defines the pulse line-shape; when the detector is a phoswich (i.e., a sandwich of scintillators), the different shapes associated with the various layers forming the telescope can be used to localize the material where the incident $\gamma$ radiation interacted. This is, for example, the case of the PARIS array, based on phoswich scintillation detectors [188] made of two crystals read by a single photomultiplier (PMT). Two types of phoswich are currently available: LaBr$_{3}$:Ce-NaI and CeBr$_{3}$-NaI. Both LaBr$_{3}$ and CeBr$_3$ are cubic 2"$\times$2"$\times$2" crystals while the NaI crystals are 2"$\times$2"$\times$6". The two crystals are separated by a quartz window to avoid chemical interaction between them, that can lead in some years to an unwanted yellowing of the scintillators in proximity of the common edge. Although the two crystals have very different performances in terms of energy resolution ($\sim$ 4.1% for the LaBr$_3$ compared to 7.8% for the NaI at 662 keV), the difference in the time response of the two scintillators allows to identify in which crystal the interaction took place and get the best performances for both of them using a single PMT. In the present configuration, the PARIS array consists of up to 8 clusters made of 9 phoswich each. In Ref. [177], a PSA algorithm applied to LaBr$_3$:Ce and LaCl$_3$:Ce scintillators is discussed, to distinguish between signals induced by incident $\gamma$ rays and internal $\alpha$ activity. On panel a of Fig. 15 an example of charge comparison applied to PARIS detector is shown. Signals of the LaBr$_3$ and NaI are given in inset of the figure. Since the LaBr$_3$ signals are faster than the NaI, the short (Q$_{\mathrm {S}}$) and long (Q$_{\mathrm L}$) integration window gives the same result, while in the case of NaI signal the short integration represents only a fraction of the longer one. This gives rise to two diagonal distributions: the steeper one represents the events in which the measured $\gamma$-ray interacted in the LaBr$_3$:Ce. The less steep diagonal is populated by $\gamma$-rays interacting in the NaI crystal. Mixed events are seen in between. The 6 MeV line is referred to the 6.13 MeV $\gamma$-ray emitted from an excited state of $^{16}$O produced by the reaction $^{13}$C($\alpha$,n)$^{16}$O, taking place in the Pu$^{13}$C radioactive source. Thanks to its large efficiency and good energy resolution, the PARIS array opens the way for $\gamma$-ray spectroscopy at medium to large $\gamma$-ray energy.

The signals produced by a scintillator have always the same line-shape, regardless of the radiation interaction point. As a consequence, the localization of the impact point requires the use of segmented photocathodes and the acquisition, on an event-by-event basis, of the image of the scintillation light on the photocathode [194,195,196]. This information is naturally provided by a SiPM array, while in the case of a PMT the use of a Position Sensitive PMT (PSPMT) is required.

The growth of the SiPM technology made a fine segmentation of the photocathodes possible. To better reconstruct the impact point, machine learning algorithms are under study [197]. Moreover, the research on ceramic scintillating materials will open new perspectives in terms of detector resolution, maximum available volume and cost/performance ratio.

4.3.3 LUNA

LUNA applies the PSA technique to discriminate the intrinsic background of the used detectors (due to their intrinsic radioactivity) with respect to the signal associated with neutrons. For the $^{13}$C($\alpha$,n)$^{16}$O measurement, a detector array based on 18 $^{3}$He proportional counters at a pressure of 10 bars was designed. They are arranged in two concentric rings around the target chamber: 12 counters of 40 cm active length are located at a radius of 11 cm, and 6 of 25 cm active length are located at 6 cm radius. Since the average neutron energy from the reaction is 2.5 MeV, counters are embedded in a polyethylene block used as moderator to obtain thermal neutrons for the final detection.

The output signal fed charge sensitive preamplifiers, whose signal was then digitized and directly written to disk for further analysis. Once the neutron is captured by $^3$He, the reaction $^3$He(n, p)$^3$H takes place and two charged particles release their energy in the detector working as a proportional chamber.

Charge-sensitive preamplifier (i.e., current integrated) signals can be converted in current sensitive preamplifier signals by a first order digital high pass filter (CR). After the conversion, when a neutron is captured (and a p and a $^{3}$H are produced inside the detector) the output pulse has a typical structure with a double peak waveform (this is not true in few cases, i.e. in case of the wall effect³) [198]. On the contrary, $\alpha$ background signals (due to the natural radioactivity of the Th and U chains coming from contaminants in the counter case) are characterized by only one particle releasing energy in the gas and the output signal has a single peak. In Fig. 16a, the reader can find an example of the filter performance: the blue and the dark green waveform are the preamplifier output and its CR shaping, respectively.

After the CR shaping, the PSA parameter M can be defined as:

$$\begin{aligned} M(t_{\mathrm 0},t_{\mathrm 1},t_{\mathrm 2})=\frac{I(t_{\mathrm 0},t_{\mathrm 1})}{I(t_{\mathrm 0},t_{\mathrm 1})+I(t_{\mathrm 1},t_{\mathrm 2})}, \end{aligned}$$

(3)

where I(a, b) is the charge integrated between time a and b. In the LUNA analysis $t_{\mathrm 1}-t_{\mathrm 0}$ = 1 $\upmu$s and $t_{\mathrm 2} - t_{\mathrm 1}$ = 7 $\upmu$s were used for the optimization of the neutron/$\alpha$ PSD.

Fig. 16

LUNA. a The input charge sensitive preamplifier and filtered current sensitive preamplifier waveforms for a $^3$He(n, p) event. Typical features of the waveform, i.e. amplitude, rise-time and pre-sample are indicated by corresponding arrows. The signal refers to an event in which one neutron is detected. The light green and orange parts of the filtered waveform correspond to the fast and slow integral regions, respectively. Adapted from [116]. b Scatter plot of M parameter—energy. Blue and red datasets indicate measurement of background and Am/Be source, respectively. From [116]

The method was tested plotting the M parameter vs energy deposited in a scatter plot for two sources: an AmBe source (almost only neutrons are detected by the setup) and a background measurement (mainly $\alpha$ particles are detected, because neutrons from outside were absorbed by borated PE). In Fig. 16b the main results are shown: red and blue points indicated events from AmBe source and environmental background, respectively. The acquisition time was about 1 day for the AmBe source and 1 week for the background, to acquire enough statistics for both dataset. After the test with these two data sets, the value for M = 0.81 was chosen to maximize the neutron detection and the $\alpha$ rejection efficiencies, at about 90% and 98% of the level without PSA.

The use of these PSA techniques reduced the overall background of the detector from 3.3 down to 1 counts/h, allowing to measure lower cross sections, in the region of energies of astrophysical interest [115]. With the installation of the facility LUNA MV at LNGS foreseen in the end of this year, the LUNA scientific program will include the $^{22}$Ne($\alpha$,n)$^{25}$Mg cross section measurement [199]. The described PSA method will allow also in this case to increase the sensitivity of the measurement providing for the first time direct cross section data below the 704 keV resonance.

4.3.4 n_TOF

In n_TOF, the PSA technique is used to discriminate among $\gamma$, $\alpha$ particles and neutrons. The detection of the prompt $\gamma$ rays resulting from the neutron capture events, i.e. the electromagnetic transitions leading to the de-excitation of the compound nucleus, is performed using either a calorimeter made of BaF$_2$ crystals [200] (called Total Absorption Calorimeter) or an array of C$_6$D$_6$ liquid scintillators [201]. The calorimeter is designed to detect the full $\gamma$-ray cascade using detectors of high intrinsic efficiency and large solid-angle coverage [200]. The other experimental setup is based on a detector with extremely low neutron sensitivity and exploiting the total energy technique [202] in combination with the pulse height weighting technique.

The main background source is related to the neutrons scattered by the sample and interacting with the surrounding materials. This background component is particularly critical as it follows the same energy dependence and resonant pattern as the capture events.

The different operating principles of the two detectors require a good $\alpha$/$\gamma$ and n/$\gamma$ discrimination. A convenient solution to perform particle identification and, in the mean time, to identify and reconstruct pile-up events generated by the high instantaneous neutron flux is based on the acquisition of the complete waveforms of the signals, using Flash Analogue to Digital Converters (FADC). The important advantage of this approach is the possibility of deducing the physical information contained in the digitized signals through off-line analyses.

Total Absorption Calorimeter (TAC) This is a segmented 4$\pi$ detector array made of 40 BaF$_2$ crystals suited for neutron capture cross-section measurements on low-mass and/or radioactive samples. The light output of the BaF$_2$ has two main components with decay times of (0.6$-$ 0.8e) ns and 630 ns for the fast and the slow emission, respectively. The crystals are 12 pentagonal and 28 hexagonal in shape, and each of them is coupled with a 12.7 cm Photonis XP4508B PMT.

The neutron sensitivity is minimized thanks to a spherical neutron moderator/absorber made of an inert non-flammable lithium salt (C$_{12}$H$_{20}$O$_4$($^6$Li)$_2$) inserted in the central cavity, surrounding the sample, and also by the encapsulation of each crystal in a $^{10}$B-loaded carbon-fiber shield. The neutrons can be captured by the absorber producing a $\gamma$ cascade, which can be recognized by the Total Absorption technique, i.e. reconstructing the deposited-energy distribution of the corresponding $\gamma$ cascades [203].

The other non-negligible background contribution is due to the radioactive impurities in the BaF$_2$ ($^{226,228}$Ra and their daughters), which emit $\alpha$ and $\gamma$-rays with energies up to a few MeV [204]. Signals produced by $\alpha$-particles can be discriminated from $\gamma$-induced events by the absence of the fast component in the light output; the time dependence of each light component can be expressed by an exponential formula with a proper decay constant. Therefore, the $\alpha$/$\gamma$ discrimination is achieved by fitting the pulse shape. The event selection is based on the total pulse duration versus the ratio of the fast over the slow components of the scintillation light output (Fig. 17a).

Fig. 17

n_TOF. a TAC detector: Signal duration versus the ratio of the fast and slow component of the scintillation light output. From [205]. b C$_6$D$_6$ liquid scintillators: ratio between the slow and fast component of the light response as a function of the fast component. The upper and lower branches correspond to neutrons and $\gamma$, respectively (projection of B/A ratio shown in the inset; the first peak is associated with $\gamma$ and the second peak corresponds to neutrons). Adapted from [207]

In addition to rejecting background events, identification of $\alpha$ particles permits one to continuously monitor the gain of each module by the position of the energy spectrum lines of radium and its progeny [204]. Moreover, the information on the multiplicity (i.e. the number of hits registered in BaF$_2$ crystals) can be used for the selection of $\gamma$-ray events, as the range of charged particles is much smaller than the crystal dimension.

C$_6$D$_6$ liquid scintillators In the array of C$_6$D$_6$ liquid scintillators each module consists of a cylindrical cell with carbon-fiber walls, 12 cm in diameter and 9 cm thick, read out by an EMI 9823QKA PMT [206]. The low sensitivity to background signals induced by scattered neutrons is achieved by the minimization of the amount of material surrounding the detector and using only materials characterized by a small neutron capture cross section. However, since the component of neutron diffusion is particularly significant, it is necessary to take it carefully into account. In fact the neutron scattering cross section can be some order of magnitude larger than capture ($\sigma _{\mathrm n}$/$\sigma _{\gamma }~\sim$ 10$^3 -$10$^4$). Also in this case the discrimination n/$\gamma$ is performed through the shape of the signal produced by the two particles in the detector. The signal shape analysis from scintillation detectors can be obtained by the convolution of the exponential decay spectrum of the scintillation light with the response function of the PMT and readout system [207]. Since the decay constants of the scintillator do not depend on the particle type, the only expected difference between $\gamma$- and neutron-induced signals is due to the relative contributions of the fast and slow components. The branches corresponding to neutrons and $\gamma$ are well identified in the slow to fast component ratio as a function of the fast component (Fig. 17b).

4.3.5 NUCLEX

The detection of fast neutrons with respect to the $\gamma$ background can be achieved with commercially available solid scintillators.

In organic systems, the scintillation process is based on the energy transfer between aromatic groups of the either solid or liquid matrix and the dispersed dye molecules characterized by high quantum efficiency. In fast neutrons and $\gamma$ particles detection, the particles actually measured by the scintillators are recoil protons from fast neutrons and recoil Compton electrons from $\gamma$ rays. Protons produce, along their path, a higher ionization density (which causes the emission of delayed photons) with respect to electrons. This delayed fluorescence has characteristic times of the order of tens of ns, with respect to the prompt emission whose time scale is 1–2 ns, maintaining the same spectral response. Therefore recoil protons generate scintillation pulses with a more intense long living component with respect to Compton electrons, thus allowing their discrimination through pulse shape identification techniques, as shown in Fig. 18, where the $n/\gamma$ discrimination obtained with solid polyoxane-based scintillators (cylinder shaped with a 2” diameter and 2 cm height, doped with 8% PPO) is shown. The scintillator was irradiated with a pulsed flux of 4.5 MeV neutrons from p+$^7$Li reactions.

Fig. 18

NUCLEX. n/$\gamma$ discrimination with solid polysiloxane-based scintillators. a PSD correlation plot between fast and slow components obtained through shapers with different integrating constant. b The same correlation where colours indicate particle identification obtained with an independent method (i.e. time of flight measurement, as shown in the inset)

This research line is in progress with siloxane-based scintillators highly doped (up to 8% in weight) with PPO (2,5-diphenyloxazole) [208].

4.4 $\gamma$-ray tracking with HPGe detectors

The PSA can be used to perform the $\gamma$-ray tracking, to significantly improve the quality of the $\gamma$ spectroscopy which can be achieved with an HPGe array. One of the most important positive effects of this technique is the correction of the Doppler effect.

4.4.1 GAMMA

The AGATA array [60, 210, 211], designed and built by an international collaboration in which GAMMA significantly contributes, fully exploits the PSA technique to obtain extremely good position and energy resolutions. The key element required to perform the $\gamma$-ray tracking is to build a position sensitive HPGe crystal. This can be achieved using detector segmentation in conjunction with the possibility to sample and process the output signals from the detector pre-amplifiers. The detector segmentation is realized, for obvious production limits, on the outer surface of the germanium crystal. A peculiar geometry of dopants, conduction overlays and isolation trenches divide the AGATA crystals surface into 36 areas, called “segments” [210]. The inner part of the detector presents a highly doped cylindrical cavity, that constitutes the inner common detector electrode connected to the high voltage. The outer surface is n-doped, while the inner one is p-doped and collects electrons. For this reason the energy information is generally taken from the common electrode: in fact, the neutron damage produces amorphous pockets that generally work as hole traps that leave the electron signal mostly unaffected.

Different interaction positions inside the crystal lead to the release of free charge carriers with different spatial distributions. The drift motion of these carriers across the detector volume following the electric field lines induces current signals not only at the terminals of the segment where the interaction happened (signal that contains the energy information and the radial position) but also on the nearby segments, according to the Ramo theorem. Since the preamplifiers bandwidth is high enough to preserve the detector signal high-frequency content, it is possible to retrieve the information about the interaction position inside the crystal analyzing the leading edge of the preamplifier wave-forms.

To keep the position information, a dedicated differential preamplifier was developed [212]. Signals coming from the 36 segments and the central contact are continuously digitized using high-resolution, 100 Msps (Megasample per second) ADC. A specific readout electronics and trigger have been developed, allowing AGATA to maintain optimal performances, in terms of energy resolution and dead-time with rates up to 80 kHz per crystal.

To reconstruct the position information, each AGATA crystal must be previously characterized. Illuminating the detector with precisely collimated source with known position (with the support of GEANT4 simulations, see Ref. [213]) it is possible to build a digital library of preamplifier signals. Incoming signals are then compared to the reference ones using grid search algorithms. The analysis is performed online, with dead-time below few percents, up to rates of about 4–5 kHz per crystal.

Typically, the PSA will give the interaction positions within the crystal with a resolution of the order of $5\, \hbox {mm}$ FWHM [214]. Implementation of position uncertainty determination is currently under study with, for example, bootstrapping methods [215].

The first main improvement due to the PSA is related to the fact that thanks to the position determination inside the crystals, the interaction path of a $\gamma$ ray inside the array can be reconstructed, allowing for the detection of its full energy. Several algorithms have been developed over the years and are still being improved [216]. Reconstruction of the full energy of the $\gamma$ rays, taking into account all the possible interactions processes: photo-electric, Compton-scattering, pair-creation at the typical energies observed in nuclear structure studies (few keV to hundreds of MeV) allows to reach performances in terms of P/T⁴ close to the one of Compton-Suppressed arrays, with a huge efficiency gain.

Second improvement, thanks to the precise determination of the $\gamma$-ray interaction point in the crystal, the probability of the charge carriers to be trapped at local defects can be evaluated, allowing the correction of the measured energy.

The third main result of the position resolution, obtained with the PSA, is the unprecedented Doppler correction capabilities, when AGATA is coupled to spectrometers allowing for the measurement of the velocity or to high-resolution charge particle detectors and the kinematic reconstructions of the recoil vector is performed. In this case, it is possible to obtain energy resolution only $\sim$ 5% larger than what is observed for $\gamma$ rays emitted at rest, thus allowing to obtain unprecedented results for the study of exotic nuclei and also opening new perspectives in the study of high-energy $\gamma$ rays [209].

Fig. 19

GAMMA. a Energy spectrum measured by AGATA in the region of the 6.13 MeV gamma-ray, emitted by the $^{16}$O nucleus with a recoil velocity v/c = 20%. The grey spectrum is without Doppler correction, while the others were corrected using different position information, as described in the legend. From [209]. b Performances of AGATA during a radioactive ion-beam experiment. The SPIRAL1 post-accelerated $^{19}$O beam was impinging on a 3-$\upmu$m-thick CD$_2$ target deposited on a 11 $\upmu$m Au backing for lifetime measurement in $^{20}$O. In the inset the comparison between the Doppler corrected and non corrected spectra in linear scale is shown. The presence of the high energy transitions, above 2500 keV, can only be observed thanks to the unique performances of the setup

In Fig. 19a, the energy resolution which can be obtained by AGATA fully exploiting the PSA is shown as a red curve, to be compared with the grey line obtained without Doppler correction, as explained in the caption. In Fig. 19b, one of the latest results of the AGATA array, using a post-accelerated radioactive ion beam at GANIL, is reported. A 10$^5$ pps $^{19}$O beam was produced and post-accelerated to 8 MeV/nucleon at SPIRAL1 (GANIL, France); it impinged on a deuterated polyethylene (CD$_2$) target deposited on a thick (20 mg/cm$^2$) Au backing. The direct spectrum (blue curve) is dominated by the background radioactivity (natural radioactivity and radioactive beam implantation). Combining the detection of a proton and the detection of the recoiling nucleus with the position of the first interaction of the $\gamma$ ray within AGATA, it is possible to obtain the green line, which corresponds to the Doppler corrected spectrum of $^{20}$O populated by the $^{19}$O(d,p) transfer reaction, with an energy resolution similar to that obtained at rest. Therefore the line shape of the transition can be used to perform direct lifetime measurement even with relatively low statistics ($\sim$ 200 counts) in the photopeak.

In the next future, the solid angle coverage of the AGATA array will be progressively increased from the current 1$\pi$ to 2$\pi$, thus requiring an increase of high-resolution readout channels up to 1100; new back-end electronics is currently under test. Moreover, new algorithms for the PSA and $\gamma$-ray tracking based on machine learning algorithms are under study.

5 X and ${\gamma }$ spectroscopy

In many nuclear physics experiments, the reaction products cannot be directly detected and identified. This may be caused either by a short lifetime of the searched products or by their low energy, not allowing them to leave the target or to be directly measured. However, since these products have internal structures, they emit characteristic X or $\gamma$ radiation that can be used to tag their presence in the reaction. The large mean free path of X and $\gamma$ rays allows to detect them outside of target or interaction region and their identification requires a good spectroscopic capability, to resolve interesting energy lines from, generally large, correlated and uncorrelated backgrounds. The uncorrelated background, typically, can be reduced by a narrow-gate coincidence with other detectors, suggesting to select fast spectrometers.

The spectroscopy of X-rays is typically performed with silicon drift detector (SDD) combining high-energy resolution of about 100 eV with very fast response time of the order of 1 ns. Also charge-coupled device (CCD) can be used when background rate is not overwhelming.

For $\gamma$-ray spectroscopy HPGe detectors with their resolution of few keV, high efficiency and fast response are most indicated for this kind of experiments. Inorganic scintillator crystals are less expensive and much easier to handle, providing similar efficiency and timing, but with 20–60 times larger energy resolution.

In this section, we describe X-ray spectroscopy by SDD and CCD and $\gamma$-ray spectroscopy with HPGe and CsI(Tl) detectors as used in KAONNIS, PANDORA and CHIRONE experiments.

5.1 CHIRONE: identification of Pygmy Dipole Resonance and of $^{12}$C excited states with $\gamma$ spectroscopy

The CHIMERA 4$\pi$ multidetector at LNS is primarily a charged particle detector. However, the CsI(Tl) crystals, belonging to the spherical part and read by a photodiode [217] (see Sect. 3.2.1), are also suitable to detect $\gamma$-rays due to the high atomic number of the material. Indeed, due to the large solid angle coverage of the single detector and to the small yield of charged particles, the sphere has a larger signal-to-noise ratio for $\gamma$-detection with respect to the forward part of CHIMERA. The efficiency of the crystals depends both on $\gamma$ energy and thickness of CsI(Tl); as an example an efficiency of $\approx$ 50% is obtained in the energy range of 4–5 MeV. The energy resolution is 500 keV, while timing resolution is $\approx$ 100 ns. Such CHIMERA peculiarities allow to detect $\gamma$-rays in a wide energy range (from an energy threshold of $\approx$ 1 MeV to at least 20 MeV), with a good detection efficiency, and to reconstruct their angular distributions. The method used for the identification of $\gamma$-rays is based on the so-called fast–slow technique described in Sect. 4.1.

Fig. 20

CHIRONE. a $\gamma$-ray energy spectra measured with CHIMERA CsI(Tl) in the reaction $\alpha$+$^{12}$C at 16 MeV/nucleon (figure adapted from Ref. [219]). Various levels of C are indicated with different colours and their scale factors. b $\gamma$-ray energy spectra in $^{68}$Ni + $^{12}$C reaction, Doppler shift corrected. The black dots represent the spectrum in coincidence with $^{68}$Ni, detected at forward angles. The blue dots represent the spectrum in coincidence with $^{66,67}$Ni. The bump at around 10 MeV is the contribution of the Pygmy Dipole Resonance decay (figure adapted from Ref. [144])

With this method, the collaboration has performed several experiments in the framework of the $\gamma$-ray spectroscopy. The energy resolution of CsI(Tl) can not compete with HPGe detectors, however the large solid angle and the efficiency allow to extract data in cases of low-intensity radioactive beams or for broad resonances, as, for instance, the Pygmy Resonance. Two examples are described in the following.

The collaboration has investigated the $\gamma$-decay of $^{12}$C levels, in particular the Hoyle and the 9.64 MeV states [218]. In this case, the main advantage of CsI(Tl) crystals is the high efficiency that allows to access information about the levels with a low decay probability. Figure 20a shows $\gamma$-ray energy spectra, measured in the reaction $\alpha$+$^{12}$C. In the figure one might note that it was possible to observe the 12.7 MeV $\gamma$-decay of $^{12}$C level with a relative probability of occurrence of $4\times 10^{-5}$, obtained as a combination of cross section and $\gamma$-decay probability of the channel. Kinematic methods are also useful to improve resolution and background suppression (see Sect. 9.1.2).

Another relevant topic concerns the investigation of the Pygmy Dipole Resonance in the exotic nucleus $^{68}$Ni above the neutron emission threshold [144]. Figure 20b shows $\gamma$-ray energy spectra obtained in the reaction $^{68}$Ni + $^{12}$C at 28 MeV/nucleon. The enhancement at around 10 MeV comes from the contribution of the Pygmy Dipole Resonance decay of $^{68}$Ni. The cross section of such Pygmy decay was evaluated from the difference between spectra measured in coincidence with $^{68}$Ni and $^{66,67}$Ni, as discussed in detail in Ref. [144].

The collaboration is currently improving the detection of $\gamma$-rays, employing the new electronics [187], that allows the digitization of the total shape of signals. The offline computation on the pulse waveform, using several filters, will allow to improve the identification of $\gamma$-rays, based on the fast–slow method, and to remove, in a better way, the background.

5.2 KAONNIS: kaonic atom identification by X-ray spectroscopy

In SIDDHARTA (see Sect. 2.1.3), large-area X-ray detectors with spectroscopic capabilities were required to measure the low yield of X-rays from kaonic atom transitions, isotropically emitted from the large-volume gaseous targets used to enhance the K$^-$ stopping. The silicon-based solid-state devices have typical values of FWHM < 160 eV at Fe$_{\mathrm {K\alpha }}$(6.4 keV), a $\simeq$ 90% detection efficiency in the 5–10 keV range and a linearity of $\varDelta E / E~<~10^{-3}$: for these properties, SDD were selected as the best option in terms of achievable spectral resolution.

In addition, the requirement of few hundreds of ns read out times, to exploit the possibility to trigger the acquisition of the X-ray signals and reduce the machine background, oriented the final choice on 1 cm$^2$ SDD [28, 29]. In the SIDDHARTA experiment, indeed, a triple timing coincidence between the TOF system and SDDs (see Sect. 6.1.2) allowed to reduce the background dramatically, as shown in Fig. 21. In panel a, the comparison of SDD spectra with and without the triple coincidence show an overall background reduction by a factor $\simeq ~10^5$. In panel b, the lines of interest are the blue ones, corresponding to the K$^3$He transitions to the $n~=~2$ level; the K$_{\alpha }$ line, corresponding to the 3d$\rightarrow$2p transition is clearly visible, as well as the 4$\rightarrow$2. Like for kaonic hydrogen, the interesting parameters to be extracted are the strong interaction-induced shift and width of the atomic levels. The very good resolution of the SDD allows to extract the almost $-300/+600$ eV shift/width of the kaonic hydrogen $n~=~1$ level [32, 33] and $-800/+750$ eV of kaonic deuterium [36]; unfortunately it is not possible to properly measure the width of the kaonic helium $n~=~2$, which are expected to be at the level of eV [34, 35].

Therefore, the energy resolution of SDDs is limiting kaonic atom X-ray spectroscopy. Bragg spectrometers, owning a much higher resolution, were not used so far because of their extremely low efficiencies and very small source size. In the future, measurements with sub-eV precision could be achieved, thanks to the development of the Highly Annealed Pyrolytic Graphite (HAPG) mosaic crystals. The VOXES collaboration at LNF [220,221,222] reported the possibility to combine HAPG crystal properties with the vertical focus of the Von Hamos configuration, to realize a spectrometer able to maintain a resolution in the order of $0.1\%$ (FWHM/E), for energies below 10 keV, and of 0.3$\%$ up to 20 keV, using a source size ranging from 500 $\upmu$m to 2 mm in the Bragg dispersion plane. This development paves the way for deeper understanding of the low energy strangeness QCD.

Fig. 21

KAONNIS. a Effect of the triple coincidence implemented in the SIDDHARTA experiment [32,33,34,35]. The spectra of the SDDs corresponding to 9 pb$^{-1}$ of integrated luminosity for K$^3$He run with (blue) and without (red) the triple coincidence between TOF and SDDs. b Background subtracted K$^3$He spectrum. The green lines identify the titanium K$_{\alpha ,\beta }$ peaks, coming from the calibration targets, the red and pink ones identify, respectively, signals from the kaonic Carbon and Nitrogen formed in the Kapton target cell, while the blue ones correspond to the $7,6,5,4,3\rightarrow 2$p K$^3$He transitions

5.3 PANDORA: ion identification with X-ray spectroscopy and isotope identification with $\gamma$ spectroscopy

The most relevant goal of the PANDORA project is to correlate the nuclear decay rate to the plasma environment properties, by simultaneously measuring X and $\gamma$-rays. This can be achieved through an innovative multi-diagnostic detection system based on a simultaneous identification and discrimination of the photons emitted by the plasma (from microwave to hard X-ray) and the $\gamma$-rays emitted after the isotope $\beta$-decay.

The overall structure of PANDORA experimental setup consists of three main pillars (see also Sect. 2.4.5): Magnetic Trap, Array of 14 HPGe detectors and Plasma multi-diagnostics system [122, 223].

Due to the inhomogeneous and anisotropic nature of magnetoplasma the identification of plasma self-emitted photons has to be done using space and time-resolved techniques. Quantitative elemental composition and plasma morphology investigations are performed by the powerful pin-hole CCD technique, in single photon-counted mode (SPhC) [224, 225]. It allows to perform high-resolution soft X-ray space-resolved spectroscopy, thus evidencing the local displacement of electrons at different energies, as well as of plasma ions, highlighted by fluorescence line emission. The setup consists of a CCD camera (sensitive range 2–20 keV, 1024$\times$1024 pixels), a Pb pin-hole (400 $\upmu$m of hole diameter) and a Pb multi-disk collimator designed to increase signal-to-noise ratio [226]. In SPhC mode, thousands of image-frames are acquired by setting an exposure time to tens of ms and by extracting a spectrally resolved image and a space-resolved spectrum. The system reaches high spatial and energy resolutions of 500 $\upmu$m and 0.326 keV at 8.1 keV, respectively. Figure 22a shows a typical X-ray SPhC spectrum, where it is possible to identify X-rays coming from plasma due to ionized K$_\alpha$ Ar lines and X-rays emitted from materials of the plasma chamber walls (due to excited Ti and Ta). As shown in Fig. 22b, using the same SPhC image is it also possible to distinguish the spatial emission coming from Ar plasma, compared to the Ti axial losses or the Ta radial losses. SPhC image analysis allows to measure plasma radius with an uncertainty of about 5$\%$. In perspective, using two CCD pin-hole cameras, it will be possible to estimate also the plasma volume.

Fig. 22

PANDORA. a X-ray spectrum collected with the pin-hole CCD system in SPhC mode. b SPhC image of fluorescence X-rays coming from plasma (Ar, red colour-scale) and from plasma chamber walls materials (Ti and Ta, blue and green colour-scale, respectively). Figure adapted from Ref. [227]

The plasma environment properties can thus be correlated to nuclear $\beta$-decay, determined through $\gamma$-ray spectroscopy. The design of $\gamma$-ray spectroscopy system was optimized by GEANT4 simulations. Since the harsh environment (the noise is represented by the intense plasma self-emission) strongly affects the signal-to-noise ratio, HPGe (70$\%$ of relative efficiency) detectors were chosen for their high resolution (0.2$\%$ at 1 MeV) [228]. Due to limited number of possible holes in the magnetic trap, the best compromise was obtained using 14 HPGe detectors. The total photopeak efficiency of the array, including the geometrical acceptance, was estimated between 0.1 and 0.2$\%$, depending on the energy of the detected $\gamma$-ray. With this setup the in-plasma (expected) lifetime measurements for the main targets of this experiment are expected to take from a couple of weeks for the simplest physical case ($^{134}$Cs) to about 3 months for the long living $^{176}$Lu case.

6 Particle identification by means of time of flight combined with energy or magnetic field analysis

In this section, PID techniques based on TOF measurements, associated with magnetic analysis or energy measurements, are described. In the first case measurements of the start/arrival time and track length provide the velocity, while the momentum is measured via a magnetic spectrometer. In the second case, usually adopted for low-momentum nuclei, the identification is performed correlating timing measurement with the energy loss inside the detector or the energy measured for completely absorbed nuclei: while the former provides Z discrimination, the latter is sensitive to mass, but sometimes the solution adopted profits of both approaches.

In this section, the experiments are grouped on the basis of the momentum range of the identified particle or nuclei, above or below $\approx$100 MeV/nucleon. In the first group the experiments are mainly interested in single particle or very light nuclei identification, while in the second one the studies concentrate on nuclei production. The time resolution requirements depend on the type and momentum of the analysed particle/nuclei, ranging from tens of ps up to few ns. A variety of detectors are used, including gas detectors like Multigap Resistive Plate Chambers (MRPC) or MicroChannel Plates (MCP), scintillating materials or silicon sensors.

6.1 Particle and very light nuclei identification in the $\approx$100 MeV to GeV energy range

6.1.1 ALICE TOF: MRPCs for particles up to 5 GeV/c

The time of flight detector [229,230,231] is one of the ALICE central barrel detectors and it is based on the Multigap Resistive Plate Chambers (MRPC) technology with ten gaps of 250 $\upmu$m. It is located at 3.7 m from the beam axis and it covers a cylindrical area of 141 m$^2$ at $-0.9~<~\eta ~<~0.9$ with a total of 153,000 readout pads of area 3.5$\times$2.5 cm$^2$. A time resolution of less than 50 ps has been measured on a test beam for the single MRPC strip [232]. The ALICE TOF can both provide charged particle PID in the intermediate momentum range and a trigger for cosmic ray events and ultraperipheral collisions. Since its installation in 2008, no sign of degradation has been observed [233].

Fig. 23

ALICE. a Particle velocity ($\beta ~=$ v/c) measured by the TOF as a function of momentum in Pb−Pb collisions at $\sqrt{s_{\mathrm{NN}}}~=$ 5.02 TeV (from  [233]). Tracks with transverse momentum lower than 0.3 GeV/c do not reach the TOF due to the magnetic field. b Squared-mass distribution around the anti-deuterium mass as calculated by TOF starting from a selection in the energy loss in the ALICE TPC (from  [235])

A simultaneous momentum and time-of-flight measurement can lead to the mass determination. The momentum is provided by the tracking of the ALICE TPC and ITS detectors placed inside the 0.5 T ALICE magnet (see Sect. 3.3). Two particles with the same momentum but different masses, i and j, after travelling a distance L will have a time difference of

$$\begin{aligned} \varDelta t_{ij}\simeq \frac{Lc}{2p^2} \bigl ( m_i^2-m_j^2\bigr ) \,. \end{aligned}$$

(4)

The final PID with the TOF detector can be performed considering the difference $\varDelta t=t_{\mathrm {TOF}}-t_{\mathrm {event}}-t_{k}$, with $t_{k}$ the expectation time for several mass hypotheses k ($\pi$, K, p,...) and $t_{\mathrm {event}}$ the event (or starting) time of the collision. The starting time for the ALICE TOF is provided by a weighted average between the measurements from the ALICE T0 detector [41, 229] and from the TOF itself [234] (for a track multiplicity larger than 100, the $t_{\mathrm {TOFevent}}$ is lower than 10 ps), when both are available.⁵

The detailed calibration procedure consists of mainly three steps: a common offset correction (due to a shift between the LHC clock and the actual collision time), a channel by channel offset adjustment (due to the different path and then different time delays of each channel) and a channel by channel time slewing correction (to disentangle the time from the charge information that is measured via the time over threshold of the signal). Note that a time alignment resolution of about 15 ps is obtained among all channels. A final 56 ps time resolution has been reached in Pb–Pb collisions at 5.02 TeV [233], including all the jitter contributions: the intrinsic MRPC time resolution, the electronics and the calibration term. The particle velocity measured by the TOF as a function of the momentum is reported in Fig. 23a. It can be noticed that the electron, pion, kaon, proton and deuteron bands are very well separated at low momentum. This allows a two $\sigma$ separation up to 3 GeV for K/$\pi$ and up to 5 GeV for p/K. In Fig. 23b an example of the physics analysis applications is reported: the invariant squared-mass distribution has been evaluated from TOF, starting from a selection in the energy loss in the ALICE TPC for pp collisions at 7 TeV. A pronounced peak around the anti-deuterium mass is observed, well distinguished from the background [235].

6.1.2 KAONNIS: kaon identification at $DA\varPhi NE$-LNF

In $DA\varPhi NE$, collisions of e$^+$e$^-$ pairs with a momentum of 510 MeV/c produce $\phi$ mesons almost at rest, which in turn decay into back-to-back K$^+$+K$^-$ pairs with a momentum of 127 MeV/c  [30, 31]. The low momentum kaons are identified, during the SIDDHARTA experiment, via TOF by the two plastic 1.5-mm-thick scintillators, placed 6 cm above and below the interaction point and read at both sides by PMTs. The very good time resolution (FWHM $\simeq ~100$ ps) of the two plastic scintillators allowed to improve the background rejection using the TOF separation between the kaons and the synchronous background events, mainly due to MIPs produced in time with the machine radiofrequency (RF). This separation is shown in Fig. 24, where the regions corresponding to kaons (red circles) are clearly identified in the correlation plot of the two PMTs of one of the two scintillators.

Fig. 24

KAONNIS. MIPs and kaons identification. Time correlation plot of the two PMTs of one of the scintillators: the regions corresponding to kaons (red circle) are clearly separated from MIPs shifted by 23 channels (0.81 ns). The two replica of this structure are due to the fact that, due to the very high rate of the $DA\varPhi NE$ machine RF signal (368 MHz), a RF/2 signal was used as time reference

When the kaons enter the gaseous target, the kaonic atoms are formed and the X-rays emitted during the radiative transitions of the kaonic atoms are then detected by the SDDs (see Sect. 5.2). A triple timing coincidence between the two scintillators and the SDDs allows to dramatically reduce the background, reaching an overall background reduction of a factor $\simeq ~10^5$ (see Fig. 21).

The SIDDHARTA-2 experiment plans to perform the kaonic-deuterium measurement in 2021–2022 [36] with an upgraded version of SIDDHARTA that includes a large area, L-shaped scintillators around the target cell, aiming to detect via TOF the pions produced after the K$^-$ absorption from the deuterium nuclei.

6.1.3 n_TOF: identification of neutron-induced elastic reactions

At n_TOF, a fundamental ingredient for high-precision and accurate measurements of any reaction cross-section is the knowledge of the incident neutron flux as a function of energy. Two counter telescopes (Recoil Proton Telescope, RPT) have recently been developed to extract the neutron flux in the energy region above 10 MeV, by exploiting the well known neutron–proton elastic scattering and measuring the recoil nucleus energy via kinematic constraints. Both telescopes consist of a compact trapezoidal structure, placed at a small angle with respect to the neutron beam and pointing to a polyethylene (C$_2$H$_4$) sample, placed in the neutron beam line. The RPTs [236] consist of four independent BC408 plastic scintillators with increasing thickness: 0.5, 3.0, 6.0 and 6.0 cm, each of them is coupled with a 1" PMT, and one of the two telescopes is supplemented by two stages of silicon detectors.

The selection of signals in temporal coincidence among the different slabs of the telescope, within a window of 10 ns for the scintillators and 500 ns for the silicon detectors, guarantees the identification of the events originating only from the polyethylene sample and the suppression of the $\gamma$ and electron background. However, neutrons impinging on the C$_2$H$_4$ sample can initiate n–p scattering as well as n+C inelastic reactions which can produce light particles in the final state, i.e. protons, deuterons, tritons, $\alpha$ particles. Therefore, PID capability of the RPTs is crucial to select only protons from elastic scattering and reject background signals. The timing information from RPT ($t_{\mathrm {RPT}}$) is referred to the neutron production time in the spallation target and can be related to its energy: the higher value corresponds to a lower energy of the impinging neutron. The measured $t_{\mathrm {RPT}}$ and the multi-stage structure of the RPTs ensure the event selection criteria in terms of number of detectors in coincidence: as the $t_{\mathrm {RPT}}$ decreases the number of the hit detectors increases. As an example, Fig. 25a shows the behavior of the energy deposited in the second scintillator as a function of the $t_{\mathrm {RPT}}$: events with $t_{\mathrm {RPT}}$ down to 1000 ns, where the secondary particle deposited energy is at the maximum, stop in the second scintillator while at lower $t_{\mathrm {RPT}}$ the secondaries reach the next scintillators and the energy deposited in the second scintillator decreases. It should be noticed that, thanks to the good timing (about 1 ns) properties of the scintillators, it is possible to perform the time–to–neutron-energy calibration with a good resolution $\varDelta E_{\mathrm n}/E_{\mathrm n}$ $\sim$ 10$^{-3}-$10$^{-2}$.

The discrimination between protons and deuterons in the secondaries is then performed using the $\varDelta E$ vs E plots, as reported in Fig. 25b for a given $t_{\mathrm {RPT}}$ interval. Because of the kinematic properties of the reaction, protons coming from n–p scattering are identifiable counting only the events localized in the maximum (e.g. the accumulation of events with $\varDelta E$ and E of about 12 and 60 MeV respectively). The n+C reactions are characterized by a negative Q value, therefore the protons emitted energy distribution has a lower mean value and the kinematic of the nuclear reaction does not produce a peaked distribution in energy populating the tail.

Fig. 25

n_TOF. a Deposited energy in the second scintillator as a function of the time of flight. b $\varDelta E - E$ matrices produced by events with a time of flight from 0.965 to 1.04 $\upmu$s hitting the C$_2$H$_4$ sample. The protons generated by the n–p scattering are localized in the peak ($\varDelta E~\sim ~$12 MeV and $E~\sim$ 60 MeV), which is the characteristic kinematic locus of the reaction

An extensive study through Monte Carlo simulations with neutrons impinging on a realistic setup was performed to estimate the performances of the techniques used in the analysis [237]. The correlation between $\varDelta E - E$ and TOF enables a selection of proton events at the level of 1% accuracy, for protons with energy up to 180 MeV. Above this energy, protons do not stop anymore inside the telescope therefore the techniques $\varDelta E-E$ and TOF$- E$ need to be combined with other strategies to disentangle the contribution of protons from all background events.

The above-described PID techniques are presently being applied for the first time in the $^{235}$U(n,f) analysis, and pave the way for the study of neutron-induced reactions above 20 MeV of neutron energy.

6.2 Nuclei identification in energy range of the order of 10 MeV/nucleon

6.2.1 ASFIN: $\alpha$ identification to define elastic and inelastic interactions

A nuclear cluster is defined as a group of nucleons, collectively acting as a single particle whose internal degrees of freedom can be neglected, such as $\alpha$ particles [238]. A very useful method to study this kind of structures is represented by the Thick Target in Inverse Kinematics (TTIK) [239]. Briefly, in TTIK resonant scattering, a low-intensity beam is incident on an extended gas target. As the projectiles slow down in the gas, elastic scattering reactions across a wide range of center-of-mass (c.m.) energies can take place (corresponding to a range of depths within the gas) allowing to measure large-range excitation functions in one irradiation with the same initial beam energy. A light recoil created in an elastic scattering event of the beam particle on the nucleus of the target gas can easily penetrate further through the gas and be detected by an appropriate array of detectors, while the other fragments remain in the gas target.

An experimental limitation of using the TTIK method is represented by light particles coming from other possible reaction mechanisms, such as inelastic scattering [240]. Indeed, only by analyzing the particle energy deposition spectra, it is not possible to identify the reaction mechanisms for the particles production. For this reason, it was decided to improve the TTIK method by introducing the TOF measurement since the measured energy of a detected light particle depends on the reaction process in which it was produced, as well as on the position in the gas target where the reaction has occurred. Therefore, the TOF measurement allows to discriminate elastic from inelastic reaction events.

Fig. 26

ASFIN. Experimental detected energy in DSSSD versus TOF plot. Since inverse time logic has been used, large time intervals ($\approx$ 220 ns) correspond to events which occur at the entrance of the chamber, while smaller intervals ($\approx$ 175 ns) correspond to events which take place closer to the detectors. The $\alpha$-particle punch-through energy is around 8 MeV. In the picture the green full lines represent loci for elastic scattering $\alpha$-particles events, while the dashed red lines represent the ones for the inelastic $\alpha$ related to the first three states of $^8$Li at an excitation energy of E$_x$=0.9808, 2.255, 3.21 MeV, respectively. Figure adapted from [240]

This technique was successfully applied to support the picture of $\alpha$-$^8$Li cluster configurations for excited states in $^{12}$B by means of the measurement of $^8$Li + $^4$He resonant elastic scattering. The $^8$Li beam was produced by the radioactive beam facility EXCYT at LNS [241] and delivered into a scattering chamber filled with $^{4}$He gas at a pressure of 700 mbar [240]. The stop signal for the TOF measurement is provided by a micro channel plate (MCP), placed before the entrance of the scattering chamber, while the start signal is given by a 500 $\upmu$m DSSSD, in an inverse time logic. The DSSSD also provides the energy information. The resulting energy versus TOF plot is shown in Fig. 26 where the calculation for $\alpha$ particles that are elastically (solid green line) or inelastically scattered (short-dashed red lines) are superimposed on the experimental data, proving that TOF measurements allowed for the discrimination between elastic and inelastic scattering [240].

Recently, the TTIK method with TOF measurement opened the possibility of studying exotic cluster structures in nuclei, of relevance for both nuclear physics and nuclear astrophysics [242].

6.2.2 CHIRONE: light and heavy nuclei identification with silicon detectors

The TOF technique is extensively used in the CHIMERA apparatus for direct velocity measurements of ions with $Z>$ 2 and for mass determination of particles stopped in the Si detectors [45, 243]. This is realized thanks to the long base-of-flight, in the range of 1–3.5 m, for the 688 telescopes of the forward part of the apparatus. Time of arrival of particles in the detectors is measured by a $30\%$ constant fraction discrimination (CFD) acting on silicon signal, and a $\varDelta t$ time interval is measured with respect to a common stop given by the RF signal for beams delivered by the LNS Cyclotron. An example of correlation between the energy loss in a silicon detector, $\varDelta E$, and $\varDelta t$ is given in Fig. 27a for the reaction $^{124}$Sn + $^{64}$Ni at 20 MeV/nucleon. The slower particles stopped in the silicon detector are the ones sitting in the left zone of the plot ($\varDelta t$  < 480 ns). In this case, $\varDelta E$ is simply the kinetic energy of ions and in the $\varDelta E$-$\varDelta t$ plot the lines correspond to different masses. Whereas, particles passing through silicon detectors are the ones sitting in the right part of the plot ($\varDelta t>$ 480 ns). In this case, lines in the plot correspond to different Z. Therefore, the region at $\varDelta t~>~$480 ns contains information only on the Z of particles, that is already attainable by the $\varDelta E$-E method (see 3.2.1). The identification in mass needs to correct the measured $\varDelta t$ for the effects related to Z, A and E dependence of the time profile of the signals, due to plasma delay effects, and for the time-charge walk effect, for low amplitude signals. Mass determination is performed through a semi-automatic and iterative procedure, and parameters describing $\varDelta t$ correction for the above mentioned effects are obtained by a fit. As an example, the inset of Fig. 27a shows the masses of selected loci corresponding to A = 7, 9, 11, 13 and 15, as a function of $\varDelta E$, as obtained using the $\varDelta t$ correction functional form. The typical resolution obtained is $\varDelta {{A/A}}~\sim ~1/20$ and effective thresholds for mass determination are around 5 MeV.

The collaboration is also involved in experiments with radioactive ions beams (RIBs), using the FRIBs facility at INFN-LNS with the in-flight fragmentation method [4]. The fragmentation reaction produces several stable and unstable isotopes at the same time. Optical elements are used to select and to transport the exotic beam. However, a magnetic selection does not allow for the separation of isotopes with the same m/q ratio. For this reason, it is necessary to proceed with the characterization of beam components, event-by-event, to select the isotope of interest for the specific study off-line. In the CHIMERA beam line the identification takes place through the $\varDelta E$-TOF method, using a tagging system, specifically implemented and developed [244], that allows to measure event-by-event the isotopic composition of the exotic beam. This tagging system consists of a Micro-Channel Plate detector (MCP) and of a DSSSD. The start signal is given by the MCP, located at a distance of 12.9 m from the DSSSD. The stop signal and the $\varDelta E$ are provided by the strips of the DSSSD, mounted about 2 m before the reaction target. Time resolutions around 500 ps are reached. Figure 27b shows the $\varDelta E$-TOF plot obtained with the tagging system, using a fragmentation reaction of a stable $^{70}$Zn beam accelerated at 40 MeV/nucleon and a $^{9}$Be (250 $\upmu$m) target [144]. At this energy, the probability to produce not fully stripped ions is significant. It was indeed interesting to measure the presence of different charge states, after the $^{9}$Be production target. The population was evaluated changing the magnetic field of the optical elements and measuring the beam current of the various charge states obtained. This experiment represents an upper limit for the FRIBs performance and a point of reference for the tagging system of the future FraISe facility at LNS [4].

Fig. 27

CHIRONE. a Energy loss in a silicon detector ($\varDelta E$) vs "time-of-flight" for the reaction $^{124}$Sn + $^{64}$Ni at 20 MeV/nucleon, as typical for a CHIMERA telescope placed around $\theta ~=~10.75^{\circ }$ and at 180 cm from target. The inset shows the reconstructed atomic mass number as a function of $\varDelta E$ for selected loci corresponding to given isotones (A = 7, 9, 11, 13 and 15), as resulting from the identification procedures. b $\varDelta E$-TOF plot obtained with the tagging system of the multidetector CHIMERA, using a fragmentation reaction of a stable $^{70}$Zn beam accelerated at 40 MeV/nucleon and a $^{9}$Be 250 $\upmu$m target (figure adapted from Ref. [144])

6.2.3 FOOT: particle identification for heavy fragment cross section measurements with E-TOF method

As mentioned in Sect. 2.5.1, in the FOOT setup focusing on detecting high Z fragments the identification of the charge Z is performed exploiting the measurement of the TOF and the energy released $\varDelta E$ in a thin wall of plastic scintillators TOF-Wall (TW), while the momentum p from the magnetic spectrometer and the kinetic energy $E_k$ measured in the calorimeter provide the isotopic identification.

The fragment charge identification via the $\varDelta E$-TOF method is based on the signals provided by a start counter (SC) and the TW. The SC [245] is the first detector encountered by the beam, providing the particle rate and the crossing time of the primary particles. It is a thin (250 $\upmu$m) foil of plastic scintillator material with an active area of $5 \times 5$ cm$^2$. The TW [246, 247], located about 1 m behind the target, measures the energy loss $\varDelta E$ of the fragments and provides their arrival time. It consists of 40 bars of plastic scintillator material, arranged in two orthogonal layers of 20 each. Each bar has an active area of $44 \times 2$ cm$^2$ and is 3 mm thick. The light produced in the bars is collected at each end by four silicon photomultipliers. Fragment charge discrimination is achieved by correlating the energy $\varDelta E$ deposited in the bars with the measured TOF.

Table 1 FOOT: TOF, energy and Z resolutions obtained from the data for various projectiles

Fig. 28

FOOT. Measured distribution of $\varDelta E$ versus TOF of the fragments produced during the irradiation of a 5-mm-thick carbon target with 400 MeV/nucleon oxygen ions. The various nuclei atomic numbers can be distinguished

Table 1 reports the TOF, energy and Z resolutions obtained during test beam acquisitions at the CNAO (Pavia, Italy) and GSI (Darmstadt, Germany) facilities for various projectiles. The Z-resolution for carbon and oxygen ranges from 2.5 to 3.9%, compatible with the FOOT requirements. The resolution for protons is 6.1%, however the emulsion chambers (see Sect. 3.4) are expected to perform better for such low Z nuclei.

In Fig. 28, the $\varDelta E$ versus TOF distribution obtained from irradiation of a 5-mm-thick carbon target with a 400 MeV/nucleon oxygen beam during a test beam at GSI is reported. Further improvements to the TW are foreseen in the near future, with a new mechanical frame and a better optical insulation of the bars.

Regarding the mass A of the fragments, this will be determined combining $\beta$, p and $E_k$, using the TOF, the tracking system and calorimeter, respectively. The mass will be extracted using a $\chi ^2$ minimization approach, and using the Augmented Lagrangian Method (ALM) [248]. The construction of all components of the FOOT detector is being finalized. New data, including not only Z but also A determination, are expected for 2022 at CNAO and GSI, where the full setup will take data.

6.2.4 FORTE: separation of fusion–fission and quasi-elastic events

The mass and total kinetic energy (TKE) of two binary-reaction fragments are reconstructed using the so-called two-velocity (2V) method, namely, by measuring their velocity vectors in coincidence [249]. The FORTE collaboration makes use of a TOF spectrometer consisting of 4 arms, each one containing a start and a stop detector. The conceptual design is based on the CORSET one [249]. The stop detectors are position sensitive. The information on the time of flight and on the position of the fragments in each respective arm along with the two-body kinematics allows the reconstruction of the mass and kinetic energies of the fragments. Two pairs of arms placed on opposite sides with respect to the beam axis on the same reaction plane constitute the basic element. It is then possible to span a folding angle⁶ between 80$^{\circ }$ and 140$^{\circ }$, namely, a larger mass asymmetry of the produced fragments.

The long measurements of highly ionizing particles (large doses) require detectors with a high radiation hardness and stability. Hence, start and stop detectors are built using two MCPs chevron assembled. The stop detector consists of a conversion entrance foil upstream of two MCPs (the fragment is stopped inside the MCPs) and provides a timing stop signal and two coordinates determined via delay lines. It has an active area of $70 \times 90$ mm$^{2}$ to cover the solid angle of the start detector. The flight path is 30 cm long. A coincidence of two opposite arms with stop signals and at least one start signal usually defines a trigger. Each arm provides a spatial and time resolutions of about 1 mm and 180 ps (full width at half-maximum), respectively.

The primary mass and energy of binary fragments are reconstructed in an iterative procedure that considers the fragment-velocity vectors, momentum and nucleon conservation laws, and corrections due to heavy fragment energy losses in different media. Then, the TKE of reaction products is determined as the sum of the fragment energies in the center-of-mass system.

Fig. 29

FORTE. TOF matrix (a) and Mass-TKE distribution (b) of the binary fragments measured in coincidence using two opposite TOF arms in the $^{32}$S + $^{109}$Ag reaction at beam energy of 180 MeV. Quasi-elastic (QE) and fusion–fission (FF) events are well separated in TOF matrix. The fission-like fragments are inside the blue rectangle in the Mass-TKE matrix. The mass and energy resolutions of the spectrometer are 3 a.m.u. and 5 MeV, respectively

The result of this procedure and the corresponding raw TOF–TOF matrix for the $^{32}$S + $^{109}$Ag reaction at 180 MeV are shown in Fig. 29. The three clusters in TOF–TOF matrix well identify the products of fusion–fission (FF) and quasi-elastic (QE) collisions. In case of FF events, the symmetric split produces the central cluster with equal mean TOF values registered in left and right CORSET arms. The other two clusters are produced by QE events. Here the TOF values of projectile-like fragments are small and narrowly distributed, while those of target-like fragments are large and broadly distributed. The fragment mass-TKE distributions represent the most sensitive observables to improve the knowledge of the reaction dynamics. These quantities are used to cleanly separate the products of competing processes, to estimate the intensity and nature of nuclear viscosity and measure the contribution of different fission modes [250].

The ongoing upgrade involves larger angular coverage, position sensitive passing-through stop detectors, Bragg chambers for Z identification, new electronics for pulsed beams/higher rates. A foreseen application concerns the study of exotic nuclei located in the Terra Incognita of the nuclear chart produced via multinucleon transfer reactions.

6.2.5 NUCLEX: identification of charged products fragments with silicon detectors

In TOF measurements, when it is not possible to install a start detector or the beam is not pulsed, the NUCLEX collaboration has developed a new method to recover the start time mark. First, a fully identified reference ion is selected and it is used to calculate the interaction time. This is done knowing the flight base $d_\mathrm {ref}$, the kinetic energy $E_\mathrm {ref}$ (well measured by silicon sensors) and the mass $m_\mathrm {ref}$ (from $\varDelta E-E$ or PSA correlations, see 4.1.2).

Fig. 30

NUCLEX. $E - TOF$ correlation for a FAZIA silicon detector. TOF measurement is affected by the signal rise time walk, thus the correlation shows a dependence on Z and not only on particle mass. Data comes from $^{48}$Ca + $^{12}$C reactions at 25 MeV/nucleon (adapted from [251])

Once the time of the interaction is obtained, the timing of all other particles is referred to it as a pseudo-TOF measurement, as described in detail in a recent FAZIA work [251]. The TOF signal is provided by the silicon sensors of the detector telescopes, with an intrinsic time resolution around 500 ps for the nuclei under investigation. An example of the energy-time correlation obtained with this procedure is shown in Fig. 30 for particles stopped in the first silicon layer.

It should be noted that reverse mounted silicon detectors have rather slow signals (rise times from 10 to 100 ns): this feature is useful to better exploit the pulse shape discrimination technique (see Sect. 4.1.2), but affects the pseudo-TOF measurement. In fact, the rise time strongly depends on Z, so we observe also a Z (and not only A) separation in the $E-$pseudo-TOF correlation ridges (Fig. 30). For example it is possible to distinguish $^3$H and $^3$He, or $^{10}$Be and $^{10}$B. However, on the other side, the degraded time resolution limits the present Z range to about 10.

Overall, in FAZIA, (mounted with a flight base of 1 m) the identification with timing allows to achieve A discrimination from $Z=1$ to 10, opening the door to the study of light particles emitted by quasi-target fragments in deep inelastic collisions.

6.2.6 PRISMA: heavy nuclei identification with a magnetic spectrometer

PRISMA is a magnetic spectrometer installed at LNL, optimized for ions in the mass range A = 20–200 and energies of $2{-}10$ MeV/nucleon, well suited for the beams provided by the Tandem-ALPI-PIAVE accelerator complex [252]. It is characterized by the large solid angle coverage ($\approx$ 80 msr), momentum acceptance of ± 10%, mass resolution of 1/300 and energy resolution up to 1/1000 (exploiting TOF measurement) [253]. In addition, the spectrometer can be aligned over a wide angular range from − 20$^{\circ }$ to 130$^{\circ }$ with respect to the beam line.

The ion trajectories are reconstructed from the target to the focal plane detectors event-by-event, using an algorithm that takes into account detailed magnetic field maps, measured entrance and exit positions of the particles, the time of flight and the geometry of the instrument [254]. Ions produced in the target go through an entrance detector consisting of microchannel plates, providing two-dimensional position information and the start signal for the time of flight [255]. Then, a quadrupole magnet focuses incoming ions in the vertical plane before they enter the dipole magnet. When crossing the dipole, ions with different momentum–charge ratio follow different trajectories. Therefore, tuning the dipole magnetic field it is possible to detect a specific range of nuclear products on the focal plane of the magnet.

Fig. 31

PRISMA. a Mass–charge ratio vs. horizontal position correlation in the MWPPAC focal-plane detector. Ions with higher momentum–charge ratio are less deflected in the dipole magnetic field. Nuclear charge is derived from the energy loss inside the ionization chamber. b Examples of obtained mass spectra for channels corresponding to different proton pick-up and stripping channels (here pick-up and stripping are referred to the light partner of the reaction). All proton-stripping reaction channels from (+4p) to (−5p) were identified. Both plots refer to the results obtained with the reaction $^{40}$Ar + $^{208}$Pb at $E_{\mathrm {lab}}$ = 260 MeV (adapted from [256])

The detection system at the focal plane consists of a set of multi-wire parallel plate avalanche counters (MWPPAC), providing the two-dimensional arrival position of ions and the stop signal for the time of flight (with a typical time resolution of about 300 ps), followed by an array of ionization chambers for energy loss and total energy measurements, used to derive the atomic number of reaction products. Detailed descriptions of the focal plane detectors can be found in [253].

Typical performances of the spectrometer in terms of detection efficiency and resolution are displayed in Fig. 31, which shows the correlation mass–charge ratio vs. position in the MWPPAC detector and the yields for multi-nucleon transfer reaction channels populated in the reaction $^{40}$Ar + $^{208}$Pb with a $^{40}$Ar beam at $E_{\mathrm {lab}}$ = 260 MeV [257].

Recently, the spectrometer was equipped with a second arm used to identify the fragments produced in low energy heavy-ion nuclear reactions and reconstruct the kinematics of binary reactions [258]. The second arm consists of a position sensitive MWPPAC followed by a Bragg Chamber. The performances of the second arm have been evaluated in experimental conditions using different beam–target systems [91, 258]. The position resolution of the MWPPAC was established to be 1 mm in both X and Y directions, while the energy and atomic number resolution of the Bragg chamber were found to be $\varDelta E/E~\sim$ 1% and $\varDelta$Z/Z$~\sim$ 1.7%.

7 Calorimeters and muon identification

In this section, the identification capabilities of experiments using the calorimetric technique or spectrometers for muon selection are described. Various detectors designed to measure the total energy of particles have been already described in this review, but, as the energy increases, more sophisticated solutions must be developed. Calorimetry has become the natural option and allowed not only the possibility to measure the energy of single particles, but also the global energy of groups of particles (jet studies) or events with missing energy (a signature of specific processes). Indeed, the specific role of calorimeters is the measurement of the energy of a particle by completely absorbing its momentum through interaction with passive layers interleaved with sensitive layers (segmented calorimeters) or using a unique sensitive volume (homogeneous design): in all cases the given material is best adapted to the development of an electromagnetic shower or the containment of hadronic processes. It is common that the energy information is supported by angle, position or time information. A plethora of implementations have appeared, the specific design depending on the kind and the energy of the particles to be investigated: given that the resolution improves with energy, the achievable shower signal and the electronic noise must be tuned to minimize the associated uncertainties.

In the following three experiments, in alphabetical order which happens to be of decreasing beam energy, present their calorimeters in three very different experimental contexts and four specific goals, witnessing to the robustness and the wide diffusion of the principle. The energy of the particles to be detected determines of course the thickness of the material to be traversed. In the first example, the BGOOD experiment (of the MAMBO collaboration), the detector has also high granularity (about 20 msr per detector element) to keep the angular resolution good enough for detection of photons coming from meson decay. In the second case, JLAB experiment, the focus is on electron detection in the forward direction, with emphasis on time and energy resolution and two complementary detectors for the photon-electron separation and electron tracking. The last calorimeter presented is from ALICE, which has the specific goal to measure high momentum photons and electrons and jets, opportunities expanded by the addition at a later stage of further modules. An example of muon spectrometer has been added that, while not belonging properly to the PID class of detectors, it is ipso facto a method to select muons over a huge background of hadrons and leptons, using the standard technique of absorbing all the other particles in a dense material.

7.1 ALICE: electrons, photons and muons tagging in a high-multiplicity, high-energy environment

7.1.1 Electromagnetic calorimeter

The ElectroMagnetic Calorimeter (EMCal) [41, 259] is one of the central barrel ALICE detectors and it is based on a Pb-scintillator sampling technique. It is located at 4.5 m from the beam axis and it has a cylindrical coverage of $|\eta |< 0.7$ and $\varDelta \varPhi ~=~107^\circ$. Since 2015 the EMCal acceptance has been enlarged in azimuth with DCal, an additional set of modules (DCal: 0.22 $<~\eta ~<$ 0.7 $\varDelta \varPhi ~=~67^\circ$), opening the possibility to study di-jets. In total EMCal and DCal have 17,644 cells, consisting of towers of 6.0 $\times$ 6.0 $\times$ 24.6 cm$^3$, corresponding to 20.1 radiation lengths. The plastic scintillators have longitudinal wavelength shifting fibers to collect the light which are read by Avalanche PhotoDiodes (APDs).

Fig. 32

ALICE. a Distribution of electron energy-over-momentum E/p ratio. b Electron identification purity in central, 0–10$\%$, Pb–Pb collisions at $\sqrt{s_\mathrm {NN}}$ = 5.02 TeV ( from [259])

The EMCal can identify electrons and provide trigger on jets, high-momentum photons and electrons. To distinguish between electrons and charged hadrons, it uses the E/p method, with p measured by the central ALICE-TPC: the EMCAL measures the energy deposition and compares it to the measured momentum. Indeed, while electrons deposit their full energy in the calorimeter (E/p $\approx$ 1), hadrons tend to lose only a small fraction. In Fig. 32a, the E/p distribution for Pb–Pb collisions at $\sqrt{s_\mathrm {NN}}$ = 5.02 TeV is shown. A clear separation between hadrons and electrons is visible. The separation between electrons and hadrons is further increased considering the different shape of the shower. When two clusters overlap partially, the shower cross section assumes an elliptical shape, whose long axis is characterized by the $\sigma ^2_{\text {long}}$ parameter. As an example of application, in the standard analysis, the neutral pions production, in Pb–Pb collisions at $\sqrt{s}$ = 2.76 GeV the mass width is $\approx$ 10 MeV/$c^2$ at $p_\mathrm {T}$ = 5 GeV/c, with an upper limit on $p_\mathrm {T}$ of 20 GeV/c due to the cluster size, which sets the minimum photons relative angle. However, analysing the shape of the electromagnetic shower defined above in analogy with the electron-hadron separation, it is possible to measure neutral pions up to 200 GeV/c with a purity of 81–89 $\%$ in pp collisions, decreasing with $p_{\mathrm {T}}$ (see [260]). In Fig. 32b, the electron identification purity in central Pb–Pb collisions is reported. Together with electron identification in the ALICE TPC, the EMCal detector allows the reconstruction and identification of electrons up to $p_{\mathrm{T}}~=~$ 30 GeV/c.

7.1.2 Muon spectrometer

The ALICE muon spectrometer covers the pseudorapidity region 2.5 $<~\eta ~<$ 4; it consists of a front hadron absorber, followed by a set of five tracking stations, a dipole magnet, an iron wall acting as muon filter and two trigger stations [40].

The absorber downstream the interaction point corresponds to 10 interaction lengths ($\lambda _\mathrm{I}$). Ten multi-wire proportional chambers arranged in five stations provide the space points to reconstruct the muon trajectories, bent by a 0.7 T magnetic field generated by means of a 5 m long dipole magnet. An iron wall of 7.2 $\lambda _\mathrm{I}$ filters the residual hadrons and muons with a momentum approximately greater than 4 GeV/c, to reduce the background due to pion and muon decays which survived the front absorber. It is placed between the tracking chambers and the trigger resistive plate chambers (RPCs), also used for tracking.

The ALICE muon spectrometer is used to study the light vector mesons (${\rho }$, ${\omega }$, ${\phi }$) and quarkonia ($J/\psi$ and $\varUpsilon$ families) in their dimuon decay channel, and to measure the production of single muons from decays of heavy-flavour hadrons and W$^{\pm }$, Z bosons.

Track reconstruction in the muon spectrometer is based on a Kalman filter algorithm [261, 262]; the tracks are then extrapolated to the vertex position measured by the Inner Tracking System (the inner six layer of silicon detectors [40], see Sect. 3.3) and a correction for energy loss and multiple Coulomb scattering in the absorber is applied [262].

Figure 33a shows the dimuon invariant mass spectrum, after background subtraction, in the 0–10% most central Pb–Pb collisions at $\sqrt{s_{\mathrm {NN}}}~=~2.76$ TeV, with the fit to the $J/\psi$ peak by an extended Crystal Ball function [263]: the residual background is negligible and the mass resolution at the $J/\psi$ peak is around $\sim$ 73 MeV/$c^2$ [41].

Fig. 33

ALICE. a Dimuon invariant mass spectrum in 0–10% most central Pb–Pb collisions at $\sqrt{s_{\mathrm {NN}}}~=~2.76$ TeV, with fit to the $J/\psi$ peak by a Crystal Ball function (from Ref. [41]). b Measured muon track reconstruction efficiency in Pb–Pb collisions as a function of the collision centrality

The muon detection efficiency (see Fig. 33b) shows a drop for central Pb–Pb collisions ($< 20\%$), largely due to fake tracks and that can be strongly reduced applying an additional cut on both the $p \times$ DCA (momentum $\times$ distance of closest approach) and the normalized $\chi ^2$ of the tracks ($\chi ^2~<~3.5$) [41].

The mass resolution at low masses is limited by multiple scattering inside the front absorber. This effect will be mitigated by the insertion of a silicon pixel detector (the Muon Forward Tracker), which will be placed upstream of the front absorber during the LHC Run3 [264].

7.2 JLAB: electron–photon discrimination at an electron beam facility

The CLAS12 Forward Tagger (FT) calorimeter [265] was built to detect the electrons scattered at very small angles in the kinematics of quasi-real photo-production. This regime is of special interest for the search of exotic mesons and rare states, such as scalars and strange mesons [25]. The FT was designed for high efficiency electron–photon discrimination in this angular range, given the large number of photons produced in the target. It consists of an electromagnetic calorimeter (FT-Cal), to identify the electron in the energy range 0.5–4.5 GeV and provide a fast trigger signal. A Micromegas tracker (FT-Trk) is used to measure the scattering angles and a scintillation counter (FT-Hodo) provides e$-\gamma$ particle discrimination.

The FT-Cal design is driven by demanding requirements in terms of radiation hardness, compactness, energy and time resolution. To match these requirements, lead tungstate (PbWO$_{4}$) was used as scintillating material. The FT-Cal is composed of 332 crystals with dimensions $15 \times 15 \times 200$ mm$^3$, read out by avalanche photodiodes, with full azimuthal acceptance and forward angle 2$^{\circ }~<~\theta ~<$ 5$^{\circ }$.

The discrimination between photons and electrons producing electromagnetic showers in the FT-Cal is performed via the FT-Hodo. This detector consists of 232 plastic scintillator tiles, read out by SIPMs, segmented in two layers to suppress the splash-back contribution from the FT-Cal.

The precise determination of the scattered electron angle is obtained with a tracker complementing the FT-Cal and FT-Hodo detectors. The FT-Trk uses the same technology adopted by the CLAS12 central and forward Micromegas tracker [266]; it consists of two double-layer detectors and is located in front of the FT-Hodo with geometry chosen to enable the determination of the (x, y) coordinates (perpendicular to the beam z-axis) of a track.

The energy and centroid of the clusters in the FT-Cal are used as an initial seed to define the three-momentum of the incident particles. FT-Hodo hits are reconstructed and grouped into clusters, matching position and time in the tiles of the two layers of the detector. These are then matched to clusters in the calorimeter to distinguish charged particles from neutrals that do not give a signal in the FT-Hodo. Calibration and performance assessment were carried out through the analysis of data recorded with the CLAS12 production triggers [265]. Using the calibration constants obtained with the beam-on data, an energy resolution of $3.3 \%$ at 2.2 GeV beam energy was extracted from the fit of the elastic peak in the e p$\rightarrow$ e p process (see Fig. 34a). With the same calibration constants, the $\pi ^0 \rightarrow \gamma \gamma$ decay was reconstructed at 10.6 GeV beam energy selecting events with both photons detected in the FT-Cal, finding a resolution of 4.4 MeV, corresponding to $3.2\%$ (see Fig. 34b).

The calibration of the FT-Hodo was performed by studying the energy deposition of MIPs, being these the typical signals expected from charged particles impinging on the detector. The time information is critical for background rejection and for fast-trigger purposes. The study of the timing resolutions of the FT-Cal and FT-Hodo was performed by analyzing the time correlation of signals in the FT with the CLAS12 forward time-of-flight (FTOF) detector [267] and the RF signal that is synchronous with the CEBAF accelerator beam bunches. A resolution of $\sigma ~\simeq ~140$ ps was obtained for electrons using the beam RF signal. A consistent value of $\sigma ~\simeq ~150$ ps was found for photons, determining the event start time from other particles detected in the FTOF.

Fig. 34

JLAB. a Electron energy spectrum reconstructed in the FT-Cal at 2.2 GeV beam energy. b $\pi _0 \rightarrow \gamma \gamma$ invariant mass spectrum reconstructed at 10.6 GeV beam energy: the $\pi ^0$ peak is fitted with a Gaussian with $\sigma ~\sim$ 4.4 MeV. From [265]

Since photons usually do not interact in the FT-Trk and FT-Hodo, the combined information of presence of clusters, position and timing of the sub-detectors allow to achieve a high photon-electron discrimination efficiency: the probability of a photon being erroneously identified as an electron has been estimated to be $\sim 4\%$ using the FT-Cal and FT-Hodo combined information and $< 1\%$ with the contribution of the FT-Trk.

7.3 BGOOD (MAMBO): neutral particles discrimination with BGO

The BGO calorimeter of the BGOOD experiment is segmented into 480 crystals 24-cm-thick ($\simeq ~21$ radiation lengths), arranged in $15 \times 32$ sectors in the polar and azimuthal angles, respectively. The coverage on the polar angle is $\theta ~=~(25^\circ \div 155^\circ )$ and full in azimuth. The calorimeter is preceded by the cylindrical scintillator barrel, which is used as a dE/dx detector for charged particles and its granularity in the azimuthal angle is the same of the BGO sectors. Finally, closest to the target, two cylindrical multi-wire proportional chambers (MWPCs) allow charged particle tracking.

A first fundamental discrimination neutral/charged particles in the central detector is provided by the geometrical coincidence between the BGO sectors, the plastic scintillators of the barrel and the MWPCs. Signals in the BGO which are not associated with hits in any other detector are considered as interactions of neutral particles (photons or neutrons). We define a “cluster” as the group of contiguous crystals associated with the interaction of the same particle with the detector and its “multiplicity” is the number of crystals composing the cluster.

For photon/neutron discrimination, the different processes underlying the detection of the two types of particles in the BGO calorimeter must be considered: in the energy range explored ($E_{\gamma }~\simeq ~20-300$ MeV) while photons produce an electromagnetic shower in the high density, high atomic number inorganic material of the BGO, neutrons are mainly detected via their elastic and inelastic scattering (or even induced fission) on the different components of the BGO (oxygen, germanium, bismuth).

The main features of the clusters produced by high-energy photons or by neutrons are different. Cluster multiplicity is: (1) roughly proportional to the energy of the detected photon; (2) small and independent of the released energy for the neutron. To define further PID criteria, a clean sample of $\pi ^0$ photoproduction events on deuterons has been selected by means of stringent kinematic cuts on the 2-body reaction. The following PID criteria have been derived:

• (1) the ratio between the total cluster energy and the cluster multiplicity is always <100 MeV/crystal for photons, while for neutrons also hits with larger amount of energy per crystal are observed (see Fig. 35a);

• (2) the ratio between the maximum energy released in a crystal of a cluster and the total cluster energy has a different distribution for neutrons and photons with energies > 25 MeV. This allows to apply a graphical cut on the neutron distribution for neutrons with multiplicity $>~2$ (see Fig. 35b);

• (3) the TOF (defined with respect to an arbitrary $t_0$) is in average higher for neutrons ($\simeq ~1$ ns) than for photons ($\simeq -0.5$ ns) (see bisector in Fig. 35c). This allows to apply an ellipsoidal cut (in red in Fig. 35c) to suppress the background due to low-energy photons and out-of-time events.

Fig. 35

MAMBO. a Ratio between the total cluster energy and the cluster multiplicity for neutrons and photons (in black and red the more and less energetic $\pi ^0$ decay photons, respectively). b Ratio between the maximum energy released in a crystal and the total cluster energy for neutrons with multiplicity $>~2$ and photons (sum of red and black distributions from a).The applied graphical cut is the red contour. c photon TOF versus neutron TOF distribution for selected events, the applied cut is presented in red. Ambiguity between two neutral signals with the same multiplicity is solved assigning the neutron tag to the signal with larger TOF (see 45$^{\circ }$ black line in the picture)

The time measurement also allows one to solve the ambiguity between low-energy neutral clusters with the same multiplicity, since the cluster with the larger time value is associated with the neutron. Applying the previously described selection criteria to the same sample of events before the kinematical cuts, the sample is reduced of $\sim 40\%$. In further detail, for a global reduction of 40% of the sample, cut (1) causes a reduction of $\sim 5\%$, cut (2) of $\sim 10\%$ and cut (3) contributes with an additional 25%.

8 Ring-imaging Cherenkov detectors

The discovery of the emission of photons by a charged particle travelling in a material at a speed greater than the in medium speed of light (the Cherenkov effect) opened the possibility to design a full class of detectors. The principle can be implemented in several ways. The use of the bare emission of light above a velocity threshold proved to be very effective even in very narrow phase space, the so-called differential Cherenkov detector, as it turned out for example in the experiment which discovered the antiproton [268]. Arthur Roberts proposed in 1960 the Cherenkov light-ring imaging “for the accurate measurement of particle velocity and direction” exploiting the directional properties of Cherenkov light. The seminal work of Seguinot and Ypsilantis [269] demonstrated the applicability to large area detectors. The early 80’s saw a first generation of devices, which suffered of performance problems, while the second generation, in the late 80s, worked well enough for the experiments, even with a reduced quantum efficiency of the converters. The evolution of the techniques to detect photons (from the first photon-sensitive vapors coupled to multiwire chambers, to photomultipliers, to modern silicon photomultipliers) has been critical for the feasibility of devices covering large fractions of the phase space, eventually a key interest point. The dependence of the momentum range of particles identifiable with this technique represented an opportunity to better adapt the detectors to the experimental conditions and, where it could represent a limit for the wide momentum range to explore, it triggered ingenious optical solutions and the development of new radiators materials.

RICH counters are always complementary to the other PID techniques, extending the energy range of the particle identification. In this section few applications in CSN3 experiments are described, emphasizing the different technical solutions and demonstrating the versatility of the technique.

In the ALICE and CLAS12 experiments, although the energy range of detected particles is similar and below 10 GeV/c, the RICH detectors differ in the radiators and in the design of the optical paths: at ALICE C$_6$F$_{14}$ is used as radiator together with a proximity focus (no optics), providing also a position measurement of the charged particles on the cathodes, while at CLAS12 aerogel was chosen as radiator and geometrical constraints were matched thanks to a mixed spherical/plane mirrors solution.

The EIC experiment, whose first measurement is foreseen in 2030, is considering various options for their RICH detector with the aim to extend the particle separation up to 60 GeV/c. It is an opportunity to explore the most recent technical advances, on the front of the radiators (with an eco-friendly possibility), of the design which demands for compactness, and of single-photon detectors like SiPM’s or micro-pattern gaseous detectors.

8.1 ALICE: the largest CsI RICH application for pion, kaon, proton separation

The ALICE HMPID (High-Momentum Particle IDentification) detector [270] represents the largest-scale application of CsI photocathodes, setting the standard for many detectors using the same technology, and is the largest device of its kind operated at a collider. It consists of seven proximity-focusing RICH counters and exploits MWPCs, coupled with a pad segmented CsI coated photo-cathode, to detect both Cherenkov photons and charged particles. With an active area of 10.3 m$^2$, it covers $\approx$ 5% of the ALICE central barrel acceptance in the pseudo-rapidity range $|\eta |<0.5$. The information of the pads is used to define clusters whose centroid is used as the reconstructed position of the photon. The HMPID identifies charged hadrons combining the measurement of the emission angle of the Cherenkov photons produced in a 1.5-cm-thick layer of low chromaticity C$_6$F$_{14}$ (perfluorohexane) liquid radiator with an index of refraction of n = 1.2989, with the momentum information provided by the main ALICE tracking detectors, the ITS and the TPC (see Sect. 3.3). This requires the track extrapolation from the central tracking detectors to the MIPs reconstructed position on the HMPID photo-cathode. Starting from this coordinates, candidate photon interaction points are selected around the MIP and the photon emission angle is calculated. This procedure is called ${backtracing}$ [270]. To associate the Cherenkov emission angle, deduced from the photon ring reconstruction, to the track and reject the background contribution, the Hough Transform Method (HTM) [271] is applied. Figure 36, left panel, shows the scatter plot of the measured Cherenkov angle as a function of the track momentum for pp collisions at $\sqrt{s}$ = 13 TeV collected in 2015. The three bands of pions, kaons and (anti-)protons are clearly visible and centered on the theoretical values (black curves).

Fig. 36

ALICE. a Cherenkov angle measured in the HMPID vs track momentum. b The separation in units of $\sigma$ for $\pi$/K and K/p as a function of transverse momentum in the HMPID, from [272]

The particle yields are then extracted from a three-Gaussian fit to the Cherenkov angle distribution in narrow transverse momentum bins. The multiplicity of $\approx$ 90 primary tracks plus secondaries produced in the most central (0–5%) Pb–Pb collisions in the HMPID acceptance corresponds to an average detector occupancy of $\approx$ 3.5%. In these conditions the probability that HTM detects fake Cherenkov patterns increases. The larger the emission angle, the larger the probability to find background clusters while scanning for Cherenkov photons. The background on the photo-cathodes is uniform and for a larger emission angle a larger area is scanned, so background clusters can reproduce Cherenkov patterns. To remove the background a polynomial function of 6th order is used to fit the distribution of the identified fake patterns.

Figure 36, right panel, shows the separation in units of $\sigma$ for $\pi$/K and K/p as a function of transverse momentum in the HMPID, for pp collisions at $\sqrt{s}$ = 13 TeV and Pb–Pb collisions at $\sqrt{s_{\mathrm{NN}}}$ = 5.02 TeV, respectively. The precision of the fitting of the background distribution represents a source of systematic uncertainty. In pp and p–Pb collisions, where the background is negligible and the background fitting is not applied, the total systematic error is smaller. Exploiting the statistical unfolding, the HMPID has provided pion and kaon $p_{\mathrm{T}}$ spectra between 1.5 GeV/c and 4 GeV/c and (anti-)proton spectra in the $p_{\mathrm{T}}$ interval 1.5–6 GeV/c. After ten years from the first operation, the HMPID performance is stable and the PID capabilities are at the level of expectations.

8.2 EIC: perspective of PID techniques at the electron-ion collider

Different PID technologies are proposed at EIC to identify hadrons over a wide kinematic range and to reinforce electron/hadron separation where electromagnetic calorimetry is the main player.

For hadron PID at high momenta, there are no alternatives to a gaseous RICH. The INFN groups are actively contributing to the development of the modular RICH (mRICH) for low momenta PID, in the R&D activities toward a dual RICH (dRICH) and in developing gaseous detectors of single photons based on MicroPattern Gaseous Detector (MPGD) technologies, to be used in a windowless RICH. An approach to eco-friendly gaseous RICHes has also been proposed.

The mRICH aims to provide $\pi$-K separation in the low-momentum range (3–10 GeV/c) and e-$\pi$ separation up to 2 GeV/c [273,274,275,276]. It is an aerogel RICH, where the simple proximity focusing scheme is enhanced using Fresnel lenses with the goal of raising the upper limit of the effective momentum range, keeping a mandatory compact design.

The need for an extended momentum range can be fulfilled exploiting the availability of high clarity, hydrophobic aerogel⁷ radiators, which has driven the proposal of the dRICH [277, 278]. The dRICH foresees C$_2$F$_6$ as gas radiator ($n~\simeq ~1.0008$) and an aerogel radiator ($n~\simeq ~1.02$) for $3\sigma$ $\pi /K$ separation in the range 3–60 GeV/c and efficient e$/\pi$ separation from few hundred MeV up to $\sim$ 15 GeV/c in the EIC spectrometer forward region. The design has been supported with a complete Geant4 [279] simulation study and extensively using AI techniques with the Bayesian optimization to determine the optimal design parameters [280]. Figure 37 shows a typical simulated event in the dual RICH. A first prototype has been designed and is presently under construction, in view of a test beam exercise in 2021. The readout of the Cherenkov light is another field of development: the well deployed MultiAnode PMTs (MAPMT) which are being used to test the initial RICH prototypes, are not suitable for the setup at EIC because they should operate in a strong magnetic field. SiPMs as photon sensors make an appealing alternative, even if more tests are needed to establish the procedures to keep under control the noise rate, especially after irradiation. Dedicated studies are being performed to reach the goal of SiPM that can operate up to an integrated fluxes of 10$^{11}$ 1-MeV neutron equivalent per cm$^2$ [281], to ensure several years of operation at maximum EIC luminosity, along with the coupling to the front-end ALCOR chip [282], developed for the SiPMs of the DarkSide experiment. A possible direction to explore comes from recent evidence [283] that the target radiation hardness is reachable when operating SiPMs at low temperature (in the range − 30 to − 40 $^\circ$C) and undertaking annealing cycles at high temperature (170 $^\circ$C). An initial exercise of mRICH read-out using SiPMs as photon sensors has been performed. To take advantage of the higher density of Cherenkov photons in the far UV (the distribution depending on $1/\lambda ^2$) and to cope with compactness requirements, the windowless design has been introduced [284], which avoids light absorption, using gaseous detectors like the PHENIX HBD [285].

Fig. 37

EIC. Dual RICH detector configuration after AI-driven optimization. Multiple mirror panels (gray) focus rings from both aerogel and C$_2$F$_6$ per-fluorocarbon radiators onto the same focal plane (GEANT4 simulation). Adapted from [280]

Gaseous detectors are established cost effective solutions to cover large-area single photon detection surface in magnetic field with low material budget. So far, CsI is the only available photo-cathode (PC) in the far UV domain with high quantum efficiency (QE). MPGD based photon detectors (PDs) demonstrated natural answer to control ion backflow (IBF) and photon feedback: few examples are the COMPASS RICH upgrade [286, 287], the windowless RICH prototype and test beam with quintuple GEM PDs [284], the TPC-Cherenkov (TPCC) tracker prototype with quadruple GEM PDs [288].

Fig. 38

EIC. a The formation of the ring image on the photon detector prototype by Cherenkov photons generated in a quartz radiator crossed by beam particles. b 2-D histogram of the hits produced by the Cherenkov photons in the small pad-size prototype

In the EIC context a multi-directional R & D program is led by INFN:

• establishment of the hybrid PD for a windowless RICH approach to increase the number of detected photons;

• increasing the granularity of the readout elements for fine resolution with limited lever arm. Figure 38 shows a schematic drawing of the COMPASS-like photon detector in the 2018 beam test and an example of the detected Cherenkov ring [289];

• comparison the detector performance using either THGEM (as in COMPASS) or GEMs for the first multiplication stages;

• identification of an adequate front-end chip: studies for coupling the hybrid PD with VMM3 ASIC have been initiated;

• coupling of the THGEMs with a novel and more robust PCs by Hydrogenated Nano Diamond powder (HND) to overcome the limitation imposed by the use of CsI [290]. Set of systematic studies are ongoing for complete validation [291, 292].

Due to the Global Warming Power of fluorocarbons, their application is expected to be more and more limited. For this reason, pressurised Ar at a few bar level has been proposed as alternative [293]. Initial performance studies have started [294], while the mechanical challenge posed by the need of a light-material vessel standing the pressure is still to be addressed.

8.3 JLAB: advanced compact and optimised design of RICH at CEBAF

The baseline detectors composing the CLAS12 spectrometer (time-of-flight and threshold gas Cherenkov counters) are able to efficiently identify electrons, and separate hadron species at momenta below 3 GeV/c. The realization of a different kind of detector, based on Cherenkov ring imaging technique (RICH), has been led by INFN to properly identify particles at higher momenta up to 8 GeV/c. The design of the CLAS12 RICH posed many challenges. It had to fit inside the CLAS12 spectrometer, imposing geometrical and material budget constraints. The momentum range of interest suggested the use of aerogel (see note 7) as radiator, with refraction index in between gases and liquids (n = 1.05), with an unprecedented clarity [295]. A unique hybrid-optic solution, with photons at different angles undergoing different path lengths, has been adopted using plane and spherical mirrors [296, 297]. The planar mirrors exploit for the first time a 0.7 mm glass-skin technology, developed for the terrestrial telescopes, to obtain a material budget comparable to carbon fiber at a much reduced cost [298]. The CLAS12 RICH works in the visible and near-UV wavelength range to avoid the more and more evident Rayleigh scattering inside aerogel in the UV region, and it is the first large scale device using flat-panel large area multi-anode photo-multipliers (MAPMTs). The RICH front-end electronics, counting 25,000 channels, ensures 100% efficiency at 1/3 of a photoelectron level, 1:4 gain spread compensation, and time resolution of the order of 1 ns to distinguish direct from reflected photon hits, while accepting trigger rates up to 20 kHz with a latency of $8 \,\upmu \hbox {s}$.

The first RICH sector was installed on January 2018, in time for the start of the CLAS12 data-taking [299].

Although the alignment of the various sub-components and the fine calibration of the Cherenkov angle response is still ongoing, the preliminary results show that the detector matches the required performance in discriminating between pions and kaons over the full range between 3 and 8 GeV/c, see Fig. 39. For a single detected photon, the measured time resolution is better than 1 ns and the angular resolution is better than 5 mrad. In the direct configuration (expected to be largely unaffected by the ongoing sub-component alignment), the complete ring reconstruction meets a 1.5 mrad resolution per track, corresponding to the design $4\sigma$ pion-kaon Cherenkov angle separation at the highest 8 GeV/c momentum. A second RICH sector is under construction and expected to be installed in late 2021.

Fig. 39

JLAB. RICH reconstructed mean Cherenkov angle as a function of the particle momentum for positive hadron tracks, impinging on aerogel tile 13 in layer 0. Pions, kaons and protons are separated over the full 3 to 8 GeV/c momentum range. The small deviations with respect to the expected pattern (dashed lines) for the three particle hypotheses are due to the not yet optimized alignment of the RICH components

9 Kinematic and Bayesian methods

Measurement of the yields of rare nuclear processes can be done using kinematic methods. Examples of these are the THM (Trojan Horse Method) [98] largely used by the ASFIN experiment (see Sect. 2.4.1) and the kinematical constraints used by the CHIRONE (see Sect. 2.3.1) and NUCLEX (see Sect. 2.3.4) experiments.

The Bayesian approach is a method to combine the PID signals obtained from different detectors of the same experiment by folding the probabilities with the expected abundances of each particle species. ALICE experiment (see Sect. 2.2.1) has used this approach in many analyses  [300, 301], showing the large improvement obtained in particle identification [302].

9.1 Kinematic method

9.1.1 ASFIN: identification of undetected particles through momentum conservation

The Trojan Horse Method (THM) [99] allows to study the nuclear reaction with three bodies in the final state by detecting and identifying only two of the three particles and measuring their kinematic quantities (angle of emission and energy). Indeed, the experiment can be considered kinematically complete, since all kinematic variables can be derived from the measured quantities.

This procedure cannot be used when the reaction takes place on unknown target nuclei, e.g. on target contamination. Let us consider the reaction $P + T \rightarrow a + b + s$, where P is the projectile nucleus and T is the target nucleus, a, b and s the produced particles. In case of target contamination, detecting only a and b particles implies that the system can be left undetermined due to the overlapping of different kinematic loci in the same phase-space region, corresponding to reactions having different undetected particles. Therefore, identification of particle s is pivotal to the following data analysis, to reject possible background events.

A useful procedure that allows the determination of the mass number of the undetected particle s and also of the Q-value spectrum of the reaction of interest consists in the introduction of two new variables [303]:

$$\begin{aligned} X= & {} \frac{p_{s}^{2}}{2u} \end{aligned}$$

(5)

$$\begin{aligned} Y= & {} E_{P} - E_{a} - E_{b}, \end{aligned}$$

(6)

where $E_{P}$, $E_{a}$ and $E_{b}$ are the kinetic energies of projectile P and particle a and b; and $p_s$ is the momentum of s, $u~\sim ~931.5$ MeV/$c^2$ is the atomic mass unit. The momentum $p_s$ is deduced from the energies and emission angles of a and b particles by applying the momentum conservation equation, thus the mass unit is not included in the variable X. The quantities X and Y are related through the relation:

$$\begin{aligned} Y=\frac{1}{A_s}X-Q \end{aligned}$$

(7)

since $p_{s}^2~=~2E_{s}A_{s}u$, with $p_{s}$, $E_{s}$ and $A_{s}$ momentum, kinetic energy and mass in units of u of the s particle and Q the Q-value of the reaction. At this point, $A_s$ and Q are unknown quantities and if experimental points corresponding to the measured coincidence events are reported on the X-Y plane, one expects them to fall around a straight line, defined by Eq. 7. This line intercepts the Y-axis at $Y=-Q$ and has a slope given by $1/A_s$, hence the values of Q and $A_s$ can now be deduced from a fit to the data.

Fig. 40

ASFIN. Energy–momentum plot for $\alpha$-$^{16}$O coincidences as reported in [304]. The line is calculated assuming $A_s$ = 1 and a theoretical Q-value of 5.889 MeV. Events not following the line of unitary mass are discarded in the further analysis. Figure adapted from [304]

This so-called energy–momentum plot (EP-plot) is widely used to cross check the right channel selection in experiments which use THM. For example, in Fig. 40 it is reported the kinematic technique described above for selecting the $^{19}$F($p,\alpha _0$)$^{16}$O reaction channel, i.e. with $^{16}$O in the ground state, from the measured three-body $^2$H($^{19}$F,$\alpha {}^{16}$O)n reaction [304]. In this figure, the events corresponding to the channel of interest gather around the straight line of equation $Y~=~X-5.889$, as expected if a particle of A = 1 unit mass is emitted in a reaction with a Q-value of 5.889 MeV.

9.1.2 CHIRONE: background rejection through kinematic coincidences

For a 4$\pi$ multidetector like CHIMERA the measurement of kinematical coincidences, in binary or complex reactions, is possible thanks to the complete angular coverage of the detector. The CHIRONE collaboration developed various techniques, based on imposing kinematical constraints, useful to improve the results of data analysis [218, 219]. A typical improvement is the extraction of precise angular distributions of emitted particles [305].

Even more important is the cleaning effect on random coincidences obtained using kinematic constraints on momentum and energy conservation. This is a very powerful method that allows to measure very low probability channels with a good signal over background ratio. A relevant example was recently obtained in the measurement of the $\gamma$-ray decay channel of the Hoyle and of the 9.64 MeV excited levels of $^{12}$C. Such levels are very important for the carbon production in astrophysical environments. Their decay probability is very low, 10$^{-4}$ for the Hoyle state [306], while it is of the order of $10^{-6}$ for the 9.64 MeV level, see Ref. [219]. The CHIRONE collaboration was able to perform such measurement using an $\alpha$ beam, accelerated at 64 MeV, and a target of $^{12}$C. The background was strongly suppressed, with the request of momentum and energy conservation applied to all detected particles and $\gamma$-rays. In the case of this experiment, this implies a quadruple coincidence of two charged particles ($\alpha$ and $^{12}$C, identified by means of $\varDelta$E-E (see Sect. 3.2.1) and $\varDelta$E-TOF (see Sect. 6.2.2), respectively) and two $\gamma$-rays.

Fig. 41

CHIRONE. a Kinematic loci obtained plotting the energy of recoiling $^{12}$C against the energy of scattered $\alpha$ particle, in the $\alpha$+$^{12}$C scattering at 64 MeV. The lines and regions of interest are the expected kinematics loci for the elastic scattering (green), 4.44 MeV level (black), 7.65 MeV Hoyle state (purple), 9.64 MeV (blue) and 12.7 MeV level (red). b As in a in coincidence with two $\gamma$-rays. The upper inset shows the Q$_{\mathrm {ME}}$ obtained for the same events (figure adapted from Ref. [219])

Figure 41a shows the kinematic loci obtained plotting the energy of the $^{12}$C (y-axis) and the energy of the scattered $\alpha$ particle (x-axis). Lines and regions of interest with different colors show the expected kinematic loci for different levels of $^{12}$C. In this case, only the two kinematic loci of elastic scattering and 4.44 MeV level are evidently populated; events of the 12.7  MeV level are also present, while the other levels are overwhelmed by the background. On the contrary, Fig. 41b shows the same correlation after the kinematics coincidence events with two $\gamma$-rays. In this figure, the contribution of elastic scattering is completely suppressed while the contribution produced by the tail of the 4.44 MeV level, due to spurious coincidences, emerges. This result is visible also in the inset of Fig. 41b showing the $Q_{\mathrm {ME}}$ spectrum obtained for the same events of Fig. 41b. The $Q_{\mathrm {ME}}$ is given by the difference between the total detected kinetic energy and the available beam energy: $Q_{\mathrm {ME}}$ =  Energy($\alpha _{\mathrm {scattered}}$)+Energy($^{12}$C)-Energy($\alpha _{\mathrm {beam}}$). With this method a background rejection factor of the order of $\approx$ 10$^5$, that allows to extract information about the Hoyle state, is obtained [219].

9.1.3 NUCLEX: correlation analysis for rare event selection

In nuclear reactions, several isotopes are produced in their internal unbound states. These states decay into two or more particles and precise measurements of their momentum vectors allow to reconstruct the invariant mass of their original decaying parent isotope that can, therefore, be identified experimentally. This can be accomplished with OSCAR, FAZIA and GARFIELD multi-detector arrays (see Sect. 3.2.2 for details). The energy position and the shape of the observed resonance peaks carry information also about structure properties of the unbound isotope. Within this context, the NUCLEX collaboration has studied the three $\alpha$ decay of the Hoyle state at E$_X$ = 7.654 MeV in $^{12}$C, playing a key role in cluster structure and in nuclear astrophysics. Special attention has been devoted to the branching ratios of a direct three-$\alpha$ decay (DD) vs. a sequential decay path passing through the production of $^8$Be, namely $^{12}$C$\rightarrow \alpha$ + $^8$Be followed by $^8$Be$\rightarrow \alpha$ + $\alpha$. In Ref. [307], the Hoyle state was produced with the transfer reaction $^{14}$N(d,$\alpha$)$^{12}$C$^{Hoyle}$, studied with deuteron beams at E = 10.5 MeV accelerated at the LNS, using a hodoscope designed by the NUCLEX groups and constituting also the OSCAR detector project. A $\varDelta$E-E Silicon telescope was used to detect the 1+3 $\alpha$ particles produced in the final state, thus deducing the residual excitation energy of the produced $^{12}$C nucleus, E$_X$, shown in Fig. 42a as a blue-line histogram. The observed resonance peaks correspond to $^{12}$C internal states. By correlating the detected $\alpha$ particle with other three-$\alpha$ coincidences detected by a 64 Silicon pads hodoscope, it was possible to precisely identify the Hoyle state at E$_X$ = 7.654 MeV with negligible background (see blue-filled histogram on Fig. 42). A Dalitz plot analysis of these three $\alpha$ coincidences is shown in Fig. 42b in the form of special two-dimensional Dalitz plots. The top-left Dalitz plot is constructed with the experimental events falling within the Hoyle state peak (see  [307] for details on the analysis and variables used). The top-right and bottom-left two-dimensional Dalitz plots are built with a Monte Carlo simulation of the Hoyle state decay into three-$\alpha$’s in sequential and direct mode, respectively. Using this kinematic approach, the comparison to experimental data clearly shows how the sequential mode fulfills the whole decay width of the Hoyle state. Similar kinematic multi-$\alpha$ coincidence studies have been performed with the GARFIELD array coupled to the the RCo ring counter at the LNL [308, 309]. Similar methods are used also with the FAZIA detector in heavy-ion collisions, where a large number of decaying states can be isolated and explored.

Fig. 42

NUCLEX. a $^{12}$C excitation energy spectrum reconstructed with three- and four-$\alpha$ particle coincidences in $^{14}$N(d,$\alpha$)$^{12}$C at E = 10.5 MeV. b Dalitz plot analyses of the three alpha coincidences produced by the Hoyle state. From  [307]

9.2 Bayesian methods

9.2.1 ALICE: combining PID techniques using a Bayesian approach

In ALICE charged particles as $\pi ^{\pm }$, K$^{\pm }$, and ($\bar{\mathrm{p}}$)p are identified independently [310,311,312,313] by the ITS (see Sect. 3.3), TPC (see Sect. 3.3), TOF (see Sect. 6.1.1) and HMPID (see Sect. 8.1) sub-detectors. However there is a large superposition among the transverse momentum $p_{\mathrm{T}}$ ranges of the ALICE subdetectors with a pion-kaon and kaon–proton separation power equal or larger than 2$\sigma$ (see Figure 46 of [41]). The measured $p_{\mathrm{T}}$ spectra are usually combined in the overlapping ranges using a weighted average with the systematic and statistical uncertainties as weights. In this way it is possible to measure charged hadron $p_{\mathrm{T}}$ spectra from few hundreds of MeV/c up to 20 GeV/c

Starting from the detector signals it is possible to evaluate the probability in a specific detector for a given track to be one of the five charged particle species (electron, muon, pion, kaon, (anti-)proton). As an alternative to the previous described method, a Bayesian approach [300, 301] to combine PID probabilities from different detectors was also used by ALICE.

The response of each detector can be expressed in terms of its raw signal S, e.g. the time of flight $t_{\mathrm {TOF}}$ from the TOF detector, or the energy loss dE/dx measured by the ITS or TPC, or the Cherenkov emission angle measured by the HMPID. $P(S_{\alpha }|H_{i})$ is defined as the conditional probability that a particle of species $H_{i}$ will produce a signal $S_{\alpha }$ in a detector $\alpha$. The index i can refer to electrons, pions, protons, etc. The combination of the probabilities from different detectors, $P_{\alpha }$, can thus be written as a product:

$$\begin{aligned} P(\overrightarrow{S}|H_{i}) = \prod _{\alpha } P_{\alpha }(S_{\alpha }|H_{i}), \end{aligned}$$

(8)

where $\overrightarrow{S}~=~(S_{\mathrm{ITS}},S_{\mathrm {TOF}},...)$. $P(\overrightarrow{S}|H_{i})$ is then the conditional probability that the set of detector signals $\overrightarrow{S}$ will be observed for a given particle species $H_{i}$.

However, the variable of interest in this case is the conditional probability $P(H_{i}|\overrightarrow{S})$ that the detected particle is of the species $H_{i}$, given a certain signal S. The relation between the two conditional probabilities, for a combined set of detectors, can be expressed with Bayes theorem [314]:

$$\begin{aligned} P(H_{i}|\overrightarrow{S}) = \frac{P(\overrightarrow{S}|H_{i})C(H_{i})}{\varSigma _{k=e,\pi ,p,...} P(\overrightarrow{S}|H_{k})C(H_{k})}, \end{aligned}$$

(9)

Fig. 43

ALICE. a Invariant mass spectra of $\varLambda _{\mathrm {c}}^{+}$ in the range $3~< p_{\mathrm {T}}~<~4$ GeV/c, when $\pi$, K and p are identified using $n_{\sigma }$ PID, minimum-$\sigma$ PID and Bayesian PID in pp collisions at $\sqrt{s}$ = 7 TeV, from [302]. b Invariant mass spectrum of $\varLambda _{\mathrm {c}}^{+}$ in the range 3 $<~p_{\mathrm {T}}~<~4$ GeV/c measured in pp collisions at $\sqrt{s}$ = 7 TeV when Bayesian PID method is used to identify $\pi$, K and p, from [315]

where $C(H_{i})$ is the a priori probability of measuring the particle species $H_{i}$ (i.e. the prior), and the conditional probability $P(H_{i}|\overrightarrow{S})$ is the posterior probability.

The choice of the prior represents the “best guess” one can make of an unknown quantity (in this case, the true particle yields per event). The subjectivity of the priors choice is then eliminated by means of an iterative procedure described in Ref. [302].

Usually, the $n_{\sigma }$ variable is the most used discriminating variable for PID and it is defined as the deviation of the measured signal from that expected for a given species $H_{i}$, in terms of the detector resolution $\sigma$. The minimum-$\sigma$ PID method is based on the deviation from the expected detector signal, but in this case only the species resulting in the smallest $n_{\sigma }$ value is chosen for each track, making this an exclusive selection. In case of the ALICE experiment, the TPC and TOF responses are combined by adding their respective $n_{\sigma }$ values in quadrature. This approach uses a similar logic to the Bayesian approach, but without requiring the input of any priors. Figure 43a is a clear example of the improvement of the $\varLambda _{\mathrm {c}}^{+} \rightarrow$ pK$^- \pi ^+$ identification in pp collisions at $\sqrt{s}$ = 7 TeV [302] when a Bayesian PID approach is used. The figure panel a shows the invariant mass spectra for pK$\pi$ candidates in the 3 $< p_{\mathrm {T}}~<$ 4 GeV/c range obtained using the standard $n_{\sigma }$ PID approach, the alternative minimum-$\sigma$ PID and the Bayesian approach. The signal-to-background ratio improves significantly when the Bayesian approach is used. This PID method has been used in $\varLambda _{\mathrm {c}}^{+}$ measurements in different systems [315]. The $\varLambda _{\mathrm {c}}^{+}$ invariant mass distribution in 3$~<~p_{\mathrm {T}}~<$ 4 GeV/c range in pp collisions at $\sqrt{s}$ = 7 TeV is shown in Fig. 43b as an example.

Table 2 Summary table: left part reports the type of particles and energy range for each experiment, while the right part gives the techniques described in the present review

10 Summary

The present review described the latest trends in detector and analysis methods for particle and nuclei identification techniques, as currently adopted in nuclear physics experiments where INFN-CSN3 is involved. Although the basic physics processes underneath the identification are well established since several decades, the wide energy range to be covered by such experiments has pushed researchers to develop new hardware and software tools that profit of the new technological achievements, as described in these pages.

Table 2 summarizes the PID techniques presented in this review and the energy interval of application for each experiment. Few points emerged clearly: (i) the increasing importance of solid-state detectors (silicon or germanium), both for precise tracking and energy determination, (ii) the possibility to make a complete analysis of the signal shape, further strengthening the capabilities of techniques like PSA or timing, (iii) time resolutions of the order of 100 ps or below can now be achieved, (iv) the still intense use and R&D on scintillators (liquids or crystals) and (v) the possibility to combine different techniques also profiting of the continuous increase of the data that can be collected.

Particle identification will remain a fundamental ingredient for all nuclear physics studies and there are still many opportunities for improvements in the techniques.