Abstract
This study reports the second research cycle on students’ understanding of directional derivatives of two-variable functions. We applied Action-Process-Object-Schema (APOS) Theory as theoretical framework as in the first cycle. As a result of the first research cycle, a refined genetic decomposition describing the constructions that students may do to understand directional derivatives was proposed. Following the first cycle, we used the genetic decomposition to design didactical materials (a set of activities) to help students do the proposed constructions. The APOS theory pedagogical strategy, the ACE cycle, consisting of work on the activities in collaborative groups of three or four students, followed by whole class discussion and take-home exercises, was implemented in the classroom. In this study, we empirically test the genetic decomposition and the activity set resulting from the first research cycle by performing semi-structured interviews with a group of eleven students to see whether the GD as a model and the activity set were effective, needed to be refined, or to be rejected. We validated the genetic decomposition by showing that the didactical materials and the pedagogical method were productive and supported students’ construction of directional derivatives. Some aspects in which students’ understanding can be further improved are discussed.















Similar content being viewed by others
Data Availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
Notes
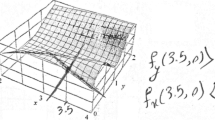
Questions I-6a and I-6b were not about directional derivatives. I-6a) What can you say about the change in the value of the function [Fig. 4] if \(x\) increases 0.02 units and \(y\) decreases 0.02 units? I-6b) Find the differential of \(f\) [Fig. 4] at the point \((1, 2)\), \(df(\mathrm{1,2})\). If it is not possible, explain why.
By the construction of “deep understanding” we mean the construction of Process or Object conceptions.
References
Al Dehaybes, M., Deprez, J., van Kampen, P., & De Cock, M. (2023 to appear). Students’ understanding of Laplacian and gradient in mathematics and physics contexts. In T. Dreyfus, A. González-Martín, J. Monaghan, E. Nardi, & P. Thompson (Eds.). Proceedings of the conference on the teaching and learning of Calculus across disciplines (June 5–9, 2023). MatRIC: University of Bergen.
Arnon, I., Cotrill, J., Dubinsky, E., Oktaç, A., Roa Fuentes, S., Trigueros, M., & Weller, K. (2014). APOS Theory: A framework for research and curriculum development in mathematics education. Springer Verlag.
Asiala, M., Brown, A., DeVries, D. J., Dubinsky, E., Mathews, D., & Thomas, K. (1996). A framework for research and development in undergraduate mathematics education. In J. Kaput, E. Dubinsky, & A. H. Schoenfeld (Eds.), Research in collegiate mathematics education (Vol. 2, pp. 1–32). Providence, RI: AMS.
Asiala, M., Cottrill, J., Dubinsky, E., & Schwingendorf, K. (1997). The development of students’ graphical understanding of the derivative. The Journal of Mathematical Behavior, 16, 399–431. https://doi.org/10.1016/S0732-3123(97)90015-8
Bajracharya, R. R., Emigh, P. J., & Manogue, C. A. (2019). Students’ strategies for solving a multirepresentational partial derivative problem in thermodynamics. Physical Review Physics Education Research, 15(2), 020124. https://doi.org/10.1103/physrevphyseducres.15.020124
Borji, V., & Martínez-Planell, R. (2020). On students’ understanding of implicit differentiation based on APOS theory. Educational Studies in Mathematics, 105, 163–179. https://doi.org/10.1007/s10649-020-09991-y
Confrey, J., & Smith, E. (1994). Exponential functions, rates of change, and the multiplicative unit. Educational Studies in Mathematics, 26(2), 135–164. https://doi.org/10.1007/BF01273661
Confrey, J., & Smith, E. (1995). Splitting, covariation, and their role in the development of exponential functions. Journal for Research in Mathematics Education, 26(1), 66–86. https://doi.org/10.2307/749228
Carlson, M. P., Jacobs, S., Coe, E., Larsen, S., & Hsu, E. (2002). Applying covariational reasoning while modeling dynamic events: A framework and a study. Journal for Research in Mathematics Education, 33(5), 352–378. https://doi.org/10.2307/4149958
Dubinsky, E. (1991). Reflective abstraction in advanced mathematical thinking. In D. Tall (Ed.), Advanced mathematical thinking (pp. 95–123). Kluwer Academic Press.
Dubinsky, E., & McDonald, M. (2001). APOS: A constructivist theory of learning in undergrad mathematics education research. In D. Holton (Ed.), The teaching and learning of mathematics at university level: An ICMI study (pp. 273–280). Kluwer Academic Publishers.
Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61(1), 103–131. https://doi.org/10.1007/s10649-006-0400-z
Ferrini-Mundy, J., & Graham, K. G. (1993). Research in calculus learning: Understanding of limits, derivatives and integrals. In J. Kaput & E. Dubinsky (Eds.), Research issues in undergraduate mathematics learning. Preliminary analyses and results, MAA Notes Volume 33 (pp. 31–46). Washington, DC: Mathematical Association of America.
Gravesen, K. F., Grønbæk, N., & Winsløw, C. (2017). Task design for students’ work with basic theory in analysis: The cases of multidimensional differentiability and curve integrals. International Journal of Research in Undergraduate Mathematics Education, 3(1), 9–33. https://doi.org/10.1007/s40753-016-0036-z
Harel, G. (2021). The learning and teaching of multivariable calculus: A DNR perspective. ZDM, 58, 709–721. https://doi.org/10.1007/s11858-021-01223-8
Jones, S. R. (2022). Multivariation and students’ multivariational reasoning. Journal of Mathematical Behavior, 67. https://doi.org/10.1016/j.jmathb.2022.100991
Kertil, M., & Gülbağcı Dede, H. (2022). Promoting prospective mathematics teachers’ understanding of derivative across different real-life contexts. International Journal for Mathematics Teaching and Learning, 23(1), 1–24.
McGee, D., & Moore-Russo, D. (2015). Impact of explicit presentation of slopes in three dimensions on students’ understanding of derivatives in multivariable calculus. International Journal of Science and Mathematics Education, 13(2), 357–384. https://doi.org/10.1007/s10763-014-9542-0
Martínez-Planell, R., Trigueros, M., & McGee, D. (2015). On students’ understanding of the differential calculus of functions of two variables. The Journal of Mathematical Behavior, 38, 57–86. https://doi.org/10.1016/j.jmathb.2015.03.003
Martínez-Planell, R., Trigueros, M., & McGee, D. (2017). Students’ understanding of the relation between tangent plane and directional derivatives of functions of two variables. The Journal of Mathematical Behavior, 46, 13–41. https://doi.org/10.1016/j.jmathb.2017.02.001
Martínez-Planell, R., Borji, V., & Trigueros, M. (2022). Slope and the differential calculus of two variable functions. Karunakaran, S. S., & Higgins, A. (Eds.). Proceedings of the 24th Annual Conference on Research in Undergraduate Mathematics Education, 366–373. Boston, MA.
Mkhatshwa, T. P. (2021). A quantitative and covariational reasoning investigation of students’ interpretations of partial derivatives in different contexts. International Journal of Mathematical Education in Science and Technology. https://doi.org/10.1080/0020739X.2021.1958941
Moore-Russo, D., Conner, A., & Rugg, K. (2011). Can slope be negative in 3-space? Studying concept image of slope through collective definition construction. Educational Studies in Mathematics, 76(1), 3–21. https://doi.org/10.1007/s10649-010-9277-y
Moreno-Arotzena, O., Pombar-Hospitaler, I., & Barraguéz, J. I. (2021). University student understanding of the gradient of a function of two variables: An approach from the perspective of the theory of semiotic representation registers. Educational Studies in Mathematics, 106, 65–89. https://doi.org/10.1007/s10649-020-09994-9
Nagle, C., Martínez-Planell, R., & Moore-Russo, D. (2019). Using APOS theory as a framework for considering slope understanding. The Journal of Mathematical Behavior, 54. https://doi.org/10.1016/j.jmathb.2018.12.003
Park, J. (2015). Is the derivative a function? If so, how do we teach it? Educational Studies in Mathematics, 89(2), 233–250. https://doi.org/10.1007/s10649-015-9601-7
Stewart, J. (2012). Calculus (7th ed.). Cengage Learning.
Tall, D. (1992). Visualizing differentials in two and three dimensions. Teaching Mathematics and Its Applications, 11(1), 1–7. https://doi.org/10.1093/teamat/11.1.1
Thompson, J. R., Manogue, C. A., Roundy, D. J., & Mountcastle, D. B. (2012). Representations of partial derivatives in thermodynamics. AIP Conference Proceedings, 1413, 85.
Trigueros, M., Martínez-Planell, R., & McGee, D. (2018). Student understanding of the relation between tangent plane and the total differential of two-variable. International Journal of Research in Undergraduate Mathematics Education, 4, 181–197. https://doi.org/10.1007/s40753-017-0062-5
Wangberg, A., Gire, E., & Dray, T. (2022). Measuring the derivative using surfaces. Teaching Mathematics and Its Applications: An International Journal of the IMA, 41, 110–124. https://doi.org/10.1093/teamat/hrab030
Wangberg, A., & Johnson, B. (2013). Discovering calculus on the surface. Primus, 23(7), 627–639. https://doi.org/10.1080/10511970.2013.775202
Weber, E. D. (2012). Students’ Ways of Thinking about Two-Variable Functions and Rate of Change in Space (Unpublished doctoral dissertation). Arizona State University, USA
Weber, E. D. (2015). The two-change problem and calculus students’ thinking about direction and path. The Journal of Mathematical Behavior, 37, 83–93. https://doi.org/10.1016/j.jmathb.2014.12.003
Weber, E., Tallman, M., Byerley, C., & Thompson, P. W. (2012). Introducing derivative via the calculus triangle. Mathematics Teacher, 104(4), 274–278. https://doi.org/10.5951/mathteacher.106.4.0274
Weber, E., & Thompson, P. W. (2014). Students’ images of two-variable functions and their graphs. Educational Studies in Mathematics, 87(1), 67–85. https://doi.org/10.1007/s10649-014-9548-0
Yerushalmy, M. (1997). Designing representations: Reasoning about functions of two variables. Journal for Research in Mathematics Education, 28, 431–466. https://doi.org/10.2307/749682
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
We have no conflicts of interest to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Borji, V., Martínez-Planell, R. & Trigueros, M. University Students’ Understanding of Directional Derivative: An APOS Analysis. Int. J. Res. Undergrad. Math. Ed. (2023). https://doi.org/10.1007/s40753-023-00225-z
Accepted:
Published:
DOI: https://doi.org/10.1007/s40753-023-00225-z