First-Year Engineering Students’ Interpretations of Differentials and Definite Integrals

Abstract

In this paper we focus on Norwegian first-year engineering students’ interpretations of differentials and definite integrals. Through interviews with 15 engineering students, we investigated how the students interpreted the different symbols involved in the Fundamental Theorem of Calculus (FTC), as displayed in the textbook used in their calculus course. Through the students’ reflections, we aimed to gain insight into the students’ interpretations of differentials, infinitesimals, and limits, and how these concepts were used to interpret the definite integral. Despite a rather rigorous limit-based approach to definite integrals, provided in teaching and in the students’ textbook, we observed that most students offered conceptual interpretations closer linked with an infinitesimal approach, in terms of integrals being regarded as sums of narrow bars, in line with Leibniz.

Introduction

This study was carried out and funded as a part of MatRIC’s (Centre for Research, Innovation and Coordination of Mathematics Teaching) research activity on the teaching and learning of mathematics in higher education. Rooted in a social constructivist’s perspective and symbol interactionism, our study is motivated by a preceding master study on upper-secondary students, where findings suggested that students primarily associate integration with “actions to be carried out” (Knutsen, 2020) found that integration was interpreted almost solely as the “area under a curve” or “anti-derivative,” and that “sum-based” interpretations were not emphasized by the students. From our review of the course plans in introductory calculus courses for engineering programs offered at universities and university colleges in Norway, we found that the Norwegian curricula for engineering programs tend to emphasize limit-based interpretations of the definite integral. For instance, the University of Stavanger’s (2022, our translation) mathematics course description states that “…students should know the concept of limits, and should be able to define continuity, differentiability, and integration by the limit concept”, and the University of Oslo’s (2022, our translation) course description states that “…students should know how to define and calculate continuity, limits, derivatives and integrals in a precise manner”. On the other hand, for example demonstrated through the study of González-Martin and Hernandes Gomes (2017), textbooks at specific professional engineering courses, in students’ posterior education, to a large extent tend to emphasize the sum-based aspects of integration. With this in mind, we were curious to see if engineering students would offer other types of interpretations than the students at upper-secondary.

Since several studies (see the Didactical Research section) accounts for students’ general perceptions of integration techniques, integrals, and the relations to Riemann-sums, we aimed to investigate deeper into the nuances of students’ reasoning related to differentials, infinitesimals, and limits, with the goal of enrichening the existing body of research literature, from a student perspective. As differentials and infinitesimals from a teaching perspective are prominent in recent research literature, for example Ely (2017, 2021) and Thompson and Harel (2021), our research could be regarded as a supplement to such literature. Aiming to grasp the nuances of the engineering students’ reasoning around these issues, we pose the following research question:

What characterizes first year engineering students’ interpretations of the symbols involved in the Fundamental Theorem of Calculus, with respect to differentials, infinitesimals, and limits, and how do these interpretations affect upon their interpretations of definite integrals?

In the Norwegian educational system, integration is introduced at upper secondary school, and to put the engineering students in our study into a proper context, we find it useful to provide a brief insight into the students’ educational background. At upper secondary school in Norway, there are two main directions that the students can choose between – vocational study programs and general study programs. Vocational study programs aim to prepare students for certain professions (like plumbers, electricians, carpenters and so forth), while general study programs aim to prepare students for higher education. In 2020, a new national curriculum called “The professional renewal” (“Fagfornyelsen”) was introduced in Norway, replacing the “Knowledge promotion” (“Kunnskapsløftet”) from 2006. This curriculum applies to the first 12 years of schooling, prior to students’ higher education at universities or university colleges. Since the Knowledge promotion was the prevailing curricula for students both from Knutsen’s (2020) master study and the engineering students in the study presented in this article, we will only focus on the curriculum from 2006. Integration is only a part of the curricula for the general study program, but for these students several choices of mathematics courses could be made, and integration as a topic is only relevant for students choosing the so called R2-course. This course is considered to be the most theoretically demanding course at upper secondary school. In the Norwegian national curricula, relevant for R2, three bullet points containing the word “integral” are listed under the headline “functions” (Utdanningsdirektoratet, 2020, our translation):

• give an account of the definition of a definite integral as a limit of a sum and an indefinite integral as an antiderivative.

• calculate integrals of the central functions by antidifferentiation, substitution, partial fraction decomposition with linear denominators, and integration by parts.

• interpret the definite integral in models of practical situations and use it to compute plane areas and volumes of rotating bodies.

One notices that the Fundamental Theorem of Calculus (FTC) is not explicitly mentioned, which implied a certain flexibility related to if and how this theorem might be presented in textbooks or in teaching. One should mention that R2 was not a direct requirement for admission to the engineering program, but students without R2 were required to pass different kinds of preparation courses, which were meant to cover the same content as R2.

Some Historical and Epistemological Considerations

In order to analyze students’ interpretations of the symbols involved in the FTC, we find it appropriate to provide a brief historically rooted overview of the main epistemological aspects connected to our research question, in which we regard as relevant for our group of students. The brief historically rooted overview is meant to identify the epistemological roots of the core ideas that we could expect the students to be acquainted with. Through our observations, we saw that several students’ reasoning could relate to some of these historical aspects, for example infinitesimals as understood by Leibniz. Recapitulating our research question, we focus particularly on differentials, infinitesimals and limits, and how this relates to the concept of definite integrals.

The behavior of infinitesimals was known to create some difficulties also in Greek mathematics at the time Euclid wrote his Elements, where he through his definitions, states that “magnitudes are said to have a ratio to one another which are capable, when multiplied, of exceeding one another” (Kline, 1972, p. 69). From this, one immediately notices that infinitesimals are kept out of the definition, valid only if one for instance applies the “Archimedean local model” in which quantities may be small but remain real-valued (Oehrtman & Simmons, 2023). Newton, however, varied his vocabulary when describing infinitesimals in the 17th century, and related to infinitesimals and ratios he wrote the following:

Ultimate ratios in which the quantities vanish are not, strictly speaking, ratios of ultimate quantities, but limits to which the ratios of these quantities, decreases without limit, approach, and which, though they can come nearer than any given difference whatever, they can neither pass over nor attain before the quantities have diminished indefinitely. (Kline, 1972, p. 365).

In some sense, this quote from Newton displays the fine-grained demarcation line between what later became formalized through a rigorous development of limits, and at the time, rather informal treatments of infinitesimals and differentials. Around the same time, Leibniz regarded the area under a graph as a series of small rectangles and let the width of these rectangles approach infinitely small. In turn, the definite integral was defined as a sum of these differentials. Leibniz first considered a curve defined over an interval divided into subintervals and erected ordinates ${y}_{i}$ over each point ${x}_{i}$. The sequence $\left\{\delta {y}_{i}\right\}$ was defined as a difference of ordinates, with the sum ${\sum }_{i}\delta {y}_{i}$ being equal to the difference ${y}_{n}-{y}_{0}$ (Katz, 2004, pp. 316–317). This approximated the area under the curve, and by introducing $\int$for the sum and $dx$ for the infinitely small difference between ordinates, the notions of integration as we know it from modern times was established. Related to early versions of the FTC, and in the sense that integrals could be considered as antiderivatives, Boyer (1959) writes:

Newton here determined first the rate of change of the area, and then from this found the area itself by what we should now call the indefinite integral [antiderivative] of the function representing the ordinate. It is to be noted, furthermore, that the process which is made fundamental in this proposition is the determination of rates of change. In other words, what we should now call the derivative is taken as the basic idea and the integral is defined in terms of this (Boyer, 1959, p. 191).

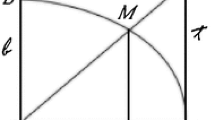
Without a properly defined limit concept, Newton based his observation on methods of exhaustion, which probably emerged from considerations as illustrated in Fig. 1 below, where $A\left(x\right)$ is the area function of $f$, from $x=a$.

Fig. 1

The area function and the interval from ${x}_{0}$ to $x$ and a visual proof of its connection to antiderivatives (adapted from Clausen et al., 1993, p. 12)

Through the rigorous development of limits in the 18th century, Riemann integrals were conceptualized as the limit between the lower and the upper Riemann sums. The core idea in this way of conceptualizing integrals, which differs from Leibniz’s and Newton’s approach, is that one through a rigorous formalization of the limit concept, could postulate the existence of an exact value that the Riemann sums approaches, without being concerned about the behavior of the infinitesimals. In this sense, the notions ∫ and $dt$ become vestigial as they are no longer needed in the calculations. How these rather rigorous limit approaches were expressed in lessons and textbooks in our study is exemplified later.

In what is labeled as “nonstandard analysis”, Abraham Robinson in 1960 succeeded in developing a rigorous fundament for infinitesimal, through so-called hyperreal numbers:

“One defines a hyperreal number $x$ to be an infinitesimal if $\left|x\right|<r$ for all positive real numbers $r$, finite if $\left|x\right|<r$ for some real number $r$, and infinite if $\left|x\right|<r$ for all real numbers $r$. The only real infinitesimal is 0; all other are nonreal hyperreal numbers. (Eves, 1990, p. 295).

In an attempt to describe this in everyday language, one could say that the notion of infinitely small numbers, has been formalized through defining infinitesimals smaller than any real number. In turn, this could be regarded as an extension of the field of real numbers, $\mathbb{R}$, to the field of so-called hyperreal numbers, ${\mathbb{R}}^{*}$. This intervention made it possible to establish a certain degree of rigor, regarding the formalization of infinitesimals, as an alternative to the classical limit approach that had prevailed in calculus teaching for the last couple of centuries. Keisler was the first to apply this approach in calculus textbooks in 1976 (Eves, 1990) and since this, some researchers have argued for an infinitesimal approach to calculus, rather than the more usual limit approach (e.g., Ely, 2017, 2021; Thompson & Milner, 2018; Stevens & Jones, 2023).

Didactical Research on Integration: A Brief Overview

The topic of integration and integrals plays a major role in most calculus courses around the world, and are often described, together with limits and derivatives, as one of the main ingredients of such courses (Bressoud et al., 2016; Larsen et al., 2017). Educational research has been carried out, focusing on both the teaching, and learning of integrals, and in this section, we will mainly focus on literature that we find to be of direct relevance for our study. Related to our section above, on infinitesimals, Bressoud (2011, 2019) points to the discrepancy between the sequence the different topics in calculus historically developed, and the sequence these normally are taught in higher education. He suggests reordering the sequence, so that students early in the calculus courses get familiar with the core ideas of integration, namely by estimations through the sum of area of bars, rather than to start with limits and then introduce integration through limits of Riemann-sums. Several researchers have followed the idea of introducing the concept of integrals through such estimations and alludes to ideas of differentials and infinitesimals instead of limits. This could be exemplified through “an informal approach to infinitesimals” (Ely, 2017) and DIRACC (Developing and Investigating a Rigorous Approach to Conceptual Calculus) (Thompson, 2018). In DIRACC one emphasizes that variables vary smoothly, and that differentials are variables. Differentials are conceptualized by letting 𝑥 vary “by $dx$ through intervals of length $\varDelta x$” and be letting $dy$ vary “at a constant rate with respect to $dx$” (Thompson, 2018, p. 2). Ely (2017) approaches differentials in similar terms, by letting the differentials refer to actual, small quantities that varies. The underpinning theory of hyperreal numbers, briefly mentioned in the previous section, is not made explicit to the students and the approach is therefore labeled as an “informal infinitesimal approach” (p. 155). Drawing on studies from the U.S., including Thompson (2018) and the DIRACC project, Ely (2021) discusses such approaches further and points to the aim of a more direct referential meaning, for example by letting $dy/dx$ be “an actual quotient rather than code language for $\underset{h\to 0}{\text{lim}}\frac{f\left(x+h\right)-f\left(x\right)}{h}$” (p. 591). Common to both Thompson’s (2018) and Ely’s (2017) suggestions for teaching, is that differentials are treated more in line with the historical origins and development of these concepts, emphasizing infinitesimals and differentials rather than limits, as opposed to what commonly is preferred in modern calculus textbooks. In this sense, this also strongly relates to the ideas of Bressoud (2011, 2019). Further, Thompson and Silverman (2008) argue for the importance of students to regard the integral as an accumulation function, and that this is crucial for their understanding and conceptual development. This is of particular importance since students tend to neglect the accumulated “bits”, represented by the products in the accumulated sums (Thompson & Silverman, 2008). This point is also raised in Kouropatov’s (2016) dissertation, where a teaching unit is developed and implemented, suggesting that students could benefit from approaches emphasizing the accumulative aspect of integrals. The idea of focusing more on integrals as accumulation functions of actual sums, are also put forward by González-Martín and Hernandes-Gomes (2017), who points to the contextual differences of how integration is implemented respectively in textbooks for professional engineering courses and the traditional calculus courses. Since the students involved in our study all attended engineering study programs, this point becomes highly relevant.

From a student perspective, some research has been carried out with several foci. A rather old study from Tall (1980), where students’ interpretations of differential notations was investigated stands out as particular relevant to our research. 60 first-year university students were asked about the symbols in the expression $\frac{dy}{dx}=\underset{\delta \to 0}{\text{lim}}\frac{\delta y}{\delta x}$. The following interpretation of $dy$ were offered (Tall, 1980, p. 2):

$dy$ has no meaning by itself $\left(15\right)$

$dy$ means “with respect to $y$” (as in integration) $\left(7\frac{1}{2}\right)$

$dy$ is the differential of $y$$\left(7\frac{1}{2}\right)$

$dy$ is an infinitesimal increase in $y$$\left(11\frac{1}{2}\right)$

$dy$ is a “very small” or “smallest possible” increase in $y \left(4\frac{1}{2}\right)$

$dy$ is the limit of $\delta y$ as it gets small $\left(6\right)$

No response $\left(8\right)$

The number in each parenthesis is the number of student responses, and the $\frac{1}{2}$ represents students that gave more than one answer. This overview demonstrates that even though about half the students only showed procedural meanings, a considerable amount also offered conceptual interpretations. Without being provided with a formal approach to infinitesimals prior to the survey, 22 students were still placed in the three latter categories that contained “pre-conceptual infinitesimal notions” (p. 2). These findings relate to Thompson (1994), which investigated students reasoning through problems involving differentials, and suggested that students, through practical tasks involving differentials, demonstrated to possess some basic preconceptions that could be built upon in the introduction of integrals and differentials. Although limits also were briefly discussed by Tall (1980), Oehrtman (2009) conducted a study involving 120 students from an introductory calculus course. All these students completed a pre- and post-course survey, consisting of limits in various problems, and clinical interviews were conducted on nine of these students. Among Oehrtman’s (2009) main findings was that students turned out to have different metaphors for limits. One of these metaphors was the so-called “collapse metaphor, where students justified “the fundamental theorem of calculus by describing a volume collapsing to an area, or an area collapsing to a length” (p. 420). In the case of “the limit (e.g., the thickness of a slice $\varDelta h$) going to zero, this dimension was ultimately to vanish in a “collapsed” object of reduced dimension” (p. 410). In the case of definite integrals, such metaphors could result in students imagining the Riemann integral “graphically as a “sum” of infinitely many one-dimensional vertical lines over the interval $[a,b]$, extending from the $x$-axis to a height $f\left(x\right)$ and produced by a collapse of two-dimensional rectangles from the Riemann sums as their width becomes zero” (p. 413). Variants of this type of reasoning could also be observed frequently in our study. Related to limits, Oehrtman (2009) identified “approximation metaphors” as the most common, where students in different ways expressed an awareness of magnitudes to the limit process getting closer and closer, always with a certain error margin. For such metaphors, Oehrtman (2009) draw parallels to the historical development as “they comprise much of the historical motivation for calculus” (p. 414).

Related to definite integrals, several studies focus on students’ general conceptions of integrals (e.g., Hong & Thomas, 1997; Mahir, 2009; Orton, 1983; Rösken & Rolka, 2007). In these studies, students’ conceptions of integrals and techniques, through specific tasks and questionnaires were investigated. Jones (2015) presents a survey on 157 university students from two universities in the U.S., that had just completed a first-year calculus course. The questionnaire consisted of four open-ended questions, aiming to grasp the underlying meanings of definite integrals. His findings suggest that students tend to interpret definite integrals as either an area or an anti-derivative, rather than “multiplicatively based summation ideas” (p. 721). These three main categories of students’ ways of understanding integrals (area-, antiderivative- or sum-based interpretations) also influenced on Ely’s (2017) descriptions and further elaboration of these categories. Inspired by Jones’ (2015) and Ely’s (2017) grouping, this made us focus our follow-up questions almost entirely on aspects belonging to the third category, as this emerged as the most relevant, from a conceptual point of view. A study from Wagner (2018) stands out with a particular resemblance to our study and findings, as he sought to investigate the relations the students made between Riemann sum-based reasoning and solution processes relevant through applying the antiderivative, as presented in the FTC. Through relevant tasks and problems, he interviewed two groups of students studying physics: eight beginning students formed one group, and seven upper-level students, in their third year, formed the other. Wagner (2018) found that common to all these students was their inability to connect Riemann sums with anti-derivatives, and he concluded that “too many students dismiss Riemann sums as an unpleasant stepping-stone to be endured in a curriculum whose goal was really to get to the FTC” (p. 354). Although our study has similarities to Wagner’s (2018) study, our focus was on the definitions and sense-making of the symbols involved in FTC, and their interpretations of the underlying ideas such as infinitesimals, differentials, and limits. So, rather than to investigate their ability to actively use and compare respectively Riemann-sums and anti-derivatives when solving problems, we aimed for insights into students’ more general interpretations of symbols, and through such interpretations make them reflect on the very conceptual issues and connections. While Wagner (2018) focused on “how the students understand the process of using Riemann sums, and how they understand the computational process of evaluating a definite integral” (p. 331) we focused on students’ general interpretations of symbols and definitions. This seeking of students’ interpretations of definitions was operationalized for example through asking the students about the relation between definite integrals and area (as opposed to Wagner’s (2018) focus on the relation between the definite integral and Riemann sums). To sum up, based on the literature above, our research is meant to add to the already existing body of literature that promotes innovative approaches to teaching, by focusing on it from a student perspective.

Theoretical Framework for the Study

From a social constructivist’s perspective, we consider the learning of mathematics primarily to be an individual cognitive process, shaped by the social interaction with other human beings (Ernest, 1998; Jaworski, 1994). This perspective could be linked to “symbol interactionism”, since, according to Ernest (1998), “semiotic tools and rhetoric in learning mathematics stresses the transformations of signs”. The foundations for symbol interactionism were elaborated by Blumer (1969), where one important premise is that “the meaning […] is derived from, or arises out of, the social interaction that one has with one’s fellows” (p. 2). Other important premises for symbolic interactionism are that one acts based on meaning and that such meanings are “handled in, and modified through, an interpretative process used by the person in dealing with the things he encounters” (Blumer, 1969, p. 2). Our research should be understood in the light of these premises, as students’ meaning making are captured through the formulation “students’ interpretations”, in our research question. The students’ interpretative processes when dealing with the FTC should be viewed in direct relation to Blumer’s (1969) premises (quoted above) and constitutes the focus of our forthcoming analysis.

In our detailed analysis of students’ interpretations, we draw on Duval’s (2006) terms “treatments” and “conversions”, with an emphasis on the latter. When defining these terms, Duval (2006) make use of the term “registers”, which could be understood as main categories of representations, for example numbers, algebraic symbols, geometrical figures, or graphs. While treatments are defined as “transformations within the same register” (p. 111), and involves for example calculations and symbol manipulations, conversions are transformations from one register to another. A conversion is “more complex than treatment because any change of register first requires recognition of the same represented object between two representations whose contents have very often nothing in common” (p. 112). Further, “when a conversion is congruent the representation of the starting register is transparent to the representation of the target register. In other words, conversion can be seen like an easy translation unit to unit” (Duval, 1999, p. 10). Contrary, non-congruent conversions could not be carried out in a similar and transparent manner. Whether a conversion is congruent or non-congruent will also depend on the direction in which the conversion takes place. In students’ efforts of explaining the meaning of the notations involved in the FTC, conversions took place, by converting mathematical symbols into verbal language. Conversions from mathematical symbols into iconic representations like drawings or graphs were also sometimes included in students’ interpretations, as some students made use of illustrations and graphs to visualize the meaning of certain symbols, like for example differentials. A non-congruent conversion of particular interest in our study was related to interpretations of the differential $dt$ as “an infinitely small magnitude”. According to Duval’s definition this is non-congruent since one cannot “draw” something that is infinite small. It is therefore not possible to fully visualize through a figurative representation, like one can through the use of symbols. This non-congruent nature of the conversions between limits of Riemann-sums and drawings of series of bars will be further investigated in our analysis. The terms “conceptual” and “procedural” are used in accordance with Hiebert and Lefevre (1986), where conceptual knowledge is a “connected web of knowledge, a network in which the linking relationships are as prominent as the discrete pieces of information” (p. 4) and procedural knowledge is understood as “algorithms, or rules, for completing mathematical tasks” (p. 6).

To depict conversions and the meaning that students assigned to them, we found it useful to also apply Steinbring’s (2005) epistemological triangle. In Steinbring’s model one considers each sign (or symbol) to be associated with a “reference context” and a “concept”. The reference context represents what the sign or symbol may refer to, and concept is the mediated epistemologically grounded mathematical meaning, gained from the interplay between the reference context and the signs. Based on this, one could also construct semiotic chains where one can “draw up a sequence of epistemological triangles for the interaction, or a sequence of learning steps to reflect the development of interpretations made by the subject” (Steinbring, 2005, p. 23). Combined with Duval (1999, 2006), this analytical tool enables us to trace and identify conversions in students’ interpretations as parts of a continuous argument. In addition, the reciprocal effect between “symbol” and “reference context”, also provides some explanatory power related to how the students interpret the mathematical object at hand. Except from one occasion, we do not explicitly depict the chain of epistemological triangles in our analyses, but we are frequently referring to the interplay between “symbols” and “reference context” in our analysis.

Methodology

Methodologically, our qualitative study is rooted within the interpretivist’s paradigm, where the research aims to “grasp the subjective meaning of social action” (Bryman, 2016, p. 692). Within this paradigm we take on a phenomenographic research tradition, focusing on students’ subjective experiences and a descriptive presentation of these (Patton, 2002). Adapted to mathematics education, we draw on Neuman’s (1999) accounts, where he states that the intentions with the phenomenographic approach “is to map the variation of ways a phenomenon can appear” (p. 102). In line with this, we aim to seek insight into university students multifaceted interpretations of differentials, infinitesimals, limits, and definite integrals.

Research Design

Our study was designed as a case-study, involving first-year engineering students attending the same calculus class, but from two different engineering programs, respectively the mechatronic- and computer engineering programs. Together with the teacher responsible for the actual course, a mandatory set of tasks was designed for the students, meant to be solved in groups. Four of the groups, two of which included students from the mechatronic engineering program and the other two containing students from the computer engineering program, were observed while working on these tasks for two hours. The study was conducted in the middle of the first semester at the university, and the topic of integration had just been completed. 15 students volunteered for individual interviews, subsequent to their group work, whereof seven attended the mechatronic engineering program and eight attended the computer engineering program. In this article, we will mainly focus on the interviews. The students were interviewed individually for about 40 min through semi-structured interviews. During the interviews, the students were asked to describe the content of the FTC, as displayed in the textbook, in their own words. A reproduction of the FTC, as displayed in their textbook is provided in Fig. 2.

Fig. 2

The Fundamental Theorem of Calculus as presented to the students (adapted from Adam & Essex, 2018, pp. 313–314)

After a “free” interpretation of the FTC, where the students were asked to account for the theorem in their own words, the students were asked to interpret the symbols $dt$ and $dx$. During the interview, all the students were also asked about the relation between the integral and area. This main structure was kept for all the 15 students, but the content of the dialogues to some extent varied depending on the students’ responses and what they individually specifically brought up. The interviews mainly followed the principles of task-based interviews as suggested by Goldin (2000): (1) Posing the question, (2) Minimal heuristic suggestions, (3) The guided use of heuristic suggestions, (4) Exploratory, metacognitive questions (p. 523). Follow-up questions were mostly based on the students’ own statements. All the interviews were voice recorded and transcribed, and the students were given pseudonyms, revealing only their gender. In addition to the methods described above, we observed all 10 lessons devoted to the topic “integration”, through video recordings. In this paper these observations are only used to provide a brief contextual background, accounted for below.

Glimpse from the Students’ Educational Context and the Limit-Based Approach to Definite Integrals

It is not our intention to create a dichotomy between limit-based reasoning and infinitesimal reasoning, since it could be difficult to make clear distinctions between the multitude of underlying ways of reasoning when it comes to these terms. For example, limit-based reasoning builds on the ideas of approximation, as argued for by for example Oehrtman (2009) through students’ use of “approximation metaphors”. The same is also the case for infinitesimals. From students’ utterings alone it could therefore be difficult to categorize one specific type of reasoning, on the expense of the other, and one should not neglect the fact that several interpretations could be inferred. On the other hand, the Riemann integrals’ emphasis on an “upper” and “lower” limit in principle offers a rather different approach to definite integrals than the infinitesimal approach, in terms of a series of rectangles with an “infinitely small” width. To illustrate what we denote as a “rigorous limit-based approach” to integrals, we present two excerpts from the students’ textbook. Both examples were presented by their teacher in the lessons, which to a large extent was the case with the rest of the content and chronology of the textbook’s integration chapter. Hence, the following examples could be understood as partly representing how the Riemann-integral was presented to the students (Fig. 3).

Fig. 3

Lower- and upper Riemann sums for $f\left(x\right)={x}^{2}$ (Adams & Essex, 2018, p. 303)

In this example, one observes how the partitioning was constructed, namely by letting $\varDelta x=a/n$. Subsequently, the upper and lower Riemann sums were calculated, resulting in respectively two different expressions. In the next example, these results are used to find the Riemann integral (Fig. 4).

Fig. 4

A limit-based approach to finding the definite integral ${\int }_{0}^{a}{x}^{2}dx$ (Adams & Essex, pp. 304–305)

The results in the example above are carried out solely through known procedures for calculating limits, and the meaning assigned to ${\int }_{0}^{a}{x}^{2}dx$ is attained through limits, as acquired in the first example. The approach to definite integrals provided from the examples above, where definite integrals are defined through limits of upper and lower Riemann sums, illustrates what we denote as the “rigorous” limit-based approach to definite integrals. Furthermore, when we apply the term “limit-based interpretation” in our analysis, it is this interpretation we are alluding to, although other perceptions of limits are possible.

Data Analysis Strategy

Transcribed data from the student interviews were coded through several stages. First, we applied an open coding, to get a sense of what our data contained. We gave the passages different labels, in terms of keywords describing core issues in our data. After identifying core issues, like “infinitesimal reasoning” and “integral as a sum”, et cetera, we went through the data again, by an axial coding process, described by Pidgeon and Henwood (2004) as the “exhaustive coding of the intersecting properties of core conceptual categories” (p. 640). This was an important step, which to a large extent informed the exact phrasing of our research question. Performing this coding enabled us to discover relations between how symbols was interpreted, and how these syntactically was related to other concepts and ideas. When we got to the stage of axial coding, the general codes that emerged fit very closely with the constructs of “reference contexts” and “conversions” from the literature. Therefore, even though we had not decided ahead of time to use these codes, we adopted these categories. This resulted in the development of two main categories, inspired by our theoretical framework, namely reference contexts for differentials in definite integrals and conversions between definite integrals and areas. It is important to stress that these main categories were colored by our theoretical lenses, presented in our theoretical framework section, and were not a direct result of the empirical data alone. A third phase of selected coding was then performed, based on these categories, which resulted in the emergence of different sub-categories, as depicted in Table 1. To ensure the validity of our findings, both authors of this paper carried out the open and axial coding individually, while the selective coding was primarily carried out by the main author, who also conducted the student interviews.

Table 1 Overview of the categories applied in the analysis

The categories displayed in Table 1 should not be interpreted as strictly hierarchical, meaning that a preceding category is contained in the next, in a successive manner. Still, to a certain extent, this was often the case. For example, students that regarded $dt$ as width of a bar approaching zero would probably recognize the symbol $dt$ from differentiation and in a sense belong in the category of association with differentiation as well. Successively, several of these students would offer procedural interpretations, as in the preceding category. However, in several cases we lack sufficient data to conclude in this manner, and the nuances in students’ interpretations sometimes enlightens very different aspects. Therefore, this categorization should be viewed more like an attempt of sorting and systematizing our data, rather than a tool for categorizing the students by different labels.

Results and Analysis

We systematize our analysis through the main categories “reference contexts for differentials in definite integrals” and “conversions between area and integrals”, and the belonging subcategories presented in the “Methodology” section. “Reference contexts” points to Steinbring’s (2005) term, as accounted for in our theory section, and deals with students’ ways of making meaning to the symbols related to differentials. “Conversions” alludes to the terminology from Duval (2006) and focus on how students in different ways argued for the symbolic notations involved in the FTC, in relation to areas. Further, we have selected excerpts from the transcripts with the aim of covering the diversity in the students’ interpretations rather than analyzing students one by one. This is primarily done due to space limitations, but also because many students share certain reference contexts. For the sake of painting a better picture, we provide an overview of all the 15 engineering students that participated at the end of our analysis section. Our goal is to provide both an intrinsic analysis of the students’ interpretations and a general overview.

Reference Contexts for Differentials in Definite Integrals

During the interviews, all students were asked to interpret $dt$ and dx the way they understood these symbols as applied in the FTC, from their own point of view. Below we provide examples from all the subcategories that emerged from the main category, during our analysis.

Procedures and Conventions

This category aims to grasp students’ interpretations of the symbol $dt$, where $dt$ is interpreted as a procedure or a way of writing without being related to other notions. Common to these interpretations is that the reference context only consists of a procedure or an action to be carried out.

Robert: At the end it says $dt$, so that is basically all between that $S$ and the $dt$, which is what actually should be integrated, and in this case, this is $f$ of $t$. Since it is $dt$ instead of the usual $dx$, that means that it should be in relation to, or with respect to $t$. So not just the standard $dx$ but specifically for $dt$.

Robert interpreted $\int$as the starting point and $dt$ as the endpoint of “what actually should be integrated”, which in this case is the function $f\left(t\right).$ Further, he emphasized that the $t$ in $dt$ alludes to what “it should be in relation to, or with respect to $t$”. The interpretation solely seems to be linked to the procedure of integrating a function, by finding its antiderivative, and no other interpretation of $dt$ was offered by Robert.

Tara: I am very bad at such substitutions, like delta $t$, of $d$ of $x$, I think this is very difficult […]. I would guess it is just the way we write it, with respect to $t$.

Tara expressed her uncertainty by relating $dt$ to the reference context of “substitutions”, probably by recognizing that this expression is often used in such tasks and examples. She ended by interpreting $dt$ as a convention, by saying “I would guess it is just the way we write it”, adding also the procedural aspect “with respect to $t$”.

Associations with Differentiation

By “associations with differentiation” we refer to interpretations involving that the students in different ways drew parallels between $dt$ and differentiation and derivatives. Possibly, the students have been using differentials to express the derivative, in terms of $\frac{dy}{dx}$ or $\frac{d}{dx}f\left(x\right)$, and might recognize and associate the $dt$ with such expressions. We let Milo represent this group of students, as his statements contains the main aspects that were found among the students fitting this category.

Milo: I have reflected a bit on if that $d$ actually is delta, change in $x$, but I have understood this as yes, but no, maybe not quite

Interviewer: Could you elaborate a bit more here?

Milo: [draws a graph, a point, and a corresponding slope]. When you take the derivative, you have a graph, and then you have the triangle here in this little area, and then you have delta $x$ and delta $y$, change in $x$ and change in $y$, which you use to differentiate. And then I wondered if that’s taken further, to this notation, and that this actually would have been delta $y$ delta $x$ f of $x$, but I realize that this probably is not quite correct, and I have thought that this is just the way it is.

In addition to differentiation as a reference context for $dt$, Milo hypothesized that $d$ “actually is delta”, entailing a “change in $x$”. To illustrate this, he converted the symbolic notations into an iconic representation by drawing a graph and marking a point. He then added the line in which forms the slope of the graph in the marked point, and he drew a triangle indicating the $\varDelta y$ and the $\varDelta x$ in “which you use to differentiate”. His thoughts about this, “taken further”, through the symbol $dt$ are somewhat unclear, and he ends up by expressing uncertainty about his comparison. Milo’s interpretation offers a possible link between $dt$and $\varDelta t$. Furthermore, exemplified through his illustration of the slope, that such expressions possess the ability to “change”.

Width of a Vertical Line

Through the interviews, several students used “width of bars” as reference context for interpreting $dt$ and $dx$. Since this reference context results in non-congruent conversions between the differential and the iconic representation of “width of bars”, when the width is made infinitely small, some of the students’ interpretations were directed towards physical interpretations like “poles” or vertical lines.

Sean: That is, in a way, what is the name again, like differentials, that is, in a way a small change in $t$, in a way. I guess you can say.

Interviewer: Ok, what kind of change is this?

Sean: It’s an infinitely small change, I think […] you could say that it only becomes the height of the graph in a way, it might be something there, I don’t know [laughs].

As one of very few students, Sean actively used the word “differential” in his interpretation and described this as a “small change”. When asked what kind of change this is, he described it as “an infinitely small change”. Up to this point, Sean’s descriptions were much in line with infinitesimal-based interpretations. However, when the interviewer challenged Sean on the nature of this change, Sean seemed to conceptualize this as “becoming zero” instead of “approaching zero”, which resulted in a reference context consisting only of poles, or vertical lines. The same is observed through Michaels accounts:

Michael: I don’t really like this – I understand that we think of it as an infinitely small bar, but in my world, this is just a line.

Both Michael and Sean seemed to be aware that their interpretations of vertical lines were problematic. In Sean’s case this doubt was expressed through laughter and by adding “it might be something there, I don’t know”. Through the statement “but in my world, that is just a line”, Michael also seemed convinced that something was problematic with this interpretation.

Width of a Bar Approaching Zero

The previous category, “width of a vertical line”, could in some sense be described as a special case of this next category. Here we collected interpretations pertaining to differentials being interpreted through the reference context of width of bars that approaches zero, without explicitly being regarded as problematic from the students’ point of view. The students expressed the “approaching zero”-aspect in different ways, for example “eternal small” or “infinitely small”, and common to the interpretations in this category was the decrement of differentials, towards small magnitudes or infinitely small magnitudes.

Mateo: Yeah, that is the given width […] because it is when the widths approach infinitely small, and you add this, then it is a certain accuracy, or it has to be a certain accuracy when they become infinitely small, because then [silent].

Interviewer: So, if this $dt$ corresponds to the width, what can we say about the width then?

Mateo: Yeah, that is infinitely small.

From Mateo’s way of reasoning, and his use of plural form (“widths”) one can observe that $dt$ was interpreted through an iconic representation, in terms of $dt$ being the width of a series of bars, and that his statement “it has to be a certain accuracy” referred to the total area made up of such bars. In such bars, $dt$ is a width that “approaches infinitely small” which results in a “certain accuracy”. Mateo’s interpretation also entailed that $dt$ is the end-result of a varying magnitude (the widths) and something that has the characteristics of being “infinitely small”.

Elias: The practical is that from $a$ to $x$ we should integrate the function $f$ of $t$, with respect to $t$. But you also have the picture, you have a row, in a way, of bars, from $a$ to $x$ in this case, and the width of those bars that are $dt$, and we should sum them up when dt approaches zero […]

Interviewer: And how does what you just said connects to the $dt$?

Elias: We had the width of the bars, and when it approaches zero, then we get the perfectly estimated value.

Interviewer: But this $dt$, is that related to delta $t$ in some sense?

Elias: […] $dt$ is only the notation for saying that, yes, now delta $t$ has approached zero. So, then it is wrong to say that $dt$ approaches zero.

Elias’ interpretations were much in line with Mateo’s, but he started by describing what he denotes as “the practical” interpretation, in accordance with our first category “procedures and conventions”. Then, in similar terms as Mateo, he explicitly related $dt$ to the width of bars. However, Elias initially stated that “$dt$ approaches zero”, which differs from Mateo that consequently described $dt$ as “infinitely small widths”. It is therefore interesting to notice how Elias corrected this himself, when he was asked about the relations between $\varDelta t$ and $dt$, in terms of “$dt$ is only the notation for saying that, yes, now delta $t$ has approached zero. So, then it is wrong to say that $dt$ approaches zero”. Hence, reference contexts for respectively $\varDelta t$and $dt$ are slightly different, with $dt$ acting as the end-result of an approximation process.

Conversions Between Definite Integrals and Areas

Through this second main category “conversions between definite integrals and areas” our aim is two-folded. On the one hand, to present the students’ reflections on the conversions from definite integrals to areas. On the other hand, we attempt to capture if and how students used their interpretations of differentials (in the first main category) when accounting for the conversions between integrals and areas.

None or Procedural

Several of the students provided none or only procedural interpretations concerning the conversions between definite integrals and area.

Anna: I’m a bit on just passing the exam, instead of just contemplating on everything, because I don’t feel I have the time to understand everything. How things work. Then I don’t feel I would handle the time-pressure we have at school, I only have to get used to see and to recognize. So that you get the feeling of what to do.

We let Anne represent the six students’ that did not offer any mathematical justifications on the conversions between integrals and areas. Like Anna, several expressed their lack of capacity to engage with “how things work”. For these students it seems to exist an underlying premise in their answers, that being able to solve integration tasks by using procedures and techniques are more important than the conceptual aspects.

Sum of Areas of Bars

In this category we have collected interpretations that are not explicitly linked to differentials or limits, but somehow refer to integrals as sums of bars.

Mateo: That is because you multiply up a $y$-value, or a $f$ of $x$-value, with a given $x$, or a width, which you sum up until you get a total area under the curve.

Mateo was pointing to the sum of area of bars when reflecting on why the integral results in an area. By the statement “you multiply up a $y$-value, or an $f$ of $x$-value, with a given $x$, or a width” Mateo could be misinterpreting the $x$-value to equate the ${\Delta }x$, since he seems to describe $x$ as “a width”. Another possible interpretation is that Mateo is just trying to clarify the meaning of “$f$ of $x$”, which in turn should be summarized. However, if this is the case, the role of the “width” becomes unclear.

Steven: Well, we started before we used this sign [points to the integral sign] then we thought about this as the sum of several bars, under the graph, and the area of those altogether would then be the same as the area under the graph, and integration is an accurate method for the exact area while the bars are an approximation.

By the statement “we started before we used this sign” Steven’s reference context probably referred to prior teaching sequences, where sums of series of bars were calculated (see Figs. 3 and 4) by the use of ${\Sigma }$ (later in the interview Steven denoted ${\Sigma }$ as “E”). By stating that “integration is an accurate method for the exact area”, Steven came close to a sum-based area-definition of integrals, but he was not offering detailed descriptions of how the area of such bars are calculated.

Sums of Areas of Bars Involving Infinitesimals

This category contains students’ that somehow employed reasoning involving infinitesimals or differentials in addition to the sums of areas of bars.

Tara: I think that has something to do with the distribution, or that you take this bar distribution, only with very, very small bars and that you don’t get this deviation on what is outside.

Even though Tara described this in everyday language, she indirectly alludes to the use of differentials through her description of “very, very small bars”. She probably simplified her description, and did not mention sums, but instead she said, “I think that has something to do with the distribution”. It is possible that she visualized a row of bars, covering a certain area, but she did not actively make use of the function value or the width of bars, in her descriptions.

Sam: Well, that is the sum of these quadrangles that you make, for $f$ of $t$ multiplied by $dt$. And then you get the area […] but when you take the integral, then you make a lot of them, or eternal many. Because I guess that is the definition, that you take the sum from, eh, when it approaches infinity.

In the last sentence of the excerpt, Sam demonstrated that he saw a connection between areas and sum-based definitions of definite integrals. He emphasized that “when you take the integral, then you make a lot of them, or eternal many”. Sam is the only student that explicitly is referring to the definition, in terms of “that you take the sum form, eh, when it approaches infinity”. This is an allusion to the sum of quadrangles, mentioned at the beginning of the excerpt, where these quadrangles are described as “$f$ of $t$ multiplied by $dt$”. Sam did not define the variable $t$, but in his first sentence $dt$ represents the width of the quadrangles.

Limit-Based Interpretations

To fit this category, students had to somehow relate integrals to the Riemann definition, in terms of a value between a lower Riemann sum, $L(f, P)$and an upper Riemann sum, $U (f, P).$ This is not to say that interpretations in the categories above do not involve types of reasoning that relates to limits, or could be built on in that sense (e.g. Oehrtman’s (2009) “metaphors for limit”). However, based on our empirical data and the approaches observed (see Figs. 3 and 4), we found it useful to make a distinction and investigate if what we denote as “rigorous limit-based approaches” could somehow be traced in students’ responses. Only two out of the 15 students came up with such description, even though this was emphasized both in teaching and in the textbook used.

Mattew: I know that when you have an upper-bound and a lower-bound and that when you get one minus the other, then it should equate the area under a graph, and that when you know the area of something, you could formulate this as an equation.

Even though Mattew were rather broad and imprecise in his descriptions, he mentioned a lower-bound and an upper-bound. However, instead of referring to the area as something in between, he mistakenly stated that “when you get one minus the other, then it should equate the area under a graph”. He continued with saying “when you know the area of something, you could formulate this as an equation”. Here it is unclear what he meant, but he might think of the antiderivative, as displayed in the FTC.

Jack: Wasn’t that that he found that if you took upper part, or the sum of upper part of these rectangles, and then you also have a lower part, then you will have a kind of estimated value of what the area is, below the curve […] you will never get it exact. But if you want it pretty accurate, then you can put infinitely many rectangles underneath, and then you will have a pretty accurate answer, but you will not get it complete accurate.

Interviewer: But if you have infinitely many, will you not get it completely accurate then?

Jack: I thought it was an infinitely small error.

In Jacks first uttering, he described the area as related to upper- and lower bounds, in similar terms as Mattew. As a response to the question of accuracy, his explanations related to our category “sums of areas of bars involving infinitesimals”. The idea that there exists an accurate value, which the integrals approach by decreasing the distance between the lower- and upper bound, as described by Jack in his first statement, was not made explicit when Jack continued his reasoning. His last remark, “I thought it was an infinitely small error” seems to be more in accordance with an infinitesimal way of reasoning.

Table 2 is meant to represent a simplified overview of how the students’ interpreted differentials, and how they were interpreting the conversions between definite integrals and areas. In accordance with our descriptions earlier, categories could be overlapping and contained in each other. This table should therefore only be understood as a way of structuring our findings, in line with our descriptions provided in the data analysis section. Still, a tendency here seems to be that the level of complexity and refinement in students’ interpretations of differentials to a large extent was mirrored in students’ interpretations of definite integrals in general.

Table 2 Overview of the students’ interpretations

Discussion

In this section we synthesize our findings from the analysis by discussing the main content from our two overarching categories “reference contexts for differentials in definite integrals” and “conversions between the integrals and areas”. In an attempt of gaining a holistic understanding of our empirical data, we will mainly focus our discussions on the relations between the different categories.

According to Thompson (1994), a developed concept of differentials is crucial to students understanding of definite integrals. From our analysis, one can observe that students offer various interpretations of the differential notions $dt$ and $dx$. 7 out of the 15 students seemed to focus on differentials as a convention or a description of a procedure to be carried out, which is in accordance with for example the findings from Tall (1980). This might have different reasons, but an explanation for this could be the focus on integration techniques, through routine tasks. To solve such tasks, it is often sufficient to hold a procedural interpretation of differentials, in terms of integrating “with respect to $t$”. This is also in line with the results from Knutsen (2020) on upper secondary students, which to a large extent motivated this study. Another explanation might be the vestigial use of the symbols $\int$ and $dt$ in Riemann integrals, as pointed out by Ely (2017). Since Riemann integrals are defined as a limit between lower- and upper Riemann sums, there is a discrepancy between the symbols applied in the FTC, and the meaning for example Leibniz attributed to these. The challenge of not conceiving $dy/dx$ as a quotient $\left(\frac{dy}{dx}\right)$, is problematized by Ely (2021) in what he describes as a “code language” for limits (p. 592). The point of differentials being a code language for limits, could also be made for $dx$ in integration and limits of Riemann sums. The vestigial nature of symbols in the Riemann integral can manifest itself in several ways, but the most striking example was found in a passage from the interview with Michael.

Michael: You solve the integral, right, and then it disappears [refers to $dt$]. I never calculated with it. I never multiplied with it. It was just there until it suddenly disappeared.

The sudden “disappearance” of $dt$ could indicate that the vestigial nature of $dt$ not only prevents students from assigning a proper meaning to the notation itself, but also its role in specific tasks. For example, in substitution tasks, students treat differentials as if they are actual quotients. However, some student’s previous acquaintances with differentials are that they are not really fractions. In turn, such experiences might stand out as contradicting. This is exemplified later in the interview with Michael:

Michael: For example, when it says as its written here, $\frac{dt}{dx}$ [points to a substitution task from his notebook]. Then it looks like a fraction, and sometimes I can do calculations with it as if it is a fraction, but not always.

As reflected in our analysis, in the sub-category “width of bar approaching zero”, students showed clear signs of relating differentials to actual quantities in terms of a width of a bar becoming smaller and smaller. This interpretation is in a reciprocal manner also mirrored in their reflections on definite integrals in the sub-category “sum of areas of bars involving infinitesimals”. Since this seemed to be the natural way of reasoning for many students, despite being exposed to the Riemann approach, we regard this as a strong argument for building further on this in the way calculus are being taught. By letting $dt$ represent actual quantities, one could expect an infinitesimal approach to be more productive for students’ understanding. Infinitesimal-based approaches to calculus, where differentials are treated as real quantities has been applied in teaching, for example by Thompson and Milner (2018), were one regards differentials as variables by letting $x$ vary “by $dx$ though intervals of length $\varDelta x$” (p. 2). By treating differentials in this manner, one could also achieve clearer envisions of integrals as accumulation functions. According to Thompson and Silverman (2008), seeing integrals as an accumulation function is crucial for students’ conceptions of definite integrals. Related to this issue, it was a bit surprising that as many as 7 out of 15 students did not offer any explanations on the conversions between integrals and areas. Since areas are included in the very definition of integrals, through the accumulative Riemann summation of “bits”, the students could in principle answer this question by simply just referring to the sum-based definition. However, an explicit reference to the definition was only made by one student. For the rest of the students, one can only assume a possible awareness of such a connection.

For students in the category “width of a vertical line”, the infinitely small magnitude was equated with zero. This led to a seemingly paradox, as $dx$ in the reference context of bars with decreasing widths, became zero, instead of approaching zero. These observations correspond to what Oehrtman (2009) describes as “collapsed metaphors” for limits.

In Fig. 5, we build on the conceptual framework from Steinbring, to construct a semiotic chain that illustrate students’ meaning making as the interplay between signs and reference contexts. The figure illustrates how juxtaposed bars are used as reference context for summation and differentials, and how these bars, by becoming more narrow, in turn provides the reference context for the definite integral and the symbols involved in the FTC. Trough the lenses of limit-based approaches, one should note that the conversion from $\int$and $dx$ into the iconic reference context of narrow bars, is non-congruent in a strong sense, as it fails to grasp the infinity aspect. The limitation of this reference context to some extent was manifested in students reasoning concerning “poles” and “bars with no width”. Ely (2021) points out that for example in physics, one always deals with actual magnitudes, although often very small, and that regarding differentials as such actual magnitudes is an advantage, rather than an obstacle. These points are also raised by Thompson (1994) and Kouropatov (2016), who promotes the idea of letting students get acquainted with differentials, rooted in actual physical problems. Linked to these kinds of approaches and utilization of infinitely small magnitudes as an entrance to differentials, the iconic conversions in Fig. 5 could have obtained a more intrinsic meaning related to what they represent.

Fig. 5

Semiotic chain of epistemological triangles to illustrate students’ interpretations of definite integrals and differentials

Students that offered an explanation on the conversions between integrals and areas mostly did this by alluding to sums of bars, but rarely in the Riemann sense, understood as a limit between lower- and upper Riemann sums. On the other hand, the bars provided by the students implied resemblance to the bars used by Leibniz. This also concerned the meaning they attributed, in the sense of the word “limits” rarely being explicitly used, and few students drew attention to upper and lower Riemann sums. Instead, by the exception of Mattew and Jack, the students frequently did use the word “approach”, although the nature of the “approached value” and its role in definite integrals, was not expressed in rigorous limit-based terms. This seem to be in line with Oehrtman’s (2009) study of students’ limit concept, where “approximation metaphors were the most ubiquitous metaphor revealed” (p. 421). Students placed in the “limit” category, expressed an awareness of the existence of some value between a “lower bound” and an “upper bound”. Although, when elaborating further on this, their terminology seemed to resonate more with infinitesimal descriptions. Further, we observe a strong relation between the way students interpret the differentials in the FTC and how they make sense of the conversions between integrals and area. That is, for six of the students in our study, $dt$ in different ways represents the width of a rectangular bar. For four out of these students, $dt$ represented an “infinitely small” width, which in this sense could be regarded as a “special case” of the more general width of these bars, ${\Delta }t$. In turn, the integral corresponds to the sum of all these bars. During our interviews we also came across some examples where the strict width of bar- approach to differentials seemed disadvantageous for some of the students’ syntactical interpretations, mainly linked to arclengths.

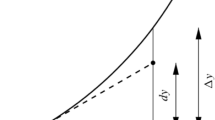
Michael: When you should find the integral of just the line. The curve in itself. And when the integrated no longer is the area. Then I have a problem connecting.

Integrals used to find arclengths constituted a challenge for Michael, as he did not manage to connect the sum of areas of bars-interpretation to the length of just the curve. This raises the question on whether a strict bar-interpretation of differentials and integrals, in some sense restrict students more general conception of differentials as mathematical objects.

In Fig. 6, concerning arclengths, the small “piece” is estimated by applying Pythagoras theorem to the differentials $\varDelta y$ and $\varDelta x$, and the total length is determined by the sum of all such $\varDelta x$ intervals. In this example the differential does no longer represent a width of a bar, as most often referred to by the students, but an interval, in a more general sense. A more general perception, where integrals are regarded as sum of differentials, rather than widths of bars, might therefore benefit students in the long run. One could imagine such development to take place if students were offered examples of differentials in several settings and contexts, as suggested for example by Thompson (1994) and Kouropatov (2016). The use of differentials in different settings might also give the students fitting in our sub-category “associating with differentiation” the possibility to refine their interpretations. Furthermore, it might enable them to describe the syntactical aspects, such as the common features of differentials and whether they appear in differentiation or in integration.

Fig. 6

Arclengths and integrals

Summary and Conclusion

Initially we posed the research question:

What characterizes first year engineering students’ interpretations of the symbols involved in the Fundamental Theorem of Calculus, with respect to differentials, infinitesimals, and limits, and how do these interpretations affect upon their interpretations of definite integrals?

Through our analysis and discussions, we found that among the students that offered conceptual interpretations, terminology consistent with infinitesimal approaches was prevailing when interpreting integrals, as the description of $dt$ or $dx$ as an infinitely small magnitude were mirrored in their ways of connecting definite integrals to areas. Only two students provided what we denote as “rigorous limit-based interpretations” of definite integrals, even though this approach was prevailing both in teaching and in the textbook used, as demonstrated in Figs. 3 and 4. We regard this as an important finding, as this could indicate that students’ reasoning has a lot in common with infinitesimal approaches as described in our historical and epistemological considerations, in our initial section. Students’ reference contexts when interpreting differentials and integrals were rather consistently linked to “width of bars” that served as a basis for sum-based approaches, where definite integrals were interpreted as sums of such bars. For four of the students, it was emphasized that the width of the bars should approach zero, which in turn was interpreted as becoming “infinitely small”. For two students, confusion occurred when they let the width of bars become zero resulting of an infinite sum of vertical lines, denoted by Oehrtman (2009) as “collapse metaphor”. Non-congruent iconic representations of this reference context are incompatible with the symbolic, and this might give rise to such “confusing” interpretations. Among the students that did offer interpretations on the conversion between the integral and the area, only one student referred directly to the definition, in terms of a sum-based approach, and it was unclear if the others just associate areas to sum-based interpretations or if they implicitly alluded to the definition. That as many as seven students did not offer any kind of mathematical justifications on the conversion between the integral and areas, we found a bit surprising and somewhat concerning. By analyzing textbook for both calculus courses and for specific professional engineering courses, González-Martín and Hernandes-Gomes (2017) found considerable discrepancies between textbooks used in calculus courses and textbooks used in professional engineering courses, as textbooks in professional engineering courses have a much stronger emphasis on sum-based applications of integration. In turn, as these findings suggests that a sum-based understanding of accumulative sums is essential for engineering students, and our findings related to the lack of accumulation interpretations among the participants in our study, to a large extent substantiate this concern. In Jones and Ely’s (2023) review of research literature on “quantitatively-based approaches to integration” (p. x), “adding up pieces” (AUP) and “accumulation from rate” (AR) are denoted as different paradigms. Dressed in these terms, our study suggests that AUP approaches dominated students’ interpretations of FTC. Compared to the limit approach, AUP has its advantages in modelling (Jones & Ely, 2023) and for example within an “Archimedean local model”, the partitioning could result in numbers that can be regarded as real-valued numbers, and hence more in line with the practical needs of engineering students (Oehrtman, 2023; González-Martín & Hernandes-Gomes, 2017).

From our point of view, the novelty of this study is achieved through the student perspective, and by allowing for rather free reflections on the meaning of symbols in the FTC, and interpretations of the relation between these symbols. To some extent our findings correspond with other studies (e.g. Wagner 2018) although our focus on symbol-interpretations provides more details on specific conceptual issues, such as differentials and the role these play in definite integrals. We conclude by emphasizing the infinitesimal-based approaches to definite integrals, which prevailed the interpretations provided by the students. The interviews revealed few traces of rigorous limit-based interpretations, although this approach was offered both in the textbook used and in teaching. It is our view that these findings could influence teaching approaches in ways that to a larger extent build on the conceptions (and preconceptions) that students possess. For example, historical, infinitesimal-based approaches could be built on to substantiate the core ideas of the more modern limit concept, so that notions such as $\varDelta t$ and $dt$ could be bridged in a conceptual more meaningful sense. One could describe the outcome of our research to somewhat be in line with phylogenetic perspectives, as promoted by Bressoud (2011, 2019), as infinitesimals and differentials historically preceded the development of the limit concept, and therefore for example could be used as a meaningful gateway into the formalization of definite integrals, in terms of more rigorous limit-based approaches. Our findings also substantiate the need for a developed differential concept, beneficial for grasping the idea of integration as accumulation functions (Kouropatov, 2016; Thompson, 1994; Thompson & Silverman, 2008; Thompson, 2018). Finally, out findings could support non-standard alternatives to Calculus teaching, like informal infinitesimal approaches as suggested by Ely (2017, 2021), but our results do not allow for definitive conclusions in such directions. Like Oehrtman (2009) suggests, a solution could also be to build more strongly on students’ acquainted ideas when limits are dealt with. A clear parallel in this sense could be made to definite integrals, where students could benefit from teaching approaches that more actively built on their own preconceptions and reference contexts.