The Limit Notion at Three Educational Levels in Three Countries

Abstract

This paper documents how the limit concept is treated in high school, at a university and in teacher education in England, France and Sweden. To this end we make use of vignettes, data-grounded accounts of the situation at the three levels in the three countries. These are analysed using the Anthropological Theory of the Didactic (ATD). While university praxeologies are relatively similar across the three countries, greater differences manifest themselves in high school and teacher education. For instance, at the high school level, in France a local praxeology on the limits of sequences is taught, which is not the case in England or Sweden. Results from the analysis of limits are extrapolated to comment on implications for the teaching of calculus, and for teacher education, in the three countries. The paper also raises methodological issues in our approach.

Introduction

This paper stems from a nascent international calculus database that we, the authors, manage, which currently has 14 national reports¹ of calculus at three levels: school; beginning university; and teacher education. In considering how to document similarities and differences in the reports we discussed our three countries (England, France and Sweden) and noted differences in approaches with special reference to the limit notion; our work on this led to this paper, which is guided by the following research question (RQ) and two follow up questions (FQ). The data analysis reported in this paper is directed towards addressing RQ. The paper also develops a methodological approach to addressing RQ and the Discussion section reflects on this approach.

RQ With regard to limits, what similarities and differences exist in the three countries at each of the three levels?²

FQ1 What does our response to RQ say about similarities and differences in the calculus taught in the three countries?

FQ2 What are the implications of our study for teacher education?

The paper is structured as follows. The literature review consists of two sections: the limit notion; and calculus around the world. This is followed by a presentation of the theoretical framework used, the Anthropological Theory of the Didactic (ATD), and the methodology we designed for the study. Then nine vignettes on limits in high school, university and teacher training in England, France and Sweden are presented. These vignettes form a basis for the ATD analysis. The discussion section addresses all three questions and is followed by a section on limitations and implications.

Literature review

The limit notion

“Limit” was not an explicit construct in the early development of calculus (e.g., Leibniz and Newton) but, since the “rigorous” formulation of the fundamental ideas of calculus in the 19th century, it is a (arguably “the”) central construct of calculus. In a first high school course in differentiation teachers may use an informal and dynamic language of limits, “the slope of the secant gets closer and closer to the slope of the tangent,” and may introduce limit notation, $\underset{h\to 0}{\text{lim}}\frac{f\left(x+h\right)-f\left(x\right)}{h}$. As “calculus” changes to “real analysis”, $\epsilon -\delta$ notation is introduced, for example, “a function $f$ approaches a limit $L$ near $a$” means: ${\forall _\varepsilon } > 0\,\exists \delta > 0\left[ {0 < \left| {x - a} \right| < \delta \Rightarrow \left| {f\left( x \right) - L} \right| < \varepsilon } \right]$.This static “language of limits” is a 19th century invention which was not present when calculus was invented. Educational studies on limits initially focused on students’ cognitive difficulties with limits. Calculus teachers have, undoubtedly, long known of these, but this knowledge was not the focus of research until the 1970s. Orton (1983) reports on student difficulties in finding the limits of numerical sequences and finding the limits of sequences expressed in general terms, for instance, $\frac{n-1}{n}$. Davis & Vinner (1986) published an early paper on students’ understanding of limits presented via $\epsilon -\delta$ definitions and commented on the now well-documented “temporal order” phenomenon, where “for every $\epsilon$, there exists a $\delta$…” is often internalized as “for every $\delta >0$, there exists an $\epsilon >0$…”. Monaghan (1991) reports on students’ problems with the language of limits, the interference of everyday meanings in the mathematical meanings ascribed to the terms “tends to”, “approaches”, “converges” and “limit”; the paper notes similarities to findings in some French studies, tend vers and limite (Cornu, 1980).

Barbé et al., (2005) focus on Spanish high school teachers’ problems in teaching the “limit of functions”. The study, using ATD, identified two disconnected mathematical organizations (MO): MO₁, related to the algebra of limits and calculations; MO₂ related to the limit definition and the topology of $\mathbb{R}$. Hardy (2009) uses ATD to examine instructors’ and students’ perceptions of the knowledge to be learned about limits of functions in a first Calculus course. Instructors’ perceptions could be modelled in mathematical terms but students’ choices for limit techniques were based on norms, e.g. “we do this because that’s what we usually do under the circumstances” (p. 355). In France, several studies have focused on sequences: Chorlay (2019) reports a design of a situation for introducing infinite limits of sequences in high school based on examples and aimed at setting the formal definition.

Calculus around the world

There are surprisingly few comparative studies on how calculus is taught around the world. Our search located: Törner et al., (2014), which includes brief overviews of calculus curricula and teaching in Belgium, Cyprus, England, France, Germany, Greece and Italy; Thomas et al., (2015), which examines key mathematical concepts in the transition from secondary to university; Bressoud et al., (2016), which includes overviews of calculus instruction in France, Germany, Uruguay and the USA; and, Bosch et al., (2021), which considers 10 case studies from universities in Canada, Denmark, France, Germany, and Spain to examine how the content of university programs is selected and structured. Further to these, a special issue of ZDM (volume 53, issue 3, 2021) on Calculus in High School and College Around the World, although not focusing on comparative studies, includes reports on calculus in Germany, Israel, Singapore, South Korea, Tunisia and the USA. We use the above to provide an overview of what is known about calculus around the world in schools, universities and teacher education courses. We note a bias towards European and North American accounts in this literature-base. We now consider each level.

School

With the exception of state schools in Peru, calculus is taught in high schools (HS) in every country mentioned above (and in our database) but it is not taught to all students in this category; to whom it is taught depends on the programmes offered (we do not have space to provide details). Törner et al., (2014) make an historical claim that three periods exist in the evolution of school calculus curricula:

The first period started at the beginning of the twentieth century and lasted until the start of the 1960s when modern mathematics appeared. The second period was dominated by the modern mathematics approach and lasted until the beginning of the 1980s. The third period is traced from the beginning of the 1980s to the present. (p.550).

The first period offered informal approaches to calculus. The second period emphasised $\epsilon -\delta$ definitions and proofs of theorems. The third period returned to the informal approaches of the first period. We return to this comment on the third period in the Discussion.

University

We restrict attention to the first year of university and note: (i) significant differences in what is covered in calculus/analysis courses in the first year, not least because most students who follow such courses are not mathematics majors; (ii) issues in the transition from school to university is a focus of mathematics education research (e.g., Thomas et al., 2015). These transition issues are linked to the first part of Klein’s (1908/1932, p.1) double discontinuity: (i) university students are “confronted with problems, which did not suggest […] the things with which he had been concerned at school”; (ii) When the same student becomes a teacher, “he suddenly found himself expected to teach the traditional elementary mathematics in the old pedantic way.” With regard to (i), a measure of difference is the extent to which a university Calculus course repeats high school calculus. For example, Bressoud (2021, p.531) states, “The United States has created a system in which the overwhelming majority of students […] take the same calculus course twice, once in the last year of high school and again in the first semester of university.” Bosch et al., (2021) focus on the first year of Mathematics programmes in a selection of Canadian and European universities and how knowledge to be taught is developed; they note, “The Canadian programs usually offer several calculation-oriented courses labelled Calculus, while the European programs […] contain fewer or even no courses of this type” (p.159). In our paper we also focus on first year Mathematics programmes but, as shall be raised in the Discussion section, we note differences, with regard to the treatment of limits, in three European curricula considered.

Teacher education

The second part of Klein’s double discontinuity concerns what would, today, be called teacher education. Winsløw & Grønbæk (2014) note a tendency of school calculus to emphasise algebraic techniques, and downplay definitions and existence problems; “From the point of view of university mathematics, this means that [school] students’ work mainly consists in ‘finding’ objects (such as limits) for which they have no formal definition or criteria of existence” (p. 77).

We note variations in teacher education over and within countries. There are two routes to becoming a qualified teacher.

• School-based, the student teacher receives training in a school or set of schools. This route is the dominant route into teaching in England.

• University-based, with two variants:

  • The ‘consecutive’ model. After obtaining a degree, the student teacher follows a course leading to a teaching qualification. This is the common route in France.

  • The ‘concurrent’ model. The student teacher simultaneously studies mathematics and ways of teaching mathematics. This is a common route in Sweden.

Several recent studies have focused on Klein’s second discontinuity in university-based routes with regards to calculus. For instance, Yan et al., (2020) investigate mathematicians’ views of how a calculus course for prospective teachers should be designed; respondents argue for less content and greater emphasis on connections and underlying ideas. Our paper does not deal with the design of courses to bridge Klein’s second discontinuity but it does raise issues with regard to the limit notion for each of the three routes to qualified teacher status described above.

Theoretical framework and methodology

This section provides an overview of the rationale and constructs behind the ATD, and describes the methodology of the study. We introduce symbolic abbreviations, common practice in ATD analysis in order to provide succinct references to specific constructs.

Praxeological Organization

In the ATD, mathematical activity is considered as a human activity within institutions. To enable a precise description of mathematical activity, Chevallard (1999) introduces the notion of Praxeological Organization (PO), comprising the following components in a single institution:

• Type of tasks, T, with certain similarities (e.g., compute the limit of a sequence);

• Technique, τ, enabling the performance of a type of task T (e.g., to squeeze a sequence between two sequences with the same limit);

• Technology, θ, a discourse on the technique, making it possible to explain, justify or (re)produce it (e.g., comparison theorem or definition of the limit of a sequence);

• Theory, Θ, the rationale/discourse related to the technology, making it possible to explain, justify or produce it (e.g., real analysis).

The block [T,τ] is called the know-how block, or praxis, and the block [θ,Θ] is called the knowledge block, or logos; hence the term praxeology. In an institution, for a type of task T, the quadruple [T,τ,θ,Θ] is called a punctual praxeology (of the institution). A local praxeology is a praxeology centred on a technology θ, which can therefore contain several types of tasks and techniques depending of θ. A regional praxeology is a praxeology centred on a theory Θ, which can therefore contain several types of tasks, techniques and technologies depending of Θ. At the domain level (explained below) these regional praxeologies need to be linked in a global praxeology. When we refer to praxeological organizations related to mathematics, we follow Barbé et al., (2005) and write MO for “mathematical organizations”.

There are many conditions outside the classroom which influence MOs. To identify these, Chevallard (2002) proposed a scale of “levels of determination” (later called “codetermination”) (Fig. 1). For our study, we focus on levels 1–4, limiting ourselves to the MOs relating to the domain of analysis/calculus, the two sectors of sequences and functions, the two themes of limits of sequences and of functions and the two subjects of computation of limits of sequences and of functions. This is shown in Fig. 1.

Fig. 1

Levels of didactic codetermination

Didactic transposition

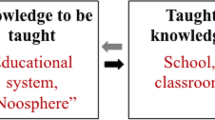
The didactic transposition (Fig. 2) of mathematical knowledge is concerned with the transformation of knowledge across institutions. This emanates from an institution producing and using knowledge, which is organized in an MO. This scholarly knowledge needs to be transformed to become an object that can be taught in an educational institution (MO to be taught); this is carried out by people in the “noosphere”, “sphere of those who think about education” (Bosch & Gascón, 2005, p. 112). The knowledge to be taught then has to be transposed to become knowledge actually taught by teachers (MO taught) and then to knowledge learnt by students (MO learnt).

Fig. 2

The didactic transposition (Bosch & Gascón, 2005, p. 117)

However, from an anthropological viewpoint, scholarly knowledge cannot be absolute. It is subject to change and the history of the limit notion is an example of such a change. To emphasize this, Bosch and Gascón introduce the notion of reference epistemological model (REM, see Fig. 1) “that constitutes the basic theoretical model for the researcher and can be elaborated from the empirical data of the three corresponding institutions: the mathematical community, the educational system and the classroom” (ibid., p. 117). The aim of a REM is to support a researcher’s analysis of the steps of the didactic transposition.

Methodology

The methodology of this paper is designed to facilitate an ATD analysis addressing RQ:

RQ With regard to limits, what similarities and differences exist in the three countries at the three levels?

The aim is to design an operational methodology, easy to use, and easy to modify if adding new countries for analysis and comparison. For this study, we focus on the limit notion. The methodology consists of four steps:

• 1. We first designed a REM on limit (see next section) based on the national HS curricula of the three countries, complemented with the curricula of the three universities of the study, but without taking into account new mathematical notions that are not taught in HS, as trainee teachers will have to teach HS notions, not university notions. The REM thus constructed is specifically adapted to the study of the three countries.

• 2. For each of the nine levels considered we wrote a vignette providing information with respect to seven questions described below. These questions and vignettes were written avoiding technical language, to improve readability while still providing a basis for ATD analysis.

• 3. We then applied our REM in order to interpret the nine vignettes from an ATD perspective. The result is a praxeological organization (PO) for each level for the limit notion.

• 4. These POs are then used to make comparisons within countries, for the double discontinuity, and between countries, at the same level.

Reference Epistemological Model.

The aim of this REM is to provide a basis from which to analyse the teaching of limits in the three countries and at the three levels. To avoid too large a REM, we made some choices and we do not treat of all the elements related to limits. However, our REM includes the two local praxeologies (LP) for limits of functions that constitute the REM of Barbé et al., (2005).

We designed the REM by identifying, in the three national HS curricula and HS textbooks, the national punctual praxeologies for the limit notion. We then looked at the types of tasks identified at the HS, university and teacher education levels: what are the new techniques and the new technologies with respect to these HS types of tasks. Throughout this process, we drew on the same data as when constructing the vignettes. Mostly, concerning the university level we discarded the new objects and new types of tasks in order to focus on the HS notions that future teachers will have to teach. For instance, the REM does not take into account series and topology. It should be mentioned that a praxeology component is taken into account as soon as it appears in one country. Finally, based on our experience as researchers and teachers both in mathematics and didactics, we used all these punctual praxeologies to build a REM for the limit notion.

Within the calculus Domain, we consider two fundamental objects for which limits can be defined: sequences of real numbers and functions of a real variable (we do not consider series in this paper, since they are hardly considered at the HS level in any of the three countries). We consider regional praxeologies (RP) for functions and sequences: RP(Θ_f) is defined by theory Θ_f consisting of the definition of functions together with properties of $\mathbb{R}$; RP(Θ_s) is defined by theory Θ_s consisting of the definition of sequences together with properties of $\mathbb{R}$. We focus on the following types of tasks:

T₁: compute the limit of a sequence (T_1s) or a function (T_1a at a point a and T_1∞ at infinity); state whether the limit is finite or infinite.

T₂: prove the convergence of a sequence (T_2s) or a function (T_2a and T_2∞).

To describe the REM in more detail, we list the main technologies:

θ₀: definition of limits, distinguishing functions (θ_0f) and sequences (θ_0s); we do not specify cases but we say whether definitions are informally/formally set;

θ₁: algebra of limits for functions (θ_1f) or sequences (θ_1s);

θ₂: existence theorems for convergence, including existence for monotonic bounded sequences, the Bolzano-Weierstrass theorem and Cauchy’s sequences;

θ₃: comparison theorems to compute limits, θ_3s and θ_3f ;

θ₄: Taylor expansion theorem (mainly for functions, for indeterminate forms (IF));

θ₅: continuity (for functions);

θ₆: composition of limits (θ_6ff for two functions and θ_6fs for a function and a sequence);

θ₇: induction principle (important for sequences).

These technologies all have related techniques, τ₀-τ₆, enabling the accomplishment of tasks falling under T₁ and T₂.

We end this section with Tables 1 and 2, detailing how the regional praxeologies, tasks, technologies and techniques listed immediately above relate to the three lowest levels in Fig. 1.

Table 1 Regional Praxeologies for functions

Table 2 Regional Praxeologies for sequences

Note that T₂ is typically also accomplished by techniques of computation. For instance, computing a limit using the algebra of limits proves more than the value of the limit, it also proves convergence. But the computation of limits usually does not emphasize convergence, rather the computation usually focuses on the limit value. However, it is different for recursively defined sequences (and for series): applying the techniques of computation (τ₂ and τ_6fs or τ₅) leads to an equation of the form $f\left(l\right)=l$, but without certainty that one of its solutions is an actual limit of the sequence. Hence, for a recursive sequence, knowledge of convergence is important and, for that purpose, we distinguish between T₁ and T₂. Moreover, for the types of tasks on recursive sequences, it is necessary to deal also with functions and the related local praxeologies, which contributes to the emergence of a global praxeology with RP(Θ_s) and RP(Θ_f). Our REM is thus not actually complete because, for reasons of space, we omitted some objects (e.g., sub-sequences) and properties (e.g., boundedness). Still, we claim that this REM is sufficient for this paper, as it provides us with what we need to conduct an analysis to address RQ.

Constructing the vignettes

Data on limits in the three countries is reduced into nine (3⋅3) vignettes that constitute an intermediary between data and our proposed POs.

To structure and standardize the vignettes we address the first four questions below:

• (1) In which areas of mathematics do limits appear?

• (2) What definitions, properties and theorems concerning limits are employed in these areas?

• (3) What tasks involving limits are used in these areas?

• (4) What methods are students encouraged to use in limit tasks?

We also note representations and digital tools used.

In addition, for teacher education we also considered:

• (5) Are didactical issues regarding limits and/or calculus raised in teacher education?

• (6) Are differences between high school and university knowledge of limits and/or calculus raised in teacher education?

• (7) What specific preparation, if any, for teaching limits and/or calculus is offered in teacher education?

Questions (1) to (4) concern praxeological organisation, respectively: theory; technology; task types; and techniques. Questions (5) to (7) explore three aspects of teacher education regarding limits and/or calculus. We now consider sampling, data collection and data analysis used to address these questions.

Regarding sampling, we first note variation over and within the three countries. All three countries: have a national curriculum for HS; have a range of university mathematics courses (from research-centred universities providing Mathematics degrees to service courses for subjects that require post-high school mathematics); have different trajectories for teacher education. Our approach to HS is to focus on the national curricula and related textbooks and high stakes examinations. For universities we focus, for reasons of space, on a Mathematics degree in one research-centred university in each country, as the logos for scholarly knowledge of limits is most likely to appear in such universities/degrees; we selected universities which we were familiar with. At the level of teacher education, we describe the main national trajectory/ies and supplement this, as appropriate, with details concerning specific teacher education programs or initiatives.

At the HS and university levels, data collected included: curricula documentation, for instance, syllabi; textbooks used or recommended; mathematical tasks given to students; and, final examinations. At the level of teacher education, we examined national guidelines which specify requirements for teacher education (general guidelines for all teacher education and, where they existed, specific guidelines for high school mathematics).

Having collected data to address these seven questions we wrote draft vignettes which were sent to experts in the field to validate and/or modify; “experts in the field” included individuals considered to have a deep knowledge of HS mathematics and/or teacher education in each country and the directors of undergraduate mathematics at the three universities considered.

Nine vignettes

We present vignettes on limit at three educational levels (high school, university and teacher education) describing the situation in England, France and Sweden. These vignettes were written in the summer of 2020 and curricula documents cited are those which applied at that time.

England

High school

High school corresponds to Years (grades) 7 to 13, students are typically 11 to 18 years of age; the first five years are compulsory and include a large number of subjects. Academic stream students in the last two years specialize in, typically, three subjects at Advanced level (A-level). A-level Mathematics consistently has a higher number of students than other subjects, about 30% of students study it³. Calculus is a major part of the A-level Mathematics curriculum. In the current Department for Education (DfE) curricular document on A-level Mathematics⁴, the word ‘limit’ appears three times:

• Understand … the gradient of the tangent as a limit.

• Understand and use integration as the limit of a sum.

• In the appendix on ‘notation’: $\underset{x\to a}{\text{lim}}f\left(x\right)$, the limit of $f\left(x\right)$ as $x$ tends to $a$

This curriculum is the foundation upon which the ‘examination boards’ (EB) design mathematical content specification and examinations. There are three EBs, AQA⁵, OCR⁶ and Pearson Edexcel⁷; their documentation is very similar so we report on the first one here. The specification of mathematics content in the AQA specification is identical to that in the DfE document.

There are many textbooks but no prescribed textbooks for A-level Mathematics. In recent decades, textbooks associated with EBs have become popular in schools. A textbook linked to the first year of AQA A-level Mathematics is Goldie et al., (2017). Limits are mentioned in Chap. 10 (Differentiation) and 11 (Integration). Chapter 10 starts with a section The gradient of the tangent as a limit; after numeric examples on the gradient to $y={x}^{2}$ at (1,1) we read, “the gradient of the chord becomes closer to the gradient of the tangent” (p.191). The use of technology, “spreadsheets or graphing software” is suggested. In Sect. 2, the notation $\underset{h\to 0}{\text{lim}}\frac{f\left(x+h\right)-f\left(x\right)}{h}$ is introduced. Tasks ask students to show or find derivatives of polynomials: “Find, from first principles, the derivative of ${x}^{3}-6x-1.$”

In Chap. 11, integration is introduced as the reverse of differentiation and tasks involve finding integrals (often set as finding the area under a curve). Limit (other than “the limits of integration”) is only mentioned on one page, “In the limiting case the ${\Sigma }$ sign is written as $\int$and $\delta x$ is written as $dx$” (p.236) and there are no tasks related to this.

The AQA assessment of A-level Mathematics⁸ takes place via three two-hour written examinations. The latest papers available at the time of writing were for the June 2018 examinations (published May 2019⁹). The word “limit” does not appear in any of these papers. Graphical calculators are allowed in these examinations.

The University of Leeds

The curriculum for the first year of the Mathematics BSc at the University of Leeds has 120 credits¹⁰. Limits are a focus in modules: Mathematics 1 & 2 (semesters 1 & 2 respectively, 25 credits each); Sets, Sequences and Series (semester 2, 15 credits).

The summary for Mathematics 1 & 2 states “consolidates basic calculus material from A-level, extending it to more advanced techniques, such as functions of several variables, and introducing elements of the analysis required to formalize the subject.” It also provides an introduction to linear algebra. Limits are treated informally but provide the basis for the definitions of the derivative and the definite integral. The module reading list cites well-known university calculus textbooks, for instance, Spivak (2008).

The most recent past examination papers¹¹ (80% of assessment) have the following limit questions:

• Determine whether each of the following limits exists. Where a limit does exist, compute it using any appropriate technique.

• (a) $\underset{x\to 3}{\text{lim}}\frac{{x}^{2}+4x+3}{{x}^{2}+2x-3}$ (b) $\underset{x\to 0}{\text{lim}}\frac{\text{sinh}x}{x}$ (c) $\underset{x\to 1}{\text{lim}}\frac{x}{\sqrt{{x}^{2}-1}}$

Limits also appear in an application question regarding a particle of mass $m$ which is dropped to Earth giving a force of magnitude $F\left(z\right)=\frac{GMm}{{(z+a)}^{2}}$.

• Show that the force $F$ is conservative by finding its potential function $U\left(z\right)$ such that $\underset{z\to \infty }{\text{lim}}U\left(z\right)=0$.

Sets, Sequences and Series is a semester 2 module and employs $\epsilon -\delta$ approaches. The word “limit” is not mentioned in the module objectives or syllabus but limits are clearly a focus of the work as the syllabus includes: supremum and infimum; convergence of sequences; the Bolzano-Weierstrass Theorem; absolute and conditional convergence of series. The module reading list includes Applebaum (2012).

Questions in the most recent past examination paper for Sets, Sequences and Series are oriented towards definitions and proofs, for example: “Prove that inf$\left\{\frac{1}{n}-\frac{3}{m}|n,m\in \mathbb{N}\right\}=-3$. Start by stating the definition of the infimum.” The examination ends with a question concerning the Bolzano-Weierstrass Theorem. Students may use “approved calculators” in examinations.

Mathematics teacher education

There are various ways to become a mathematics teacher: through university courses and through various school-based training routes¹². Since 2010, university courses have declined and school-based routes are the norm. University courses include undergraduate courses (e.g., Bachelor of Education) and post-graduate courses, typically a one-year course combining university modules and school-based practice for people with relevant first degrees. In all of these routes to secondary mathematics teaching there are likely to be “pockets of excellence” in preparing preservice teachers to teach calculus but there is no requirement to do it. Given this, no vignette for limits, for calculus, for the link between university and school mathematics can be provided for initial teacher education in England. With regard to in-service teacher education, there is a course, Teaching A-level Mathematics ¹³ (TAM), designed to deepen mathematical knowledge and develop teaching approaches. Calculus is a major focus but no specific knowledge of, or approach to, limits is suggested.

France

High school

The term “analysis” is used, rather than “calculus”. High school corresponds to Years 6–12, and is compulsory up to and including grade 10. In grades 11 and 12, mathematics is not compulsory; what is presented here concerns the mathematics speciality option in these grades (taken by 41% of the students in 2020–2021¹⁴).

In grade 11¹⁵, limits appear in two different areas: limits of sequences, in algebra, and limits of functions, in analysis. However, examining a commonly used textbook (Barbazo et al., 2019), we can see that there is little emphasis on limits. In algebra, limits appear, without mentioning properties, in the task of estimating the possible limit of a sequence (finite or infinite) using mainly numerical or graphical tools. In analysis, limits occur in connection to finding the derivative of a function at a point. Again, no theory of limits is presented; rather, the expression “tends to” is used. Furthermore, limits are implicitly present in the task of computing $f\text{'}\left(a\right)$ using differential quotients, the algebra of limits and an implicit idea of continuity. Digital tools, such as graphing calculators, Geogebra and spreadsheets are frequently used.

In grade 12¹⁶, the notions of limits of sequences and functions are brought together and definitions, properties and theorems concerning these are presented. Again, examining an established textbook (Barbazo et al., 2020), we can see that although graphs and tables of values are still used to make conjectures, the focus is on using theoretical tools. Formal definitions (albeit not using symbolic quantifiers) are initially given for limits at infinity – first for sequences, then for functions. Limits of functions at specific points are then defined, leading to the definition of continuity. Tasks mainly concern the computation of limits, using the algebra of limits or (rarely for functions) comparisons. Definitions for limits are only used for sequences. Software, calculators, graphs and tables of values are used.

Regarding sequences, the notion of convergence is used to prove the existence of limits. Nothing similar is done for limits of functions although composition of functions, continuity of functions, monotonic bounded sequences and graphic interpretations of asymptotes as limits of functions are considered. Limits of functions and limits of sequences are linked through (simple) recursive sequences.

In the national final HS exam (required to enter university), Baccalauréat, in 2019, Metropole subject¹⁷, there were the following tasks concerning limits: compute the limit of a function (specifically, an exponential function) at infinity; prove the convergence and compute the limit of a recursive sequence (the first term being in $\left[\text{0,1}\right]$).

The University of Paris Cité

The first year of the bachelor programme in mathematics at the University of Paris Cité (in the academic year 2019–2020) consisted of three courses¹⁸: (1) elementary algebra and analysis, aimed at consolidating and developing knowledge of HS mathematics; (2) a course covering the basics of analysis, including all main definitions; and (3) a course providing deepened knowledge of analysis.

Concerning limits, definitions are given using $\epsilon -\delta$ notation. Properties of limits are developed, with theorems concerning, for instance, subsequences (Bolzano-Weierstrass’ Theorem), asymptotes, left and right limits and the uniqueness of limits. Indeterminate forms, however, are covered in the second semester using MacLaurin polynomials. The main type of task is ‘compute the limit for a given function (or sequence)’, but there are many other types of tasks, some stated quite generally, for example, proving that “if $f\left(x+1\right)-f\left(x\right)$ converges to 0 at $+\infty$, then $\frac{f\left(x\right)}{x}$ converges to 0” and investigating the convergence of ${(1+\frac{1}{n})}^{n}$. Apart from “compute the limit”-type tasks, there are not many clearly procedural tasks. Further to this, the second course introduces the topology of $\mathbb{R}$, defining limits using neighbourhoods and discussing issues of closure of sets through limits of sequences.

In contrast to the situation in HS, there is no use of digital tools in the exercises and exams given to students (in 2019–2020). As in HS, the subdomains of sequences and functions are connected through recursive sequences.

Mathematics teacher education

The main path to becoming a mathematics teacher in France¹⁹ is to pass a master degree, mainly in specific university-situated Instituts Nationaux Supérieurs du Professorat et de l’Éducation (INSPÉ), after a bachelor degree in mathematics. This is done in two parallel steps, M1 and M2, where M1 is mainly a preparation for the national competitive exam (“certificat d’aptitude pour l’enseignement secondaire” – CAPES) and M2 includes school-based training.

In the CAPES curriculum²⁰, there are two written examinations, one on advanced mathematics and one on secondary mathematics, sometimes containing questions on limits. According to the CAPES jury, limits are considered among the most difficult notions for future teachers. There are also two oral examinations, one of which consists of delivering a lecture on a theme. Of 37 possible themes, two concern limits, of sequences and functions, respectively. From 2020, there is also a theme on recursive sequences. For the second oral examination, concerning student responses to specific questions, one of more than 20 concerns limits.

In M1 of the INSPE de Paris²¹, there are 42 h of analysis plus 24 h of analysis for secondary school, including some didactic issues. In M2, there are six compulsory and nine optional hours on analysis. In the last three years, limits were covered in the optional course, building on Chorlay (2019). However, in 2020, this was removed as it was considered too far from the future practice of most mathematics teachers.

Sweden

High school

High school corresponds to Years (grades) 7 to 12, students are typically 12 to 18 years of age. Grades 7–9 are mandatory. More than 98% of Swedish youth enrol in upper secondary school (years 10–12), 60% in academic preparatory programs.²² The mathematics curriculum²³ is divided into five courses, and calculus content is included in Mathematics 3²⁴, 4 and 5, with limits covered in Mathematics 3, which is taken by about 40%²⁵ of students.

Calculus content appears in the curriculum under the heading “Relationships and change.” The word “limit” appears once, in the syllabus for Mathematics 3: “orientation to continuous and discrete functions, as well as the concept of limits.” In Alfredsson et al., (2012), a widely used textbook, limits are introduced explicitly to define derivatives, which were already introduced geometrically as the slope of the tangent line: “In the next section we will define derivatives mathematically. To do this we first have to introduce the concept of limit.”²⁶ (p. 77). The definition given is informal: “$\underset{x\to a}{\text{lim}}f\left(x\right)=L$. The function $f\left(x\right)$ can take values as close to $L$ as one wishes by choosing $x$ close enough to $a$” (p. 77).

Of the worked examples, one concerns limits at infinity, and one the nonexistence of a limit. Typical tasks (which are few) concern the computation of limits, either using algebra, mostly in work with differential quotients, or through numerical computation using calculators.

The four example Mathematics 3 national tests available online²⁷ contain limit tasks corresponding to between 0 and 6 out of 72 points. The tasks either concern the computation of a limit given using limit notation or examining the behaviour of a given function for large values of $x$.

Uppsala University

In the first year of the Mathematics BSc at Uppsala University²⁸, courses in single- and multiple-variable calculus and differential equations include calculus content. Limits are introduced in the first-semester 10-ECTS-credit course Single Variable Calculus (SVC), with a more rigorous treatment given in the second-year course Real Analysis. As in France, the term “analys” (analysis) is used, rather than “calculus”. The single-variable calculus course has two variants: SVC-M²⁹ for the bachelor programme in mathematics; SVC-Eng³⁰ for the engineering programmes (and for prospective teachers). Two learning outcomes of the SVC-Eng syllabus mention limits explicitly: “give an account of the concepts of limit, continuity, derivative and integral”, and “reproduce a number of standard limits and how to use them in computations”. The content concerning limits simply reads: “Limits and continuity: notions and rules.” The corresponding wordings in the SVC-M syllabus are slightly more substantial: “give an account of the notion of limit both for real-valued functions and for sequences of numbers, and compute limits of functions and sequences using standard formulas,” and “Limits and continuity: notions, proof of existence and rules.” Apart from limits being used to prepare the ground for the definition of continuity, derivatives and integrals, in both courses work on limits focuses on computation using standard limit formulas and, later, using approximation with MacLaurin polynomials to compute limits of indeterminate forms.

SVC-Eng uses Adams & Essex (2017) as a textbook, but replaces the informal definition of limit of a function suggested there with an $\epsilon -\delta$ definition. Limits of sequences are introduced in connection to infinite series, as a special case of limit at infinity of a function. Tasks mostly concern the computation of limits of functions at specific points, often using standard limit formulas, but there are some examples of tasks where students are expected to apply the idea behind the definition, for instance, finding a $\delta$ given an $\epsilon$ for a specific function at a specific point.

SVC-M uses Månsson & Nordbeck (2011) with additional material, including coverage of limits, provided by the lecturer. The limit notion is first formally defined for sequences, with some examples and theorems, including the Bolzano-Weierstrass Theorem (not taught in SVC-Eng). Then limits of functions are introduced, first at infinity and then at specific points. In addition to limit computation tasks there are also tasks on showing convergence or the existence of a limit.

In the final exams of SVC-Eng and SVC-M, there is at most one task explicitly concerning limits, typically a computational task involving the use of Maclaurin polynomials. However, graph sketching tasks commonly appearing in exams often require limit computation to find asymptotes.

Mathematics teacher education

There are two main paths to becoming a mathematics teacher in Sweden³¹: a BSc in mathematics followed by a one-and-a-half-year master programme, or a concurrent five-year upper secondary teacher education programme, which includes the study of two subjects and general pedagogy. The majority of prospective teachers enrol in a teacher education programme. Although teacher education in Sweden is regulated by law³², details of the content of the study programmes are largely left to each university to decide. General claims about these programmes can therefore not be made. At Uppsala University³³, prospective upper secondary mathematics teachers take the SVC-Eng course. Hence, they will have seen a formal definition of the limit of a function but will not be very familiar with limits of sequences. They will have had little or no experience with the formal limit definition, as few take the optional Real Analysis course.

The curriculum of the mathematics education course for prospective secondary teachers at Uppsala University does not specify mathematical content. It allows for including didactical aspects of calculus (including limits), but whether this is done depends on the lecturer giving the course. The course on the history of mathematics contains some material on the historical development of calculus, including the limit concept.

Analysis of the vignettes

In the language of ATD, each vignette gives information on an MO related to limits in a particular institution. In this section, we use this information to address RQ: With regard to limits, what similarities and differences exist in the three countries at each of the three levels? We use the following abbreviations to refer to the nine institutions:

• E_HS, F_HS and S_HS for English, French and Swedish High Schools;

• E_UL, F_UP and S_UU for the Universities of Leeds, Paris Cité and Uppsala;

• E_TE, F_TP and S_TU for teacher education in England, in the INSPE of Paris and at Uppsala University.

In each of these institutions, we use the REM presented above to analyse the vignettes in terms of regional praxeologies for functions and sequences, defined by theories Θ_f and Θ_s. We use abbreviations for praxeologies building on the notation used in the REM: regional, e.g., RP(Θ_f); local, e.g., LP(θ₀); and, punctual, e.g., PP(T₁).

High school

At the level (of didactic codetermination) of the Discipline, the notion of limits appears in Domains with different names: “Calculus” for E_HS, “Analysis” for F_HS, “Relationships and change” for S_HS. At the Sector level, for functions, the teaching of limits starts with similar punctual praxeologies defined by tasks within T₁: compute the limits of difference quotients. Examining the descriptions of typical tasks in the HS vignettes, two techniques are available in this punctual praxeology: (1) algebraic transformations (with continuity implicitly assumed) with the calculation of the value at (or near) $h=0$ of the differential quotient $\frac{f\left(a+h\right)-f\left(a\right)}{h}$; (2) using a sequence of approximate values and a statement to the effect that the sequence is approaching a specific value. The technology θ_0f is expressed in terms of closeness, “as close as you wish…”, seemingly favouring techniques based on graphs or numerical values and, also, the use of an implicit notion of continuity. We denote by ⁱθ_0f this informal technology and ⁱτ₀ the related techniques. In F_HS the technology θ_0f is further formalized in grade 12.

The same types of tasks are the norm in F_HS and S_HS: computing the limits of a function either at a point $a$ (T_1a) or at infinity (T_1∞, less so in S_HS), determining whether the limit is finite or infinite, with the technique τ₁ based on the algebra of limits, θ₁. The technology of limit comparison, θ₃, and the associated technique τ₃ of inequalities, is present in F_HS, but not in E_HS or S_HS. The notion of continuity (θ₅) also appears at this level: implicitly in E_HS, in terms of limits in F_HS and S_HS. Thus, in F_HS and S_HS we have the development of a regional praxeology RP(Θ_f) of functions with local praxeologies of limits focusing on the types of tasks T₁. However, in S_HS and E_HS, a local praxeology related to the notion (though not the definition) of limit is developed, mainly to support future work on differentiation and integration (and in E_HS, apparently, only for this future work since questions on limits do not appear in the final exam). Moreover, there is a difference concerning θ_0f, which is expressed informally for E_HS and S_HS, and formally for F_HS (albeit in natural language without logical symbolism). Technological tools are used or suggested in E_HS, are often used for justification purposes in S_HS and used only for conjectures in F_HS.

In F_HS, but not in E_HS or S_HS, in parallel with the regional praxeology on functions, a regional praxeology RP(Θ_s) of sequences also appears. In grade 11, in the domain of algebra, there appears a technology θ_0s for limits of sequences; the techniques relate to using graphs and approximated values but this is formalized in grade 12. Further to this, in F_HS, a local praxeology is developed for T_2s with regard to the convergence of recursive sequences. This involves an existence theorem for monotone bounded sequences which gives rise to another local praxeology LP(θ_2s), providing a link between the two regional praxeologies RP(Θ_f) and RP(Θ_s).

In summary, the three HS institutions start from similar punctual praxeologies for derivatives focusing on finite limits at specific points but the development of limits from this point differs. In E_HS and S_HS a local praxeology is developed to support future work on differentiation and integration but in F_HS two regional praxeologies are developed, with the beginnings of a global praxeology.

University

In the three universities in the study, limits appear in domains with different names: “calculus” in E_LU, “analys” in S_UU and “analyse” in F_UP. University syllabi take the respective HS curricula into account: starting with the limit in S_UU; consolidating HS knowledge in E_UL and F_UP.

In the three universities, E_UL, F_UP and S_UU (SVC-M variant), there is the constitution of a global praxeology with RP(Θ_f) and RP(Θ_s). Comparing the REM with the university vignettes, we note the following local praxeologies: LP(θ_0f), LP(θ_1f), LP(θ_3f), LP(θ_0s), LP(θ_1s), LP(θ_3s) and a local praxeology for convergence LP(θ_2s) with, notably, the Bolzano-Weierstrass theorem. The main type of task is still T₁, but there are more types of functions with more and different cases to be treated by students. In all three universities, MacLaurin polynomials are used as a technique for computing limits of indeterminate forms (specifically those which cannot be handled through the algebra of limits).

However, there are some differences: in E_UL, limits are defined first informally, for functions, and then formally. In semester 2, there then appears a new regional praxeology, for sequences. In contrast, in S_UU, the SVC-M variant starts with limits of sequences. In F_UP, the constitution of the global praxeology that already appeared in F_HS is pursued. In S_UU, limits are introduced less rigorously in SVC-Eng than in SVC-M. The focus is still on T₁ but SVC-Eng starts with limits of functions (at $a$ and then at infinity), with limits of sequences presented as a particular case of limits of functions at infinity, without specific theorems such as the Bolzano-Weierstrass theorem.

In summary, despite differences in the knowledge concerning limits that students bring to the beginning of university, and despite different domain names, similar praxeologies are taught for functions, RP(Θ_f), and also for sequences, RP(Θ_s), although at S_UU this is done only in SVC-M.

Teacher education

In E_TE, there are multiple pathways to qualified teacher status but it is, in the opinion of the UK author, reasonable to assume that there is little or nothing on didactical aspects of limits in the majority of these pathways. In S_TU, the lecturer’s choice determines what didactical aspects of calculus are taught. In F_TP, it is different, mainly because of the CAPES competitive exam. The first year of the master course (INSPE) includes a focus on regional praxeologies, RP(Θ_s) and RP(Θ_f), that appear in HS and at the beginning of university. The second year is more oriented towards didactic issues, calculus is an option but depends on the lecturer’s choice.

In conclusion, the English and Swedish teacher education institutions have large local variations and there is apparently little on the didactics of limit. In France, largely due to preparation for CAPES, both HS and university limit praxeologies are taught, but in the professional year after CAPES, dealing with the teaching of limits in HS is the choice of the lecturer, such as recently with a specific situation in F_TP (Chorlay, 2019).

Discussion

We discuss RQ, FQ1 and FQ2 and then consider methodological implications for analysis of the nascent international calculus database.

With regard to RQ, significant differences appear at the level of HS. In E_HS, in Calculus, a local praxeology related to the notion (though not the definition) of the limit of a function is developed but apparently only as a basis for future work on differentiation and integration. In S_HS, in Relationships and change, this same local praxeology is also developed but with local praxeologies for θ_1f and θ₅. These local praxeologies exist within a regional praxeology RP(Θ_f). In F_HS, in Analysis, there is a more complete RP(Θ_f) with local praxeologies mainly related to θ_0f and θ_1f, but also with θ_3f, θ₅, θ_6ff; there is also another RP(Θ_s) with local praxeologies related to θ_0s, θ_1s, the specific θ_2s, θ_3s and θ_6fs with connections between the two regional praxeologies. Expressing this without ATD constructs, it could be said that E_HS pays lip service to the limit notion, S_HS goes beyond E_HS by linking limits with continuity and F_HS provides a wider (including sequences) and more rigorous approach to limits. In summary, the limit notion at the HS level should be regarded as a nationally-situated construct.

In contrast to the HS level, the treatment of limits at the university level in the three countries is similar in that they all develop regional praxeologies for both functions, RP(Θ_f), and sequences, RP(Θ_s), though there are slight differences in the local praxeologies developed. The fact that all the Mathematics courses, by the end of the year, cover the Bolzano-Weierstrass theorem attests to the claim that T₂ tasks are prominent and the courses relate to the topology of $\mathbb{R}$ which is, arguably, too austere for HS work on limits. Perhaps this similarity at the university level is related to the REM underlying each course being similar to the REM we outline in the Theoretical Framework.

At the level of teacher education, a significant difference appears in the vignettes: in E_TE and in S_UU there is nothing in written documentation about limits whereas, in F_TP, limits appear in the CAPES examinations. Beyond this one difference, not much more can be said because teacher education documentation appears to ignore the limit notion; in particular our questions (5), (6) and (7) above can all be answered in the negative for England and Sweden. Given the literature documenting student difficulties with the limit notion, a lack of an explicit comment on limit at this level can be seen as a cause for concern. We return to this in FQ2 below.

We turn to FQ1. With regard to university Mathematics courses, Bosch et al., (2021), as mentioned above, state that Canadian programmes offer calculation-oriented Calculus courses but European programs contain fewer or no courses of this type. Our analysis, with regard to limits, largely supports the claim with regard to the three European programs considered in this paper, though we do note differences with regard to local praxeologies developed. It seems safe to say that the limit approach could be the dominant approach in university calculus courses for other European Mathematics degrees today. But the “transfer” of this approach to school has been problematic. To consider this we return to Törner et al.’s (2014) description of three periods in the history of school calculus curricula in Europe and note the claim that, in all seven countries studied, calculus notions were introduced informally. Although we regard the three periods described by Törner et al., (2014) as broadly accurate, it should not be assumed that ‘intuitive’ approaches in the third period are identical. These approaches at the school level result from the first step in the didactic transposition where a rigorous approach, which presents limit notions as the basis for calculus, is being transposed to become a teaching object at school level. Limit-first approaches can and do exist at school level, for instance, Advanced Placement Calculus in the USA³⁴, but non-limit-first approaches to rate of change and accumulation are also possible and exist. The HS courses described above are three such approaches. All start with “intuitive” approaches in the first year of study: in England, “the gradient of the chord becomes closer to the gradient of the tangent”; in France, “there is not much emphasis on limits in grade 11” but limit definitions are employed in grade 12; in Sweden, “limits are explicitly introduced to define derivatives, which have already been introduced geometrically as the slope of the tangent line”. Thereafter the three courses differ. Both courses in France and Sweden develop to embrace limit definitions (though not in identical ways). England is the exception. Limit definitions exist (minimally) in the curriculum document and in textbooks but limit tasks are not examined. The limit concept remains in the curriculum as a remnant of a former mathematical object.

We turn to FQ2. The vignettes reveal differences in teacher education in the three countries: no discernible focus on limits (or calculus) in E_TE; didactical aspects of calculus are taught in S_TU, but what is taught depends on the lecturer; and limits and calculus are addressed in F_TP due to the CAPES exam. Behind these differences are national policies on teacher education determined by a noosphere (not necessarily the same national noosphere that determines the first step of the didactical transposition). The noospheres in France and Sweden evidently accept a dominant role of universities in teacher education but this is not the case in England:

the ‘universitisation’ of teacher education should not be understood as an irreversible process […] there have been two trends in the past period: on one hand, further integration within the logic of higher education and research and, on the other hand, there have also been, as in the case of the UK, “policies designed to reduce the role of universities in teacher education” (Zgaga, 2013, p.359).

The papers cited in the literature review on teacher education do not mention the noosphere (by name or by description). Consideration of the noosphere may seem to take us a long way from limits and calculus but this consideration is important in the sense that the noosphere creates the conditions in which limits and calculus can feature in teacher education. Our study does not add to what the literature on Klein’s double discontinuity already says except for this point – the potential to address the double discontinuity at a national level relies on the noosphere providing affordances for it to be addressed.

Limitations of our research include: (i) space restrictions forced us to present only one university course in each country; (ii) we focused on the limit notion and similarities or differences may occur with other objects; (iii) the study is at a large scale and some notions, like the use of infinitesimals, may be invisible; (iv) we focused on the curriculum content and not how it is taught; that would require consideration of didactical praxeologies and the collection of pertinent data from classrooms and/or teachers; (v) The situation regarding teacher education needs further consideration, our a priori expectations were clearly naïve.

We now consider implications for the nascent international calculus database. This study is a first step in a larger project to compare calculus around the world. We employed our methodology on our three countries with a focus on the limit notion: the methodology seems robust and flexible enough for comparing calculus education. First, the REM, built on HS punctual praxeologies and completed with universities approaches appears adequate for interpreting vignettes via ATD analysis, with only slight modifications. It is reasonable to think that adding more countries will require only minor modifications to this REM on limits but that considering other calculus notions will lead to new REMs. Second, the vignettes, constructed to enable interpretation using ATD, have been checked by experts; we believe that they reflect well the actual situation in each level and country.