Abstract
Calculus courses have been attracting the attention of mathematics education researchers over the last decades. Recent publications and special issues dedicated to calculus highlight the diverse roles of calculus courses in the pathways for STEM studies within and across educational levels, as well as issues related to the academic preparation of future STEM professionals, including mathematicians, non-mathematics professionals (NMPs) and teachers. In this paper, we review recent literature, mostly since 2015, to identify and characterize explicit references to such diverse roles of calculus courses. The review highlights an intrinsic tension between two institutional roles of calculus: scaffolding and filtering. We find nuanced yet substantial variation in how the dual role of calculus is experienced and managed across different groups of students and stakeholders. With regard studies on calculus for mathematics students, recent studies attend to changes in the rules underpinning calculus notions and processes, and highlight the scaffolding potential of calculus courses towards abstraction and reasoning. In contrast, studies on calculus for NMPs report that such courses often promote filtering rather than scaffolding and question transferability and relevance of those courses for NMPs. Finally, studies challenge the perception that traditional tertiary calculus courses scaffold school teaching and underline the need for empirical research that would explain the nature of this scaffolding and how it can be realized in practice. We conclude that further empirical research, in particular theory development, is needed to address the diverse roles of calculus at the intersection of institutions, disciplines and communities.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Attending to the Diverse Social, Cultural and Institutional Contexts of the Teaching and Learning of Calculus: An Emerging Need
The teaching and learning of calculus has been attracting the attention of the mathematics education research community over the last decades. Even more, in recent years, our community has been particularly active in disseminating findings from research studies on calculus in review chapters, special issues and specialized conferences. Some recent indicative examples include: special issues on the Teaching and Learning of Calculus in 2014 (Rasmussen et al., 2014) and recently on Calculus in High School and College Around the World (Thompson & Harel, 2021); the ICME13-Topical Survey on the Teaching and Learning of Calculus (Bressoud et al., 2016); book chapters such as Generalization, Covariation, Functions, and Calculus (Hitt & González-Martín, 2016) and Understanding the Concepts of Calculus (Larsen et al., 2017); and, the first Calculus in Upper Secondary and Beginning University Mathematics Conference (Monaghan et al., 2019) where we conceived the special issue which we guest-edit and which includes this paper. These studies discuss students’ difficulties with calculus (Bressoud et al., 2016; Hitt & González-Martín, 2016; Larsen et al., 2017; Rasmussen et al., 2014; Thompson & Harel, 2021) and students’ learning experiences and meaning making of calculus across educational levels (Rasmussen et al., 2014; Thompson & Harel, 2021). Often the central focus of the discussion is around specific topics of calculus – such as limits, derivatives or integrals (Bressoud et al., 2016; Larsen et al., 2017; Rasmussen et al., 2014; Thompson & Harel, 2021). In other works, the focus shifts beyond attending to students’ learning of specific topics. Such works highlight the critical role of calculus courses in the pathways for STEMFootnote 1 studies at and within certain educational levels (e.g., Bressoud, 2021; Bressoud et al., 2016; Larsen et al., 2017; Rasmussen et al., 2014; Törner et al., 2014); the role of student affiliations (e.g., engineering or mathematics) in their learning and working with calculus topics (e.g., Bingolbali et al., 2007); and, the quality of the academic preparation of future professionals, including engineers, scientists, and mathematics teachers (e.g., Hitt & González-Martín, 2016; Winsløw & Grønbæk, 2014).
We contend that, to explore and address issues that go beyond the learning of specific topics, research on calculus education needs to acknowledge the diverse social, cultural and institutional contexts of the teaching and learning of calculus (Rasmussen et al., 2014). In this paper, we review recent studies that are attentive to this diversity and resonate with the overarching question of the special issue in which this paper appears: How do calculus courses address the varied – sometimes conflicting – goals, values, and needs of different institutions, disciplines, and communities? Specifically, in this review, we explore, identify and characterize the various roles of calculus courses at the intersection of: educational levels (e.g., in the transition from secondary to tertiary education); mathematical domains and practices students may encounter before (e.g., algebra or geometry), during (e.g., from calculations to proof) or after calculus courses (e.g., real analysis); communities of students (e.g., calculus for mathematics or engineering students); different professions (e.g., mathematicians, economists or engineers); and, calculus courses and teaching primary and secondary mathematics in the preparation of mathematics teachers.
Before describing the methodology of the literature review, we note that we found a substantial variation of what ‘calculus’ means in terms of content, rigor (e.g., the role of definition and proof), range of techniques and applications. We also noticed that calculus content appears at various educational levels in different educational systems, usually at upper secondary (or high school), post-compulsory, and tertiaryFootnote 2 levels. In this paper, we adopted a general definition of a ‘calculus course’, as a courseFootnote 3 that relates to the mathematical study of continuous change in the context of real numbers and typically includes limits, continuity of functions, derivatives, integrals and the fundamental theorem of calculus (other notions, such as infinite sequences and series may also be included). This content can be seen in the same course, or sometimes split over two courses of differential and integral calculus. Some calculus courses may solely focus on one-variable functions, while in other courses the focus may extend to two-variable (and rarely multivariable) functions (e.g., Trigueros et al., 2018). In some educational systems, calculus courses are separated from proof-based real analysis courses (Kondratieva & Winsløw, 2018). However, in many educational systems the distinction between calculus and real analysis courses is blurred, and post-compulsory and tertiary calculus courses may include elements of real analysis. Furthermore, calculus courses at the tertiary level very often are offered to groups of students from different programs (e.g., mathematics, engineering, science, teacher education, etc.) or to students who have not chosen their specialisation yet. The fact that calculus is often taught in large classes, makes addressing diverse student needs even more difficult. To address such variations in educational systems and target audiences, we have conducted this review with attention to contextual and institutional characteristics of the reviewed studies. We describe how we did so in what follows.
Literature Review Method
In the selection of studies, we used two criteria. Firstly, we selected studies that report insights specific to calculus courses. In such studies, calculus is pertinent to their research questions or aims and not merely incidental to the context in which the study was conducted. Secondly, we looked for studies which make explicit reference to the diverse roles of calculus, especially at the intersection of institutions, disciplines, and communities. Such reference was sought: in the research questions or the aims of the study; in the conceptual framework (e.g., its affordances to study cultural and institutional differences); and, in the interpretation of the findings. In each item we reviewed, we searched for explicit elaboration regarding the institutions, disciplines and/or communities involved in the study. With these two criteria in mind, we reviewed the literature through the following stages:
-
a)
Initially, we selected six seminal journals in mathematics education with a range of specializations including teaching and learning of mathematics at the upper/post-secondary and tertiary levels. These journals are: Educational Studies in Mathematics, International Journal of Mathematical Education in Science and Technology, International Journal of Research in Undergraduate Mathematics Education, Journal for Research in Mathematics Education, Journal of Mathematical Behavior and ZDM – Mathematics Education. We started our review considering papers published in these journals from 2015 onwards. We chose 2015 as a starting point of our review because around that year several reviews of studies on the teaching and learning of calculus came out (Bressoud et al., 2016; Hitt & González-Martín, 2016; Larsen et al., 2017), which we have included and built on in our review. We have also included the ZDM-Mathematics Education special issue on calculus (Rasmussen et al., 2014).
-
b)
Inspired by studies presented at the first Calculus in Upper Secondary and Beginning University Mathematics Conference (Monaghan et al., 2019), we initially agreed that our review will focus on the areas of: transitions across secondary, post-secondary and tertiary education; connections across mathematical domains; education and professional needs of engineers and other professionals; education and professional needs of teachers; equity, access and gender issues; and, affect, beliefs and identity.
-
c)
We searched the journals listed in (a), selected papers that satisfied the two aforementioned criteria, and recorded our work in a shared spreadsheet in which we kept account of citation information (authors, year, journal, abstract, keywords) and brief notes on each paper, including whether the paper relates to the areas described in (b). Finally, we drew on publications cited in the papers we reviewed to identify additional studies that met our two criteria or could provide a broader perspective on some of the issues we identified in our calculus-focused review (e.g., non-calculus specific studies regarding access to STEM).
-
d)
Areas (see (b)) that were connected to a small number of papers (less than 5) were not included in the review or were merged with other areas. This led to the four areas we discuss in "Calculus in the Transition Across Educational Levels", "Calculus and other Mathematical Areas", "Calculus for Engineers and other Non-Mathematics Professionals" and "Calculus for Mathematics Teachers". Within each of these areas, we identified the questions that guided our review.
-
e)
With the areas and the questions agreed, we read thoroughly the studies shortlisted in stage (c). During this stage, some initially selected publications were filtered out and others emerged from citations within the papers we were reading. Overall, we prioritized journal publications and book chapters over conference papers.
In what follows, we discuss findings in relation to the four areas we agreed in stage (d): calculus in the transition across educational levels; calculus and other mathematical areas; calculus for engineers and other non-mathematics professionals; and, calculus for mathematics teachers. Each section opens with the questions that guided our review in each area.
Calculus in the Transition Across Educational Levels
Issues related to the transition from secondary to tertiary mathematics have been discussed extensively in the literature (Biza et al., 2016; Gueudet, 2008; Hochmuth et al., 2021). Such studies identify tensions in relation to “(dis)connections between mathematics and between students’ attitudes, practices, and performances at school and tertiary level” as well as in relation to “the transition to abstraction and formal mathematical thinking” (Biza et al., 2016, p. 16). Calculus courses, specifically, have an essential role in the transitions across institutions and their practices (institutional role) and are essential in students’ first tertiary (or post-compulsory) experiences of mathematics (Bressoud et al., 2016), a role that is often at the heart of their decision to continue or not with STEM studies. In what follows, we synthesize insights from recent literature guided by the following questions: (1) What is the institutional role of calculus courses in the transition across educational levels? (2) What is the impact of this role on students’ experiences and study choices?
The Institutional Role of Calculus Courses in the Transition Across Educational Levels: Scaffolding and Filtering
Calculus courses are often institutionally located at critical positions in students’ pathways through secondary and post-compulsory education and towards their preparation for STEM studies (Thompson & Harel, 2021; Törner et al., 2014). In the studies we reviewed, we observed two (intended or unintended) roles of calculus courses in post-compulsory and/or early tertiary level: (a) calculus courses support students towards their preparation for STEM studies, and (b) success to those courses is part of the selection process towards STEM studies at tertiary level. This observation is not new, and several metaphors have been used in the past to highlight that the former role should prevail the latter: “pump rather than a filter” or “to become a door, not a barrier” (Steen, 1987, p. 12). In this section, we introduce a variation of the pump / filter metaphor, the metaphor of scaffolding, to describe the support calculus courses intend to offer towards students’ transition from one institution to another while maintaining the metaphor of filtering to describe the (intended or unintended) role of calculus courses in the selection of students who aspire to pursue STEM studies at tertiary level. These two roles are interconnected as we discuss in what follows.
In the educational contexts of the seven European countriesFootnote 4 discussed by Törner et al. (2014), calculus is offered in schools since the beginning of the twentieth century as an effort “to bridge the gap between mathematics at university and at school” (p. 550) (scaffolding). The described approach to calculus in schools is more intuitive, with less or no attention to proofs and more emphasis on student engagement, problem-solving, applications, modelling and the gradual introduction/use of digital technologies. Calculus is compulsory for students who aspire to pursue STEM-related studies and it is included in their university entrance examinations (filtering). Furthermore, teaching approaches are mainly procedure-oriented with a focus on student preparation for exams. Calculus notions are not introduced through their formal definition. Such informal introduction, “especially of the concept of limit, does not seem to encourage the progression to the formal definitions later at university” (p. 558).
In the US, calculus is offered in some schools (currently, 20% of high school students take calculus) while it is a prerequisite for selective colleges and universities (Bressoud, 2021). Because of the lack of uniformity in students’ background, many tertiary level institutions offer a series of calculus courses (Calculus I, II and III). Over 50% of the students who take Calculus I have already taken a calculus course in secondary school (Ellis et al., 2014). In comparison to secondary, Calculus I, II and III courses are usually more rigorous in the discussion of notions such as limits, graphical interpretations, definitions, etc., and applications of these notions. Proofs, however, are typically not part of these courses (Ellis et al., 2014). Tertiary level calculus courses serve as a prerequisite for STEM studies and filtering takes place during the first year of university studies (see also section "Calculus for Engineers and other Non-Mathematics Professionals"). For some of the students, a calculus course might be the last mathematical course they take (Bressoud, 2021).
Besides the European and the US educational systems, within which the majority of the studies we reviewed have been conducted, calculus courses in many countries play similar roles in terms of preparing the students at the upper secondary level (scaffolding) and then selecting (filtering) those who will continue for STEM studies – e.g., in Cameroon (e.g., González-Martín & Nseanpa, 2021), Canada (Hitt & Dufour, 2021), Israel (Dreyfus et al., 2021), Singapore (Toh, 2021), South Korea (Yoon et al., 2021) and Tunisia (Ghedamsi & Lecorre, 2021). In most of the cases we reviewed, calculus courses put limited attention to proof. Moreover, the integration of applications of calculus notions to real life or to non-mathematical problems varies. In some cases, applications are included in the secondary or post-secondary calculus curriculum (e.g., Bressoud, 2021 for the US; Törner et al., 2014, for some European countries), whereas, in other cases, research reports that examples and applications are scarce or are not emphasized by teachers (e.g., González-Martín et al., 2018, in Canada). Finally, there are cases in which calculus notions are discussed in mathematics courses while their applications are included in other courses such as physics (Lyublinskaya & Petrova, 2021, in Russia).
The scaffolding and filtering institutional roles of calculus courses are interrelated: students are allegedly prepared for their tertiary studies and this preparedness is assessed through university admission examinations (Toh, 2021; Törner et al., 2014; Yoon et al., 2021) or at the first year of university studies and before students proceed with their specialization (Bressoud, 2021; Ellis et al., 2014). However, teaching oriented towards high stake examinations intends to support students on the development of certain routines that may not be appropriate for their specialization at tertiary level (Frank & Thompson, 2021; Toh, 2021; Törner et al., 2014). We discuss this in section "Calculus for Engineers and other Non-Mathematics Professionals". Also, such filtering keeps students who have not been prepared appropriately away from STEM studies (Ellis et al., 2014; Frank & Thompson, 2021); we elaborate this in the discussion of the second question.
The Impact of Calculus Courses on Students’ Experiences and Study Choices: Different Experiences and Views of Filtering and Scaffolding
We now examine how the scaffolding and filtering institutional roles of calculus courses impact on student experiences and study choices. Calculus courses – especially elementary calculus courses such as Calculus I in the US – are essential in students’ first academic engagement with the tertiary institutions’ rules and routines and their decision to continue with their intended specialization (Ellis et al., 2014). Students who withdraw from STEM degrees “often cite traditional and uninspiring instruction that emphasized rote memorization rather than conceptual understanding and applications as one of the major reasons for their departure” (p. 662). However, not all students experience these first calculus courses in the same way (Ellis et al., 2014; Rasmussen & Ellis, 2013). Moreover, students’ experiences with calculus vary across populations with different demographic characteristics. For example, in the study of Ellis et al. (2014) higher percentages of female, Asian, Pacific Islander, American Indian or Alaska Native students decide not to continue with calculus. We note that some students persist after their failure in the first calculus course. Interested in these students, Dibbs (2019) followed – all the way to graduation – a group of students who had failed their initial calculus course and chose to retake it rather than change specialization. These students identified several reasons for their success in the repeated course: processing their initial failure; having a better instructor in the repeated course; and, participating regularly in the formative assessments. Although these studies were conducted in the US, and we cannot claim that these findings are readily transferrable to other educational contexts, the observation that different groups of students experience the same calculus course differently in the US calls for further investigation in other educational contexts as well.
Students’ earlier experience with calculus from secondary school (or post-compulsory education) is critical in their transition to tertiary studies in mathematics, but also to other STEM disciplines. College students in the US who have had prior exposure to calculus in secondary school perform “half grade higher in their college calculus courses” than students without such exposure (Sadler & Sonnert, 2018, p. 321). Bressoud (2021) acknowledges that the disparity in secondary school provision in calculus creates two downsides: first, students with different background end up in the same calculus class; and, second, students who cannot attend well-resourced public schools that offer calculus are disadvantaged compared to those who can. Therefore, he proposes strengthening “the high school preparation in calculus of all students” (Bressoud, 2021, p. 532, his emphasis). In a similar spirit, Frank and Thompson (2021) claim that “investigating students’ calculus experiences should also include investigation into their prior schooling” (p. 2).
It seems to us that there is no consensus between stakeholders involved in the teaching of calculus on what students’ preparation should consist of. Yoon et al. (2021) looked at how stakeholders and public opinions influenced the 2015 reform in the calculus high school curriculum in South Korea that led to a reduction of the calculus content taught at school level. Public opinion mainly from parents and students argues that calculus serves as a filter that generates excessive stress for college applicants and proposes the removal of calculus from the school curriculum. Tertiary level teachers do not agree with this argument and argue that calculus is essential in students’ preparation. We return to this point in section "Calculus for Engineers and other Non-Mathematics Professionals". In another study, Sadler and Sonnert (2018) asked 6,207 college calculus students and 216 college and high school teachers in the US their views about the best preparation for college calculus. Discrepancies between school and college teachers were observed in the responses: while high school teachers generally feel that students are well prepared, especially if they take calculus in high school, more college teachers, in comparison to school teachers, argue for more emphasis on student preparation of pre-calculus and algebraic notions at school level. We discuss the influence of students’ previous curricular experiences on their learning of calculus topics in section "Calculus and other Mathematical Areas" and we touch upon teachers’ professional development in relation to calculus teaching in section "Calculus for Mathematics Teachers".
Calculus and other Mathematical Areas
We now turn to the role of calculus in the transitions across mathematical areas met before, within and after calculus courses. In what follows, we synthesize insights from recent literature on mathematical learning and teaching guided by the following questions: (1) What are the issues in the transition across notions from pre-calculus to calculus or within calculus? (2) What is the role of calculus courses in the transition from procedural calculations to mathematical abstraction and reasoning?
Transition Across Notions from Pre-Calculus to Calculus or within Calculus: Attention to Changes in the Rules
The learning of calculus draws on students’ school experiences with pre-calculus notions such as functions, algebraic expressions, geometrical objects and representations (Biza, 2021; Frank & Thompson, 2021; Grant et al., 2016; Hitt & González-Martín, 2016; Thompson & Carlson, 2017). Such experiences are related to the curriculum students encounter (Biza, 2021; Byerley, 2019) and to their teachers’ expectations (Ayalon & Wilkie, 2019). Byerley (2019), for example, discusses the implication of three students’ fraction and measure schemes for their understanding of rate of change, while Biza (2021) looks at how tangent lines to circles and conic sections influence how students argue about tangent lines in calculus. In addition, essential ideas of calculus can be introduced with algebraic and geometrical routines without the use of limits. Some researchers argue that such routines are a better preparation for students as they overcome the formality of limits and their definition (Ely, 2021; Grant et al., 2016).
Several studies focus on the notion of function, a mathematical notion that is met in pre-calculus courses and has strong implications for the learning of calculus. Frank and Thompson (2021), for example, focus on three ideas pre-calculus addresses in school mathematics that have potential for students’ introduction to calculus (Calculus I in the US): variational reasoning, meanings for average rate of change, and representational use of function notation. Their study investigates manifestations of these ideas in Calculus I students’ responses, in secondary mathematics teachers’ responses and in pre-calculus textbooks. Their findings indicate similarities in meanings related to these notions held by teachers and students and those conveyed by textbooks. However, as the authors claim, such meanings are not always productive for understanding calculus (e.g., rate of change as average in large intervals or emphasis on functions as a calculation mechanism).
Recently, there has been more attention to changes in discursive rules (e.g., in relation to how we use definitions or regarding what makes an argument acceptable) in the transition from pre-calculus to calculus or within calculus. Learning about the differences in discursive rules is what Sfard (2008) calls metalevel learning. Such studies emphasize the importance of metalevel learning and propose teaching and learning approaches in which discursive rules are negotiated explicitly (e.g., Güçler, 2013, 2014, 2016; Schüler-Meyer, 2020). Here, we discuss three examples regarding changes in discursive rules: in the transition across mathematical areas (Biza, 2021), within one-variable calculus (Park, 2015) and from one-variable calculus to multivariable calculus (e.g., Trigueros et al., 2018).
Biza (2021) investigates how experiences with tangent lines across mathematical domains leave their marks on students’ subsequent work with tangents in calculus. The study’s commognitive analyses (Sfard, 2008) highlight the importance of students’ previous curricular experiences on how they learn in subsequent years. Specifically, Biza (2021) introduces the notion of the discursive footprint of tangents and its characteristics by reviewing how tangents are used across mathematical domains in school textbooks. Manifestations of this footprint are sought in undergraduate mathematics students’ responses to a questionnaire about tangents. Such manifestations include the identification of characteristics of sole (and combination of) discourses (geometry, algebra, calculus, real analysis) in student responses. For example, students’ responses demonstrate evidence in which geometrical properties (e.g., one point in common) are applied locally at a neighborhood of the tangency point. Students may also use terms such as derivative (calculus discourse) and only one common point (geometry discourse) in the same argument without explicit evidence of awareness that these terms are in conflict (intra-commognitive conflicts, see Kontorovich, 2019).
Park’s (2015) study focuses on changes in discursive rules within calculus, specifically on university teachers’ discourses about the derivative at a point and about the derivative as a function. Her findings indicate that teachers shift between both notions without realizing that students may not be aware, and may not follow, these shifts. Furthermore, students who are unaware of the differences between the derivative at a point and the derivative as a function might be reluctant to change routines that worked well for them for new ones without seeing the reason for doing so. This reason is less transparent when teaching emphasizes the procedures in the mathematical activities (how), by mostly focusing on actions (e.g., how we calculate the formula of a tangent line), and with less attention to why and when an existing or a new routine should be used.
Trigueros and colleagues discuss the transition from single variable functions to two- (or multi) variable functions (e.g., Trigueros et al., 2018). According to them, transition to three or more dimensions requires changes in the meaning of function and in the use of objects such as slope (e.g., from tangent line to tangent plane) and derivative (e.g., directional). Also, the visualization of graphs and slopes beyond two dimensions is not easy for students even when they manage to work out calculations with multivariable functions (Trigueros et al., 2018). As they argue, multivariable calculus “should not be considered as a simple generalization of one-variable calculus” (Trigueros et al., 2021, p. 94). In practice, the rules of how already known from single variable functions mathematical objects change in the transition to two- (or multi) variable functions.
Learning of calculus cannot be seen in isolation and without consideration of students’ previous experiences. Pre-calculus courses may fail to prepare students for what is coming in calculus whereas calculus courses may fail to acknowledge students’ previous experiences. Attention to changes in the rules can scaffold towards calculus learning but also towards what is coming after calculus (e.g., real analysis). We now discuss these opportunities for scaffolding.
The Role of Calculus Courses in the Transition from Procedural Calculations to Mathematical Abstraction and Reasoning: Opportunities for Scaffolding towards Reasoning and Abstraction
Returning to the role calculus courses play (or have the potential to play) in student introduction to abstraction and reasoning, we note that, in some educational systems, such as the US’s, calculus in the post-secondary curriculum is seen mostly as related to procedural calculations in comparison to real analysis that deals with abstraction and proving. Sometimes, Introduction to Proof (ITP) courses are seen as a bridge between calculus and real analysis, as they are “designed to support students in their mathematical training by bridging the gap between the calculus sequence, which typically focuses on calculation, and advanced mathematics courses that require skills in proof” (David & Zazkis, 2020, p. 388). In other studies, however, calculus courses are seen as a dynamic environment in which reasoning skills grow (Rasmussen & Keene, 2019; Schüler-Meyer, 2020). Such studies highlight that when calculus goes beyond applications of formulae and calculations, it can become a fruitful environment for the development of sophisticated reasoning skills (scaffolding).
Looking further on the transition from procedural calculation to abstraction, again more insight is needed into the differences between underpinning teacher and student practices. In the terms of the Anthropological Theory of Didactics (ATD, Chevallard, 1999) such differences reflect different praxeologies.Footnote 5 For example, Kondratieva and Winsløw (2018) argue that, in calculus, calculation practices focus on algebraic computational rules (praxis), which are rarely explained (logos) and are often allocated in different sections of the curriculum (e.g., differentiation techniques, integration techniques, differential equations, etc.). In real analysis courses, students learn about the theory (logos) that justifies the practices (praxis) they have seen in calculus. However, the connection is not explicitly negotiated. Kondratieva and Winsløw (2018) use the term “desyncretization of knowledge” (proposed by Verret, 1975) to describe how areas of tertiary mathematics “which were originally combined and united, for instance in the context of discovery, become separated again as they are taught” (p. 120). They propose a frame for early resyncretization experiences in calculus courses that can prepare students for real analysis. Such approach demands a careful design that connects the praxis that dominates calculus with the logos that characterizes real analysis.
We see that some studies consider calculus courses as fostering only procedural calculations, while other studies see the potential of those courses towards the transition from pre-calculus ideas to mathematical abstraction and reasoning (scaffolding). However, calculus courses are usually offered to large cohorts of STEM students, only a small number of whom will proceed with further mathematical studies that include abstraction and reasoning. Are the early resyncretization experiences (Kondratieva & Winsløw, 2018), the exploration of why and when of actions (Biza, 2021; Park, 2015) or the shift to formal narratives (Schüler-Meyer, 2020) appropriate for all the students who attend calculus courses? Whatever works as scaffolding for mathematics students might become just filtering for non-mathematics specialists. We return to this discussion in relation to engineers and other non-mathematics professionals in section "Calculus for Engineers and other Non-Mathematics Professionals". Furthermore, as we discuss in section "Calculus for Mathematics Teachers", the potential of highlighting connections between actions and reasons behind actions is maybe more pertinent for those who are trained at tertiary level to teach calculus at school (Winsløw & Grønbæk, 2014).
Calculus for Engineers and other Non-Mathematics Professionals
As we discussed in section "Calculus in the Transition Across Educational Levels", calculus courses play, explicitly or not, the institutional roles of filtering and/or of scaffolding in many academic programs for those who aspire to pursue further studies in mathematics as well as in other STEM disciplines – what Rasmussen et al. (2014) call client disciplines. We now focus specifically on calculus courses for these client disciplines with attention to how content and approaches are relevant to these disciplines. As discussed by Artigue et al. (2007), research on mathematics for non-mathematics professionals (NMPs) has received increasing attention due, among many reasons, to the increase of public accountability and scrutiny of instruction quality and student satisfaction in post-secondary institutions. However, they noted that much research on post-secondary mathematics education has been developed having in mind, implicitly or explicitly, “the mathematical education of “pure mathematicians” or mathematics teachers and their particular needs” (Artigue et al., 2007, p. 1013), and this was still the case ten years later (Artigue, 2016). It is, therefore, necessary to develop research investigating the relationships between calculus and these client disciplines (Rasmussen et al., 2014), with attention to the practices of these disciplines (Hitt & González-Martín, 2016; Yan et al., 2020). We note that mathematics teaching is seen as a part of the group of client disciplines by Rasmussen et al. (2014) while for Artigue et al. (2007) mathematics teachers are seen apart from NMPs. As mathematics teachers are expected not only to be confident with the mathematics they teach but also to draw on mathematics to inform their teaching and to address students’ needs (Ball & Bass, 2009; Wasserman, 2018a), in this paper, we have opted for the latter: we have separated teachers from other NMPs and section "Calculus for Mathematics Teachers" is entirely dedicated to tertiary calculus and mathematics teachers.
In what follows, we synthesize insights from recent literature around issues related to calculus and the training and practices of NMPs guided by the following questions: (1) What is the impact of the institutional roles of calculus courses for NMPs? (2) How do NMPs draw on content and approaches from calculus courses?
Impact of the Institutional Roles of Calculus Courses for NMPs: Filtering Rather than Scaffolding
As we mentioned in section "Calculus in the Transition Across Educational Levels", several studies indicate that calculus courses prevent many students from pursuing their intended career (filtering). Researchers have identified tertiary mathematics courses (in particular, calculus) as overemphasizing technical skills and rote memorization (Ellis et al., 2014) and being taught in a mathematical way (Loch & Lamborn, 2016). These reasons are probably among those resulting in first-year calculus high failure rates (Artigue et al., 2007) and high dropout rates (Ellis et al., 2014), particularly in engineering programs (Faulkner et al., 2019, 2020). In a large survey conducted in the US (Ellis et al., 2014), the results indicate that students in medicine, business and engineering, as well as those who are yet to decide their specialization, may change specializations after their first calculus (Calculus I) experience. We observe that engineering is one of the client disciplines with more studies about retention issues. For instance, Faulkner et al. (2019) discuss that “many students drop out of engineering not because they have failed an engineering course, but because they failed a mathematics course” (p. 98). In these programs, the strictness of the “core math sequence” (p. 98) – Calculus I, II or III, linear algebra, and differential equations – may also disadvantage students who lacked access to secondary school calculus (Faulkner et al., 2019), as well as female and minority students (Faulkner et al., 2020), as we also discussed in section "Calculus in the Transition Across Educational Levels". It is natural to wonder why calculus courses appear in the first year of many STEM programs. In the case of engineering, historically, it seems that the institutional role of calculus has been guided by the origins of the École Polytechnique, founded in 1794 in France, whose model was followed by many engineering programs in the world. Due to the decline of geometry in the nineteenth century and the rise of real analysis, Lagrange and Laplace had a critical role in introducing the study of real analysis in the training of engineers (Belhoste, 1994; González-Martín et al., 2021). If the needs of current engineers are different than those at the end of the eighteenth century, then the purpose of calculus courses towards the preparation of engineering students (scaffolding) might be compromised to mostly filtering those who can continue.
Reports from the workplace provide contrasting information about the scaffolding role of calculus courses in the preparation of NMPs. Quéré (2019) launched an online survey that was completed by 261 French engineers. Of these participants, only 24% believed their university mathematical training was adequate for their professional needs (with 51% reporting it as insufficient). Of the 129 (49.4%) participants who declared an actual need of university mathematics at work, only 43% (21.24% of the entire sample) said they required the knowledge learned in their calculus courses. This result calls for more research into the specific content of calculus that is used, and in what professional activities this content is needed. Such research may provide feedback for calculus course design, such as what content can be left out, or what modelling activities can be integrated (see some recommendations for mathematics courses from Faulkner et al., 2019, and for calculus courses from González-Martín, 2021). The results of Quéré’s survey are consistent with previous reports about the actual use of mathematics by engineering professionals (e.g., Kent & Noss, 2003). Such observations challenge the prominent presence of calculus courses in certain STEM study programs, in principle with scaffolding purposes, that result in high rates of failure (becoming rather a filter), while NMPs state they do not actually need these courses. We develop this point in the next section.
NMPs’ (Non) Use of Content and Approaches from Calculus Courses: Questioning Transferability and Relevance
Regarding how calculus content can prepare students’ work in other disciplines (scaffolding), in the case of engineering, faculty members who teach courses that have calculus as a prerequisite have stated that calculus is required “for mathematical maturity more than just the actual calculus” content, because “the way [the engineering course] is taught, you can do it without calculus” (Ferguson, 2012, cited by Faulkner et al., 2019, pp. 98–99). Faulkner et al. (2019) note that faculty teaching engineering courses having mathematics courses as prerequisite or co-requisite agree that their students have difficulties with: using and interpreting mathematical models; choosing and manipulating symbolic and graphical expressions; and, using computational tools. For instance, the participants complained about their students’ difficulties to “set up integrals and derivatives to describe physical situations” (p. 112) and that these students have a vision of calculus as just equations, preventing them from “capturing the underlying physical principles” (p. 113). Similarly, Hitt and Dufour (2021) identified college students’ difficulty to solve problems in context and to transfer knowledge from calculus to physics (e.g., in the articulation of mathematics and kinematics notions in motion problems).
Similar difficulties have also been reported in economics – such as students’ difficulties to set up, from a contextualized problem, the function that needs to be optimized (Mkhatshwa, 2019) – confirming “students’ tendency not to reason in the context of a task when interpreting quantities while solving contextualized problems” (p. 1120). Jones (2015, 2017) provides insight into how university students, who have passed a calculus course, are not able to capture physics principles, and discusses whether activities emphasized (or not) in calculus are relevant to physics. Specifically, Jones (2015) showed how the ‘area under a curve’ and ‘anti-derivative’ conceptualizations of integrals (compared with the ‘adding up pieces’ conceptualization) are less helpful to understand physics situations involving density, revolutions, pressure, or force. These physics interpretations are present in other disciplines (such as engineering). Regarding derivatives in non-kinematics contexts, Jones (2017) observed students’ low level of covariation-based reasoning. Furthermore, the interpretation of the independent variable as time – which is typical in applied problems in calculus – produced task-solving difficulties for some participants. In addition, students’ grasp of the various symbols (constants, parameters, variables) in a formula when considering derivatives was inaccurate. This resonates with concerns expressed by engineering faculty (Faulkner et al, 2019). Students’ interpretations of phenomena with negative rate of change have also been reported to be challenging (e.g., Ärlebäck & Doerr, 2018; Hitt & Dufour, 2021). These studies indicate that content and approaches of calculus courses may not be transferred or may not be relevant for transfer to other disciplines.
We now discuss some studies that report on the use (or lack thereof) of calculus content and approaches in other disciplines. González-Martín (2021) analyzed the use of integrals in two engineering courses (Strength of Materials and Electricity and Magnetism) in reference books and teaching practices. The results indicate that integrals underlie the development of techniques proper to the discipline, and that, in these courses, they are used as an addition of infinitely small things – their ‘adding up pieces’ conceptualization, resonating with Jones’ (2015) results. However, in practice, these techniques are mostly reduced to the use of ready-to-use formulae and geometric calculations. When the calculation of an antiderivative is necessary, the functions under consideration are usually very simple, putting into question the large amount of time typically dedicated in calculus courses to learn integration techniques of complicated functions. This resonates with Faulkner et al.’s (2019) results, showing that “the sentiment that students need fewer fancy techniques and more computational skills was universal [in their engineering faculty participants], regardless of engineering discipline” and that “disciplines agreed that students need not memorize formulas for infrequently used techniques of integration” (p. 118). Moreover, González-Martín’s (2021) analyses show the entanglement of rationales from calculus and from engineering, leading to justifications that could be seen as lacking the rigor of mathematics, but that are adequate to the practices of engineering (see also González-Martín & Hernandes-Gomes, 2020, for more details).
In the same vein, Faulkner et al. (2020) analyzed engineering coursework to see how well the content of calculus aligns with the mathematics used in the early engineering courses on circuits and statics. They arrive to similar results, showing the limited application of calculus ideas in both courses (8% and 20% of the coursework, respectively), as well as differences in the use of calculus content between the mathematical prerequisite course and subsequent engineering courses. Among the main differences between practices in calculus courses and in these courses, Faulkner et al. (2020) highlight: 1) the use of the simplest functions among those studied in calculus; 2) the ampler presence of discontinuous functions in the engineering courses; 3) a simpler use (or even non-use) of limits; and, 4) the reduction of many techniques to algebra and geometry. As Faulkner et al. (2020) note, the application of limits in circuits and statics is much simpler and less mathematically rigorous than the application of limits in calculus courses. This can be traced back to the historical development of these fields - for instance, “calculus had been used to develop beam theory […] nearly a century before the first epsilon-delta limit proof was published” (p. 417).
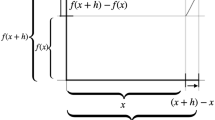
In economics, Feudel and Biehler (2021) discuss how derivatives are used to define marginal cost – the additional cost of the last unit – considering that one unit is usually small in economics. Therefore, the expression of the additional cost of the next unit C(x + h) – C(x) ≈ C΄(x).h when h ≈ 0, becomes C(x + 1) – C(x) ≈ C΄(x) when we consider h = 1. Two main differences between C΄(x) and the additional cost of the next unit need to be considered: 1) derivatives are a rate of change, while the additional cost is an amount of change; 2) mathematically, C΄(x) is generally an inaccurate approximation for C(x + 1) – C(x). It is thus important that economics students are aware of these differences and are able to relate the mathematical use of derivatives with its specific use in economics. However, Feudel and Biehler’s (2021) study shows students’ difficulties to grasp these nuances.
In contrast to the examples we listed so far in which calculus courses fail to fulfil their scaffolding purpose, there exist studies in which calculus courses tailored for a specific student profile seem to be more successful in this regard. Czocher (2017), for example, reports on a differential equations course for NMPs taught with modelling principles. Regarding tailored calculus courses for engineers, to gain more insight on what can make these courses successful, Ellis et al. (2021) analyzed two calculus courses in two US universities. One of the courses was successful while the other was discontinued. The criteria identified for the success were: “a) changes were embedded into the core departmental business; b) a noticeable improvement in student engagement was evident; c) long-term impact evaluations were carried out; and d) an ongoing focus on educational innovation and/or research was evident” (p. 382). Therefore, the researchers argue that “sustaining an innovative mathematics course for engineering students requires deep commitments among influential actors from both the engineering and mathematics communities” (p. 396). In spite of these challenges, we stress that calculus courses designed for specific disciplines seem to have higher passing rates than other calculus courses (Voigt et al., 2020). It seems, therefore, necessary to gain more insight into what makes calculus courses offered to NMPs more successful in comparison to others.
Calculus for Mathematics Teachers
Calculus is an essential aspect of the preparation and professional development of teachers in many countries around the world (Tatto et al., 2010; Thompson & Harel, 2021). For example, in the US, the Conference Board of the Mathematical Sciences (CBMS, 2012) has recommended that preparation of high school teachers comprises at least a three-course sequence of single- and multi-variable calculus, complemented by a proof-based calculus course. A similar recommendation was made in Israel by the Knowledge Base for Teaching Secondary School Mathematics Committee, who asserted that infinitesimal calculus “must be the cornerstone of the mathematical part of the teacher’s training” (Gutfreund & Rosenberg, 2012, p.55). We note that, in both cases, teachers are recommended to study calculus content that extends above and beyond what the teachers are expected to teach at school in the respective countries. Hereafter, we refer to content and approaches of calculus that are not part of the secondary curriculum of the educational system under consideration as tertiary calculus.
Rationales given for the central role of tertiary calculus in teacher education often attend to how such courses develop teachers’ knowledge of calculus and teachers’ knowledge about mathematics (Even, 2011), and how these two kinds of knowledge can scaffold the work of teaching mathematics. For example, the CBMS report (2012) suggests that studying tertiary calculus can help prospective teachers in bringing together many of the ideas in high school mathematics, in deriving results that may have been taken for granted in high school, and in clearing up common confusion among expressions, equations, and functions. We note the emphasis on how tertiary calculus has the potential to support the development of knowledge and proficiency pertinent for teaching calculus, as well as other mathematical domains, which is well aligned with the metaphor of calculus as scaffolding. At the same time, the CBSM report also stresses the important role of tertiary calculus, among other tertiary mathematics courses, in providing prospective teachers with experiences needed for developing “the habits of mind of a mathematical thinker and problem-solver, such as reasoning and explaining, modeling, seeing structure, and generalizing” (CBMS, 2012, p. 19). Here again, calculus is seen as scaffolding the professional development of teachers by promoting their understanding and appreciation of mathematics as a discipline, as well as their ability to work in ways characteristic of the discipline.
The disposition that tertiary mathematics courses scaffold school mathematics teaching is consistent with (and often supported by) a long list of studies (e.g., Ball & Bass, 2009; Schoenfeld & Kilpatrick, 2008; Wasserman, 2018a; Zazkis & Mamolo, 2011) and position papers (e.g., Cuoco, 2001; Wu, 2011). Nevertheless, there is relatively little empirical evidence that can support this disposition, and in recent years, the contribution and relevance of tertiary calculus, as well as other tertiary mathematics courses, to school mathematics teaching is undergoing increased scrutiny. Empirical research accumulated over the last decade suggests that the contribution for teachers that is attributed to such courses may not be realized in school teaching (Ticknor, 2012; Wasserman et al., 2018; Winsløw & Grønbæk, 2014; Zazkis & Leikin, 2010). Specifically, these studies indicate that pre-service teachers taking such courses find them unproductive and irrelevant for their future profession, while practicing teachers find it difficult to cite specific examples in which their learning experiences in tertiary mathematics courses were applicable in their teaching.
Growing recognition of the difficulty in translating learning experiences in tertiary mathematics courses to knowledge teachers can draw on in and for mathematics teaching has sparked increasing efforts to explicate the role of tertiary mathematics courses in teacher education. In what follows, we focus on tertiary calculus and synthesize insights from recent literature guided by the following questions: (1) How can tertiary calculus scaffold school mathematics teaching? (2) How are content and approaches usually present in tertiary calculus courses addressing teachers’ needs?
How Tertiary Calculus can Scaffold School Mathematics Teaching: The Pursuit for Empirical Evidence
The question of the contribution of tertiary mathematics to school teaching was posed already more than a century ago by the renowned mathematician Felix Klein, who identified and drew attention to the discontinuity between teachers’ experiences of studying mathematics at university and of teaching mathematics at school (Kilpatrick, 2019). Nevertheless, our knowledge and understanding of the actual contribution of tertiary courses in general, and of tertiary calculus in particular, are still far from satisfying (Even, 2011; Wasserman, 2018a, 2018b; Zazkis, 2020; Zazkis & Leikin, 2010). Moreover, documented examples of how teachers draw on content or approaches from tertiary mathematics courses in teaching are fairly rare (Zazkis, 2020). Consequently, the explication of how tertiary calculus can scaffold the work of teachers is based more on theoretical speculation and personal experience than on systematic, evidence-based inquiry.
This situation started to change over the last decade, when empirical studies of the affordances of tertiary mathematics for school mathematics teaching started to accumulate. Wasserman (2018b) provides a notable such example in the area of abstract algebra. Studies that attend specifically to the relevance and contribution of tertiary calculus courses for teachers are only starting to emerge, and mostly attend to proof-based courses (Hoffmann & Even, 2021; Mytlis & Even, 2021; Wasserman et al., 2018; Weber et al., 2020; Yan et al., 2020). For example, Hoffmann and Even (2021) identify three broad areas of contribution of tertiary calculus courses for teachers: knowledge of the essence of mathematics, knowledge of doing mathematics, and knowledge of the worth of mathematics. Yan et al. (2020) refined and elaborated these three areas in the context of real analysis on the basis of interviews of 24 research mathematicians. They found that the mathematicians expected tertiary calculus courses not only to help prospective teachers deepen their understanding of the topics they will be teaching in school but, among other goals: to communicate the nature of mathematics and promote disciplinary values and practices related to formalism, proof, and rigor; to provide opportunities for mathematical investigation; and, to highlight the human dimension of mathematical activity.
We observe that the above list of goals is well aligned with the common perception of how tertiary calculus may scaffold teachers’ knowledge about mathematics (e.g., CBMS, 2012). However, there is very little empirical research that explains whether and in what sense these goals are achieved. A few empirical studies that have explored calculus and real analysis courses for teachers from the teacher’s side warn that such courses may only have limited impact on school teaching if they attend to mathematical content and approaches without also providing teachers with opportunities to realize how they could draw on such content and approaches in the context of teaching the school curriculum (Wasserman et al., 2018; Winsløw & Grønbæk, 2014). A possible conclusion is that the scope of calculus in teacher education should be extended to include also explicit and elaborated discussions of the utilizations of tertiary calculus in and for mathematics teaching. Wasserman and Weber (2017) note that identifying such utilizations is far from straightforward, in part because these utilizations may be nonlocal in the sense of not being restricted to teaching content in the school curriculum in close proximity to calculus, as calculus may inform teaching in various mathematics areas (Wasserman, 2018a). Zazkis (2020) agreed with Wasserman (2018a), and observed further that the ways in which teachers draw on tertiary mathematics in teaching are often tacit and personal, which may explain the innate difficulty in recognizing, documenting, and explicating the ways in which tertiary calculus actually scaffolds teaching.
Nevertheless, this review suggests that there is a slow but persistent accumulation of empirical studies of the connections between tertiary calculus and school teaching and of the utilizations of these connections in school teaching. There are some initial indications that attending explicitly to these connections and utilizations may support teachers’ motivation and engagement in tertiary calculus courses (McGuffey et al., 2019) as well as teachers’ preparedness for the classroom (Biza et al., 2018). Biza et al. (2018) describe a course for prospective and practicing mathematics teachers with a focus on the teaching of calculus. Course participants were invited to engage with fictional, yet data grounded classroom situations (“mathtasks”) in which student or/and teacher responses are inspired by commonly reported issues related to calculus. Analyses suggest that deploying activities that combine the calculus content together with pedagogical issues related to the teaching of this content may contribute towards the identification – as well as reflection upon and development – of mathematics teachers’ diagnostic competences in teacher education and professional development programs.
The Content of Tertiary Calculus Courses and the Needs of Teachers: An Apparent Misalignment
While the literature on the affordances of tertiary calculus for school teaching is scarce and often does not specify how these benefits might manifest themselves in teaching, insight into our second question may be drawn from the accumulating body of research of secondary calculus teachers’ knowledge of and meanings for calculus. For example, one line of studies compared US and South Korean teachers’ mathematical meanings for core notions in calculus, such as covariational reasoning (Thompson et al., 2017), function notation (Yoon et al., 2021) and slope and rate of change (Byerley & Thompson, 2017). These studies highlighted certain mathematical meanings that should be targeted by calculus courses for teachers (in the US, but presumably in other countries as well), such as “function notation as a means to represent one quantity’s values in relation to another quantity’s values” (Yoon & Thompson, 2020, p.15) or “conceptualizing and representing the simultaneous variation in two quantities’ values” (Thompson et al., 2017, p. 109). Similarly, Moore et al. (2019) studied teachers’ meanings for graphs and their conventions and notations, such as the direction and orientation of axes, and found that the teachers in their study, who had completed the tertiary calculus sequence, had “developed mathematical meanings that, at best, limit their ability to attribute mathematical viability to school mathematics concepts presented unconventionally” (p.192). Other studies have attended to teachers’ understandings of students’ slope statements (Styers et al., 2020), and of the density of irrational numbers in the real numbers (Marmur et al., 2020).
Whereas the studies reviewed in this section have attended explicitly to tertiary calculus courses in teacher education, they highlight teachers’ views on and understandings of calculus that differ from, and in some ways may come in conflict with, content and approaches usually present in tertiary calculus courses. This apparent misalignment between tertiary calculus courses and school calculus teaching raises the question as to how appropriate the content and approaches of current tertiary calculus courses are for preservice teachers, and whether teachers should be given more opportunities to re-visit calculus as practicing teachers in programs that attend explicitly to the aforementioned misalignment.
Attending to the Scaffolding and Filtering Roles of Calculus at the Intersection of Institutions, Disciplines, and Communities: Discussion and Ways Forward
To examine the question How do calculus courses address the varied – sometimes conflicting – goals, values, and needs of different institutions, disciplines, and communities?, we reviewed recent research literature, mostly since 2015, around four interrelated areas: calculus in the transition across educational levels; calculus and other mathematical areas; calculus for engineers and other non-mathematics professionals (NMPs); and, calculus for mathematics teachers. Our review highlights an intrinsic tension between two institutional roles of calculus courses: scaffolding and filtering. The role of scaffolding relates to supporting students towards their transition to STEM studies whereas the role of filtering relates to high failure and dropout rates, which limit the number of students accessing STEM studies. We find nuanced yet substantial variation in how the dual role of calculus courses is experienced and managed across different groups of students and stakeholders. With regard to studies on calculus for mathematics students, some recent studies are more attentive to changes in the rules underpinning calculus notions and processes, and highlight the scaffolding potential of calculus courses towards abstraction and reasoning. In contrast, studies on calculus for NMPs report that such courses often favor filtering rather than scaffolding and question transferability and relevance of those courses for NMPs. Finally, studies challenge the perception that traditional tertiary calculus courses scaffold school teaching and underline the need for empirical research that would explain the nature of this scaffolding and how it can be realized in practice. In this section, we synthesize our findings across the four review areas and discuss the variations in how the dual role of scaffolding and filtering of calculus courses is experienced to challenge the view of calculus courses for all groups of students and to propose areas of further investigation together with theory developments with affordances towards such investigations.
In terms of scaffolding, in several studies, calculus courses are seen as an opportunity to introduce students to proof and mathematical abstract thinking, which are taken to be relevant for mathematics students at large. However, looking at how calculus courses are perceived by NMPs, such as engineers and economists, it seems that these courses centralize content and approaches that do not always match the needs and practices of future NMPs. Similarly, studies have indicated that tertiary calculus courses are not tailored well enough to the professional needs and practices of school mathematics teachers. Although these courses are offered to benefit teachers and improve the quality of school teaching, in practice, the learning gains do not seem to be reflected in teachers’ toolkits for teaching and these courses are not recognized by teachers as relevant or beneficial for their profession. In terms of filtering, the reviewed literature suggests that students who have not been prepared adequately in their upper secondary calculus courses may find it more difficult to continue their studies at the tertiary level. Also, students who have entered tertiary level education may dropout or be forced to change their academic path due to transition-related issues, which are particularly severe in tertiary calculus courses. The filtering effects of calculus seem to have greater impact on groups with certain demographic characteristics (e.g., gender or ethnic origin, Ellis et al., 2014) or on those who do not have access to well-resourced schools that can prepare them for calculus (Bressoud, 2021). Thus, gender, ethnic origin or socioeconomic status might be lurking factors that contribute to keeping students away from advancing to and within STEM studies. Furthermore, as we mentioned earlier, calculus courses do not seem to address the needs of NMPs. This has ethical and social implications: many students are filtered out because they failed a course that does not seem to be entirely relevant to their study specialization, not because of their lack of preparedness for such specialization.
Through our review, it seems that further attention is needed, both in research and practice, to the diverse needs of specific groups (mathematics students, NMPs and prospective and practicing teachers) who are the intended beneficiaries from calculus courses. Very often research on the learning and teaching of calculus does not address the specific needs of groups of students and teachers who are involved. We would like to challenge a research view of calculus courses for all students – without consideration of the different student cohort needs and diverse study programs that calculus courses are part of.
In the case of NMPs, calculus courses – as a pre-requisite or as an introduction to STEM courses – are assumed to provide future professionals with a mathematical toolkit and a vision of mathematics that will make them more efficient in their profession. The studies we reviewed in section "Calculus for Engineers and other Non-Mathematics Professionals" report that several professionals state that they do not need these courses and that the technical skills typically emphasized in calculus courses do not seem to be necessary in their professional practice. Moreover, the analysis of professional practices shows that, even when calculus is used, such use does not always necessitate the same techniques and rationales as in mathematics. Thus, it may be reasonable to challenge the assumption that calculus courses per se make better professionals, or that their content is easily transferred to other subjects. Further research should investigate the differences and connections between practices in calculus and the use of calculus in other areas – see, for instance, calculus and mechanics in Hitier & González-Martín (this issue). We also note that many of the studies related to NMPs we reviewed are written from the mathematics education point of view while they discuss the teaching and learning of other disciplines. We advocate for a balance input from mathematics educators and educators of other disciplines at practice and research levels.
In the case of scaffolding for mathematics teachers, we identified two emerging areas of research. Firstly, by and large, descriptions of the benefits of calculus courses tend to be underspecified, and documented examples of teachers’ utilizations of tertiary calculus in their teaching are relatively rare, possibly because teachers typically find it difficult to cite instances in which they draw on tertiary mathematics in their teaching (Zazkis & Leikin, 2010), or because such utilizations of calculus are tacit and personal (Zazkis, 2020). Therefore, there is need for more systematic investigations into such affordances. One methodology for producing such examples, which has been successfully implemented in a recent line of studies, is to scan the syllabuses of academic courses and identify potential pedagogical implications of topics therein (Wasserman & Weber, 2017; Weber et al., 2020). Pinto and Cooper (this issue) propose and demonstrate a different methodology in which small groups of research mathematicians and experienced secondary mathematics teachers view videotaped secondary mathematics lessons and jointly inquire into mathematical issues and pedagogical dilemmas that they recognize therein, bringing forth the knowledge and expertise of these two communities. Regarding the second area of emerging research, while there are only a few such studies to draw on, they seem to indicate that teachers may find more value in tertiary mathematics courses if they attend them as practicing teachers compared to teachers that attend such courses before gaining teaching experience (Even, 2011; Hoffmann & Even, 2021; Mytlis & Even, 2021; Pinto & Cooper, this issue). Therefore, in the future, it may be helpful to differentiate between prospective and practicing teachers when exploring teachers’ processes of learning and utilizing tertiary calculus, and how experience and expertise in school teaching may support these processes.
We note that in our literature review we could not locate an explicit discussion of the filtering role of tertiary calculus in teacher education. We find this noteworthy for at least two reasons. First, the absence of a discussion of the filtering role of tertiary calculus in teacher education stands out in its contrast to the abundance of evidence of the filtering role of tertiary calculus in other client disciplines (e.g., Ellis et al., 2014; Rasmussen & Ellis, 2013). Secondly, the acute role of tertiary calculus in the secondary-tertiary transition is well documented, and one would expect that tertiary calculus would have an even more acute role in teachers’ transition back and forth between learning secondary mathematics, to learning tertiary mathematics, and to teaching school mathematics, particularly since preservice teachers often find tertiary calculus courses to be unproductive and irrelevant for their future profession. Thus, there is space for research that investigates whether and in what ways tertiary calculus may play a filtering role for teachers.
We note that we have encountered a small number of studies that attended to perspectives and practices of tertiary teachers who teach calculus courses for NMPs (e.g., González-Martín & Hernandes-Gomes, 2021) and teachers (Moreno-Armella, 2021; Yan et al., 2020). González-Martín and Hernandes-Gomes (2021), for example, discuss how tertiary teachers with different background conceptualize in different ways what applications for engineering in a calculus course would be. In the case of teachers, Moreno-Armella (2021) narrates the experiences of one tertiary teacher in a calculus course for teachers over several semesters and illustrates that calculus courses for teachers may be adapted in ingenious ways. We still have very little information about adaptations of calculus courses to specific disciplines and the rationales behind these adaptations. Furthermore, more research is needed on what characteristics make calculus courses adapted to specific disciplines successful (e.g., Ellis et al., 2021). Again, we anticipate that joint teams across disciplines will provide important insights towards the design and the evaluation of these courses.
Another area in which we did not identify a critical body of literature for our discussion regards diversity, equity, and inclusion (DEI) in relation to calculus courses. We have reported on large surveys that have identified issues of underrepresentation and retention of students with certain demographic characteristics (Ellis et al., 2014). In recent years, increased efforts are invested in the study and conduct of teaching approaches that could disrupt negative discrepancies and support equitable learning opportunities, for example inquiry-based learning and inquiry-oriented learning (Laursen & Rasmussen, 2019). Yet the nature of instruction that promotes DEI is still mostly an uncharted research area. Two studies in this special issue help to start addressing this gap. Leyva et al. (this issue) examined practices that are generally perceived as supporting equitable learning from the perspective of calculus students and found that these practices are insufficient to cultivate equitable opportunities in calculus courses. Tremaine et al. (this issue) propose a framework for identifying the motivations of different stakeholders in calculus programs towards attending to DEI, and demonstrate how this framework can help to highlight strengths and areas in need of growth, thus fostering and facilitating productive communication about DEI within calculus programs. However, more studies are needed that zoom-in on the diverse experiences of calculus students and on how instructional approaches can support equitable opportunities in calculus courses.
In our review, we noted that studies on affect, beliefs and identity, although with increasing presence in our field at large, rarely focus on calculus specifically. Given that a range of these studies are on transition from school to tertiary studies, calculus is often merely the context rather than the focus of the research. This is a signal that more research is needed on how calculus courses, which are so critical in the transition from school to tertiary level, impact on students’ beliefs, affect and identity building in relation to mathematics. This is also related to mathematics teachers and other professionals.
We also note that a substantial body of the studies we reviewed were conducted in the US or Europe. In awareness of the significance that contextual and sociocultural characteristics of the educational systems in which research is conducted has on findings, we cannot claim that our findings are automatically applicable to other educational contexts. However, some observations and conclusions of these studies – such as how different groups of students experience the same calculus course differently or are prevented from continuing their STEM studies – might be (e.g., González-Martín & Nseanpa, 2021, for the case of Cameroon). To this end, it is crucial to look closely at how the teaching and learning of calculus vary across countries and educational contexts, as done for instance by Viirman et al. (this issue), who show important differences in content and approaches of calculus courses across three European countries, and three educational levels therein.
Studies that address the diverse roles of calculus at the intersection of institutions, disciplines and communities need support from theoretical perspectives that can capture the goals, the rules and the values of these institutions, disciplines and communities effectively. We see some capacity for this in socio-cultural, institutional and discursive perspectives (Nardi et al., 2014). Yoon et al. (2021), for example, argue that there is a need of a “socio‐political perspective on the deliberation process regarding mathematics curriculum” (p. 2) that can employ methodologies beyond “traditional mathematics education research”, such as discourse and content analysis of curricular documents, textbooks, media, public reports, etc. Such theoretical and methodological perspectives have the capacity to contextualize teaching and learning experiences and to study curricular changes in relation to stakeholder and public perceptions of calculus.
Furthermore, a common characteristic in studies that attend to the intra-mathematical, interdisciplinary and intra-calculus differences in the use of calculus notions is the contextualization of such differences in terms of students’ curricular experiences. Some of the studies we reviewed describe such differences either as a change of discourse (e.g., Biza, 2021; Güçler, 2013, 2014, 2016; Park, 2015) or change of institutionally embedded praxeologies (e.g., González-Martín, 2021; Kondratieva & Winsløw, 2018). These studies propose that bringing discursive and institutional differences upfront and making clear connections between the different ways in which calculus terms are used can demystify mathematical meanings and enculturate students to how mathematical ideas develop and are inter-connected. In this sense, the studies by Broley and Hardy (this issue) and Bašić and Milin Šipuš (this issue) show how practices in calculus can be very distant from practices in subsequent courses such as real analysis or multivariate calculus, and highlight the necessity to address these differences explicitly. Calculus courses can therefore provide an ideal environment to initiate such enculturation, especially in relation to the transition of practices from calculations to abstract thinking for mathematics professionals or to modelling for NMPs or to reflecting on school mathematics for teachers. Similarly, studies on the needs of teachers and other professionals need to consider the values and the practices of these communities explicitly. A blanket approach to calculus teaching cannot address the disciplinary needs of different groups and cannot address the differences in student background either. It is thus important not only to be attentive to the learning of certain topics of calculus (e.g., limits, derivatives, integrals, etc.), but also to enquire about what certain groups of students, professionals and teachers need to learn about these topics and why. Such enquiries may yield calculus courses that serve the purposes of scaffolding together with filtering through – and not filtering out – those who aspire to continue with STEM studies.
Notes
For the purpose of this paper, we use the acronym STEM, which was initially proposed for Science, Technology, Engineering, and Mathematics, with S representing also Social Science subjects such as Psychology, Economics or (Teacher) Education.
Post-compulsory education is for students who follow specialised pathways towards admission to tertiary education. In some systems, post-compulsory courses are offered in school, while, in other systems, these courses are offered in further education institutions (e.g., colleges) or they are introductory courses offered by tertiary institutions (e.g., pre-university or foundation courses). Upper secondary level might be post-compulsory as well (in many countries, compulsory education ends at the age of 16).
The title of these courses may include the terms “calculus” (e.g., Calculus I, II and III in the US) or “ Infinitesimal Calculus” (e.g., in Greece or Israel) or may not include any reference to calculus (e.g., “Matemáticas I” at college in Spain).
Belgium, Cyprus, France, Germany, Greece, Italy and UK-England.
In ATD, knowledge is seen as including practical action (tasks and techniques; praxis), as well as the rationales about them (technologies and theories; logos). A praxeology is a basic unit used to analyse human action in general in the light of said praxis and logos.
References
Ärlebäck, J. B., & Doerr, H. M. (2018). Students’ interpretations and reasoning about phenomena with negative rates of change throughout a model development sequence. ZDM, 50(1–2), 187–200. https://doi.org/10.1007/s11858-017-0881-5
Artigue, M. (2016). Mathematics education research at university level: achievements and challenges. In E. Nardi, C. Winsløw & T. Hausberger (Eds.), Proceedings of the First Conference of the International Network for Didactic Research in University Mathematics (pp. 11–27). University of Montpellier; INDRUM.
Artigue, M., Batanero, C., & Kent, P. (2007). Mathematics thinking and learning at post-secondary level. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 1011–1049). Information Age Publishers.
Ayalon, M., & Wilkie, K. J. (2019). Exploring secondary students’ conceptualization of functions in three curriculum contexts. The Journal of Mathematical Behavior, 56, 100718. https://doi.org/10.1016/j.jmathb.2019.100718
Ball, D. L., & Bass, H. (2009). With an eye on the mathematical horizon: Knowing mathematics for teaching to learners’ mathematical futures. [Paper presentation]. 43 Jahrestagung der Gesellschaft fur Didaktik der Mathematik, Oldenburg, Germany. https://eldorado.tu-dortmund.de/handle/2003/31305. Accessed 20 April 2022.
Bašić, M., & Milin Šipuš, Z. (this issue). Geometrical reasoning in teaching and learning of integrals of multivariable functions. International Journal of Research in Undergraduate Mathematics Education.
Belhoste, B. (1994). Un modèle à l’épreuve. L’Ecole Polytechnique de 1794 au Second Empire. In B. Belhoste, A. Dahan-Dalmedico & A. Picon (Eds.), La Formation Polytechnicienne 1774–1994 (pp. 9–30). Dunod.
Bingolbali, E., Monaghan, J., & Roper, T. (2007). Engineering students’ conceptions of the derivative and some implications for their mathematical education. International Journal of Mathematical Education in Science and Technology, 38(6), 763–777. https://doi.org/10.1080/00207390701453579
Biza, I. (2021). The discursive footprint of learning across mathematical domains: The case of the tangent line. The Journal of Mathematical Behavior, 62, 100870. https://doi.org/10.1016/j.jmathb.2021.100870
Biza, I., Giraldo, V., Hochmuth, R., Khakbaz, A. S., & Rasmussen, C. (2016). Research on Teaching and Learning Mathematics at the Tertiary Level: State-of-the-art and Looking Ahead. SpringerOpen. https://doi.org/10.1007/978-3-319-41814-8
Biza, I., Nardi, E., & Zachariades, T. (2018). Competences of mathematics teachers in diagnosing teaching situations and offering feedback to students: Specificity, consistency and reification of pedagogical and mathematical discourses. In T. Leuders, K. Philipp, & J. Leuders (Eds.), Diagnostic Competence of Mathematics Teachers. Unpacking a complex construct in teacher education and teacher practice (pp. 55–78). Springer. https://doi.org/10.1007/978-3-319-66327-2_3
Bressoud, D. M. (2021). The strange role of calculus in the United States. ZDM – Mathematics Education, 53(3), 521–533. https://doi.org/10.1007/s11858-020-01188-0
Bressoud, D., Ghedamsi, I., Martinez-Luaces, V., & Törner, G. (2016). Teaching and Learning of Calculus. SpringerOpen. https://doi.org/10.1007/978-3-319-32975-8
Broley, L., & Hardi, N. (this issue). The evolution of students’ learning from calculus to analysis: how students solve analysis tasks that look like calculus tasks. International Journal of Research in Undergraduate Mathematics Education.
Byerley, C. (2019). Calculus students’ fraction and measure schemes and implications for teaching rate of change functions conceptually. The Journal of Mathematical Behavior, 55, 100694. https://doi.org/10.1016/j.jmathb.2019.03.001
Byerley, C., & Thompson, P. W. (2017). Secondary mathematics teachers’ meanings for measure, slope, and rate of change. The Journal of Mathematical Behavior, 48, 168–193. https://doi.org/10.1016/j.jmathb.2017.09.003
Chevallard, Y. (1999). L’analyse des pratiques enseignantes en théorie anthropologique du didactique. Recherches en Didactique des Mathématiques, 19(2), 221–266. https://revue-rdm.com/1999/l-analyse-des-pratiques/. Accessed 20 April 2022.
Conference Board of the Mathematical Sciences (CBMS). (2012). The mathematical education of teachers II. American Mathematical Society; Mathematical Association of America. https://www.cbmsweb.org/archive/MET2/met2.pdf. Accessed 20 April 2022.
Cuoco, A. (2001). Mathematics for teaching. Notices of the AMS, 48(2), 168–174. https://www.ams.org/journals/notices/200102/200102FullIssue.pdf?cat=fullissue&trk=fullissue200102. Accessed 20 April 2022.
Czocher, J. A. (2017). How can emphasizing mathematical modeling principles benefit students in a traditionally taught differential equations course? The Journal of Mathematical Behavior, 45, 78–94. https://doi.org/10.1016/j.jmathb.2016.10.006
David, E. J., & Zazkis, D. (2020). Characterizing introduction to proof courses: a survey of U.S. R1 and R2 course syllabi. International Journal of Mathematical Education in Science and Technology, 51(3), 388–404. https://doi.org/10.1080/0020739X.2019.1574362
Dibbs, R. (2019). Forged in failure: Engagement patterns for successful students repeating calculus. Educational Studies in Mathematics, 101(1), 35–50. https://doi.org/10.1007/s10649-019-9877-0
Dreyfus, T., Kouropatov, A., & Ron, G. (2021). Research as a resource in a high-school calculus curriculum. ZDM – Mathematics Education, 53(3), 679–693. https://doi.org/10.1007/s11858-021-01236-3
Ellis, J., Kelton, M. L., & Rasmussen, C. (2014). Student perceptions of pedagogy and associated persistence in calculus. ZDM – International Journal on Mathematics Education, 46(4), 661–673. https://doi.org/10.1007/s11858-014-0577-z
Ellis, B., Larsen, S., Voigt, M., & Vroom, K. (2021). Where calculus and engineering converge: An analysis of curricular change in calculus for engineers. International Journal of Research in Undergraduate Mathematics Education, 7(2), 379–399. https://doi.org/10.1007/s40753-020-00130-9
Ely, R. (2021). Teaching calculus with infinitesimals and differentials. ZDM – Mathematics Education, 53(3), 591–604. https://doi.org/10.1007/s11858-020-01194-2
Even, R. (2011). The relevance of advanced mathematics studies to expertise in secondary school mathematics teaching: practitioners’ views. ZDM – Mathematics Education, 43(6–7), 941–950. https://doi.org/10.1007/s11858-011-0346-1
Faulkner, B., Earl, K., & Herman, G. (2019). Mathematical maturity for engineering students. International Journal of Research in Undergraduate Mathematics Education, 5(1), 97–128. https://doi.org/10.1007/s40753-019-00083-8
Faulkner, B., Johnson-Glauch, N., San Choi, D., & Herman, G. L. (2020). When am I ever going to use this? An investigation of the calculus content of core engineering courses. Journal of Engineering Education, 109(3), 402–423. https://doi.org/10.1002/jee.20344
Ferguson, L. (2012). Understanding calculus beyond computations: A descriptive study of the parallelmeanings and expectations of teachers and users of calculus. (doctoral dissertation). Indiana University, Bloomington, Indiana.
Feudel, F., & Biehler, R. (2021). Students’ understanding of the derivative concept in the context of mathematics for economics. Journal Für Mathematik-Didaktik, 42(1), 273–305. https://doi.org/10.1007/s13138-020-00174-z
Frank, K., & Thompson, P. W. (2021). School students’ preparation for calculus in the United States. ZDM – Mathematics Education, 53(3), 549–562. https://doi.org/10.1007/s11858-021-01231-8
Ghedamsi, I., & Lecorre, T. (2021). Transition from high school to university calculus: a study of connection. ZDM – Mathematics Education, 53(3), 563–575. https://doi.org/10.1007/s11858-021-01262-1
González-Martín, A. S. (2021). The use of integrals in engineering programmes: a praxeological analysis of textbooks and teaching practices in Strength of Materials and Electricity and Magnetism courses. International Journal of Research in Undergraduate Mathematics Education, 7(2), 211–234. https://doi.org/10.1007/s40753-021-00135-y
González-Martín, A. S., Gueudet, G., Barquero, B., & Romo Vázquez, A. (2021). Mathematics and other disciplines, and the role of modelling: advances and challenges. In V. Durand-Guerrier, R. Hochmuth, E. Nardi & C. Winsløw (Eds.). Research and Development in University Mathematics Education (pp. 169–189). Routledge. https://doi.org/10.4324/9780429346859
González-Martín, A. S., & Hernandes-Gomes, G. (2020). Mathematics in engineering programs: what teachers with different academic and professional backgrounds bring to the table. An institutional analysis. Research in Mathematics Education, 22(1), 67–86. https://doi.org/10.1080/14794802.2019.1663255
González-Martín, A. S., & Hernandes-Gomes, G. (2021). Applications in calculus for engineering. The cases of five teachers with different backgrounds. In M. Inprasitha, N. Changsri & N. Boonsena, N. (Eds). Proceedings of the 44th Conference of the International Group for the Psychology of Mathematics Education (vol. 2, pp. 406–415). PME.
González-Martín, A. S., Nardi, E., & Biza, I. (2018). From resource to document: Scaffolding content and organising student learning in teachers’ documentation work on the teaching of series. Educational Studies of Mathematics, 98(3), 231–252. https://doi.org/10.1007/s10649-018-9813-8
González-Martín, A. S., & Nseanpa, C. J. (2021). Teachers’ practices and resource use in teaching derivatives. A study of the African context: the case of Cameroon. In M. Inprasitha, N. Changsri & N. Boonsena, N. (Eds), Proceedings of the 44th Conference of the International Group for the Psychology of Mathematics Education (vol. 2, pp. 397–405). PME.
Grant, M. R., Crombie, W., Enderson, M., & Cobb, N. (2016). Polynomial calculus: Rethinking the role of calculus in high schools. International Journal of Mathematical Education in Science and Technology, 47(6), 823–836. https://doi.org/10.1080/0020739X.2015.1133851
Güçler, B. (2013). Examining the discourse on the limit concept in a beginning-level calculus classroom. Educational Studies in Mathematics, 82(3), 439–453. https://doi.org/10.1007/s10649-012-9438-2
Güçler, B. (2014). The role of symbols in mathematical communication: The case of the limit notation. Research in Mathematics Education, 16(3), 251–268. https://doi.org/10.1080/14794802.2014.919872
Güçler, B. (2016). Making implicit metalevel rules of the discourse on function explicit topics of reflection in the classroom to foster student learning. Educational Studies in Mathematics, 91(3), 375–393. https://doi.org/10.1007/s10649-015-9636-9
Gueudet, G. (2008). Investigating the secondary–tertiary transition. Educational Studies in Mathematics, 67(3), 237–254. https://doi.org/10.1007/s10649-007-9100-6
Gutfreund, H., & Rosenberg, Y. (Eds.). (2012). Knowledge and training of secondary school mathematics teachers. The Israel Academy of Sciences and Humanities.
Hitier, M., & González-Martín, A. G. (this issue). Derivatives and the study of motion at the intersection of calculus and mechanics: A praxeological analysis of practices at college level. International Journal of Research in Undergraduate Mathematics Education.
Hitt, F., & Dufour, S. (2021). Introduction to calculus through an open-ended task in the context of speed: representations and actions by students in action. ZDM – Mathematics education, 53(3), 635–647, https://doi.org/10.1007/s11858-021-01258-x
Hitt, F., & González-Martín, A. S. (2016). Generalization, covariation, functions, and Calculus. In A. Gutiérrez, G. L. Leder & P. Boero (Eds.), Second Handbook of Research on the Psychology of Mathematics Education. The Journey Continues (pp. 3–38). Sense Publishers. https://doi.org/10.1007/978-94-6300-561-6_1
Hochmuth, R., Broley, L., & Nardi, E. (2021). Transition to, across and beyond university. In V. Durand-Guerrier, R. Hochmuth, E. Nardi & C. Winsløw (Eds.), Research and Development in University Mathematics Education (pp. 193–215). Routledge. https://doi.org/10.4324/9780429346859
Hoffmann, A., & Even, R. (2021). What do teachers learn about the discipline of mathematics in academic mathematics courses? In M. Inprasitha, N. Changsri & N. Boonsena (Eds.). Proceedings of the 44th Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 51–60). PME.
Jones, S. R. (2015). Areas, anti-derivatives, and adding up pieces: Definite integrals in pure mathematics and applied science contexts. The Journal of Mathematical Behavior, 38, 9–28. https://doi.org/10.1016/j.jmathb.2015.01.001
Jones, S. R. (2017). An exploratory study on student understandings of derivatives in real-world, non-kinematics contexts. The Journal of Mathematical Behavior, 45, 95–110. https://doi.org/10.1016/j.jmathb.2016.11.002
Kent, P., & Noss, R. (2003). Mathematics in the University Education of Engineers (A Report to The Ove Arup Foundation). https://www.ovearupfoundation.org/public/data/chalk/file/a/5/Kent-Noss-report.pdf. Accessed 20 April 2022.
Kilpatrick, J. (2019). A double discontinuity and a triple approach: Felix Klein’s perspective on mathematics teacher education. In H. G. Weigand, W. McCallum, M. Menghini, & M. Neubra (Eds.), The legacy of Felix Klein, ICME-13 Monographs (pp. 215–225). ICME-13 Monographs. Springer. https://doi.org/10.1007/978-3-319-99386-7_15
Kondratieva, M., & Winsløw, C. (2018). Klein’s Plan B in the early Teaching of Analysis: Two theoretical cases of exploring mathematical links. International Journal of Research in Undergraduate Mathematics Education, 4(1), 119–138. https://doi.org/10.1007/s40753-017-0065-2
Kontorovich, I. (2019). What can be more challenging than square-rooting from squared things? In G. Hine, S. Blackley, & A. Cooke (Eds.), Proceedings of the 42nd annual conference of the Mathematics Education Research Group of Australasia (pp. 412–419). MERGA.
Larsen, S., Marrongelle, K., Bressoud, D., & Graham, K. (2017). Understanding the concepts of calculus: Frameworks and roadmaps emerging from educational research. In J. Cai (Ed.), The compendium for research in mathematics education (pp. 526–550). National Council of Teachers of Mathematics.
Laursen, S. L., & Rasmussen, C. (2019). I on the prize: Inquiry approaches in undergraduate mathematics. International Journal of Research in Undergraduate Mathematics Education, 5(1), 129–146. https://doi.org/10.1007/s40753-019-00085-6
Leyva, L. A., Amman, K., Wolf, E. A., Igbinosun, J., & Khan, N. (this issue). Support for all? Confronting racism and patriarchy to promote equitable learning opportunities through undergraduate calculus instruction. International Journal of Research in Undergraduate Mathematics Education.
Loch, B., & Lamborn, J. (2016). How to make mathematics relevant to first-year engineering students: Perceptions of students on student-produced resources. International Journal of Mathematical Education in Science and Technology, 47(1), 29–44. https://doi.org/10.1080/0020739X.2015.1044043
Lyublinskaya, I., & Petrova, E. (2021). Mathematics learning in physics classrooms of Russian schools: a changing landscape from the Soviet period to the present. ZDM – Mathematics Education, 53(3), 1485–1498. https://doi.org/10.1007/s11858-021-01248-z
Marmur, O., Moutinho, I., & Zazkis, R. (2020). On the density of ℚ in ℝ: Imaginary dialogues scripted by undergraduate students. International Journal of Mathematical Education in Science and Technology. Advance online publication. https://doi.org/10.1080/0020739X.2020.1815880
McGuffey, W., Quea, R., Weber, K., Wasserman, N., Fukawa-Connelly, T., & Mejia Ramos, J. P. (2019). Pre- and in-service teachers’ perceived value of an experimental real analysis course for teachers. International Journal of Mathematical Education in Science and Technology, 50(8), 1166–1190. https://doi.org/10.1080/0020739X.2019.1587021
Mkhatshwa, T. P. (2019). Students’ quantitative reasoning about an absolute extrema optimization problem in a profit maximization context. International Journal of Mathematical Education in Science and Technology, 50(8), 1105–1127. https://doi.org/10.1080/0020739X.2018.1562116
Monaghan, J., Nardi, E., & Dreyfus, T. (Eds.). (2019). Calculus in upper secondary and beginning university mathematics – Conference proceedings. MatRIC. https://matric-calculus.sciencesconf.org/. Accessed 20 April 2022.
Moreno-Armella, L. (2021). The theory of calculus for calculus teachers. ZDM – Mathematics Education, 53(3), 621–633. https://doi.org/10.1007/s11858-021-01222-9
Moore, K. C., Silverman, J., Paoletti, T., Liss, D., & Musgrave, S. (2019). Conventions, habits, and US teachers’ meanings for graphs. The Journal of Mathematical Behavior, 53, 179–195. https://doi.org/10.1016/j.jmathb.2018.08.002
Mytlis, Y., & Even., R. (2021). Contribution of academic mathematics studies to teaching topics from the high-school curriculum. In M. Inprasitha, N. Changsri & N. Boonsena (Eds.). Proceedings of the 44th Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 360–369). PME.
Nardi, E., Biza, I., González-Martín, A. S., Gueudet, G., & Winsløw, C. (2014). Institutional, sociocultural and discursive approaches to research in university mathematics education. Research in Mathematics Education, 16(2), 91–94. https://doi.org/10.1080/14794802.2014.918344
Park, J. (2015). Is the derivative a function? If so, how do we teach it? Educational Studies in Mathematics, 89(2), 233–250. https://doi.org/10.1007/s10649-015-9601-7
Pinto, A., & Cooper, J. (this issue). The road not taken—Investigating affordances of infinitesimal calculus for enriching the repertoire of secondary mathematics teachers. International Journal of Research in Undergraduate Mathematics Education.
Quéré, P. V. (2019). Les mathématiques dans la formation des ingénieurs et sur leur lieu de travail: études et propositions (cas de la France). Doctoral dissertation, Université de Bretagne Occidentale, Rennes, France]. HAL theses. https://hal.archives-ouvertes.fr/tel-02281937. Accessed 20 April 2022.
Rasmussen, C., & Ellis, J. (2013). Who is switching out of calculus and why? In A. M. Lindmeier & A. Heinze (Eds.), Proceedings of the 37th Conference of the International Group for the Psychology of Mathematics Education (Vol. 4, pp. 73–80). PME.
Rasmussen, C., & Keene, K. (2019). Knowing solutions to differential equations with rate of change as a function: Waypoints in the journey. The Journal of Mathematical Behavior, 56, 100695. https://doi.org/10.1016/j.jmathb.2019.03.002
Rasmussen, C., Marrongelle, K., & Borba, M. C. (2014) Research on calculus: what do we know and where do we need to go? ZDM – Mathematics Education, 46(4), 507–515. https://doi.org/10.1007/s11858-014-0615-x
Sadler, P., & Sonnert, G. (2018). The path to college calculus: The impact of high school mathematics coursework. Journal for Research in Mathematics Education, 49(3), 292–329. https://doi.org/10.5951/jresematheduc.49.3.0292
Schoenfeld, A. H., & Kilpatrick, J. (2008). Toward a theory of proficiency in teaching mathematics. In T. Wood & D. Tirosh (Eds.). International handbook of mathematics teacher education: Vol. 2. Tools and Processes in Mathematics Teacher Education (pp. 321–354). Sense Publishers.
Schüler-Meyer, A. (2020). Mathematical routines in transition: Facilitating students’ defining and proving of sequence convergence. Teaching Mathematics and Its Applications, 39, 237–247. https://doi.org/10.1093/teamat/hrz019
Sfard, A. (2008). Thinking as communicating. Human development, the growth of discourse, and mathematizing. Cambridge University Press. https://doi.org/10.1017/CBO9780511499944
Steen, L. A. (Ed.). (1987). Calculus for a New Century: A Pump, Not a Filter. Mathematical Association of America. https://www.maa.org/sites/default/files/pdf/pubs/books/members/NTE8_optimized.pdf. Accessed 20 April 2022.
Styers, J. L., Nagle, C. R., & Moore-Russo, D. (2020). Teachers’ noticing of students’ slope statements: Attending and interpreting. Canadian Journal of Science, Mathematics and Technology Education, 20(3), 504–520. https://doi.org/10.1007/s42330-020-00107-5
Tatto, M. T., Lerman, S., & Novotna, J. (2010). The organization of the mathematics preparation and development of teachers: A report from the ICMI Study 15. Journal of Mathematics Teacher Education, 13(4), 313–324. https://doi.org/10.1007/s10857-009-9139-7
Ticknor, C. S. (2012). Situated learning in an abstract algebra classroom. Educational Studies in Mathematics, 81(3), 307–323. https://doi.org/10.1007/s10649-012-9405-y
Thompson, P. W., & Carlson, M. (2017). Variation, covariation, and functions: Foundational ways of thinking mathematically. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 421–456). National Council of Teachers of Mathematics.
Thompson, P. W., & Harel, G. (2021). Ideas foundational to calculus learning and their links to students’ difficulties. ZDM – Mathematics Education, 53(3), 507–519. https://doi.org/10.1007/s11858-021-01270-1
Thompson, P. W., Hatfield, N. J., Yoon, H., Joshua, S., & Byerley, C. (2017). Covariational reasoning among US and South Korean secondary mathematics teachers. The Journal of Mathematical Behavior, 48, 95–111. https://doi.org/10.1016/j.jmathb.2017.08.001
Toh, T. L. (2021). School calculus curriculum and the Singapore mathematics curriculum framework. ZDM – Mathematics Education, 53(3), 535–547. https://doi.org/10.1007/s11858-021-01225-6
Törner, G., Potari, D., & Zachariades, T. (2014). Calculus in European classrooms: curriculum and teaching in different educational and cultural contexts. ZDM – International Journal on Mathematics Education, 46(4), 549–560. https://doi.org/10.1007/s11858-014-0612-0
Tremaine, R., Ellis Hagman, J., Voigt, M., Damas, S., & Gehrtz, J. (this issue). You don’t want to come into a broken system: Perspectives for increasing diversity in STEM among undergraduate calculus program stakeholders. International Journal of Research in Undergraduate Mathematics Education.
Trigueros, M., Bridoux, S., O’Shea, A. N., & Branchetti, L. (2021). Challenging issues in the teaching and learning of calculus and analysis. In V. Durand-Guerrier, R. Hochmuth, E. Nardi & C. Winsløw (Eds.). Research and Development in University Mathematics Education (pp. 83–103). Routledge. https://doi.org/10.4324/9780429346859
Trigueros, M., Martínez-Planell, R., & McGee, D. (2018). Student understanding of the relation between tangent plane and the total differential of two-variable functions. International Journal of Research in Undergraduate Mathematics Education, 4(1), 181–197. https://doi.org/10.1007/s40753-017-0062-5
Verret, M. (1975). Le temps des études I. Librairie Honoré Champion.
Voigt, M., Apkarian, N., Rasmussen, C., & the Progress through Calculus Team. (2020). Undergraduate course variations in precalculus through Calculus 2. International Journal of Mathematical Education in Science and Technology, 51(6), 858–875. https://doi.org/10.1080/0020739X.2019.1636148
Wasserman, N. H. (2018a). Knowledge of nonlocal mathematics for teaching. The Journal of Mathematical Behavior, 49, 116–128. https://doi.org/10.1016/j.jmathb.2017.11.003
Wasserman, N. H. (2018b). Exploring advanced mathematics courses and content for secondary mathematics teachers. In N.H. Wasserman (Ed.). Connecting Abstract Algebra to Secondary Mathematics, for Secondary Mathematics Teachers (pp. 1–15). Springer. https://doi.org/10.1007/978-3-319-99214-3_1
Wasserman, N., Weber, K., Villanueva, M., & Mejia-Ramos, J. P. (2018). Mathematics teachers’ views about the limited utility of real analysis: A transport model hypothesis. The Journal of Mathematical Behavior, 50, 74–89. https://doi.org/10.1016/j.jmathb.2018.01.004
Wasserman, N., & Weber, K. (2017). Pedagogical applications from real analysis for secondary mathematics teachers. For the Learning of Mathematics, 37(3), 14–18. https://www.jstor.org/stable/26548463. Accessed 20 April 2022.
Weber, K., Mejía-Ramos, J. P., Fukawa-Connelly, T., & Wasserman, N. (2020). Connecting the learning of advanced mathematics with the teaching of secondary mathematics: Inverse functions, domain restrictions, and the arcsine function. The Journal of Mathematical Behavior, 57, 100752. https://doi.org/10.1016/j.jmathb.2019.100752
Winsløw, C., & Grønbæk, C. (2014). Klein’s double discontinuity revisited: contemporary challenges for universities preparing teachers to teach calculus. Recherches en Didactique des Mathématiques, 34(1), 59–86. https://revue-rdm.com/2014/kleins-double-discontinuity-revisited/. Accessed 20 April 2022.
Wu, H. (2011). The mis-education of mathematics teachers. Notices of the AMS, 58(3), 372–384. https://www.ams.org/journals/notices/201103/201103-full-issue.pdf?cat=fullissue&trk=fullissue201103. Accessed 20 April 2022.
Yan, X., Marmur, O., & Zazkis, R. (2020). Calculus for teachers: Perspectives and considerations of mathematicians. Canadian Journal of Science, Mathematics, and Technology Education, 20(2), 355–374. https://doi.org/10.1007/s42330-020-00090-x
Yoon, H., Bae, Y., Lim, W., & Kwon, O. N. (2021). A story of the national calculus curriculum: how culture, research, and policy compete and compromise in shaping the calculus curriculum in South Korea. ZDM – Mathematics Education, 53(3), 663–677. https://doi.org/10.1007/s11858-020-01219-w. Accessed 20 April 2022.
Yoon, H., & Thompson, P. W. (2020). Secondary teachers’ meanings for function notation in the United States and South Korea. The Journal of Mathematical Behavior, 60, 100804. https://doi.org/10.1016/j.jmathb.2020.100804
Zazkis, R. (2020). Personal, nonlocal, tacit: On mathematical knowledge in teaching. Canadian Journal of Science, Mathematics and Technology Education, 20(4), 647–656. https://doi.org/10.1007/s42330-020-00118-2
Zazkis, R., & Leikin, R. (2010). Advanced mathematical knowledge in teaching practice: Perceptions of secondary mathematics teachers. Mathematical Thinking and Learning, 12, 263–281. https://doi.org/10.1080/10986061003786349
Zazkis, R., & Mamolo, A. (2011). Reconceptualizing knowledge at the mathematical horizon. For the Learning of Mathematics, 31(2), 8–13. https://www.jstor.org/stable/41319556. Accessed 20 April 2022.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
On behalf of all the authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Biza, I., González-Martín, A.S. & Pinto, A. ‘Scaffolding’ or ‘Filtering’: A Review of Studies on the Diverse Roles of Calculus Courses for Students, Professionals and Teachers. Int. J. Res. Undergrad. Math. Ed. 8, 389–418 (2022). https://doi.org/10.1007/s40753-022-00180-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40753-022-00180-1