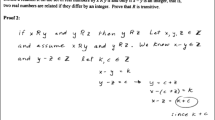Comprehending written proofs is central to success in tertiary mathematics, and pivotal to becoming a successful mathematician (Mejía-Ramos et al., 2017). In their systematic review of the proof-related literature, Mejia-Ramos and Inglis (2009) found that most research into students’ understanding of proof focused on how students construct proofs. They found little research on how students comprehend the proofs they read. One reason for this is that while it is relatively straightforward to design tasks to assess students’ construction of their own proofs, it is less obvious how to design tasks that assess students’ comprehension of presented proofs. The last decade has seen an increase in research focused explicitly on students’ reading comprehension regarding proof (e.g., Hodds et al., 2014; Lew et al., 2020; Selden & Selden, 2017).

In particular, two programs of research have sought to develop standardized tasks and methods for assessing undergraduates’ proof reading comprehension. First, Mejia-Ramos et al. (2012) developed a theoretical model for proof comprehension, based on the triangulation of interview and survey data. Three aspects of their model are relevant here: “summarizing via high-level ideas”, “identifying the modular structure” and “justification of claims” (p. 15). Mejia-Ramos et al. used their model to develop multiple-choice tests based on three proofs from an undergraduate ‘introduction to proof’ course (Mejía-Ramos et al., 2017). The outcome was the first empirically validated tests for assessing students’ proof reading comprehension. However, developing and validating the tests was time-consuming and resource-intensive, and the process must be repeated for every new proof that is to be the focus of the assessment.

Second, Davies et al. (2020) sought to develop assessments of comprehension of presented proofs quickly and efficiently, without the need to design and empirically validate a new multiple-choice test for every proof. Building on Mejia-Ramos and colleagues’ work, they collected students’ written summaries of presented proofs, and applied a comparative judgement (CJ) technique (Jones et al., 2019) to assess the summaries. The CJ technique involved presenting pairs of summaries to mathematicians and asking them to decide which summary was ‘better’. The binary decision data from many pairwise judgements by different mathematicians were statistically modelled to produce a unique score for each summary. Davies et al. explored the validity and reliability of the scores using standard methods from the CJ literature (e.g., Jones et al., 2019; Pollitt, 2012). They reported that mathematicians were reliable (consistent with one another) when making pairwise decisions about students’ proof summaries. Good reliability has often been reported when CJ is applied to educational assessment across different subjects and contexts (Verhavert et al., 2019), and was the initial motivation for Davies et al. to apply it to proof comprehension assessment.

However, Davies et al. highlighted the need for a more nuanced understanding of how mathematicians read and comprehend proof summaries. Their findings contrast with research demonstrating localized inconsistencies across mathematicians when evaluating the validity of particular proofs (Inglis & Aberdein, 2015; Inglis & Alcock, 2012; Weber & Czocher, 2019).

Our purpose in the present research is to extend our earlier, primarily quantitative work by exploring mathematicians’ decision-making processes with regard to students’ proof summaries. In doing so, we develop deeper understandings of the locus and nature of differences between mathematicians’ behavior in this setting, leading to commentary about the nature and utility of proof summaries for researchers and practitioners alike.

Before presenting our empirical work, we consider the literature on proof writing and ‘key ideas’ in proof. We then offer a theoretical account of proof summaries and three research questions.

Proof Summaries and Features of Good Proof Writing

We now consider the literature on proof construction. In particular, we focus on recent works on the characteristics and conventions of proof writing in undergraduate mathematics, as highlighted by Moore (2016) and Lew and Mejía-Ramos (2019).

Moore (2016) identified four characteristics of good undergraduate proof writing: logical correctness, clarity, fluency, and demonstration of understanding. These characteristics came from a two-stage task-based interview, in which mathematicians were asked to evaluate several student-produced proofs from an undergraduate course in discrete mathematics. In each interview, mathematicians were first asked to assign each proof a numerical score, and then asked to discuss their decision with the interviewer. Based on our theoretical conception of proof summaries, we conjecture that Moore’s (2016) four characteristics of good proof writing may also feature in our work based on proof summaries. In lieu of explicit definitions for his four characteristics, Moore provided several excerpts and examples of each, noting their confounding and interconnected nature. Following the thematic analysis of our data, we discuss these characteristics and associated excerpts in parallel with our own findings.

In a similar vein, Lew and Mejía-Ramos (2019) investigated mathematicians’ and students’ perspectives on conventional mathematical proof writing. Lew and Mejia-Ramos used a breaching experiment methodology to identify conventions of mathematical proof writing by presenting mathematicians with potential violations of these norms and attending to their attempts to “repair the breach” (p. 10). The authors made three important observations: 1) mathematicians believe proofs should follow the rules of general academic language; 2) students and mathematicians differ on their understanding of conventions regarding the introduction of new mathematical objects; and 3) unlike students, mathematicians attend to the context of a proof to determine appropriate levels of formality and rigor. We return to these findings later, contrasting our own empirical work on proof summaries with the extant literature on proof construction itself.

On Proof, Key Ideas, And the Activity of Summarizing

Written proofs often include (sometimes minimal) commentary guiding the reader through the deductive argument. Mathematicians rarely write out a mathematical proof with explicit mentions of axioms defining their operational space (Aberdein, 2009). Rather, they rely on shared conventions to abbreviate their mathematical arguments, invoking implicit warrants, explicating only the most salient derivations. As such, summarizing and distilling key ideas is central to mathematical practice (Raman, 2003). Yet, the extent to which these conventions are truly shared remains a contested topic (Czocher & Weber, 2020), and for those that are largely agreed, the mechanisms by which agreement is reached remain opaque. Dawkins and Weber (2017) framed this notion of shared understandings via the series of values and norms held by mathematicians and students, and conjectured that students’ difficulty with proof-based activities is the result of various mismatches between the values and norms of student and research communities.

Several researchers have argued that focusing students’ attention on identifying and articulating the key idea of a proof is a productive pedagogical activity (Hanna & Mason, 2014; Robinson, 2000; Yan, 2019). And hence, given the connection between key ideas and proof summaries, we suggest that engaging students in summarizing proofs is likely to be similarly productive. Moreover, rigor and precision are likely to be less salient in the context of summaries and hence the conjectured mismatch of values and norms between mathematicians and students creates less of a barrier to productive engagement than in traditional proof construction settings.

The educational literature on key ideas refers to, and relies heavily upon, the notion of summarizing. Yan (2019) described this literature as constituting two camps of research: either as “the most important mathematical ideas, methods or strategies used in a proof” or “as an outline, overview, or architecture of a proof” (p. 2). The former implicitly characterizes proofs as active entities constructed by individuals who must implement, or use, an idea. The latter implicitly adopts a more passive approach, wherein the proof appears to be fixed in time and space. However, in both cases, the key idea is characterized as an idea, or series of activities or statements, that lead the reader back to the original text.

Raman (2003) considered the key idea leading to proof production as a heuristic that maps ‘to a formal proof with …appropriate sense of rigor’ (ibid). Again, we find an overlap between the notion of a key idea, and the (re)-production of a full or ‘formal’ proof.

Defining Proof Summaries

Before proceeding, we must define what is meant by a ‘proof summary’. To this end, we rely on three influential works reviewed above, each contributing their own properties to our definition; Raman (2003), Yan (2019), and Mejia-Ramos and Inglis (2009) whose work we discussed in the previous section.

From Raman’s (2003) work on key ideas, we take the notion mapping to a formal proof with an appropriate sense of rigour or detail. From Yan’s more recent work on the same topic, we take the notion of leading the reader back to (a version of) the original proof. Note that the formal proof from Raman’s mapping need not be the original text to which the reader is led in Yan’s work. As discussed earlier, mathematicians’ rarely communicate to each other in ‘formal’ proofs, satisfied in the knowledge that such a formalization likely exists if it is every needed.

And finally, from Mejia-Ramos and Inglis (2009), we take the duopoly of proof construction and comprehension tasks. However, unlike the literature reviewed in this survey, we view the proof summary task as a hybrid of both categories. The summary task is a construction task in the sense that it demands a novel piece of text from the respondent, and it is a comprehension task in the sense that the text produced is heavily dependent on one’s ability to read and understand the original.

This leaves us with the following tripartite definition of a proof summary to which we return later:

  1. 1.

    A proof summary invokes an appropriate level of rigour or detail to generate a mapping to a formal proof.

  2. 2.

    An effective proof summary should lead the reader back to (a version of) the original text.

  3. 3.

    The proof summary task is a hybrid ‘construction/comprehension’ task demanding knowledge from both domains.

Research Questions

In the present paper, we address the following three research questions:

  1. RQ1:

    What features of student-produced proof summaries do mathematicians’ attend to in a comparative judgement setting?

Our previous work used quantitative data to identify features common to ‘successful’ proof summaries. Here, we use clinical interview data to delve deeper into mathematicians’ decision-making process when evaluating students’ proof summaries.

  1. RQ2:

    How do these features relate to the characteristics and conventions of proof writing identified in the literature?

Moore (2016) and Lew and Mejía-Ramos (2020) made a series of empirical observations regarding mathematicians’ conceptions of good proof writing. We conjecture that many of these features will be common to both proofs and proof summaries, and seek to understand the relationship between construction and summary tasks through these features.

  1. RQ3:

    How can these features be used to account for the consistency amongst judging mathematicians identified in Davies et al. (2020)?

We know from Davies et al. (2020) that mathematicians’ judge proof summaries reliably, and that the resulting scores are likely valid reflections of students’ understanding of proof. However, the literature suggests that mathematicians’ often vary in their evaluations of purported proofs. We aim to use our answers to RQ1, regarding mathematicians’ decision-making processes, to understand RQ3 regarding reliability and consistency.

Methods

Participants

Nine participants from the same English university, referred to as M1 to M9 throughout, were interviewed in this study. All participants were active researchers in mathematics or mathematics education, holding a postgraduate degree in mathematics or a related discipline.

Materials

In these interviews, participants were asked to make pairwise comparisons of students’ summaries of a proof demonstrating the uncountability of the open unit interval, see Fig. 1. These proof summaries were a subset of an existing dataset, presented in Davies et al. (2020), and were responses to the prompt shown in Fig. 2. Figures 4, 5 and 6 exemplify the responses given.

Fig. 1
figure 1

An adaptation of Cantor’s diagonalization proof of the uncountability of the open unit interval, used by the authors of Mejia-Ramos et al. (2017)

Full size image
Fig. 2
figure 2

A reproduction of the task sheet given to students in Davies et al. (2020)

Full size image

Procedures

Each interview lasted between 40 and 60 min and comprised three parts. Part 1 saw participants complete a series of 20 comparative judgements in a laboratory setting, announcing their decisions (‘left’ or ‘right’) aloud. Each judge was given a copy of the task sheet, including the proof itself (Fig. 1) and the prompt for a summary (Fig. 2). The interviewer verbally explained that students had been asked to ‘summarize the given proof’ and had received no additional instructions beyond those presented on the task sheet. Mathematicians were invited to refer to the proof throughout their judgements, as was the case for the students when producing their summaries. All nine participants saw the same 20 pairings in the same order. Part 2 was a semi-structured interview, first addressing broad features of participants’ experience, before narrowing to more specific questions targeting possible judging strategies and attendance to certain features of students’ summaries. Part 3 was a think-aloud protocol wherein participants reviewed the final 10 pairings. During this part, participants were asked to explain ‘how’ and ‘why’ they made their decisions. The interviewer also drew attention to several predetermined features of particular summaries to elicit comments regarding attitudes to explicit errors and abuses of notation.

Both participant and interviewer were audio-recorded during parts 2 and 3, while the decisions from part 1 were recorded manually to facilitate an elementary analysis of consistency between mathematicians.

Data Analysis

We conducted a thematic analysis of these interviews, driven by latent themes identified in the transcribed data. Following Braun and Clarke (2006) this decision was based on an essentialist assumption of a shared understanding of meaning between researcher and participant. Similarly, we understand the utterances of the participant mathematician as a window into their reasons for endorsing or rejecting mathematical texts.

Coding the Data

We first transcribed all nine interviews in full, then read and re-read the resulting transcripts making informal notes on potential codes related to mathematicians’ decision-making processes. This initial parse included codes related to content-related features of students’ proof summaries, as well as contextual factors motivating the judging process. A more structured third reading saw the initial list of 45 grounded codes systematically assigned to all transcripts, and the data pertaining to each code collated into four overarching themes.

After defining and exemplifying each theme, we then generated brief numerical summaries indicative of the prevalence of each subtheme in the data. We defined prevalence as the number of participants who provided at least one utterance related to the given code, hence quantities are expressed at the participant level in the form ‘subtheme x was identified in the transcripts of n participants’. This ancillary analysis intends to provide a holistic overview of the data and should not be interpreted as a summation of the relative density.

Results

Consistency Amongst Mathematicians

Before presenting a thematic analysis of mathematicians’ decision-making, we note the degree of consistency amongst mathematicians, based on the frequency of agreement on each pairwise comparison. Based on the diverse range of features upon which mathematicians may disagree (discussed later), and the extant literature on reliability in comparative judgement, we deem the ~ 85% pairwise agreement amongst mathematicians as an indicator of moderate to good consistency. Figure 3 demonstrates this agreement, where each row is a mathematician judge (M1 to M9) and each column is a pairing. A dark cell indicates that a judge held the majority view on that pairing. Given the qualitative focus of our research questions, and the corresponding nature of the data collected, we are not able to provide a more standardized metric of reliability or agreement.

Fig. 3
figure 3

A visualization of agreement across pairings. A dark cell indicated that judge i held the majority view on pairing j

Full size image

However, an expected outcome for each of the 20 pairings in this study can be produced by comparing the comparative judgement-based scores generated in the earlier study (Davies et al., 2020). In each case, the majority decision of the interviewed participants (illustrated by dark cells in Fig. 3) was consistent with the higher score from Davies et al. in 19 of the 20 pairings. For the outlier (pairing 2), the comparative judgement-based scores were separated by < 1% of a standard deviation. Given that only 5 of 9 participants selected the ‘lower scoring’ summary in the present study, we conclude that this pairing was either difficult or divisive and does not present a substantive threat to validity.

Four Themes Governing Participants’ Decision-Making

We identified four themes, with associated subthemes, in the data, each regarding different justifications of mathematicians’ decisions (Table 1). In all cases, the evidence came from self-reported reasons, was drawn from the semi-structured interview, or from the think-aloud task, where values or justifications were inferred by the researchers.

Table 1 Summary of thematic analysis
Full size table

We present the subthemes and associated excerpts in turn, followed by brief discussion sections after each of the four main themes. In these discussions, we examine connections between our observations and the literature, before exploring the theoretical and practical implications of our findings in the final section.

Theme 1: Influencing Features

This theme refers to the non-specific mathematical features attended to by the participating mathematicians. The subthemes here refer directly to meta-level mathematical features of students’ summaries. We identified four meta-level features that influenced participants’ reasons for endorsement: mathematical accuracy, technical detail, mathematical fluency and brevity.

Mathematical Accuracy

Accuracy was an important feature of several participants’ decisions, who often strongly rejected summaries featuring abuses of notation or isolated objective errors. M7 focused on the precision of the mathematical notation, noting that ‘it really depends on [incorrect] notation, that’s one thing that’s a bugbear for me’. The same judge went on to comment that one response ‘[claimed] that “b is equal to f or not equal to f” which is complete nonsense [because] b is not an element of f, it’s not equal to it in any sense or form and that’s just bad’. This excerpt arose from the second part of the interview in which no particular response was specified, we assume this participant was referring to the transcribed summary shown in Fig. 4.

Fig. 4
figure 4

A transcribed version of the proof summary, identified by M7 as ‘just bad’, based on the abuse of notation in the final sentence

Full size image

This summary appears to compare b, a real number from the interval (0,1), to the function f(n), asserting that these two objects are not equal. M7 was particularly dismissive of this ‘nonsense’, appearing to interpret it as an indication that its author did not understand the proof or the associated mathematical objects. Two other mathematicians raised similar objections to the proof summary in Fig. 4. However, M7’s perspective was not unanimous. Others were more willing to ‘cut some slack, particularly with students of this level’ (M4). To this end, M2 focused on readability, saying ‘it’s clear what it understands... It’s not correct mathematically but with undergraduate students especially I don’t know... They confuse a lot of the elements with functions and so on. So yea, let’s be a little bit generous’.

The summary shown in Fig. 5 features the incorrect assertion that ‘(0,1) is countable’. M3 said of their approach to evaluating proof summaries that they ‘look for whether the students got their claims right and then how much detail they provided…There was one that says this shows the interval was uncountable… [in this case, the other] is obviously better, even if the detail isn't right’.

Fig. 5
figure 5

An example proof summary focused on a countably infinite subset of the open unit interval

Full size image

Notice that the summary in Fig. 5 appears to rely on a countably infinite subset to justify the uncountability of the open interval. Arguably, there are several potentially problematic aspects of this unusually short summary. It is interesting to note that the confusion (or possible ‘typo’) between countability and uncountability was the most salient feature for at least one judge.

While it is clear that not all participants agreed on the relative importance of mathematical accuracy, this subtheme was a recurrent feature in at least five of the interviews.

Technical Detail

By technical detail, we refer to what M4 called ‘the book-keeping of the proof’. This subtheme highlights participants’ attention to the notation-heavy elements of the proof, and in particular, to the presence of word use specific to the discourse of mathematics (rather than mathematical accuracy, as highlighted in the previous subtheme). Three participants explicitly commented on a desire to see technical detail expressed symbolically, rather than described using natural language. For example, M6 said: ‘If one of [the summaries] used words and one of them used the actual notation for it, I would go for notation on the reason that if the logic is correct [in one], that’s fine but, they’ve not actually shown that you can write something in such a way [that is mathematical]’. Similarly, M9 explicitly reported using technical detail as a tiebreaker for some pairings: ‘If I had two [similar] proofs [summaries], one was giving a little more details [sic], I would choose that one’.

However, the importance of such technical details varied across participants. Two participants preferred summaries focused on meta-level objects. For example, M8 was explicitly ‘not looking for details of the proof, but their structure of the proof. So, the key parts of the proof [were most important]’. Similarly, M1 ‘…had the impression that if someone started doing the summary by going too much into the details, it gave the impression that they had focused on the details, but they’d lost the context of the general picture’.

The lack of consistency across participants regarding technical details contrasts with the consistency across the next subtheme, focused on students’ demonstrations of understanding.

Demonstrations of (a Lack of) Understanding

Participants’ comments about demonstrations of understanding were about the overall impression of the given summary, accompanied by an inference that the student did not understand the proof and/or its associated concepts. For example, M5 noted that ‘…it’s probably more of a feeling of the overall thing, but it feels like it’s... I don’t know. There’s something a bit strange about the way they’ve written…[their summary]’. M4 justified one of their decisions by reporting ‘a gut feeling that they haven’t understood it’, concluding that they are ‘less likely to forgive them for [other omissions]’.

When discussing the summary in Fig. 4, M5 commented that ‘they tried to, sort of, give an example... I don’t know. I don’t think I liked it very much. … it felt like they really went off-topic and they didn’t seem to understand what was happening’. It seems that M5 identified a weakness in this particular proof summary, on the premise that the example did not provide the reader with any insight as to how to produce the original text.

In sum, mathematicians’ references to instinctual responses characterized excerpts identified as demonstrations of (a lack of) understanding. We interpret these excerpts as meta-level commentaries on normative aspects of mathematical word use. As is evidenced here, violations of these norms can be difficult to articulate but can produce strong, sometimes emotional, reactions to mathematical texts.

Brevity

Brevity refers to the length and density of the summary. Interview excerpts assigned this subtheme had more bearing on mathematicians’ interpretation of ‘summary’ than they did on their orientations to evaluating mathematical texts.

M1 referenced brevity explicitly, asserting on one occasion ‘this one is better than [the other] because, at the least, it’s shorter’. M8 appeared to value brevity for a different reason, apparently related to the communication of a key idea: ‘It was very beautiful, it did not do any math it just said this is how they prove it. It is proved by contradiction; “assume this, assume that. The contradiction…” I like it’. We interpret this excerpt to indicate that this participant valued directness in a proof summary. Possibly M8 conceptualized the summary task as requiring the author to identify and outline the key ideas necessary to reconstruct the proof. Earlier in the interview, the same participant had made explicit references to ‘finding the key parts of the proof’, and the notion that when constructing a proof, ‘you should first find a road map…’, implying that a proof summary could function as such.

By contrast, M7 valued completeness, noting that longer summaries were likely to contain more important information regarding the proof. For example, this participant ‘would punish [sic] for not covering all the points. So in my head, if you’re summarizing something, the idea of summarizing usually means it’s shorter, but, if every single part of what is written, has to be written, then you can’t really shorten it’.

Unnecessary Content

In contrast to the key ideas identified in the next theme, participants also identified particular objects or ideas that they deemed reflective of weaker comprehension.

For example, the original proof (Fig. 1) begins with a brief three-line argument establishing that the open unit interval is infinite, before proceeding to establish that it is uncountably infinite. Several participants appeared to view this sub-argument as superfluous. M6 said this argument, ‘isn’t too relevant. I was not focusing on … the fact that it has infinite subsets. … Well, it’s not the point, so I think I ignored that and the way it was done’.

Similarly, M2 noted that ‘I think I probably wouldn’t have included that from the outset because, in a way, a finite set is obviously denumerable’.

On the other hand, M3 noted the potential ‘pedagogical’ value of including this possibly superfluous sub-argument. M3 went on to comment that it may well be worth including it, asserting that the ‘extent students understand why it’s there is a different matter. I think there were one or two proofs or summaries where that observation was pretty much the only relevant content there was. So in that case, it makes a difference’. It is interesting to note that M3, the only judge who argued for the inclusion of this sub-argument, did so on the premise that it provides an additional opportunity for the student to present accurate material, and not because they claim it is a pivotal aspect of the proof.

A second frequently referenced example of unnecessary content came from the sub-argument addressing the conflict between different decimal representations resulting from infinite strings of 0’s and 9’s. This sub-argument was deemed unnecessary by four participants. M9 said ‘Obviously, many of them had this argument with the infinite string of 9’s, which I think is just not necessary for the summary’. In total there were four mathematicians who made comments similar to M7’s assertion that ‘… the 0’s and 9’s didn’t matter to me… these are just details…’.

We return to participants’ expectations of object-level inclusions in our discussion. For now, we pivot toward themes explicitly addressing participants’ reasons when evaluating the summaries.

Theme 2: Key Idea(s)

This theme highlights the object-level mathematical content salient in participants’ decisions. The original proof (in Fig. 1) uses Cantor’s diagonalization argument, to show that there can be no bijective mapping from \(N\) to the open unit interval. This is demonstrated by contradiction, supposing the existence of such a function, say \(f:N\to \left(\mathrm{0,1}\right)\), and producing an element of the codomain, labeled b, that does not have a preimage in the domain of f. Based on our analysis of mathematicians’ judgements, this proof had three key ideas/objects that should be included in a summary of the proof. We present these as three subthemes: the construction of f, the construction of b, and references to the structure of the argument as a proof by contradiction.

Construction of f

Four participants noted that many summaries did not introduce the function f, commenting that it needs to be defined for the text to have meaning. For example, M1 noted that one particular summary ‘... misses that here we cannot find the set to map all of the interval one-to-one. So what kind of set are they trying to map? If you don’t provide any kind of information on that, then how do you conclude that the interval is uncountable?’ This sentiment was echoed by three others in various forms. M7 noted that the proof summary in Fig. 4 appeared to ‘miss the key point, that the function has to be denumerable. It’s implied by saying f(n), but they’ve not said what f is’. Of the same summary, M8 read aloud “…thus, b is not f(n)…”, before exclaiming ‘Who is f? [f] was not in the picture before. And, “thus” is a big word to use when you have not explained anything’. All the mathematicians choose the other summary in the one pairing in which Fig. 4 appeared.

Finally, we present an excerpt from M7, justifying why they did not like the summary in Fig. 4 (shown earlier): ‘[it] is just missing too much information… The first [sentence] is not relevant to me, also not the second and the third. Then, where the actual idea starts with b is a number different from f, f is not defined and I don’t know what the range of f is. So that’s just not enough’.

Construction of b

In a similar vein to that discussed above, many mathematicians also asserted or implied that a good summary of this proof should include an explicit construction of b, the element of the domain used to contradict the assumption of surjectivity. M5, for example, noted that the ‘heart of the proof…would be the construction of a number b that is different from each one of the countably many Ai’. M5 went on to comment on the summary in Fig. 6, saying.

Fig. 6
figure 6

An example proof summary featuring an open admission about the student’s understanding of the original text

Full size image

that ‘what [the author] calls “the part about b”, he clearly hasn’t understood’, and hence concluded that he was highly disinclined to choose this summary in most pairings.

In total, six mathematicians made similar comments indicating the centrality of the constructed b to the key idea of this proof, and hence to a successful summary.

Proof by Contradiction

Six participants commented on the importance of explicit references to the method of proof: contradiction. For example, during the think-aloud part of the interview, M9 observed that ‘somehow [a summary referencing contradiction] feels nicer. A nicer summary. Because perhaps the main reason is because [the author] told me I’m gonna proceed with proof by contradiction’. This excerpt echoes aspects of Moore’s (2016) notion of clarity. In particular, for Moore, clarity is achieved not only by the use of correct language and notation (discussed earlier) but also by ‘organizing a proof to make it readable and flow smoothly’ (p. 266). We interpret commentary on the method of proof as a commentary on clarity, in so far as it allows the reader to have a sense of the flow of the original text.

Theme 3: Assessment Approaches

This theme refers to approaches used by the participants to identify the most important features upon which to base their decisions. That is, we focus on two opposing approaches to evaluating the relative merit of student-produced summaries; we refer to them as positive and negative grading.

Positive Grading

Positive grading excerpts were those in which participants actively sought elements or phrases to reward. This was typified by M1: ‘I was looking for good things… I read to make sense. And then, I think in the next step, I try to … I ask myself if that’s enough for me… I would say I read and try to collect the valid arguments. And then, see if they add up to what I would assume is an appropriate summary’.

This self-reported approach appeared most akin to traditional modes of assessment in which assessors commonly seek to give credit to student responses (Crisp, 2008). It should be noted that the above excerpt from M1 does not explicitly address the process for comparing two texts. However, any comparison they make is at least reportedly based on the positive attributes of the two summaries. For example, M1 decided between two summaries by explaining ‘the one on the right is better because [it] identifies that it’s a proof by contradiction’.

This positive approach was also adopted by M6 and M9. The archetypal explanation of a positive marker’s decision-making was characterized by the following construction: 'I chose response A because of (possibly implicitly) positive feature X'.

Negative Grading

Negative marking excerpts were those in which participants actively sought errors in each summary. M7 self-identified as a negative marker: ‘I usually go for the negative rather than the positive, it’s a judgement, it’s faster. When I’m comparing, it’s faster to see the negative one because this sounds really cynical, students are more likely to make mistakes. They usually make a mistake somewhere, not every student is perfect so if they’re likely to make a mistake you can usually pick up the mistakes faster which means that you can see if one of them has made quite a few logical errors you know that one’s not as rigorous as the other…’.

In a similar vein, M8 noted that seeing ‘incorrect statements influences the decision more than showing correct things’. In the think-aloud task, negative marking appeared in the form ‘I choose B because A had an undesirable attribute’. For example, M3 chose between two summaries stating: ‘the left one misstates the claim, so that already pretty much means it’s weaker than the other’. In total, three participants (M3, M7 and M8) identified as negative markers. However, there was evidence that all nine participants emphasized errors, rather than positive contributions, on at least one occasion.

On many occasions, participants identified both positive and negative elements of one or both responses. In such cases, it became a question of weighing the influence of the various features. As a researcher, the inference of these unstated weights could only be based on the participants’ final decision and was necessarily an imprecise process. Moreover, no participant adhered exclusively to positive or negative grading throughout their judgements, even if having communicated a clear preference/bias when asked during the semi-structured interview.

Theme 4: Non-Content-Related Features

This final theme captures a series of three non-content-related features of participants’ evaluative decisions: context-dependence, legibility, and arbitrary decision-making. The first of these subthemes has important bearings on the validity of participants’ evaluations and can be used to partially account for variations in other aspects of participants’ behavior. The third is a feature of the comparative judgment-based approach and are addressed in relation to previous work from the same research tradition.

Context-Dependence of the Task

M4 noted that their approach to decision-making in a real-world setting (i.e. grading their own students’ work) would be context-dependent. ‘While [abuse of notation] doesn’t bother me… [they] would in some more formal context. If they gave it to me as a piece of course work, I would be less happy than if it was in a class test or exam’. M6 said of some summaries lacking mathematical accuracy (i.e. featuring abuses of notation) that ‘I think this is ok for a summary’, again implying that in a different context their reasons may differ.

The context of the task was also raised by M3, who focused on a different feature of the context, regarding the experience of the students: ‘The proof hinges on a proof by contradiction on the fact they can’t… From the students, I would want to know whether, for example, if they remember how to construct [the infinite subset using \({1}/{{2}^{\mathrm{k}}}\)]… because this may be a standard procedure that they need to implement and this is why in the beginning I asked you, who are these students [and what do they know]?’ It is interesting that the absence of this contextual information did not perturb the other eight participants, yet all of M3’s decisions except one were consistent with the majority decisions.

Legibility

Several participants commented on the poor handwriting of several summaries, making it difficult to parse some summaries in full. We remind the reader, here, that the proof summaries included in this manuscript are transcriptions of the originals, to allow the reader to focus primarily on their mathematical context. Poor handwriting also served to distract some participants who noted that ‘at a certain point if the handwriting is too bad, you just have to assume it’s bad’ (M7). While this may have been an important confound for some participants, legibility had little influence on the reasons mathematicians’ gave for their decisions. We note that previous comparative judgement-based studies have focused on confounding variables such as handwriting and presentation (e.g. Jones et al., 2019), and none have found a systematic influence on the material nature of mathematicians’ decisions.

Arbitrary Decision-Making

Other participants commented that some decisions were necessarily arbitrary. M5 reported not being able to ‘choose between two equally terrible summaries’, while M3 observed that sometimes the ‘crimes committed were different but equally problematic’, concluding that their decision was therefore meaningless.

Discussion

We have reported a study in which mathematicians chose the ‘better’ undergraduate proof summary in presented pairings, and then talked about their decisions in an interview. Our analysis resulted in four themes, as shown in Table 1, which we now use to address our three research questions enumerated earlier: RQ1) What features of student-produced proof summaries do mathematicians’ attend to in a comparative judgement setting? RQ2) How do these features relate to the characteristics and conventions of proof writing identified in the literature? and RQ3) How can these features be used to account for the consistency amongst judging mathematicians identified in Davies et al. (2020)?

To address research question 1, we return to each of our four themes, summarizing our findings and drawing parallels with the literature where appropriate. We then address research questions 2 and 3 based on the discussion of the first.

Theme 1: Influencing Features

We identified five features of students’ summaries influencing mathematicians’ decisions: mathematical accuracy, technical details, demonstrations of understanding, brevity, and unnecessary content. Our understanding of accuracy was similar to Moore’s notion of ‘clarity’, described as encompassing ‘[correct] use of mathematical language and notation’ (p. 266), among other factors. Our subtheme, ‘technical detail’, is also related to Moore’s notions of clarity, but also overlapped with Moore’s ‘fluency’, described as the ‘correct use of mathematical language… as well as the English grammar, punctuation and capitalization [used] to make [a] proof flow…’ (p. 266). We also note the overlap between our grounded ‘technical detail’ subtheme and the ‘conventions of academic language’ (p. 121) highlighted by Lew and Mejía-Ramos (2019). The overlap between our observations associated with proof summaries and Moore’s work is even greater with respect to demonstrations of understanding.

Theme 1 appears to contain greater disagreement across interviewees than any of the other themes. This was particularly for the case of the subthemes technical detail and whether brevity or comprehensiveness was a positive feature of proof summaries.

Theme 2: Key Idea(s)

There were three key ideas invoked by the original proof demonstrating the uncountability of the open unit interval, related to the construction of f, the construction of b and proof by contradiction. While these are idea are specific to the proof at hand, we conjecture that similarly discrete key ideas feature in the majority of proofs from undergraduate mathematics curricula. While the very notion of ‘key ideas’ is well-established in the proof comprehension literature (e.g. Raman, 2003), we also note the importance of the introduction of new objects to mathematicians’ evaluations of students’ proof summaries. This is consistent with another observation of Lew and Mejía-Ramos (2019), that mathematicians paid careful attention to new mathematical objects, reacting negatively to, amongst other things, students’ use of variables that have not been appropriated introduced. Again, it is interesting to note that these conventions of good proof-writing were applied in the context of our summary task.

Our qualitative analysis of the interviews pointed towards overall agreement amongst participant mathematicians as to the nature and importance of the three identified key ideas that underpin the proof. Therefore, the presence of these key ideas in summaries can be taken to be considered important across the participants collectively. It is possible that this agreement about the key ideas was the substantive basis of many of the decisions provided by the participants, and explains much of the consistency in Fig. 3.

Themes 3 and 4: Assessment Approaches and Non-Content-Related Features

We consider these two themes together. Theme 3 contains the subthemes positive grading and negative grading, and Theme 4 contains the subthemes context-dependence of the task, legibility and arbitrary decision-making. The subthemes associated with both themes 3 and 4 represented reasons that appear to be novel to the proof summary task and comparative judgement. We highlight a parallel between our work and the extant literature, based on comments associated with the ‘context-dependence’ of the task. This topic was highlighted in Lew and Mejía-Ramos (2019) with respect to the relative degrees of ‘formality’ expected by mathematicians’ in different settings. This is also a focal point of Davies et al. (2021), who demonstrated that context-dependence is a systematic feature of mathematicians’ grading of student-produced proofs.

In particular, we note a potential impact of the comparative judgement protocol on mathematicians’ evaluation of student-produced texted. That is, some mathematicians’ appeared to adopt a deficit model of assessment, focusing only on the negative aspects of students’ work. We note that this arbitrary decision-making seemed to be connected to a more negative perspective that we saw in negative grading, as we observed no instances of arbitrary decision making because summaries were viewed equally positively. We also acknowledge that the judgments here suggest that the mathematicians were particularly critical of the student work.

Once again, our qualitative analysis pointed towards agreement across the participant mathematicians around both Theme 3 (assessment approaches) and Theme 4 (non-content-related features).

The Role and Definition of Summaries in Proof Comprehension Research

Our second research question asks about the relationship between features of traditional good proof writing, and the features of good proof summaries identified above. The discussion above demonstrates that our students’ proof summaries were evaluated similarly to how the literature predicts traditional proofs would be evaluated. In particular, we note the prevalence of the observations regarding good proof writing by Lew and Mejía-Ramos (2019), in our novel context of proof summaries. On the other hand, it seems that features like technical details and brevity serve to distinguish proof summaries from their more formal counterparts: proofs. For at least some judges, these features are pivotal in the evaluation of the quality of a given summary. However, we conjecture that these judges would be willing to endorse traditional proofs with greater variations in detail and length.

Our data suggest that summarizing and proving are closely related tasks and hence, that asking students to summarize a given proof may be a productive task for those (practitioners and researchers) wishing to evaluate students’ understanding of the proofs that they read. In further support of this conclusion, we note the consistency between the thematic analysis presented here, and the content-based regression analysis presented in Davies et al. (2020). Davies et al. identified four features of students’ responses acted as significant predictors of a high comparative judgment-based score: introduction of the objects b and f, alongside appeals to ‘proof by contradiction’ and [an explication of] that contradiction (p. 14). This suggests a duality of validities with respect to both qualitative analysis presented here, and our primarily quantitative earlier work. The parallel with our earlier work supports the validity of the think-aloud protocol used in the present work. More importantly, the triangulation across studies (Davies et al., 2020) and analytical methods support the validity of our earlier conjecture that proof summaries can profitably be used as a proxy for students’ understanding of the given proof.

On Mathematicians’ (Dis-)Agreement Regarding Proof Summaries

We found that mathematicians were consistent with one another when making their decisions, as shown in Fig. 3. The parallels the reliability analysis of Davies et al. (2020), and is largely unsurprising given the overlapping datasets (recall that the parings in the present study were a subset of those used in our previous work). This consistency was expected, and provides further support for the use of comparative judgement for evaluating students’ proof comprehension in both research and practice contexts.

It remains, however, to account for the agreement amongst mathematicians’ pairwise decision-making, in light of the vast diversity of justifications mathematicians gave for their judgements. While our data does not shed significant light on this topic, we note that our findings mirror Weber and Czocher (2019), who reported on mathematicians’ evaluations of various forms of proof. Weber and Czocher demonstrated two key findings: 1) that mathematicians disagreed on the status of particular proofs, and 2) that these disagreements ‘only occurred for inferential methods that mathematicains found to be atypical’ (p. 12). We conjecture that our results follow a similar pattern. That is, judgements about proof summaries can largely be governed by the shared values and norms of the mathematical community, but that fringe cases exist generating isolated disagreements giving the artificial impression of disorder amongst otherwise largely homogeneous behaviour. While beyond the scope of this work, one might investigate this claim by generating a series of proof summary pairs, and conjecturing about the level of agreement each would generate.

Final Remarks

In this paper, we have made two distinct contributions to understanding of mathematical proof summaries and their value to proof comprehension assessment. First, we outlined a theoretical conception of proof summaries with respect to key ideas, proof construction and comprehension tasks, and notions of rigour. We then presented an interview study adding to the existing empirical literature promoting the value of proof summaries in the realm of proof comprehension. In particular, we have shown that the task of summarizing a given proof has substantive similarities with existing notions of good proof-writing, and the resulting evaluation of students’ summaries share important features with previously published applications to more quantitative notions of proof comprehension assessment. While it remains the case that further research is required to investigate the scope of our findings and their application to novel mathematical contexts, here we have made progress toward understanding and demonstrating the value of proof summaries as a tool for researchers and instructors wishing to access students’ understanding of the proofs that they read.