A novel CE-PT-MABAC method for T-spherical uncertain linguistic multiple attribute group decision-making

Abstract

A T-spherical uncertain linguistic set (TSULS) is not only an expanded form of the T-spherical fuzzy set and the uncertain linguistic set but can also integrate the quantitative judging ideas and qualitative assessing information of decision-makers. For the description of complex and uncertain assessment data, TSULS is a powerful tool for the precise description and reliable processing of information data. However, the existing multi-attribute border approximation area comparison (MABAC) method has not been studied in TSULS. Thus, the goal of this paper is to extend and improve the MABAC method to tackle group decision-making problems with completely unknown weight information in the TSUL context. First, the cross-entropy measure and the interactive operation laws for the TSUL numbers are defined, respectively. Then, the two interactive aggregation operators for TSUL numbers are developed, namely T-spherical uncertain linguistic interactive weighted averaging and T-spherical uncertain linguistic interactive weighted geometric operators. Their effective properties and some special cases are also investigated. Subsequently, a new TSULMAGDM model considering the DM’s behavioral preference and psychology is built by integrating the interactive aggregation operators, the cross-entropy measure, prospect theory, and the MABAC method. To explore the effectiveness and practicability of the proposed model, an illustrative example of Sustainable Waste Clothing Recycling Partner selection is presented, and the results show that the optimal solution is h₃. Finally, the reliable, valid, and generalized nature of the method is further verified through sensitivity analysis and comparative studies with existing methods.

Introduction

The process by which multiple DMs, including experts or stakeholders in different fields, select optimal option from multiple alternatives regarding multiple attributes or criteria is known as MAGDM [1, 2]. In contrast to single agent-based decision-making models, group decision-making can integrate the knowledge, experience, and preferences of various individuals and fully display democracy in the decision-making process. Currently, group decision-making models are widely applied in practical scenarios, such as service evaluation, credit evaluation, strategic planning evaluation and investment decision, and so on. Due to the complexity and uncertainty of the actual MAGDM problems, ambiguous, unquantifiable, incomplete, and unrealized information may occur in the information processing process. At this point, it is clearly unreasonable for DMs to use precise data to express individual judgments and preferences. DMs prefer to use linguistic evaluations when evaluating system performance [3, 4], for example, “good”, “very likely”, “low”, etc. This type of linguistic term can be close to people’s daily judgment habit and cognition, but a single linguistic variable cannot fully portray the DM’s actual ideas. To break through this dilemma, some scholars have proposed various linguistic information models, such as hesitant fuzzy linguistic term sets [5], intuitionistic linguistic sets [6], 2-tuple fuzzy linguistic representation model [7], etc. Xu [8] argued that the linguistic term interval form can more accurately portray the uncertainty of evaluation information in a way that is not achievable with a single linguistic tem variable. Therefore, Xu [8] introduced the concept of uncertain linguistic variables for the first time. So far, ULS have been the focus of numerous scholars, and various extension studies have further enriched the theory of ULSs.

Liu and Jin [9] raised the intuitionistic uncertain linguistic set (IULS) that combines the merits of ULS and intuitionistic fuzzy sets (IFS). It is obvious that its mathematical structure consists of an uncertain linguistic part and an intuitionistic fuzzy part, where the former describes the qualitative evaluation value of the alternative given by the DM regarding a certain attribute, while the latter quantifies the degree of support and opposition to the uncertain linguistic part [10,11,12].

The intuitionistic fuzzy part is required to satisfy that the sum of membership degree (MD) and non-membership degree (ND) is not over one [13]. On the contrary, IULSs cannot be adopted. Further, scholars have proposed the Pythagorean uncertain linguistic sets (PyULSs) [14,15,16,17,18] integrated by ULS and Pythagorean fuzzy set [19]. The modeling ability regarding uncertain information is improved to some extent. However, if the sum of the squares of MD and ND is over1, then PyULSs fail to be applied. After this, some scholars have studied q-rung orthopair uncertain linguistic sets (q-ROULSs) with generalization [20,21,22,23,24,25], which consists of the ULSs and q-rung orthopair fuzzy sets [26]. If the value of the parameter q in the q-rung orthopair fuzzy part is regulated to become larger, the expression range of q-ROULS is enlarged, and its ability to model uncertain information is further improved. IULS and PyULS are special cases of q-ROULS (when q = 1 and q = 2, respectively). Thus, q-ROULS is more flexible and comprehensive than IULS and PyULS in terms of expressing uncertain information.

Cuong [27] added abstinence degree (AD) to the intuitionistic fuzzy set binary structure to form a ternary structure concept, i.e., picture fuzzy set. This set can handle awkward and complex information more reliably [28, 29]. Combining ULS and picture fuzzy set, picture uncertain linguistic sets (PULSs) were defined by Wei [30], where the sum of MD, AD, and ND of the picture fuzzy part is required to be no more than 1. For the supplier selection problem, interval-valued PULSs were proposed by Naeem et al. [31]. Meanwhile, some interval-valued PULS Hamacher aggregation operators were developed by Garg et al. [32].

spherical fuzzy set (TSFS) is an advanced form of fuzzy set extension, which was presented by Mahmood et al. [33]. This set has the same ternary structure as the PFS and satisfies that the sum of the q-power of the membership functions is not larger than 1. In this way, the TSFS has a larger and more flexible information description space. Obviously, the TSFS is a generalized form of spherical fuzzy set, PFS, q-ROFS, PyFS, and IFS. As an unrestricted generalized function, TSFS is widely used by numerous scholars. At present, the academic research of scholars on TSFS is concentrated on the following aspects: the information measures [34, 35], the aggregation operators [36,37,38,39,40,41,42], and the alternative ranking techniques [37, 38, 43,44,45,46]. However, there are few studies on TSULS based on ULS and TSFS extensions. For example, Wang and Ullah [47] defined TSULS which contains both uncertain linguistic and T-spherical fuzzy parts, and proposed the generalized distance measure and Heronian mean aggregation operator in the TSULS setting, respectively. And then the MARCOS method was extended and improved to solve the MAGDM problem with TSULNs.

The MABAC method is called a good tool for solving the MAGDM problem to choose the optimal alternative. It was first proposed by Pamucar and Cirovic [48] in 2015 and used to deal with the logistics centers selection problem. The key step in the MABAC method is to select the best option by computing the distance between each alternative and the bored approximation area (BAA), which is different from existing decision approaches like TOPSIS, VIKOR, EDAS, MARCOS, MAIRCA, and TODIM. The MABAC method not only has the characteristics of simple calculation process and reliable results, but also has the advantages of considering the potential value of profit and loss and easy integration with other decision-making methods [49, 50]. Currently, scholars have carried out a variety of extensions and applications of the MABAC methodology with rich results, as shown in Table 1. As can be seen from Table 1, there are some extension and improvement challenges when applying the MABAC method to solve the MAGDM problems. The details are as follows:

• 1. The traditional MABAC method has been extended in various decision contexts, such as IFS [52, 54, 62] and its generalized forms [49, 51, 57, 60, 63, 68], linguistic [53, 61, 64, 66] and uncertain linguistic [65, 67], etc. However, these decision theories do not fully express vague, ambiguous, and uncertain subjective evaluative information. Moreover, the traditional MABAC approach has not been extended and improved in the TSUL environment.

• 2. In terms of DM weight determination. In the process of solving the MAGDM problem, most of the literatures on DM weight determination assume subjectively, and some literatures use AHP [50] and BWM [61, 69] to determine the DM weight subjectively. However, the determination of expert weights by these methods is rife with subjectivity and arbitrariness. Therefore, how to obtain DM objective weights in the TSULS environment is one of the key issues addressed in this paper.

• 3. In the aspect of attribute weight determination. The existing attribute weight determination methods mainly focus on the subjective approaches, such as AHP [50], SWARA [58], DEMATEL [59], and BWM [61, 63, 65, 69] methods. There are relatively few methods to determine the objective weights of attributes, such as maximization deviation method (MDM) [52, 61, 65], ITARA [57, 60], CRITIC [53, 66, 68, 70], and entropy [62]. There are also few studies on the combined weight of attributes [53, 61, 65]. And the correlation between the attributes has been ignored in many current studies, which is expected for the literatures [54, 59]. However, there is no comprehensive consideration on the attribute combined weight and the interrelationship of the attributes at present.

• 4. In the process of evaluation information aggregation, scholars proposed various aggregation operators, which not only enriched various decision-making theories and methods, but also provided strong support for the successful implementation of MABAC method. However, the existing aggregation operators are based on the AOLs, especially in the context of IFS, PyFS, and q-ROFS, there may be counterintuitive phenomena in the aggregation of evaluation information. For example, let δ_i = ([s_αi, s_βi],(τ_i, η_i, ν_i)) (i = 1, 2,…, m) be a family of TSULNs. If δ_k = ([s_αk, s_βk],(τ_k, η_k, 0)) and τ_k and η_k ≠ 0, then by traditional AOLs, we derive ν_δi×δk = 0, which means the NDs of the product result of ν_δi and ν_δk will always be zero if ν_k = 0. Obviously, ν_δi (i = 1, 2,…, m, i ≠ k) will not influence of the final aggregation results, which is somewhat counterintuitive. How to eliminate this phenomenon in the TSUL environment is one of the major challenges.

• 5. Determining the distance matrix is the core step in the traditional MABAC method. The Hamming or Euclidean distance measure has been used in the existing literatures [49, 51,52,53, 56,57,58, 61, 63]. Due to the different forms of Hamming or Euclidean distance measure in different decision environments, there may be different results between the alternative and BAA, which has affected the accuracy and reliability of the MABAC method. However, the use of distance measures in some studies is not well-considered, for example, ignoring the rejection degree in the q-ROFS distance measure [49, 51, 57], which may make the decision results inaccurate. In addition, some existing studies on the integration of PT and MABAC methods can reflect the behavioral preferences and psychology of DMs [62, 66,67,68]. However, in literature review, we can find that there is no research regarding the MABAC method based on CE and PT.

Table 1 MABAC methods for MAGDM problems in different decision environments

Throughout the above challenges, how to effectively handle TSUL information in solving the TSUL MAGDM problem and how to consider the decision maker's preference during the extension of the MABAC method are the research topics of this paper. To this end, this paper proposes the TSUL CE measure, the TSULIWA and TSULIWG operators, and an improved MABAC method based on CE-PT. These studies not only enrich the system of uncertain language set theory, but also extend the application areas of MABAC methods. These studies have significant theoretical and practical value implications. Therefore, some of the main highlights and contributions are described in this manuscript as follows:

• 1. The TSUL CE measure, a novel TSULS information measure, is first defined. This measure can synthetically handle the data from both TSFS and ULS, and it can realize a deviation measure between arbitrary TSULNs. This provides a reliable basis for obtaining experts, attribute weights and improving the MABAC method in this paper.

• 2. We develop some IOLs of TSULNs, and then the TSULIWA and TSULIWG operators are proposed, some related properties and particular cases are discussed. These operators eliminate counterintuitive phenomena and make TSULNs aggregation more rational and efficient.

• 3. The traditional distance measure was replaced by the TSUL CE measure. Based on this, we define TSUL similarity and construct MDM to obtain expert and attribute objective weights respectively. At the same time, the DEMATEL method, which considers the attribute correlation, is extended in the TSULS environment to obtain the attribute subjective weight, and then the combined weight is obtained.

• 4. Finally, we use the TSUL CE measure to replace the distance measure in the existing MABAC methods and integrate with the PT to determine the prospect matrix. And the applicability and validity of the TSUL CE-PT-MABAC model is verified by solving the SWCRP selection problem.

To this end, the other sections of this article are organized as follows: “Preliminaries” briefly reviews some related basic concepts, and TSUL CE measure is defined. “TSUL Aggregation operators based on IOLs” develops the IOLs of TSULNs and the TSULIWA and TSULIWG operators. “Proposed CE-PT-MABAC-based TSUL MAGDM model” builds the TSUL CE-PT-MABAC model for the MAGDM problems. “Illustrative example” illustrates the applicability of the proposed methodology using an example of SWCRP selection. A sensitivity analysis and a comparative study are also conducted. “Discussion” summarizes the research in this manuscript and outlines future plans.

Preliminaries

ULS, TSFS, and TSULS

This section outlines some of the basic definitions of ULS, TSFS, and TSULS.

Definition 1

[3]. The set of linguistic terms S = {s₀, s₁,…, s_k−1} consists of k hierarchical terms, where k is an odd number. Generally k can take values 3, 5, 7, and 9. e.g., k = 7, S = {s₀, s₁, s₂, s₃, s₄, s₅, s₆} = {very low, low, medium–low, medium, medium–high, high, very high}.

The conditions below should all be met for any linguistic set S:

• 1. If m > n, then s_m > s_n;

• 2. If there is a negative operator neg(s_m) = s_n, then n = k – 1 − m;

• 3. If s_m ≥ s_n, then max(s_m, s_n) = s_m;

• 4. If s_m ≤ s_n, then min(s_m, s_n) = s_m.

Definition 2

[8] Let $\tilde{S}$ be the set of uncertain linguistic variables $\tilde{s}_{i}$(i = 1, 2,…, n), i.e., $\tilde{S}$ is named as the ULS, which is denoted as $\tilde{S} = \{ \tilde{s}_{1} ,\tilde{s}_{2} , \ldots ,\tilde{s}_{n} \}$. And the uncertain linguistic variable $\tilde{s}_{i}$ can be denoted as $\tilde{s} = [s_{\alpha } ,s_{\beta } ]$, s_α, s_β ∈ S and α ≤ β, where s_α and s_β are the lower and upper bounds.

Since the uncertain linguistic variable operational rules proposed by Xu [8] may cause the calculation result to be over than grade k in linguistic terms. For this reason, Liu and Zhang [12] developed some new operational rules, which are defined as follows:

Definition 3

[12] Suppose $\tilde{s}_{1} = [s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ]$, $\tilde{s}_{2} = [s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ]$ are any two uncertain linguistic variables in linguistic term set $S = \{ s_{0} ,s_{1} ,s_{2} , \ldots ,s_{k - 1} \}$, the uncertain linguistic variables’ operational laws is presented as below:

• 1. $\tilde{s}_{1} \oplus \tilde{s}_{2} = \left[ {s_{{x_{1} + x_{2} - \frac{{x_{1} x_{2} }}{k}}} ,s_{{y_{1} + y_{2} - \frac{{y_{1} y_{2} }}{k}}} } \right]$;

• 2. $\tilde{s}_{1} \otimes \tilde{s}_{2} = \left[ {s_{{\frac{{x_{1} x_{2} }}{k}}} ,s_{{\frac{{y_{1} y_{2} }}{k}}} } \right]$;

• 3. $\lambda \tilde{s}_{1} = \left[ {s_{{k - k\left( {1 - \frac{{x_{1} }}{k}} \right)^{\lambda } }} ,s_{{k - k\left( {1 - \frac{{y_{1} }}{k}} \right)^{\lambda } }} } \right],\lambda \ge 0$;

• 4. $\left( {\tilde{s}_{1} } \right)^{\lambda } = \left[ {s_{{k\left( {\frac{{x_{1} }}{k}} \right)^{\lambda } }} ,s_{{k\left( {\frac{{y_{1} }}{k}} \right)^{\lambda } }} } \right],\lambda \ge 0$.

Definition 4

[33] Assuming that X is a non-empty set, the TSFS is described in the following form:

$$ \Im { = }\left\{ {\left\langle {x,\left( {\tau_{\Im } (x),\eta_{\Im } (x),\vartheta_{\Im } (x)} \right)} \right\rangle |x \in X} \right\} $$

(1)

where $\tau_{\Im } (x),\eta_{\Im } (x),\vartheta_{\Im } (x) \in [0,1][0,1]$ are the MD, AD, and ND of element x ∈ ℑ in X, respectively, and satisfying $0 \le \tau_{\Im }^{q} (x) + \eta_{\Im }^{q} (x) + \vartheta_{\Im }^{q} (x) \le 1$, q ≥ 1 for ∀x ∈ X. In addition, $\pi_{\Im } (x) = \sqrt[q]{{1 - \tau_{\Im }^{q} (x) - \eta_{\Im }^{q} (x) - \vartheta_{\Im }^{q} (x)}}$ is known as the refusal degree. For convenience, the ternary structure of T-spherical fuzzy number (TSFN) is denoted as ρ = (τ, η, ϑ).

Definition 5

[38] For a TSFN ρ = (τ, η, ϑ), the score function sc(ρ) and accuracy function ac(ρ) of this TSFN are described as follows, respectively:

$$ sc(\rho ) = \frac{{1 + \tau^{q} - \eta^{q} - \vartheta^{q} }}{2}, $$

(2)

$$ ac(\rho ) = \tau^{q} + \eta^{q} + \vartheta^{q} . $$

(3)

For arbitrary two TSFNs ρ₁ = (τ₁, η₁, ϑ₁) and ρ₂ = (τ₂, η₂, ϑ₂), judging the priority of both can be according to the following rules:

• 1. If sc(ρ₁) > sc(ρ₂), then ρ₁ is greater than ρ₂, namely, ρ₁ > ρ₂;

• 2. If sc(ρ₁) = sc(ρ₂), then if ac(ρ₁) > ac(ρ₂), then ρ₁ is greater than ρ₂, namely, ρ₁ > ρ₂; (ii) if ac(ρ₁) = ac(ρ₂), then ρ₁ is equal to ρ₂, namely, ρ₁ = ρ₂.

Since the operational rules proposed by Mahmood et al. [33] do not take the interaction among the MD, AD, and ND of TSFNs into account. If AD or ND in any two TSFNs is zero, then AD or ND in result value is also zero based on the TSFNs algebraic sum operation, which is counterintuitive. To eliminate this phenomenon, the IOLs of TSFNs proposed by Ju et al. [38] are adopted in this paper.

Definition 6

[38] Assuming that ρ = (τ, η, ϑ), ρ₁ = (τ₁, η₁, ϑ₁) and ρ₂ = (τ₂, η₂, ϑ₂) are any three TSFNs, then they have the following IOLs:

• 1. $\rho_{1} \oplus \rho_{2} = \left( {\sqrt[q]{{1{ - }\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )} }}} \right)$;

• 2. $\rho_{1} \otimes \rho_{2} = \left( {\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} - \eta_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} - \eta_{i}^{q} - \tau_{i}^{q} )} }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} - \eta_{i}^{q} )} }},\sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} )} }}} \right)$;

• 3. $\lambda \cdot \rho = \left( {\sqrt[q]{{1 - (1 - \tau^{q} )^{\lambda } }},\sqrt[q]{{(1 - \tau^{q} )^{\lambda } - (1 - \tau^{q} - \eta^{q} )^{\lambda } }},\sqrt[q]{{(1 - \tau^{q} - \eta^{q} )^{\lambda } - (1 - \tau^{q} - \eta^{q} - \vartheta^{q} )^{\lambda } }}} \right)$, λ > 0;

• 4. $\rho^{\lambda } = \left( {\sqrt[q]{{(1 - \vartheta^{q} - \eta^{q} )^{\lambda } - (1 - \vartheta^{q} - \eta^{q} - \tau^{q} )^{\lambda } }},\sqrt[q]{{(1 - \vartheta^{q} )^{\lambda } - (1 - \vartheta^{q} - \eta^{q} )^{\lambda } }},\sqrt[q]{{1 - (1 - \vartheta^{q} )^{\lambda } }}} \right)$, λ > 0.

Wang and Ullah [47] defined the TSULS concept based on the TSFS and ULS. This concept is described below:

Definition 7

[47]. Let X be a universe set, there is an uncertain linguistic variable, i.e., $\left[ {s_{\alpha (x)} ,s_{\beta (x)} } \right] \in X$, then

$$ \tilde{Q}{ = }\left\{ {\left\langle {x\left( {[s_{\alpha (x)} ,s_{\beta (x)} ],(\tau_{{\tilde{Q}}} (x),\eta_{{\tilde{Q}}} (x),\vartheta_{{\tilde{Q}}} (x))} \right)} \right\rangle \left| {x \in X} \right.} \right\} $$

(4)

is named an TSULS. In the TSF part, $\tau_{{\tilde{Q}}} (x)$, $\eta_{{\tilde{Q}}} (x)$,$\vartheta_{{\tilde{Q}}} (x) \in [0,1]$ mean the MD, AD, and ND of elements x to uncertain linguistic variable $[s_{\alpha (x)} ,s_{\beta (x)} ]$, and satisfying $0 \le \left( {\tau_{{\tilde{Q}}} (x)} \right)^{q} + \left( {\eta_{{\tilde{Q}}} (x)} \right)^{q} + \left( {\vartheta_{{\tilde{Q}}} (x)} \right)^{q} \le 1$, q ≥ 1, for ∀x ∈ X. $\pi_{{\tilde{Q}}} (x) = \sqrt[q]{{1 - \tau_{{\tilde{Q}}}^{q} (x) - \eta_{{\tilde{Q}}}^{q} (x) - \vartheta_{{\tilde{Q}}}^{q} (x)}}$ is called the refusal degree $\tilde{Q}$ in X. For simplicity, the TSULN is noted as $\delta = ([s_{\alpha } ,s_{\beta } ],(\tau ,\eta ,\vartheta ))$.

Definition 8

[47] For a TSULN $\delta = ([s_{\alpha } ,s_{\beta } ],(\tau ,\eta ,\vartheta ))$, the following describes the score function sc(δ) and accuracy function ac(δ) of TSULN, respectively:

$$ sc(\delta ) = \frac{1}{2}\left( {1 + \tau^{q} - \eta^{q} - \vartheta^{q} } \right) \times s_{{\frac{1}{2}\left( {\alpha + \beta } \right)}} = s_{{\frac{1}{4}\left( {\alpha + \beta } \right)\left( {1 + \tau^{q} - \eta^{q} - \vartheta^{q} } \right)}} $$

(5)

$$ ac(\delta ) = \left( {\tau^{q} + \eta^{q} + \vartheta^{q} } \right) \times s_{{\frac{1}{2}\left( {\alpha + \beta } \right)}} = s_{{\frac{1}{2}\left( {\alpha + \beta } \right)\left( {\tau^{q} + \eta^{q} + \vartheta^{q} } \right)}} $$

(6)

To judge the priority of any two TSULNs $\delta_{1} = ([s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ],(\tau_{1} ,\eta_{1} ,\vartheta_{1} ))$ and $\delta_{2} = ([s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ],(\tau_{2} ,\eta_{2} ,\vartheta_{2} ))$, the rules are described as follows:

• 1. If sc(δ₁) > sc(δ₂), then δ₁ is greater than δ₂, namely, δ₁ > δ₂;

• 2. If sc(δ₁) = sc(δ₂), then (i) if ac(δ₁) > ac(δ₂), then δ₁ is greater than δ₂, namely, δ₁ > δ₂; (ii) if ac(δ₁) = ac(δ₂), then δ₁ is equal to δ₂, namely, δ₁ = δ₂.

TSUL cross-entropy measure

To represent the discrimination of uncertain information between any two TSULNs, we define the concept of TSUL CE measure, which contains two CE measures in uncertain linguistic part and T-spherical fuzzy part.

Definition 9

For any two TSULNs $\delta_{1} = ([s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ],(\tau_{1} ,\eta_{1} ,\vartheta_{1} ))$ and $\delta_{2} = ([s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ],(\tau_{2} ,\eta_{2} ,\vartheta_{2} ))$ (q ≥ 1, k ≥ 3), the cross-entropy between TSULNs δ₁ and δ₂ is defined as follows:

$$ {\text{CE}}(\delta_{1} ,\delta_{2} ) = {\text{CE}}_{{{\text{UL}}}} (\delta_{1} ,\delta_{2} ) + {\text{CE}}_{{{\text{TSF}}}} (\delta_{1} ,\delta_{2} ) $$

(7)

where

$$ \begin{gathered} {\text{CE}}_{UL} (\delta_{1} ,\delta_{2} ) = \frac{{\alpha_{1} + \beta_{1} }}{2(k - 1)}\ln \frac{{2(\alpha_{1} + \beta_{1} )}}{{\alpha_{1} + \beta_{1} + \alpha_{2} + \beta_{2} }}\hfill \\ \qquad + \left( {1 - \frac{{\alpha_{1} + \beta_{1} }}{2(k - 1)}} \right)\ln \frac{{4(k - 1) - 2(\alpha_{1} + \beta_{1} )}}{{4(k - 1) - (\alpha_{1} + \beta_{1} + \alpha_{2} + \beta_{2} )}}\hfill \\ \qquad + \frac{{\beta_{1} - \alpha_{1} }}{k - 1}\ln \frac{{2(\beta_{1} - \alpha_{1} )}}{{\beta_{1} - \alpha_{1} + \beta_{2} - \alpha_{2} }} + \left( {1 - \frac{{\beta_{1} - \alpha_{1} }}{k - 1}} \right)\hfill \\ \qquad \ln \frac{{2\left( {(k - 1) - (\beta_{1} - \alpha_{1} )} \right)}}{{2(k - 1) - (\beta_{1} - \alpha_{1} + \beta_{2} - \alpha_{2} )}} + \frac{{\alpha_{2} + \beta_{2} }}{2(k - 1)}\hfill \\ \qquad \ln \frac{{2(\alpha_{2} + \beta_{2} )}}{{\alpha_{1} + \beta_{1} + \alpha_{2} + \beta_{2} }} + \left( {1 - \frac{{\alpha_{2} + \beta_{2} }}{2(k - 1)}} \right)\hfill \\ \qquad \ln \frac{{4(k - 1) - 2(\alpha_{2} + \beta_{2} )}}{{4(k - 1) - (\alpha_{1} + \beta_{1} + \alpha_{2} + \beta_{2} )}} + \frac{{\beta_{2} - \alpha_{2} }}{k - 1}\hfill \\ \qquad \ln \frac{{2(\beta_{2} - \alpha_{2} )}}{{\beta_{1} - \alpha_{1} + \beta_{2} - \alpha_{2} }} + \left( {1 - \frac{{\beta_{2} - \alpha_{2} }}{k - 1}} \right)\hfill \\ \qquad \ln \frac{{2\left( {(k - 1) - (\beta_{2} - \alpha_{2} )} \right)}}{{2(k - 1) - (\beta_{1} - \alpha_{1} + \beta_{2} - \alpha_{2} )}}, \hfill \\ \end{gathered} $$

$$ \begin{gathered} {\text{CE}}_{{{\text{TSF}}}} (\delta_{1} ,\delta_{2} ) = \sqrt {\frac{{\tau_{1}^{q} + \tau_{2}^{q} }}{2}} - \left({\frac{{\sqrt {\tau_{1}^{q} } + \sqrt {\tau_{2}^{q} }}}{2}} \right)\hfill \\ \qquad + \sqrt{\frac{{\eta_{1}^{q} + \eta_{2}^{q} }}{2}} - \left( {\frac{{\sqrt {\eta_{1}^{q} } + \sqrt {\eta_{2}^{q} } }}{2}} \right) \hfill \\ \qquad + \sqrt {\frac{{(1 - \eta_{1}^{q} ) + (1 - \eta_{2}^{q} )}}{2}} - \left( {\frac{{\sqrt {1 - \eta_{1}^{q} } + \sqrt {1 - \eta_{2}^{q} } }}{2}} \right)\hfill \\ \qquad + \sqrt {\frac{{\vartheta_{1}^{q} + \vartheta_{2}^{q} }}{2}} - \left( {\frac{{\sqrt {\vartheta_{1}^{q} } + \sqrt {\vartheta_{2}^{q} } }}{2}} \right)\hfill \\ \qquad + \sqrt {\frac{{\pi_{1}^{q} + \pi_{2}^{q} }}{2}} - \left({\frac{{\sqrt {\pi_{1}^{q} } + \sqrt {\pi_{2}^{q} } }}{2}}\right). \hfill \\ \end{gathered} $$

Theorem 1

For any two TSULNs δ₁ and δ₂, the cross-measure CE(δ₁, δ₂) satisfies the following properties:

• 1. CE(δ₁, δ₂) ≥ 0;

• 2. CE(δ₁, δ₂) = 0, iff δ₁ = δ₂;

• 3. CE(δ₁, δ₂) = CE(δ₂, δ₁);

• 4. CE(δ₁, δ₂) = CE(δ₁^c, δ₂^c), where $\delta_{i}^{c} = ([s_{{k - 1 - \beta_{i} }} ,s_{{k - 1 - \alpha_{i} }} ],(\vartheta_{i} ,\eta_{i} ,\tau_{i} ))$ (i = 1, 2).

Proof

(i) For the uncertain linguistic part in TSULN, we can easily prove ${\text{CE}}_{{{\text{UL}}}} (\delta_{1} ,\delta_{2} ) \ge 0$ based on Shannon’s inequality. For the T-spherical fuzzy part in TSULN, since for all the real numbers x and y, the inequality $\sqrt {\frac{{x^{q} + y^{q} }}{2}} \ge \frac{{\sqrt {x^{q} } + \sqrt {y^{q} } }}{2}$ holds. It’s easy to get ${\text{CE}}_{{{\text{TSF}}}} (\delta_{1} ,\delta_{2} ) \ge 0$.

So, CE(δ₁, δ₂) ≥ 0, which completes the proof of property (1).

(ii) We can easily prove that properties (2)–(4) hold.

Example 1

Suppose δ₁ = ([s₁, s₃], (0.5, 0.6, 0.1)) and δ₂ = ([s₄, s₅], (0.7, 0.1, 0.3)) are TSULNs, k = 7, q = 2. We use Eq. (11) to measure these two TSULNs, and the specific calculation is as follows:

First, we calculate the cross-entropy value of uncertain linguistic part in the TSULNs.

$$ \begin{gathered} {\text{CE}}_{{{\text{UL}}}} (\delta_{1} ,\delta_{2} ) = \frac{1 + 3}{{2 \times (7 - 1)}}\ln \frac{2 \times (1 + 3)}{{1 + 3 + 4 + 5}}\hfill \\ \qquad + \left( {1 - \frac{1 + 3}{{2 \times (7 - 1)}}} \right) \ln \frac{4 \times (7 - 1) - 2 \times (1 + 3)}{{4 \times (7 - 1) - (1 + 3 + 4 + 5)}}\hfill \\ \qquad + \frac{3 - 1}{{7 - 1}}\ln \frac{2 \times (3 - 1)}{{3 - 1 + 5 - 4}}+ \left( {1 - \frac{3 - 1}{{7 - 1}}} \right)\hfill \\ \qquad \ln \frac{{2 \times \left( {(7 - 1) - (3 - 1)} \right)}}{2 \times (7 - 1) - (3 - 1 + 5 - 4)} + \frac{4 + 5}{{2 \times (7 - 1)}}\hfill \\ \qquad \ln \frac{2 \times (4 + 5)}{{1 + 3 + 4 + 5}} + \left( {1 - \frac{4 + 5}{{2 \times (7 - 1)}}} \right)\hfill \\ \qquad \ln \frac{4 \times (7 - 1) - 2 \times (4 + 5)}{{4 \times (7 - 1) - (1 + 3 + 4 + 5)}} + \frac{5 - 4}{{7 - 1}}\hfill \\ \qquad\ln \frac{2 \times (5 - 4)}{{3 - 1 + 5 - 4}} + \left( {1 - \frac{5 - 4}{{7 - 1}}} \right)\hfill \\ \qquad \ln \frac{{2 \times \left( {(7 - 1) - (5 - 4)} \right)}}{2 \times (7 - 1) - (3 - 1 + 5 - 4)}{ = }0.2181 \hfill \\ \end{gathered} $$

Then, the refusal degrees of TSFNs in T-spherical fuzzy parts of TSULNs are calculated as π₁ = 0.616 and π₂ = 0.640. From this, we can calculate the cross-entropy value of TSF part in TSULNs.

$$ \begin{gathered} CE_{TSF} (\delta_{1} ,\delta_{2} ) = \sqrt {\frac{{0.5^{2} + 0.7^{2} }}{2}} - \left( {\frac{{\sqrt {0.5^{2} } + \sqrt {0.7^{2} } }}{2}} \right)\hfill \\ \qquad + \sqrt {\frac{{0.6^{2} + 0.1^{2} }}{2}} - \left( {\frac{{\sqrt {0.6^{2} } + \sqrt {0.1^{2} } }}{2}} \right) \hfill \\ \qquad + \sqrt {\frac{{(1 - 0.6^{2} ) + (1 - 0.1^{2} )}}{2}} - \left( {\frac{{\sqrt {1 - 0.6^{2} } + \sqrt {1 - 0.1^{2} } }}{2}} \right) \hfill \\ \qquad + \sqrt {\frac{{0.1^{2} + 0.3^{2} }}{2}} - \left( {\frac{{\sqrt {0.1^{2} } + \sqrt {0.3^{2} } }}{2}} \right) + \sqrt {\frac{{0.616^{2} + 0.640^{2} }}{2}}\hfill \\ \qquad - \left( {\frac{{\sqrt {0.616^{2} } + \sqrt {0.640^{2} } }}{2}} \right) = 0.1174 \hfill \\ \end{gathered} $$

So, $CE(\delta_{1} ,\delta_{2} ) = CE_{UL} (\delta_{1} ,\delta_{2} ) + CE_{TSF} (\delta_{1} ,\delta_{2} ) = 0.2181 + 0.1174 = 0.3355$.

TSUL aggregation operators based on IOLs

In this section, the IOLs of TSULNs are developed, two new TSULIWA and TSULIWG operators are developed on the basis of IOLs, and related properties and special cases are discussed.

TSUL IOLs

To eliminate the counterintuitive problem, inspired by the IOLs of TSFNs developed by Ju et al. [46], we define the IOLs of TSULNs as follows:

Definition 10

Suppose $\delta = ([s_{\alpha } ,s_{\beta } ],(\tau ,\eta ,\vartheta ))$, $\delta_{1} = ([s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ],(\tau_{1} ,\eta_{1} ,\vartheta_{1} ))$ and $\delta_{2} = ([s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ],(\tau_{2} ,\eta_{2} ,\vartheta_{2} ))$ are three random TSULNs, then the IOLs of these TSULNs are defined as follows:

$$ \delta_{1} \oplus \delta_{2} = \left( {\left[ {s_{{\alpha_{1} + \alpha_{2} - \frac{{\alpha_{1} \alpha_{2} }}{k}}} ,s_{{\beta_{1} + \beta_{2} - \frac{{\beta_{1} \beta_{2} }}{k}}} } \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )} }} \hfill \\ \end{gathered} \right)} \right); $$

(8)

$$ \delta_{1} \otimes \delta_{2} = \left( {\left[ {s_{{\frac{{\alpha_{1} \alpha_{2} }}{k}}} ,s_{{\frac{{\beta_{1} \beta_{2} }}{k}}} } \right],\left( \begin{gathered} \sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} - \eta_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} - \eta_{i}^{q} - \tau_{i}^{q} )} }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} - \eta_{i}^{q} )} }},\sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {(1 - \vartheta_{i}^{q} )} }} \hfill \\ \end{gathered} \right)} \right); $$

(9)

$$ \lambda \cdot \delta = \left( {\left[ {s_{{k - k\left( {1 - \frac{\alpha }{k}} \right)^{\lambda } }} ,s_{{k - k\left( {1 - \frac{\beta }{k}} \right)^{\lambda } }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - (1 - \tau^{q} )^{\lambda } }},\sqrt[q]{{(1 - \tau^{q} )^{\lambda } - (1 - \tau^{q} - \eta^{q} )^{\lambda } }}, \hfill \\ \sqrt[q]{{(1 - \tau^{q} - \eta^{q} )^{\lambda } - (1 - \tau^{q} - \eta^{q} - \vartheta^{q} )^{\lambda } }} \hfill \\ \end{gathered} \right)} \right),\lambda > 0; $$

(10)

$$ \delta^{\lambda } = \left( {\left[ {s_{{k\left( {\frac{\alpha }{k}} \right)^{\lambda } }} ,s_{{k\left( {\frac{\beta }{k}} \right)^{\lambda } }} } \right],\left( \begin{gathered} \sqrt[q]{{(1 - \vartheta^{q} - \eta^{q} )^{\lambda } - (1 - \vartheta^{q} - \eta^{q} - \tau^{q} )^{\lambda } }}, \hfill \\ \sqrt[q]{{(1 - \vartheta^{q} )^{\lambda } - (1 - \vartheta^{q} - \eta^{q} )^{\lambda } }},\sqrt[q]{{1 - (1 - \vartheta^{q} )^{\lambda } }} \hfill \\ \end{gathered} \right)} \right),\lambda > 0 $$

(11)

Theorem 2

Let $\delta = ([s_{\alpha } ,s_{\beta } ],(\tau ,\eta ,\vartheta ))$, $\delta_{1} = ([s_{{\alpha_{1} }} ,s_{{\beta_{1} }} ],(\tau_{1} ,\eta_{1} ,\vartheta_{1} ))$ and $\delta_{2} = ([s_{{\alpha_{2} }} ,s_{{\beta_{2} }} ],(\tau_{2} ,\eta_{2} ,\vartheta_{2} ))$ be three TSULNs, λ₁, λ₂, λ ≥ 0. Then their operational properties are as below:

• 1. $\delta_{1} \oplus \delta_{2} = \delta_{2} \oplus \delta_{1}$;

• 2. $\delta_{1} \otimes \delta_{2} = \delta_{2} \otimes \delta_{1}$;

• 3. $\lambda \cdot (\delta_{1} \oplus \delta_{2} ) = \lambda \cdot \delta_{2} \oplus \lambda \cdot \delta_{1}$;

• 4. $\lambda_{1} \cdot \delta \oplus \lambda_{2} \cdot \delta = (\lambda_{1} + \lambda_{2} ) \cdot \delta$;

• 5. $\delta^{{\lambda_{1} }} \otimes \delta^{{\lambda_{2} }} = \delta^{{(\lambda_{1} + \lambda_{2} )}}$;

• 6. $\delta_{1}^{\lambda } \otimes \delta_{2}^{\lambda } = (\delta_{1} \otimes \delta_{2} )^{\lambda }$.

Proof

(i) By the Eqs. (8–9), properties (1–2) are not difficult to prove.

(ii) With respect to property (3), since

$$ \delta_{1} \oplus \delta_{2} = \left( {\left[ {s_{{\alpha_{1} + \alpha_{2} - \frac{{\alpha_{1} \alpha_{2} }}{k}}} ,s_{{\beta_{1} + \beta_{2} - \frac{{\beta_{1} \beta_{2} }}{k}}} } \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )} }} \hfill \\ \end{gathered} \right)} \right) $$

According to Eq. (10), we can have

$$ \lambda (\delta_{1} \oplus \delta_{2} ) = \lambda \left( {\left[ {s_{{\alpha_{1} + \alpha_{2} - \frac{{\alpha_{1} \alpha_{2} }}{k}}} ,s_{{\beta_{1} + \beta_{2} - \frac{{\beta_{1} \beta_{2} }}{k}}} } \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )} }} \hfill \\ \end{gathered} \right)} \right) $$

$$ = \left( {\left[ \begin{gathered} s_{{k - k\left( {1 - \frac{{\alpha_{1} + \alpha_{2} - \frac{{\alpha_{1} \alpha_{2} }}{k}}}{k}} \right)^{\lambda } }} , \hfill \\ s_{{k - k\left( {1 - \frac{{\beta_{1} + \beta_{2} - \frac{{\beta_{1} \beta_{2} }}{k}}}{k}} \right)^{\lambda } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \left( {1 - 1 + \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} } \right)^{\lambda } }},\sqrt[q]{\begin{gathered} \left( {1 - 1 + \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} } \right)^{\lambda } - \hfill \\ \left( {1 - 1 + \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} + \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} } \right)^{\lambda } \hfill \\ \end{gathered} } \hfill \\ \sqrt[q]{\begin{gathered} \left( {1 - 1 + \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} + \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} } \right)^{\lambda } - \hfill \\ \left( \begin{gathered} 1 - 1 + \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )} + \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} - \hfill \\ \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )} + \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )} \hfill \\ \end{gathered} \right)^{\lambda } \hfill \\ \end{gathered} } \hfill \\ \end{gathered} \right)} \right) $$

$$ = \left( {\left[ \begin{gathered} s_{{k - k\left( {1 - \frac{{\alpha_{1} }}{k} - \frac{{\alpha_{2} }}{k} + \frac{{\alpha_{1} \alpha_{2} }}{{k^{2} }}} \right)^{\lambda } }} , \hfill \\ s_{{k - k\left( {1 - \frac{{\beta_{1} }}{k} - \frac{{\beta_{2} }}{k} + \frac{{\beta_{1} \beta_{2} }}{{k^{2} }}} \right)^{\lambda } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )}^{\lambda } }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )^{\lambda } } - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )^{\lambda } } }} \hfill \\ \end{gathered} \right)} \right) $$

$$ = \left( {\left[ \begin{gathered} s_{{k - k\prod\nolimits_{i = 1}^{2} {\left( {1 - \frac{{\alpha_{i} }}{k}} \right)^{\lambda } } }} , \hfill \\ s_{{k - k\prod\nolimits_{i = 1}^{2} {\left( {1 - \frac{{\beta_{i} }}{k}} \right)^{\lambda } } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )}^{\lambda } }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )^{\lambda } } - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )^{\lambda } } }} \hfill \\ \end{gathered} \right)} \right) $$

Then, since

$$ \lambda \cdot \delta = \left( {\left[ {s_{{k - k\left( {1 - \frac{\alpha }{k}} \right)^{\lambda } }} ,s_{{k - k\left( {1 - \frac{\beta }{k}} \right)^{\lambda } }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - (1 - \tau^{q} )^{\lambda } }},\sqrt[q]{{(1 - \tau^{q} )^{\lambda } - (1 - \tau^{q} - \eta^{q} )^{\lambda } }}, \hfill \\ \sqrt[q]{{(1 - \tau^{q} - \eta^{q} )^{\lambda } - (1 - \tau^{q} - \eta^{q} - \vartheta^{q} )^{\lambda } }} \hfill \\ \end{gathered} \right)} \right) $$

According to Eq. (8), we can have

$$ \begin{gathered} \lambda \delta_{1} \oplus \lambda \delta_{2} = \left( {\left[ {s_{{k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{\lambda } }} ,s_{{k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{\lambda } }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - (1 - \tau_{1}^{q} )^{\lambda } }},\sqrt[q]{{(1 - \tau_{1}^{q} )^{\lambda } - (1 - \tau_{1}^{q} - \eta_{1}^{q} )^{\lambda } }}, \hfill \\ \sqrt[q]{{(1 - \tau_{1}^{q} - \eta_{1}^{q} )^{\lambda } - (1 - \tau_{1}^{q} - \eta_{1}^{q} - \vartheta_{1}^{q} )^{\lambda } }} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \, \oplus \left( {\left[ {s_{{k - k\left( {1 - \frac{{\alpha_{2} }}{k}} \right)^{\lambda } }} ,s_{{k - k\left( {1 - \frac{{\beta_{2} }}{k}} \right)^{\lambda } }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - (1 - \tau_{2}^{q} )^{\lambda } }},\sqrt[q]{{(1 - \tau_{2}^{q} )^{\lambda } - (1 - \tau_{2}^{q} - \eta_{2}^{q} )^{\lambda } }}, \hfill \\ \sqrt[q]{{(1 - \tau_{2}^{q} - \eta_{2}^{q} )^{\lambda } - (1 - \tau_{2}^{q} - \eta_{2}^{q} - \vartheta_{2}^{q} )^{\lambda } }} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} $$

$$ = \left( {\left[ \begin{gathered} s_{{k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{\lambda } + k - k\left( {1 - \frac{{\alpha_{2} }}{k}} \right)^{\lambda } - \frac{{\left( {k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{\lambda } } \right)\left( {k - k\left( {1 - \frac{{\alpha_{2} }}{k}} \right)^{\lambda } } \right)}}{k}}} , \hfill \\ s_{{k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{\lambda } + k - k\left( {1 - \frac{{\beta_{2} }}{k}} \right)^{\lambda } - \frac{{\left( {k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{\lambda } } \right)\left( {k - k\left( {1 - \frac{{\beta_{2} }}{k}} \right)^{\lambda } } \right)}}{k}}} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {\left( {1 - 1 + (1 - \tau_{i}^{q} )^{\lambda } } \right)} }}, \hfill \\ \sqrt[q]{\begin{gathered} \prod\nolimits_{i = 1}^{2} {\left( {1 - 1 + (1 - \tau_{i}^{q} )^{\lambda } } \right)} - \hfill \\ \prod\nolimits_{i = 1}^{2} {\left( {1 - 1 + (1 - \tau_{i}^{q} )^{\lambda } - (1 - \tau_{i}^{q} )^{\lambda } + (1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } \right)} \hfill \\ \end{gathered} }, \hfill \\ \sqrt[q]{\begin{gathered} \prod\nolimits_{i = 1}^{2} {\left( {1 - 1 + (1 - \tau_{i}^{q} )^{\lambda } - (1 - \tau_{i}^{q} )^{\lambda } + (1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } \right)} - \hfill \\ \prod\nolimits_{i = 1}^{2} {\left( \begin{gathered} 1 - 1 + (1 - \tau_{i}^{q} )^{\lambda } - (1 - \tau_{i}^{q} )^{\lambda } + (1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } - \hfill \\ (1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } + (1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )^{\lambda } \hfill \\ \end{gathered} \right)} \hfill \\ \end{gathered} } \hfill \\ \end{gathered} \right)} \right) $$

$$ = \left( {\left[ \begin{gathered} s_{{k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{\lambda } \left( {1 - \frac{{\alpha_{2} }}{k}} \right)^{\lambda } }} , \hfill \\ s_{{k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{\lambda } \left( {1 - \frac{{\beta_{2} }}{k}} \right)^{\lambda } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )^{\lambda } } }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )^{\lambda } } - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )^{\lambda } } }} \hfill \\ \end{gathered} \right)} \right) $$

$$ = \left( {\left[ \begin{gathered} s_{{k - k\prod\nolimits_{i = 1}^{2} {\left( {1 - \frac{{\alpha_{i} }}{k}} \right)^{\lambda } } }} , \hfill \\ s_{{k - k\prod\nolimits_{i = 1}^{2} {\left( {1 - \frac{{\beta_{i} }}{k}} \right)^{\lambda } } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )}^{\lambda } }},\sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} )^{\lambda } } - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} )^{\lambda } } - \prod\nolimits_{i = 1}^{2} {(1 - \tau_{i}^{q} - \eta_{i}^{q} - \vartheta_{i}^{q} )^{\lambda } } }} \hfill \\ \end{gathered} \right)} \right) $$

Thus, $\lambda \cdot (\delta_{1} \oplus \delta_{2} ) = \lambda \cdot \delta_{2} \oplus \lambda \cdot \delta_{1}$, the property (3) completes the proof.

(iii) The proofs of properties (4–6) are the same as for property (3). It is omitted.

TSUL interactive weighted aggregation operators

Based on the IOLs for TSULNs above, two new TSULIWA and TSULIWG operators are developed in this subsection, with the relevant definitions described below:

Definition 11

Let $\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))$ (j = 1, 2,…, n) be a collection of TSULNs. A weight vector of δ_j (j = 1, 2,…, n) is w = (w₁, w₂,…, w_n)^T, with w_j > 0 and $\sum\nolimits_{j = 1}^{n} {w_{j} = 1}$. The TSULIWA and TSULIWG operators are defined as the.

$$ {\text{TSULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \sum\limits_{j = 1}^{n} {w_{j} \delta_{j} } $$

(12)

$$ {\text{TSULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \prod\limits_{j = 1}^{n} {(\delta_{j} )^{{w_{j} }} } $$

(13)

Theorem 3

Let $\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))$ (j = 1, 2,…, n) be a family of TSULNs. Then the aggregation values by the Eqs. (12)–(13) are still TSULNs, and even

$$ {\text{TSULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{q} )^{{w_{j} }} } }},\sqrt[q]{{\prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } }}, \hfill \\ \sqrt[q]{{\prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{q} - \eta_{j}^{q} - \vartheta_{j}^{q} )^{{w_{j} }} } }} \hfill \\ \end{gathered} \right)} \right) $$

(14)

$$ {\text{TSULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{\prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{q} - \eta_{j}^{q} - \tau_{j}^{q} )^{{w_{j} }} } }}, \hfill \\ \sqrt[q]{{\prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } }},\sqrt[q]{{1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{q} )^{{w_{j} }} } }} \hfill \\ \end{gathered} \right)} \right) $$

(15)

Proof

The results from the TSULIWA and TSULWG operators, respectively, are still TSFNs, which is not difficult to prove. It is omitted. Then, we prove that the Eqs. (14)–(15) hold by mathematical induction. We first focus on the proof of TSULIWA, which follows:

• 1. When n = 1, the Eq. (14) holds.

• 2. Based on the Definition 10, when n = 2, we can obtain

  $$ w_{1} \cdot \delta_{1} = \left( {\left[ {s_{{k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{{w_{1} }} }} ,s_{{k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{{w_{1} }} }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - (1 - \tau_{1}^{q} )^{{w_{1} }} }},\sqrt[q]{{(1 - \tau_{1}^{q} )^{{w_{1} }} - (1 - \tau_{1}^{q} - \eta_{1}^{q} )^{{w_{1} }} }}, \hfill \\ \sqrt[q]{{(1 - \tau_{1}^{q} - \eta_{1}^{q} )^{{w_{1} }} - (1 - \tau_{1}^{q} - \eta_{1}^{q} - \vartheta_{1}^{q} )^{{w_{1} }} }} \hfill \\ \end{gathered} \right)} \right); $$
  $$ w_{2} \cdot \delta_{2} = \left( {\left[ {s_{{k - k\left( {1 - \frac{{\alpha_{2} }}{k}} \right)^{{w_{2} }} }} ,s_{{k - k\left( {1 - \frac{{\beta_{2} }}{k}} \right)^{{w_{2} }} }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - (1 - \tau_{2}^{q} )^{{w_{2} }} }},\sqrt[q]{{(1 - \tau_{2}^{q} )^{{w_{2} }} - (1 - \tau_{2}^{q} - \eta_{2}^{q} )^{{w_{2} }} }}, \hfill \\ \sqrt[q]{{(1 - \tau_{2}^{q} - \eta_{2}^{q} )^{{w_{2} }} - (1 - \tau_{2}^{q} - \eta_{2}^{q} - \vartheta_{2}^{q} )^{{w_{2} }} }} \hfill \\ \end{gathered} \right)} \right). $$

  Then,

  $$ \begin{gathered} {\text{TSULIWA}}(\delta_{1} ,\delta_{2} ) = w_{1} \delta_{1} \oplus w_{2} \delta_{2} \hfill \\ = \left( \begin{gathered} \left[ {s_{{k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{{w_{1} }} + k - k\left( {1 - \frac{{\alpha_{2} }}{k}} \right)^{{w_{2} }} - \frac{{\left( {k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{{w_{1} }} } \right)\left( {k - k\left( {1 - \frac{{\alpha_{2} }}{k}} \right)^{{w_{2} }} } \right)}}{k}}} ,s_{{k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{{w_{1} }} + k - k\left( {1 - \frac{{\beta_{2} }}{k}} \right)^{{w_{2} }} - \frac{{\left( {k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{{w_{1} }} } \right)\left( {k - k\left( {1 - \frac{{\beta_{2} }}{k}} \right)^{{w_{2} }} } \right)}}{k}}} } \right], \hfill \\ \left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{j = 1}^{2} {(1 - 1 + (1 - \tau_{j}^{q} )^{{w_{j} }} )} }},\sqrt[q]{{\prod\nolimits_{j = 1}^{2} {(1 - 1 + (1 - \tau_{j}^{q} )^{{w_{j} }} )} - \prod\nolimits_{j = 1}^{2} {(1 - 1 + (1 - \tau_{j}^{q} )^{{w_{j} }} - (1 - \tau_{j}^{q} )^{{w_{j} }} + (1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} )} }}, \hfill \\ \sqrt[q]{\begin{gathered} \prod\nolimits_{j = 1}^{2} {(1 - 1 + (1 - \tau_{j}^{q} )^{{w_{j} }} - (1 - \tau_{j}^{q} )^{{w_{j} }} + (1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} )} - \hfill \\ \prod\nolimits_{j = 1}^{2} {(1 - 1 + (1 - \tau_{j}^{q} )^{{w_{j} }} - (1 - \tau_{j}^{q} )^{{w_{j} }} + (1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} - (1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} + (1 - \tau_{j}^{q} - \eta_{j}^{q} - \vartheta_{j}^{q} )^{{w_{j} }} )} \hfill \\ \end{gathered} } \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} $$
  $$ \begin{gathered} = \left( {\left[ {s_{{k - k\left( {1 - \frac{{\alpha_{1} }}{k}} \right)^{{w_{1} }} \left( {1 - \frac{{\alpha_{2} }}{k}} \right)^{{w_{2} }} }} ,s_{{k - k\left( {1 - \frac{{\beta_{1} }}{k}} \right)^{{w_{1} }} \left( {1 - \frac{{\beta_{2} }}{k}} \right)^{{w_{2} }} }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} )^{{w_{j} }} } }},\sqrt[q]{{\prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } - \prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} - \eta_{j}^{q} - \vartheta_{j}^{q} )^{{w_{j} }} } }} \hfill \\ \end{gathered} \right)} \right) \hfill \\ = \left( {\left[ {s_{{k - k\prod\limits_{j = 1}^{2} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k - k\prod\limits_{j = 1}^{2} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} )^{{w_{j} }} } }},\sqrt[q]{{\prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } }}, \hfill \\ \sqrt[q]{{\prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } - \prod\nolimits_{j = 1}^{2} {(1 - \tau_{j}^{q} - \eta_{j}^{q} - \vartheta_{j}^{q} )^{{w_{j} }} } }} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} $$

  Obviously, the Eq. (14) is true.

• 3. The Eq. (14) is true when n = m, i.e.,

  $$ {\text{TSULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{m} ) = \left( {\left[ \begin{gathered} s_{{k - k\prod\limits_{j = 1}^{m} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k - k\prod\limits_{j = 1}^{m} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } }},\sqrt[q]{{\prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } }}, \hfill \\ \sqrt[q]{{\prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} - \vartheta_{j}^{q} )^{{w_{j} }} } }} \hfill \\ \end{gathered} \right)} \right) $$

  Then, when n = m + 1, we have

  $$ \begin{gathered} {\text{TSULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{m} ,\delta_{m + 1} ) = {\text{TSULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{m} ) \oplus w_{m + 1} \delta_{m + 1} \hfill \\ = \left( {\left[ {s_{{k - k\prod\limits_{j = 1}^{m} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k - k\prod\limits_{j = 1}^{m} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } }},\sqrt[q]{{\prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } }}, \hfill \\ \sqrt[q]{{\prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} - \vartheta_{j}^{q} )^{{w_{j} }} } }} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \oplus \left( {\left[ {s_{{k - k\left( {1 - \frac{{\alpha_{m + 1} }}{k}} \right)^{{w_{m + 1} }} }} ,s_{{k - k\left( {1 - \frac{{\beta_{m + 1} }}{k}} \right)^{{w_{m + 1} }} }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - (1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} }},\sqrt[q]{{(1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} - (1 - \tau_{m + 1}^{q} - \eta_{m + 1}^{q} )^{{w_{m + 1} }} }}, \hfill \\ \sqrt[q]{{(1 - \tau_{m + 1}^{q} - \eta_{m + 1}^{q} )^{{w_{m + 1} }} - (1 - \tau_{m + 1}^{q} - \eta_{m + 1}^{q} - \vartheta_{m + 1}^{q} )^{{w_{m + 1} }} }} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} $$
  $$ = \left( \begin{gathered} \left[ {s_{{k - k\prod\limits_{j = 1}^{m} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } + k - k\left( {1 - \frac{{\alpha_{m + 1} }}{k}} \right)^{{w_{m + 1} }} - \frac{{\left( {k - k\prod\limits_{j = 1}^{m} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } } \right)\left( {k - k\left( {1 - \frac{{\alpha_{m + 1} }}{k}} \right)^{{w_{m + 1} }} } \right)}}{k}}} ,s_{{k - k\prod\limits_{j = 1}^{m} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } + k - k\left( {1 - \frac{{\beta_{m + 1} }}{k}} \right)^{{w_{m + 1} }} - \frac{{\left( {k - k\prod\limits_{j = 1}^{m} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } } \right)\left( {k - k\left( {1 - \frac{{\beta_{m + 1} }}{k}} \right)^{{w_{m + 1} }} } \right)}}{k}}} } \right], \hfill \\ \left( \begin{gathered} \sqrt[q]{{1 - \left( {1 - \left( {1 - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } } \right)} \right)\left( {1 - \left( {1 - (1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} } \right)} \right)}}, \hfill \\ \sqrt[q]{\begin{gathered} \left( {1 - \left( {1 - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } } \right)} \right)\left( {1 - \left( {1 - (1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} } \right)} \right) - \hfill \\ \left( {1 - \left( {1 - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } } \right) - \left( {\prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } } \right)} \right)\left( \begin{gathered} 1 - \left( {1 - (1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} } \right) - \hfill \\ \left( {(1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} - (1 - \tau_{m + 1}^{q} - \eta_{m + 1}^{q} )^{{w_{m + 1} }} } \right) \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} }, \hfill \\ \sqrt[q]{\begin{gathered} \left( {1 - \left( {1 - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } } \right) - \left( {\prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } } \right)} \right)\left( \begin{gathered} 1 - \left( {1 - (1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} } \right) - \hfill \\ \left( {(1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} - (1 - \tau_{m + 1}^{q} - \eta_{m + 1}^{q} )^{{w_{m + 1} }} } \right) \hfill \\ \end{gathered} \right) - \hfill \\ \left( {1 - \left( {1 - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } } \right) - \left( {\prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } } \right) - \left( {\prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m} {(1 - \tau_{j}^{q} - \eta_{j}^{q} - \vartheta_{j}^{q} )^{{w_{j} }} } } \right)} \right) \hfill \\ \left( {1 - \left( {1 - (1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} } \right) - \left( \begin{gathered} (1 - \tau_{m + 1}^{q} )^{{w_{m + 1} }} - \hfill \\ (1 - \tau_{m + 1}^{q} - \eta_{m + 1}^{q} )^{{w_{m + 1} }} \hfill \\ \end{gathered} \right) - \left( \begin{gathered} (1 - \tau_{m + 1}^{q} - \eta_{m + 1}^{q} )^{{w_{m + 1} }} - \hfill \\ (1 - \tau_{m + 1}^{q} - \eta_{m + 1}^{q} - \vartheta_{m + 1}^{q} )^{{w_{m + 1} }} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} } \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right) $$
  $$ = \left( {\left[ {s_{{k - k\prod\limits_{j = 1}^{m + 1} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} ,s_{{k - k\prod\limits_{j = 1}^{m + 1} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\limits_{j = 1}^{m + 1} {(1 - \tau_{j}^{q} )^{{w_{j} }} } }},\sqrt[q]{{\prod\limits_{j = 1}^{m + 1} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m + 1} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } }}, \hfill \\ \sqrt[q]{{\prod\limits_{j = 1}^{m + 1} {(1 - \tau_{j}^{q} - \eta_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{m + 1} {(1 - \tau_{j}^{q} - \eta_{j}^{q} - \vartheta_{j}^{q} )^{{w_{j} }} } }} \hfill \\ \end{gathered} \right)} \right) $$

  It is clearly that the Eq. (14) is true when n = m + 1. Thus, the Eq. (14) is true for any j. Similarly, we can prove that the Eq. (15) is true for any j.

The following properties of the TSULIWA and TSULIWG operators can be proved without difficulty to according to Theorems 1 and 3:

Theorem 4

Let δ_j (j = 1, 2,…, n) be a group of TSULNs,

• 1. (Idempotency). If δ_j = δ for all j, then

  $$ {\text{TSULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = {\text{TSULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \delta $$

  (16)

• 2. (Monotonicity). If δ_j^*(j = 1, 2,…, n) is also a set of TSULVs, and δ_j ≤ δ_j^*, then

  $$ {\text{TSULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le {\text{TSULIWA}}(\delta_{1}^{*} ,\delta_{2}^{*} , \ldots ,\delta_{n}^{*} ) $$

  (17)
  $$ {\text{TSULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \ge {\text{TSULIWG}}(\delta_{1}^{*} ,\delta_{2}^{*} , \ldots ,\delta_{n}^{*} ) $$

  (18)

• 3. (Boundedness). If $P^{ - } = \min \delta_{j} = \left( {[s_{{\mathop {\min }\limits_{j} \alpha_{j} }} ,s_{{\mathop {\min }\limits_{j} \beta_{j} }} ],(\mathop {\min }\limits_{j} (\tau_{j} ),\mathop {\max }\limits_{j} (\eta_{j} ),\mathop {\max }\limits_{j} (\vartheta_{j} ))} \right)$,

  $P^{ + } = \max \delta_{j} = \left( {[s_{{\mathop {\max }\limits_{j} \alpha_{j} }} ,s_{{\mathop {\max }\limits_{j} \beta_{j} }} ],(\mathop {\max }\limits_{j} (\tau_{j} ),\mathop {\min }\limits_{j} (\eta_{j} ),\mathop {\min }\limits_{j} (\vartheta_{j} ))} \right)$, then

  $$ P^{ - } \le {\text{TSULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le P^{ + } $$

  (19)
  $$ P^{ - } \le {\text{TSULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) \le P^{ + } $$

  (20)

Next, the TSULIWA and TSULIWG operators have the following special cases are discussed in different scenarios when elements in TSULN $\delta_{j} = ([s_{{\alpha_{j} }} ,s_{{\beta_{j} }} ],(\tau_{j} ,\eta_{j} ,\vartheta_{j} ))$ are assigned different values.

• 1. If q = 2, the TSULIWA/TSULIWG degenerates to the picture uncertain linguistic interaction weighted averaging or geometric operator, i.e., PULIWA or PULIWG.

  $$ {\text{SULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[{}]{{1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} )^{{w_{j} }} } }},\sqrt[{}]{{\prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} - \eta_{j}^{2} )^{{w_{j} }} } }}, \hfill \\ \sqrt[{}]{{\prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} - \eta_{j}^{2} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} - \eta_{j}^{2} - \vartheta_{j}^{2} )^{{w_{j} }} } }} \hfill \\ \end{gathered} \right)} \right) $$

  (21)
  $$ {\text{SULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[{}]{{\prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} - \eta_{j}^{2} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} - \eta_{j}^{2} - \tau_{j}^{2} )^{{w_{j} }} } }}, \hfill \\ \sqrt[{}]{{\prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} - \eta_{j}^{2} )^{{w_{j} }} } }},\sqrt[{}]{{1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} )^{{w_{j} }} } }} \hfill \\ \end{gathered} \right)} \right) $$

  (22)

• 2. If q = 1, the TSULIWA/TSULIWG degenerates to the spherical uncertain linguistic interaction weighted averaging or geometric operator, i.e., SULIWA or SULIWG.

  $$ {\text{PULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} 1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j} )^{{w_{j} }} } ,\prod\limits_{j = 1}^{n} {(1 - \tau_{j} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \tau_{j} - \eta_{j} )^{{w_{j} }} } , \hfill \\ \prod\limits_{j = 1}^{n} {(1 - \tau_{j} - \eta_{j} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \tau_{j} - \eta_{j} - \vartheta_{j} )^{{w_{j} }} } \hfill \\ \end{gathered} \right)} \right) $$

  (23)
  $$ {\text{PULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} - \eta_{j} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} - \eta_{j} - \tau_{j} )^{{w_{j} }} } , \hfill \\ \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} - \eta_{j} )^{{w_{j} }} } ,1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} )^{{w_{j} }} } \hfill \\ \end{gathered} \right)} \right) $$

  (24)

• 3. If η_j = 0, the TSULIWA/TSULIWG degenerates to the q-rung orthopair uncertain linguistic interaction weighted averaging or geometric operators, i.e., q-ROULIWA or q-ROULIWG.

  $$ q{\text{ - ROULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( {\sqrt[q]{{1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{q} )^{{w_{j} }} } }},\sqrt[q]{{\prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{q} - \vartheta_{j}^{q} )^{{w_{j} }} } }}} \right)} \right) $$

  (25)
  $$ q{\text{ - ROULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( {\sqrt[q]{{\prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{q} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{q} - \tau_{j}^{q} )^{{w_{j} }} } }},\sqrt[q]{{1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{q} )^{{w_{j} }} } }}} \right)} \right) $$

  (26)

• 4. If q = 2, η_j = 0, the TSULIWA/TSULIWG degenerates to the Pythagorean uncertain linguistic interaction weighted averaging or geometric operators, i.e., PyULIWA or PyULIWG.

  $$ {\text{PyULIWA(}}\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( {\sqrt[{}]{{1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} )^{{w_{j} }} } }},\sqrt[{}]{{\prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \tau_{j}^{2} - \vartheta_{j}^{2} )^{{w_{j} }} } }}} \right)} \right) $$

  (27)
  $$ {\text{PyULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( {\sqrt[{}]{{\prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} - \tau_{j}^{2} )^{{w_{j} }} } }},\sqrt[{}]{{1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j}^{2} )^{{w_{j} }} } }}} \right)} \right) $$

  (28)

• 5. If q = 1, η_j = 0, the TSULIWA/TSULIWG degenerates to the intuitionistic uncertain linguistic interaction weighted averaging or geometric operators, i.e., IULIWA or IULIWG.

  $$ {\text{IULIWA}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k - k\prod\limits_{j = 1}^{n} {\left( {1 - \frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( {1 - \prod\limits_{j = 1}^{n} {(1 - \tau_{j} )^{{w_{j} }} } ,\prod\limits_{j = 1}^{n} {(1 - \tau_{j} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \tau_{j} - \vartheta_{j} )^{{w_{j} }} } } \right)} \right) $$

  (29)
  $$ {\text{IULIWG}}(\delta_{1} ,\delta_{2} , \ldots ,\delta_{n} ) = \left( {\left[ \begin{gathered} s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\alpha_{j} }}{k}} \right)^{{w_{j} }} } }} , \hfill \\ s_{{k\prod\limits_{j = 1}^{n} {\left( {\frac{{\beta_{j} }}{k}} \right)^{{w_{j} }} } }} \hfill \\ \end{gathered} \right],\left( {\prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} )^{{w_{j} }} } - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} - \tau_{j} )^{{w_{j} }} } ,1 - \prod\limits_{j = 1}^{n} {(1 - \vartheta_{j} )^{{w_{j} }} } } \right)} \right) $$

  (30)

To illustrate the advantages of the proposed aggregation operators, the following example is provided:

Example 2

Suppose δ₁ = ([s₂, s₃], (0.6, 0.3, 0.1)), δ₂ = ([s₃, s₄], (0.3, 0.2, 0.5)), δ₃ = ([s₁, s₂], (0.4, 0.3, 0.2)) and δ₄ = ([s₄, s₆], (0.1, 0.8, 0.1)) are four TSULNs (whose weighting vector is w = (0.2, 0.1, 0.3, 0.4)^T), k = 7, q = 1. The TSULIWA and TSULIWG operators are utilized to fuse these TSULNs, and they are compared with the PULWA and PULWG operators suggested by Wu and Wei (2017). Subsequently, we change δ₁ and δ₄ to δ₁’ = ([s₂, s₃], (0.6, 0.3, 0.0)) and δ₄’ = ([s₄, s₅], (0.0, 0.8, 0.1)), and again implement the above aggregation operators. The results of the application of the above operators are listed in Table 2.

Table 2 Information fusion results

As can be seen from Table 2, the TSULIWA and TSULIWG operators developed in this paper are able to fuse the TSULNs given in this example. In the information aggregated results before the change, there is a small difference between the aggregated results of the operators proposed by Wu and Wei [72] and the results of new operators in both the UL and TSF parts. However, in the changed information aggregated results, there is no significant change in the UL part of the operators’ results proposed by Wu and Wei [72], and there are zeros in the positions of MD and ND in the TSF part. The main reason is that the role of MD or ND with a value of zero is enlarged during the information aggregation process, thus masking the information of MD or ND in other TSULNs, which results in partial loss of information and counterintuitive phenomena. However, our proposed aggregation operators eliminate the above drawbacks because the TSUL aggregation operators is developed based on IOLs, which can take into account the interactions between MDs, Ads and NDs in the TSF part, and the proposed operators can maintain the validity and integrity of the evaluation information.

Proposed CE-PT-MABAC-based TSUL MAGDM model

In this section, we present the CE-PT-MABAC-based TUSL MAGDM model, which builds on the TSULS foundation of our proposed TSULCE and TSULIWA/TSULIWG operators, thereby defining and extending the TSUL similarity measure, TSUL MDM, TSUL DEMATEL, and CE-PT-MABAC method, and each of these methods or techniques has a well-defined purpose in this decision model, such as determining expert and attribute weights, developing TSUL CE-PT-MABAC method, and using these as inputs to solve the TSUL MAGDM problems. The logical framework of this paper is shown in Fig. 1.

Fig. 1

The logical framework of this work

Let H = {h₁, h₂,…, h_i,…, h_m}be a finite collection of alternatives, A = {a₁, a₂,…, a_j,…, a_n} is a set of attributes, and the attribute weight vector be denoted as W = {w₁, w₂,…, w_j,…, w_n}^T, ${\sum }_{j=1}^{n}{w}_{j}=1, {w}_{j}\in [0, 1]$. A set of invited experts vector is denoted as E = {e₁, e₂,…, e_ε,…, e_p}. In light of the characteristics of experts with different industry experience and knowledge, individual experts have different opinions and preferences on the evaluation of various attributes, assigning different weights to different experts under each attribute is more in line with the actual decision-making scenario than assuming that the weights of all experts under each attribute are equal, and the decision-making results obtained are more reasonable. Let the weight of expert e_ε corresponding to attribute a_j be${\omega }_{\varepsilon }^{(j)}$, with$0\le {\omega }_{\varepsilon }^{\left(j\right)}\le 1, {\sum }_{\varepsilon =1}^{p}{\omega }_{\varepsilon }^{(j)}=1$. The evaluation value for the alternative h_i (i = 1, 2,…, m) with respect to the attribute a_j (j = 1, 2,…, n) is given by expert e_ε(ε = 1, 2,…, p), which is expressed by TSULN and denoted as $d_{ij}^{\varepsilon } = \left( {[s_{{\alpha_{ij}^{\varepsilon } }} ,s_{{\beta_{ij}^{\varepsilon } }} ],\left( {\tau_{ij}^{\varepsilon } ,\eta_{ij}^{\varepsilon } ,\vartheta_{ij}^{\varepsilon } } \right)} \right)$. Then, the evaluation matrix of the individual expert is constructed and denoted as D^ε = [d_ij^ε]_m×n, (i = 1, 2,…, m; j = 1, 2,…, n; ε = 1, 2,…, p). Meanwhile, expert e_ε (ε = 1, 2,…, p) evaluates the correlation degree between attributes and constructs the individual initial TSUL direct relation matrix (TSULDRM) $\aleph^{\varepsilon } = \left[ {\gamma_{jl}^{\varepsilon } } \right]_{n \times n}$, $\gamma_{jl}^{\varepsilon } = \left( {[s_{{\alpha_{jl}^{\varepsilon } }} ,s_{{\beta_{jl}^{\varepsilon } }} ],(\tau_{jl}^{\varepsilon } ,\psi_{jl}^{\varepsilon } ,\vartheta_{jl}^{\varepsilon } ,)} \right)$(j, l = 1, 2,…, n; ε = 1, 2,…, p), if j = l, then $\gamma_{jl}^{\varepsilon } = \left( {[s_{0} ,s_{0} ],(0,0,0)} \right)$.

Calculating expert weights by TSUL similarity

The expert weight is one of the crucial factors in the process of dealing with MAGDM problems, and the use of similarity measure to calculate the expert weight is an effective way to reflect the importance of experts using the degree of similarity between the evaluation values of individual experts and the average evaluation values. In this subsection, referring to the conversion relationship between similarity measure and distance measure, we use the TSUL CE measure proposed above to define the new similarity in the TSUL environment, and then calculate the expert weights from it, so the detailed process is as follows:

In general, there are cost-based and benefit-based attributes. The individual TSUL decision matrix D^ε = [d_ij^ε]_m × n is standardized to the normalized individual TSUL decision matrix R^ε = [r_ij^ε]_m × n.

$$ r_{ij}^{\varepsilon } = \left\{ {\begin{array}{*{20}c} {d_{ij}^{\varepsilon } = \left( {[s_{{\alpha_{ij}^{\varepsilon } }} ,s_{{\beta_{ij}^{\varepsilon } }} ],\left( {\tau_{ij}^{\varepsilon } ,\eta_{ij}^{\varepsilon } ,\vartheta_{ij}^{\varepsilon } } \right)} \right),} & {a_{j} \in \Psi_{1} } \\ {d_{ij}^{\varepsilon } )^{c} = \left( {[s_{{z - 1 - \beta_{ij}^{\varepsilon } }} ,s_{{z - 1 - \alpha_{ij}^{\varepsilon } }} ],\left( {\vartheta_{ij}^{\varepsilon } ,\eta_{ij}^{\varepsilon } ,\tau_{ij}^{\varepsilon } } \right)} \right),} & {a_{j} \in \Psi_{2} } \\ \end{array} } \right. $$

(31)

where $(d_{ij}^{\varepsilon } )^{c}$ is the complement of TSULN $d_{ij}^{\varepsilon }$, Ψ₁ and Ψ₂ denote the benefit-type and cost-type attributes, respectively. Then, the normalized individual TSUL decision matrix R^ε is converted into an evaluation matrix with respect to each attribute, i.e.,$F^{(j)} = [\xi_{\varepsilon i}^{(j)} ]_{p \times m}$, where $\xi_{\varepsilon i}^{(j)}$ is equivalent to d_ij^ε.

For the matrix F^(j), the average of the experts’ evaluated values for each alternative h_i with respect to the attribute a_j is $\hat{\xi }_{i}^{(j)} = \left( {[s_{{\hat{\alpha }_{i}^{(j)} }} ,s_{{\hat{\beta }_{i}^{(j)} }} ],(\hat{\tau }_{i}^{(j)} ,\hat{\eta }_{i}^{(j)} ,\hat{\vartheta }_{i}^{(j)} )} \right)$.

$$ s_{{\hat{\alpha }_{i}^{(j)} }} = s_{{\frac{1}{p}\sum\limits_{\varepsilon = 1}^{p} {\alpha_{\varepsilon i}^{(j)} } }} ,\;s_{{\hat{\beta }_{i}^{(j)} }} = s_{{\frac{1}{p}\sum\limits_{\varepsilon = 1}^{p} {\beta_{\varepsilon i}^{(j)} } }} ,\;\hat{\tau }_{i}^{(j)} = \frac{1}{p}\sum\limits_{\varepsilon = 1}^{p} {\tau_{\varepsilon i}^{(j)} } ,\;\hat{\eta }_{i}^{(j)} = \frac{1}{p}\sum\limits_{\varepsilon = 1}^{p} {\eta_{\varepsilon i}^{(j)} } ,\;\hat{\vartheta }_{i}^{(j)} = \frac{1}{p}\sum\limits_{\varepsilon = 1}^{p} {\vartheta_{\varepsilon i}^{(j)} } . $$

(32)

The existing transformation relationship between similarity measure and distance measure is referenced, then the TSUL CE-based similarity measure $sim_{\varepsilon i}^{(j)}$ between $\xi_{\varepsilon i}^{(j)}$ and $\hat{\xi }_{i}^{(j)}$ can be defined as

$$ {\text{sim}}_{\varepsilon i}^{(j)} = 1 - \frac{{{\text{CE}}(\xi_{\varepsilon i}^{(j)} ,\hat{\xi }_{i}^{(j)} )}}{{\sum\nolimits_{\varepsilon = 1}^{p} {CE(\xi_{\varepsilon i}^{(j)} ,\hat{\xi }_{i}^{(j)} )} }}, $$

(33)

where $CE(\xi_{\varepsilon i}^{(j)} ,\hat{\xi }_{i}^{(j)} )$ is the TSUL CE measure between $\xi_{\varepsilon i}^{(j)}$ and $\hat{\xi }_{i}^{(j)}$.

Then, we can construct the similarity matrix $S^{(j)} = \left[ {{\text{sim}}_{\varepsilon i}^{(j)} } \right]_{p \times m}$ for attribute a_j ∈ A. the weight of expert e_ε regarding the attribute a_j are calculated via Eq. (34).

$$ \omega_{\varepsilon }^{(j)} = \frac{{\sum\nolimits_{i = 1}^{m} {{\text{sim}}_{\varepsilon i}^{(j)} } }}{{\sum\nolimits_{\varepsilon = 1}^{p} {\sum\nolimits_{i = 1}^{m} {{\text{sim}}_{\varepsilon i}^{(j)} } } }} $$

(34)

Obviously, $0\le {\omega }_{\varepsilon }^{\left(j\right)}\le 1, {\sum }_{\varepsilon =1}^{p}{\omega }_{\varepsilon }^{(j)}=1$.

Determining the attribute combined weights

In this subsection, the subjective weights of the attributes are computed by the DEMATEL method extended in the TSUL context, the TSUL CE-based MDM is utilized to compute the objective attribute weights, and then the optimal combined weights the attributes are determined.

Determining subjective weight by TSUL DEMATEL

The DEMATEL method considering attribute associations is extended in the TSUL setting, where we give detailed steps for determining the subjective weight calculation inspired by Gül [73].

• 1. We utilize the TSULIWA (Eq. (14)) or TSULIWG (Eq. (15)) operator to aggregate individual initial TSULDRM into group initial TSULDRM.

• 2. Based on the matrix operation, the group initial TSULDRM ℵ is separated into low linguistic sub-matrix ℵ^LL, up linguistic submatrix ℵ^UL, MD submatrixℵ^M, AD submatrixℵ^A, and ND submatrixℵ^N. We employ the Eq. (35) to normalize the five submatrices respectively, and then obtain the normalized low linguistic submatrix X^LL, normalized up linguistic submatrix X^UL, normalized MD submatrix X^M, AD submatrix X^A, and ND submatrix X^N.

  $$ x_{jl} = \frac{{y_{jl} }}{{\max \left\{ {\mathop {\max }\limits_{l} \sum\nolimits_{j = 1}^{n} {y_{jl} ,} \mathop {\max }\limits_{j} \sum\nolimits_{l = 1}^{n} {y_{jl} } } \right\}}}. $$

  (35)

The three total relation submatrices are identified by Eq. (36), and the total relation matrix $T = \left[ {t_{jl} } \right]_{n \times n}$ is derived from the conversion of the five submatrices given the form of $t_{jl} = \left( {[s_{{\Lambda_{jl} }} ,s_{{\Delta_{jl} }} ],\left( {t_{jl}^{M} ,t_{jl}^{A} ,t_{jl}^{N} } \right)} \right)$.

$$ \left\{ {\begin{array}{*{20}l} {s_{{\Lambda_{jl} }} = s_{{X^{LL} (1 - X^{LL} )^{ - 1} }} ;s_{{\Delta_{jl} }} = s_{{X^{UL} (1 - X^{UL} )^{ - 1} }} \, } \\ \left[ {t_{jl}^{M} } \right] = X^{M} \left( {1 - X^{M} } \right)^{ - 1} ;\left[ {t_{jl}^{A} } \right] = X^{A} \left( {1 - X^{A} } \right)^{ - 1} ; \\ \left[ {t_{jl}^{N} } \right] = X^{N} \left( {1 - X^{N} } \right)^{ - 1} \\ \end{array} } \right. $$

(36)

The TSULIWA operator (see Eq. (14)) is applied to compute the sum of the rows and columns of the total influence matrix T by Eq. (37), where the weights are assumed to be equal, respectively, denoted $\Gamma_{l}$($\Gamma_{j}$) and $\Upsilon_{j}$. Subsequently, the subjective weights of the attributes are calculated by combining the TSULN score function (see Eq. (5)) in Eq. (38).

$$ \Gamma_{l} = \sum\limits_{j}^{n} {t_{jl} } = {\text{TSULIWA}}(t_{1l} ,t_{2l} , \ldots ,t_{nl} ),\qquad\qquad\qquad\qquad\Upsilon_{j} = \sum\limits_{l = 1}^{n} {t_{jl} } = {\text{TSULIWA}}(t_{j1} ,t_{j2} , \ldots ,t_{jn} ) $$

(37)

$$ w_{j}^{s} = \frac{{\sqrt {\left( {sc(\Gamma_{j} ) + sc(\Upsilon_{j} )} \right)^{2} + \left( {sc(\Gamma_{j} ) - sc(\Upsilon_{j} )} \right)^{2} } }}{{\sum\nolimits_{j = 1}^{n} {\sqrt {\left( {sc(\Gamma_{j} ) + sc(\Upsilon_{j} )} \right)^{2} + \left( {sc(\Gamma_{j} ) - sc(\Upsilon_{j} )} \right)^{2} } } }} $$

(38)

Calculating objective weights via TSUL MDM

In the scenario where the attribute weight information is completely unknown, irrational attribute weight assignment can affect the accuracy of the decision result. The MDM method proposed by Wei [74] argues that if the deviation between the attribute values r_ij(or r_lj) (i, l = 1, 2,…, m; j = 1, 2,…, n) of the alternatives under attribute a_j is small, the attribute is assigned a smaller weight value, and vice versa, a larger weight value is assigned. Based on this principle, we utilize CE measure to replace the distance measure of traditional MDM, and the new TSUL CE-based MDM is established to calculate the objective weights of attributes.

The deviation between alternative h_i and the other alternatives h_l (l = 1, 2,…, m, l ≠ i) with respect to attribute a_j ∈ A can be calculated by TSUL CE as expressed in Eq. (39).

$$ D_{ij} (w^{o} ) = \sum\limits_{l = 1}^{m} {CE(r_{ij} ,r_{lj} )w_{j}^{o} } $$

(39)

A linear CE-based mathematical model is built to assign the optimal weight vector w^o of attributes with the objective of maximizing the total deviation of all attributes.

$$ \left\{ {\begin{array}{*{20}c} {{\text{Max }}D(w^{o} ) = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{m} {D_{ij} (w^{o} )} } = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{m} {\sum\limits_{l = 1}^{m} {{\text{CE}}(r_{ij} ,r_{lj} )w_{j}^{o} } } } } \\ {{\text{s}}{\text{.t}}{. }\sum\limits_{j = 1}^{n} {(w_{j}^{o} )^{2} } = 1, \, 0 \le w_{j}^{o} \le 1 \, } \\ \end{array} } \right. $$

(40)

The following Lagrange function with multiplierλ is built to solve the above model.

$$ L(w_{j}^{o} ,\lambda ) = \sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{m} {\sum\limits_{l = 1}^{m} {{\text{CE}}(r_{ij} ,r_{lj} )w_{j}^{o} } + \lambda \left( {\sum\limits_{j = 1}^{n} {(w_{j}^{o} )^{2} } - 1} \right)} } $$

From this, the optimal weight of the attribute is calculated by Eq. (41).

$$ w_{j}^{o*} = \frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{l = 1}^{m} {{\text{CE}}(r_{ij} ,r_{lj} )} } }}{{\sqrt {\sum\nolimits_{j = 1}^{n} {\left( {\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{l = 1}^{m} {{\text{CE}}(r_{ij} ,r_{lj} )} } } \right)^{2} } } }} $$

(41)

The attribute objective weight w_j^o is obtained by normalizing w_j^o* derived from the Eq. (41).

$$ w_{j}^{o} = \frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{l = 1}^{m} {{\text{CE}}(r_{ij} ,r_{lj} )} } }}{{\sum\nolimits_{j = 1}^{n} {\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{l = 1}^{m} {{\text{CE}}(r_{ij} ,r_{lj} )} } } }} $$

(42)

Calculate attribute combined weights

We employ Eq. (43) to obtain the combined weight w_j^c of the attribute by combining the attribute subjective weight w_j^s and objective weight w_j^o(j = 1, 2,…, n). Clearly, it satisfies $0\le {w}_{j}^{{\text{c}}}\le 1, {\sum }_{j=1}^{n}{w}_{j}^{c}=1$.

$$ w_{j}^{c} { = }\frac{{\sqrt {w_{j}^{s} w_{j}^{o} } }}{{\sum\nolimits_{j = 1}^{n} {\sqrt {w_{j}^{s} w_{j}^{o} } } }}. $$

(43)

Determine the alternatives ranking based on TSUL CE-PT-MABAC

In this subsection, the MABAC method is extended and improved to solve the MAGDM problem with TSULNs. The specific steps are described below:

Step 1: The expert weight value ${\omega }_{\varepsilon }^{\left(j\right)}$(j = 1, 2,…, n; ε = 1, 2,…, p) with respect to the attribute a_j is determined by the method described in “Calculating expert weights by TSUL similarity”.

Step 2: The individual evaluation information provided by the experts is fused by the TSULIWA (Eq. (44)) or TSULIWG (Eq. (45)) operator and consequently the TSUL group decision matrix G = [g_ij]m × n, $g_{ij} = \left( {[s_{{\theta_{ij} }} ,s_{{\rho_{ij} }} ],\left( {\tau_{ij} ,\eta_{ij} ,\vartheta_{ij} } \right)} \right)$ (i = 1, 2,…, m; j = 1, 2,…, n) is obtained.

$$ \begin{gathered} g_{ij} = {\text{TSULIWA}}(r_{ij}^{1} ,r_{ij}^{2} , \ldots ,r_{ij}^{p} ) \hfill \\ = \left( {\left[ \begin{gathered} s_{{k - k\prod\limits_{\varepsilon = 1}^{p} {\left( {1 - \frac{{\alpha_{ij}^{\varepsilon } }}{k}} \right)^{{\omega_{\varepsilon } }} } }} , \hfill \\ s_{{k - k\prod\limits_{\varepsilon = 1}^{p} {\left( {1 - \frac{{\beta_{ij}^{\varepsilon } }}{k}} \right)^{{\omega_{\varepsilon } }} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\limits_{\varepsilon = 1}^{p} {(1 - (\tau_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } }},\sqrt[q]{{\prod\limits_{j = 1}^{n} {(1 - (\tau_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } - \prod\limits_{j = 1}^{n} {(1 - (\tau_{ij}^{\varepsilon } )^{q} - (\eta_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } }}, \hfill \\ \sqrt[q]{{\prod\limits_{j = 1}^{n} {(1 - (\tau_{ij}^{\varepsilon } )^{q} - (\eta_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } - \prod\limits_{j = 1}^{n} {(1 - (\tau_{ij}^{\varepsilon } )^{q} - (\eta_{ij}^{\varepsilon } )^{q} - (\vartheta_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } }} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} $$

(44)

Or

$$ \begin{gathered} g_{ij} = {\text{TSULIWG}}(r_{ij}^{1} ,r_{ij}^{2} , \ldots ,r_{ij}^{p} ) \hfill \\ = \left( {\left[ \begin{gathered} s_{{k\prod\limits_{\varepsilon = 1}^{p} {\left( {\frac{{\alpha_{ij}^{\varepsilon } }}{k}} \right)^{{\omega_{\varepsilon } }} } }} , \hfill \\ s_{{k\prod\limits_{\varepsilon = 1}^{p} {\left( {\frac{{\beta_{ij}^{\varepsilon } }}{k}} \right)^{{\omega_{\varepsilon } }} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{\prod\limits_{\varepsilon = 1}^{p} {(1 - (\vartheta_{ij}^{\varepsilon } )^{q} - (\eta_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } - \prod\limits_{\varepsilon = 1}^{p} {(1 - (\vartheta_{ij}^{\varepsilon } )^{q} - (\eta_{ij}^{\varepsilon } )^{q} - (\tau_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } }}, \hfill \\ \sqrt[q]{{\prod\limits_{\varepsilon = 1}^{p} {(1 - (\vartheta_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } - \prod\limits_{\varepsilon = 1}^{p} {(1 - (\vartheta_{ij}^{\varepsilon } )^{q} - (\eta_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } }},\sqrt[q]{{1 - \prod\limits_{\varepsilon = 1}^{p} {(1 - (\vartheta_{ij}^{\varepsilon } )^{q} )^{{\omega_{\varepsilon } }} } }} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \end{gathered} $$

(45)

Step 3: The attribute combined weight w_j^c (j = 1, 2,…, n) can be obtained by the approach mentioned in “Determining the attribute combined weights”.

Step 4: The TSUL weighted matrix $G_{w} = [g_{ij}^{w} ]_{n \times m}$ is obtained based on the TSUL group decision matrix G and attribute combined weight w_j^c (j = 1, 2,…, n).

$$ g_{ij}^{w} = w_{j}^{c} \times g_{ij} = \left( {\left[ {s_{{k - k\left( {1 - \frac{{\alpha_{ij} }}{k}} \right)^{{w_{j}^{c} }} }} ,s_{{k - k\left( {1 - \frac{{\alpha_{ij} }}{k}} \right)^{{w_{j}^{c} }} }} } \right],\left( \begin{gathered} \sqrt[q]{{1 - (1 - \tau_{ij}^{q} )^{{w_{j}^{c} }} }},\sqrt[q]{{(1 - \tau_{ij}^{q} )^{{w_{j}^{c} }} - (1 - \tau_{ij}^{q} - \eta_{ij}^{q} )^{{w_{j}^{c} }} }}, \hfill \\ \sqrt[q]{{(1 - \tau_{ij}^{q} - \eta_{ij}^{q} )^{{w_{j}^{c} }} - (1 - \tau_{ij}^{q} - \eta_{ij}^{q} - \vartheta_{ij}^{q} )^{{w_{j}^{c} }} }} \hfill \\ \end{gathered} \right)} \right) $$

(46)

Step 5: We utilize the TSULIWA (Eq. (47)) or TSULIWG (Eq. (48)) operator to calculate the BAA value and construct the BAA matrix $B = [b_{j} ]_{1 \times n}$.

$$ b_{j} = {\text{TSULIWA}}(g_{1j} ,g_{2j} , \ldots ,g_{mj} ) = \left( {\left[ \begin{gathered} s_{{k - k\prod\limits_{i = 1}^{m} {\left( {1 - \frac{{\alpha_{ij} }}{k}} \right)^{\frac{1}{m}} } }} , \hfill \\ s_{{k - k\prod\limits_{i = 1}^{m} {\left( {1 - \frac{{\beta_{ij} }}{k}} \right)^{\frac{1}{m}} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{1 - \prod\limits_{i = 1}^{m} {(1 - \tau_{ij}^{q} )^{\frac{1}{m}} } }},\sqrt[q]{{\prod\limits_{i = 1}^{m} {(1 - \tau_{ij}^{q} )^{\frac{1}{m}} } - \prod\limits_{i = 1}^{m} {(1 - \tau_{ij}^{q} - \eta_{ij}^{q} )^{\frac{1}{m}} } }}, \hfill \\ \sqrt[q]{{\prod\limits_{i = 1}^{m} {(1 - \tau_{ij}^{q} - \eta_{ij}^{q} )^{\frac{1}{m}} } - \prod\limits_{i = 1}^{m} {(1 - \tau_{ij}^{q} - \eta_{ij}^{q} - \vartheta_{ij}^{q} )^{\frac{1}{m}} } }} \hfill \\ \end{gathered} \right)} \right) $$

(47)

Or

$$ b_{j} = {\text{TSULIWG}}(g_{1j} ,g_{2j} , \ldots ,g_{mj} ) = \left( {\left[ \begin{gathered} s_{{k\prod\limits_{i = 1}^{m} {\left( {\frac{{\alpha_{ij} }}{k}} \right)^{\frac{1}{m}} } }} , \hfill \\ s_{{k\prod\limits_{i = 1}^{m} {\left( {\frac{{\beta_{ij} }}{k}} \right)^{\frac{1}{m}} } }} \hfill \\ \end{gathered} \right],\left( \begin{gathered} \sqrt[q]{{\prod\limits_{i = 1}^{m} {(1 - \vartheta_{ij}^{q} - \eta_{ij}^{q} )^{\frac{1}{m}} } - \prod\limits_{i = 1}^{m} {(1 - \vartheta_{ij}^{q} - \eta_{ij}^{q} - \tau_{ij}^{q} )^{\frac{1}{m}} } }}, \hfill \\ \sqrt[q]{{\prod\limits_{i = 1}^{m} {(1 - \vartheta_{ij}^{q} )^{\frac{1}{m}} } - \prod\limits_{i = 1}^{m} {(1 - \vartheta_{ij}^{q} - \eta_{ij}^{q} )^{\frac{1}{m}} } }},\sqrt[q]{{1 - \prod\limits_{i = 1}^{m} {(1 - \vartheta_{ij}^{q} )^{\frac{1}{m}} } }} \hfill \\ \end{gathered} \right)} \right) $$

(48)

Step 6: Obtain the prospect matrix P. The traditional MABAC method requires that the distance between each alternative and the BAA be calculated at this step. Nevertheless, the behavioral preferences and psychology of DMs have been neglected by conventional MABAC, and these factors may have an impact on the decision outcome. Therefore, considering finite rationality, we utilize the prospect matrix instead of the distance matrix. When $sc(g_{ij}^{w} ) \ge sc(b_{j} )$, the alternative h_i regards with a_j belongs to upper approximation area (G⁺), whereas $sc(g_{ij}^{w} ) < sc(b_{j} )$ means the alternative h_i regards with a_j belongs to lower approximation area (G⁻). And the BAA denotes a reference point used to determine gains and losses. For this purpose, we utilize the TSUL CE measure instead of the distance measure in the traditional MABAC to calculate the prospect matrix P = [Ξ_ij]_n×m as shown in Eq. (49) below.

$$ \Xi_{ij} = \left\{ {\begin{array}{*{20}c} {\left( {{\text{CE}}(g_{ij}^{w} ,b_{j} )} \right)^{\alpha } ,} & {{\text{ if }}sc(g_{ij}^{w} ) > sc(b_{j} )} \\ {0,} & {{\text{if }}sc(g_{ij}^{w} ) = sc(b_{j} )} \\ { - \gamma \left( {{\text{CE}}(g_{ij}^{w} ,b_{j} )} \right)^{\beta } ,} & {{\text{if }}sc(g_{ij}^{w} ) < sc(b_{j} )} \\ \end{array} } \right. $$

(49)

where $CE(g_{ij}^{w} ,b_{j} )$ represents the deviation or discrimination between $g_{ij}^{w}$ and b_j, which is calculated by the Eq. (7). 0 ≤ α, β ≤ 1 denote the coefficients of risk attitude. The higher the value of α, β, the more inclined the DMs is to seek risk. γ > 1 is the loss aversion coefficient, which denotes how sensitive the DM’s attitude is to loss aversion. This article set α = β = 0.88 and γ = 2.25 [75] in Eq. (49).

Step 7: The total prospect value σ_i of each alternative is calculated from Eq. (50). According to this value σ_i, the alternatives are ranked in descending order, the larger the better to determine the best option.

$$ \sigma_{i} = \sum\limits_{j = 1}^{n} {\Xi_{ij} } $$

(50)

The decision-making algorithm

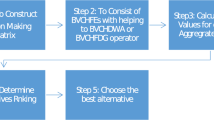
To address the TSUL MAGDM issue, we propose a three-phase decision-making process as shown in Fig. 2, and the detailed algorithm is as below:

Fig. 2

Flowchart of the proposed methodology

Phase 1 Problem description and data collection

Step 1: Obtain initial individual TSUL assessment matrix D^ε from expert ε.

Step 2: Obtain individual initial TSULDRM I^ε from expert ε.

Phase 2 Determine the weight of experts and attributes

Step 3: The normalized individual TSUL assessment matrix R^ε is obtained by Eq. (31).

Step 4: calculate the expert weight ${\omega }_{\varepsilon }^{\left(j\right)}$ regarding the attribute by the Eqs. (32–34).

Step 5: the group initial TSULDRM I is obtained via the TSULIWA (Eq. (14)) or TSULIWG (Eq. (15)) operator.

Step 6: the attribute subjective weight w_j^s is determined by TSUL DEMATEL approach (Eqs. (35–38)).

Step 7: the TSUL group decision matrix G is obtained via the TSULIWA (Eq. (44)) or TSULIWG (Eq. (45)) operator.

Step 8: the attribute objective weight w_j^o is determined by TSUL MDM (Eq. (42)).

Step 9: the attribute combined weight w_j^c is calculated by Eq. (43).

Phase 3 Determination of the best alternative based on the TSUL CE-PT-MABAC method

Step 10: the TSUL weighted group decision matrix G^w is determined by Eq. (46).

Step 11: the BAA matrix B is constructed by the TSULIWA (Eq. (47)) or TSULIWG (Eq. (48)) operator.

Step 12: the prospect matrix P is obtained by Eq. (49).

Step 13: the total prospect is calculated using Eq. (50) and ranking alternatives.

Illustrative example

In China, a large amount of recycling and renewable resource enterprises have emerged in the recycling market in the last decade with the development of circular economy. QL is a waste textile reuse and remanufacturing enterprise in Nanchang city, which was established in 2004. Its business involves recycling of waste textiles, processing and sales of second-hand raw materials, such as garments, needles, and textiles. In the business of waste textile remanufacturing and second-hand raw material processing, the waste clothing is an important production input. These waste clothes are mainly sourced from recycling partners with different recycling channels. The company has implemented supplier selection to ensure a sustainable supply of used garments.

We present an illustrative example of the SWCRP selection of the company QL to illustrate the developed methodology. There are four recycling organizations as alternatives in the used clothing recycling industry, namely H = {h₁, h₂,…, h₄}. The five organizations are evaluated primarily based on a given set of attributes A = {a₁, a₂,…, a₇}, these attributes are operating cost per unit (a₁), quality utility value (a₂), resource use efficiency (a₃), pollution and waste production (a₄), environmental management information system (a₅), employee turnover rate (a₆), and customer satisfaction (a₇) [76]. Among them, a₁ and a₄ are cost-type attributes, while the others are benefit-type attributes. The weight information for these attributes is completely unknown. A decision committee E = {e₁, e₂, e₃} composed of three experts is established to evaluate the performance of each recycling partner h_i (i = 1, 2,…, 5) for attribute a_j (j = 1, 2,…, 7), and the evaluation values are represented by the TSULNs.

Decision analysis

Step 1–2: The experts used TSULNs to evaluate the alternatives regarding attributes, in which the linguistic term set is S = {s₀ = very bad, s₁ = bad, s₂ = moderate bad, s₃ = moderate, s₄ = moderate good, s₅ = good, s₆ = very good}. The evaluation information of three experts is shown in Table 3. Meanwhile, the initial TSULDRMs of seven attributes given by three experts are shown in Table 4.

Table 3 SWCRP evaluation information from experts

Table 4 The individual initial TSULDRMs from experts

Steps 3–4: Since attributes a₁ and a₄ are cost-type, we can obtain normalized decision matrix R^ε according to Eq. (31). For example,$d_{11}^{1} = \left( {[s_{4} ,s_{5} ],(0.5,0.2,0.6)} \right)$ is normalized to get $r_{11}^{1} = \left( {[s_{1} ,s_{2} ],(0.6,0.2,0.5)} \right)$. The standardized individual decision matrix R^ε provided by experts is converted into the evaluation matrix F^(j) regarding attribute a_j. The expert’s weights on attributes are obtained based on Eqs. (32–34) as follows:

$$ \omega_{1}^{(1)} = 0.302,\;\omega_{2}^{(1)} = 0.411,\;\omega_{3}^{(1)} = 0.286;\qquad\qquad\qquad\qquad \omega_{1}^{(2)} = 0.318,\;\omega_{2}^{(2)} = 0.375,\;\omega_{3}^{(2)} = 0.307; $$

$$ \omega_{1}^{(3)} = 0.381,\;\omega_{2}^{(3)} = 0.342,\;\omega_{3}^{(3)} = 0.277;\qquad\qquad\qquad\qquad\omega_{1}^{(4)} = 0.338,\;\omega_{2}^{(4)} = 0.310,\;\omega_{3}^{(4)} = 0.352; $$

$$ \omega_{1}^{(5)} = 0.352,\;\omega_{2}^{(5)} = 0.405,\;\omega_{3}^{(5)} = 0.244;\qquad\qquad\qquad\qquad\omega_{1}^{(6)} = 0.338,\;\omega_{2}^{(6)} = 0.276,\;\omega_{3}^{(6)} = 0.387; $$

$$ \omega_{1}^{(7)} = 0.352,\;\omega_{2}^{(7)} = 0.289,\;\omega_{3}^{(7)} = 0.359. $$

Steps 5–6: we apply TSUL DEMATEL method to determine the subjective weight of attributes. Firstly, the TSULIWA operator is used to aggregate individual initial TSULDRMs into group initial TSULDRM. The results are shown in Table 5. This matrix is decomposed into five sub-matrices and normalized by the Eq. (35). The total relation matrix T is determined by the Eq. (36). The results are listed in Table 6. The subjective weight vector of attributes is determined by Eqs. (37–38), w^s = (0.237, 0.151, 0.134, 0.151, 0.145, 0.076, 0.105)^T.

Table 5 The aggregated initial TSULDRM

Table 6 The total relation matrix T

Step 7: The TSULIWA operator (Eq. (44)) is employed to fuse individual decision matrices R^ε into TSUL group decision matrix G as shown in Table 7.

Table 7 TSUL group decision matrix G

Steps 8–9: We use the Eq. (42) to compute the objective weight vector of attributes: w^o = (0.126, 0.112, 0.164, 0.133, 0.113, 0.181, 0.170)^T. The attribute combined weight vector can be obtained by the Eq. (43): w^c = (0.178, 0.134, 0.153, 0.146, 0.132, 0.121, 0.138)^T.

Step 10: Based on the Table 4 and the attribute combined weight vector, we use the Eq. (46) to get the TSUL weighted matrix G_w, as shown in the Table 8.

Table 8 TSUL weighted decision matrix G_w

Step 11: We use the TSULIWA operator (Eq. (47)) to construct the BAA matrix B.

$$ b_{1} = \left( {[s_{0.702} ,s_{1.255} ],(0.264,0.170,0.340)} \right),\;b_{2} = \left( {[s_{0.568} ,s_{1.072} ],(0.288,0.196,0.290)} \right), $$

$$ b_{3} = \left( {[s_{0.403} ,s_{0.869} ],(0.297,0.190,0.201)} \right),\;b_{4} = \left( {[s_{0.544} ,s_{0.978} ],(0.211,0.185,0.289)} \right), $$

$$ b_{5} = \left( {[s_{0.564} ,s_{1.032} ],(0.289,0.204,0.181)} \right),\;b_{6} = \left( {[s_{0.553} ,s_{0.926} ],(0.238,0.204,0.273)} \right), $$

$$ b_{7} = \left( {[s_{0.466} ,s_{0.853} ],(0.296,0.201,0.208)} \right). $$

Step 12: The prospect matrix P can be obtained by the Eq. (49) (α = β = 0.88, γ = 2.25).

$$ P = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - 0.096} & { - 0.028} & { - 0.050} & {\begin{array}{*{20}c} { \, 0.012} & { - 0.057} & { \, 0.035} & { \, 0.005} \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} { \, 0.011} & { - 0.035} & { - 0.036} & {\begin{array}{*{20}c} { - 0.017} & { \, 0.023} & { - 0.085} & { - 0.043} \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} { \, 0.022} & { \, 0.011} & { \, 0.040} & {\begin{array}{*{20}c} { \, 0.015} & { \, 0.005} & { \, 0.009} & { \, 0.034} \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} { \, 0.014} & { \, 0.027} & { - 0.012} & {\begin{array}{*{20}c} { - 0.041} & { - 0.029} & { - 0.021} & { - 0.052} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] $$

Step 13: The total prospect value of each alternative is determined by the Eq. (50).

$$ \sigma_{{1}} = - 0.{179},\sigma_{{2}} = - 0.{182},\sigma_{{3}} = 0.{137},\sigma_{{4}} = - 0.{113} $$

And the alternatives are ranked as h₃ > h₄ > h₁ > h₂. Therefore, h₃ is the best option.

Discussion

In this section, the impact of the parameters contained in the proposed model on the decision-making results is discussed. Further, we compare and analyze the proposed method with the existing methods.

Sensitivity analysis

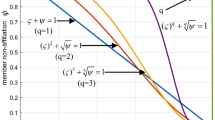
To explore the influence of the parameters on the decision-making outcome, we implement a sensitivity analysis for the parameters α, β and γ taking various values in this subsection. When β = 0.88 and γ = 2.25, α takes different values in the range of [0, 1] and the total values of prospect for each alternative changes as shown in Fig. 3a. The change in the ranking of the alternatives is shown in Fig. 3b. When α = 0.88 and γ = 2.25, β takes different values in the range of [0, 1] and the total values of prospect for each alternative changes as shown in Fig. 4a. And the change in the ranking of the alternatives is shown in Fig. 4b.

Fig. 3

Sensitivities regarding parameters α

Fig. 4

Sensitivities regarding parameters β

From Figs. 3 and 4, it can be found that as the values of α and β become larger, the difference between the total values of the prospect of the alternatives becomes smaller, but alternative h₃ is always the optimal option. This can show that the change of α and β has no effect on the decision results when γ = 2.25.

Subsequently, we take various values of γ in the range of 2–12 when α = β = 0.88, and the change in the total prospect values for each alternative is shown in Fig. 5a. The change in ranking of the alternatives is shown in Fig. 5b. As can be seen from Fig. 5, the total prospect value of alternative h₃ does not change as the value of γ becomes larger, while the total prospect values of the remaining alternatives become progressively smaller, and there is no change in the ordering of the alternatives. It can be found that the prospect value of alternative h₃ under different attributes belong to G⁺, in other words, the parameter γ has no effect on alternative h₃.

Fig. 5

Sensitivity regarding parameter γ

Comparative analysis

In this subsection, we apply various multi-attribute decision methods, including PULWA and PULWG (picture uncertain linguistic weighted averaging and geometric) [72], PULWBM and PULWGBM (picture uncertain linguistic weighted Bonferroni mean and geometric) [30] operators and TSUL MARCOS [47] to solve the SWCRP selection problem in this manuscript. The alternative rankings are listed in Table 9.

Table 9 Comparison of results with various approaches

As shown in Table 9, the existing approaches, such as PULWA, PULWG, PULWBM, and PULWGBM operators, are not suitable for this example in this paper. We can know from Table 3 that the evaluation values of some attributes cannot be expressed by pictures uncertain linguistic numbers. Thus, the smallest integer value of qis set to 2 according to the TSULNs in Table 3. The TSUL MARCOS method can obtain calculation results, and the ranking of alternatives is h₃ > h₁ > h₂ > h₄. And the best solution can be obtained as h₃, which indicates that the method proposed in this manuscript is feasible and valid.

The proposed methodology integrating the TSULIWA, TSULIWG, and TSUL CE-PT-MABAC efficiently handles the TSUL information in Table 3. It is clear that the proposed methodology has wider range of applications the existing methods. Therefore, the following example is further provided to demonstrate that the proposed method has the advantage of generalization and effectiveness.

Example 3

[10, 12] Assume that there are four potential company as alternatives (h₁, h₂,…, h₄) in which to invest the money. The panel selected four attributes (risk analysis a₁, growth analysis a₂, social-political impact analysis a₃, environmental impact analysis a₄) to evaluate the four alternatives. The IULNs are used to indicate alternative assessment values regarding attributes (the linguistic term set S = {s₀, s₁, s₂, s₃, s₄, s₅, s₆}) by three DMs (whose weight vector ω = (0.4, 0.32, 0.28)^T), and the attribute weight vector is W = (0.32, 0.26, 0.18, 0.24)^T. the decision matrices R^ε (ε = 1, 2, 3) are constructed as listed in Table 10. We can calculate the results using the proposed method in the case of η_ij = 0, q = 1. The results calculated by this proposed under different conditions are compared with the results of Liu and Jin [9], Liu et al. [10], Liu and Zhang [12] in Table 11.

Table 10 The decision matrices with IULNs

Table 11 Comparison of results with different methods

From Table 11, we can find that the IULWGA, IULWGHM, IULWAHM (s = t = 1) and IULWABM (s = t = 1) operators obtained results consistent with the ranking of alternatives with the proposed method under condition 0 ≤ β < 0.2, i.e., h₂ > h₄ > h₁ > h₃. Hence, h₂ is the optimal choice alternative at this time. However, under different constraints, the ranking of the obtained alternatives for the IULWAHM (s > 2 or t > 2), IULWABM (s > 2 or t > 2, s ≠ t) operators and the proposed method (0.2 ≤ β ≤ 1) is consistent, and alternative h₄ is the optimal option. Although the proposed method obtains two consistent results with the existing aggregation operator-based methods under different conditions, these methods are fundamentally different. Existing methods based on the aggregation operators mainly consider interrelationship between attributes, and the degree of association is related to the values of the parameters s and t. As the values of parameters s and t becomes larger, the degree of association of attributes becomes larger, and the best option changes from h₂ to h₄, while the method proposed in this paper focuses on the consideration of the DMs’ behavioral preferences and psychological factors. Specifically, the DM’s preference tends to avoid risk (at this timeβ is small), the ranking of alternatives is h₂ > h₄ > h₁ > h₃, while the DM’s preference tends to seek risk (at this time β is large), the ranking of alternatives becomes h₄ > h₂ > h₁ > h₃.

In summary, the TSULS is a generalized form of SULS, PULS, q-ROULS, PyULS, and IULS. It has a more powerful ability to handle uncertain and ambiguous information. In this setting, the new TSULCE synthesizes the uncertain information measures of the uncertain linguistic and T-spherical fuzzy parts in TSULSs, and the TSUL CE was used in this paper as a deviation metric tool to obtain expert and attribute objective weights, as well as to replace the distance measure in the tradition MABAC method. The DEMATEL method was extended in the TSULS environment to compute attribute subjective weights, in which association relationships between attributes were considered. The IOL-based TSULIWA and TSULIWG operators developed in this paper are able to take into account the interactions between MD, AD, and ND in the TSF part of TSULNs. These operators are able to aggregate TSULNs efficiently and can ensure the integrity of information fusion and avoid counterintuitive phenomena. The MABAC method, which integrated CE and PT, was extended in the TSULS environment, not only to take into account the behavioral preferences and psychology of the MD in the decision-making process, but also to achieve flexibility in the decision-making process based on risk preferences.

Conclusion

In this article, we defined TSUL CE measure and IOLs based on TSULS. Then we proposed the TSULIWA and TSULIWG operators with TSULNs, and their properties and special cases were also discussed. Subsequently, the MAGDM framework was constructed utilizing TSUL information. In it, the expert weights regarding attributes were calculated by the defined TSUL CE-based similarity. The attribute objective weights were obtained by the TSUL CE-based MDM, while the attribute subjective weights were determined by the extended TSUL DEMATEL method. The combined attribute weight was determined. Integrated with the proposed aggregation operator, the TSUL CE-PT-MABAC method implements the ranking of alternatives. Lastly, the illustrative examples were provided, and the sensitivity analysis and comparative study were performed to illustrate the effectiveness and superiority.

However, the TSUL CE-PT-MABAC model has also some limitations. In this paper, the subjective weights of attributes are determined by the TSUL DEMATEL method, which is relatively complex and computationally intensive although it is able to take into account the correlations between attributes. In addition, the developed TSULIWA and TSULIWG operators only consider the interactions between MD, AD, and ND in the TSF part of the TSULNs, and the operators have not yet taken into account the correlative, prioritized relational characteristics of the inputs, which do not reflect realistic decision-making scenarios well.

In future, the full consistency method [77] will be used to determine the attribute subjective weights and with the MABAC method will be integrated in the TSULS environment. A series of novel aggregation operators will be further designed in the TSULS context to synthesize factors, such as interaction, priority, and multi-association relationships. Meanwhile, some alternative ranking techniques or approaches, such as WASPAS, CoCoSo, MARCOS, EDAS, etc., will be extended and applied in TSULS environment. In addition, the developed method will be tested in real decision-making scenarios.