Abstract
The complex interval-valued intuitionistic fuzzy set (CIIFS), as an extension of the complex intuitionistic fuzzy set (CIFS), is one of the better tools for dealing with time-periodic information in a single set of two-dimensional information. So, this paper makes some new operators based on Aczel-Alsina’s t-norm and t-conorm in the CIIFS environment. First, some Aczel-Alsina t-norm and t-conorm operational laws are defined for complex interval-valued intuitionistic fuzzy numbers (CIIFNs). Then, using the proposed operational laws, Aczel-Alsina The operators Complex interval-valued intuitionistic Aczel-Alsina weighted average (CIIFAAWA), Complex interval-valued intuitionistic Aczel-Alsina weighted geometric (CIIFAAWG), Complex interval-valued intuitionistic Aczel-Alsina ordered weighted average (CIIFAAOWA), and Complex interval-valued intuitionistic Aczel-Alsina ordered weighted geometric (CIIFAAOWG) are developed. Further, some properties of the proposed operators are discussed and investigated in detail. A group decision-making method is also suggested based on developed operators in the CIIFS environment. The proposed operators are more adaptable and give more accurate results than existing ones. Furthermore, a multi-criteria decision-making technique is developed based on the proposed operators. A decision-making problem for healthcare facilities in public hospitals is provided to demonstrate the benefits and applicability of the proposed method. Finally, a comparative study is also investigated using the existing methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Due to the increased emergencies, health care systems etc., decision-making and information management have become very important. However, to handle complex, imprecise and ambiguous information [1, 2], it isn’t easy to use classical tools. Therefore, to overcome this situation, Zadeh introduced the theory of fuzzy set (FS) [3]. FS is characterized by membership function (MF) in the closed interval [0, 1]. For transportation problems, an approach namely, P. Senthil Kumar (PSK) method was developed in order to obtain an optimal solution in terms of triangular fuzzy numbers [4, 5].
The theory of FS was further extended by Al-shami et al. [6] and introduced the notion of (a, b)-fuzzy soft set. Further, some aggregation operators are developed in order to aggregate the (a, b)-fuzzy soft set. Ibrahim et al. [7] initiated the notion of (3,2)-fuzzy sets and discussed their relationship with other kinds of fuzzy sets.
Further, Atanassov extended the notion of FS and initiated the concept of an intuitionistic fuzzy set (IFS) [8]. The IFS is characterized by MF and nonmembership function (NMF) belonging to the closed interval [0, 1] such that the \(MF + NMF \le 1\). For aggregating intuitionistic fuzzy numbers, Xu and Yager [9] presented a geometric aggregation operator. In addition, related to IFS, some authors proposed several other tools to handle vague and imprecise information whereby two or more sources of vagueness appear simultaneously [10,11,12,13,14]. The notion of SR-Fuzzy Sets was first introduced by Al-Shami et al. [15] as a generalization of FS. Further, the authors developed weighted aggregated operators for the aggregation of SR-Fuzzy sets and applied the concept to MCDM problem. Moreover, Al-shami and Mhemdi [16] introduced the concept of (m, n)-fuzzy sets and proposed an MCDM approach with the (m, n)-fuzzy set setting Al-Shami [17] further initiated the concept of (2,1)-Fuzzy sets and developed some weighted aggregated operators.
Kumar [18] developed an algorithm for solving real-life optimization problems based on fuzzy and IFS. Kumar [19] developed a software-based approach for solving the intuitionistic fuzzy solid assignment problem (IFSAP). A numerical example was also presented for the application of the proposed method. In order to deal with uncertainty and hesitation in transportation problems an intuitionistic fuzzy zero point method was developed by Kumar [20] to find the optimal solution to the type-2 intuitionistic fuzzy transportation problem (IFTP). Kumar [21] proposed a computationally simple and efficient method for solving real-life mixed intuitionistic fuzzy 3D assignment problems. Further, Kumar [22] further formulated a transportation problem in which costs are triangular intuitionistic fuzzy numbers, and supplies and demands are crisp numbers.
Atanassov and Gargov [23] introduced an interval-valued intuitionistic fuzzy set (IIFS) characterized by a membership function and a nonmembership function with interval values. Xu [24] presented an averaging operator (AO) to deal with multi-criteria decision-making (MCDM) problems in the IIFS environment. Garg used Einstein’s t-norm techniques to create numerous interactive AO for interval-valued intuitionistic fuzzy numbers (IIFNs) [25, 26]. The ordered weighted aggregate (OWA) operator was initiated by Yager [27], adding weights to every input depending on their ranking positions. Garg et al. [28] used Hamacher TN operators to provide different AOs under IIFS. For IIFN aggregation, Wang and Liu [29] suggested an Einstein hybrid weighted geometric aggregation operator. Liu [30] presented IIFN AOs based on Hamacher norms. Chen et al. [31] introduced several new AOs for solving the MCDM problem in the IIFS context based on transformation approaches. Triangular norms play an important role and are the basis of many AOs addressed in many fuzzy frameworks. Menger [32] pioneered the use of triangular norms in statistical data. Deschrijver et al. [33] studied tnorm (TN) and tconorm (TCN) in the context of IFSs. Several triangular norms were established to collect knowledge in various mathematical frameworks. Lukasiewicz TN and TCN [34], product TN and probabilistic sum TCN [35], Archimedean TN and TCN [36], Drastic TN and TCN [37], Einstien TN and TCN [38], and Dombi TN and TCN [39] are some of the TN and TCN that have been proposed. Nevertheless, in complex data sets, ambiguity and vagueness within the data occur concurrently with changes in the data’s phase (periodicity). Complex data sets include vast amounts of data generated by medical research and government databases for biometric and face identification, sound and photographs, all of which may contain large amounts of incomplete, confusing, and inaccurate information. To overcome these concerns, Ramot et al. [40] proposed the concept of a complex fuzzy set (CFS), which expands the membership function’s range from the real number subset to the unit disc. Ramot et al. [40] investigated several characteristics of CFSs, such as complements, unions, and intersections, using many illustrative instances. Because the CFS model does not tell anything about the disagreement of any element in any setting, Alkouri and Salleh [41] extended the concept of CFS to complex intuitionistic fuzzy set (CIFS) by including the degree of non-membership and defining their primary operations, such as union, intersection, complement, and so on. Alkouri and Salleh [42] also defined complex intuitionistic fuzzy connection, structure, and projections, and even a similarity measure among two CIFSs. Kumar and Bajaj [43] gave many distance and entropy metrics for complex intuitionistic fuzzy soft sets. Rani and Garg [44] proposed a set of distance measures for use in decision-making in a CIFS context. Rani and Garg [45] developed power AOs to integrate the various CIFS and handle the MCDM issue. Garg and Rani [46] proposed several general aggregating operators for different CIFS. In 1982, Aczel and Alsina [47] developed a novel family of TN and TCN for the condition \(0\le p\le \infty \) in 1982, dubbed Aczel–Alsina TN and TCN. When the value of p increases, the AATN and AATCN are strictly growing and continuous. Many scholars have utilised the ideas of AATN and AATCN to discover the superiority of modifying active parameters in many sectors. Different triangular norms of parametric TN, product TN, Dombi product TN, AATN, Frank product TN, and Schweizer and Sklar TN were studied by Babu and Ahmed [48].
Senapati and Chen [49] first defined Aczel-Alsina aggregation operators for IFS. He also defined [50] the same operators for IIFS. In [51], Mehmood et al. developed some complex intuitionistic fuzzy aggregation operators based on Aczel-Alsina t-norm and t-conorm. However, complex intuitionistic fuzzy set (CIFS) deal only with single-valued membership degrees but cannot deal with interval values. Therefore, to give experts more freedom, Rani and Garg [52] introduced the concept of complex interval-valued intuitionistic fuzzy set (CIIFS). CIIFS is characterized by a complex-valued membership degree and a complex-valued non-membership degree range from the real number subset to the unit disc. Motivated by the CIIFS and Aczel-Alsina t-norm and t-conorm in this paper, some new Aczel-Alsina t-norm and t-conorm based operators namely the complex interval-valued intuitionistic fuzzy Aczel-Alsina t-norm and t-conorm (CIIFAA) operators are developed. Then some properties of the proposed operators are discussed, and the concept is applied to multi-criteria decision-making problems. The following are the key contributions of this paper:
-
(1)
To define operational laws based on Aczel-Alsina t-norm and t-conorm for complex interval-valued intuitionistic fuzzy numbers (CIIFNs).
-
(2)
To develop Aczel-Alsina t-norm and t-conorm based aggregation operators for CIIFNs.
-
(3)
To propose an MCDM method based on the developed operators.
-
(4)
A case study, a numerical example of COVID-19 healthcare facilities, is given to show how the proposed operators can be used.
The rest of the text reads as follows: Section “Preliminaries” presents some basic definitions that are preliminary results. Section “Operational laws for CIIFNs based on A-A t-norm and A-A t-conorm” deals with some operational laws for CIIFNs based on Aczel-Alsina t-norm and t-conorm. Its order and hybrid form are proposed using the proposed operational laws in Section “CIIF Aczel-Alsina average aggregation operators”, complex interval-valued intuitionistic fuzzy Aczel-Alsina t-norm and t-conform-based weighted average (CIIFAAWA) operator. Some properties of the proposed operators are also discussed in detail. Section “CIIF Aczel-Alsina geometric aggregation operators” investigates a complex interval-valued intuitionistic fuzzy Aczel-Alsina t-norm and t-conorm-based weighted geometric (CIIFAAWG) operator, its order, hybrid form, and the properties of the proposed operators. Section “Model for MADM using CIF data” presents an MCDM approach based on the developed operators in a CIIFS environment. Section “Health care facility for COVID-19 in hospitals” is a numerical example regarding COVID-19 facilities in public sector hospitals for demonstrating and applying the proposed method. Section “Conclusions” presents a concluding remark.
Preliminaries
This section discusses some basic definitions and operational laws, which can be utilized in the next sections. In 1986 Attanasov initiated the notion of IVIFS [23] as a generalization of IFS. It consists of IVMD and IVNMD and can be defined as
Definition 1
[23] The IIFS A on T is defined as
where \(\alpha _{A}=[\overset{-}{\alpha _{A}}(x),\overset{+}{\alpha _{A}} (x)]\subseteq [0,1],\beta _{A}=[\overset{-}{\beta _{A}}(x),\overset{+}{\beta _{A}}(x)]\subseteq [0,1]\) denotes the IVMD and IVNMD.
Rani and Garg [52], generalizing the concept of IIFS, presented the notion of CIIFS. It is characterized by a complex interval-valued membership degree and a complex interval-valued nonmembership degree. It can be defined as
Definition 2
[52] The CIIFS A on T is defined as
where \(a^{-},a^{+}\) and \(b^{-},b^{+}\) denotes the lower bound degrees of the membership and upper bound degrees of the non-membership, which is defined as, \(a ^{-}(x)=\lambda ^{-}(x)e^{i\zeta _{\lambda }^{-}(x)}\), \(a ^{+}(x)=\lambda ^{+}(x)e^{i\zeta _{\lambda }^{+}(x)}\), \(b ^{-}(x)=\eta ^{-}(x)e^{i\xi _{\eta }^{-}(x)}\), \(b ^{+}(x)=\eta ^{+}(x)e^{i\xi _{\eta }^{+}(x)}\) and \(\lambda ^{-},\lambda ^{+},\eta ^{-},\eta ^{+}\subseteq [0,1]\) and \(0\le \lambda ^{+}+\eta ^{+}\le 1\) for all \(x\in T\). We denote the CIIFN by
Aczel-Alsina t-norm and t-conorm
The Aczel-Alsina t-norm [47] \((J_{A}^{\eta })_{\eta \in [0,\infty ]}\) is ascertained by
The Aczel-Alsina t-conorm [47] \((S_{A}^{\eta })_{\eta \in [0,\infty ]} \) is ascertained by
Operational laws for CIIFNs based on A-A t-norm and A-A t-conorm
We briefly discussed the A-A operation concering CIIFNs based on A-A t-norm and A-A t-conorm.
Definition 3
Let, \(CIIF_{i}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \(\left( i=1,2\right) \) be two CIIFNs, \( \beta>0,\varphi >0\) and \((\lambda =1,2)\). Then the A-Al t-norm and A-A t-conorm operator of CIIFNs is defined as:
The following presents an example based on the above operational laws.
Example 1
Let \(CIIF=\left( \left[ 0.2,0.4\right] e^{i2\pi \left[ 0.3,0.4\right] },[0.3,0.4]e^{i2\pi [0.3,0.5]}\right) ,\) \(CIIF_{_{1}}=\left( [0.3,0.4]e^{i2\pi [0.2,0.4]},[0.3,0.5]e^{i2\pi [0.3,0.4]}\right) \) and \(CIIF_{_{2}}=\left( [0.4,0.5]e^{i2\pi [0.2,0.6]},[0.2,0.5]e^{i2\pi [0.4,0.5]}\right) \) is three CIIFNs. Then by applying Aczel-Alsina operation on CIIFNs, and for \(\lambda =5\), \(\varphi =3\). Then
(ii)
(iii)
(iv)
Theorem 1
Let \(CIIF_{i}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \(\left( i=1,2,3\right) \) be the three CIIFNs, then we have
-
(i)
\(CIIF_{_{1}}\oplus CIIF_{_{2}}=CIIF_{_{2}}\oplus CIIF_{_{1}};\)
-
(ii)
\(CIIF_{_{1}}\otimes CIIF_{_{2}}=CIIF_{_{2}}\otimes CIIF_{_{1}};\)
-
(iii)
\(\varphi (CIIF_{_{1}}\oplus CIIF_{_{2}})=\varphi CIIF_{_{1}}\oplus \varphi CIIF_{_{2}}\);
-
(iv)
\((\varphi _{1}+\varphi _{2})CIIF_{1}=\varphi _{1}CIIF_{1}\oplus \varphi _{2}CIIF_{1},\varphi _{1},\varphi _{2}>0\)
-
(v)
\(\left( CIIF_{_{1}}\otimes CIIF_{_{2}}\right) ^{\varphi }=CIIF_{_{1}}^{\varphi }\otimes CIIF_{_{2}}^{\varphi };\)
-
(vi)
\(CIIF_{1}^{\varphi _{1}}\otimes CIIF_{1}^{\varphi _{2}}=CIIF_{1}^{(\varphi _{1}+\varphi _{2})},\varphi _{1},\varphi _{2}>0.\)
Proof
For the three CIIFNs \(CIIF,CIIF_{_{1}}\) and \(CIIF_{_{2}},\) and \(\phi , \phi _{1}, \phi _{2}>0,\) as stated in Definition 1, we can get
(ii) It is straightforward.
(iii) Let
Then \(\log (1-t)\)
Using this, we get \(\varphi (CIIF_{_{1}}\oplus CIIF_{_{2}})\)
(iv)
\(\square \)
CIIF Aczel-Alsina average aggregation operators
Utilizing the operational laws developed in Sect. “Operational laws for CIIFNs based on A-A t-norm and A-A t-conorm”, in this section, we develop CIIFAAWA operator, CIIFAAOWA operator and CIIFAAHA operators. Some properties of the proposed operators are also discussed in detail.
Definition 4
Let \(CIIF=\) \(\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) \((i=1,2, \ldots ,n)\) be collection of CIIFNs, then CIIF Aczel-Alsina weighted average (CIIFAAWA) operator is a mapping CIIFAAWA: \(CIIFAAWA_{\varphi }(CIIF_{_{1}},CIIF_{_{2}}, \ldots ,CIIF_{_{n}})=\oplus _{i=1}^{n}(\varphi CIIF_{_{\lambda }})=\varphi _{1}CIIF_{_{1}}\oplus \varphi _{2}CIIF_{_{2}}\oplus \cdots \oplus \varphi _{n}CIIF_{_{n}}\), where \(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})^{T}\) be weight vector of \(CIIF_{_{\lambda }}\) \((i=1,2, \ldots ,n)\) with \(\varphi _{i}\in \left[ 0,1\right] \) and \(\sum _{i=1}^{n}\varphi _{i}=1\).
We develop the succeeding theorem that follows the Aczel-Alsina operations on CIIFNs.
Theorem 2
Let \(CIIF_{{}}=\) \(\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) be a collection of CIIF elements, then accumulated value by use of CIIFAAWA operators also a CIIFNs, and \(CIIFAAWA_{\varphi }(CIIF_{_{1}},CIIF_{_{2}}, \ldots ,CIIF_{_{n}})\) \(=\oplus _{i=1}^{n}(\varphi _{i}CIIF_{_{i}}) \)
where \(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})\) is weight vector of \(CIIF_{_{i}}(i=1,2, \ldots ,n)\) in a manner that \(\varphi _{i}\in \left[ 0,1\right] ,\) and \(\sum _{i=1}^{n}\varphi _{i}=1.\)
Proof
We may establish the Theorem using the mathematical induction approach in the following way:
(i) When \(n=2,\) depending on Aczel-Alsina operations on CIIFNs, we obtain
Based on Definition 4, we obtain
Hence, it is right for \(n=2.\)
(ii) Assume that the Eq. (5) is holds true for \(n=k,\) then
Now, for \(n=k+1,\) we get \(CIIFAAWA_{\varphi }(CIIF_{_{1}},CIIF_{_{2}}, \ldots ,CIIF_{_{k+1}}) =\oplus _{i=1}^{n}(\varphi _{i}CIIF_{_{i}})\oplus (\varphi _{k+1}CIIF_{_{k+1}})\)
Thus, Eq. (5) is true for \(n=k+1.\) Therefore, from (i) and (ii), we may conclude that Eq. (5) holds for any n. \(\square \)
We easily prove the subsequent properties by applying the CIIFAAWA operator.
Theorem 3
(Idempotency property) \(CIIF_{_{i}}=\) \(\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) \( (i=1,2, \ldots ,n)\) are collection equal to CIIFNs, i.e., \(CIIF_{_{i}}=CIIF\) for all i, then
Proof
As by the operational laws
Thus, \(CIIFAAWA_{\varphi }\) \(\varphi (CIIF_{_{1}},CIIF_{_{2}}, \ldots ,CIIF_{_{n}})=CIIF\) holds. \(\square \)
Theorem 4
(Boundedness property) Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) be a number of CIIFNs Let \(CIIF_{_{i}}^{-}=\min (CIIF_{_{1}},CIIF_{_{2}}, \ldots ,CIIF_{_{n}})\) and \(CIIF^{+}=\max (CIIF_{_{1}},CIIF_{_{2}}, \ldots , CIIF_{_{n}}).\) Then,
Proof
Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) be a number of CIIFNs. Let
and
We have
and
Hence, there have the subsequent inequalities,
Therefore
\(\square \)
Theorem 5
(Monotonicity property) Let \(CI_{IF_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \(CI_{IF_{i}}^{^{\prime }}=\left( \left[ \alpha _{i}^{^{\prime }},\beta _{i} \right] e^{i2\pi [\gamma _{i}^{^{\prime }},\delta _{i}^{^{\prime }}]}, \left[ \mu _{i}^{^{\prime }},\nu _{i}^{^{\prime }}\right] e^{i2\pi [\eta _{i}^{^{\prime }},\phi _{i}^{^{\prime }}]}\right) \) and \((i=1,2, \ldots ,n)\) be two sets of CIIFNs,
Now, we introduce CIF Aczel-Alsins ordered weighted averaging (CIFAAOWA) operator.
Definition 5
Assume that \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) are several CIIFNs. An \(n-\) dimensional CIIFAAOWA operator is a function CIIFAAOWA: \(\hbox {CIFN}^{n}\) \(\longrightarrow \) CIIFN along side relating vector \(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})^{T}\) in such a way as to allow \(\varphi _{i}\in [0,1],\) and \(\sum _{i=1}^{n}\varphi _{1}=1.\) Therefore, \(\hbox {CIIFAAOWA}_{\varphi }\)
where \(k(1),k(2), \ldots ,k(n)\) are permutation of \(i=1,2, \ldots ,n,\) for which \( CIIF_{_{k(i-1)}}\ge CIIF_{_{k(i)}}\) for all \(i=1,2, \ldots ,n.\) The succeeding theorem is developed based on Aczel-Alsina product operation on CIIFNs.
Theorem 6
Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) be a number of CIIFNs. A \(n-\)dimensional CIIF Aczel-Alsina ordered weighted average (CIIFAAOWA) operator is a function CIIFAAOWA: \(\hbox {CIIFN}^{n}\rightarrow \hbox {CIIFN}\) with the corresponding vector \(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})^{T}\) in such a way as to allow \(\varphi _{i}\in [0,1],\)and \( \sum _{i=1}^{n}\varphi _{i}=1.\) Then, \(\hbox {CIIFAAOWA}_{\varphi }\)
where \((k(1),k(2), \ldots ,k(n))\) are permutation of \((i=1,2, \ldots ,n),\)in such a manner \(CIIF_{_{k(i-1)}}\ge CIIF_{_{k(i)}}\) for all \(i=1,2, \ldots ,n.\) The subsequent properties may be shown by CIIFAAOW operator without any problem.
Theorem 7
(Idempotency property) If \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) are several CIIFNs, which are all equal, i.e., \(CIIF_{_{i}}=CIIF\) for all i, then
Theorem 8
(Boundedness property) Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}e^{i2\pi [\gamma _{i},\delta _{i}]}\right] , \left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) be a number of CIIFNs and Let \(CIIF^{-}=\min _{i}CIIF_{_{i}},\)and \(CIIF^{+}=\max _{i}CIIF_{_{i}}.\) Then
If \(CIIF_{i}\le \) \(CIIF_{i}^{^{\prime }}\) for all i, then
Theorem 9
(Commutative property) Let \(CI_{IF_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \(CI_{IF_{i}}^{^{\prime }}=\left( \left[ \alpha _{i}^{^{\prime }},\beta _{i} \right] e^{i2\pi [\gamma _{i}^{^{\prime }},\delta _{i}^{^{\prime }}]}, \left[ \mu _{i}^{^{\prime }},\nu _{i}^{^{\prime }}\right] e^{i2\pi [\eta _{i}^{^{\prime }},\phi _{i}^{^{\prime }}]}\right) \) be two sets of CIIFNs, then
where \(CI_{IF_{i}}^{^{\prime }}(i=1,2, \ldots ,n)\) is any permutation of \( CIIF_{_{i}}(i=1,2, \ldots ,n).\)
In Definition 2, we comprehend that the CIIFAAWA operator weights the CIIFNs, and in Definition 3, we recognize that the CIIFAAOWA operator weights only the ordered position of the CIIFNs. As such, the above-mentioned two average operators indicate the weights in two ways. But the weight can be shown by one operator without being directed in two ways by two operations. To overcome this difficulty, we put forward CIIF Aczel-Alsina hybrid averaging (CIIFAAHA) operator, which weighs both the given CIIFN and its ordered position.
Theorem 10
Let \(CIIF_{_{i}}(i=1,2, \ldots ,n)\) be a number of CIIFNs. An n-dimensional CIIF Aczel-Alsina hybrid average (CIIFAAHA) operator is a function \(CIIFAAHA:CIIFN^{n}\rightarrow CIIFN\), in such a way as to allow
where \(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})^{T}\) is weighting vector closely related to the CIIFAAHA operator, with \(\varphi _{i}\in [0,1]\) \((i=1,2, \ldots ,n)\) and \(\sum _{i=1}^{n}\varphi _{i}=1\) \(CIIF_{_{(i)}}^{-}=n\varphi _{i}CIIF_{_{i}},i=1,2,\ldots ,n,(CIIF_{_{k(1)}}^{-},CIIF_{_{k(2)}}^{-}, \ldots ,CIIF_{_{k(n)}}^{-}) \)is any permutation of weighted CIIFNs \((CIIF_{_{(1)}}^{-},CIIF_{_{(2)}}^{-}, \ldots ,CIIF_{_{(n)}}^{-}),\) to allow \( CIIF_{_{k(i-1)}}^{-}\ge CIIF_{_{k(i)}}^{-}\) \((i=1,2, \ldots ,n);\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})^{T}\) is weighted vector if \(CIIF_{_{i}}(i=1,2, \ldots ,n),\) with\(\varphi _{i}\in [0,1]\) \((i=1,2, \ldots ,n)\) and \(\sum _{i=1}^{n}\varphi _{i}\) and n is the balancing coefficient, which plays a role in balance.
Based on Aczel-Alsina operations with CIIFNs information, we can deduce the subsequent theorem.
Theorem 11
Let \(CIIF_{_{i}}(i=1,2, \ldots ,n)\) be a family of CIIFNs. Then accumulated value by the CIIFAAHA operator is still a CIIFN, and \(CIIFAAHA_{\varphi }(CIIF_{1},CIIF_{2}, \ldots ,CIIF_{n})=\oplus _{i=1}^{n}(\varphi _{i}CIIF_{_{k(i)}}^{-})\)
Just like the above Theorem, we can easily obtain the following theorem.
Theorem 12
The CIIFAAWA and CIIFAAOWA operators are special cases of the CIIFAAHA operator.
Proof
(1) Let \(\varphi =(\frac{1}{n},\frac{1}{n}, \ldots ,\frac{1}{n})^{T}.\) Then
(2) Let \(\varphi =(\frac{1}{n},\frac{1}{n}, \ldots ,\frac{1}{n})^{T}.\) Then \(CIIF_{_{i}}^{-}=CIIF_{_{i}}(i=1,2,\ldots , n)\) and
which complete the proof. \(\square \)
CIIF Aczel-Alsina geometric aggregation operators
Utilizing the operational laws developed in Sect. “Operational laws for CIIFNs based on A-A t-norm and A-A t-conorm”, we develop the CIIFAAWG operator, CIIFAAOWG operator and CIIFAAHG operator. Some properties of the proposed operators are also discussed in detail in this section.
Definition 6
Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) be collection of CIIFNs. Then CIIF Aczel-Alsina weighted geometric (CIFAAWG) operator is a mapping CIIFAAWG:
where \(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})^{T}\) be weight vector of \(CIIF_{_{i}}\) \((i=1,2, \ldots ,n)\) with \(\varphi _{i}\in \left[ 0,1 \right] \) and \(\sum _{^{i}=1}^{n}\varphi _{i}=1.\)
We develop the succeeding theorem that follows the Aczel-Alsina operations on CIIFNs.
Theorem 13
Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) be several CIIF elements, then accumulated value by use of CIIFAAWG operator is also a CIIFNs, and \(CIIFAAWG_{\varphi }(CIIF_{1},CIIF_{2}, \ldots ,CIIF_{n}) =\otimes _{i=1}^{n}(\varphi _{i}CIIF_{_{i}}) \)
where \(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})\) is weight vector of \(CIIF_{_{i}}(i=1,2, \ldots ,n)\) in a manner that \(\varphi _{i}\in \left[ 0,1\right] ,\) and \(\sum _{i=1}^{n}\varphi _{i}=1.\)
Proof
We are able to prove this Theorem with aid of mathematical induction technique in a subsequent manner:
(i) when \(n=2,\) depending on Aczel-Alsina operations on CIFNs, we obtain
Based on above Definition 5, we obtain \(CIIFAAWG_{\varphi }(CIIF_{_{1}},CIIF_{_{2}})=\varphi _{1}CIIF_{_{2}}\otimes \varphi _{2}CIIF_{_{1}}\)
Hence, it is right for \(n=2.\)
(ii) Suppose that it is true for \(n=k\), then we have \(CIIFAAWG_{\varphi }(CIIF_{_{1}},CIIF_{_{2}}, \ldots ,CIIF_{_{k}})=\otimes _{i=1}^{k}(\varphi _{i}CIIF_{_{k}})\)
Now, for \(n=k+1,\) then \(CIIFAAWG_{\varphi }(CIIF_{_{1}},CIIF_{_{2}}, \ldots ,CIIF_{_{k+1}})=\otimes _{i=1}^{n}(\varphi _{i}CIIF_{_{i}})\otimes (\varphi _{k+1}CIIF_{_{k+1}})\)
Thus, it is true for \(n=k+1.\)
Therefore, from (i) and (ii), we may conclude that (3) holds for any n. \(\square \)
We easily prove the subsequent properties by using the CIFAAWG operator.
Theorem 14
(Idempotency property) Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) be several equal CIFNs, i.e., \(CIIF_{_{i}}=\) CIIF for all i, then
Proof
Since \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) \((i=1,2, \ldots ,n),\) then we have, \(CIIFAAWG_{\varphi }(CIIF_{_{1}},CIIF_{_{2}}, \ldots ,CIIF_{_{n}})=\otimes _{i=1}^{n}(\varphi _{i}CIIF_{_{i}})\)
As a result, \(CIIFAAWG_{\varphi }(CIIF_{1},CIIF_{2}, \ldots ,CIIF_{n})=CIIF\) holds. \(\square \)
Theorem 15
(Boundedness property) Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) \((i=1,2, \ldots ,n)\) be a number of CIIFNs. Let \(CIIF^{-}=\min (CIIF_{1},CIIF_{2}, \ldots ,CIIF_{n})\) and \(CIIF^{+}=\max (CIIF_{1},CIIF_{2}, \ldots ,CIIF_{n}).\) Then,
Proof
Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}e^{i2\pi [\gamma _{i},\delta _{i}]}\right] , \left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) be a number of CIIFNs. Let \(CIIF_{_{i}}^{-}=\min (CIIF_{1},CIIF_{2}, \ldots ,CIIF_{n}) =\left( \left[ \alpha _{i}^{-},\beta _{i}^{-}\right] e^{i2\pi [\gamma _{i}^{-},\delta _{i}^{-}]},\left[ \mu _{i}^{-},\nu _{i}^{-}]e^{i2\pi [\eta _{i}^{-},\phi _{i}^{-}]}\right] \right) \) and \(CIIF_{_{i}}^{+}=\max (CIIF_{1},CIIF_{2}, \ldots ,CIIF_{n})=\left( \left[ \alpha _{i}^{+},\beta _{i}^{+}\right] e^{i2\pi [\gamma _{i}^{+},\delta _{i}^{+}]},\left[ \mu _{i}^{+},\nu _{i}^{+}\right] e^{i2\pi [\eta _{i}^{+},\phi _{i}^{+}]}\right) \). Then, we get \(\left( \left[ \alpha _{i}^{-},\beta _{i}^{-}\right] e^{i2\pi [\gamma _{i}^{-},\delta _{i}^{-}]}\right) =\min _{i}\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i}^{-},\nu _{i}^{-}\right] e^{i2\pi [\eta _{i}^{-},\phi _{i}^{-}]}\right) =\min _{i}\left( \left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \) and \(\left( \left[ \alpha _{i}^{+},\beta _{i}^{+}\right] e^{i2\pi [\gamma _{i}^{+},\delta _{i}^{+}]}\right) =\max _{i}\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi [\gamma _{i},\delta _{i}]},\left[ \mu _{i}^{+},\nu _{i}^{+}\right] e^{i2\pi [\eta _{i}^{+},\phi _{i}^{+}]}\right) =\max _{i}\left( \left[ \mu _{i},\nu _{i}\right] e^{i2\pi [\eta _{i},\phi _{i}]}\right) \). Hence, there have subsequent inequalities,
Therefore, \(CIIF^{-}\le \) \(CIIFAAWG_{\varphi }(CIIF_{1},CIIF_{2}, \ldots ,CIIF_{n})\le CIIF^{+}.\) \(\square \)
Theorem 16
(Monotonicity property) Let \(CIIF_{_{i}}\) and \(CIIF_{_{i}}^{ {\acute{}} }(i=1,2, \ldots ,n)\) be two sets of CIIFNs, if \(CIIF_{_{i}}\le CIIF_{_{i}}^{ {\acute{}} }\) for all i, then
We introduce the CIF Aczel-Alsins ordered weighted geometric (CIIFAAWG) operator.
Definition 7
Assume that \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i[\gamma _{i},\delta _{i}]},\left[ \mu _{i},\nu _{i}\right] e^{i[\eta _{i},\phi _{i}]}\right) \) and \((i=1,2, \ldots ,n)\) are several CIIFNs. An n-dimensional CIIFAAOWG operator is a function CIIFAAOWG \(:CIIFN^{n}\longrightarrow CIIFN\) alongside relation vector \(\varphi =(\varphi _{1},\varphi _{2},\cdots \varphi _{n})^{T}\) in such a way as to allow \(\varphi _{i}\in [0,1],\) and \(\sum _{i=1}^{n}\varphi _{1}=1.\) Therefore,
where \((k(1),k(2),\ldots ,k(n))\) are permutation of \((i=1,2, \ldots ,n)\), for which \(CIIF_{_{k(i-1)}}\ge CIIF_{_{k(i)}}\) for all \(i=1,2, \ldots ,n.\) The succeeding theorem is developed based on the Aczel-Alsina product operation on CIIFNs.
Theorem 17
Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i\left[ \gamma _{i},\delta _{i}\right] },\left[ \mu _{i},\nu _{i}\right] e^{i\left[ \eta _{i},\phi _{i}\right] }\right) \) and \((i=1,2, \ldots ,n)\) be a number of CIIFNs. An n-dimensional CIIF Aczel-Alsina ordered weighted geometric (CIIFAAOW) operator is a function \( CIIFAAOWG:CIIFN^{n}\rightarrow CIIFN\) with the corresponding vector \(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})^{T}\) in such a way as to allow \(\varphi _{i}\in [0,1],\) and \(\sum _{i=1}^{n}\varphi _{i}=1.\) Then,
where \((k(1),k(2),\ldots ,k(n))\) are permutation of \((i=1,2, \ldots ,n),\) in such a manner \(CIIF_{_{k(i-1)}}\ge CIIF_{_{k(i)}}\) for all \(i=1,2, \ldots ,n.\)
The CIIFAAOW operator may show the subsequent properties without any problem.
Theorem 18
(Idempotency property) If \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i\left[ \gamma _{i},\delta _{i}\right] },\left[ \mu _{i},\nu _{i}\right] e^{i\left[ \eta _{i},\phi _{i}\right] }\right) \) \((i=1,2, \ldots ,n)\) are several CIIFNs, which are all equal, i.e., \(CIIF_{_{(i)}}=CIIF\) for all i, then
Theorem 19
(Boundedness property) Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i2\pi \left[ \gamma _{i},\delta _{i}\right] },\left[ \mu _{i},\nu _{i}\right] e^{i\left[ \eta _{i},\phi _{i}\right] }\right) \) and \((i=1,2, \ldots ,n)\) be a number of CIIFNs. Let \(CIIF^{-}=\min _{i}CIIF_{_{(i)}},\)and \(CIIF^{+}=\max _{i}CIIF_{_{(i)}}.\) Then
Theorem 20
(Monotonicity property) Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i}e^{i2\pi (\gamma _{i})},\beta _{i}e^{i2\pi (\delta _{i})}\right] , \left[ \mu _{i}e^{i2\pi (\eta _{i})},\nu _{i}e^{i2\pi (\phi _{i})}\right] \right) \) and \(CIIF_{_{i}}^{^{\prime }}=\left( \left[ \alpha _{i}^{^{\prime }},\beta _{i} \right] e^{i\left[ \gamma _{i}^{^{\prime }},\delta _{i}^{^{\prime }}\right] },\left[ \mu _{i}^{^{\prime }},\nu _{i}^{^{\prime }}\right] e^{i\left[ \eta _{i}^{^{\prime }},\phi _{i}^{^{\prime }}\right] }\right) \) and \((i=1,2, \ldots ,n)\) be two sets of CIFNs, if \(CIIF_{_{(i)}}\le \) \( CIIF_{_{(i)}}^{ {\acute{}} }\) for all i, then
Theorem 21
(Commutative property) Let \(CIIF_{_{i}}=\left( \left[ \alpha _{i},\beta _{i}\right] e^{i\left[ \gamma _{i},\delta _{i}\right] },\left[ \mu _{i},\nu _{i}\right] e^{i\left[ \eta _{i},\phi _{i}\right] }\right) \) and \(CIIF_{_{i}}^{^{\prime }}=\left( \left[ \alpha _{i}^{^{\prime }},\beta _{i}^{^{\prime }} \right] e^{i\left[ \gamma _{i}^{^{\prime }},\delta _{i}^{^{\prime }}\right] } \left[ \mu _{i}^{^{\prime }},\nu _{i}^{^{\prime }}\right] e^{i\left[ \eta _{i}^{^{\prime }},\phi _{i}^{^{\prime }}\right] }\right) \) and \((i=1,2, \ldots ,n)\) be two sets of CIIFNs, then
where \(CIIF_{_{(i)}}^{ {\acute{}} }(i=1,2, \ldots ,n)\) is any permutation of \(CIIF_{_{(i)}}(i=1,2, \ldots ,n).\)
In the above definition, we comprehend that the CIIFAAWG operator weights solely the CIIFNs. In this definition, the CIIFAAOWG operator only considers the CIIFNs’ ordered position. As such, the two above geometric operators indicate the weights in two ways. But the weight can be shown by one operator without being directed in two directions by two operations. We suggest using the CIIF Aczel-Alsina hybrid geometric (CIIFAAHG) operator to solve this problem. This operator takes into account both the given CIIFN and its ordered position.
Definition 8
Let \(CIIF_{_{(i)}}(i=1,2, \ldots ,n)\) be a number of CIIFNs. An n-dimensional CIIF Aczel-Alsina hybrid geometric (CIIFAAHG) operator is a function \(CIIFAAHG:CIIFN^{n}\rightarrow CIIFN\), in such a way as to allow
where \(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})^{T}\) is weighting vector closely related to the CIIFAAHG operator, with \(\varphi _{i}\in [0,1]\) \((i=1,2, \ldots ,n)\) and \(\sum _{i=1}^{n}\varphi _{i}=1;CIIF_{_{i}}^{-}=n\varphi _{i}CIIF_{_{i}},\) \(i=1,2, \ldots ,n,(CIIF_{_{k(1)}}^{-},CIIF_{_{k(2)}}^{-}, \ldots ,CIIF_{_{k(n)}}^{-})\) is any permutation of weighted CIIFNs \((CIIF_{_{(1)}}^{-},CIIF_{_{(2)}}^{-}, \ldots ,CIIF_{_{(n)}}^{-}),\) so as to allow \(CIIF_{_{k(i-1)}}^{-}\ge CIIF_{_{k(i)}}^{-}(i=1,2, \ldots ,n);\varphi =(\varphi _{1},\varphi _{2},\ldots , \varphi _{n})^{T}\) is weighted vector if \(CIIF_{_{i}}(i=1,2, \ldots ,n),\)with \(\varphi _{i}\in [0,1]\) \((i=1,2, \ldots ,n)\) and \(\sum _{i=1}^{n}\varphi _{i}\) and n is the balancing coefficient, which plays a role in balance.
We can deduce the subsequent theorem based on Aczel-Alsina operations with CIIFNs information.
Theorem 22
Let \(CIIF_{_{i}}(i=1,2, \ldots ,n)\) be a family of CIIFNs. Then accumulated value by CIIFAAHG operator is still a CIIFN, and
From the above theorem, we can easily obtain the following theorem:
Theorem 23
The CIIFAAWG and CIIFAAOWG operators are special cases of the CIIFAAHG operator.
Proof
(1) Let \(\varphi =(\frac{1}{n},\frac{1}{n}, \ldots ,\frac{1}{n})^{T}.\) Then
(2) Let \(\varphi =(\frac{1}{n},\frac{1}{n}, \ldots ,\frac{1}{n})^{T}.\) Then
which complete the proof. \(\square \)
Model for MADM using CIF data
This section will utilize the recommended operators for a MADM issue in the CIF environment. MADM techniques make decisions by analyzing trade among alternative exhibitions over multiple attributes [30]. Basic data required in a MADM technique incorporates attribute values or performance measures (individual assessments on alternatives against each attribute), attribute weights (which take into account how important each attribute is to the whole decision issue), and a way to put all of this information together into a total value or assessment for each option. Simply put, a MADM problem is finding a good compromise solution out of all the possible options after weighing them on multiple factors. Here, we might also advise a MADM process controlling CIF Aczel Alsina aggregation operators where characteristic values are inside the shape of CIFEs, and characteristic weights are inside the shape of actual numbers. Assume that \(\Gamma _{CIIF}=\{ \Gamma _{CIIF_{(1)}},\Gamma _{CIIF_{(2)}}, \ldots ,\Gamma _{CIIF_{(m)}}\}\) are the discretely preparations of alternatives,\(\chi =\{ \chi _{1},\chi _{2}, \ldots ,\chi _{n}\}\)are the discretely preparations of attributes and ’\(\varphi =(\varphi _{1},\varphi _{2}, \ldots ,\varphi _{n})\) are the weight vector of the characteristic \(\chi _{\lambda }(\lambda =1,2, \ldots ,n)\) in any such manner as ’\(\varphi _{\lambda }\in [0,1]\) and \(\sum _{\lambda =1}^{n}=1\). Suppose that R \(=(CIIF_{s(\lambda )})_{m\times n}\) \(=\) \((\Gamma _{CIIF_{s(\lambda )}},\Lambda _{CIIF_{s(\lambda )}})_{m\times n}\) is the CIF selection matrix, as seemed in Table 1, where \(\Gamma _{\acute{C}_{CIIF_{s(\lambda )}}}\) in constitute club diploma with the aid of using which opportunity \(\Gamma _{CIIF_{s}}\) fulfils the characteristic \(\chi _{\lambda }\), and \(\Lambda _{CIIF_{\acute{C} _{CIIF_{s(\lambda )}}}}\) constitute non-club diploma with the aid of using which opportunity \(\mu _{\lambda }\) does now no longer fulfil the characteristic \(\chi _{\lambda }\), where\(\Gamma _{CIIF_{\acute{C}_{CIIF_{s(\lambda )}}}}\subset [0,1]\), and \(\Lambda _{CIIF_{\acute{C}_{CIIF_{s(\lambda )}}}}\subset [0,1]\) permitting \(0\le \Gamma _{CIIF_{\acute{C}_{CIIF_{s(\lambda )}}}}+\Lambda _{CIIF_{\acute{C}_{CIIF_{s(\lambda )}}}}\le 1\), \((s=1,2, \ldots ,m)\) and \((\lambda =1,2, \ldots ,n).\)
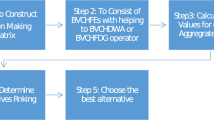
The following algorithm constructs a method for searching for the best opportunity(s) in light of the CIIFAAWA operators for MADM difficulty, which includes the following steps:
Step I: For a MADM difficulty with CIIFEs, we formulate the CIIF selection matrix \(R=(\acute{C}_{CIF_{s(\lambda )}})_{m\times n}\) where the factors \(\acute{C}_{CIF_{s(\lambda )}}\) \((s=1,2, \ldots ,m,\lambda =1,2, \ldots ,n)\) are the value determinations of the opportunity \(\mu _{m}\) concerning the criterion \( \chi _{n}\).
Step II: In the occasion that there are numerous varieties of criteria, in particular benefit (B) and cost (C), at that factor, we convert the CIIF selection matrix \(R=(\acute{C}_{s\lambda })_{m\times n}\) into the normalized one\(R^{\sim }\) \(=(\mu _{_{s\lambda }})_{m\times n}\) via way of means of making use of the accompanying equation \(\Gamma _{CIF_{s\lambda }}=\left\{ \begin{array}{c} \acute{C}_{CIF_{s(\lambda )}},\lambda \in B \\ \acute{C}_{CIF_{s(\lambda )}}^{c},\lambda \in C_{CIF} \end{array} \right\} \), where \(\acute{C}_{CIF_{s(\lambda )}}^{c}\) is the compliment of \(\acute{C} _{CIF_{s(\lambda )}}\).
Step III: On the basis of the decision matrix \(R^{\sim }\), as derived from Step 2, the total accumulated value of the alternative \(\Gamma _{CIF_{s}}(s=1,2,\ldots ,m)\) under the different criteria \(\chi _{\lambda }\)is acquired by utilizing CIIFAAWA operator and hence get the general decision values \(\Gamma _{CIF_{s}}(s=1,2,\ldots ,m)\) for each alternative \(\mu _{s}\), i.e.,

Step IV: We decide the rating values \(S^{\sim }(\Gamma _{CIF_{s}})(s=1,2,\ldots ,m)\) at the basis of the overall CIF records \(\Gamma _{CIF_{s}}(s=1,2,\ldots ,m)\) with the reason of ranking all of the opportunity \(\Gamma _{CIF_{s}}(s=1,2,\ldots , m) \) to choose wonderful desire \(\Gamma _{CIF_{s}}\). If you discover equal rating capabilities \(S^{\sim }(\Gamma _{CIF_{s}})\) and \(S^{\sim }(\Gamma _{CI_{IF}})\), at that factor we retain to parent accuracy tiers of \(L^{\sim }(\Gamma _{CIF_{s}})\) and \(L^{\sim }(\Gamma _{CI_{IF}})\) in view of standard CIF records of \(\Gamma _{CIF_{s}}\) and \(\Gamma _{CI_{IF}}\), and we rank the selection \(\Gamma _{CIF_{s}}\) consistent with the accuracy tiers of \(L^{\sim }(\Gamma _{CIF_{s}})\) and \(L^{\sim }(\Gamma _{CI_{IF}})\).
Step V: We rank all of the opportunity \(\Gamma _{CIF_{s}}(s=1,2,\ldots ,m)\) in accordance with the descending price of the rating values, choose the most suited opportunity.
Step VI: End.
Health care facility for COVID-19 in hospitals
COVID-19 is the name of the new coronavirus strain driving the current epidemic. On January 7, 2020, Chinese authorities identified this virus strain [53]. It began to spread worldwide from country to country [54], and the number of cases grew by the day [55]. Every year, the global health budget is $7.5 trillion [53]. This epidemic has served as a harsh wake-up call for Pakistan’s inadequate health infrastructure, which has been under unsustainable strain throughout this time [56]. The COVID-19 pandemic for 2019–2020 was expected to enter Pakistan in February 2020, with approximately 255,769 cases and 5386 deaths (World Health Organization 2020b) as of July 15, 2020. In a developing country like Pakistan, disease outbreaks are a big problem for the health care system. There aren’t enough basic medical facilities or health policies, the government isn’t doing a good job, and people aren’t interested in broad protective measures [57].
This paper presents a numerical example regarding healthcare facilities in Khyber Pakhtunkhwa, Pakistan. After initial scrutiny, four hospitals in Khyber Pakhtunkhwa are taken as alternatives \(A_{i}=(i=1,2,3,4,5).\) The four hospitals are evaluated based on the following four criteria:
-
1.
RT-PCR Facilities (RT-PCR),
-
2.
Personal protective equipment (PPE),
-
3.
Shortage of Isolation Ward (SIW),
-
4.
Hight Qualified Staff (HQS).
A group of three experts is nominated in order to evaluate the four hospitals based on four criteria. The experts present their evaluation values in the form of CIIFNs, indicated in Tables 2, 3, 4.
By Using CIIFAAWA operator
Step 1. In this step, we construct the complex interval-valued intuitionistic fuzzy decision matrices and are presented in Tables 2, 3, and 4.
Step 2. Since all the attributes \(A_{i}\) \((i=1,2,3,4)\) are of the benefit type, there is no need for normalization.
Step 3. By utilizing the CIIFAAWA operator to aggregate all the preference values presented by the experts and the collective complex intuitionistic fuzzy information is presented in Table 5.
Step 4. Utilizing the CIIFAAWA operator to aggregate all attributes \(CI_{j}(j=1,2,3,4)\) of the ith line and obtain the overall performance values concerning alternative \(A_{i}\). Here we take \(k=3\). Then,
Step 5. Utilizing the score function for ranking the alternatives \( A_{i}(i=1,2,3,4)\), we have,
Step 6. Based on the score values, ranking of the alternatives \(A_{i}(i=1,2,3,4)\) are
Therefore, we have
where the symbol “\(\succ \)” means “superior to”. Thus, the best choice is \(A_{2}\).
By using the CIIFAAWG operator
Here, we apply the CIIFAAWG operator to the above numerical example:
Step \(3'\). Utilizing the CIIFAAWG operator to aggregate all preference value \(CI_{j}(j=1,2,3,4)\) of the ith line and obtain the overall performance value \(CI_{i}\) concerning alternative \(A_{i}\). Here we take \(k=3\). Then
Step \(4'\). Utilizing the score function for ranking the alternatives \( A_{i}(i=1,2,3,4)\), we have,
Step \(5'\). Based on the score values, ranking of the alternatives \(A_{i}(i=1,2,3,4)\) are:
Therefore, we have
where the symbol “\(\succ ''\) means “superior to”. So according to CIIFAAWG operator \(A_{2}\) is the best choice.
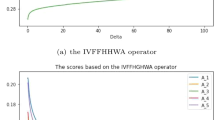
Discussion about the influence of the parameter k
To reflect the effect of changing, we utilise a separate parameter k in our suggested technique to rank the alternatives based on the value of the parameter k. Table 6 displays the ranking results.
Table 6 shows that when the parameter k is changed, the ranking order derived from the CIIFAAWA operator in each parameter k remains the same in this example. Also, as the parameter k for the same alternative goes up, the score function values made by the CIIFAAWA operator go up.
Comparison with different existing methods
This section compares the proposed method with existing methods under the CIIF, CIF, and IIF environments.
Comparison with different CIIF methods
This subsection compares the proposed method to previously developed methods [52]. The proposed method is compared with the CIIFWG, CIIFWA, CIIFOWA, and CIIFOWG operators [52]. The score values and ranking of alternatives are presented in Table 7.
Table 7 shows that by utilizing the proposed CIIFAAWA operator, CIIFAAWG operator, CIIFAAOWG operator, and CIIFAAOWA operator, the same best alternative \(A_{2}\) is obtained. The ranking result of alternatives by using the CIIFWA operator [52] and CIIFWG operator [52] is \(A_{4}>A_{1}>A_{3}>A_{2}\) and \(A_{4}>A_{3}>A_{1}>A_{1}\), respectively. The proposed operators are more flexible than existing operators and the existing operators are special cases of the developed operators. In addition, the ranking order of the alternatives by utilizing the CIIFOWA operator [52] and CIIFOWG operator [52] are \(A_{2}>A_{3}>A_{4}>A_{1}\) and \(A_{2}>A_{3}>A_{4}>A_{1}\) which is the same as obtained by developed operators. However, the proposed operators show more flexibility than the existing operators. But based on changing decision conditions, the above table shows that the best alternatives change with various operators. Hence the present method is more reliable and valid as compared with the existing methods.
Comparison with different CIF methods
To evaluate the performance of the developed method a comparative study was conducted with the methods developed in [45] and [51]. The score values and ranking of alternatives are presented in Table 8.
From Table 8, it is clear that the method developed in this paper gives \(A_{2}\) as the best alternative. In addition, when comparing the proposed method with other existing methods, it gives the same alternative, \(A_{2}\), except for the two existing methods, which are the CIFAAWA operator and CIFAAWG operator \(A_{4}\). The key benefit of developed operators is that they are more professional. It deals with an MCDM problem with both interrelationships among the criteria. The mathematical example validates the application and the effectiveness of the developed method. But based on changing decision conditions, Table 8 shows that the best alternatives change with various operators. Subsequently, our developed techniques are generally more extensive and adaptable than some prevailing techniques to manage the CIIF MCDM problem.
Comparison with different IIF methods
By taking the phase term as zero, the CIIFS reduced to IIFS. This shows that IIFS is a special case of the CIIFS. Therefore, the developed approach is compared with the methods developed under IIFS environments in this subsection. The score values and ranking of alternatives are presented in Table 9.
In Table 9, it is clear that our proposed methods that as CIIFAAWA operator, CIIFAAWG operator, CIIFAAOWG operator and CIIFAAOWA operator have the same and best alternatives, which is \(A_{2}\). In addition, when we compare our suggested method with another existing method, it gives the same alternative, \(A_{2}\), except for the two existing methods, IIFAAWA and IIFWG operators, which are \(A_{4}\). According to Table 9, the ranking of alternatives obtained by using the IIFAAWA operator [50] operator and IIFWG operator is \(A_{2}>A_{3}>A_{1}>A_{4}\) and \(A_{3}>A_{2}>A_{1}>A_{4}\), respectively. In addition, IIFAAWA operator [50] operator is \(A_{2}>A_{4}>A_{1}>A_{3}\), while the ranking achieved by using the IIFAAWG operator [50] operator is \(A_{2}>A_{4}>A_{1}>A_{3}\) which is the same ranking as the CIIFAAWA operator and CIIFAAWG operator. The fundamental reason is that present operators, but not all, examine interrelationships among criteria.
Comparison with different IF methods
In this part, we compare the provided MCDM technique to other existing methods to assess the performance of our suggested model. First, we convert the expert’s decision matrix into IFNs by taking phase terms equal to zero of each CIFN. We now utilize this information by applying the existing aggregation techniques to it. To check the application and effectiveness of the proposed method, we compare our approach to the IFAAWA operator [49], IFAAWG operator [49], IFAAWOA operator [49], IFAAOWG operator [49], IFWG operator [10] and IFWA operator [10]. The ranking results are shown in Table 10.
It is clear that our proposed methods, including CIIFAAWA and CIIFAAWG, have the same ranking as other existing methods, including IFWA [10], IFWG [10], IFOWA [10], and IFOWG [10]. In addition, the ranking result of IFAAWA [49], IFAAWG [49], IFAAOWA [49] and IFAAOWG [49] are slightly different from our proposed method. The ranking result of IFAAWA [49], IFAAWG [49], IFAAOWA [49] and IFAAOWG [49] operator is \(A_{4}\). But based on changing decision conditions, Table 10 shows that the best alternatives change with various operators.
Conclusions
In daily life, while dealing with the two-phase information in decision-making problems, the concept of CIIFS is one of the better tools as it gives experts more freedom compared to other existing theories. In this paper, we develop some new operators under the CIIFS environment, namely the CIIFAAWA operator, CIIFAAOWA operator, CIIFAAHA operator, CIIFAAWG operator, CIIFAAOWG operator and CIIFAAHG operator. Some properties of the developed operators are discussed and investigated. Moreover, we developed a decision-making method based on the proposed operators with a CIIFS setting. Further, for the application and effectiveness of the proposed method, we presented a numerical example for selecting the best hospital in the COVID-19 situation with complex interval-valued intuitionistic fuzzy data. Finally, a comparative study was conducted with the existing method and found that the proposed approach is more effective than other methods. Because the proposed method deal with the two-phase information while the evaluating values are complex-valued membership and non-membership degrees. The results also showed that the proposed operators are more flexible than the existing method because of the parameter k. In future, we will extend the present concept to other theories, such as complex Pythagorean fuzzy sets, complex q-rung orthopair fuzzy sets and complex interval-valued intuitionistic fuzzy soft sets.
Data Availability
The data used in this manuscript are hypothetical and can be used by anyone by just citing this article.
References
Garg H (2018) Some arithmetic operations on the generalized sigmoidal fuzzy numbers and its application. Granular Comput 3(1):9–25
Garg H (2018) Arithmetic operations on generalized parabolic fuzzy numbers and its application. Proc Natl Acad Sci India Sect A 88(1):15–26
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353
Kumar PS (2016) A simple method for solving type-2 and type-4 fuzzy transportation problems. Int J Fuzzy Logic Intell Syst 16(4):225–237
Kumar PS (2016) PSK method for solving type-1 and type-3 fuzzy transportation problems. IJFSA 5(4):121–146
Al-shami TM, Alcantud JCR, Mhemdi A (2023) New generalization of fuzzy soft sets:(a, b)-Fuzzy soft sets. AIMS Math 8:2995–3025
Ibrahim HZ, Al-Shami TM, Elbarbary OG (2021) (3, 2)-Fuzzy sets and their applications to topology and optimal choices. Comput Intell Neurosci (2021)
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 28:87–96
Xu ZS, Yager RR (2006) Some geometric aggregation operators based on intuitionistic fuzzy sets. Int J Gen Syst 35:417–433
Ye J (2009) Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment. Expert Syst Appl 36(3):6899–6902
Xu ZS (2010) A method based on distance measure for intervalvalued intuitionistic fuzzy group decision making. Inf Sci 180(1):181–190
Tan C, Chen X (2010) Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making. Expert Syst Appl 37(1):149–157
Xu ZS, Xia MM (2011) Induced generalized intuitionistic fuzzy operators. Knowl-Based Syst 24(2):197–209
Yu X, Xu ZS (2013) Prioritized intuitionistic fuzzy aggregation operators. Inf Fusion 14:108–116
Al-shami TM, Ibrahim HZ, Azzam AA, EL-Maghrabi AI (2022) SR-fuzzy sets and their weighted aggregated operators in application to decision-making. J Funct Space 2022:1–14
Al-shami TM, Mhemdi A (2023) Generalized Frame for Orthopair fuzzy sets:(m, n)-fuzzy sets and their applications to multi-criteria decision-making methods. Information 14(1):56
Al-shami TM (2022) (2, 1)-Fuzzy sets: properties, weighted aggregated operators and their applications to multi-criteria decision-making methods. Complex Intell Syst pp 1–19
Kumar PS (2020) Algorithms for solving the optimization problems using fuzzy and intuitionistic fuzzy set. Int J Syst Assur Eng Manag 11(1):189–222
Kumar PS (2018) A note on ‘a new approach for solving intuitionistic fuzzy transportation problem of type-2’. Int J Log Syst Manag 29(1):102–129
Kumar PS (2019) Intuitionistic fuzzy solid assignment problems: a software-based approach. Int J Syst Assur Eng Manag 10(4):661–675
Kumar PS (2020) Intuitionistic fuzzy zero point method for solving type-2 intuitionistic fuzzy transportation problem. Int J Oper Res 37(3):418–451
Kumar PS (2022) Computationally simple and efficient method for solving real-life mixed intuitionistic fuzzy 3D assignment problems. Int J Softw Sci Comput Intell. https://doi.org/10.4018/ijssci.291715
Atanassov K, Gargov G (1989) Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst 31(3):343–349
Xu ZS (2007) Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis 22(2):215–219
Garg H (2016) Generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision making. Comput Ind Eng 101:53–69
Garg H (2017) Novel intuitionistic fuzzy decision making method based on an improved operation laws and its application. Eng Appl Artif Intell 60:164–174
Yager RR (1988) On ordered weighted avergaing aggregation operators in multi-criteria decision making. IEEE Trans Syst Man Cybern 18(1):183–190
Garg H (2018) Some robust improved geometric aggregation operators under interval-valued intuitionistic fuzzy environment for multi-criteria decision -making process. J Ind Manag Optim 14(1):283–308
Wang W, Liu X (2013) The multi-attribute decision making method based on interval-valued intuitionistic fuzzy Einstein hybrid weighted geometric operator. Comput Math Appl 66:1845–1856
Liu P (2014) Some Hamacher aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making. IEEE Trans Fuzzy Syst 22(1):83–97
Chen SM, Cheng SH, Tsai WH (2016) Multiple attribute group decision making based on interval-valued intuitionistic fuzzy aggregation operators and transformation techniques of interval - valued intuitionistic fuzzy values. Inf Sci 1:367–368
Menger K (1942) Statistical metrics. Proc Natl Acad Sci USA 28:535
Deschrijver G, Cornelis C, Kerre EE (2004) On the representation of intuitionistic fuzzy t-norms and t-conorms. IEEE Trans Fuzzy Syst 12:45–61
Drossos CA (1999) Generalized t-norm structures. Fuzzy Sets Syst 104:53–59
Pap E, Bošnjak Z, Bošnjak S (2000) Application of fuzzy sets with different t-norms in the interpretation of portfolio matrices in strategic management. Fuzzy Sets Syst 114:123–131
Stamou GB, Tzafestas SG (2001) Resolution of composite fuzzy relation equations based on Archimedean triangular norms. Fuzzy Sets Syst 120:395–407
Wang S (2007) A fuzzy logic for the revised drastic product t-norm. Soft Comput 11:585–590
Garg H (2016) Generalized intuitionistic fuzzyinteractive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision making. Comput Ind Eng 101:53–69
Ullah K, Garg H, Gul Z, Mahmood T, Khan Q, Ali Z (2021) Interval valued T-spherical fuzzy information aggregation based on Dombi t-Norm and Dombi t-Conorm for multi-attribute decision making problems. Symmetry 13:1053
Ramot D, Milo R, Fiedman M, Kandel A (2002) Complex fuzzy sets. IEEE Trans Fuzzy Syst 10(2):171–186
Alkouri A, Salleh A (2012) Complex intuitionistic fuzzy sets, volume 1482, chapter 2nd International Conference on Fundamental and Applied Sciences, pp. 464–470
Alkouri AUM, Salleh AR (2013) Complex Atanassov’s Intuitionistic Fuzzy Relation. Abstract and Applied Analysis
Kumar T, Bajaj RK (2014) On complex intuitionistic fuzzy soft sets with distance measures and entropies. J Math
Rani D, Garg H (2017) Distance measures between the complex intuitionistic fuzzy sets and its applications to the decision - making process. Int J Uncertain Quantif 7(5):423–439
Rani D, Garg H (2018) Complex intuitionistic fuzzy power aggregation operators and their applications in multi-criteria decision-making. Exp Syst pp e12325
Garg H, Rani D (2018) Some generalized complex intuitionistic fuzzy aggregation operators and their application to multicriteria decision-making process. Arab J Sci Eng, pp 1–20
Aczel J, Alsina C (1982) Characterization of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgements. Aequationes Math 25(1):313–315
Babu MS, Ahmed S (2017) Function as the generator of parametric T-norms. Am J Appl Math 5:114–118
Senapati T, Chen G (2021) Aczel–Alsina aggregation operators and their application to intuitionistic fuzzy multiple attribute decision making. Int J Intell Syst
Senapati T, Chen G (2021) Novel Aczel–Alsina operations-based interval-valued intuitionistic fuzzy aggregation operators and their applications in multiple attribute decision-making process. Int J Intell Syst
Mahmood T, Ali Z, Baupradist S, Chinram R (2022) Complex intuitionistic fuzzy Aczel-Alsina aggregation operators and their application in multi-attribute decision-making. Symmetry 14(11):2255
Rani D, Grage (2019) Complex interval-valued intuitionistic fuzzy sets and their aggregation operators. Fund Inf 164(1):61–101
World Health Organization (2020a) Coronavirus (COVID-19) events as they happen. Accessed 13 July 2020. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/events-as-they-happen
World Health Organization (2020b) WHO coronavirus disease (COVID-19) dashboard. Accessed 13 July 2020. https://covid19.who.int/
Prompetchara E, Ketloy C, Palaga T (2020) Immune responses in COVID-19 and potential vaccines: lessons learned from SARS and MERS epidemic. Asian Pac J Allergy Immunol 38(1):1–9. https://doi.org/10.12932/AP-200220-0772
Spinelli A, Pellino G (2020) COVID-19 pandemic: perspectives on an unfolding crisis. Br J Surg 107(7):785–787. https://doi.org/10.1002/bjs.11627
Jaffery R (2020) Pakistan struggles to fight COVID-19. The Diplomat, 15 April 2020. https://thediplomat.com/2020/04/pakistan-struggles-to-fight-covid-19/
Acknowledgements
The authors would like to thank the contributions of the different partners of the SENATOR project (https://www.senatorproject.eu/ (accessed on 16 November 2022)).
Funding
This article was partially funded by the European Commission through the SENATOR project (H2020MG-2018-2020, RIA, project n. 861,540).
Author information
Authors and Affiliations
Contributions
All authors have contributed equally to this article.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest regarding the publication of the research article
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Khan, M.S.A., Jan, S.U., Jan, R. et al. Complex interval-valued intuitionistic fuzzy decision support system with application to COVID-19 healthcare facilities. Complex Intell. Syst. 9, 7103–7132 (2023). https://doi.org/10.1007/s40747-023-01090-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-023-01090-8