Introduction

The so-called imbalanced data refer to the extreme difference in the number of samples between classes in the data [1,2,3]. Both the noise hidden in the data and imbalance ratio between the classes have seriously negative effects on classification methods and classifiers [4]. From the view of data level, highlighting class attributes is likely to encounter those unpredicted traps due to noise can blur class attributes (so-called noise interference) [5]. Additionally, from the view of algorithm level, the noise has the capability to induce classifiers or classification methods to treat minority classes as noise [6]. Consequently, the above complex issue nature brings challenges for the classification aiming at imbalanced data containing the noise.

Recently, some efforts have been gained to address this issue. For instance, (i) sampling-based techniques addressing the classification of imbalanced data. The distribution between classes is balanced via applying oversampling techniques on the minority classes or adopting under-sampling techniques on the majority classes. Unfortunately, data distribution is likely to be damaged during sampling, causing incorrect classification results. Particularly, when the density of the noise is close to that of the minority classes, sampling techniques are embarrassed in noise resistance. (ii) Label noise-based methods, which apply spatial distribution of sample points to filter the label noise [4]. (iii) Fuzzy theory-based methods. Fuzzy approaches are used in classification tasks, decision-making tasks and security tasks. Such as, the fuzzy set method proposed by [7], the fuzzy set method in [8], the orthopair fuzzy sets method [9], and the method proposed in [10]. Additionally, to address noise interference, the [11] designed the optimal ARX models and the [12] robust Kalman filtering method.

Motivation

The study goal of this work is binary classification aiming at the imbalanced data containing noise. However, we are eager to demonstrate that the method can separate the noise from majority and minority classes, so as to provide the valuable insights for noise resistance, and there also supplies a reference for the development of the classifier. Certainly, the final motivation is to learn these boundaries separating the noise from majority and minority classes, which can promote the classified precision during classifying highly imbalanced data containing the noise. Here, this paper proposed the twin-hyperspheres with density fuzzy, namely DHS-DF. To suppress the interference created by the noise, from a data level of perspective, using the density fuzzy judges whether an unknown point is the noise. From an algorithm level point of view, the hypersphere itself has the natural ascendency to classify imbalanced data.

Contributions

The specific contributions of this work are summarized, as follows.

  1. (i)

    The twin-hyperspheres utilizing the density fuzzy is proposed to classify imbalanced data containing the noise. The fuzzy membership of importing the label density estimator, i.e., so-called the density fuzzy, quantizes the contributions provided by instance points, thereby suppressing noise resistance.

  2. (ii)

    These efforts gained by the density fuzzy are effectiveness in the identification of the noise; moreover, they also do not rely on specific classifiers or specific scenarios.

The rest of this paper is organized as follows. Related works are summarized in "Related works". Section "Methodology" describes the problem formalization, the theory and the implementation of the model. The details regarding experiment settings and the design are illustrated in "Experiment settings". "Results" section displays experiment results, and then we discuss the results in "Discussion". Finally, a conclusion is drawn in section "Conclusion".

Related works

Sampling-based approaches

Oversampling techniques and under-sampling techniques are used to handle the classification issue of imbalanced data. For example, the AB-Smote method [13]-based oversampling gains good classified results via paying more attention to boundary points. Neighborhood approach [14]-based under-sampling gain the advanced results through finding the nearest neighbor points. Similarly, the under-sampling approach implemented in [15]. Generally, sampling approaches need to generate the data points in minority classes or to remove the data points in majority classes. Considering binary classification, the number of points after sampling is twice in that of points in the minority class (i.e., under-sampling) or in the majority classes (i.e., oversampling) [4]. Consequently, sampling methods are prone to gain high classification accuracy, by contrary, they get poor efficiency in treating large-scale classification.

Label noise-based approaches

The [16] defines that label noise is these points with incorrect labels. For instance, the MadaBoost [17], AveBoost [18] and AveBoost2 [18] are proposed to reduce the sensitivity of boosting to label noise, which improve classification results in the presence of label noise. Similarly, including the A-Boost (average boosting) [19]. Additionally, the method-based semi-supervised learning in [20] is proposed to perform semi-supervised learning in the presence of label noise. Indeed, label noise-based approaches are sensitive to the density of labels so that the number of labels directly impacts their classification capabilities.

Deep learning-based approaches

Deep learning-based classification models have moved from theory to practice, and have been widely used in data classification, for example, the CNNs (convolutional neural networks) [21] are used for classification tasks and gain good classified precision. Deep architectures not only extract deeper representations of the input data by utilizing deep nonlinear network structures, but also have strong capabilities to learn the essential features of the input data. Therefore, many excellent deep learning-based classification models have been proposed for different application backgrounds, such as, the CNN using 3D convolution kernel [22], and the deep models proposed in [23]. Deep learning-based classification models may involve complex feature decomposition in the classification process [24, 25], which need to carry out more efforts on feature decomposition. As including, these classification models in [26,27,28].

Deep long-tailed learning attempts to learn deep neural network models from a training dataset with a long-tailed class distribution, where a small fraction of classes have massive samples and the rest classes are associated with only a few samples [29, 30]. For instance, Wang [31] et al. proposed a routing diverse experts (RDE) classifier to reduce model variance and bias, which allow the model to be less confused for long-tail classes. Cui et al. [32] and Jamal et al. [33] adopted deep long-tailed learning for classification. The imbalance of the classes causes deep models biased to head classes so as to perform poorly to tail classes [34]. Due to the lack of tail-class samples, it is more challenging to train a model for tail-class classification [35].

Fuzzy-based approaches

The fuzzy membership of a point can be used to judge whether the point provides contributions for the construction of classes [36]. If the point cannot provide the contributions, it allows to be regarded as the noise. For instance, Richhariya et al. [37] proposed a fuzzy least squares twin support vector machine (RFLSTSVM), because of utilizing the fuzzy membership function, RFLSTSVM achieves good noise immunity. Whereas, it needs to afford dear computation to solve a pair of system of linear equations. Similarly, the model with fuzzy implemented in [38].

Methodology

Problem formalization

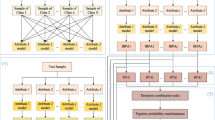
For an unknown point \(x_{k}\) in Fig. 1, it was assigned into the majority class, illustrated in Fig. 1a, or was classified into the minority class, as shown in Fig. 1b, or was treated as noise in Fig. 1c. However, these classification results cause some concern, (i) we are eager to how to avoid noise interference during classification. (ii) We pay attention to whether point \(x_{k}\) is noise.

Fig. 1
figure 1

Classification illustration of an unknown point. a, b Show that unknown point \(x_{k}\) was assigned into the majority class or the minority class. c Indicates unknown point \(x_{k}\) was treated as the noise. The majority classes and the minority classes are marked as purple squares, gold triangles, respectively. The red circle is an unknown point. The purple and black curves are the boundaries

Full size image

Several definitions are given, and Table 1 gives the details of symbols.

Table 1 Illustrations of symbols
Full size table

Definition 1

Imbalanced dataset \(D_{{{\text{im}}}} = \{ M^{ + 1} , N^{ - 1} , \varsigma^{0} \} \in \Re^{h}\) consists of majority class \(M^{ + 1}\), minority class \(N^{ - 1}\) and noise \(\varsigma^{0}\).\(\Re^{h}\) is the h-dimensional Euclidean space.\(|M^{ + 1} |\), \(|N^{ - 1} |\) are the number of the majority class and the minority class, respectively.\(|\varsigma^{0} |\) indicates noise ratio. If \(|\varsigma^{0} | = 0\) holds, this means that there is no noise in \(D_{im}\). By contrary, if \(|\varsigma^{0} | > 0\) holds, there is noise in \(D_{{{\text{im}}}}\).

Definition 2

The class centers of \(M^{ + 1}\) and \(N^{ - 1}\) are denoted as \(C_{M}^{ + 1}\) and \(C_{N}^{ - 1}\), respectively. The hypersphere of learning \(M^{ + 1}\) and the hypersphere of learning \(N^{ - 1}\) are defined as \(S_{M}^{ + 1}\), \(S_{N}^{ - 1}\), respectively, and as follows

$$ \begin{gathered} S_{M}^{ + 1} = \min R_{ + 1}^{2} + \delta_{ + 1} \sum\limits_{{i \in M^{ + 1} }} {\xi_{ + 1} } - \sum\limits_{{j \in N^{ - 1} }} {||\phi (x_{j} ) - {\mathbf{a}}_{ + 1} ||}^{2} \hfill \\ {\text{s.t.}} { ||}\varphi (x_{i} ) - {\mathbf{a}}_{ + 1} ||^{2} \le R_{ + 1}^{2} + \xi_{ + 1} \, , \, i \in M^{ + 1} , \hfill \\ \end{gathered} $$
(1)
$$ \begin{gathered} S_{N}^{ - 1} = \min R_{ - 1}^{2} + \delta_{ - 1} \sum\limits_{{j \in N^{ - 1} }} {\xi_{ - 1} } - \sum\limits_{{i \in M^{ + 1} }} {||\phi (x_{i} ) - {\mathbf{a}}_{ - 1} ||}^{2} \hfill \\ {\text{s.t.}} { ||}\varphi (x_{j} ) - {\mathbf{a}}_{ - 1} ||^{2} \le R_{ - 1}^{2} + \xi_{ - 1} \, , j \in N^{ - 1} , \hfill \\ \end{gathered} $$
(2)

where \(\delta_{ \pm 1} > 0\) are a penalty factor.\({\mathbf{a}}_{ \pm 1}\) and \(R_{ \pm 1}\) are the centers and radii of \(S_{M}^{ + 1}\), \(S_{N}^{ - 1}\).\(\xi_{ \pm 1} \ge 0\) are slack variables.\(\phi ( \cdot )\) is a nonlinear function.

Definition 3

Binary classification tasks on \(D_{im}\) is to train \(\Im (S_{M}^{ + 1} , S_{N}^{ - 1} )\) to learn class labels.\(\Im (S_{M}^{ + 1} , S_{N}^{ - 1} )\) is the proposed model, which consists of both \(S_{M}^{ + 1}\) and \(S_{N}^{ - 1}\).

Theory

The noise is suppressed through evaluating the contributions provided by each point for the training of \(S_{M}^{ + 1}\) and \(S_{N}^{ - 1}\).The contributions are quantized through calculating the fuzzy membership of each point in \(D_{im}\). Using the contributions employs the decision which a point should be regarded as noise or be assigned into corresponding classes. Therefore, this can address (i) and (ii) in "Problem formalization" from a data level of perspective. The details are as follows, illustrated in Fig. 2.

Fig. 2
figure 2

Illustrated chart of contribution assessment. The classification procedure of (a), (b), (c) correspond to Scenario (1), Scenario (2) and Scenario (3), respectively. The majority classes and the minority classes are marked as purple squares, gold triangles, respectively. Sample points are marked as red circles. The purple and black curves are the boundaries

Full size image

Given sample \(X = \{ x_{1} , x_{2} , x_{3} , ....\}\), we consider three types of scenarios regarding the contributions provided by a point, including Scenario (1), (2) and (3) in Fig. 2. To simplify, let point \(x_{1}\), \(x_{2}\), \(x_{3}\) be taken as an example, respectively.

Scenario (1). Point \(x_{1}\) is close to the class center \(C_{M}^{ + 1}\) of \(M^{ + 1}\), then it is considered to provide great contributions for the training of \(S_{M}^{ + 1}\). Therefore, point \(x_{1}\) is assigned into \(M^{ + 1}\), and gains a majority class label \(+ 1\), illustrated in Fig. 2a.

Scenario (2). Point \(x_{2}\) is close to the class center \(C_{N}^{ - 1}\) of \(N^{ - 1}\), then it provides major contributions for the training of \(S_{N}^{ - 1}\), so that it can be classified into \(N^{ - 1}\) in Fig. 2b, and gains a minority class label.

Scenario (3). Point \(x_{3}\) just provides a weak contribution for the training of either \(S_{M}^{ + 1}\) or \(S_{N}^{ - 1}\), unfortunately, point \(x_{3}\) is treated as noise, as shown in Fig. 2c.

There needs to determine how to evaluate the so-called far distance or near distance mentioned in Fig. 2. Let us define that the distance between point \(x_{i} \in X\) and \(C_{M}^{ + 1}\) is \(d_{M}^{i}\), i = 1, 2, 3, …, and that the distance between point \(x_{i}\) and \(C_{N}^{ - 1}\) is \(d_{N}^{i}\).The average distance between sample X and \(C_{M}^{ + 1}\), \(C_{N}^{ - 1}\) is \(\overline{d}_{M}^{X}\) and \(\overline{d}_{N}^{X}\), respectively. For example, taking point \(x_{1}\) in Fig. 2a as an example, \(d_{M}^{1}\) must be less than \(d_{N}^{1}\) and \(\overline{d}_{M}^{X}\) at the same time, which is the so-called near distance appeared by point \(x_{1}\) and \(C_{M}^{ + 1}\). By contrast with near distance, \(d_{N}^{1}\) is greater than \(\overline{d}_{N}^{X}\), which is the so-called far distance exhibited by point \(x_{1}\) and \(C_{N}^{ - 1}\). Similarly, for point \(x_{2}\) in Fig. 2b and point \(x_{3}\) in Fig. 2c.

Calculation of density fuzzy

The distance between point \(x_{i}\) and \(C_{M}^{ + 1}\) is calculated by Eq. (3)

$$ d_{M}^{i} = ||x_{i} - C_{M}^{ + 1} ||^{2} . $$
(3)

Similarly, the distance between \(x_{i}\) and \(C_{N}^{ - 1}\) is given in Eq. (4), where \(\kappa\) is a kernel function.

$$ d_{N}^{i} = ||x_{i} - C_{N}^{ - 1} ||^{2} . $$
(4)

The average distance between sample X and \(C_{M}^{ + 1}\), \(C_{N}^{ - 1}\) is, respectively, calculated, as follows:

$$ \overline{d}_{M}^{X} = \frac{1}{\alpha - 1}\sum\limits_{i = 1}^{\alpha } {(d_{M}^{1} + d_{M}^{2} + , \ldots , d_{M}^{i - 1} } , d_{M}^{i + 1} , d_{M}^{i + 2} , \ldots , d_{M}^{\alpha } ), $$
(5)
$$ \overline{d}_{N}^{X} = \frac{1}{\beta - 1}\sum\limits_{i = 1}^{\beta } {(d_{N}^{1} + d_{N}^{2} + , \ldots , d_{N}^{i - 1} } , d_{N}^{i + 1} , d_{N}^{i + 2} , \ldots , d_{N}^{\beta } ). $$
(6)

The calculation of the proposed fuzzy membership \(f( \cdot )\) is as follows

$$ f( \cdot ) = \left\{ \begin{gathered} 1 - 1/\sqrt {d_{M}^{i} + o_{f} } {\text{ if }}d_{M}^{i} < d_{N}^{i} {\text{ and }}d_{M}^{i} < \overline{d}_{M}^{X} \hfill \\ 1 - 1/\sqrt {d_{N}^{i} + o_{f} } {\text{ if }}d_{N}^{i} < d_{M}^{i} {\text{ and }}d_{N}^{i} < \overline{d}_{N}^{X} \hfill \\ - \infty {\text{ otherwise, }} \hfill \\ \end{gathered} \right. $$
(7)

where \(o_{f} \ge 1\) is a constant item to avoid the situation where the denominator appears zero.\(- \infty\) is a very small value specified by the users, e.g., \(- \infty = 1{\text{e}} - 7\).

To determine \(C_{M}^{ + 1}\) in Eq. (3) and \(C_{N}^{ - 1}\) in Eq. (4), the method of estimating class label density used in the [39] is selected, which estimates the density of class labels from a probabilistic view. Since there exists the difference of the density between majority classes and minority classes, the method is suitable to be used to determine class center. As follows:

$$ C_{M}^{ + 1} = \sum\limits_{k} {I(z_{k} \in M^{ + 1} )} , $$
(8)
$$ C_{N}^{ - 1} = \sum\limits_{j} {I(y_{j} \in N^{ - 1} )} , $$
(9)

where \(\sum I\) is a density estimator, which is used to estimate label density of the majority class and the minority class, respectively. For the calculation of \(\sum I\), please refer to the Proposition 1 in [39]. According to the above derivation, it can be known that the density estimator was introduced into the fuzzy membership, i.e., namely the proposed dense fuzzy.

Evaluation of contributions

The \(f( \cdot )\) is used to quantize the contributions. For above Scenarios (1), (2) and (3), the contributions created by point \(x_{i}\) are illustrated, respectively. As following:


Manner (I). If \(d_{M}^{i} < d_{N}^{i}\) and \(d_{M}^{i} < \overline{d}_{M}^{X}\), i.e., Scenario (1) in Fig. 2a, \(f( \cdot ) = 1 - 1/\sqrt {d_{M}^{i} + 1}\) evaluates the contributions provided by point \(x_{i}\) for the training of \(S_{M}^{ + 1}\). Here, an example was given to interpret the details. Assuming that \(o_{f} = 1\), \(d_{M}^{i} = 4\), \(d_{N}^{i} = 10\) and \(\overline{d}_{M}^{X} = 6\). Clearly, \(d_{M}^{i} < d_{N}^{i}\) and \(d_{M}^{i} < \overline{d}_{M}^{X}\) hold, so that \(x_{i}\) can provide the contributions for the training of \(S_{M}^{ + 1}\). Consequently, the contribution \(\Xi (x_{i} )\) is \(1 - 1/\sqrt {d_{M}^{i} + 1} = 1 - 1/\sqrt {4 + 1} = 0.8\), i.e., \(\Xi (x_{i} ) = 0.8.\)


Manner (II). If \(d_{N}^{i} < d_{M}^{i}\) and \(d_{N}^{i} < \overline{d}_{N}^{X}\), i.e., Scenario (2) in Fig. 2b, \(1 - 1/\sqrt {d_{N}^{i} + 1}\) evaluates the contributions provided by point \(x_{i}\) for the training of \(S_{N}^{ - 1}\). Similarly, assuming that \(d_{M}^{i} = 14\), \(d_{N}^{i} = 9\) and \(\overline{d}_{N}^{X} = 12\). Clearly, \(d_{N}^{i} < d_{M}^{i}\) and \(d_{N}^{i} < \overline{d}_{N}^{X}\) hold, therefore, \(x_{i}\) can provide the contributions for the training of \(S_{N}^{ - 1}\). The contribution is \(1 - 1/\sqrt {d_{N}^{i} + 1} = 1 - 1/\sqrt {9 + 1} = 0.9\), i.e., \(\Xi (x_{i} ) = 0.9\).


Manner (III). Otherwise, i.e., Scenario (3) in Fig. 2c, point \(x_{i}\) is treated as noise, because this scenario provides little or no contribution for the training of \(S_{M}^{ + 1}\) or \(S_{N}^{ - 1}\). For example, for this scenario \(d_{M}^{i} = 14\), \(d_{N}^{i} = 9\) and \(\overline{d}_{N}^{X} = 6\), although \(d_{N}^{i} < d_{M}^{i}\) holds, \(d_{N}^{i} < \overline{d}_{N}^{X}\) does not hold, therefore, point \(x_{i}\) is treated as the noise, and \(f( \cdot ) = - \infty \, \) assesses the contributions of the noise point \(x_{i}\), i.e., \(\Xi (x_{i} ) = 1{\text{e}} - 7\). In this scenarios, point \(x_{i}\) is closer to the minority class, compared with the majority class, i.e., \(d_{N}^{i} < d_{M}^{i}\), however, point \(x_{i}\) is still far away from the class center of the minority class, i.e., \(d_{N}^{i} > \overline{d}_{N}^{X}\), so point \(x_{i}\) just creates little contribution for the training of \(S_{N}^{ - 1}\). Certainly, also including another scenario, \(d_{M}^{i} = 4\), \(d_{N}^{i} = 10\) and \(\overline{d}_{M}^{X} = 3\). Similarly, \(d_{M}^{i} = 20\), \(\overline{d}_{M}^{X} = 13\) and \(d_{N}^{i} = 20\), \(\overline{d}_{N}^{X} = 16\).

Noting that regarding the Manner (I), (II) and (III), there displays a relative comparison. For an unknown point \(x_{i}\), we are prone to that it can create great contributions to which of the two hyperspheres, so the relative comparison is considered.

Model \(\Im (S_{M}^{ + 1} , S_{N}^{ - 1} )\)

Fuzzy membership \(f( \cdot )\) in Eq. (7) is added into hypersphere \(S_{M}^{ + 1}\), \(S_{N}^{ - 1}\), so Eqs. (1) and (2) can be converted into Eqs. (10), (11), respectively. As follows:

$$ \begin{gathered} S_{M}^{ + 1} = \min R_{ + 1}^{2} + \delta_{ + 1} \sum\limits_{{i \in M^{ + 1} }} {f( \cdot ) * \xi_{ + 1} } - \sum\limits_{{j \in N^{ - 1} }} {||\phi (x_{j} ) - {\mathbf{a}}_{ + 1} ||}^{2} \hfill \\ {\text{s.t.}}\,\,{ ||}\varphi (x_{i} ) - {\mathbf{a}}_{ + 1} ||^{2} \le R_{ + 1}^{2} + \xi_{ + 1} \, , \, i \in M^{ + 1} , \hfill \\ \end{gathered} $$
(10)
$$ \begin{gathered} S_{N}^{ - 1} = \min R_{ - 1}^{2} + \delta_{ - 1} \sum\limits_{{j \in N^{ - 1} }} {f( \cdot ) * \xi_{ - 1} } - \sum\limits_{{i \in M^{ + 1} }} {||\phi (x_{i} ) - {\mathbf{a}}_{ - 1} ||}^{2} \hfill \\ {\text{s.t.}}\,\,{ ||}\varphi (x_{j} ) - {\mathbf{a}}_{ - 1} ||^{2} \le R_{ - 1}^{2} + \xi_{ - 1} \, , j \in N^{ - 1} . \hfill \\ \end{gathered} $$
(11)

As such, Eqs. (10) and (11) are the twin-hyperspheres with density fuzzy, that is, the proposed model \(\Im (S_{M}^{ + 1} , S_{N}^{ - 1} )\) is composed of Eqs. (10) and (11). The implementation of \(\Im (S_{M}^{ + 1} , S_{N}^{ - 1} )\) is given in Algorithm 1 and Algorithm 2.

Algorithm 1 displays the training of \(\Im (S_{M}^{ + 1} , S_{N}^{ - 1} )\).Training sample \(X = \{ x_{1} , \ldots , x_{i} , \ldots , \}\) is used for the input of \(\Im (S_{M}^{ + 1} , S_{N}^{ - 1} )\).The final input of \(\Im (S_{M}^{ + 1} , S_{N}^{ - 1} )\) is the learned class label \(\{ \ldots , {\text{label}}_{j}^{ + 1} , \ldots , {\text{label}}_{k}^{ - 1} , \ldots , \}\). First, the parameters are initialized in Step 1. We configured a greater initialization value for the \(\overline{d}_{M}^{X}\) and \(\overline{d}_{N}^{X}\). The procedure of Step 2 and Step 6 displays the assigned process of each point in \(X\) through calculating the corresponding contributions. The details are as follows.

Utilizing Eqs. (3), (4) calculates the distance between point \(x_{i}\) and \(C_{M}^{ + 1}\), \(C_{N}^{ - 1}\), denoted as \(d_{ + 1}^{i}\) and \(d_{ - 1}^{i}\), respectively, illustrated in Step 4 and Step 5 in Algorithm 1. Thereafter, Step 6 in Algorithm 1 invokes Algorithm 2 to calculate the fuzzy membership of point \(x_{i}\). The calculated description is below.

The output of Algorithm 2 is class center and class labels. For point \(x_{i}\), if \(d_{ + 1}^{i} < d_{ - 1}^{i}\) and \(d_{ + 1}^{i} < \overline{d}_{M}^{X}\) holds, i.e., Scenario (1), using \(f( \cdot ) = 1 - 1/\sqrt {d_{M}^{i} + o_{f} }\) in Eq. (7) calculates the fuzzy membership. Point \(x_{i}\) is assigned into the majority class \(M^{ + 1}\), and gains a majority class label \({\text{label}}_{i}^{ + 1}\). Using Eq. (8) calculates the class center \(C_{M}^{ + 1}\) of the majority class \(M^{ + 1}\); meanwhile, using Eq. (5) updates the average distance \(\overline{d}_{M}^{X}\) between sample \(X\) and \(C_{M}^{ + 1}\). The quantized contributions, i.e., the value of \(f( \cdot )\), are used for the training of hypersphere \(S_{M}^{ + 1}\), and then the class center \(C_{M}^{ + 1}\) and the learned class label \({\text{label}}_{i}^{ + 1}\) are returned, illustrated in the procedure between Step 2 and Step 16 in Algorithm 2. Similarly, for the procedure of between Step 17 and Step 31 in Algorithm 2, i.e., Scenario (2), if point \(x_{i}\) is assigned into the minority class, the corresponding contribution is used for the training of hypersphere \(S_{N}^{ - 1}\). Otherwise, point \(x_{i}\) is treated as noise, i.e., Scenario (3), the fuzzy membership is calculated using \(f( \cdot ) = - \infty\), as shown in Step 32–Step 35 in Algorithm 2.

According to the returned results in Step 6 in Algorithm 1, these learned class labels are obtained in Step 7 in Algorithm 1. The training of the model is terminated once each point in sample is judged, illustrated in Step 8 to Step 11 in Algorithm 1. Finally, the learned class labels are outputted in Step 12 in Algorithm 1.

figure a
figure b

Experiment settings

Illustrations of datasets

Five imbalanced datasets were synthesized using random distribution, denoted as S1–S5, and Gaussian noise with different ratio was added into the five synthetic datasets, as shown in Table 2. There did not consider specific distribution to synthesize the dataset, since those data distributions in applications are usually complex and unknown. Using the random distribution is to objectively analyze classification performance of the proposed model.

Table 2 The five synthetic datasets
Full size table

Five UCI datasets with different imbalanced ratio were also used, denoted as U1–U5, illustrated in Table 3. To verify the ability of the model to resist noise, without changing the attributes of the five UCI datasets, Gaussian noise with different noise ratio was added into them. The noise ratio is increased as imbalanced ratio (IR) increases. The UCI datasets adding the Gaussian noise are named as UG6–UG10. The details are displayed in Table 4.

Table 3 The five UCI datasets
Full size table
Table 4 The five UCI datasets with noise
Full size table

Assessment metrics and comparison models

Evaluated metrics are accuracy metric and F1-score, as follows

$$ {\text{Accuracy}} = \frac{{\text{TP + TN}}}{{\text{TP + FP + TN + FN}}}, $$
(12)
$$ {\text{F1-score}} = \frac{{2{\text{TP}}}}{{2{\text{TP}} + {\text{FP}} + {\text{FN}}}}, $$
(13)

where TP, TN are the indicator that correctly predicts the number of the minority class and the majority class, respectively. FP is the indicator that predicts the majority class as the number of the minority class. FN is the indicator that predicts the minority class as the number of the majority class.

The AB-Smote [13] model-based sampling, MadaBoost [17] model-based label noise, CNNs [21] model-based deep learning, RDE [31] model-based deep long-tailed learning and RFLSTSVM [37] model-based fuzzy are used for comparisons. Additionally, the benchmark model, namely DHS-B, was designed referring as our DHS-DF. DHS-B has the same structure and parameters as DHS-DF, while it does not apply the proposed density fuzzy. This is to analyze the effects of the proposed density fuzzy on resisting noise.

Regarding the selection of parameters, RBF (radial basis function) is used for the DHS-B and DHS-DF, and the kernel parameter was tuned in rang of {0.1, 0.3, 0.5, 0. 7, 1, 1.5, 2, 3, 5}. For these parameters of competitors, there applied the parameters observed in the corresponding literature. We implemented the corresponding algorithms of these models by Python 3.8 in Tensorflow framework on the Linux system.

Experiment description

Experiment (i), to observe the results of separating noise from minority classes and majority classes, these models were run on the five synthetic datasets S1–S5, then the learned classification boundaries were visualized.

Experiment (ii), to test the ability of resisting noise, these models were run on the five UCI datasets UG6–UG10, and then the results were analyzed by using Accuracy and F1-score metrics.

Experiment (iii), to test classification ability on imbalanced datasets, these models were run on the five UCI datasets U1–U5, then, using accuracy and F1-score metrics assess the classification results.

Ablation experiment. To demonstrate that the proposed density fuzzy can resist noise, the ablation experiments were also implemented.

Results

Classification boundaries

The results in Fig. 3 show that the proposed DHS-DF outperforms the competitors and the benchmark model. In terms of the seven models (DHS-DF, DHS-B and the five competing models), although the capabilities of resisting noise decrease quickly as noise ratio increases, the dropped tendency of DHS-DF is slower than that of the competitors and the benchmark model DHS-B.

Fig. 3
figure 3

Classification results on the five synthetic datasets. a Displays the accuracy metric. b Displays the F1-score metric. The measurement results of the two metrics drop as noise ratio increases

Full size image

To observe the results of separating noise from the majority and minority classes, Fig. 4 visualized the classification boundaries learned by these models on the synthetic dataset S5 when noise ratio is 90%. In this case, it can be seen that DHS-DF still learned the desired boundaries so that it can separate noise from minority and majority classes well, correspondingly, DHS-DF gained the classification precision well. By contrary, the competitors and benchmark model learned poor classification boundaries, however, the competitor with fuzzy RFLSTVM outperforms the four competitors without fuzzy and the benchmark model DHS-B.

Fig. 4
figure 4

Visualization of classification results on the synthetic dataset S5. The minority classes and majority classes are marked as red circles, blue circles, respectively. The noise is marked as yellow squares. The black curves are the learned boundaries

Full size image

The results of ablation experiments in Fig. 5 shown that DHS-DF and RFLSTSVM with fuzzy are significantly superior to these models without fuzzy (DHS-B, AB-Smote, MadaBoost, CNNs, RDE) in terms of classification performance. DHS-DF has more advantages than RFLSTSVM. However, compared the benchmark model DHS-B with the competitors without fuzzy, some of they win over DHS-B on most datasets. These indicate that the benefit of resisting noise with fuzzy is greater than that of with the model structures itself. Clearly, these models with fuzzy can gain more efforts than these without fuzzy in terms of noise resistance.

Fig. 5
figure 5

Comparisons between fuzzy and non-fuzzy on the five synthetic datasets. The models with fuzzy are marked as the symbol +. Otherwise, they are marked as the symbol −. a Displays the accuracy metric. b Displays the F1-score metric

Full size image

Ability of noise resistance

The results in Fig. 6 show that DHS-DF is still a winner on the five datasets UG6–UG10 in terms of noise resistance. Even on the dataset UG10 with highly imbalanced ratio (IR = 87.8:1) and with high noise ratio (\(|\varsigma^{0} | = 90\%\)), DHS-DF gains the advanced classification results, i.e., accuracy = 0.611, F1-socre = 0.623, observing the competitors; however, they get the poor classification results, and the accuracy and F1-score all are below 0.5. Hence, on datasets UG6–UG10, DHS-DF gains the advanced classification results of being similar to these on the five synthetic datasets.

Fig. 6
figure 6

Classification results on the datasets UG6–UG10. a Displays the accuracy metric. b Displays the F1-score metric. The measurement results of the two metrics drop as noise ratio increases

Full size image

The results of ablation experiments in Fig. 7 show that these models with fuzzy are superior to these without fuzzy in suppressing noise. These comparison results confirm that they are consistent with those in Fig. 5. Together, these results in Figs. 3, 4, 5, 6 and 7 demonstrate that fuzzy indeed promotes these models to resist noise.

Fig. 7
figure 7

Comparisons between fuzzy and non-fuzzy on the datasets UG6–UG10. The models with fuzzy are marked as the symbol +. Otherwise, they are marked as the symbol −. a Displays the accuracy metric. b Displays the F1-score metric

Full size image

Classification ability

Figure 8 displays the classification results of these models on the five UCI datasets U1–U5 without noise. DHS-DF outperforms the six models on most datasets, e.g., datasets U1, U3, U4 and U5. Especially, on highly imbalanced dataset U6 (IR = 87.8:1), DHS-DF has outstanding ascendency than the six models. Additionally, the competitor with fuzzy RFLSTSVM wins over the four competitors without fuzzy AB-Smote, MadaBoost, CNNS and RDE (noting DHS-B is the benchmark model) on the three datasets U1, U2 and U5. However, in Fig. 7, RFLSTSVM outperforms the four competitors without fuzzy and the benchmark model DHS-B on the five datasets UG6–UG10 with noise. Together, these indicate that fuzzy can suppress noise.

Fig. 8
figure 8

Classification results on UCI datasets without noise. The models with fuzzy are marked as the symbol +. Otherwise, they are marked as the symbol −. a Displays the accuracy metric. b Displays the F1-score metric

Full size image

Discussion

Insights

Compared with the six models, the proposed model shows ascendency since an unknown point should be assigned into majority or minority classes, or be treated as the noise, depending on the contributions that the point provides for the hypersphere training. The contributions provided by the point for the hypersphere training can be assessed by Eq. (7). Then, the decision on which points are noise can be made based on the contributions provided by points. Therefore, from a data level of view, this can address the issue of noise interference. Overall, the proposed model gains good classification accuracy and shows better noise resistance on imbalanced datasets with noise.

Cost-sensitive learning aims at rebalancing classes by adjusting loss values for different classes during training [40], including class-level re-weighting and class-level re-margining. As for class-level re-weighting, the most methods are to directly utilize label frequencies of training samples for loss re-weighting, namely weighted softmax loss [41]. The [42] proposed that the label frequencies are used to adjust model predictions during training, so as to alleviate the bias of class imbalance by using the prior knowledge, called balanced softmax. To disentangle the learned model from the long-tailed training distribution, Hong et al. [29] applied a label distribution to disentangle loss, and indicate that models can adapt arbitrary testing class distributions if the testing label frequencies are available. Unlike the [29], Cui et al. [32] introduced a concept of effective number to approximate the expected sample number of different classes, rather than using label frequencies. So-called the effective number refers to an exponential function of the training sample number. To address class imbalance, the [32] enforces a new class-balanced weighting item that is inversely proportional to the effective number of classes, also including equalization loss [43], seesaw loss [44], and adaptive class suppression loss [45].

Model limitations

Certainly, the proposed model also has disadvantages. During the training of the model, the number of iterations relies on data dimensionality Id and data volume Iv, i.e., c1*Id + c2* Iv, where c1 and c2 are constants. The model depends on the fuzzy membership function in Eq. (7), when large-scale data are used as the training set, the convergence epochs of our model may be increased. Whereas, this does not imply that our model cannot converge, but the training epochs become long. In addition, Eqs. (8) and (9) invoke the density estimator \(\sum I\) in [39], due to \(\sum I\) has high computational complexity, the overall computational complexity of the proposed model is increased. Therefore, the time complexity T(O) of the model is n3 > T(O) > n2.

Conclusion

The noise hidden in the data has negative effects on classification capabilities of those classifiers. To address the issue of noise interference, this paper proposed the twin-hyperspheres model for binary classification on imbalanced datasets containing noise. Utilizing the proposed density fuzzy, the noise is effectively suppressed during classification. Results on the synthetic datasets and UCI datasets containing Gaussian noise show that the proposed model outperforms the competitors in noise resistance and classification accuracy, moreover, the classification boundaries learned by the proposed model are better than these learned by the competitors. These efforts gained by the density fuzzy are not only effectiveness in suppressing noise, but also they do not rely on specific classifiers or specific scenarios. In future work, we will look at addressing multi-classification on those datasets containing noise. Due to multi-classification tasks are more complex than binary classification tasks, classification capabilities of those classifiers are challenged.