Introduction

Data envelopment analysis (DEA) is a non-parametric method for evaluating the performance of decision-making units (DMUs) with multiple inputs and outputs. It was first introduced by Charans et al. [6] and has been widely extended over the past 3 decades. DEA evaluates each unit from an optimistic standpoint and obtains the best relative efficiency of the unit under evaluation by maximizing its relative efficiency compared to remaining decision-making units and by determining the most desirable weights. Any unit with an optimistic efficiency score of one will be efficient; otherwise, it will be inefficient. Such a view causes more than one unit to be evaluated as efficient unit, and therefore, it is not possible to distinguish between such units.

To improve the diagnostic power of DEA, some researchers have also considered performance appraisal from a pessimistic perspective. In this regard, Wang and Lu [31] first introduced the best and worst relative efficiency of each DMU by introducing ideal point (IP) and anti-ideal point (AIP). Then, by combining optimistic efficiency and pessimistic efficiency, they obtained a relative closeness index to the ideal unit for each unit as its final evaluation index. Finally, they used the TOPSIS approach for the total ranking of units. Wu [33] modified the approach proposed by Wang and Lu [31] by overcoming the shortcomings of the pessimistic model. On the other hand, DEA assigns different weights to each unit, making DMUs not ranked and compared on the same basis. To address this issue, researchers proposed the use of common-weight methods first introduced by Cook et al. [8] that assign the same weights to each of the indicators of DMUs and provide a reasonable criterion for evaluating and comparing units.

The classical DEA models evaluate units based on desired inputs and outputs. However, in some real applications, there are undesirable factors in the production process that have a notable impact on evaluation discussion. For instance, in airport evaluation, the number of delayed flights is considered as an undesirable output and should be minimized to improve the airport’s performance. To this end, there are various approaches to dealing with undesirable outputs, which fall into two main categories: direct and indirect approaches. In the indirect approach, the undesirable outputs are changed to the desirable ones after linear or nonlinear transformations, and in the direct approach, the undesirable outputs are entered directly into the DEA models. One of the main approaches to deal with these factors has been suggested by Korhanen and Lopestic [21] in the way that efficiency was considered as a ratio with negative weights for undesirable outputs. Puri and Yadav [25] then enumerated the shortcomings of this approach and presented a modified model for handling undesirable outputs.

Conventional DEA models are widely used to evaluate the relative efficiency of similar DMUs, such as universities, hospitals, and banks. However, they are unable to accurately evaluate the efficiency of DMUs in the presence of uncertainty. To address this issue, fuzzy DEA models can provide an appropriate solution. In fact, the main assumption in DEA models is that the data are accurate; however, in the real world, data are often presented in terms such as good or bad and is usually inaccurate. Therefore, the performance evaluation with conventional methods involving such data can lead to errors in the evaluation process. In such a situation, the conventional DEA models cannot accurately measure the performance of DMUs. In order to make sensible decisions and be more in line with the real world, it is essential to use fuzzy logic tools to achieve the ultimate goals that lead to the fuzzy DEA (FDEA). There are several approaches to handle the fuzzy data in the DEA literature, the most important of which are alpha-cut and fuzzy arithmetic approaches.

The methods proposed by Kao and Liu [16] and Saati et al. [26] are the two main methods based on the alpha-cut approach for solving FDEA models. Kao and Liu’s [16] method transforms each FDEA model into linear models based on the principle of the expander and alpha-cuts, and obtains the upper and lower bounds of the alpha-cut of the efficiency membership functions. In addition, Kao and Liu [17] introduced another approach for ranking units with fuzzy data that does not require a membership function with a precise form. Their proposed approach for two-stage structures consisting of fuzzy data was used by Lao and Liu [18]. Lozano [22] developed the same approach and proposed another method for finding fuzzy efficiency in two-stage systems. Saati et al. [26] method converted each FDEA model into an interval linear model based on alpha-cut and then converted the resulting interval problem into a linear programming problem for the given alpha. Saati and Memariani [27] developed this approach and proposed an approach to determine the common sets of weight (CSW) in fuzzy data envelopment analysis models. Hatami-Marbini et al. [14] developed their approach using fuzzy ideal and anti-fuzzy units. Puri and Yadav [25] used the alpha-cut approach to compute the efficiency in a fuzzy environment with undesirable outputs. Using the concept of the ideal point, Kazemi et al. [19] used this approach to determine CSWs in fuzzy models containing non-discretionary factors. Fathi and Farzipour Saen [12] evaluated the performance of supply chain by combining dual boundaries and common-weight sets in FDEA. Tabatabaei et al. [28] developed the alpha-cut approach for solving the fuzzy relational network model based on the CWS method. Abbasi Shureshjani et al. [1] extended the alpha-cut approach for evaluating the performance of DMUs in fuzzy two-stage DEA models. Tavssoli et al. [20] developed this approach for assessing the efficiency of Iran’s EDNs components with sustainability considerations in fuzzy network DED model. Eydi and Rastgra [11] have used the alpha-cut technique in fuzzy DEA models to select an appropriate third-party logistics provider considering dual role data. However, this approach cannot provide a fuzzy efficiency score of each DMU directly and only approximates the fuzzy efficiency score of each DMU from the given alpha level.

Moreover, the most important weakness of the alpha-cut method for computing the fuzzy efficiency is that a sequence of linear models must be solved based on a set of different alpha-cuts, which significantly increases the computation complexities. To overcome this shortcoming, the fuzzy arithmetic approach in FDEA models has been proposed by Wang et al. [32]. Since this approach solves three different fractional DEA models to find the fuzzy efficiency components, it obtains different weights for the units. To solve this problem, Bardaj et al. [5] proposed a new approach based on a fractional objective function and linear constraints. In addition, Azar et al. [4] generalized the fuzzy arithmetic approach to the additive model and used it to find CWS in the FDEA model to calculate the fuzzy efficiency of units and rank them. Kachuei et al. [15] developed this method for finding fuzzy efficiency in the presence of undesirable outputs. Ebrahimnejad and Amani [10] used the concept of fuzzy ideal point (FIP) and fuzzy anti-ideal point (FAIP) to evaluate the units in the FDEA model in the presence of undesirable outputs. Addressing the weaknesses of Wang et al.’s [32] method, they extended the fuzzy arithmetic approach to find the fuzzy efficiency of FIP and FAIP in the presence of undesirable outputs. Then, they ranked all DMUs by finding the best and worst relative efficiency of each unit in the presence of undesirable outputs. However, the most important weakness of this method is that it requires considerable computational effort to find the best and worst fuzzy efficiency of each DMU.

As far as we know, in traditional DEA models, each unit is evaluated with the most favorable weight. Although the selection of different and flexible weights for the input and output of DMUs is one of the advantages of DEA models, it hinders the comparison between units with the same efficiency scores. To address this issue, a technique has been proposed in which a set of common weights is determined and the efficiency of all units is maximized. In this way, the comparison between DMUs with the same efficiency scores is possible. In this paper, the proposed approach of Ebrahimnejad and Amani [10] is generalized so that by finding common weights, the best and worst relative efficiencies of each unit can be calculated by solving only one linear model, leading to a significant reduction in calculations. The advantages of using the common-weight DEA method based on the fuzzy arithmetic approach are reduced computational complexities and the ability to evaluate the best and worst fuzzy efficiencies equitably on the same base. The main contributions of this study are summarized as follows:

  • In this study, a novel model for the overall assessment of DMUs with undesirable factors in the fuzzy environment based on a common set of weights is developed.

  • The proposed method is based on fuzzy arithmetic approach. In addition, a set of common weights is derived from two optimistic and pessimistic perspectives, which improves the power of discrimination between units.

  • In contrast to existing methods, the efficiency of all units is measured on the same scale, resulting in more accurate rankings.

  • Compared to the existing methods, there is less computational complexity and also fewer linear models are solved.

The rest of the paper is organized as follows. “Preliminaries” first reviews the basic concept of fuzzy set theory and defines fuzzy ideal and anti-ideal points and formulates the fuzzy DEA models based on the undesirable outputs. This section also provides an overview of the existing fuzzy arithmetic approach for solving FDEA models based on fuzzy virtual DMUs. “The proposed method” presents our proposed common-weight method based on the developed fuzzy arithmetic approach to measure the best and worst fuzzy efficiency of decision-making units consisting of undesirable outputs. “Numerical example” presents a numerical example taken from the literature to illustrate the proposed method. Finally, conclusions and future research scopes are provided in “Conclusions”.

Preliminaries

Some concepts such as fuzzy set theory and fuzzy data envelopment analysis are reviewed in this section [4, 10, 15, 32].

Fuzzy set theory

Definition 1.

If the membership function for the fuzzy number \(\tilde{C} = (c^{L} ,c^{M} ,c^{U} )\) is defined as follows:

$$ \begin{array}{*{20}c} {\mu_{{\tilde{C}}} (x) = \left\{ \begin{gathered} \frac{{x - c^{L} }}{{c^{M} - c^{L} }},\,\,\,c^{L} \, \le x\, \le c^{M} , \\ \frac{{c^{U} - x}}{{c^{U} - c^{M} }},\,\,\,c^{M} \, \le x\, \le c^{U} . \\ \end{gathered} \right.} & {\,\,} \\ \end{array} $$
(1)

Then, the number \(\tilde{C}\) is called a triangular fuzzy number.

Definition 2.

A triangular fuzzy number \(\tilde{C} = (c^{L} ,c^{M} ,c^{U} )\) is said to be a non-negative (positive) fuzzy number if and only if \(c^{L} \ge 0\) (\(c^{L} > 0\)).

Definition 3.

Arithmetic operations such as addition, subtraction, multiplication, and division for two triangular fuzzy numbers \(\tilde{C} = (c^{L} ,c^{M} ,c^{U} )\) and \(\tilde{D} = (d^{L} ,d^{M} ,d^{U} )\) are defined as follows:

$$ \begin{aligned} \tilde{C} + \tilde{D}& = (c^{L} + d^{L} ,c^{M} + d^{M} ,c^{U} + d^{U} ), \\ \tilde{C} - \tilde{D} &= (c^{L} - d^{U} ,c^{M} - d^{M} ,c^{U} - d^{L} ), \\ \tilde{C} \times \tilde{D}& \approx (c^{L} \times d^{L} ,c^{M} \times d^{M} ,c^{U} \times d^{U} ),\,\,\,\,\,\,c^{L} ,d^{L} \ge 0 \\ \frac{{\tilde{C}}}{{\tilde{D}}} &\approx \frac{{(c^{L} ,c^{M} ,c^{U} )}}{{(d^{L} ,d^{M} ,d^{U} )}} \approx \Big(\frac{{c^{L} }}{{d^{U} }},\frac{{c^{M} }}{{d^{M} }},\frac{{c^{U} }}{{d^{L} }}\Big)\quad c^{L} \ge 0,\,d^{L} > 0. \end{aligned} $$
(2)

Definition 4

Consider \(m\) triangular fuzzy numbers \(\tilde{C}_{t} = (c_{t}^{L} ,c_{t}^{M} ,c_{t}^{U} )\), and also let \(x_{\min } = \inf \bigcup\nolimits_{t = 1}^{T} {(c_{t}^{L} ,c_{t}^{U} )}\), \(x_{\max } = \sup \bigcup\nolimits_{t = 1}^{T} {(c_{t}^{L} ,c_{t}^{U} )}\) and \(\alpha \in [0,1]\), then, the fuzzy relative closeness index (\(RC\)) to rank the fuzzy numbers is defined as follows [10]:

$$ \begin{array}{*{20}c} {RC^{\alpha } (\tilde{C}_{i} ) = \frac{1}{2}\left[ {\frac{{\alpha (c_{t}^{M} + c_{t}^{U} ) + (1 - \alpha )(c_{t}^{L} + c_{t}^{M} ) - 2x_{\min } }}{{x_{\max } - x_{\min } }}} \right]} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\ \end{array} $$
(3)

The larger is the proposed index value (\(RC^{\alpha } (\tilde{C}_{t} )\)), the higher the fuzzy number (\(\tilde{C}_{t}\)) rank.

FDEA model with undesirable outputs

Suppose there are \(K\) homogeneous DMUs. Each \(DMU_{k} :k = 1,...,K\) consumes the fuzzy input \(\tilde{x}_{tk} = (\tilde{x}_{tk}^{L} ,\tilde{x}_{tk}^{M} ,\tilde{x}_{tk}^{U} ) \ge 0:t = 1,...,T\) and produces the fuzzy output \(\tilde{w}_{nk} = (\tilde{w}_{nk}^{L} ,\tilde{w}_{nk}^{M} ,\tilde{w}_{nk}^{U} ) \ge 0:n = 1,...,N\). The fuzzy efficiency for \(DMU_{k}\) is determined as follows:

$$ \begin{array}{*{20}c} {\tilde{E}_{k} = \frac{{\sum\nolimits_{n = 1}^{N} {h_{n} \tilde{w}_{nk} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{tk} } }} \approx \left[ {\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{nk}^{L} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{U} } }},\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{nk}^{M} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{M} } }},\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{nk}^{U} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{L} } }}} \right]} & {\,\,} \\ \end{array} $$
(4)

Pursuant to the fuzzy arithmetic, Wang et al. [32] introduced the following model to measure the fuzzy efficiency of \(DMU_{o}\):

$$\begin{aligned} \tilde{E}_{o}^{*} & = Maximize\,\,\,\,\tilde{E}_{o} \approx \left( {E_{o}^{L} ,\,E_{o}^{M} ,\,\,E_{o}^{U} } \right)\\ & \quad = \left( {\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{no}^{L} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{to}^{U} } }},\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{no}^{M} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{to}^{M} } }},\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{no}^{U} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{to}^{L} } }}} \right) \\ & s.t.\\ & \tilde{E}_{k} \approx \left( {E_{k}^{L} ,\,E_{k}^{M} ,\,\,E_{k}^{U} } \right)\\& \quad = \left( {\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{nk}^{L} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{U} } }},\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{nk}^{M} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{M} } }},\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{nk}^{U} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{L} } }}} \right) \\ &\quad \le 1,\,\,\,\,k = 1,...,K, h_{n} ,\,q_{t} \ge 0,\\ & \quad n = 1,...,N,\,\,\,t = 1,...,T. \\ \end{aligned} $$
(5)

It should be noted that if the set of constraints of the model (5) is established for the upper bound \(E_{k}^{U}\), then it is also satisfied for other bounds (\(E_{k}^{L}\),\(E_{k}^{M}\)). Therefore, model (5) is reformulated as follows:

$$\begin{aligned} \tilde{E}_{o}^{*} &= Max\,\,\,\,\tilde{E}_{o} \approx \left[ {E_{o}^{L} ,\,E_{o}^{M} ,\,\,E_{o}^{U} } \right] \\ &\quad= \left[ {\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{no}^{L} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{to}^{U} } }},\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{no}^{M} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{to}^{M} } }},\frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{no}^{U} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{to}^{L} } }}} \right] \\ & s.t. \\ E_{k}^{U}& = \frac{{\sum\nolimits_{n = 1}^{N} {h_{n} w_{nk}^{U} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{L} } }} \le 1,\,\,\,\,k = 1,...,K, \\& h_{n} ,\,q_{t} \ge 0,\,\,\,n = 1,...,N,\,\,\,t = 1,...,T. \end{aligned} $$
(6)

Wang et al. [32] transformed the model (6) into three models and calculated the optimal values of \(E_{o}^{*L}\), \(E_{o}^{*M}\) and \(E_{o}^{*U}\), separately.

Two main shortcomings of Wang et al.’s [32] method are:

  • By solving three separate models, different weights are produced for each unit under evaluation which cannot be the optimal solution of model (6) and contradicts the definition (4).

  • The fuzzy efficiency of the unit under evaluation may not satisfy the condition of the triangular membership function. To solve these two problems, Ebrahimnejad and Amani [10] proposed the lexicographic approach to solve the model (6).

Now, assume each \(DMU_{k} :k = 1,...,K\) consists of \(T\) fuzzy inputs \(\tilde{x}_{tk} \,(t = 1,...,T)\) and \(N\) fuzzy outputs that are a combination of \(N_{1}\) desirable fuzzy output \(\tilde{w}_{nk}^{g} \,(n = 1,...,N_{1} )\) and \(N_{2}\) undesirable fuzzy output \(\tilde{w}_{mk}^{b} \,(m = 1,...,N_{2} )\). Puri and Yadav [25] modified the proposed model of Korhonen and Luptacik [21] and introduced the following model to evaluate the fuzzy relative efficiency of \(DMU_{o}\) in the presence of undesirable outputs:

$$\begin{aligned} &\tilde{E}_{o}^{*} = Max\,\tilde{E}_{o} = \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{no}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mo}^{b} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{to} } }} \\& s.t.\,0 \le \\ & \tilde{E}_{k} = \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nk}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mk}^{b} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{tk} } }} \le 1,\,\,k = 1,...,K, \\ & h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\,\forall n,\,m,\,t. \\ \end{aligned} $$
(7)

Puri and Yadav [25] used Saati et al.’s [26] approach to solve the model (7).

Table 1 depicts the used notations.

Table 1 Notations
Full size table

The common-weights FDEA approach

The fuzzy arithmetic approach of Wang et al. [32] to solve the model (6) assigns different weights to the unit under evaluation. To solve this problem, Azar et al. [4], presented the following model, based on the proposed additive model of Charnes et al. [7], to determine the common sets of weights:

$$ \begin{aligned} & Max\,\mathop {Min}\limits_{k \in K} \,\Bigg\{ \sum\limits_{n = 1}^{N} {h_{n} (w_{nk}^{L} ,w_{nk}^{M} ,w_{nk}^{U} )} \\ &\qquad\qquad\qquad\quad - \sum\nolimits_{t = 1}^{T} {q_{t} (x_{tk}^{L} ,x_{tk}^{M} ,x_{tk}^{U} )} \Bigg\}\, \\ &s.t. \\& \frac{{\sum\nolimits_{n = 1}^{N} {h_{n} (w_{nk}^{L} ,w_{nk}^{M} ,w_{nk}^{U} )} }}{{\sum\nolimits_{t = 1}^{T} {q_{t} (x_{tk}^{L} ,x_{tk}^{M} ,x_{tk}^{U} )} }} \le 1,\,\,\,k = 1,...,K, \\ &\sum\nolimits_{n = 1}^{N} {h_{n} } \ge 1, \\ & \sum\nolimits_{t = 1}^{T} {q_{t} } \ge 1, \\ & h_{n} ,\,q_{t} \ge \varepsilon ,\,\,\,n = 1,...,N,\,\,t = 1,...,T.\, \\ \end{aligned} $$
(8)

in which \(\varepsilon\) is a non-Archimedean value to prevent weights \(h\) and \(q\) from being zero.

In contrast to the proposed model of Wang et al. [32], model (9) can only be solved one time and it is the most important advantage of this approach. Kachouei et al. [15] extended the model (8) by considering the undesirable factors as follows:

$$ \begin{aligned} & Max\,\mathop {Min}\limits_{k \in K} \,\left\{ \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} (w_{nk}^{Lg} ,w_{nk}^{Mg} ,w_{nk}^{Ug} )}\right.\\ &\quad- \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} (w_{mk}^{Lb} ,w_{mk}^{Mb} ,w_{mk}^{Ub} )}\\ &\left.\quad - \sum\limits_{t = 1}^{T} {q_{t} (x_{tk}^{L} ,x_{tk}^{M} ,x_{tk}^{U} )} \right\}\, \\ & s.t. \\ &\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} (w_{nk}^{Lg} ,w_{nk}^{Mg} ,w_{nk}^{Ug} )} - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} (w_{mk}^{Lb} ,w_{mk}^{Mb} ,w_{mk}^{Ub} )} }}{{\sum\nolimits_{t = 1}^{T} {q_{t} (x_{tk}^{L} ,x_{tk}^{M} ,x_{tk}^{U} )} }} \le 1,\\ &\quad k = 1,...,K, \\ &\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} (w_{nk}^{Lg} ,w_{nk}^{Mg} ,w_{nk}^{Ug} )} - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} (w_{mk}^{Lb} ,w_{mk}^{Mb} ,w_{mk}^{Ub} )} \ge 0,\\ &\qquad \,k = 1,...,K, \\ & \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} } \ge 1, \\ & \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} } \ge 1, \\ &\sum\limits_{t = 1}^{T} {q_{t} } \ge 1, \\ & h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\,\forall n,\,m,\,t. \\ \end{aligned}$$
(9)

Kachouei et al. [15] by solving model (9) based on the arithmetic fuzzy approach and finding the optimal weights \((q_{t}^{*} ,h_{n}^{*g} ,\,h_{m}^{*b} )\), calculated the fuzzy efficiency for \(DMU_{k}\) as follows:

$$ \begin{aligned} &\tilde{E}_{k}^{*} = \left[ {E_{k}^{*L} ,\,E_{k}^{*M} ,\,E_{k}^{*U} } \right] \\ &\quad = \left[ \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{Lg} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{Ub} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t}^{*} x_{tk}^{U} } }},\,\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{Mg} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{Mb} } }}{{\sum\nolimits_{t = 1}^{T} {v_{t}^{*} x_{tk}^{M} } }},\right.\\ &\qquad \left.\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{Ug} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{Lb} } }}{{\sum\nolimits_{t = 1}^{T} {v_{t}^{*} x_{tk}^{L} } }} \right] \\ \end{aligned} \\ $$
(10)

FDEA model with undesirable outputs based on FIP and FAIP

By defining two hypothetical units as the ideal unit and the anti-ideal unit, Wang and Lou (2006) developed two models to assess units in terms of the best and worst efficiencies. Then, by combining two obtained efficiencies, they determined the total efficiency for each unit based on the relative closeness index. The relative closeness index calculates the distance of each DMU from its ideal and anti-ideal, simultaneously. After that, Wu [33] modified the proposed model of Wang and Luo [31].

Ebrahimnejad and Amani [10], according to the proposed models of Puri and Yadav [25] and Wang and Luo [31] and Wu [33], presented a new method for assessing triangular fuzzy units. In this way, they first defined two hypothetical fuzzy units, FID and FAID, and then determined the best fuzzy efficiency of FID (BFID) and the worst fuzzy efficiency of FAID (WFAID) using the lexicographic approach. After that, they used the obtained results to compute the best and the worst fuzzy efficiency for each unit. Finally, based on the fuzzy relative closeness index, the total efficiency of each DMU was determined.

Assume that the triangular fuzzy inputs, the triangular fuzzy desirable and undesirable outputs are represented, respectively, by \(\tilde{x}_{tk} \, = (x_{tk}^{L} ,\,x_{tk}^{M} ,\,x_{tk}^{U} ):t = 1,...,T\), \(\tilde{w}_{nk}^{g} \, = (w_{nk}^{Lg} ,\,w_{nk}^{Mg} ,\,w_{nk}^{Ug} ):n = 1,...,N_{1}\) and \(\tilde{w}_{nk}^{b} \, = (w_{nk}^{Lb} ,\,w_{nk}^{Mb} ,\,w_{nk}^{Ub} ):n = 1,...,N_{2}\). In addition, inputs and outputs of the two virtual fuzzy units, namely \({\text{FIP}}\,{ = }(\tilde{x}^{\min } ,\tilde{w}^{g\max } ,\tilde{w}^{b\max } )\) and \({\text{FAIP}}\, = (\tilde{x}^{\max } ,\tilde{w}^{g\min } ,\tilde{w}^{b\min } )\) are defined as follows:

$$ \begin{aligned} & \tilde{x}_{t}^{\min } = (x_{t}^{L\min } ,\,x_{t}^{M\min } ,\,x_{t}^{U\min } ) \\ &\quad = \left( {\mathop {\min }\limits_{k} \{ x_{t}^{L} \} ,\,\mathop {\min }\limits_{k} \{ x_{t}^{M} \} ,\,\mathop {\min }\limits_{k} \{ x_{t}^{U} \} } \right):t = 1,...,T, \\ &\tilde{x}_{t}^{\max } = (x_{t}^{L\max } ,\,x_{t}^{M\max } ,\,x_{t}^{U\max } ) \\ &\quad= \left( {\mathop {\max }\limits_{k} \{ x_{t}^{L} \} ,\,\mathop {\max }\limits_{k} \{ x_{t}^{M} \} ,\,\mathop {\max }\limits_{k} \{ x_{t}^{U} \} } \right):t = 1,...,T, \\ &\tilde{w}_{n}^{g\min } = (w_{n}^{Lg\min } ,\,w_{n}^{Mg\min } ,\,w_{n}^{Ug\min } ) \\ &\quad = \left( {\mathop {\min }\limits_{k} \{ w_{n}^{Lg} \} ,\,\mathop {\min }\limits_{k} \{ w_{n}^{Mg} \} ,\,\mathop {\min }\limits_{k} \{ w_{n}^{Ug} \} } \right):n = 1,...,N_{1} , \\ &\tilde{w}_{n}^{g\max } = (w_{n}^{Lg\max } ,\,w_{n}^{Mg\max } ,\,w_{n}^{Ug\max } )\\ &\quad = \left( {\mathop {\max }\limits_{k} \{ w_{n}^{Lg} \} ,\,\mathop {\max }\limits_{k} \{ w_{n}^{Mg} \} ,\,\mathop {\max }\limits_{k} \{ w_{n}^{Ug} \} } \right):n = 1,...,N_{1} , \\ &\tilde{w}_{m}^{b\min } = (w_{m}^{Lb\min } ,\,w_{m}^{Mb\min } ,\,w_{m}^{Ub\min } ) \\ &\quad = \left( {\mathop {\min }\limits_{k} \{ w_{m}^{Lb} \} ,\,\mathop {\min }\limits_{k} \{ w_{m}^{Mb} \} ,\,\mathop {\min }\limits_{k} \{ w_{m}^{Ub} \} } \right):m = 1,...,N_{2} , \\ &\tilde{w}_{m}^{b\max } = (w_{m}^{Lb\max } ,\,w_{m}^{Mb\max } ,\,w_{m}^{Ub\max } )\\ &\quad = \left( {\mathop {\max }\limits_{k} \{ w_{m}^{Lb} \} ,\,\mathop {\max }\limits_{k} \{ w_{m}^{Mb} \} ,\,\mathop {\max }\limits_{k} \{ w_{m}^{Ub} \} } \right):m = 1,...,N_{2} , \\ \end{aligned} $$
(11)

The following model determines the best fuzzy efficiency of FIP (BFIP), (\(\tilde{\delta }_{I}^{*}\)):

$$ \begin{aligned} &\tilde{\delta }_{I}^{*} = Max\,\tilde{\delta }_{I}^{*} \approx [\delta_{I}^{L} ,\delta_{I}^{M} ,\delta_{I}^{U} ]\\ &\quad = \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} (w_{n}^{Lg\max } ,w_{n}^{Mg\max } ,w_{n}^{Ug\max } )} - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} (w_{m}^{Lb\max } ,w_{m}^{Mb\max } ,w_{m}^{Ub\max } )} }}{{\sum\nolimits_{t = 1}^{T} {q_{t} (x_{t}^{L\min } ,x_{t}^{M\min } ,x_{t}^{U\min } )} }} \\ &s.t. \\ &\tilde{\delta }_{j} = \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} (w_{nk}^{Lg} ,w_{nk}^{Mg} ,w_{nk}^{Ug} )} - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} (w_{mk}^{Lb} ,w_{mk}^{Mb} ,w_{mk}^{Ub} )} }}{{\sum\nolimits_{t = 1}^{T} {q_{t} (x_{tk}^{L} ,x_{tk}^{M} ,x_{tk}^{U} )} }} \\ &\quad \le 1,\,\,k = 1,...,K, \\ &\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} (w_{nk}^{Lg} ,w_{nk}^{Mg} ,w_{nk}^{Ug} )} - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} (w_{mk}^{Lb} ,w_{mk}^{Mb} ,w_{mk}^{Ub} )} \ge \tilde{0},\\ &\quad \,\,k = 1,...,K, \\ &\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} (w_{n}^{Lg\max } ,w_{n}^{Mg\max } ,w_{n}^{Ug\max } )} \\ &\quad- \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} (w_{m}^{Lb\max } ,w_{m}^{Mb\max } ,w_{m}^{Ub\max } )} \ge 0, \\ &h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\forall n,m,t. \\ \end{aligned} $$
(12)

To find the fuzzy efficiency of FIP, the model (12) is solved based on the proposed approach of Ebrahimnejad and Amani [10].

After calculating the fuzzy efficiency of FIP, \(\tilde{\delta }_{I}^{*} \approx [\delta_{I}^{L} ,\delta_{I}^{M} ,\delta_{I}^{U} ]\), the worst efficiency of FAIP (WFAIP) (\(\tilde{\beta }_{AI}^{*}\)) is determined as follows:

$$ \begin{aligned} &\tilde{\beta }_{AI}^{*} = Min\,\tilde{\beta }_{AI} \approx [\beta_{AI}^{L} ,\beta_{AI}^{M} ,\beta_{AI}^{U} ] \\ &\,\,\,\,\,\,\,\,\, = \left[ \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{Lg\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{Ub\min } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{U\max } } }},\right.\\ &\quad \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{Mg\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{Mb\min } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{M\max } } }},\\ &\quad \left.\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{Ug\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{Lb\min } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{L\max } } }} \right] \\ s.t. \\ &\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{Lg\max } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{Ub\max } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{U\min } } }} \ge \delta_{I}^{*L} , \\ &\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{Mg\max } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{Mb\max } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{M\min } } }} \ge \delta_{I}^{*M} , \\ &\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{Ug\max } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{Lb\max } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{L\min } } }} \ge \delta_{I}^{*U} , \\ &\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{Ug} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{Lb} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{L} } }} \le 1,\,\,j = 1,...,n, \\ &\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{Lg} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{Ub} } \ge 0,\,\,j = 1,...,n, \\ &\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{Lg\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{Ub\min } } \ge 0 \\ & h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\,\forall n,m,t. \\ \end{aligned} $$
(13)

To calculate the optimal value of model (13), similarly, the approach of Ebrahimnejad and Amani [10] is applied to obtain the WFAIP, \(\tilde{\beta }_{AI}^{*} \approx [\beta_{AI}^{*L} ,\beta_{AI}^{*M} ,\beta_{AI}^{*U} ]\).

According to the BFIP (\(\tilde{\delta }_{I}^{*}\)), the following model was introduced to determine the best fuzzy efficiency (BFE) of each DMU:

$$ \begin{gathered} \tilde{\delta }_{o}^{*} = Max\,\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{no}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mo}^{b} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{to} } }} \\ s.t. \\ \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{n}^{g\max } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{m}^{b\max } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{t}^{\min } } }} = \tilde{\delta }_{I}^{*} ,\,\, \\ \tilde{\delta }_{k} = \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nk}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mk}^{b} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{tk} } }} \le 1,\,\,k = 1,...,K, \\ \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nk}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mk}^{b} } \ge 0,\,\,k = 1,...,K, \\ h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\forall n,m,t. \\ \end{gathered} $$
(14)

In addition, according to the FAIP (\(\tilde{\beta }_{AI}^{*}\)), the following model was introduced to determine the worst fuzzy efficiency (WFE) of each DMU:

$$ \begin{aligned} &\tilde{\beta }_{o}^{*} = Min\,\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{no}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mo}^{b} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{to} } }} \\ &\quad s.t. \\ &\quad \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{n}^{g\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{m}^{b\min } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{t}^{\max } } }} \ge \tilde{\beta }_{AI}^{*} , \\ &\quad \tilde{\beta }_{k} = \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nj}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mj}^{b} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{tj} } }} \le 1,\,\,k = 1,...,K, \\ &\quad \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nj}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mj}^{b} } \ge 0,\,\,k = 1,...,K, \\ &\quad h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\forall n,m,t. \\ \end{aligned} $$
(15)

Based on the fuzzy arithmetic and the proposed lexicographic approach proposed by Ebrahimnejad and Amani [15], the fuzzy efficiency of models (14) and (15) is computed. Then, the index of the fuzzy relative closeness to provide the total fuzzy efficiency for each unit is calculated as follows:

$$ {\mathop {RC}\limits_{o}^{ \sim } = \frac{{\tilde{\beta }_{o}^{*} - \tilde{\beta }_{AI}^{*} }}{{(\tilde{\beta }_{o}^{*} - \tilde{\beta }_{AI}^{*} ) + (\tilde{\delta }_{I}^{*} - \tilde{\delta }_{o}^{*} )}}\,\,:\,\,o = 1,...,K.} $$
(16)

It should be noted that the value of \({\tilde{RC}}_{o}\) shows the ranks of \(DMU_{o}\). Therefore, if the value of \({\tilde{RC}}_{o}\) is large, it means that the \(DMU_{o}\) has performed better. Due to the fuzzy nature of \({\tilde{RC}}_{o}\), it ranks according to Eq. (3).

The proposed method

In this section, the fuzzy efficiency for each unit is determined based on the common set of weights by use of FIP and FAIP containing undesirable outputs.

BFE by the common set of weights

The following fuzzy model is introduced to obtain the CSWs for determining the BFE of each DMU:

$$ \begin{aligned} & Max\,\left\{ {\mathop {Min}\limits_{k \in K} \,\left[ {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nk}^{g} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mk}^{b} } - \sum\limits_{t = 1}^{T} {q_{t} \tilde{x}_{tk} } } \right]} \right\} \\ &s.t. \\ &\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{n}^{g\max } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{m}^{b\max } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{t}^{\min } } }} = \tilde{\delta }_{I}^{*} , \\ &\tilde{\delta }_{k} = \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nk}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mk}^{b} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{tk} } }} \le 1,\,k = 1,..,K, \\ &\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nk}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mk}^{b} } \ge 0,\,\,k = 1,...,K, \\ &\sum\nolimits_{t = 1}^{T} {q_{t} } + \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} } + \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} } = 1,\, \\ &h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\,\forall n,\,m,\,t.\, \\ \end{aligned} $$
(17)

It is noteworthy that this model does not determine the efficiency score, but by maintaining the optimal value of the BFIP (\(\tilde{\delta }_{I}^{*}\)), the common sets of weights \((q_{t}^{*} ,\,h_{n}^{*g} ,\,h_{m}^{*b} )\) is determined to measure the BFE. According to the fuzzy arithmetic operations, model (17) is reformulated as follows:

$$ \begin{aligned} &Max\,\left\{ \mathop {Min}\limits_{k \in K} \,\left[ \left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{U} } } \right), \left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{M} } } \right),\right.\right.\\ &\quad \left.\left.\left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{L} } } \right) \right] \right\} \\ &s.t. \\ &\,[\delta_{I}^{*L} ,\delta_{I}^{*M} ,\delta_{I}^{*U} ] \\ &=\left[ {\frac{{\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gL\max } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bU\max } } }}{{\sum\limits_{t = 1}^{T} {q_{t} x_{t}^{U\min } } }},\,\frac{{\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gM\max } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bM\max } } }}{{\sum\limits_{t = 1}^{T} {q_{t} x_{t}^{M\min } } }},\,\frac{{\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gU\max } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bL\max } } }}{{\sum\limits_{t = 1}^{T} {q_{t} x_{t}^{L\min } } }}} \right] \\ &\left[ {\frac{{\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } }}{{\sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{U} } }},\,\frac{{\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } }}{{\sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{M} } }},\,\frac{{\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } }}{{\sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{L} } }}} \right] \le 1,\,\,k = 1,...,K, \\ &\left[ {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } ,\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } ,\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } } \right] \ge 0,\,k = 1,...,K, \\ &\sum\limits_{t = 1}^{T} {q_{t} } + \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} } + \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} } = 1,\, \\ &h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\,\forall n,\,m,\,t. \\ \end{aligned}$$
(18)

For solving this model, let

\(\delta = \mathop {Min}\limits_{k \in K} \,\left[ \left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{U} } } \right),\right.\break\left. \left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{M} } } \right),\right.\break\left.\left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{L} } } \right) \right].\) Therefore, we have

$$ \left\{ \begin{gathered} \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{U} } \ge \delta ,\,k = 1,...,K, \\ \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{M} } \ge \delta ,\,k = 1,...,K, \\ \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{L} } \ge \delta ,\,k = 1,...,K. \\ \end{gathered} \right. $$

If the first set of restrictions, \(\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } - \sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{U} } \ge \delta\) is established, the remaining set constraints will redundant and can be removed.

The first set of restrictions in model (18) is rewritten as follows:

$$ \left\{ \begin{gathered} \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gL\max } } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bU\max } } = \delta_{I}^{*L} \times \sum\limits_{t = 1}^{T} {q_{t} x_{t}^{U\min } } , \\ \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gM\max } } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bM\max } } = \delta_{I}^{*M} \times \sum\limits_{t = 1}^{T} {q_{t} x_{t}^{M\min } } , \\ \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gU\max } } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bL\max } } = \delta_{I}^{*U} \times \sum\limits_{t = 1}^{T} {q_{t} x_{t}^{L\min } } . \\ \end{gathered} \right. $$

In addition, if the upper bound \(\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{L} } }}\) is less than or equal to one, it is also satisfied for the other bounds such as \(\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{U} } }} \le 1\), and \(\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{M} } }} \le 1\). Similarly, if \(\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } \ge 0\), then it is also satisfied for the other bounds \(\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } \ge 0\), and \(\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } \ge 0\). According to the mentioned changes, model (18) is rewritten as follows:

$$ \begin{aligned} &\delta^{*} = Max\,\delta \, \\ &s.t. \\ &\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{U} } \ge \delta ,\,k = 1,...,K, \\ &\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gL\max } } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bU\max } } = \delta_{I}^{*L} \times \sum\limits_{t = 1}^{T} {q_{t} x_{t}^{U\min } } , \\ &\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gM\max } } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bM\max } } = \delta_{I}^{*M} \times \sum\limits_{t = 1}^{T} {q_{t} x_{t}^{M\min } } , \\ &\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gU\max } } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bL\max } } = \delta_{I}^{*U} \times \sum\limits_{t = 1}^{T} {q_{t} x_{t}^{L\min } } ,\, \\ &\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{L} } \le 0,\,\,k = 1,...,K, \\ &\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } \ge 0,\,k = 1,...,K, \\ &\sum\limits_{t = 1}^{T} {q_{t} } + \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} } + \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} } = 1,\, \\ &h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\,\forall n,\,m,\,t, \\ \end{aligned}$$
(19)

Based upon the optimal value of model (19), i.e., the common set of weights \((q_{t}^{*} ,\,h_{n}^{*g} ,\,h_{m}^{*b} )\) for all DMUs, the BFE for each \(DMU_{k} :k = 1,...,K\) is calculated as follows:

$$ \begin{aligned} &\tilde{\delta }_{k}^{*} = [\delta_{I}^{*L} ,\delta_{I}^{*M} ,\delta_{I}^{*U} ] \\ &\quad = \left[ \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bU} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t}^{*} x_{t}^{U} } }},\right.\\ &\qquad\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bM} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t}^{*} x_{t}^{M} } }},\\ &\qquad\left.\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bL} } }} {{\sum\nolimits_{t = 1}^{T} {q_{t}^{*} x_{t}^{L} } }} \right] \end{aligned} $$
(20)

Theorem 1

The BFE of \(DMU_{k}\) derived from Eq. (20) maintains the form of a non-negative triangular fuzzy number.

Proof

Let the common set of weights \((q_{t}^{*} ,\,h_{n}^{*g} ,\,h_{m}^{*b} )\) be the optimal solution of model (19). The feasibility of this solution implies that \(q_{t}^{*} ,\,h_{n}^{*g} \,h_{m}^{*b} \ge 0\) for all \(1 \le t \le T,\,\,1 \le n \le N_{1} ,\,1 \le m \le N_{2}\). On the other hand, owing to the form of the non-negative fuzzy input \(\tilde{x}_{tk} \, = (x_{tk}^{L} ,\,x_{tk}^{M} ,\,x_{tk}^{U} )\), fuzzy desirable output \(\tilde{w}_{nk}^{g} \, = (w_{nk}^{Lg} ,\,w_{nk}^{Mg} ,\,w_{nk}^{Ug} )\), and fuzzy undesirable output \(\tilde{w}_{mk}^{b} \, = (w_{mk}^{Lb} ,\,w_{mk}^{Mb} ,\,w_{mk}^{Ub} )\), we have

$$ \begin{gathered} 0 \le x_{tk}^{L} \le x_{tk}^{M} \le \,x_{tk}^{U} ,\,\,\,\,\,\,\,\,\,\,\,\,1 \le t \le T, \\ 0 \le w_{nk}^{Lg} , \le w_{nk}^{Mg} \le w_{nk}^{Ug} ,\,\,\,\,\,1 \le n \le N_{1} \\ 0 \le w_{mk}^{Lb} \le w_{mk}^{Mb} \le w_{mk}^{Ub} ,\,\,\,\,\,\,1 \le m \le N_{2} \\ \end{gathered} $$

Therefore,

$$ \begin{aligned} & 0 \le \sum\limits_{t = 1}^{T} {q_{t}^{*} x_{t}^{L} } \le \sum\limits_{t = 1}^{T} {q_{t}^{*} x_{t}^{M} } \le \,\sum\limits_{t = 1}^{T} {q_{t}^{*} x_{t}^{U} } , \\ & 0 \le \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gL} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bU} } , \\& \le \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gM} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bM} }\\ & \le \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gU} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bL} } \\ \end{aligned} $$

Hence,

$$ 0 \le \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bU} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t}^{*} x_{t}^{U} } }} \le \frac{{\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gM} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bM} } }}{{\sum\limits_{t = 1}^{T} {q_{t}^{*} x_{t}^{M} } }} \le \frac{{\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gU} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bL} } }}{{\sum\limits_{t = 1}^{T} {q_{t}^{*} x_{t}^{L} } }} $$

This implies that \(0 \le \delta_{I}^{*L} \le \delta_{I}^{*M} \le \delta_{I}^{*U}\) and so \(\tilde{\delta }_{k}^{*} = [\delta_{I}^{*L} ,\delta_{I}^{*M} ,\delta_{I}^{*U} ]\) keeps the form of a non-negative triangular fuzzy number.

The WFE by the common set of weights

In a similar way, the following fuzzy model is suggested to determine the CSWs for calculating the WFE of each DMU:

$$ \begin{array}{*{20}c} \begin{gathered} Min\,\left\{ {\mathop {Max}\limits_{k \in K} \,\left[ {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nk}^{g} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mk}^{b} } - \sum\limits_{t = 1}^{T} {q_{t} \tilde{x}_{tk} } } \right]} \right\} \\ s.t. \\ \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{n}^{g\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{m}^{b\min } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{t}^{\max } } }} = \tilde{\beta }_{AI}^{*} , \\ \tilde{\beta }_{k} = \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nk}^{g} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mk}^{b} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} \tilde{x}_{tk} } }} \le 1,\,\,k = 1,...,K, \\ \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} \tilde{w}_{nk}^{g} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} \tilde{w}_{mk}^{b} } \ge 0,\,\,k = 1,...,K, \\ \sum\limits_{t = 1}^{T} {q_{t} } + \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} } = 1,\, \\ h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\,\forall n,\,m,\,t.\, \\ \end{gathered} & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\ \end{array} $$
(21)

In this model, by maintaining the optimal value of the BFAIP (\(\tilde{\beta }_{AI}^{*}\)), the common set of weights \((q_{t}^{*} ,\,h_{n}^{*g} ,\,h_{m}^{*b} )\) is determined to measure the WFE. According to the triangular fuzzy arithmetic operations, model (21) is rewritten as follows:

$$ \begin{aligned} & Min\,\left\{ \mathop {Max}\limits_{k \in K} \,\left[ \left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{U} } } \right),\right.\right.\\ &\left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{M} } } \right),\\ &\left.\left.\left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{L} } } \right) \right] \right\} \\ &s.t. \\ &[\beta_{AI}^{*L} ,\beta_{AI}^{*M} ,\beta_{AI}^{*U} ] \\ &\quad=\left[ \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gL\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bU\min } } }} {{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{U\max } } }},\right.\\ &\qquad \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gM\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bM\min } } }} {{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{M\max } } }},\\ &\qquad \left.\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gU\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bL\min } } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{L\max } } }} \right] \\ &\left[ \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } }} {{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{U} } }},\,\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } }} {{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{M} } }},\right.\\ &\quad \left.\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } }} {{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{L} } }} \right] \le 1,\,\,k = 1,...,K, \\ &\left[ \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } ,\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } ,\right.\\ &\quad \left.\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } \right] \ge 0,\,k = 1,...,K, \\ &\sum\nolimits_{t = 1}^{T} {q_{t} } + \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} } + \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} } = 1,\, \\ &h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\,\forall n,\,m,\,t. \\ \end{aligned} $$
(22)

Let

$$ \begin{aligned} &\beta = \mathop {Max}\limits_{k \in K} \,\left[ \left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{U} } } \right),\right.\\ &\quad \left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{M} } } \right),\\ &\quad \left.\left( {\sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{L} } } \right) \right] \end{aligned} $$

Then, we have

$$ \left\{ \begin{gathered} \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{U} } \le \beta ,\,k = 1,...,K, \\ \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{M} } \le \beta ,\,k = 1,...,K, \\ \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } - \sum\limits_{t = 1}^{T} {q_{t} x_{tk}^{L} } \le \beta ,\,k = 1,...,K. \\ \end{gathered} \right. $$

If the third set of restrictions \(\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } - \sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{L} } \le \beta\) is established, the other two sets of constraints will be redundant and can be removed.

The first set of restrictions of model (21) is rewritten as follows:

$$ \begin{gathered} \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gL\min } } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bU\min } } = \beta_{AI}^{*L} \times \sum\limits_{t = 1}^{T} {q_{t} x_{t}^{U\max } } , \\ \sum\limits_{r = 1}^{{s_{1} }} {u_{r}^{g} y_{r}^{Mg\min } } - \sum\limits_{p = 1}^{{s_{2} }} {u_{p}^{b} y_{p}^{Mb\min } } = \beta_{AI}^{*M} \times \sum\limits_{t = 1}^{T} {q_{t} x_{t}^{M\max } } , \\ \sum\limits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gU\min } } - \sum\limits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bL\min } } = \beta_{AI}^{*U} \times \sum\limits_{t = 1}^{T} {q_{t} x_{t}^{L\max } } . \\ \end{gathered} $$

Similarly, if the upper bound \(\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{L} } }}\) is less than or equal to one, it is also satisfied for other bounds such as \(\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{U} } }} \le 1\) and \(\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{M} } }} \le 1\). In addition, if the lower bound \(\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} }\) is more than or equal to zero, then the other bounds such as \(\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bM} } \ge 0\), and \(\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } \ge 0\) will be satisfied. According to the mentioned changes, model (22) reformulated as follows:

$$ \begin{aligned} & \beta^{*} = Max\,\beta \, \\ & s.t. \\ & \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} } \\ &\qquad- \sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{L} } \le \beta ,\,k = 1,...,K, \\ & \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gL\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bU\min } } \\ &\qquad= \beta_{AI}^{*L} \times \sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{U\max } } , \\ & \sum\nolimits_{r = 1}^{{s_{1} }} {u_{r}^{g} y_{r}^{Mg\min } } - \sum\nolimits_{p = 1}^{{s_{2} }} {u_{p}^{b} y_{p}^{Mb\min } }\\ &\qquad = \beta_{AI}^{*M} \times \sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{M\max } } , \\ & \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{n}^{gU\min } } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{m}^{bL\min } } \\ &\qquad= \beta_{AI}^{*U} \times \sum\nolimits_{t = 1}^{T} {q_{t} x_{t}^{L\max } } ,\, \\ & \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bL} }\\ &\qquad - \sum\nolimits_{t = 1}^{T} {q_{t} x_{tk}^{L} } \le 0,\,k = 1,...,K, \\ & \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} w_{nk}^{gL} }\\ &\qquad - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} w_{mk}^{bU} } \ge 0,\,k = 1,...,K, \\ & \sum\nolimits_{t = 1}^{T} {q_{t} } + \sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{g} } + \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{b} } = 1,\, \\ & h_{n}^{g} ,\,h_{m}^{b} ,\,q_{t} \ge \varepsilon ,\,\,\forall n,\,m,\,t. \\ \end{aligned} $$
(23)

After obtaining the common set of weights \((q_{t}^{*} ,\,h_{n}^{*g} ,\,h_{m}^{*b} )\) by solving model (23), the WFE of each \(DMU_{k} :k = 1,...,K\) is calculated as follows:

$$ \begin{aligned} \tilde{\beta }_{k}^{*}& = [\beta_{AI}^{*L} ,\beta_{AI}^{*M} ,\beta_{AI}^{*U} ] \\ & = \left[ \frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gL} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bU} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t}^{*} x_{tk}^{U} } }},\right.\\ &\quad\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gM} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bM} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t}^{*} x_{tk}^{M} }}},\\ &\quad \left.\frac{{\sum\nolimits_{n = 1}^{{N_{1} }} {h_{n}^{*g} w_{nk}^{gU} } - \sum\nolimits_{m = 1}^{{N_{2} }} {h_{m}^{*b} w_{mk}^{bL} } }}{{\sum\nolimits_{t = 1}^{T} {q_{t}^{*} x_{tk}^{L} } }} \right] \\ \end{aligned} $$
(24)

Theorem 2

The WFE of \(DMU_{k}\) derived from Eq. (24) maintains the form of a non-negative triangular fuzzy number.

Proof

This can be proved similar to Theorem 1:

Total ranking of DMUs

In this subsection, we explore how it is possible to rank all DMUs. To this end, first the fuzzy efficiency of FIP and the fuzzy efficiency of FAIP are calculated, respectively, by models (12) and (13) based on Ebrahimnejad and Amani’s [10] approach. Then, in the second step, the BFD is computed based on formulation (20) by the help of CSW derived from model (19). In the third step, the WFD is computed based on formulation (24) by the help of CSW derived from model (23). After that, the fuzzy relative closeness is calculated by Eq. (16) for all DMUs. The fuzzy relative closeness allows units to be compared and ranked. Therefore, the larger is the value of fuzzy relative closeness, the better rank of DMU under consideration. Since the fuzzy relative closeness index is a fuzzy number, all DMUs can be ranked according to Eq. (3) at different levels of \(\alpha \in (0,1]\). The algorithm of our proposed approach is shown in Fig. 1.

Fig. 1
figure 1

The proposed approach algorithm

Full size image

The main advantages of the proposed technique for solving fuzzy DEA models in the present of undesirable outputs over the existing approaches can be summarized as follows:

  • The proposed approach by Puri and Yadav [25] evaluates DMUs in the present of undesirable outputs in fuzzy environment only based on optimistic point of view. However, the proposed approach in this study improves the distinguishing power of DMUs by considering both optimistic and pessimistic perspectives.

  • The alpha-cut approach proposed by Puri and Yadav [25] approximates the fuzzy efficiency score of each DMU from the given alpha level. However, the extended fuzzy arithmetic approach proposed in this study provides the exact form of membership function of fuzzy efficiency score for each DMU.

  • Unlike the existing approaches that are unable to solve the flexibility of the weights in performance evaluation by fuzzy DEA models, the extended fuzzy arithmetic approach in this study solves this issue by generating common weights in order to evaluate all DMUs based on a same basis.

  • Unlike the existing methods, the proposed approach in this study, by taking into account both pessimistic and optimistic aspects and simultaneously generating common weights, improves the distinguishing power of units in performance evaluation in the presence of unfavorable outputs in the fuzzy environment.

  • The main advantages of using common-weight DEA method based upon fuzzy arithmetic approach over the existing fuzzy DEA techniques are reduction of the computational complexities and evaluation of equitably the best and the worst fuzzy efficiencies on the same base.

Numerical example

To illustrate the validity of the proposed common-weight FDEA approach, a numerical example taken from Puri and Yadav [25] is given, and the obtained results are compared with those derived by Puri and Yada’s method [25] and Ebrahimnejad and Amani’s [10] method.

In this example, 12 units consisting of two inputs (\(\tilde{x}_{1} ,\,\tilde{x}_{2}\)), two desirable outputs (\(\tilde{w}_{1}^{g} ,\,\tilde{w}_{2}^{g}\)) and one undesirable output (\(\tilde{w}^{b}\)) represented by positive triangular fuzzy data are considered. Data are given in Table 2.

Table 2 Fuzzy triangular inputs, desirable and undesirable outputs
Full size table

Two last rows in Table 2 show the fuzzy inputs and outputs of virtual units, namely FIP and FAIP in accordance with the formulation (11). Given the proposed algorithm, first the best and the worst fuzzy efficiencies of two virtual units, i.e., FID and FAIP, are calculated by models (12) and (13). The results are shown in the two last rows of Table 3. Then, according to the resulting efficiencies, the common sets of weights for all units are calculated by models (19) and (23) leading to the optimal values (0.2577, 0.2099, 0.1301, 0.2394) and (0.2326, 0.1842, 0.1152, 0.2110, 0.2569), respectively. After that, based on the obtained optimal weights, the BFD and the WFD are computed by formulations (20) and (24), respectively. In the end, the fuzzy relative closeness is determined for each DMU via formulation (3). The results can be seen in Table 3.

Table 3 The results of BFE, WFE, BFIP, WFAIP, and RC
Full size table

Table 3 shows that the upper bound of the BFP of units 1, 2, and 4 is equal to 1, while the upper bounds of the other units are less than one. It means that only the upper bound of the BFE of three units 1, 2, and 4 is efficient at and the others are inefficient.

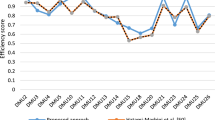
It should be noted that the upper bounds of the obtained efficiencies are the same as the evaluated results of crisp data. Figure 2 shows the graphical representation of the efficiency results obtained with crisp data in accordance with Puri nd Yadav’s [25] approach.

Fig. 2
figure 2

Efficiency results with crisp data Puri and Yadav [25]

Full size image

According to Fig. 2, the best and the worst efficiency of all units with crisp data, except of units 1, 2 and 4, are less than one. The results indicate that data evaluation in a fuzzy environment shows more accurate evaluation than crisp data. Therefore, the fuzzy relative closeness index at different \(\alpha\) levels is calculated and the units are ranked for further investigation.

The fuzzy relative closeness (\(R\tilde{C}_{k}^{\alpha }\)) for 12 DMUs at different levels of \(\alpha \in (0,1]\) by Eq. (3) is computed, and the obtained results are shown in Table 4.

Table 4 The fuzzy relative closeness \(\mathop {RC_{k}^{\alpha } }\limits^{ \sim }\)
Full size table

As seen from Table 4, the fuzzy relative closeness values (\(R\tilde{C}_{k}^{\alpha }\)) are increased for all DMUs by increasing the value of \(\alpha\) at different levels \(\{ 0.1,\,0.2,\,0.3,\,0.4,\,0.5,\,0.6,\,0.7,\,0.8,\,0.9,\,1\,\}\). This issue is shown in Fig. 3.

Fig. 3
figure 3

The fuzzy relative closeness (\(R\tilde{C}_{k}^{\alpha }\)) at levels \(\alpha \in (0,\,1]\)

Full size image

According to the fuzzy relative closeness values given in Table 4, all DMUs were ranked at different levels. \(\alpha \in (0,\,1]\) The results are presented in Table 5.

Table 5 Ranks of DMUs
Full size table

As seen in Table 5, there are differences in the ranking DMUs at different alpha levels but these differences do not seem to be significant.

In general, DMUs 1, 12, 11, 7, 3, 8, 6, and 5 have the ranks 3, 4, 5, 6, 7, 10, 11, and 12 at different levels \(\alpha = (0,1]\), respectively. DMU 5 has the last rank among 12 units. In more details, DMU 2 at levels \(\{ 0.1,\,0.2,\,0.3,\,0.4,\,0.5,\,0.6,0.7,0.8\}\) and \(\{ 0.9,1\}\) has the ranks of 2 and 1, respectively, while the ranks of DMU 4 in the same levels are 1 and 2, respectively. In addition, the rank of DMU 9 at levels \(\{ 0.1,0.2\}\) and \(\{ 0.3,\,0.4,\,0.5,\,0.6,0.7,0.8,0.9,1\}\) are 8 and 9, respectively, while the ranks of DMU 10 in the same levels are 9 and 8, respectively.

Table 5 shows the ranking changes of 12 units by the three different methods: Puri and Yadav [25], Ebrahimnejad and Amani [10] and the proposed method.

Table 6 shows that unit 5 has the last rank for \(\alpha = \{ 0.6,\,0.7,\,0.8,\,0.9,\,1\}\). In addition, unit 2 has the first rank when \(\alpha\) takes 0.9 and 1 values for all three approach. Puri and Yadav [25] evaluated and ranked DMUs involving undesirable fuzzy data from an optimistic perspective, while Ebrahimnejad and Amani [10] evaluated and ranked DMUs involving undesirable fuzzy data from both optimistic and pessimistic perspectives. However, in our proposed approach, by maintaining the BFIP and also the WFAIP, a common set of weights for all fuzzy units is determined. Then, the BFP and WFP for each decision-making unit are determined. Since the proposed method uses a common set of optimal weights to evaluate all units, it can be said that a more accurate evaluation has been done than the two previously proposed approaches. Moreover, our proposed approach needs less computational effort than the approaches proposed by Puri and Yadav [25] and Ebrahimnejad and Amani [10].

Table 6 Comparing the rank of units at different alpha levels
Full size table

The different ranks show that in addition to the change in efficiency scores, the rank of the units also changes at different levels of \(\alpha\). Figures 4, 5, and 6 show the ranking changes according to Puri and Yadav [25] and Ebrahimnejad and Amani [10] methods and the proposed method, respectively. As you can see in these figures, the changes in the ranking of units in Puri and Yadav [25] methods are more than the other two methods. In general, the ranking changes in the proposed method are much less than the previous methods.

Fig. 4
figure 4

Ranks of DMUs at levels \(\alpha \in (0,\,1]\) Puri and Yadav [25]

Full size image
Fig. 5
figure 5

Ranks of DMUs at levels \(\alpha \in (0,\,1]\) (Ebrahimnejad and Amani [10]

Full size image
Fig. 6
figure 6

Ranks of DMUs at levels \(\alpha \in (0,\,1]\)

Full size image

In sum, the main advantages of our proposed approach compared to those ones proposed by Ebrahimnejad and Amani [10] and Puri and Yadav [25] are summarized as follows:

  • Ebrahimnejad and Amani [10] used the concept of ideal and anti-ideal points to evaluate the units including undesirable outputs in a fuzzy environment. They applied the fuzzy arithmetic approach to find the best and worst fuzzy efficiency of each DMU. However, the most important weakness of this method is that it requires considerable computational effort to find these efficiencies. In our proposed method, by finding common weights, the best relative efficiency of each unit is calculated by solving only one linear model, and the worst efficiency of each unit is calculated by solving only one linear model.

  • Puri and Yadav [25] evaluated and ranked the units including undesirable outputs in the fuzzy environment only from an optimistic perspective, based on the alpha-cut approach. However, the most important weakness of the alpha-cut approach in finding the fuzzy efficiency is that a sequence of linear models must be solved based on a set of different alpha-cuts, which significantly increases the calculations. One of the advantages of our proposed method compared to this method is providing the fuzzy efficiencies of DMUs from two optimistic and pessimistic perspectives.

Another advantage of the proposed method in this study over the both approaches proposed by Ebrahimnejad and Amani [10] and Puri and Yadav [25] is the use of a common-weight approach which leads to reducing the complexity of calculations and solving fewer problems to achieve the optimal solution. In addition, the use of the common-weight technique will reduce the variability in the ranking.

Conclusions

Uncertainty or ambiguity of data in some real-world applications has led to the design of methods for evaluating such systems in recent years in which the fuzzy data envelopment analysis is one of the existing techniques in dealing with such cases. After evaluating the performance of production processes, the issue of ranking units in terms of how they work in the system is one of the most important issues. Hence, researchers are always trying to provide appropriate methods for evaluating decision-making units that can increase the differentiation power among units. One approach in DEA to solve this problem based on common set of weights that can simultaneously with determining the optimal common weights for all units, maximize their efficiency and give a complete ranking for all efficient units. Accordingly, in this paper, first, two virtual fuzzy ideal and anti-ideal virtual units, namely FIP and FAIP have defined and based on the proposed method of Ebrahimnejad and Amani [10], the best and the worst fuzzy efficiency of virtual units have calculated. Then, according to the obtained efficiency scores, models for determining a set of common weights have presented and the best and worst efficiency of all units with fuzzy triangular data and in the presence of undesirable outputs have determined. Finally, the fuzzy relative closeness index for fuzzy efficiencies at different levels has been computed and the units have been ranked. A comparison has been made between the proposed method and the other two methods, which indicates a more logical evaluation of the proposed method because it reduces the scatter of weights assigned to inputs and outputs and allows comparison and ranking of all units on a same base.

However, the proposed approach in this study assumes all fuzzy inputs and fuzzy outputs can be varied at the discretion of decision makers. In real applications of DEA, there are non-discretionary variables that are beyond the management control, but need to be taken into account in the performance evaluation. Therefore, further research on extending the proposed method to overcome these shortcomings is an interesting stream of future research. Moreover, the proposed approach can be developed for DEA models with network structure [34]. This approach can also be extended to find common weights in DEA models with type-2 Gaussian fuzzy numbers [29]. Another topic includes handling the polygonal fuzzy sets using fuzzy enhanced Russell graph measure proposed by Arana-Jiménez et al. [3]. Other extension of the proposed approach is formulating the DEA model with fuzzy production possibility set [2]. We also attempt to solve fuzzy multi-objective transportation problems [13, 23, 24], with fuzzy DEA technique proposed in this study. Comparison of the evaluation results of the fuzzy DEA technique with other assessment methods such as fuzzy MCDM methods [30] and fuzzy Dombi EDAS model [9] can also be considered as a further research avenue.