Introduction

For the practical decision-making problem, preference relation is an important technique, which can be constructed by making pairwise comparison over a set of alternatives or criteria. Given a preference relation, the consistency property should be analyzed, because inconsistent preference relation may lead to unreasonable conclusion. In the literature, there exist two important consistency definitions: the additive consistency and the multiplicative consistency. The consistency analysis of fuzzy preference relations (FPRs) have been extensively investigated [1, 2]. However, the preference values in FPR can only offer the membership degree of an object over another. To overcome this issue, the intuitionistic fuzzy preference relation (IFPR) based on the intuitionistic fuzzy set (IFS) and the intuitionistic fuzzy number (IFN) was proposed [3]. The IFPR can provide the preferred and non-preferred degrees simultaneously. Yang et al. [4] discussed the additive consistency of IFPRs, while the multiplicative consistency was considered in [5]. Sometimes, the sum of membership degree and non-membership degree may be bigger than 1, but their square sum is equal to or less than 1. Then, the Pythagorean fuzzy set (PFS) and the Pythagorean fuzzy number (PFN) were introduced [6]. Mandal and Ranadive [7] further defined the Pythagorean fuzzy preference relation (PFPR). The consistency of PFPRs have been discussed by some scholars [8, 9]. Recently, Yager [10] proposed the q-rung orthopair fuzzy set (q-ROFS), which generalized the IFS and the PFS. The corresponding q-rung orthopair fuzzy number (q-ROFN) (\(\mu ,\nu \)) satisfies \(\mu ^{q}+\nu ^{q}\le 1\), where \(q\ge 1\) [11]. For an evaluation value (0.9, 0.5), we can see that it is a q-ROFN for \(q\ge 3\), but (0.9, 0.5) is neither an IFN nor a PFN. Thus, compared to the IFPR and the PFPR, the q-rung orthopair fuzzy preference relation (q-ROFPR) defined by Li et al. [12] can offer more flexible and uncertain information. Zhang et al. [13] and Zhang and Chen [14] both investigated the additive consistency of q-ROFPRs, while the multiplicative consistency analysis was conducted in [15, 16].

Research gap and motivation

In real decision-making problems, the experts may want to provide the qualitative judgements using the linguistic variables. Then, a linguistic preference relation (LPR) can be constructed based on the discrete linguistic term set (LTS) \(S=\{s_{i}\mid i=0,1,\ldots ,\tau \}\). Several researchers have discussed the consistency of LPRs [17, 18]. Similar to the FPR, the qualitative non-preferred degree of an object over another is also not considered in a LPR. Motivated by the IFS and the IFN, the linguistic intuitionistic fuzzy set (LIFS) and the linguistic intuitionistic fuzzy number (LIFN) were, respectively, introduced [19, 20]. Subsequently, Pei et al. [21] proposed the linguistic intuitionistic fuzzy preference relation (LIFPR) and studied the additive consistency, where the qualitative positive and negative judgements can be offered simultaneously. Meng et al. [22] also considered the additive consistency of LIFPRs and applied to an MCDM problem. Jin et al. [23] dealt with the multiplicative consistency of LIFPRs and presented a group decision-making (GDM) method. Afterwards, Garg [24] defined the linguistic Pythagorean fuzzy set (LPFS) and the linguistic Pythagorean fuzzy number (LPFN). Liu et al. [25] introduced the linguistic Pythagorean fuzzy preference relation (LPFPR) and considered the multiplicative consistency. Recently, Liu and Liu [26] generalized the LIFS and the LPFS to the linguistic q-rung orthopair fuzzy set (Lq-ROFS). The corresponding linguistic q-rung orthopair fuzzy number (Lq-ROFN) \((s_{\mu },s_{\nu })\) satisfies \(\mu ^{q}+\nu ^{q}\le \tau ^{q}\), where \(q\ge 1\).

Let \(S=\{s_{0}: \mathrm{very~ slow},s_{1}: \textrm{slow}, s_{2}: \mathrm{slightly~slow}, s_{3}: \textrm{normal}, s_{4}: \mathrm{slightly ~fast}, s_{5}: \textrm{fast}, s_{6}: \mathrm{very~ fast}\}\) be a LTS, we can see that \((s_{4},s_{5})\) is a Lq-ROFN for \(q\ge 3\), but it is neither a LIFN nor a LPFN. Clearly, when \(q=1\), the Lq-ROFN reduces to a LIFN. And when \(q=2\), the Lq-ROFN becomes a LPFN. Thus, the Lq-ROFN can be regarded as a generalization form of LIFN and LPFN, which can offer more qualitative uncertain information. Taking into account the advantages of Lq-ROFN, the research of Lq-ROFS has become a hot topic. More and more researchers have paid their attentions to the decision-making problems under linguistic q-rung orthopair fuzzy environment. At present, the study of Lq-ROFS is mainly focused on the aggregation operators, various types of linguistic q-rung orthopair fuzzy aggregation operators have been proposed [26,27,28,29,30]. However, as far as we know, there is no research about the corresponding Lq-ROFPRs, and it will be an interesting issue to deal with Lq-ROFPRs. Therefore, in this paper, on the basis of Lq-ROFS and Lq-ROFN, we will define the Lq-ROFPR and conduct the multiplicative consistency analysis.

In practical decision-making problems, the experts may be unable to provide complete preference relations due to the limitations of professional knowledge and experience. For a preference relation, if some evaluation elements are unknown, it is called an incomplete preference relation. Many scholars have discussed different kinds of incomplete preference relations, such as incomplete FPR [31], incomplete IFPR [32], incomplete interval-valued IFPR [33], incomplete q-ROFPR [16], incomplete interval-valued q-ROFPR [34], incomplete LPR [35], incomplete LIFPR [22], incomplete interval-valued LIFPR [36] and incomplete multiplicative LIFPR [37]. In this paper, we also assume the Lq-ROFPR can be incomplete with missing values. After introducing the concept of multiplicative consistent Lq-ROFPR, we define a consistency index to measure the consistency level. To estimate the unknown values from an incomplete Lq-ROFPR, a programming model is constructed by minimizing the consistency index.

Considering that uncertainty and inaccuracy exist in most real decision-making problems, the Lq-ROFS with corresponding decision making algorithms can be employed in fault detection [38, 39], robot selection problem [40, 41], non-zero-sum game [42, 43], global supplier searching [44, 45] and impulsive decision-making [46, 47]. Readers can also refer to [48,49,50]. In this paper, we will use the proposed Lq-ROFPRs to deal with three practical MCDM problems: the company manager selecting problem, the typhoon emergency plan choosing problem and the mobile phones evaluating problem.

Main contributions

The main contributions and originalities of this paper are presented as follows: (1) a new preference relation called Lq-ROFPR based on the Lq-ROFS is introduced; (2) the multiplicative consistency of Lq-ROFPRs is defined and studied; (3) a transformation formula is proposed to convert the normalized Lq-ROFPWV into a multiplicative consistent Lq-ROFPR; (4) a consistency-based model is built to derive the normalized Lq-ROFPWV; (5) a programming model is constructed to improve the consistency level of an unacceptably multiplicative consistent Lq-ROFPR; (6) a mathematical model is established to ascertain the unknown linguistic variables from an incomplete Lq-ROFPR; (7) the Lq-ROFPRs are applied to solve three MCDM problems.

Paper organization

The remainder of the paper is organized as follows. “Preliminaries” mainly reviews some related knowledge and introduce the concept of Lq-ROFPR. In Multiplicative consistency analysis for Lq-ROFPRs”, the multiplicative consistency is defined and a consistency-based programming model is built to obtain the normalized Lq-ROFPWV. For an incomplete and unacceptably multiplicative consistent Lq-ROFPR, two different optimization models are, respectively, constructed to estimate the missing values and improve the consistency level. “An approach for MCDM with Lq-ROFPRs” proposes an MCDM method and offers a multiplicative consistency-based algorithm. “Application examples and comparison analysis” applies the new approach to practical decision making problems and conducts the comparison analysis. Finally, “Conclusion” gives the conclusion of this paper.

Preliminaries

In the abstract and “Introduction”, we can see that many symbols are defined. To enhance the readability of this paper, we offer a Table 1 to list the used symbols again.

Table 1 The used symbols and their meanings
Full size table

In the following, some related knowledge are reviewed and the concept of Lq-ROFPR is defined.

Definition 1

[10] Let X be a universe of discourse, the q-ROFS in X is defined as

$$\begin{aligned} A = \{\langle x,\mu _{A}(x),\nu _{A}(x)\rangle \mid x \in X\}, \end{aligned}$$

where \(\mu _{A}(x):X \longrightarrow [0,1]\) and \(\nu _{A}(x):X \longrightarrow [0,1]\) represent the membership degree and non-membership degree of the element \(x \in X\) to the set A, respectively. In addition, \(\mu _{A}^q(x) + \nu _{A}^q(x) \le 1\) (\(q \ge 1\)) should be satisfied, and the hesitation degree can be given by \(\pi _{A}(x) = \big (1-\mu _{A}^q(x) - \nu _{A}^q(x)\big )^{1/q}\).

For the convenience of representation, a q-ROFN can be written as \((\mu , \nu )\), where \(\mu , \nu \in [0,1]\) and \(\mu ^{q} + \nu ^{q} \le 1\) (\(q \ge 1\)) [11]. Moreover, the q-ROFPR was introduced by Li et al. [12].

Definition 2

[12] A q-ROFPR on \(X=\{x_{1},x_{2},\) \(\ldots ,x_{n}\}\) is characterized by a comparison matrix \(R= (r_{ij})_{n\times n}\subset X\times X\), where \(r_{ij}= (\mu _{ij}, \nu _{ij})\) is a q-ROFN, and \(0\le \mu _{ij}, \nu _{ij}\le 1\), \(\mu _{ij}= \nu _{ji}, \nu _{ij}= \mu _{ji},\) \(\mu _{ii}= \nu _{ii}=2^{-1/q}\), \(\mu _{ij}^q + \nu _{ij}^q \le 1\), for all \(i,j =1,2,\ldots ,n\), \(q \ge 1\).

Definition 3

[15] A q-ROFPR \(R=(r_{ij})_{n\times n}\) with \(r_{ij}=(\mu _{ij},\nu _{ij})\) is called multiplicative consistent if

$$\begin{aligned} \mu _{ij}\mu _{jk}\mu _{ki}=\nu _{ij}\nu _{jk}\nu _{ki}, \end{aligned}$$
(1)

for all \(i,j,k=1,2,\ldots ,n\).

Given a finite ordered discrete LTS \(S=\{s_{i}\mid i=0,1,\ldots ,\tau \}\) with odd cardinality, Xu [51] extended the discrete LTS S to a continuous LTS \(\overline{S}=\{s_{\alpha }\mid \alpha \in [0,\tau ]\}\) to preserve more original information. If \(s_{\alpha },s_{\beta }\in \overline{S}\), then \(s_{\alpha }<s_{\beta }\Leftrightarrow \alpha <\beta \). Moreover, there exist two functions \(I(\cdot )\) and \(I^{-1}(\cdot )\), such that [18]:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} I(\cdot ): \overline{S}\rightarrow [0,\tau ], I(s_{\alpha })=\alpha , \forall s_{\alpha }\in \overline{S},\\ I^{-1}(\cdot ): [0,\tau ]\rightarrow \overline{S}, I^{-1}(\alpha )=s_{\alpha }, \forall \alpha \in [0,\tau ]. \end{array}\right. } \end{aligned} \end{aligned}$$

Definition 4

[26] Let X be a universe of discourse, the Lq-ROFS in X is defined as

$$\begin{aligned} L = \{\langle x,s_{\mu }(x),s_{\nu }(x)\rangle \mid x \in X\}, \end{aligned}$$

where \(s_{\mu }(x):X \longrightarrow \overline{S}\) and \(s_{\nu }(x):X \longrightarrow \overline{S}\) represent the linguistic membership degree and linguistic non-membership degree of the element \(x \in X\) to the set L, respectively. In addition, \(I^{q}(s_{\mu }(x)) +I^{q}(s_{\nu }(x)) \le \tau ^{q}\) (\(q \ge 1\)) should be satisfied, and the linguistic hesitation degree can be given by \(s_{\pi }(x) = I^{-1}\Big (\big (\tau ^{q}-I^{q}(s_{\mu }(x)) -I^{q}(s_{\nu }(x))\big )^{1/q}\Big )\).

For the convenience of representation, a Lq-ROFN can be written as \((s_{\mu }, s_{\nu })\), where \(s_{\mu }, s_{\nu }\in \overline{S}\) and \(I^{q}(s_{\mu })+I^{q}(s_{\nu })\le \tau ^{q}\) (\(q \ge 1\)) [26].

Definition 5

[26, 28] Let \(\gamma _{1}=(s_{\mu _{1}},s_{\nu _{1}})\), \(\gamma _{2}=(s_{\mu _{2}},s_{\nu _{2}})\), \(\gamma =(s_{\mu },s_{\nu })\) be any three Lq-ROFNs and \(\lambda >0\), then some operational rules can be given as follows:

$$\begin{aligned} \gamma _{1}\oplus \gamma _{2}&=(s_{\mu _{1}},s_{\nu _{1}})\oplus (s_{\mu _{2}},s_{\nu _{2}})\\&=\Big (s_{\big (\mu _{1}^{q}+\mu _{2}^{q}-\mu _{1}^{q}\mu _{2}^{q}/\tau ^{q}\big )^{1/q}},s_{\frac{\nu _{1}\nu _{2}}{\tau }}\Big );\\ \gamma _{1}\otimes \gamma _{2}&=(s_{\mu _{1}},s_{\nu _{1}})\otimes (s_{\mu _{2}},s_{\nu _{2}})\\&=\Big (s_{\frac{\mu _{1}\mu _{2}}{\tau }},s_{\big (\nu _{1}^{q}+\nu _{2}^{q}-\nu _{1}^{q}\nu _{2}^{q}/\tau ^{q}\big )^{1/q}}\Big );\\ \lambda \gamma&=\lambda (s_{\mu },s_{\nu })=\Big (s_{\tau \big (1-(1-\mu ^{q}/\tau ^{q})^{\lambda }\big )^{1/q}},s_{\tau \big (\frac{\nu }{\tau }\big )^{\lambda }}\Big );\\ \gamma ^{\lambda }&=(s_{\mu },s_{\nu })^{\lambda }=\Big (s_{\tau \big (\frac{\mu }{\tau }\big )^{\lambda }},s_{\tau \big (1-(1-\nu ^{q}/\tau ^{q})^{\lambda }\big )^{1/q}}\Big ). \end{aligned}$$

Definition 6

[28] Let \(\gamma =(s_{\mu },s_{\nu })\) be a Lq-ROFN, the linguistic score function \(LS(\gamma )\) and the linguistic accuracy function \(LH(\gamma )\) can be, respectively, defined as

$$\begin{aligned} LS(\gamma )=s_{\big (\frac{\tau ^{q}+\mu ^{q}-\nu ^{q}}{2}\big )^{1/q}},\quad LH(\gamma )=s_{(\mu ^q + \nu ^q)^{1/q}}. \end{aligned}$$

For two different Lq-ROFNs \(\gamma _{1}=(s_{\mu _{1}},s_{\nu _{1}})\) and \(\gamma _{2}=(s_{\mu _{2}},s_{\nu _{2}})\), Lin et al. [28] proposed the following comparison law:

(a) if \(LS(\gamma _{1})>LS(\gamma _{2})\), then \(\gamma _{1}\succ \gamma _{2}\), and \(\gamma _{1}\) is superior to \(\gamma _{2}\);

(b) if \(LS(\gamma _{1})=LS(\gamma _{2})\), then

     \(LH(\gamma _{1})>LH(\gamma _{2})\) means \(\gamma _{1}\succ \gamma _{2}\), and \(\gamma _{1}\) is better than \(\gamma _{2}\);

     \(LH(\gamma _{1})=LH(\gamma _{2})\) means \(\gamma _{1}=\gamma _{2}\), and \(\gamma _{1}\) is equal to \(\gamma _{2}\).

During the decision-making theories, constructing the preference relation to solve a problem is an important technique. Motivated by the LIFPR [22, 23] and the LPFPR [25], we can introduce the concept of Lq-ROFPR as follows.

Definition 7

A Lq-ROFPR on \(X=\{x_{1},x_{2},\) \(\ldots ,x_{n}\}\) is characterized by a comparison matrix \(R= (r_{ij})_{n\times n}\subset X\times X\), where \(r_{ij} =(s_{\mu _{ij}}, s_{\nu _{ij}})\) is a Lq-ROFN, and \(s_{\mu _{ij}}, s_{\nu _{ij}}\in \overline{S}\), \(s_{\mu _{ij}}=s_{\nu _{ji}}\), \(s_{\nu _{ij}}=s_{\mu _{ji}}\), \(s_{\mu _{ii}}=s_{\nu _{ii}}=s_{2^{-1/q}\tau }\), \(I^{q}(s_{\mu _{ij}})+I^{q}(s_{\nu _{ij}})\le \tau ^{q}\), for all \(i, j =1, 2,\ldots , n\), \(q\ge 1\).

In Definition 7, for the Lq-ROFN \((s_{\mu _{ij}}, s_{\nu _{ij}})\), \(s_{\mu _{ij}}\) can be explained as the linguistic preference degree of the object \(x_{i}\) over \(x_{j}\), while \(s_{\nu _{ij}}\) is the linguistic preference degree of the object \(x_{j}\) over \(x_{i}\). Especially, when \(q=1\), the Lq-ROFPR \(R=(r_{ij})_{n\times n}\) becomes a LIFPR [22, 23]; when \(q=2\), the Lq-ROFPR \(R=(r_{ij})_{n\times n}\) reduces to a LPFPR [25].

Multiplicative consistency analysis for Lq-ROFPRs

The multiplicative consistency of Lq-ROFPRs is defined as follows:

Definition 8

A Lq-ROFPR \(R=(r_{ij})_{n\times n}\) with \(r_{ij} =(s_{\mu _{ij}}, s_{\nu _{ij}})\) is called multiplicative consistent if

$$\begin{aligned} I(s_{\mu _{ij}})I(s_{\mu _{jk}})I(s_{\mu _{ki}})&=I(s_{\nu _{ij}})I(s_{\nu _{jk}})I(s_{\nu _{ki}}), \nonumber \\ ~~ i,j,k&=1,2,\ldots ,n. \end{aligned}$$
(2)

Theorem 1

A Lq-ROFPR \(R=(r_{ij})_{n\times n}\) with \(r_{ij} =(s_{\mu _{ij}}, s_{\nu _{ij}})\) is of multiplicative consistency if one of the following equations is satisfied:

$$\begin{aligned} (i)~&I(s_{\mu _{ij}})I(s_{\mu _{jk}})I(s_{\mu _{ki}})=I(s_{\nu _{ij}})I(s_{\nu _{jk}})I(s_{\nu _{ki}}),\\&~~ i,j,k=1,2,\ldots ,n,\\ (ii)~&I(s_{\mu _{ij}})I(s_{\mu _{jk}})I(s_{\mu _{ki}})=I(s_{\nu _{ij}})I(s_{\nu _{jk}})I(s_{\nu _{ki}}),\\&~~ 1\le i<j<k\le n,\\ (iii)~&\ln I(s_{\mu _{ij}})+\ln I(s_{\mu _{jk}})+\ln I(s_{\mu _{ki}})=\ln I(s_{\nu _{ij}})\\ +&\ln I(s_{\nu _{jk}})+\ln I(s_{\nu _{ki}}), ~~ i,j,k=1,2,\ldots ,n,\\ (iv) ~&\ln I(s_{\mu _{ij}})+\ln I(s_{\mu _{jk}})+\ln I(s_{\mu _{ki}})=\ln I(s_{\nu _{ij}})\\ +&\ln I(s_{\nu _{jk}})+\ln I(s_{\nu _{ki}}),~~1\le i<j<k\le n. \end{aligned}$$

Proof

Clearly, it is only need to prove Eq. (i) is equivalent to Eq. (ii). This equivalence can be easily proved using Definition 7 and the six possible position cases of i, j, k, which is omitted here. \(\square \)

Theorem 2

A Lq-ROFPR \(R=(r_{ij})_{n\times n}\) with \(r_{ij} =(s_{\mu _{ij}}, s_{\nu _{ij}})\) is multiplicative consistent if and only if \(\Phi (ij)=\Phi (ik)\cdot \Phi (kj)\) for all \(i,j,k=1,2,\ldots ,n\), where \(\Phi (ij)=I(s_{\mu _{ij}})/I(s_{\nu _{ij}})\).

Proof

Considering Definition 7 and the first equation in Theorem 1, this theorem can be easily proved, which is omitted here. \(\square \)

Definition 9

A Lq-ROFPR \(R=(r_{ij})_{n\times n}\) with \(r_{ij} =(s_{\mu _{ij}}, s_{\nu _{ij}})\) is called of weak transitivity, if \(\Phi (ik)\ge 1\) and \(\Phi (kj)\ge 1\), then \(\Phi (ij)\ge 1\), for all \(i,j,k=1,2,\ldots ,n\).

From Theorem 2, it is obvious that if the Lq-ROFPR \(R=(r_{ij})_{n\times n}\) is multiplicative consistent, then R is weakly transitive.

For any kind preference relations, deriving the corresponding reliable weight vector is an important issue. Since the decision making problems under the linguistic environment are becoming more complicated and uncertain than ever, the quantitative priority weight vector will be inappropriate, it cannot rationally reflect the importance degrees of the objects. Considering this situation, it is reasonable to expect that the priority weights derived from the Lq-ROFPR should be Lq-ROFNs.

Given a Lq-ROFPR \(R= (r_{ij})_{n\times n}\) over the set of objects \(X=\{x_{1},x_{2},\) \(\ldots ,x_{n}\}\), let \(s_{\omega }=(s_{\omega _{1}},s_{\omega _{2}},\ldots ,s_{\omega _{n}})^\mathrm{{T}}\) be the Lq-ROFPWV, where \(s_{\omega _{i}}=(s_{\omega ^{\mu }_{i}},s_{\omega ^{\nu }_{i}})\) \((i=1,2,\ldots ,n)\) is a Lq-ROFN, such that \(s_{\omega _{i}^{\mu }},s_{\omega _{i}^{\nu }}\in \overline{S}\) and \(I^{q}(s_{\omega _{i}^{\mu }})+I^{q}(s_{\omega _{i}^{\nu }})\le \tau ^{q}\). Then, \(s_{\omega _{i}^{\mu }}\) and \(s_{\omega _{i}^{\nu }}\) can be, respectively, regarded as the linguistic membership degree and linguistic non-membership degree of the importance of object \(x_{i}\). Moreover, the Lq-ROFPWV \(s_{\omega }\) is said to be normalized if the following equations hold for all \(i=1,2,\ldots ,n\):

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \sum _{j=1,j\ne i}^{n}I^{q}(s_{\omega _{j}^{\mu }})\le I^{q}(s_{\omega _{i}^{\nu }}),\\ I^{q}(s_{\omega _{i}^{\mu }})+(n-2)\tau ^{q}\ge \sum _{j=1,j\ne i}^{n}I^{q}(s_{\omega _{j}^{\nu }}). \end{array}\right. } \end{aligned} \end{aligned}$$
(3)

Theorem 3

Let \(R=(r_{ij})_{n\times n}\) be a Lq-ROFPR, if there is a normalized Lq-ROFPWV \(s_{\omega }=(s_{\omega _{1}},s_{\omega _{2}},\ldots ,s_{\omega _{n}})^\mathrm{{T}}\), such that

$$\begin{aligned} \begin{aligned} r_{ij}&=(s_{\mu _{ij}}, s_{\nu _{ij}})\\ {}&= {\left\{ \begin{array}{ll} \Big (s_{2^{-1/q}\tau },s_{2^{-1/q}\tau }\Big ),~~i=j,\\ \bigg (I^{-1}\Big (\sqrt{I(s_{\omega _{i}^{\mu }})I(s_{\omega _{j}^{\nu }})}\Big ),\\ \qquad I^{-1}\Big (\sqrt{I(s_{\omega _{i}^{\nu }})I(s_{\omega _{j}^{\mu }})}\Big )\bigg ),~~i\ne j, \end{array}\right. } \end{aligned} \end{aligned}$$
(4)

then R is multiplicative consistent.

Proof

In fact, we can easily check that \(\bigg (I^{-1}\Big (\sqrt{I(s_{\omega _{i}^{\mu }})I(s_{\omega _{j}^{\nu }})}\Big ),I^{-1}\Big (\sqrt{I(s_{\omega _{i}^{\nu }})I(s_{\omega _{j}^{\mu }})}\Big )\bigg )\) is a Lq-ROFN, and \(s_{\mu _{ij}}=s_{\nu _{ji}}\) for all \(1\le i,j\le n\). Moreover, if \(i<j<k\),

$$\begin{aligned}&I(s_{\mu _{ij}})I(s_{\mu _{jk}})I(s_{\mu _{ki}})\\&\quad = \sqrt{I(s_{\omega _{i}^{\mu }})I(s_{\omega _{j}^{\nu }})}\sqrt{I(s_{\omega _{j}^{\mu }})I(s_{\omega _{k}^{\nu }})}\sqrt{I(s_{\omega _{k}^{\mu }})I(s_{\omega _{i}^{\nu }})}\\&\quad = \sqrt{I(s_{\omega _{i}^{\nu }})I(s_{\omega _{j}^{\mu }})}\sqrt{I(s_{\omega _{j}^{\nu }})I(s_{\omega _{k}^{\mu }})}\sqrt{I(s_{\omega _{k}^{\nu }})I(s_{\omega _{i}^{\mu }})}\\&\quad = I(s_{\nu _{ij}})I(s_{\nu _{jk}})I(s_{\nu _{ki}}). \end{aligned}$$

Therefore, according to the second equation in Theorem 1, the Lq-ROFPR \(R=(r_{ij})_{n\times n}\) is multiplicative consistent.    \(\square \)

Generally speaking, to derive a reasonable ranking result, the Lq-ROFPR \(R=(r_{ij})_{n\times n}\) provided by the decision maker should be multiplicative consistent, Then, according to Theorem 3, there will be a normalized Lq-ROFPWV \(s_{\omega }=(s_{\omega _{1}},s_{\omega _{2}},\ldots ,s_{\omega _{n}})^\mathrm{{T}}\), such that \(R=(r_{ij})_{n\times n}\) can be expressed as (4). However, in most decision-making problems, it is extremely hard for the expert to give a multiplicative consistent Lq-ROFPR \(R=(r_{ij})_{n\times n}\). In this case, there exist i and j, such that

$$\begin{aligned}&s_{\mu _{ij}}\ne I^{-1}\Big (\sqrt{I(s_{\omega _{i}^{\mu }})I(s_{\omega _{j}^{\nu }})}\Big )~~ or \\&s_{\nu _{ij}}\ne I^{-1}\Big (\sqrt{I(s_{\omega _{i}^{\nu }})I(s_{\omega _{j}^{\mu }})}\Big ),\quad i\ne j. \end{aligned}$$

Clearly, these equations are equivalent to

$$\begin{aligned}&\ln I(s_{\mu _{ij}})\ne 0.5\ln I(s_{\omega _{i}^{\mu }})+0.5\ln I(s_{\omega _{j}^{\nu }})~~ or \\&\ln I(s_{\nu _{ij}})\ne 0.5\ln I(s_{\omega _{i}^{\nu }})+0.5\ln I(s_{\omega _{j}^{\mu }}),\quad i\ne j. \end{aligned}$$

Taking into account the deviations in the above equations, some deviation variables can be introduced as follows for \(i\ne j\):

$$\begin{aligned} \varepsilon _{ij}&=\ln I(s_{\mu _{ij}})- 0.5\ln I(s_{\omega _{i}^{\mu }})-0.5\ln I(s_{\omega _{j}^{\nu }}),\\ \eta _{ij}&=\ln I(s_{\nu _{ij}})- 0.5\ln I(s_{\omega _{i}^{\nu }})-0.5\ln I(s_{\omega _{j}^{\mu }}). \end{aligned}$$

Obviously, the multiplicative consistency level of Lq-ROFPR \(R=(r_{ij})_{n\times n}\) is better if the values of \(\vert \varepsilon _{ij}\vert \) and \(\vert \eta _{ij}\vert \) are smaller. Therefore, we can build a consistency-based model 1 to obtain the normalized Lq-ROFPWV \(s_{\omega }=(s_{\omega _{1}},s_{\omega _{2}},\ldots ,s_{\omega _{n}})^\mathrm{{T}}\).

$$\begin{aligned}&{\textbf {model}}~ {\textbf {1}} ~~~~~~~ \min ~J_{1}=\sum _{i\ne j}\big (\vert \varepsilon _{ij}\vert +\vert \eta _{ij}\vert \big )\\&\begin{aligned}&s.t. {\left\{ \begin{array}{ll} \ln I(s_{\mu _{ij}})- 0.5\ln I(s_{\omega _{i}^{\mu }})-0.5\ln I(s_{\omega _{j}^{\nu }})-\varepsilon _{ij}=0,~~i,j=1,2,\ldots ,n,~ i\ne j,\\ \ln I(s_{\nu _{ij}})- 0.5\ln I(s_{\omega _{i}^{\nu }})-0.5\ln I(s_{\omega _{j}^{\mu }})-\eta _{ij}=0,~~i,j=1,2,\ldots ,n,~ i\ne j,\\ I(s_{\omega _{i}^{\mu }}),I(s_{\omega _{i}^{\nu }})\in [0,\tau ],~ I^{q}(s_{\omega _{i}^{\mu }})+I^{q}(s_{\omega _{i}^{\nu }})\le \tau ^{q}, ~~i=1,2,\ldots ,n,\\ \sum _{j=1,j\ne i}^{n}I^{q}(s_{\omega _{j}^{\mu }})\le I^{q}(s_{\omega _{i}^{\nu }}),~ I^{q}(s_{\omega _{i}^{\mu }})+(n-2)\tau ^{q}\ge \sum _{j=1,j\ne i}^{n}I^{q}(s_{\omega _{j}^{\nu }}),~~i=1,2,\ldots ,n. \end{array}\right. } \end{aligned} \end{aligned}$$

Introducing some positive slack variables \(\varepsilon _{ij}^{+}=\frac{\vert \varepsilon _{ij}\vert +\varepsilon _{ij}}{2}\), \(\varepsilon _{ij}^{-}=\frac{\vert \varepsilon _{ij}\vert -\varepsilon _{ij}}{2}\), \(\eta _{ij}^{+}=\frac{\vert \eta _{ij}\vert +\eta _{ij}}{2}\) and \(\eta _{ij}^{-}=\frac{\vert \eta _{ij}\vert -\eta _{ij}}{2}\), then \(\vert \varepsilon _{ij}\vert =\varepsilon _{ij}^{+}+\varepsilon _{ij}^{-}\), \(\varepsilon _{ij}=\varepsilon _{ij}^{+}-\varepsilon _{ij}^{-}\), \(\vert \eta _{ij}\vert =\eta _{ij}^{+}+\eta _{ij}^{-}\) and \(\eta _{ij}=\eta _{ij}^{+}-\eta _{ij}^{-}\). Moreover, according to the Definition 7, we can easily have \(\varepsilon _{ij}=\eta _{ji}\) and \(\eta _{ij}=\varepsilon _{ji}\). Thus, the model 1 can be rewritten as a model 2, where only the deviations of upper diagonal elements are considered.

$$\begin{aligned}&{\textbf {model}}~ {\textbf {2}} ~~~~~~~ \min ~J=\sum _{1\le i<j\le n}\big (\varepsilon _{ij}^{+}+\varepsilon _{ij}^{-}+\eta _{ij}^{+}+\eta _{ij}^{-}\big )\\&\begin{aligned}&s.t. {\left\{ \begin{array}{ll} \ln I(s_{\mu _{ij}})- 0.5\ln I(s_{\omega _{i}^{\mu }})-0.5\ln I(s_{\omega _{j}^{\nu }})-\varepsilon _{ij}^{+}+\varepsilon _{ij}^{-}=0,~~1\le i<j\le n,\\ \ln I(s_{\nu _{ij}})- 0.5\ln I(s_{\omega _{i}^{\nu }})-0.5\ln I(s_{\omega _{j}^{\mu }})-\eta _{ij}^{+}+\eta _{ij}^{-}=0,~~1\le i<j\le n,\\ I(s_{\omega _{i}^{\mu }}),I(s_{\omega _{i}^{\nu }})\in [0,\tau ],~ I^{q}(s_{\omega _{i}^{\mu }})+I^{q}(s_{\omega _{i}^{\nu }})\le \tau ^{q}, ~~i=1,2,\ldots ,n,\\ \sum _{j=1,j\ne i}^{n}I^{q}(s_{\omega _{j}^{\mu }})\le I^{q}(s_{\omega _{i}^{\nu }}),~ I^{q}(s_{\omega _{i}^{\mu }})+(n-2)\tau ^{q}\ge \sum _{j=1,j\ne i}^{n}I^{q}(s_{\omega _{j}^{\nu }}),~~i=1,2,\ldots ,n,\\ \varepsilon _{ij}^{+}\ge 0, ~\varepsilon _{ij}^{-}\ge 0, ~\eta _{ij}^{+}\ge 0, ~\eta _{ij}^{-}\ge 0, ~ ~1\le i<j\le n. \end{array}\right. } \end{aligned} \end{aligned}$$

In most practical decision-making problems, it is too strict for the experts to give absolutely multiplicative consistent Lq-ROFPRs. To deal with this situation, an appropriate approach is to consider the acceptable consistency. According to the fourth equation in the Theorem 1, we introduce the following concept of acceptably multiplicative consistent Lq-ROFPR.

Definition 10

Let \(\overline{CI}\) be a consistency threshold value, a Lq-ROFPR \(R=(r_{ij})_{n\times n}\) with \(r_{ij}=(s_{\mu _{ij}},s_{\nu _{ij}})\) is said to be acceptably multiplicative consistent if \(CI(R)\le \overline{CI}\), where CI(R) is the consistency index of R and can be computed by

$$\begin{aligned} CI(R)&=\dfrac{1}{C_{n}^{3}\ln \tau }\sum _{1\le i<j<k\le n}\big \vert \ln I(s_{\mu _{ij}})+\ln I(s_{\mu _{jk}})\nonumber \\&\quad +\ln I(s_{\mu _{ki}}) -\ln I(s_{\nu _{ij}})-\ln I(s_{\nu _{jk}})-\ln I(s_{\nu _{ki}})\big \vert . \end{aligned}$$
(5)

Clearly, the Lq-ROFPR \(R=(r_{ij})_{n\times n}\) is absolutely multiplicative consistent iff CI(R)=0, and a smaller CI(R) means the better multiplicative consistency level. If \(CI(R)> \overline{CI}\), on the other hand, the Lq-ROFPR R is unacceptably multiplicative consistent. It is known that an inconsistent preference relation may generate unreasonable and unreliable conclusion, to improve the multiplicative consistency level, a programming model 3 can be built.

$$\begin{aligned}&{\textbf {model}}~ {\textbf {3}} ~~~~~~~ \min ~f=\sum _{1\le i<j\le n}\Big (\big \vert \ln I(s_{\mu _{ij}})-\ln I(s_{\mu _{ij}'})\big \vert +\big \vert \ln I(s_{\nu _{ij}})-\ln I(s_{\nu _{ij}'})\big \vert \Big )\\&\begin{aligned}&s.t. {\left\{ \begin{array}{ll} \dfrac{1}{C_{n}^{3}\ln \tau }\sum \limits _{1\le i<j<k\le n}\Big \vert \ln I(s_{\mu _{ij}'})+\ln I(s_{\mu _{jk}'})+\ln I(s_{\mu _{ki}'}) -\ln I(s_{\nu _{ij}'})-\ln I(s_{\nu _{jk}'})-\ln I(s_{\nu _{ki}'})\Big \vert \le \overline{CI},\\ I(s_{\mu _{ij}'}),I(s_{\nu _{ij}'})\in [0,\tau ],~ I^{q}(s_{\mu _{ij}'})+I^{q}(s_{\nu _{ij}'})\le \tau ^{q}, ~~1\le i<j\le n. \end{array}\right. } \end{aligned} \end{aligned}$$

Definition 11

Let \(R^{k}=(r^{k}_{ij})_{n\times n}\) with \(r^{k}_{ij}=(s_{\mu _{ij}^{k}}, s_{\nu _{ij}^{k}})\) (\(k=1,2\)) be two Lq-ROFPRs, then the distance between \(R^{1}\) and \(R^{2}\) can be defined as

$$\begin{aligned} d(R^{1},R^{2})&=\frac{1}{n(n-1)\ln \tau }\sum _{1\le i<j\le n}\Big (\big \vert \ln I(s_{\mu _{ij}^{1}}) \nonumber \\&\quad -\ln I(s_{\mu _{ij}^{2}})\big \vert +\big \vert \ln I(s_{\nu _{ij}^{1}})-\ln I(s_{\nu _{ij}^{2}})\big \vert \Big ). \end{aligned}$$
(6)

Solving the model 3, an acceptably multiplicative consistent Lq-ROFPR \(R'=(r_{ij}')_{n\times n}\) can be obtained, where the upper diagonal element \(r_{ij}'\) is given as \((s_{\mu _{ij}'}, s_{\nu _{ij}'})\). Moreover, according to Eq. (6), the derived Lq-ROFPR \(R'=(r_{ij}')_{n\times n}\) has the smallest distance from the unacceptably multiplicative consistent \(R=(r_{ij})_{n\times n}\), Therefore, the adjusted Lq-ROFPR \(R'\) can keep more original information. Introducing some positive slack variables \(a_{ij}^{+}\), \(a_{ij}^{-}\), \(b_{ij}^{+}\), \(b_{ij}^{-}\), \(c_{ijk}^{+}\) and \(c_{ijk}^{-}\), the model 3 can be transformed as a model 4.

$$\begin{aligned}&{\textbf {model}}~ {\textbf {4}} ~~~~~~~ \min ~f=\sum _{1\le i<j\le n}\Big (a_{ij}^{+}+a_{ij}^{-}+b_{ij}^{+}+b_{ij}^{-}\Big )\\&\begin{aligned}&s.t. {\left\{ \begin{array}{ll} \ln I(s_{\mu _{ij}})-\ln I(s_{\mu _{ij}'})-a_{ij}^{+}+a_{ij}^{-}=0,~~1\le i<j\le n,\\ \ln I(s_{\nu _{ij}})-\ln I(s_{\nu _{ij}'})-b_{ij}^{+}+b_{ij}^{-}=0,~~1\le i<j\le n,\\ \dfrac{1}{C_{n}^{3}\ln \tau }\sum \limits _{1\le i<j<k\le n}\Big (c_{ijk}^{+}+c_{ijk}^{-}\Big )\le \overline{CI},\\ \ln I(s_{\mu _{ij}'})+\ln I(s_{\mu _{jk}'})+\ln I(s_{\mu _{ki}'}) -\ln I(s_{\nu _{ij}'})\\ \qquad ~-\ln I(s_{\nu _{jk}'})-\ln I(s_{\nu _{ki}'})-c_{ijk}^{+}+c_{ijk}^{-}=0,~~1\le i<j<k\le n,\\ I(s_{\mu _{ij}'}),I(s_{\nu _{ij}'})\in [0,\tau ],~ I^{q}(s_{\mu _{ij}'})+I^{q}(s_{\nu _{ij}'})\le \tau ^{q}, ~~1\le i<j\le n,\\ a_{ij}^{+}\ge 0,~a_{ij}^{-}\ge 0,~b_{ij}^{+}\ge 0,~b_{ij}^{-}\ge 0,~~1\le i<j\le n,\\ c_{ijk}^{+}\ge 0,~c_{ijk}^{-}\ge 0,~~1\le i<j<k\le n. \end{array}\right. } \end{aligned} \end{aligned}$$

Solving the model 4, an acceptably multiplicative consistent Lq-ROFPR \(R'=(r_{ij}')_{n\times n}\) can be constructed via the optimal solutions \(s_{\mu _{ij}'}\) and \(s_{\nu _{ij}'}\).

Remark 1

If someone wants to obtain an absolutely multiplicative consistent Lq-ROFPR \(R'=(r_{ij}')_{n\times n}\) from the unacceptably multiplicative consistent Lq-ROFPR \(R=(r_{ij})_{n\times n}\), the corresponding model 3 can be rewritten as a model 3’.

$$\begin{aligned}&{\textbf {model}}~ {\textbf {3'}} ~~ \min ~f'=\sum _{1\le i<j\le n}\Big (\big \vert \ln I(s_{\mu _{ij}})-\ln I(s_{\mu _{ij}'})\big \vert +\big \vert \ln I(s_{\nu _{ij}})-\ln I(s_{\nu _{ij}'})\big \vert \Big )\\&\begin{aligned}&s.t. {\left\{ \begin{array}{ll} \ln I(s_{\mu _{ij}'})+\ln I(s_{\mu _{jk}'})+\ln I(s_{\mu _{ki}'}) =\ln I(s_{\nu _{ij}'})+\ln I(s_{\nu _{jk}'})+\ln I(s_{\nu _{ki}'}),~~1\le i<j<k\le n,\\ I(s_{\mu _{ij}'}),I(s_{\nu _{ij}'})\in [0,\tau ],~ I^{q}(s_{\mu _{ij}'})+I^{q}(s_{\nu _{ij}'})\le \tau ^{q}, ~~1\le i<j\le n. \end{array}\right. } \end{aligned} \end{aligned}$$

For a Lq-ROFPR \(R=(r_{ij})_{n\times n}\) with \(r_{ij}=(s_{\mu _{ij}}, s_{\nu _{ij}})\), it is called an incomplete Lq-ROFPR if some unknown values exist. As shown before, to obtain a reasonable conclusion, the consistency index of a complete Lq-ROFPR should be as small as possible. Let \(U_{\mu }=\{(i,j)~\mid ~s_{\mu _{ij}}~ is ~\textrm{unknown}\}\) and \(U_{\nu }=\{(i,j)~\mid ~s_{\nu _{ij}}~ is ~\textrm{unknown}\}\), then a programming model 5 can be established to estimate the missing values.

$$\begin{aligned}&{\textbf {model}}~ {\textbf {5}} ~~~~~~~ \min ~\delta \\&\begin{aligned}&s.t. {\left\{ \begin{array}{ll} \dfrac{1}{C_{n}^{3}\ln \tau }\sum \limits _{1\le i<j<k\le n}\Big \vert \ln I(s_{\mu _{ij}})+\ln I(s_{\mu _{jk}})+\ln I(s_{\mu _{ki}}) -\ln I(s_{\nu _{ij}})-\ln I(s_{\nu _{jk}})-\ln I(s_{\nu _{ki}})\Big \vert =\delta ,\\ I(s_{\mu _{ij}})\in [0,\tau ],~ I^{q}(s_{\mu _{ij}})\le \tau ^{q}-I^{q}(s_{\nu _{ij}}), ~~(i,j)\in U_{\mu }, ~(i,j)\notin U_{\nu }, \\ I(s_{\nu _{ij}})\in [0,\tau ],~ I^{q}(s_{\nu _{ij}})\le \tau ^{q}-I^{q}(s_{\mu _{ij}}), ~~(i,j)\notin U_{\mu }, ~(i,j)\in U_{\nu }, \\ I(s_{\mu _{ij}}),I(s_{\nu _{ij}})\in [0,\tau ],~ I^{q}(s_{\mu _{ij}})+I^{q}(s_{\nu _{ij}})\le \tau ^{q}, ~~(i,j)\in U_{\mu }, ~(i,j)\in U_{\nu }. \end{array}\right. } \end{aligned} \end{aligned}$$

By introducing some slack variables \(\theta _{ijk}^{+}\) and \(\theta _{ijk}^{-}\), the model 5 can be transformed as a model 6.

$$\begin{aligned}&{\textbf {model}}~ {\textbf {6}} ~~~~~~~ \min ~\delta \\&\begin{aligned}&s.t. {\left\{ \begin{array}{ll} \dfrac{1}{C_{n}^{3}\ln \tau }\sum \limits _{1\le i<j<k\le n}\Big (\theta _{ijk}^{+}+\theta _{ijk}^{-}\Big )=\delta ,\\ \ln I(s_{\mu _{ij}})+\ln I(s_{\mu _{jk}})+\ln I(s_{\mu _{ki}}) -\ln I(s_{\nu _{ij}})\\ \qquad \qquad \qquad \qquad \quad ~-\ln I(s_{\nu _{jk}})-\ln I(s_{\nu _{ki}})-\theta _{ijk}^{+}+\theta _{ijk}^{-}=0,~~1\le i<j<k\le n,\\ I(s_{\mu _{ij}})\in [0,\tau ],~ I^{q}(s_{\mu _{ij}})\le \tau ^{q}-I^{q}(s_{\nu _{ij}}), ~~(i,j)\in U_{\mu }, ~(i,j)\notin U_{\nu }, \\ I(s_{\nu _{ij}})\in [0,\tau ],~ I^{q}(s_{\nu _{ij}})\le \tau ^{q}-I^{q}(s_{\mu _{ij}}), ~~(i,j)\notin U_{\mu }, ~(i,j)\in U_{\nu }, \\ I(s_{\mu _{ij}}),I(s_{\nu _{ij}})\in [0,\tau ],~ I^{q}(s_{\mu _{ij}})+I^{q}(s_{\nu _{ij}})\le \tau ^{q}, ~~(i,j)\in U_{\mu }, ~(i,j)\in U_{\nu },\\ \theta _{ijk}^{+}\ge 0,~\theta _{ijk}^{-}\ge 0,~~1\le i<j<k\le n. \end{array}\right. } \end{aligned} \end{aligned}$$

Solving the model 6, we can derive some upper diagonal missing values using the optimal solutions \(I(s_{\mu _{ij}^{*}})\big ((i,j)\in U_{\mu }\big )\) and \(I(s_{\nu _{ij}^{*}})\big ((i,j)\in U_{\nu }\big )\). Then, a complete Lq-ROFPR \(R=(r_{ij})_{n\times n}\) can be constructed via the Definition 7. Moreover, if the optimal objective value \(\delta ^{*}\le \overline{CI}\), the complete Lq-ROFPR \(R=(r_{ij})_{n\times n}\) will be acceptably multiplicative consistent. Otherwise, \(R=(r_{ij})_{n\times n}\) has unacceptable consistency.

An approach for MCDM with Lq-ROFPRs

Consider a decision-making problem, let \(X=\{x_{1},x_{2},\ldots ,x_{n}\}\) be the set of alternatives, \(C=\{c_{1},c_{2},\ldots ,c_{m}\}\) be the set of criteria and \(\lambda =(\lambda _{1},\lambda _{2},\ldots ,\lambda _{m})^\mathrm{{T}}\) be the weight vector of criteria, such that \(\lambda _{l}>0\) and \(\sum _{l=1}^{m}\lambda _{l}=1\). An expert team gives a complete or incomplete Lq-ROFPR \(R_{l}=(r_{l,ij})_{n\times n}\) with \(r_{l,ij}=(s_{l\mu _{ij}}, s_{l\nu _{ij}})\) by making pairwise comparison for all alternatives over each criterion \(c_{l}\) \((l=1,2,\ldots ,m)\). When a Lq-ROFPR is incomplete, the model 6 is used to get the complete Lq-ROFPR. If the complete Lq-ROFPR is unacceptably multiplicative consistent, the model 4 is utilized to improve the consistency. Without loss of generality, the Lq-ROFPRs \(R_{l}=(r_{l,ij})_{n\times n}\) \((l=1,2,\ldots ,m)\) offered by the expert team are assumed to be complete and acceptably multiplicative consistent. In the following, we first introduce the concept of comprehensive Lq-ROFPR.

Definition 12

Let \(R_{l}=(r_{l,ij})_{n\times n}\) with \(r_{l,ij}=(s_{l\mu _{ij}}, s_{l\nu _{ij}})\) be a Lq-ROFPR over the set of alternatives \(X=\{x_{1},x_{2},\ldots ,x_{n}\}\) for each criterion \(c_{l}\) \((l=1,2,\ldots ,m)\), and \(\lambda =(\lambda _{1},\lambda _{2},\ldots ,\lambda _{m})^\mathrm{{T}}\) be the weight vector of criteria, such that \(\lambda _{l}>0\) and \(\sum _{l=1}^{m}\lambda _{l}=1\), then the comprehensive Lq-ROFPR \(R_{c}=(r_{c,ij})_{n\times n}\) is defined as

$$\begin{aligned} r_{c,ij}&=(s_{c\mu _{ij}}, s_{c\nu _{ij}})\nonumber \\&=\left( I^{-1}\bigg (\prod _{l=1}^{m}I^{\lambda _{l}}\big (s_{l\mu _{ij}}\big )\bigg ) ,I^{-1}\bigg (\prod _{l=1}^{m}I^{\lambda _{l}}\big (s_{l\nu _{ij}}\big )\bigg )\right) . \end{aligned}$$
(7)

Lemma 1

[52] Let \(x_{i}\ge 0\), \(\lambda _{i}>0\) \((i=1,2,\ldots ,m)\) and \(\sum _{i=1}^{m}\lambda _{i}=1\), then

$$\begin{aligned} \prod _{i=1}^{m}x_{i}^{\lambda _{i}}\le \sum _{i=1}^{m}\lambda _{i}x_{i}, \end{aligned}$$

where equality holds only if \(x_{1}=x_{2}=\cdots =x_{m}\).

Remark 2

Based on Eq. (7), we can easily check that \(I(s_{c\mu _{ij}})\le \tau \), \(I(s_{c\nu _{ij}})\le \tau \), \(s_{c\mu _{ii}}=s_{c\nu _{ii}}=s_{2^{-1/q}\tau }\), \(s_{c\mu _{ij}}=s_{c\nu _{ji}}\) and \(s_{c\nu _{ij}}=s_{c\mu _{ji}}\). Moreover, from the Lemma 1,

$$\begin{aligned}&I^{q}(s_{c\mu _{ij}})+I^{q}(s_{c\nu _{ij}})\\&\quad =\Big (\prod _{l=1}^{m}I^{\lambda _{l}}\big (s_{l\mu _{ij}}\big )\Big )^{q}+\Big (\prod _{l=1}^{m}I^{\lambda _{l}}\big (s_{l\nu _{ij}}\big )\Big )^{q}\\&\quad = \prod _{l=1}^{m}\Big (I^{q}\big (s_{l\mu _{ij}}\big )\Big )^{\lambda _{l}}+\prod _{l=1}^{m}\Big (I^{q}\big (s_{l\nu _{ij}}\big )\Big )^{\lambda _{l}}\\&\quad \le \sum _{l=1}^{m}\lambda _{l}I^{q}\big (s_{l\mu _{ij}}\big )+\sum _{l=1}^{m}\lambda _{l}I^{q}\big (s_{l\nu _{ij}}\big )\\&\quad =\sum _{l=1}^{m}\lambda _{l}\Big (I^{q}\big (s_{l\mu _{ij}}\big )+I^{q}\big (s_{l\nu _{ij}}\big )\Big ) \le \sum _{l=1}^{m}\lambda _{l}\big (\tau ^{q}\big )=\tau ^{q}. \end{aligned}$$

Thus, according to Definition 7, \(R_{c}=(r_{c,ij})_{n\times n}\) with \(r_{c,ij}=(s_{c\mu _{ij}}, s_{c\nu _{ij}})\) is a Lq-ROFPR.

Theorem 4

If all Lq-ROFPRs \(R_{l}=(r_{l,ij})_{n\times n}\) with \(r_{l,ij}=(s_{l\mu _{ij}}, s_{l\nu _{ij}})\) \((l=1,2,\ldots ,m)\) are acceptably multiplicative consistent, then the comprehensive Lq-ROFPR \(R_{c}=(r_{c,ij})_{n\times n}\) is also of acceptable consistency.

Proof

When the Lq-ROFPR \(R_{l}=(r_{l,ij})_{n\times n}\) with \(r_{l,ij}=(s_{l\mu _{ij}}, s_{l\nu _{ij}})\) is acceptably multiplicative consistent, we will have \(CI(R_{l})\le \overline{CI}\). Let \(\chi _{ij}=\ln I(s_{c\mu _{ij}})+\ln I(s_{c\mu _{jk}})+\ln I(s_{c\mu _{ki}}) -\ln I(s_{c\nu _{ij}})-\ln I(s_{c\nu _{jk}})-\ln I(s_{c\nu _{ki}})\), from Eq. (7), we can derive

$$\begin{aligned} \chi _{ijk}=&\sum _{l=1}^{m}\lambda _{l}\ln I(s_{l\mu _{ij}})+\sum _{l=1}^{m}\lambda _{l}\ln I(s_{l\mu _{jk}})\\&+\sum _{l=1}^{m}\lambda _{l}\ln I(s_{l\mu _{ki}}) -\sum _{l=1}^{m}\lambda _{l}\ln I(s_{l\nu _{ij}})\\&-\sum _{l=1}^{m}\lambda _{l}\ln I(s_{l\nu _{jk}})-\sum _{l=1}^{m}\lambda _{l}\ln I(s_{l\nu _{ki}})\\ =&\sum _{l=1}^{m}\lambda _{l}\big (\ln I(s_{l\mu _{ij}})+\ln I(s_{l\mu _{jk}})+\ln I(s_{l\mu _{ki}})\\&-\ln I(s_{l\nu _{ij}})-\ln I(s_{l\nu _{jk}})-\ln I(s_{l\nu _{ki}})\big ). \end{aligned}$$

Hence,

$$\begin{aligned} CI(R_{c})&=\dfrac{1}{C_{n}^{3}\ln \tau }\sum _{1\le i<j<k\le n}\big \vert \chi _{ijk}\big \vert \\&=\dfrac{1}{C_{n}^{3}\ln \tau }\sum _{1\le i<j<k\le n}\big \vert \sum _{l=1}^{m}\lambda _{l}\big (\ln I(s_{l\mu _{ij}})+\ln I(s_{l\mu _{jk}})\\ {}&\quad +\ln I(s_{l\mu _{ki}}) -\ln I(s_{l\nu _{ij}})-\ln I(s_{l\nu _{jk}})-\ln I(s_{l\nu _{ki}})\big )\big \vert \\&\le \sum _{l=1}^{m}\lambda _{l}\dfrac{1}{C_{n}^{3}\ln \tau }\sum _{1\le i<j<k\le n}\big \vert \ln I(s_{l\mu _{ij}})+\ln I(s_{l\mu _{jk}})\\ {}&\quad +\ln I(s_{l\mu _{ki}})-\ln I(s_{l\nu _{ij}})-\ln I(s_{l\nu _{jk}})-\ln I(s_{l\nu _{ki}})\big \vert \\&=\sum _{l=1}^{m}\lambda _{l}CI(R_{l})\le \sum _{l=1}^{m}\lambda _{l}\overline{CI}=\overline{CI}. \end{aligned}$$

Therefore, the comprehensive Lq-ROFPR \(R_{c}\) is acceptably multiplicative consistent, which completes the proof. \(\square \)

If the consistency threshold \(\overline{CI}=0\), from Theorem 4, we can easily obtain the following corollary.

Corollary 1

If all Lq-ROFPRs \(R_{l}=(r_{l,ij})_{n\times n}\) with \(r_{l,ij}=(s_{l\mu _{ij}}, s_{l\nu _{ij}})\) \((l=1,2,\ldots ,m)\) are absolutely multiplicative consistent, then the comprehensive Lq-ROFPR \(R_{c}=(r_{c,ij})_{n\times n}\) is also of absolute consistency.

To determine the weights of criteria, the decision maker team provides a Lq-ROFPR \(A=(a_{ij})_{m\times m}\) with \(a_{ij}=(s_{a_{ij}^{\mu }}, s_{a_{ij}^{\nu }})\) by making pairwise comparison for all criteria. Without loss of generality, the Lq-ROFPR \(A=(a_{ij})_{m\times m}\) is also assumed to be complete and acceptably multiplicative consistent. Taking the Lq-ROFPR \(A=(a_{ij})_{m\times m}\) into the model 2, we can obtain a normalized Lq-ROFPWV \(s_{w}=(s_{w_{1}},s_{w_{2}},\ldots ,s_{w_{m}})^\mathrm{{T}}\) with \(s_{w_{l}}=(s_{w_{l\mu }},s_{w_{l\nu }})\) \((l=1,2,\ldots ,m)\). For a Lq-ROFN \(s_{w_{l}}=(s_{w_{l\mu }},s_{w_{l\nu }})\), it can be transformed into an interval linguistic number \(s_{w_{l}^{I}}=[s_{\underline{w_{l}}},s_{\overline{w_{l}}}]\), where \(s_{\underline{w_{l}}}=s_{w_{l\mu }}\) and \(s_{\overline{w_{l}}}=s_{\big (\tau ^{q}-(w_{l\nu })^{q}\big )^{1/q}}\). Motivated by the possibility degree of interval number [53], for two interval linguistic numbers \(s_{w_{i}^{I}}=[s_{\underline{w_{i}}},s_{\overline{w_{i}}}]\) and \(s_{w_{j}^{I}}=[s_{\underline{w_{j}}},s_{\overline{w_{j}}}]\), the possibility degree of \(s_{w_{i}^{I}}\ge s_{w_{j}^{I}}\) can be defined as

$$\begin{aligned} p(s_{w_{i}^{I}}\ge s_{w_{j}^{I}})&=\max \Bigg \{1-\max \Bigg \{\nonumber \\&\quad \frac{I(s_{\overline{w_{j}}})-I(s_{\underline{w_{i}}})}{I(s_{\overline{w_{i}}})-I(s_{\underline{w_{i}}})+I(s_{\overline{w_{j}}})-I(s_{\underline{w_{j}}})},0\Bigg \},0\Bigg \}. \end{aligned}$$
(8)

Let \(p_{ij}=p(s_{w_{i}^{I}}\ge s_{w_{j}^{I}})\) \((i,j=1,2,\ldots ,m)\), then a possibility degree matrix \(P=(p_{ij})_{m\times m}\) can be constructed. The priority vector of P can reflect the importance of criteria [54], and the weight \(\lambda _{i}\) \((i=1,2,\ldots ,m)\) is given by

$$\begin{aligned} \lambda _{i}=\frac{1}{m(m-1)}\bigg (\sum _{j=1}^{m}p_{ij}+\frac{m}{2}-1\bigg ). \end{aligned}$$
(9)

Therefore, the weight vector of criteria is derived as \(\lambda =(\lambda _{1},\lambda _{2},\ldots ,\lambda _{m})^\mathrm{{T}}\).

On the basis of the above discussions, an MCDM method with incomplete Lq-ROFPRs is put forward.

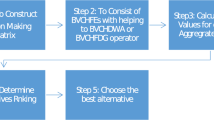
Algorithm I:

Input: Consistency threshold \(\overline{CI}\), parameter q, Lq-ROFPRs \(R_{l}\) \((l=1,2,\ldots ,m)\) and A.

Output: Priority weights and ranking order.

Step 1. For a set of alternatives \(X=\{x_{1},x_{2},\ldots ,x_{n}\}\) and a set of criteria \(C=\{c_{1},c_{2},\ldots ,c_{m}\}\), an expert team provides some Lq-ROFPRs \(R_{l}=(r_{l,ij})_{n\times n}\) by comparing these n alternatives for each criterion \(c_{l}\) \((l=1,2,\ldots ,m)\). In addition, the decision maker team also offers a Lq-ROFPR \(A=(a_{ij})_{m\times m}\) by making pairwise comparison for all criteria.

Step 2. If all the Lq-ROFPRs \(R_{l}=(r_{l,ij})_{n\times n}\) \((l=1,2,\ldots ,m)\) and \(A=(a_{ij})_{m\times m}\) are complete, go to the Step 3. Otherwise, we use the model 6 to obtain the missing values in each incomplete Lq-ROFPR, and the corresponding complete Lq-ROFPR is still denoted as \(R_{l}\) or A.

Step 3. Based on Eq. (5), we compute all the consistency indexes \(CI(R_{l})\) (\(l=1,2,\ldots ,m\)) and CI(A). Then, Definition 10 is utilized to check whether the complete Lq-ROFPR is acceptably multiplicative consistent or not. If all the Lq-ROFPRs are of acceptable consistency, let \(R_{l}'=(r'_{l,ij})_{n\times n}=(r_{l,ij})_{n\times n}=R_{l}\) and \(A'=(a_{ij}')_{m\times m}=(a_{ij})_{m\times m}=A\), go to the Step 4. Otherwise, we use the model 4 to derive the corresponding acceptably multiplicative consistent Lq-ROFPR \(R_{l}'=(r'_{l,ij})_{n\times n}\) or \(A'=(a_{ij}')_{m\times m}\).

Step 4. Inserting the acceptably multiplicative consistent Lq-ROFPR \(A'=(a_{ij}')_{m\times m}\) into the model 2 to get the normalized Lq-ROFPWV \(s_{w}=(s_{w_{1}},s_{w_{2}},\ldots ,s_{w_{m}})^\mathrm{{T}}\). Then, we adopt Eq. (8) to obtain the possibility degree matrix. According to Eq. (9), the criterion weight vector \(\lambda =(\lambda _{1},\lambda _{2},\ldots ,\lambda _{m})^\mathrm{{T}}\) can be derived.

Step 5. On the basis of all acceptably multiplicative consistent Lq-ROFPRs \(R_{l}'=(r'_{l,ij})_{n\times n}\) (\(l=1,2,\ldots ,m\)) and the criterion weight vector \(\lambda =\{\lambda _{1},\lambda _{2},\ldots ,\lambda _{m}\}^\mathrm{{T}}\), we use Eq. (7) to get the comprehensive Lq-ROFPR \(R_{c}^{*}=(r_{c,ij}^{*})_{n\times n}\).

Step 6. Taking the acceptably multiplicative consistent Lq-ROFPR \(R_{c}^{*}=(r_{c,ij}^{*})_{n\times n}\) into the model 2 to obtain the normalized Lq-ROFPWV \(s_{\omega }=(s_{\omega _{1}},s_{\omega _{2}},\ldots ,s_{\omega _{n}})^\mathrm{{T}}\).

Step 7. According to the comparison law for Lq-ROFNs, we compare the priority weights \(s_{\omega _{k}}\) (\(k=1,2,\ldots ,n\)) to gain the ranking order of alternatives.

Step 8. End.

From the Algorithm I, we can see that the computational complexity is mainly dependent on the constructed programming models 2 and 4. For a Lq-ROFPR with n order, when we use the model 2 to obtain the normalized Lq-ROFPWV, there are \(2n^{2}\) decision variables and \(3n^{2}+4n\) constraints in this model. Therefore, the computational complexity is \(O(n^{2})\). The optimization model 2 can be easily solved using the Lingo software, and the corresponding computational complexity is quite low, which does not need too much time. Similarly, when we apply the model 4 to adjust an unacceptably multiplicative consistent Lq-ROFPR, the numbers of decision variables and constraints are \(\frac{1}{3}n^{3}+2n^{2}-\frac{7}{3}n\) and \(\frac{2}{3}n^{3}+\frac{7}{2}n^{2}-\frac{25}{6}n\), respectively. The computational complexity of model 4 is \(O(n^{3})\), which is bigger than that of model 2. Clearly, the model 4 can also be solved by using the Lingo software, and the computational complexity of this model remains unchanged even the number of Lq-ROFPRs with n order is m.

Application examples and comparison analysis

Application examples

Example 1

In the modern society, the manager is a very important person in every organization, because his/her decisions can mainly determine the sustainability and development or the collapse and failure of an organization. Recently, an engineering company wants to select a manager, and there are four candidates, \(x_{1}\): the first candidate Mike, \(x_{2}\): the second candidate Lucy, \(x_{3}\): the third candidate John and \(x_{4}\): the fourth candidate James. The selection of the manager is a complex process, the influencing factors should cover the requirements and relate to the specific job description. Motivated by the manager selection problem in [55], we choose five criteria, including \(c_{1}\): personal ability (including educational background, number of diplomas and professional knowledge), \(c_{2}\): communication ability (including negotiation, presentation and problem solving skills), \(c_{3}\): management experience (including years of experience, conflict management and team management skills), \(c_{4}\): analytical ability (including creativity, design and strategic planning skills) and \(c_{5}\): performance management (including management knowledge, self-management and diversity management). Now, the company wants to use Lq-ROFNs to evaluate these four candidates based on a LTS \(S=\{s_{0}: \mathrm{extremely~ bad}, s_{1}: \mathrm{very~ bad},s_{2}: \textrm{bad}, s_{3}: \mathrm{relatively~bad}, s_{4}: a~\mathrm{little ~bad},s_{5}: \textrm{fair}, s_{6}: a~\mathrm{little ~good},s_{7}: \mathrm{relatively~good}, s_{8}: \textrm{good}, s_{9}: \mathrm{very~ good},s_{10}: \mathrm{extremely ~good}\}\). By making pairwise comparison for the four candidates with respect to each criterion, five Lq-ROFPRs \(R_{l}=(r_{l,ij})_{4\times 4}\) \((l=1,2,3,4,5)\) are offered and listed in Tables  2, 3, 4, 5 and 6, where the parameter q is assumed to be 2. When the company is unwilling or unable to give some judgements, missing values are permitted. Moreover, the company also provides a Lq-ROFPR \(A=(a_{ij})_{5\times 5}\) by making pairwise comparison for all the criteria, which is shown in Table  7.

Table 2 Lq-ROFPR \(R_{1}=(r_{1,ij})_{4\times 4}\) for the criterion \(c_{1}\)
Full size table
Table 3 Lq-ROFPR \(R_{2}=(r_{2,ij})_{4\times 4}\) for the criterion \(c_{2}\)
Full size table
Table 4 Lq-ROFPR \(R_{3}=(r_{3,ij})_{4\times 4}\) for the criterion \(c_{3}\)
Full size table
Table 5 Lq-ROFPR \(R_{4}=(r_{4,ij})_{4\times 4}\) for the criterion \(c_{4}\)
Full size table
Table 6 Lq-ROFPR \(R_{5}=(r_{5,ij})_{4\times 4}\) for the criterion \(c_{5}\)
Full size table
Table 7 Lq-ROFPR \(A=(a_{ij})_{5\times 5}\) on the criteria set C
Full size table

In the following, we adopt the proposed method to find the most suitable manager.

\({\textbf {Step 1.}}\) The corresponding Lq-ROFPRs have been offered in Tables  2, 2, 3, 4, 5, 6 and 7.

\({\textbf {Step 2.}}\) For the incomplete Lq-ROFPRs, all the upper diagonal missing values can be derived using the model 6.

$$\begin{aligned}{} & {} \displaystyle s_{1\mu _{14}}=s_{7.1414},\quad s_{1\mu _{34}}=s_{3.1757},\quad s_{1\nu _{34}}=s_{0.5833},\\{} & {} \displaystyle s_{2\nu _{23}}=s_{2.2543},\quad s_{2\mu _{24}}=s_{7.4667},\quad s_{4\nu _{12}}=s_{6.1714},\\{} & {} \displaystyle s_{4\mu _{34}}=s_{4.8980},\quad s_{5\mu _{13}}=s_{1.4694},\quad s_{5\nu _{34}}=s_{2.2959}. \end{aligned}$$

\({\textbf {Step 3.}}\) For the complete Lq-ROFPRs, according to Eq. (5), we have \(CI(R_{1})=0.0916\), \(CI(R_{2})=0.1612\), \(CI(R_{3})=0.1355\), \(CI(R_{4})=0.0669\), \(CI(R_{5})=0.0335\) and \(CI(A)=0.2789\). Let the consistency threshold \(\overline{CI}=0.1\), then the Lq-ROFPRs \(R_{2}\), \(R_{3}\) and A are unacceptably multiplicative consistent. Pluging the Lq-ROFPRs \(R_{2}\), \(R_{3}\) and A into the model 4, respectively, three adjusted Lq-ROFPRs \(R_{2}'\), \(R_{3}'\) and \(A'\) can be derived.

$$\begin{aligned} R_{2}'=\left( \begin{array}{cccccc} (s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{3},s_{7})&{}(s_{5.2171},s_{5.2385})&{}(s_{4},s_{5})\\ (s_{7},s_{3})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{5},s_{2.2543})&{}(s_{7.4667},s_{4})\\ (s_{5.2385},s_{5.2171})&{}(s_{2.2543},s_{5})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{6.3887},s_{5.0182})\\ (s_{5},s_{4})&{}(s_{4},s_{7.4667})&{}(s_{5.0182},s_{6.3887})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})\\ \end{array} \right) , \end{aligned}$$
$$\begin{aligned} R_{3}'=\left( \begin{array}{cccccc} (s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{5},s_{4})&{}(s_{4},s_{6})&{}(s_{6},s_{6})\\ (s_{4},s_{5})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{4},s_{7.5000})&{}(s_{6.3396},s_{5})\\ (s_{6},s_{4})&{}(s_{7.5000},s_{4})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{8},s_{5})\\ (s_{6},s_{6})&{}(s_{5},s_{6.3396})&{}(s_{5},s_{8})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})\\ \end{array} \right) , \end{aligned}$$
$$\begin{aligned} A'=\left( \begin{array}{cccccc} (s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{6},s_{4})&{}(s_{6},s_{5})&{}(s_{7},s_{4})&{}(s_{8},s_{3})\\ (s_{4},s_{6})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{4},s_{5})&{}(s_{6},s_{5})&{}(s_{7},s_{6})\\ (s_{5},s_{6})&{}(s_{5},s_{4})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{7},s_{4.6667})&{}(s_{6},s_{2})\\ (s_{4},s_{7})&{}(s_{5},s_{6})&{}(s_{4.6667},s_{7})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{5},s_{3.0220})\\ (s_{3},s_{8})&{}(s_{6},s_{7})&{}(s_{2},s_{6})&{}(s_{3.0220},s_{5})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})\\ \end{array} \right) . \end{aligned}$$

\({\textbf {Step 4.}}\) Taking the Lq-ROFPR \(A'\) into the model 2, we can get a normalized Lq-ROFPWV.

$$\begin{aligned} s_{w}&= \big ((s_{5.3031},s_{5.9619}),(s_{2.6837},s_{7.5143}),\\ {}&\quad (s_{4.1933},s_{6.7885}),(s_{2.9120},s_{9.2399}),(s_{1.5096},s_{8.5852})\big )^\mathrm{{T}}. \end{aligned}$$

The normalized Lq-ROFPWV \(s_{w}\) can be transformed into an interval linguistic vector:

$$\begin{aligned} s_{w^{I}}&= \big ([s_{5.3031},s_{8.0284}],[s_{2.6837},s_{6.5981}],\\ {}&\quad [s_{4.1933},s_{7.3428}],[s_{2.9120},s_{3.8242}],[s_{1.5096},s_{5.1278}]\big )^\mathrm{{T}}. \end{aligned}$$

Based on Eq. (8), the possibility degree matrix \(P=(p_{ij})_{5\times 5}\) is given by

$$\begin{aligned} P=\left( \begin{array}{cccccc} 0.5&{}0.8050&{}0.6528&{}1&{}1\\ 0.1950&{}0.5&{}0.3404&{}0.7637&{}0.6755\\ 0.3472&{}0.6596&{}0.5&{}1&{}0.8619\\ 0&{}0.2363&{}0&{}0.5&{}0.5109\\ 0&{}0.3245&{}0.1381&{}0.4891&{}0.5\\ \end{array} \right) . \end{aligned}$$

According to Eq. (9), the criterion weight vector can be derived as

$$\begin{aligned} \lambda =(0.2729,0.1987,0.2434,0.1374,0.1476)^\mathrm{{T}}. \end{aligned}$$

\({\textbf {Step 5.}}\) From the acceptably multiplicative consistent Lq-ROFPRs \(R_{1}'=R_{1}\), \(R_{2}'\), \(R_{3}'\), \(R_{4}'=R_{4}\) and \(R_{5}'=R_{5}\), using Eq. (7), a comprehensive Lq-ROFPR \(R_{c}^{*}\) can be obtained.

$$\begin{aligned} R_{c}^{*}=\left( \begin{array}{cccccc} (s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{4.0418},s_{5.7564})&{}(s_{3.0106},s_{5.6280})&{}(s_{5.3325},s_{5.8749})\\ (s_{5.7564},s_{4.0418})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{4.4320},s_{5.4266})&{}(s_{6.9112},s_{4.3576})\\ (s_{5.6280},s_{3.0106})&{}(s_{5.4266},s_{4.4320})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})&{}(s_{5.1855},s_{2.6473})\\ (s_{5.8749},s_{5.3325})&{}(s_{4.3576},s_{6.9112})&{}(s_{2.6473},s_{5.1855})&{}(s_{\frac{10}{\sqrt{2}}},s_{\frac{10}{\sqrt{2}}})\\ \end{array} \right) . \end{aligned}$$

\({\textbf {Step 6.}}\) Inserting the comprehensive Lq-ROFPR \(R_{c}^{*}\) into the model 2, a normalized Lq-ROFPWV can be derived as

$$\begin{aligned}&s_{\omega }=(s_{\omega _{1}},s_{\omega _{2}},s_{\omega _{3}},s_{\omega _{4}})^\mathrm{{T}}= \big ((s_{2.0701},s_{8.4879}),\\ {}&(s_{3.9039},s_{7.8913}), (s_{3.7317},s_{5.0315}),(s_{2.4063},s_{8.9223})\big )^\mathrm{{T}}. \end{aligned}$$

\({\textbf {Step 7.}}\) By calculating the linguistic score functions of \(s_{\omega _{i}}\) (\(i=1,2,3,4)\), we have \(LS(s_{\omega _{1}})=s_{3.4402}\), \(LS(s_{\omega _{2}})=s_{3.3531}\), \(LS(s_{\omega _{3}})=s_{5.5117}\) and \(LS(s_{\omega _{4}})=s_{2.7021}\). According to the comparison law for Lq-ROFNs, we have \(s_{\omega _{3}}\succ s_{\omega _{1}}\succ s_{\omega _{2}}\succ s_{\omega _{4}}\), which means the most suitable manager is the third candidate John.

Example 2

In the early morning of September 15th, 2016, super typhoon Meranti landed in the Xiamen City, Fujian Province, China. It was a strong typhoon hit the mainland, the maximum wind power of the landing center was 52 m/s (16 level), which caused great damage and economic loss. In Fujian, 18 people died and 11 others were missing, 18.3 thousand houses were damaged, 10.5 million hectares of crops were affected and more than 33.1 thousand people were forced to relocate. The direct economic losses in Fujian were over 16.9 billion yuan. Using “Typhoon Meranti” as the hashtag to crawl related public comments from Sina Weibo and Tencent Weibo, Wan et al. [56] collected 19,498 comments, covering the emergency and post-disaster disposal related comments. Utilizing the Python software to extract keywords, Wan et al. [56] further selected the top 300 keywords and clustered them into seven categories. By ignoring three keywords, Wan et al. [56] finally got four decision criteria, including \(c_{1}\): economic loss, \(c_{2}\): timeliness, \(c_{3}\): disaster relief and \(c_{4}\): casualties. The weights of these criteria were derived as 0.42, 0.37, 0.18 and 0.03, respectively (the details were shown in Tables  2 and  3 in [56]). On August 8th, 2020, a typhoon landed in the coastal area of a city. The wind near the center was 16 level, the wind power of the center was 52 m/s and the pressure of the center was 930 HPA [57]. To help the department of emergency management to propose an emergency plan, the government gathered some experts in meteorology, typhoon, flooding, electricity, disaster relief and other fields to form a decision team. The team searched the history database and found this typhoon is similar to the typhoon Meranti. Therefore, the decision team decided to use the historical data of Meranti. According to the experience of Xiamen City, the team offered four possible alternatives, \(A_{1}\): 800 evacuees, 1002 commanders and fighters, 170 fire engines, 100 fire boats, 3100 rescue equipment; \(A_{2}\): 650 evacuees, 900 commanders and fighters, 130 fire engines, 80 fire boats, 2980 rescue equipment; \(A_{3}\): 700 evacuees, 950 commanders and fighters, 150 fire engines, 120 fire boats, 3400 rescue equipment; \(A_{4}\): 750 evacuees, 970 commanders and fighters, 145 fire engines, 125 fire boats, 2690 rescue equipment [57]. To find the most suitable alternative, the department of emergency management decided to use Lq-ROFNs to evaluate these four alternatives based on a LTS \(S=\{s_{0}: \mathrm{extremely ~low}, s_{1}: \mathrm{very ~low}, s_{2}: \textrm{low}, s_{3}: \mathrm{sightly~ low}, s_{4}: \textrm{medium}, s_{5}: \mathrm{sightly ~high}, s_{6}: \textrm{high}, s_{7}: \mathrm{very ~high}, s_{8}: \mathrm{extremely~ high}\}\). By making pairwise comparison for the four alternatives with respect to each criterion, four Lq-ROFPRs \(R_{l,N}=(r_{l,ij}^{N})_{4\times 4}\) \((l=1,2,3,4)\) were constructed and listed in Tables  8, 9, 10 and 11.

Table 8 Lq-ROFPR \(R_{1,N}=(r_{1,ij}^{N})_{4\times 4}\) for the criterion \(c_{1}\) (economic loss)
Full size table
Table 9 Lq-ROFPR \(R_{2,N}=(r_{2,ij}^{N})_{4\times 4}\) for the criterion \(c_{2}\) (timeliness)
Full size table
Table 10 Lq-ROFPR \(R_{3,N}=(r_{3,ij}^{N})_{4\times 4}\) for the criterion \(c_{3}\) (disaster relief)
Full size table
Table 11 Lq-ROFPR \(R_{4,N}=(r_{4,ij}^{N})_{4\times 4}\) for the criterion \(c_{4}\) (casualties)
Full size table

Assuming \(q=1\) and \(\overline{CI}=0.1\), based on the proposed approach, we can derive four acceptably multiplicative consistent Lq-ROFPRs \(R_{l,N}'\) \((l=1,2,3,4)\).

$$\begin{aligned} R_{1,N}'= \left( \begin{array}{cccccc} (s_{4},s_{4}) &{}(s_{4.8000},s_{2})&{}(s_{6.0000},s_{0.6349})&{}(s_{6},s_{1})\\ (s_{2},s_{4.8000}) &{}(s_{4},s_{4})&{}(s_{5.9686},s_{1})&{}(s_{5},s_{2})\\ (s_{0.6349},s_{6.0000}) &{}(s_{1},s_{5.9686})&{}(s_{4},s_{4})&{}(s_{2.0943},s_{5})\\ (s_{1},s_{6}) &{}(s_{2},s_{5})&{}(s_{5},s_{2.0943})&{}(s_{4},s_{4})\\ \end{array} \right) , \end{aligned}$$
$$\begin{aligned} R_{2,N}'= \left( \begin{array}{cccccc} (s_{4},s_{4}) &{}(s_{3.1173},s_{1.0062})&{}(s_{7},s_{1})&{}(s_{6.0000},s_{2})\\ (s_{1.0062},s_{3.1173}) &{}(s_{4},s_{4}) &{}(s_{4.5187},s_{2})&{}(s_{1.2346},s_{1})\\ (s_{1},s_{7}) &{}(s_{2},s_{4.5187})&{}(s_{4},s_{4}) &{}(s_{2.7274},s_{4.1987})\\ (s_{2},s_{6.0000})&{}(s_{1},s_{1.2346})&{}(s_{4.1987},s_{2.7274})&{}(s_{4},s_{4})\\ \end{array} \right) , \end{aligned}$$
$$\begin{aligned}&R_{3,N}'= \left( \begin{array}{cccccc} (s_{4},s_{4}) &{}(s_{1.9852},s_{2})&{}(s_{4.5471},s_{2})&{}(s_{5},s_{2})\\ (s_{2},s_{1.9852}) &{}(s_{4},s_{4})&{}(s_{4},s_{2})&{}(s_{6},s_{2})\\ (s_{2},s_{4.5471})&{}(s_{2},s_{4})&{}(s_{4},s_{4})&{}(s_{5},s_{3})\\ (s_{2},s_{5})&{}(s_{2},s_{6})&{}(s_{3},s_{5})&{}(s_{4},s_{4})\\ \end{array} \right) ,\\&R_{4,N}'= \left( \begin{array}{cccccc} (s_{4},s_{4}) &{}(s_{4},s_{2})&{}(s_{5},s_{3})&{}(s_{6},s_{2})\\ (s_{2},s_{4}) &{}(s_{4},s_{4})&{}(s_{2.4000},s_{3})&{}(s_{4},s_{2})\\ (s_{3},s_{5})&{}(s_{3},s_{2.4000})&{}(s_{4},s_{4})&{}(s_{5},s_{2})\\ (s_{2},s_{6})&{}(s_{2},s_{4})&{}(s_{2},s_{5})&{}(s_{4},s_{4})\\ \end{array} \right) . \end{aligned}$$

According to Eq. (7), we can obtain a comprehensive Lq-ROFPR \(R_{c,N}^{*}\).

$$\begin{aligned} R_{c,N}^{*}= \left( \begin{array}{cccccc} (s_{4},s_{4}) &{}(s_{3.4713},s_{1.5511})&{}(s_{6.0100},s_{0.9675})&{}(s_{5.8063},s_{1.4948})\\ (s_{1.5511},s_{3.4713}) &{}(s_{4},s_{4})&{}(s_{4.8753},s_{1.5131})&{}(s_{3.0589},s_{1.5476})\\ (s_{0.9675},s_{6.0100})&{}(s_{1.5131},s_{4.8753})&{}(s_{4},s_{4})&{}(s_{2.7723},s_{4.1594})\\ (s_{1.4948},s_{5.8063})&{}(s_{1.5476},s_{3.0589})&{}(s_{4.1594},s_{2.7723})&{}(s_{4},s_{4})\\ \end{array} \right) . \end{aligned}$$
Table 12 Lq-ROFPWVs and ranking orders for different parameter q (\(\overline{CI}=0.1\))
Full size table
Table 13 Lq-ROFPWVs and ranking orders for different consistency threshold \(\overline{CI}\) (\(q=1\))
Full size table

Taking the comprehensive Lq-ROFPR \(R_{c,N}^{*}\) into the model 2, a normalized Lq-ROFPWV can be derived as

$$\begin{aligned} s_{\omega ,N}=\big (&(s_{3.1579},s_{2.6562}),(s_{1.3070},s_{4.5071}),\\&(s_{0.5080},s_{7.4920}),(s_{0.8412},s_{7.1588})\big )^\mathrm{{T}}. \end{aligned}$$

By calculating the linguistic score functions, the four alternatives can be ranked as \(x_{1}\succ x_{2}\succ x_{4}\succ x_{3}\), which means the optimal emergency plan is \(x_{1}\).

In Tables  12 and  13, the effect of parameter q and consistency threshold \(\overline{CI}\) on the Lq-ROFPWVs and ranking orders are, respectively, presented. From Table  12, when the parameter q changes, we can see that the optimal emergency plan is always \(x_{1}\), but the ranking order is slightly different. For different q, the unknown linguistic variables determined from the incomplete Lq-ROFPRs may be different. For example, when q varies from 1 to 5, the \(r_{1,34}^{N}\) will be derived as \((s_{2.0943},s_{5})\), \((s_{6.1934},s_{5})\), \((s_{7.2873},s_{5})\), \((s_{2.0833},s_{5})\) and \((s_{7.5015},s_{5})\), respectively. Clearly, \((s_{7.2873},s_{5})\) and \((s_{7.5015},s_{5})\) are neither LIFNs nor LPFNs, the same findings can also be discovered in the Lq-ROFPWVs. In general, the decision makers can flexibly determine the parameter q based on the practical situation, and the value of q is usually not very big. In Table  13, with the changing of consistency threshold \(\overline{CI}\), the optimal emergency plan \(x_{1}\) does not vary. When \(\overline{CI}=0\), we will get four absolutely multiplicative consistent Lq-ROFPRs. The complete Lq-ROFPRs \(R_{1,N}\), \(R_{2,N}\) and \(R_{3,N}\) are adjusted for \(\overline{CI}=0.1\), while only \(R_{1,N}\) and \(R_{2,N}\) are adjusted for \(\overline{CI}=0.2\) and \(\overline{CI}=0.3\). Moreover, when \(\overline{CI}=0.4\), all the four complete Lq-ROFPRs are acceptably multiplicative consistent. However, there is no theoretical method to determine the value of consistency threshold \(\overline{CI}\). To satisfy the acceptable consistency level, researchers usually assumed \(\overline{CI}\) to be 0.1 [16, 23, 25, 34].

Comparison analysis

For an MCDM problem with complete Lq-ROFPRs, although the aggregation operators can be used to obtain the final ranking order, the consistency analysis is not conducted. In the following, to make a comparison in view of the consistency analysis, we apply the proposed method to solve a practical decision-making problem given by Meng et al. [22].

Example 3

[22]: In China, there are five major brands of mobile phones, including \(x_{1}\): HUAWEI, \(x_{2}\): OPPO, \(x_{3}\): APPLE, \(x_{4}\): VIVO and \(x_{5}\): MI. When researchers evaluate these five brands of mobile phones, several factors should be considered, including \(c_{1}\): appearance, \(c_{2}\): price, \(c_{3}\): performance, \(c_{4}\): quality and \(c_{5}\): reputation. Based on the LTS given in the Example 1, an expert team is invited to evaluate these five brands of mobile phones using LIFNs. Then, some Lq-ROFPRs \(R_{l,M}=(r_{l,ij}^{M})_{5\times 5}\) \((l=1,2,3,4,5)\) and \(A_{M}=(a_{ij}^{M})_{5\times 5}\) are offered (see Tables  1–6 in Meng et al. [22]), where the parameter q equals to 1.

Let the consistency threshold \(\overline{CI}=0.1\), we can obtain some acceptably multiplicative consistent Lq-ROFPRs \(R_{l,M}'\) \((l=1,2,3,4,5)\) and \(A_{M}'\) using the proposed method, where the detail steps are omitted.

$$\begin{aligned}&R_{1,M}'= \left( \begin{array}{cccccc} (s_{5},s_{5})&{}(s_{3},s_{6})&{}(s_{3},s_{7})&{}(s_{4},s_{6})&{}(s_{6},s_{4})\\ (s_{6},s_{3})&{}(s_{5},s_{5})&{}(s_{4},s_{5})&{}(s_{6.5633},s_{3.4367})&{}(s_{6},s_{2.2436})\\ (s_{7},s_{3})&{}(s_{5},s_{4})&{}(s_{5},s_{5})&{}(s_{7},s_{3})&{}(s_{5.2500},s_{1})\\ (s_{6},s_{4})&{}(s_{3.4367},s_{6.5633})&{}(s_{3},s_{7})&{}(s_{5},s_{5})&{}(s_{4},s_{1.7778})\\ (s_{4},s_{6})&{}(s_{2.2436},s_{6})&{}(s_{1},s_{5.2500})&{}(s_{1.7778},s_{4})&{}(s_{5},s_{5})\\ \end{array} \right) ,\\&R_{2,M}'= \left( \begin{array}{cccccc} (s_{5},s_{5}) &{}(s_{6},s_{4})&{}(s_{7},s_{3})&{}(s_{5},s_{4})&{}(s_{5},s_{4})\\ (s_{4},s_{6}) &{}(s_{5},s_{5})&{}(s_{1.5017},s_{0.9654})&{}(s_{1.3760},s_{1.6512})&{}(s_{3},s_{3.6000})\\ (s_{3},s_{7}) &{}(s_{0.9654},s_{1.5017})&{}(s_{5},s_{5})&{}(s_{3},s_{5.6000})&{}(s_{3},s_{7})\\ (s_{4},s_{5}) &{}(s_{1.6512},s_{1.3760})&{}(s_{5.6000},s_{3})&{}(s_{5},s_{5})&{}(s_{1.2436},s_{1.2436})\\ (s_{4},s_{5}) &{}(s_{3.6000},s_{3})&{}(s_{7},s_{3})&{}(s_{1.2436},s_{1.2436})&{}(s_{5},s_{5})\\ \end{array} \right) ,\\&R_{3,M}'= \left( \begin{array}{cccccc} (s_{5},s_{5}) &{}(s_{4},s_{5})&{}(s_{3},s_{6})&{}(s_{1.3689},s_{0.7207})&{}(s_{1.7120},s_{0.9014})\\ (s_{5},s_{4}) &{}(s_{5},s_{5})&{}(s_{4},s_{5})&{}(s_{6},s_{3})&{}(s_{7},s_{2})\\ (s_{6},s_{3})&{}(s_{5},s_{4})&{}(s_{5},s_{5})&{}(s_{7},s_{1.8427})&{}(s_{1.9305},s_{0.5082})\\ (s_{0.7207},s_{1.3689}) &{}(s_{3},s_{6})&{}(s_{1.8427},s_{7})&{}(s_{5},s_{5})&{}(s_{5},s_{5})\\ (s_{0.9014},s_{1.7120})&{}(s_{2},s_{7})&{}(s_{0.5082},s_{1.9305})&{}(s_{5},s_{5})&{}(s_{5},s_{5})\\ \end{array} \right) ,\\&R_{4,M}'= \left( \begin{array}{cccccc} (s_{5},s_{5})&{}(s_{2},s_{8})&{}(s_{2.3535},s_{7.6465})&{}(s_{3},s_{5})&{}(s_{5},s_{5})\\ (s_{8},s_{2}) &{}(s_{5},s_{5})&{}(s_{4.1667},s_{5})&{}(s_{6},s_{3})&{}(s_{2.6457},s_{0.7937})\\ (s_{7.6465},s_{2.3535}) &{}(s_{5},s_{4.1667})&{}(s_{5},s_{5})&{}(s_{7},s_{2})&{}(s_{8},s_{2})\\ (s_{5},s_{3}) &{}(s_{3},s_{6})&{}(s_{2},s_{7})&{}(s_{5},s_{5})&{}(s_{1.3807},s_{0.8284})\\ (s_{5},s_{5})&{}(s_{0.7937},s_{2.6457})&{}(s_{2},s_{8})&{}(s_{0.8284},s_{1.3807})&{}(s_{5},s_{5})\\ \end{array} \right) ,\\&R_{5,M}'= \left( \begin{array}{cccccc} (s_{5},s_{5}) &{}(s_{3},s_{6})&{}(s_{2},s_{8})&{}(s_{4},s_{5})&{}(s_{5},s_{4.2857})\\ (s_{6},s_{3}) &{}(s_{5},s_{5})&{}(s_{4},s_{6})&{}(s_{6},s_{4})&{}(s_{7},s_{3})\\ (s_{8},s_{2}) &{}(s_{6},s_{4})&{}(s_{5},s_{5})&{}(s_{7},s_{2.3333})&{}(s_{8},s_{1.7143})\\ (s_{5},s_{4}) &{}(s_{4},s_{6})&{}(s_{2.3333},s_{7})&{}(s_{5},s_{5})&{}(s_{1.6681},s_{1.0723})\\ (s_{4.2857},s_{5})&{}(s_{3},s_{7})&{}(s_{1.7143},s_{8})&{}(s_{1.0723},s_{1.6681})&{}(s_{5},s_{5})\\ \end{array} \right) ,\\&A_{M}'= \left( \begin{array}{cccccc} (s_{5},s_{5})&{}(s_{4},s_{6})&{}(s_{5},s_{5})&{}(s_{3},s_{6})&{}(s_{3},s_{5})\\ (s_{6},s_{4})&{}(s_{5},s_{5})&{}(s_{4},s_{5.1983})&{}(s_{3.8730},s_{5.1640})&{}(s_{4},s_{6})\\ (s_{5},s_{5})&{}(s_{5.1983},s_{4})&{}(s_{5},s_{5})&{}(s_{4},s_{6})&{}(s_{4},s_{5})\\ (s_{6},s_{3})&{}(s_{5.1640},s_{3.8730})&{}(s_{6},s_{4})&{}(s_{5},s_{5})&{}(s_{5.4545},s_{4.5455})\\ (s_{5},s_{3})&{}(s_{6},s_{4})&{}(s_{5},s_{4})&{}(s_{4.5455},s_{5.4545})&{}(s_{5},s_{5})\\ \end{array} \right) . \end{aligned}$$

Taking the Lq-ROFPR \(A_{M}'\) into the model 2, we can get a normalized Lq-ROFPWV.

$$\begin{aligned} s_{w}^{M}&=(s_{w_{1}}^{M},s_{w_{2}}^{M},s_{w_{3}}^{M},s_{w_{4}}^{M},s_{w_{5}}^{M})^\mathrm{{T}}\\ {}&= \big ((s_{1.1806},s_{8.8194}),(s_{1.9676},s_{8.0324}),\\&(s_{2.0988},s_{7.9012}),(s_{2.3765},s_{7.6235}),(s_{2.3765},s_{7.6235})\big )^\mathrm{{T}}. \end{aligned}$$

Similar to Meng et al.’s approach [22], if we plug the Lq-ROFPRs \(R_{l,M}'\) (\(l=1,2,3,4,5\)) into the model 2, respectively, some normalized Lq-ROFPWVs can be derived as

$$\begin{aligned} s_{\omega _{1}'}&=(s_{\omega _{11}'},s_{\omega _{12}'},s_{\omega _{13}'},s_{\omega _{14}'},s_{\omega _{15}'})^\mathrm{{T}}\\ {}&= \big ((s_{1.3991},s_{8.6009}),(s_{2.9916},s_{7.0084}),\\&\quad (s_{3.5672},s_{6.4328}),(s_{1.6630},s_{8.3370}),(s_{0.3791},s_{9.6209})\big )^\mathrm{{T}},\\ s_{\omega _{2}'}&=(s_{\omega _{21}'},s_{\omega _{22}'},s_{\omega _{23}'},s_{\omega _{24}'},s_{\omega _{25}'})^\mathrm{{T}}\\ {}&= \big ((s_{3.5844},s_{6.4156}),(s_{0.2715},s_{7.0879}),\\ {}&(s_{1.2904},s_{8.7096}),(s_{0.3847},s_{6.9747}),(s_{1.8285},s_{6.9747})\big )^\mathrm{{T}},\\&\quad s_{\omega _{3}'}=(s_{\omega _{31}'},s_{\omega _{32}'},s_{\omega _{33}'},s_{\omega _{34}'},s_{\omega _{35}'})^\mathrm{{T}}\\&= \big ((s_{0.9154},s_{7.7247}),(s_{3.2364},s_{6.7636}),\\ {}&(s_{3.6963},s_{4.9438}),(s_{0.6868},s_{9.3132}),(s_{0.1052},s_{8.5348})\big )^\mathrm{{T}},\\ s_{\omega _{4}'}&=(s_{\omega _{41}'},s_{\omega _{42}'},s_{\omega _{43}'},s_{\omega _{44}'},s_{\omega _{45}'})^\mathrm{{T}}\\ {}&= \big ((s_{0.9752},s_{9.0248}),(s_{3.3467},s_{6.6533}),\\ {}&(s_{4.8124},s_{5.1876}),(s_{0.7711},s_{9.2289}),(s_{0.0947},s_{9.9053})\big )^\mathrm{{T}},\\&\quad s_{\omega _{5}'}=(s_{\omega _{51}'},s_{\omega _{52}'},s_{\omega _{53}'},s_{\omega _{54}'},s_{\omega _{55}'})^\mathrm{{T}}\\ {}&= \big ((s_{1.2423},s_{8.7577}),(s_{2.7553},s_{7.2447}),\\ {}&(s_{4.4829},s_{5.5171}),(s_{0.9868},s_{9.0132}),(s_{0.5327},s_{9.4673})\big )^\mathrm{{T}}. \end{aligned}$$

Based on the operational laws for Lq-ROFNs in Definition 5, and according to Meng et al.’s method [22], we can use the following equation to calculate the comprehensive Lq-ROFPWV:

$$\begin{aligned} s_{\omega }^{M}&=(s_{\omega _{1}}^{M},\ldots ,s_{\omega _{5}}^{M})^\mathrm{{T}}\\ {}&=\big (\oplus _{l=1}^{5}(s_{w_{l}}^{M}\otimes s_{\omega _{l1}'}),\ldots ,\oplus _{l=1}^{5}(s_{w_{l}}^{M}\otimes s_{\omega _{l5}'})\big )^\mathrm{{T}}. \end{aligned}$$

Taking the \(s_{\omega _{1}}^{M}\) as an example, we have

$$\begin{aligned} s_{\omega _{1}}^{M}&=\big ((s_{1.1806},s_{8.8194})\otimes (s_{1.3991},s_{8.6009})\big )\\ {}&\oplus \big ((s_{1.9676},s_{8.0324})\otimes (s_{3.5844},s_{6.4156})\big )\\ {}&\oplus \big ((s_{2.0988},s_{7.9012})\otimes (s_{0.9154},s_{7.7247})\big )\\ {}&\oplus \big ((s_{2.3765},s_{7.6235})\otimes (s_{0.9752},s_{9.0248})\big )\\ {}&\oplus \big ((s_{2.3765},s_{7.6235})\otimes (s_{1.2423},s_{8.7577})\big )\\&=(s_{0.1652},s_{9.8348})\oplus (s_{0.7053},s_{9.2947})\\ {}&\oplus (s_{0.1921},s_{9.5225})\oplus (s_{0.2318},s_{9.7682})\\ {}&\oplus (s_{0.2952},s_{9.7048}) =(s_{1.5008},s_{8.2519}). \end{aligned}$$

After some computation, the priority weight vector \(s_{\omega }^{M}\) will be given by

$$\begin{aligned} s_{\omega }^{M}&=(s_{\omega _{1}}^{M},s_{\omega _{2}}^{M},s_{\omega _{3}}^{M},s_{\omega _{4}}^{M},s_{\omega _{5}}^{M})^\mathrm{{T}}\\ {}&= \big ((s_{1.5008},s_{8.2519}),(s_{2.3068},s_{7.2913}),\\&\quad (s_{3.1860},s_{6.6032}),(s_{0.8072},s_{8.7115}),(s_{0.5667},s_{8.9396})\big )^\mathrm{{T}}. \end{aligned}$$

By calculating the linguistic score functions of \(s_{\omega _{i}}^{M}\) (\(i=1,2,3,4,5)\), we have \(LS(s_{\omega _{1}}^{M})=s_{1.6245}\), \(LS(s_{\omega _{2}}^{M})=s_{2.5078}\), \(LS(s_{\omega _{3}}^{M})=s_{3.2914}\), \(LS(s_{\omega _{4}}^{M})=s_{1.0479}\) and \(LS(s_{\omega _{5}}^{M})=s_{0.8136}\). According to the comparison law for Lq-ROFNs, we have \(s_{\omega _{3}}^{M}\succ s_{\omega _{2}}^{M}\succ s_{\omega _{1}}^{M}\succ s_{\omega _{4}}^{M}\succ s_{\omega _{5}}^{M}\), which means the five major brands of mobile phones can be ranked as APPLE, OPPO, HUAWEI, VIVO and MI.

Meng et al. [22] derived the ranking order as APPLE, OPPO, HUAWEI, MI and VIVO, which is slightly different from our result, but the first three brand of mobile phones are the same. Compared with Meng et al.’s method [22], the new proposed approach has the following advantages:

Table 14 Comparison with some other preference relations
Full size table

(1) This paper deals with an MCDM problem under the linguistic q-rung orthopair fuzzy environment, where the constrains of linguistic membership degree and linguistic non-membership degree are \(I^{q}(s_{\mu _{ij}})+I^{q}(s_{\nu _{ij}})\le \tau ^{q}\) (\(q=1,2,\ldots \)). Clearly, the LIFPR studied by Meng et al. [22] is a special case of Lq-ROFPR, and our proposed method has a wider range of applications.

(2) Meng et al. [22] called a LIFPR consistent if an associated consistent reverse complementary LIFPR exists. However, for a LIFPR with n order, \(2^{\frac{n(n-1)}{2}-1}\) different reverse complementary LIFPRs may exist. Therefore, it is very difficult to check the consistency of LIFPRs. In Definition 8, we use Eq. (2) to define the consistency of Lq-ROFPRs, it is an easy work to check whether a Lq-ROFPR is multiplicative consistent or not.

(3) Meng et al. [22] adjusted an inconsistent LIFPR to be with absolute consistency, this consistency analysis is too strict and may lose some information. Compared with Meng et al.’s algorithm [22], our acceptable consistency analysis is more reasonable. In addition, if the consistency threshold \(\overline{CI}\)=0, we can also obtain absolutely consistent Lq-ROFPRs.

(4) Meng et al. utilized Eq. (28) in [22] to calculate the linguistic intuitionistic fuzzy priority weight vector. This equation is actually developed based on the arithmetic mean value, and different priority weights may be obtained if some other operators are adopted. In our method, based on the relationship between the normalized Lq-ROFPWV and a consistent Lq-ROFPR, we construct a mathematical programming model 2 to obtain the linguistic q-rung orthopair fuzzy priority weights.

(5) Meng et al. used Eq. (29) in [22] to derive a normalized linguistic intuitionistic fuzzy weight vector, which was given by

$$\begin{aligned} \tilde{s}_{w}^{M}&= \big ((s_{0.1652},s_{0.2174}),(s_{0.1739},s_{0.2261}),\\ {}&\quad (s_{0.2000},s_{0.2087}), (s_{0.2435},s_{0.1652}),(s_{0.2174},s_{0.1826})\big )^\mathrm{{T}}. \end{aligned}$$

We can see that the lower indexes of all linguistic membership degrees are small, and their sum is equal to 1, i.e., \(I(s_{0.1652})+I(s_{0.1739})+I(s_{0.2000})+I(s_{0.2435})+I(s_{0.2174})=1\). Similarly, \(I(s_{0.2174})+I(s_{0.2261})+I(s_{0.2087})+I(s_{0.1652})+I(s_{0.1826})=1\). Clearly, the normalized linguistic intuitionistic fuzzy weight vector \(\tilde{s}_{w}^{M}\) obtained in [22] is not suitable. The main reason is that the operational laws for LIFNs defined by Meng et al. [22] is not closed, and they have to make the lower indexes of all linguistic membership degrees or linguistic non-membership degrees be small by “arithmetic averaging”. In contrast, our normalized Lq-ROFPWV derived from the model 2 is more reasonable.

It should be noted that the Lq-ROFPR is a new preference relation under the linguistic environment, which is not considered by other researchers. Therefore, there are no previous methods that can be applied to solve our examples, which means we cannot make numerical comparison analysis with other methods. Considering that the Lq-ROFPR and the q-ROFPR has some relations, we present a Table  14 to verify the advantages of our approach by giving several indexes about the performances of some other methods.

(1) The preference relation considered in [13,14,15,16] is q-ROFPR, which uses real values in [0,1] to offer the preferred and non-preferred information. As discussed before, the linguistic variables can offer the qualitative recognition and have some advantages in expressing the uncertain evaluations. Taking the LTS S in the “Introduction” Section as an example, the experts will know the linguistic variable \(s_{5}\) means “fast”. However, if the decision makers use the numerical values to give the similar information, one expert may believe 0.7 means “fast”, while another may take 0.8 as “fast”. Clearly, this result may lead to some confusions when comparing two different q-ROFPRs. Moreover, the LIFPR [23] and the LPFPR [25] can be regarded as special cases of Lq-ROFPR, which means our new approach has a wider range of applications.

(2) The preference relations in [13, 15, 23, 25] are complete, and the authors did not consider the missing values. Due to the limitations of knowledge and experience, the experts may be unable or unwilling to give some judgements. Clearly, in this situation, these methods are unapplicable. In our approach, we construct an optimization model to estimate the unknown linguistic variables. When establishing the Lq-ROFPRs, the missing values can give the decision makers more choices and flexibility.

(3) To guarantee the reasonable ranking order, the consistency of preference relations should be considered. Sometimes, the absolutely consistent preference relation may be too strict, and an acceptably consistent preference relation will be more suitable. Zhang et al. [13] did not consider the acceptably additive consistency of q-ROFPRs. Zhang et al. [15], Jin et al. [23] and Liu et al. [25] all designed iterative algorithm to improve the consistency level, which may need more time and computation. Moreover, how to find a suitable parameter in the iterative approach is also a problem. In contrast, we construct a programming model to repair an unacceptably multiplicative consistent Lq-ROFPR, which can be solved by the Lingo software.

(4) The methods in [13,14,15,16, 23, 25] are GDM with complete or incomplete preference relations, the researchers did not apply their approaches to solve an MCDM problem. In this paper, we consider an MCDM problem based on the incomplete Lq-ROFPRs. To reflect the importance of criteria, the decision maker team builds a Lq-ROFPR by making pairwise comparison for all criteria. Then, a possibility degree matrix is constructed using the normalized Lq-ROFPWV, and the weight vector of criteria can be further derived. Furthermore, our proposed method can be easily extended to the GDM environment.

Conclusion

As the extension of LIFPR and LPFPR, the Lq-ROFPR has powerful ability to express the qualitative fuzziness and uncertainties in decision-making problems. Considering the advantages of Lq-ROFPRs, the multiplicative consistency had been introduced and studied. We had provided a transformation function to convert the normalized Lq-ROFPWV into a multiplicative consistent Lq-ROFPR. Then, a consistency-based programming model had been constructed to obtain the priority weights. Taking into account the practical issues, we had built another two mathematical models to improve the consistency level and deal with incomplete Lq-ROFPR, respectively. Finally, the new method had been applied to three MCDM problems. The comparison analysis had been conducted to demonstrate the effectiveness and validity of the proposed approach.

There are also some drawbacks of our method: (1) the parameter q is given in advance, our method does not discuss how to determine an appropriate value; (2) the consistency threshold \(\overline{CI}\) is also predefined; (3) the approach is not considered under the GDM environment. In the future study, we can discuss the GDM with Lq-ROFPRs based on the consistency and consensus analysis. Furthermore, following the idea of this paper, we can propose a similar method under some other fuzzy situations, such as (3,2)-fuzzy set [58], (2,1)-fuzzy set [59] and SR-fuzzy set [60].