Introduction

Noise widely exists in the fitness evaluation of many problems [1,2,3], which can mislead the direction of optimization. In the past decade, many studies [4, 5] on optimization problems in noisy environments have been published, and some strategies have been introduced to traditional evolutionary algorithms (EAs) to tackle the noise. Examples include explicit averaging [6], implicit averaging [7], Fourier transform [8], fitness estimation [9], and more. Most of the previous research focuses on relatively low-dimensional problems (up to 100-D), and a few studies on noisy problems with large-scale optimization problems (LSOPs) have been published. In fact, many noisy optimization problems are high-dimensional, such as parameters and structures optimization of deep neural networks [10] and subset selection [11].

The LSOPs in noisy environments contain challenges both on the scalability and robustness to noise, which make the difficulties of problem-solving explosive. The main reasons are the following aspects: (1) the complexity of the optimization problem increases, including the increase of dimensionality and the existence of the noise. (2) The search space of LSOPs increases exponentially with the increase of dimensionality, which is known as the curse of dimensionality [12]. (3) The computational cost of building a surrogate model is expensive, and the accuracy is also affected by noise and the curse of dimensionality, which makes some algorithms limited [13, 14].

Many algorithms have been proposed to overcome the challenge of the LSOPs, such as designing optimization operators to adapt the large-scale attributes [15], building surrogate models [16], and decomposing the problem [17], which is known as the cooperative coevolution (CC). In this paper, we apply the CC framework to solve LSOPs in noisy environments. This method is inspired by the divide and conquer, which has achieved great success in solving large-scale continuous [18], combinatorial [19], and constrained [20] problems.

How to decompose the LSOPs is the key to the successful implementation of the CC framework. Many studies [21, 22] show that the CC framework is sensitive to problem decomposition strategies. Taking the linkage identification by non-linearity check for real-coded GA (LINC-R) [23] as a pioneer, many decomposition methods have been proposed. Differential grouping (DG) [24] first extends the identical mechanism of LINC-R to the 1000-D problem. Extend DG (XDG) [25] improves the shortage of DG in dealing with overlaps. DG2 [26] notices the high computational cost in DG and utilizes the transmissibility of separability to save the computational budget. Global DG (GDG) [27] regards the variable interactions matrix as the adjacency matrix of a graph and depth-first search or breadth-first search is applied to identify the interactions and formed the sub-problems. Recursive DG (RDG) [18] further reduces the computational cost by examining the interaction between a pair of sets of variables rather than a pair of variables, and forms the sub-problems recursively. Efficient RDG (ERDG) [28] uses the historical information on interaction identification to save the computational cost in redundant examinations and is more efficient than RDG. These decomposition methods are considered high-accuracy decomposition methods. These methods detect the interaction by determining the difference between fitness difference and threshold. However, they are extremely sensitive to the fidelity of observed objective value and will completely fail to detect the interactions in multiplicative noisy environments. We will explain the reason in the section “Challenges of DG-based decomposition methods in noisy environments”.

In this paper, we propose a novel decomposition method named linkage measurement minimization (LMM), our proposal allows an automatic decomposition that treats the decomposition problem as a combinatorial optimization problem, and we design the linkage measure function (LMF) based on LINC-R as the objective function of combinatorial optimization. In addition, the advanced optimizer: MDE-DS is employed to optimize the sub-problems (MDE-DSCC-LMM). More specifically, the main contributions of this paper are as follows.

  1. (1)

    Our proposal LMM provides a novel strategy to regard the decomposition problem as a combinatorial optimization problem, and the genetic algorithm is employed to actively search the interactions between decision variables. We mathematically explain the feasibility of LMF and its relationship with LINC-R. Theoretical analysis shows how our proposal detects interactions in noisy environments. In addition, we analyze the time complexity of LMM, and the fitness evaluation times (FEs) consumed in decomposition are controllable. And our proposal can be extended to decompose the higher dimensional, multi-objective, real-world problems with a limited computational budget.

  2. (2)

    MDE-DS is applied as the optimizer for sub-problems and is well performed on various benchmark functions in noisy environments. The results in this paper further demonstrate that MDE-DS can accelerate cooperative coevolutionary optimization significantly.

  3. (3)

    Numerical experiments demonstrate that LMM is competitive with some state-of-the-art decomposition methods for LSOPs in noisy environments, and the introduction of MDE-DS is efficient for sub-problems optimization. To the best of our knowledge, not much work has been reported on employing the CC framework to solve LSOPs in noisy environments.

The rest of the paper is organized as follows: the section “Preliminaries and related work” covers preliminaries, MDE-DS, a brief review of the state-of-the-art decomposition method, and reveals the challenges of DG-based decomposition methods in multiplicative noisy environments. The section “Our proposal:MDE-DSCC-LMM” provides a detailed introduction to our proposal, MDE-DSCC-LMM. The section “Numerical experiment and analysis” describes the experiments on CEC2013 LSGO Suite [29] in noisy environments and analyzes the experimental results. The section “Discussion” discusses the direction of our research in the future. Finally, the section “Conclusion” concludes the paper.

Preliminaries and related work

Preliminaries

Large-scale optimization problem

Without loss of generality, an LSOP can be defined as follows:

$$\begin{aligned} \begin{aligned}&\min f(X) \\&{\text {s.t.}}: X \in {\mathbb {R}} \end{aligned}, \end{aligned}$$

where \(X=(x_1, x_2, \ldots , x_n)\) is an n-dimensional decision vector, and each \(x_i \ (i \in [1,n])\) is a decision variable. f(X) is the objective function needed to be minimized. In our work, the large-scale optimization problem is a special case of black-box optimization, where the number of decision variables n is large (e.g., \(n \geqslant 1000\)).

Variables’ interaction

The concept of variable interaction is derived from biology. In biology, if a feature at the phenotype level is contributed by two or more genes, then we consider there are interactions between these genes, and the genome composed of these genes is called a linkage set [30]. In the definition of optimization problems. If \(\min f(x_1, x_2, \ldots ,x_n) = (\min \nolimits _{c_1}f_1(...,...), \ldots , \min \nolimits _{c_m}f_m(...,...))\), then f(x) is a partially separable function, and decision variables in identical sub-problem consist of linkage set. There are two extreme cases, when there is no interaction between all variables, which means \(\min \ f(x_{1},x_{2},\ldots ,x_{n})=\min \ \sum _{i=1}^{n}f(x_{i_{1}})\), then we call f(x) is a fully separable function. On the contrary, we call f(x) a completely nonseparable function if all variables have direct or indirect interactions with each other.

Cooperative coevolution

Inspired by divide and conquer, the CC framework was proposed to deal with LSOPs by decomposing the problem into multiple nonseparable sub-problems and optimizing them alternately. A standard CC consists of two stages: decomposition and optimization. Figure 1 shows the main steps of the CC framework.

Fig. 1
figure 1

The flowchart of CC

Full size image

CC framework first decomposes the LSOPs into k nonseparable sub-problems with a certain strategy. Due to the sub-solution \(i(i \in [1, k])\) cannot form a complete solution for evaluation, all sub-problems maintain a public context vector [31] to construct a complete solution, and after optimization, the latest information updates the context vector. Some studies found that only one context vector may be too greedy for evaluation. Therefore, the adaptive multi-context CC framework [32] is proposed, which employs multiple context vectors to co-evolve subcomponents.

Noise in objective functions

Additive noise [33] and multiplicative noise [34] widely exist in the evaluation of optimization problems. Mathematically, the noisy objective function \(f^N (\textrm{X})\) of a trial solution X is represented by

$$\begin{aligned} f^{N}(X)= & {} f(X) + \eta \end{aligned}$$
(1)
$$\begin{aligned} f^{N}(X)= & {} f(X) \cdot (1+\beta ), \end{aligned}$$
(2)

where f(X) is the real objective function. Equation (1) shows the objective function in addictive noisy environments, \(\eta \) is the amplitude of the addictive noise. Equation (2) reveals the relationship between the real objective function and objective function in multiplicative noisy environments. \(\beta \) is a random noise (such as Gaussian noise).

Anti-noise strategies in EAs

Many optimization problems suffer from noise, and to perform the optimization under the existence of noise, various anti-noise strategies have been proposed in the literature. Following the classification reported in Ref. [35], two categories of noise handling methods for EAs can be mainly classified; each category can be divided into two sub-categories:

  • Methods which require an increase in the computational cost

    1. (1)

      Explicit averaging methods

    2. (2)

      Implicit averaging methods.

  • Methods which perform hypotheses about the noise

    1. (1)

      Averaging through approximated models

    2. (2)

      Modification of the selection schemes.

Explicit averaging methods consider that re-sampling and re-evaluation can reduce the impact of noise on the fitness landscape. Increasing the re-evaluation times is equivalent to reducing the variance of the estimated fitness. Thus, ideally, an infinite sample size would reduce to 0 uncertainties in the fitness estimations.

Implicit averaging states that a larger population allows the evaluations of neighbor solutions, and thus, the fitness landscape in a particular portion of decision space can be estimated. Paper [36] has shown that a large population size reduces the influence of noise on the optimization process, and paper [37] has proved that a GA with an infinite population size would be noise-insensitive.

Both explicit and implicit averaging methods consume more fitness evaluation times (FEs) to correct the objective value, which is improper or even unacceptable for LSOPs under the FEs’ limitation. To obtain efficient noise filtering without excessive computational cost, various techniques have been proposed in the literature, such as the introduction of the approximated model [38], probability-based selection schemes [39], self-adaptative parameter adjustment [40], and so on.

Modified DE with distance-based selection

Differential evolution algorithm (DE) [41] was first proposed in 1995 and has been wildly applied in data mining [42], pattern recognition [43], artificial neural networks [44], and other fields due to its characteristics, such as easy implementation, fast convergence speed, and strong robustness. MDE-DS [45] is designed for continuous optimization problems in presence of noise with the modification in mutation, crossover, and selection, and the detailed description of MDE-DS is as follows.

Parameter control

The constants F and Cr are unnecessary, as F is randomly sampled from 0.5 to 2 for each mutation operation and Cr is randomly switched between 0.3 and 1 for each target vector. Switching F between two extreme corners of the feasible range is conducive to attaining a balance between exploration and exploitation of the search. And there is a new parameter b (the blending rate) in blending crossover, whose value is also randomly chosen from among three candidates: a low value of 0.1, a medium value of 0.5, and a high value of 0.9. The utility of such a switching scheme has been discussed in paper [46] for solving LSOPs.

Mutation

MDE-DS includes two different mutation strategies and switches them randomly with \(50\%\) probability.

In the population centrality-based mutation, the elite subpopulation (top 50%) is selected and \(\widetilde{\vec {X}}_{{\text {best}}, G}\) is calculated by the arithmetic mean (centroid) of the subpopulation individuals. Eq. (3) is adopted to mutate the ith individual

$$\begin{aligned} \begin{aligned} \vec {V}_{i, G}=\vec {X}_{r1, G}+F\left( \widetilde{\vec {X}}_{{\text {best}}, G} - \vec {X}_{r2, G}\right) , \end{aligned} \end{aligned}$$
(3)

where \(\vec {X}_{r1, G}\) and \(\vec {X}_{r2, G}\) are two different individuals corresponding to randomly chosen indices r1 and r2. \(\vec {V}_{i, G}\) is the newly generated mutant vector corresponding to the current target vector for present generation G.

In the DMP-based mutation scheme, the best individual \(\vec {X}_{{\text {best}}, G}\) in each generation is selected and the dimension-wise average is implemented for both \(\vec {X}_{{\text {best}}, G}\) and the current target individual \(\vec {X}_{i, G}\). The mutation is generated in the following way:

$$\begin{aligned} \begin{aligned} \vec {V}_{i, G}=\vec {X}_{i, G}+\Delta _{m} \cdot \left( \frac{\vec {M}_{i, G}}{\Vert \vec {M}_{i, G} \Vert } \right) \end{aligned} \end{aligned}$$
(4)

where \(\Delta _{m}=(X_{{\text {best}}_{\text {dim}}, G}-X_{i_{\text {dim}}, G})\), with \(X_{{\text {best}}_{\text {dim}}, G}=\frac{1}{D}\sum _{k=1}^{D}x_{{\text {best}}_k, G}\) and \(X_{i_{\text {dim}}, G}=\frac{1}{D}\sum _{k=1}^{D}x_{i_k, G}\). \(\frac{\vec {M}_{i, G}}{\Vert \vec {M}_{i, G} \Vert }\) is a unit vector with random direction.

The significance of the population centrality-based mutation scheme is that it balances greediness while still maintaining a certain extent of diversity. For example, it is less greedy than the DE/best/1 scheme, and hence, the probability of the optimization trapped in local optima is less. On the other hand, the DMP-based mutation scheme prefers exploration [47], and thus, in absence of any feedback about the nature of the function, an unbiased combination of these two methods is applied.

Crossover

Crossover plays an important role in generating promising offspring from two or more existing individuals within the function landscape. Blending crossover is employed in MDE-DS and described in Eq. (5)

$$\begin{aligned} \begin{aligned} u_{j,i,G}= {\left\{ \begin{array}{ll} b \cdot x_{j,i,G} + (1-b) \cdot v_{j,i,G} \\ x_{j,i,G} \end{array}\right. }, \end{aligned} \end{aligned}$$
(5)

where \(u_{j,i,G}\) and \(v_{j,i,G}\) are the jth dimensions of the trial and donor vectors, respectively, corresponding to the current index i in generation G and \(x_{j,i,G}\) is the jth dimension of the current population individual \(\vec {X}_{i, G}\). Blending recombination has one parameter b, which is randomly selected from 0.1, 0.5, and 0.9. The concrete analysis can be referred to in Ref. [45].

Selection

The canonical DE selects the offspring based on a simple greedy strategy. However, if the fitness landscape gets corrupted with noise, the greedy selection suffers a lot, because in this case, the original fitness of parent and offspring is unknown and it can be well nigh impossible to infer when an offspring is superior or inferior to its parent. Thus, the design of selection is the key to anti-noise. To handle the presence of noise, a novel distance-based selection mechanism is introduced without any extra parameter. There are three cases of the proposed selection mechanism which are described subsequently

$$\begin{aligned} \begin{aligned} \vec {X}_{i,G+1}= {\left\{ \begin{array}{ll} \vec {U}_{i,G}, \ {\text {if}} \ \frac{f(\vec {U}_{i,G})}{f(\vec {X}_{i,G})} \le 1 \\ \vec {U}_{i,G}, \ {\text {if}} \ \frac{f(\vec {U}_{i,G})}{f(\vec {X}_{i,G})} > 1 \ {\text {and}} \ p_s \le e^{-\frac{\Delta f}{Dis}} \\ \vec {X}_{i,G}, \ {\text {else}}. \end{array}\right. } \end{aligned} \end{aligned}$$
(6)

In case 1, when \(\frac{f(\vec {U}_{i,G})}{f(\vec {X}_{i,G})} \le 1\), the offspring replaces the parent and survives to the next generation.

In case 2, although the parent performs better than the offspring, the offspring still can be preserved and survive into the next generation based on a stochastic principle. And the probability is calculated by \({\text {e}}^{-\frac{\Delta f}{{\text {Dis}}}}\), where \(\Delta f=\left.{\&\#Xarrowvert;}f(\vec {U}_{i,G}) - f(\vec {X}_{i,G}) \right.{\&\#Xarrowvert;}\) represents the absolute fitness difference between \(\vec {U}_{i,G}\) and \(\vec {X}_{i,G}\), \({\text {Dis}}=\sum _{k=1}^{D}\left.{\&\#Xarrowvert;}u_{i,k}-x_{i,k} \right.{\&\#Xarrowvert;}\) is the Manhattan distance between those two vectors. Manhattan distance is applied because of its simplicity and computational efficiency, and \(p_s\) is a random number generated from 0 to 1.

In case 3, If the parent significantly outperforms than offspring, then the offspring is removed and the parent persists to the next generation.

This selection process is further illustrated in Fig. 2.

Fig. 2
figure 2

A selection works on fitness landscape in noisy environments

Full size image

Figure 2 shows a fitness landscape scenario both in noiseless environments and noisy environments, p and \(p^{'}\) represent the parent individual in the original fitness landscape and landscape in noisy environments, o and \(o^{'}\) represent the offspring individual in original fitness landscape and landscape in noisy environments, respectively. The fitness information we can observe is only in noisy environments, so in minimization problems, \(o^{'}\) will be rejected to replace the \(p^{'}\) in the next generation. The objective value of p is better than o in the real fitness landscape, and if we re-evaluate the \(o^{'}\) and \(p^{'}\), the domination may be changed. The mechanism of selection in MDE-DS allows the algorithm to give us some probabilistic flexibility to select worse solutions as in noise-affected landscapes.

In summary, the pseudocode of MDE-DS is shown in Algorithm 1

figure a

A brief review of the state-of-the-art decomposition method

Based on the divide and conquer, the CC framework decomposes the LSOPs into multiple nonseparable sub-problems and optimizes them alternately, which is the mainstream framework for solving LSOPs. In this section, we will briefly review the state-of-the-art decomposition method.

Taking the LINC-R [30] as a pioneer, perturbation-based decomposition methods become one of the most popular strategies to collaborate with the CC framework. Equation (7) defines the perturbation in the ith dimension and the jth dimension

$$\begin{aligned} \begin{aligned} s&=(x_{1},x_{2},\ldots ,x_{n}) \\ s_{i}&=(x_{1},\ldots ,x_{i}+\delta ,\ldots ,x_{n}) \\ s_{j}&=(x_{1},\ldots ,x_{j}+\delta ,\ldots ,x_{n}) \\ s_{ij}&=(x_{1},\ldots ,x_{i}+\delta ,\ldots ,x_{j}+\delta ,\ldots ,x_{n}) .\\ \end{aligned} \end{aligned}$$
(7)

LINC-R identifies the interaction between variables based on the fitness difference of perturbation with pre-defined hyperparameter \(\varepsilon \). More specifically

$$\begin{aligned} \begin{aligned}&\exists s\in {\text {Pop}}:\\&\quad {\text {if}} \ |(f(s_{ij})-f(s_{i})) - (f(s_{j})-f(s))|> \varepsilon , \\&\quad {\text {then}} \ x_{i} \ {\text {and}} \ x_{j} \ {\text {are nonseparable.}} \end{aligned} \end{aligned}$$
(8)

\(\varepsilon \) is the allowable error. DG extends Eq. (8) first to LSOPs up to 1000-D. Due to the FEs’ limitation in LSOPs, the fitness difference from the lower bound of search space to the upper bound can be accepted. The reuse of fitness and negligence of indirect interactions decreases the needed FEs to \(O(\frac{n^2}{m})\), and m is the number of sub-problems. In paper [24], a sensitivity test for threshold \(\epsilon \) is also implemented, the experimental results show that the DG is sensitive to the threshold \(\epsilon \), and \(\epsilon =10^{-3}\) is a recommended value.

Subsequently, the extended DG (XDG) [25] noticed that DG cannot identify the overlapping; thus, it divides all direct and indirect interacting variables into a sub-problem, and then, the overlappings between sub-problems are checked to identify conditional interactions. The needed FEs of XDG are approximately \(n^2\). The complexity of the XDG results in an unsuitable allocation of computational cost between decomposition and optimization and limits the development of XDG to deal with higher dimensional problems.

The high computational cost of decomposition is a critical problem. DG2 [26], a faster and more accurate DG-based decomposition method, was proposed to address this issue. DG2 utilizes the transmissibility of separability to save the FEs. For example, if \(x_1\) interacts with \(x_2\) and \(x_3\), the identification between \(x_2\) and \(x_3\) is unnecessary, as they belong to the same sub-problem, and the computational cost of DG2 is reduced to \(\frac{n^2+n+2}{2}\).

One of the most popular DG-based methods is Recursive DG (RDG) [48]. The RDG examines the interactions between a pair of sub-problems rather than a pair of single variables. For \(f:{\mathbb {R}}^D \rightarrow {\mathbb {R}}\) is an objective function, \(X_1 \subset X\) and \(X_2 \subset X\) are two mutually exclusive subsets of variables: \(X_1 \cap X_2=\emptyset \). If there are two unit vectors \({\textbf {u}}_1 \in U_{X_1}\) and \({\textbf {u}}_2 \in U_{X_2}\), two real numbers \(l_1,l_2>0\) and a solution \({\textbf {x}}^*\) to satisfy Eq. (9)

$$\begin{aligned} \begin{aligned} f({\textbf {x}}^*+l_1{u}_1+l_2{u}_2)-f({\textbf {x}}^*+l_2{u}_2) \ne f({\textbf {x}}^*+l_1{u}_1)-f({\textbf {x}}^*), \end{aligned} \end{aligned}$$
(9)

then there are some interactions between variables in \(X_1\) and \(X_2\); otherwise, \(X_1\) and \(X_2\) are considered as separable sets. If \(X_1\) and \(X_2\) interact with each other, and RDG divides \(X_2\) into two equal-sized and mutually exclusive subsets, then interactions between \(X_1\) and the two subsets are detected. Repeat the above process until RDG finds the variables which interact with \(X_1\). The computational complexity of RDG is \(O(n\log _2n)\), which is better than DG, XDG, and DG2, and more friendly to higher dimensional problems.

The hyperparameter \(\varepsilon \) also plays an important role in interaction identification, and different problems have various fitness landscape characteristics, and the identical threshold may not be suitable for all problems. Inspired by DG2, RDG2 [49] introduces an upper bound of the round-off errors incurred by the calculation of the non-linearity term and applies it as the threshold value. The experimental results in Ref. [49] showed that RDG2 improves the accuracy of RDG in identifying the interactions between variables.

Challenges of DG-based decomposition methods in noisy environments

Additive noise and multiplicative noise are two representative noises. Additive noise is often irrelevant to the fitness landscape, so we can carefully adjust the parameters to overcome the additive noise in the decomposition, although it is not easy [50]. However, multiplicative noise is related to the fitness landscape, so fitness can amplify the noise. Dealing with multiplicative noise is more difficult than additive noise in the decomposition stage. Taking the LINC-R as an example

$$\begin{aligned}{} & {} \exists s\in {\text {Pop}}: \nonumber \\{} & {} \quad \Delta ^N_{1}=f^{N}(s_{i})-f^{N}(s)=f(s_{i})(1+\beta _{1})-f(s)(1+\beta _{2}) \nonumber \\{} & {} \quad \Delta ^N_{2}=f^{N}(s_{ij})-f^{N}(s_{j})=f(s_{ij})(1+\beta _{3})-f(s_{j})(1+\beta _{4}) \nonumber \\{} & {} \quad {\text {if}} \ |\Delta ^N_{2} - \Delta ^N_{1} |> \varepsilon , \nonumber \\{} & {} \quad {\text {then}} \ x_{i} \ {\text {and}} \ x_{j} \ {\text {are nonseparable}} \end{aligned}$$
(10)

\(\beta _{i}\) is Gaussian noise. \(|\Delta ^N_{2} - \Delta ^N_{1} |= |\Delta _{2} - \Delta _{1} + f(s_{ij})\beta _3 - f(s_{j})\beta _4 - f(s_{i})\beta _1 + f(s)\beta _2 |\). When the noise \(\beta \sim N(0, \sigma ^2)\), we define the noise term \(\phi _{ij}=f(s_{ij})\beta _3 - f(s_{j})\beta _4 - f(s_{i})\beta _1 + f(s)\beta _2\) which follows the distribution: \(\phi _{ij} \sim N(0, (f^2(s_{ij}) + f^2(s_{j}) + f^2(s_{j}) + f^2(s))\sigma ^2)\). In noisy environments with multiplicative noise, LINC-R cannot identify that the fitness difference is caused by interaction or noise and the probability of \(\phi _{ij}=0\) being satisfied is almost 0 [50]. In practice, the decomposition methods developed on the LINC-R, such as DG, DG2, RDG, etc. will fail in environments with multiplicative noise. We will provide experimental results of decomposition in the section “Performance of LMM”. Therefore, grouping methods that detect interactions by perturbation face severe challenges.

Our proposal: MDE-DSCC-LMM

In this section, we will introduce the details of our proposal. Our proposal consists of two stages: decomposition and optimization. In the decomposition, we divide the decision variables into sub-problems with our proposal: LMM, and in the optimization, MDE-DS is employed as a basic optimizer to optimize the sub-problems. Next, the concrete procedures of decomposition and optimization will be explained.

Decomposition: LMM

First, we provide the flowchart of our proposal in decomposition: LMM. The flowchart is shown in Fig. 3.

Fig. 3
figure 3

The flowchart of decomposition (LMM)

Full size image

The basic idea is that we regard the decomposition problem as a combinatorial optimization problem and design the LMF based on LINC-R to lead the direction of searching for a better decomposition solution. The specific derivation of LMF is as follows.

The original LINC-R is defined as Eq. (11)

$$\begin{aligned} \begin{aligned}&\exists s\in {\text {Pop:}}\\&\quad {\text {if}} \ |(f(s_{ij})-f(s_{j})) - (f(s_{i})-f(s)) |> \varepsilon \\&\quad {\text {then}} \ x_{i} \ {\text {and}} \ x_{j} \ {\text {are nonseparable}} \end{aligned}, \end{aligned}$$
(11)

where the size of Pop is m, FEs consumed in a pair of variables based on Pop is 4m, and the interaction between every pair of variables is identified in LINC-R. Thus, in the \(n-\)D problem, the necessary FEs is \(2mn(n+1)\), which is unaffordable for LSOPs. Many studies [18, 24, 51] only detect the interactions by calculating the fitness difference from the lower bound of search space to the upper bound to save the FEs in decomposition, and we adopt the same strategy in our proposal, although it is not so robust and may fail to detect the interactions in trap functions [52].

We also notice that the original LINC-R can be transformed into the vector addition form. Equation (12) shows this variant LINC-R

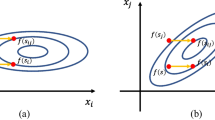
$$\begin{aligned} \begin{aligned}&{\text {if}} \ |(f(s_{ij})-f(s)) - ((f(s_{i})-f(s))+(f(s_{j})-f(s)))|\\&\quad < \varepsilon \, {\text {then}} \ x_{i} \ {\text {and}} \ x_{j} \ {\text {are separable}}. \end{aligned} \end{aligned}$$
(12)

Figure 4 shows how LINC-R and the variant LINC-R work on the separable variables \(x_i\) and \(x_j\). Although the form is different, the mechanisms of LINC-R and variant LINC-R are identical.

Fig. 4
figure 4

a LINC-R works on the separable variables. b Variant LINC-R works on the separable variables

Full size image

Based on this interesting finding, we derive LINC-R to 3-D and higher dimensions. In 3-D space, the schematic diagram is shown in Fig. 5.

Fig. 5
figure 5

The variant LINC-R works on 3-D space [53]

Full size image

Here, we define the fitness difference in 3-D

$$\begin{aligned} \begin{aligned} \Delta _{i}&= f(s_{i}) - f(s) \\ \Delta _{j}&= f(s_{j}) - f(s) \\ \Delta _{k}&= f(s_{k}) - f(s) \\ \Delta _{ijk}&= f(s_{ijk}) - f(s) .\\ \end{aligned} \end{aligned}$$
(13)

When the variant LINC-R is applied simultaneously to determine the interactions between \(x_i\), \(x_j\), and \(x_k\)

$$\begin{aligned} \begin{aligned}&{\text {if}} \ |\Delta _{ijk} - (\Delta _{i}+\Delta _{j}+\Delta _{k})|< \varepsilon , \\&\quad {\text {then }} \ x_{i},x_{j},{\text {and}} \ x_{k} \ {\text {are separable}}. \end{aligned} \end{aligned}$$
(14)

Therefore, we can reasonably infer that when the dimension reaches n

$$\begin{aligned} \begin{aligned}&{\text {if}} \ |\Delta _{1,2,\ldots ,n} - (\Delta _{1}+\Delta _{2}+\cdots +\Delta _{n})|< \varepsilon \\&\quad {\text {then}} \ x_{1},x_{2},\ldots ,.x_{n} \ {\text {are separable}}. \end{aligned} \end{aligned}$$
(15)

However, when Eq. (15) is not satisfied, we only know that interactions exist in some variables, but we cannot know in which pairs of variables. Taking 3-D space as an example

$$\begin{aligned} \begin{aligned}&{\text {if}} \ |\Delta _{ijk} - (\Delta _{i}+\Delta _{j}+\Delta _{k})|> \varepsilon \ {\text {and}} \ |\Delta _{ijk} -(\Delta _{ij}\\&\quad +\Delta _{k})|< \varepsilon \, {\text {then}} \ x_{i},x_{j} \ {\text {are nonseparabale and}} \ x_{k} \ \\&\quad {\text {is separable from }} x_{i},x_{j}. \end{aligned} \end{aligned}$$
(16)

Therefore, in the n-dimensional space, although it is difficult to detect the interactions between multiple variables through high-dimensional LINC-R directly, we can actively search for the interactions between variables through heuristic algorithms. According to the above description, in the n-dimensional problem, the linkage measurement function (LMF) is defined in Eq. (17)

$$\begin{aligned} \textrm{LMF}(s)= \left( \Delta _{1,2,\ldots ,n}-\sum _{i,j,\ldots }^{m}\Delta _{i,j,\ldots }\right) ^2; \end{aligned}$$
(17)

m is the number of sub-problems. LMF in noisy environments is defined in Eq. (18)

$$\begin{aligned} \mathrm{LMF^N}(s)=\left( \Delta ^N_{1,2,\ldots ,n}-\sum _{i,j,\ldots }^{m}\Delta ^N_{i,j,\ldots }\right) ^2, \end{aligned}$$
(18)

where \(\Delta ^N_{1,2,\ldots ,n} = f^N(s_{1,2,\ldots ,n})-f^N(s)=f(s_{1,2,\ldots ,n})(1+\beta _i)-f(s)(1+\beta _j)\). To optimize the \(\mathrm{LMF^N}(s)\), EGA is employed as the basic optimizer. Figure 6 demonstrates that how to decode from genotype to decomposition.

Fig. 6
figure 6

A demonstration of decoding from genotype to decomposition

Full size image

The length of a chromosome is LD, L is the genome length, and D is the dimension of the problem.

We decode the binary chromosome to decimal phenotype level and divide the decision variables into corresponding sub-problems, and the decision variables assigned to sub-problem 0 are regarded as separable variables. This procedure of optimization guided by LMF is named linkage measurement minimization (LMM), and the pseudocode of the decomposition is shown in Algorithm 2

figure b

As the general process of GA, we first initialize the decomposition solutions randomly in Algorithm 2, from line 2 to 8. The object E saves the best decomposition solution. Then, we repeat the procedure of selection, crossover, mutation, evaluation, and inheritance until the iteration reaches the stop criterion from line 12 to 19. The elitist strategy [54] directly replicates the best individual to the next generation, which can prevent the elite individual from destroying the superior gene and chromosome structure during optimization.

Time complexity analysis

FEs consumed in interaction identification are analyzed in this section. As the structure of an individual in Fig. 6, the best and worst time complexity for evaluating an individual is O(1) and O(D), when all decision variables are identified as nonseparable and separable, respectively. D is the dimension of problems. Suppose that the population size is N, maximum iteration is M. Thus, the best and worst time complexity of our proposal LMM is O(NM) and O(DNM).

Theoretical support for LMM in noisy environments

It is evident that the optimization guided by LMF can identify the interactions in the noiseless environment, because the individuals containing correct linkage information have lower linkage measurement values and higher fitness, which prefer to survive in the selection of EGA. An example we mentioned before is Eq. (16). And an important explanation is why LMM can identify the interactions in noisy environments. Here, we provide theoretical support.

Corollary

Let \(x_i\) and \(x_j\) be separable decision variables, and \(x_m\) and \(x_n\) be nonseparable decision variables. \(I(x_i, x_j)=(f(s_{ij})-f(s_{i}))-(f(s_{j})-f(s))\) and \(I^N(x_i, x_j)=(f^N(s_{ij})-f^N(s_{i}))-(f^N(s_{j})-f^N(s))\) represent the intensity of interaction between \(x_i\) and \(x_j\) in noiseless environment and noisy environments, respectively. In noisy environments, if we prove that the probability \(P(I^N(x_m, x_n)> I^N(x_i, x_j))>0\), which means it is possible that the intensity of the interaction between nonseparable variables can be stronger than separable variables in noisy environments, then the minimization of LMF can guide the direction to search for more interactions.

Proposition

In noisy environments, the probability \(P(I^N(x_m, x_n)> I^N(x_i, x_j))>0\), and individuals containing correct detected interactions have better fitness to survive.

Proof

In noisy environments, the noise \(\beta \sim N(0, \sigma ^2)\). The relationship between \(I^N(\cdot )\) and \(I(\cdot )\) is defined in Eq. (19)

$$\begin{aligned} \begin{aligned} I^N(x_i,x_j)&= I(x_i,x_j)+ (\beta _1f(s_{ij})-\beta _2f(s_i))\\&\quad -(\beta _3f(s_{j})-\beta _4f(s))=I(x_i,x_j) + \phi _{ij} \end{aligned}, \end{aligned}$$
(19)

where \(\phi _{ij} = (\beta _1f(s_{ij})-\beta _2f(s_i))-(\beta _3f(s_{j})-\beta _4f(s))\), and \(\phi _{ij}\) follows the distribution:

$$\begin{aligned} \phi _{ij}{} & {} \sim N(0, (f^2(s_{ij}) + f^2(s_{j})\nonumber \\{} & {} + f^2(s_{j}) + f^2(s))\sigma ^2), \end{aligned}$$
(20)

and \(I^N(x_i,x_j)\) follows the distribution:

$$\begin{aligned} I^N(x_i,x_j){} & {} \sim N(I(x_i,x_j), (f^2(s_{ij}) + f^2(s_{j}) \nonumber \\{} & {} + f^2(s_{j}) + f^2(s))\sigma ^2). \end{aligned}$$
(21)

Due to \(x_i\) and \(x_j\) are separable variables, \(x_m\) and \(x_n\) are nonseparable variables; similarly

$$\begin{aligned} I^N(x_i,x_j){} & {} \sim N(0, (f^2(s_{ij}) + f^2(s_{j}) + f^2(s_{j}) \nonumber \\{} & {} + f^2(s))\sigma ^2) I^N(x_m,x_n) \sim N(I(x_m,x_n), (f^2(s_{mn}) \nonumber \\{} & {} + f^2(s_{m}) + f^2(s_{n}) + f^2(s))\sigma ^2). \end{aligned}$$
(22)

Here, we introduce a distribution \(Y= I^N(x_m,x_n) - I^N(x_i,x_j)\), and the problem is transformed to prove \(P(Y>0)>0\). Y follows the distribution:

$$\begin{aligned} \begin{aligned} Y&\sim N(I(x_m,x_n), (f^2(s_{ij}) + f^2(s_{j}) + f^2(s_{j}) + f^2(s))\sigma ^2\\&\quad +(f^2(s_{mn}) + f^2(s_{m}) + f^2(s_{n}) + f^2(s))\sigma ^2) \\&\quad \sim N(I(x_m,x_n), \sigma _{ijmn}). \end{aligned} \end{aligned}$$
(23)

The expectation of Y is \(I(x_m,x_n)\), and there are two cases that need to be discussed:

Case 1: \(I(x_m,x_n) > 0\): In this case, \(P(Y>0)>0.5\).

Case 2: \(I(x_m,x_n) < 0\): In this case, \(0<P(Y>0)<0.5\).

In summary, \(P(I^N(x_m, x_n)>I^N(x_i, x_j))>0\) is true, and the optimization of LMF has the probability to detect more interactions in noisy environments, which can be employed as the objective function in our experiment. \(\square \)

Optimization: MDE-DSCC

Figure 7 shows the procedure of optimization.

Fig. 7
figure 7

The flowchart of optimization (MDE-DSCC)

Full size image

In the optimization, we first introduce the decomposition from Algorithm 2 to divide the decision variables into k sub-problems, and an empty set of the context vector is initialized. For each sub-problem \(i(i \in [1, k])\), we alternately optimize it with MDE-DS. The pseudocode of the whole optimization stage is shown in Algorithm 3.

figure c

In Algorithm 3, the initialization of optimization is executed from line 3 to 10. Here, we randomly generate the sub-populations for each sub-problem and update the context vector after evaluating the sub-populations. Then, sub-problems are optimized alternately from line 12 to 20 until all FEs consumed. The context vector is updated after every generation of optimization is finished.

Numerical experiment and analysis

In this section, a set of experiments are implemented to evaluate our proposal, MDE-DSCC-LMM. In the section “Experiment settings”, we introduce the experiment settings, including benchmark functions, comparing methods, and performance indicators. In the section “Performance of our proposal: MDE-DSCC-LMM”, we provide the experimental results of our proposal and comparing methods. Finally, we analyze our proposal both in the decomposition and optimization in the section “Analysis”.

Experiment settings

Benchmark functions

We design 15 test functions in noisy environments based on CEC2013 LSGO Suite, and Eq. (24) defines the benchmark functions in our experiments

$$\begin{aligned} f_i^{N}(x) = f_i(x) \cdot (1+\beta ), \quad i \in [1, 15] \end{aligned}$$
(24)

\(\beta \sim N(0,0.01)\). Briefly, this benchmark suite consists of 15 test functions with 4 categories.

  1. (1)

    \(f_1^{N}(x)\) to \(f_3^{N}(x)\): fully separable functions in noisy environments;

  2. (2)

    \(f_4^{N}(x)\) to \(f_7^{N}(x)\): partially separable functions with 7 none-separable parts in noisy environments;

  3. (3)

    \(f_8^{N}(x)\) to \(f_{11}^{N}(x)\): partially separable functions with 20 none-separable parts in noisy environments;

  4. (4)

    \(f_{12}^{N}(x)\) to \(f_{15}^{N}(x)\): functions with overlapping sub-problems in noisy environments; \(f_{13}\) and \(f_{14}\) consist of 905 decision variables, and the rest functions are 1000-D problems.

Table 1 A summary of the algorithms under comparison
Full size table
Table 2 The parameters of decomposition optimization
Full size table
Table 3 The detailed decomposition results of DG, DG2, and RDG on CEC2013 LSGO Suite in noisy environments
Full size table

Comparing methods and parameters

In our experiment design, we compare the decomposition strategy of our proposal with various grouping methods, and the algorithms applied in the comparisons are listed in Tables 1 and 2 shows the parameters of our proposal in the decomposition stage. We also conduct the experiment between MDE-DSCC-LMM and DECC-LMM to show the effect of the introduction of MDE-DS. The maximum FEs including decomposition and optimization are 3,000,000, and the population size of optimization for each sub-problem is set to 30.

Table 4 The DA and consumed FEs of DG, RDG, DG2, and LMM on CEC2013 LSGO Suite in noisy environments
Full size table
Table 5 Optimization results of DECC-D, DECC-G, DECC-DG, DECC-DG2, DECC-RDG, and DECC-LMM
Full size table

Performance indicators

There are two stages of our proposal that need to be evaluated: LMM and MDE-DSCC.

To evaluate the LMM, three metrics are employed: FEs consumed in decomposition, decomposition accuracy (DA), and optimization results. We adopt the calculation method of the DA in [49]. Essentially, DA is the ratio of the number of interacting variables that are correctly grouped to the total number of interacting variables. And to determine the existence of significance, we apply the Kruskal–Wallis test to the fitness at the end of the optimization in 25 trial runs between different decomposition methods. If significance exists, then we apply the p value acquired from the Mann–Whitney U test to do the Holm test. If LMM is significantly better than the second-best algorithm, we mark * (significance level 5%) or ** (significance level 10%) in the convergence curve.

To evaluate the MDE-DS, we apply the Mann–Whitney U test between MDE-DSCC-LMM and DECC-LMM. If MDE-DSCC-LMM is significantly better than DECC-LMM, we mark *(significance level 5%) or **(significance level 10%) at the end of optimization.

Performance of our proposal: MDE-DSCC-LMM

In this section, the performance of MDE-DSCC-LMM is studied, both on the decomposition and optimization. Experiments are conducted on the benchmark functions presented in the section “Benchmark functions”.

Performance of LMM

To verify the analysis in the section “Challenges of DG-based decomposition methods in noisy environments” that DG-based decomposition methods cannot detect the interactions in noisy environments, we apply DG, DG2, and RDG to decompose the benchmark functions. Table 3 shows the decomposition results.

Table 6 Optimization results between DECC-LMM and MDE-DSCC-LMM
Full size table

The decomposition results of DG-based methods prove our analysis, all variables are divided into a sub-problem, and interactions failed to be detected completely. Next, we provide the DA and FEs for the decomposition of DG, RDG, DG2, and LMM in Table 4, because the decomposition results of LMM are different in every trial run, the DA and consumed FEs are calculated with the mean of 25 trial runs. The best DA is in bold.

Finally, the optimization results of DECC-D, DECC-G, DECC-DG, DECC-DG2, DECC-RDG, and DECC-LMM are provided in Table 5, and the best solution is in bold.

Performance of MDE-DSCC

The mean and standard deviation of the optimum between DECC-LMM and MDE-DSCC-LMM are shown in Table 6.

And the convergence curve of 25 independent runs of all compared methods is shown in Fig. 8.

Analysis

In this section, we will analyze the performance of LMM and MDE-DS.

LMM in noisy environment

Theoretical analysis in the section “Theoretical support for LMM in noisy environments” shows that LMM has the potential to correctly detect the interactions between decision variables in noisy environments. Experimental results in the section “Performance of LMM” further support this analysis. The identification of interactions in noisy environments is a difficult task, and LMM identifies the decision variables with relatively strong intensity as nonseparable. Although the fitness difference will be affected by noise, the relative intensity of interactions between separable variables and nonseparable variables still has a possible gap, which is the main reason for successful implementation in noisy environments.

However, the optimization of LMF is not an easy task. From the DA in Table 4, the interactions which can be detected by LMM in noisy environments are limited. Although LMF can lead the direction of optimization to search for more correct interactions, a more powerful optimizer will allow LMM to find more interactions.

LMM vs DG-based decomposition methods

DG-based decomposition methods detect the interactions by determining the difference between the fitness difference and a certain parameter \(\epsilon \), and even in fully separable functions, the fitness difference will be amplified by noise and larger than \(\epsilon \) easily, which is the main reason of detection failure in noisy environments, and all decision variables are divided into a sub-problem and optimized directly. Due to the curse of dimensionality, it is difficult for DE to find an acceptable solution with this division. Thus, although the DA of DG-based methods is higher than LMM in \(f_{12}\) and \(f_{15}\), LMM still performed better than DG-based methods in the optimization of these functions, and DG-based methods are the most environmentally sensitive grouping method among the compared methods.

LMM vs D

The schematic diagram of Delta Grouping is shown in Fig. 9.

Delta grouping notices that the difference in coordinates from the initial random population to the optimized population is different in the separable variables and the nonseparable variables. In Fig. 9, when the \(\Delta _{i}\) and \(\Delta _{j}\) has large difference, Delta grouping identify \(x_{i}\) and \(x_{j}\) are separable. This rough estimation is still affected by the noise, because the Delta grouping samples in the fitness landscape and the moving vector will still be influenced by the noise. Thus, Delta grouping is second sensitive in our comparing methods, and experimental results from Table 4 and Fig. 8 all show that our proposed LMM outperforms DECC-D.

Fig. 8
figure 8figure 8

The convergence curve of DECC-D, DECC-G, DECC-DG, DECC-DG2, DECC-RDG, DECC-LMM, and MDE-DSCC-LMM. The gap in the initial period is FEs consumed for decomposition

Full size image

LMM vs random grouping

It is unnecessary to provide any information about the fitness landscape to Random grouping; therefore, Random grouping is the most environmentally insensitive decomposition method. Although paper [56] has proven that Random grouping is efficient and has a high probability to capture some interactions, it cannot detect sufficient interactions and form sub-problems properly, and LMM can detect more corrected interactions, which is the main reason that LMM outperformed than Random grouping.

The efficiency of MDE-DS

Figure 8 and Table 6 all prove that MDE-DS has a strong ability to search for better solutions compared with the canonical DE in most benchmark functions, although canonical DE performs better in \(f_9\) and \(f_{10}\). However, no optimization algorithm can solve all optimization problems perfectly. According to no free lunch theory [57] in optimization, the average performance of any pair of algorithms A and B is identical on all possible problems. Therefore, if an algorithm performs well on a certain class of problems, it must pay for that with performance degradation on the remaining problems, since this is the only way for all algorithms to have the same performance on average across all functions. Thus, although MDE-DS may perform worse than the canonical DE in noiseless functions, it is successful to introduce MDE-DS to solve problems in noisy environments.

Fig. 9
figure 9

a Delta grouping works on the separable function. b Delta grouping works on the nonseparable function

Full size image

Discussion

The above experimental results and analysis show that our proposal both the LMM and the introduction of MDE-DS have broad prospects to solve LSOPs in noisy environments. However, there are still many aspects for improvement. Here, we list some open topics for potential and future research.

How to improve the LMM

In this paper, we regard the decomposition problem as a combinatorial optimization problem and design the LMF to guide the direction of optimization by EGA. There are two parts of LMM that can be improved: (1). The design of LMF and (2). Optimizer for LMF. For LMF, we notice that it is multi-modal, especially for separable functions. For example, \(f(x)=2x_1 + x_2^2 - 0.5\sqrt{x_3}\), \(((x_1,x_2,x_3)), ((x_1,x_2),x_3)),((x_1,x_3),x_2)) , ((x_1),(x_2,x_3)), ((x_1),(x_2),(x_3))\) are all global optima, and actually, \(((x_1),(x_2),(x_3))\) is our ideal decomposition. Thus, how to design the LMF to avoid this issue is a problem that can be improved in future research. And for the optimizer, this paper employed EGA to optimize the LMF, and parts of correct interactions can be detected in noisy environments. In future research, we will apply various optimizers to optimize the LMF, and the more powerful optimizers are expected to search for more interactions in noisy environments.

Interactions’ identification in noisy environments

Although it is a difficult task to detect interactions in noisy environments, it is necessary to develop an effective interaction identification method to form sub-problems by a proper strategy. Explicit averaging [6] can alleviate the uncertainty of noise by re-evaluation. Let the re-evaluating times for \(f^N(\textrm{X})\) be m and \(f^N_i(X)\)) represents the ith re-evaluation value. Then, we apply the principle of Monte Carlo integration [58], and the mean fitness estimation \(\bar{f}^N(\textrm{X})\), standard deviation \(\sigma (f^N(X))\), and the standard error of the mean fitness \(se(f^N(X))\) are calculated as

$$\begin{aligned} \begin{aligned}&\bar{f}^N(X)=\frac{1}{m}\sum _{i=1}^{m}f_i^N(X) \\&\sigma ({f}^N(X))=\sqrt{\frac{1}{m-1}\sum _{i=1}^{m}(f_i^N(X)-\bar{f}^N(X))} \\&se(\bar{f}^N(X))=\frac{\sigma ({f}^N(X))}{\sqrt{m}}. \end{aligned} \end{aligned}$$
(25)

Equation (25) shows that sampling an individual’s objective function m times can reduce \(se(\bar{f}^N(X))\) by a factor of m to improve the accuracy in the mean fitness estimation, which means that the accuracy of sampling increases. It is a feasible method to loosen the threshold \(\varepsilon \) in DG-based methods and combine the explicit averaging strategy to identify the interactions, although it will consume lots of FEs.

Conclusion

In this paper, we proposed a novel strategy that regards the decomposition problem as a combinatorial optimization problem and designed the LMF to guide the direction of optimization. Besides, we introduce an advanced optimizer named MDE-DS to tackle optimization problems in noisy environments. Numerical experiments show that LMM can detect some interactions in noisy environments, which is competitive with the compared grouping methods. And MDE-DS has a strong ability to search for better solutions, which can accelerate the optimization in noisy environments.

In future research, we will focus on the improvement of LMM and the development of efficient interaction identification methods in noisy environments.