Introduction

Multiobjective optimization problems (MOPs) widely exist in real-world applications, such as community extraction [17], trajectory planning [13], network configuration [39], mechanism design [29], and so on. In the past 2 decades, a large number of algorithms have been designed to obtain an accurate and well-distributed approximation of the true optimal front, most of which adopt the population-based metaheuristic mechanism that can provide multiple solutions at one time [42]. In this mechanism, individuals update according to competition or cooperation principles, thus building the approximate front. Here, the definition and preservation of the elite solution are essential, since they will affect the searching preference as well as the final performance. Up to now, the static definition that bases on the current fitness values has been fully studied.

Dominance relation, crowding estimation, and aggregation cost function are the most commonly used strategies in handling elite definition and preservation [22]. Dominance relation is the primary consideration in most studies. The nondominated sorting technique has provided efficient convergence strength in MOPs with less than three objectives [7]. To guarantee selection pressure under high-dimensional problem, modified dominance relations have been studied [1]. Crowding estimation is usually required as the secondary criterion to maintain the searching diversity, where Minkowski distance and cosine distance have been studied under different problem dimensions [31]. Two approaches are commonly used to preserve solution based on the crowding estimation. The first one calculates the neighboring distance from the same nondominated front, and then selects solutions with larger distance to fill the elite archive [7]. The second one calculates the distance between the nonselected solution and its closest selected solution, and then moves the most distant solution to the selected archive one at a time until the archive’s capacity limit is reached [20]. Finally, aggregation cost function is mostly designed based on reference vectors in the objective space; therefore, it has advantages in controlling the search direction and maintaining the diversity performance. This strategy is always adopted in the decomposition-based algorithm MOEA/D and its variants [21], and also in dominance-based mechanism as a secondary criterion to guarantee the diversity performance [41]. Moreover, indicator-based methods and preference-based weightings have also been widely studied in recent years [32].

Meanwhile, the above strategies can also work in a cooperative manner. Through introducing multi-stage and multi-archive approaches, solutions under different standards are selected as elite ones to balance the searching performance. A few works introduced multiple stages focusing on convergence or diversity controls, where aggregated convergence measure and distance-based diversity estimation are, respectively, adopted in updating the approximate Pareto front. For example, Tian et al. updated the population by different selection schemes in different stages [28], while Chen et al. introduced different grouping schemes in different stages [3]. Similarly, studies adopting multiple archives also assign different elite handling methods to different archives [35]. These archives update in parallel and store elite records separately. Defining preferences in different times and archives has greatly improved the performance in many-objective optimization problems [25].

The population’s update approach is another essential process which determines the exploration and exploitation behaviors [30, 33]. To inherit from the previous generation, the existing update mechanisms can be classified into two categories, elimination-based and learning-based, respectively. Elimination-based mechanism mainly refers to the genetic and differential evolution operators, where offsprings are generated through crossover and mutation, and then, all the individuals participate in the competition following the rule of “survival of the fittest” according to the elite definition strategy [34]. Under these mechanisms, individuals are memoryless; thus, they have a rapid response for exploitation in local regions, yet it is difficult for them to fulfill the exploration based on historical information. On the other hand, the learning-based mechanisms, such as particle swarm operator, competitive swam operator, etc., are less greedy and have continuous dynamic model; thus, they have advantages in exploring the global optima [26]. However, the individual association for learning behaviors under multiple elites environment will significantly affect the optimization efficiency [38].

In conclusion, the existing studies mainly utilize the solution’s current objective values to conduct elite preservation and updating, which are not comprehensive enough to describe the searching trends. For instance, facing complex Pareto set including bias, scattered, and multimodel proprieties, estimation based on the current performance may lead to premature decision, causing diversity loss and misguided exploitation direction. Meanwhile, to enhance convergence strength and restrict computing expenses, most algorithms do not consider diversity control in the decision space, thus good alternative solutions may not be found. Since historical conditions and learning-based mechanisms show advantages in exploring the global optima, and utilizing historical evaluations does not bring additional computational costs, it makes sense to record and utilize individuals’ representative information during evolution. The information may contribute to choosing the right leader as well as preserving promising directions for evolution. Based on the above assumptions, this work attempts to define elite solutions based on their performance intervals in several historical generations. The performance includes convergence and diversity assessments, and the diversity considers the sparsity from both the objective space and the decision space. This novel idea is denoted as the robust performance evaluation (RPE). Based on the RPE, a multiobjective optimization framework with a robust archive is established.

The contributions of this paper are summarized in the following three aspects. First, a robust performance evaluation approach is introduced to define elite solutions according to the historical performance. Second, an external robust archive is established and its preservation strategy is designed. Third, a learning-based updating strategy is proposed for individuals in the external robust archive. The proposed RPE-based framework has proved to have competitive performance compared to several well-known evolutionary algorithms for solving MOPs.

The remainder of this paper is organized as follows. The preliminaries of related definitions and studies on interval dominance relation are introduced in the section “Related definitions”. The proposed robust performance evaluation and the RPE-based algorithm are detailed in the section “The proposed algorithm”. Then, the experiments on several benchmark instances and a parameter sensitivity study are presented in the section “Experiments”. Finally, the section “Discussions” presents the conclusions.

Related definitions

In this section, some basic knowledge in MOP study will be presented first. Then, a brief introduction of the interval dominance relation is given.

Multiobjective optimization problem

An MOP can be mathematically formulated as

$$\begin{aligned}{} & {} \hbox {Min} \quad {{\textbf{f}}}({\textbf{x}})= (f_{1}({\textbf{x}}),f_{2}({\textbf{x}}),\ldots ,f_{M}({\textbf{x}}))\nonumber \\{} & {} \hbox {s.t.} \qquad {\textbf{x}} \in \Omega , \end{aligned}$$
(1)

where \(\Omega =\prod _{i=1}^{D}[a_{i},b_{i}]\subseteq {\mathbb {R}}^{D}\) is the D-dimensional decision space, and \(a_{i}\) and \(b_{i}\) are the lower and upper bound of the ith dimension respectively. \({\textbf{x}}=(x_{1},x_{2},\ldots ,x_{D})^{\textrm{T}}\in \Omega \) is a candidate solution, and \({\textbf{f}}\in {\mathbb {R}}^{M}\) constitutes M objective functions.

When adopting the population-based searching mechanism to solve MOP, the position of each individual represents a candidate solution. The Pareto dominance is used to make comparison between individuals.

Definition 1

(Zhou et al. [40]) Given two individual \(p_1\) and \(p_2\), \(p_1\) Pareto dominates \(p_2\) is defined as

$$\begin{aligned} p_1 \prec p_2 \Leftrightarrow \quad{} & {} \forall j\in \{1,2,\ldots ,M\},f_j(p_1.{\textbf{x}})\le f_j(p_2.{\textbf{x}}),\nonumber \\ \wedge{} & {} \exists j\in \{1,2,\ldots ,M\},f_j(p_1.{\textbf{x}})<f_j(p_2.{\textbf{x}}). \nonumber \\ \end{aligned}$$
(2)

\(p_1\) and \(p_2\) are incomparable when they are nondominated with each other. These nondominated individuals provide the so-called trade-off solutions, which form the Pareto set (PS) in the decision space and map to the Pareto front (PF) in the objective space.

Interval comparison

Interval values have been introduced in studying optimization problems with environmental uncertainty or time-varying optima [10, 12, 23, 36]. Among these studies, on comparing interval values, several relations have been presented. The following relation is the most commonly adopted [18].

Definition 2

Given two intervals \(a=[\underline{a},\overline{a}]\) and \(b=[\underline{b},\overline{b}]\), relation \(<_{\textrm{IN}}\) is defined as

$$\begin{aligned} a<_{\textrm{IN}} b \Leftrightarrow \underline{a}\le \underline{b} \wedge \overline{a}\le \overline{b} \wedge a\ne b. \end{aligned}$$
(3)

By taking both the lower and upper boundaries into consideration, this relation is reasonable in handing interval comparison. When intervals are incomparable, it is denoted as \(a\Vert b\).

When solving an optimization through metaheuristic approaches, disturbance to the individual will provide a group of solutions and generate multiple objective values accordingly. Therefore, the individuals can be compared based on the generated objective interval, which is defined as follows.

Definition 3

Given a solution set \(\{{\textbf{x}}_1,\ldots ,{\textbf{x}}_n\}\), the jth objective interval is denoted as

$$\begin{aligned} f_j^I \triangleq [\underline{f_j}({\textbf{x}}_{1:n}), \overline{f_j}({\textbf{x}}_{1:n})] = \left[ \min _k f_j({\textbf{x}}_k), \max _k f_j({\textbf{x}}_k)\right] .\nonumber \\ \end{aligned}$$
(4)

In single-objective optimization, individuals with one-dimensional objective interval \(f^I\) can be compared according to Definition 2. When dealing with multiobjective optimization, individuals with multi-dimensional objective interval \({\textbf{f}}^I = (f_1^I,f_2^I,\ldots ,f_M^I)\) should be compared according to the interval Pareto dominance relation.

Definition 4

(Sun et al. [24]) Given two individuals \(p_1, p_2\) each related to a solution set, the jth objective interval is denoted as \(p_1. f_j^I\) and \(p_2. f_j^I\), respectively. The interval Pareto dominance relation \(\prec _{IF}\) is defined as

$$\begin{aligned} p_1 \prec _{IF} p_2 \Leftrightarrow \quad{} & {} \forall j\in \{1,2,\ldots ,M\},(p_1. f_j^I<_{\textrm{IN}} p_2. f_j^I) \nonumber \\{} & {} \quad \wedge (p_1 . f_j^I\Vert p_2. f_j^I),\nonumber \\ \wedge{} & {} \exists j\in \{1,2,\ldots ,M\},p_1. f_j^I<_{\textrm{IN}} p_2. f_j^I. \nonumber \\ \end{aligned}$$
(5)

The interval dominance relation will be adopted in our work to utilize historical performance for robust elite definition.

The proposed algorithm

In this part, the concept of the robust performance evaluation over time will be introduced, and then, the selecting and updating details in building the robust archive will be described. In the end, the framework of the proposed RPE-based algorithm is given.

Robust performance evaluation

In multiobjective metaheuristic algorithm, solutions eliminated in an elite competition must not provide guidance for subsequent generations. However, considering the multimodal, deceptive situations, or the diversity estimation affected by the whole distribution, the elite definition principle is not absolutely correct and can lead to premature situations. Therefore, the RPE technique is presented to define the suboptimal solutions according to the individuals’ states in a time window.

The individuals’ historical states include position information and objective values. The historical states over a time interval are recorded as follows. At time t, the historical positions in the last K generations are denoted as \(\{{\textbf{x}}_{t-k}\mid k=0,\ldots ,K-1\}\). According to Definition 3, for an individual p, the objective interval over time window K is \( p.f_j^I \triangleq [ \underline{f_j}({\textbf{x}}_{t-K+1:t}), \overline{f_j}({\textbf{x}}_{t-K+1:t}) ]\), \( j=1,2,\ldots ,M\). These historical states can demonstrate the stability and evolving trend of the individual.

For high-dimensional space, the selection pressure provided by the interval Pareto dominance relation is not enough; therefore, instead of comparing the objective values directly, two metrics to establish comparison during the robust evaluation are adopted. The two metrics, respectively, focus on evaluating convergence and evaluating diversity. They are defined according to the states of the individual to be evaluated relative to an elite solution set.

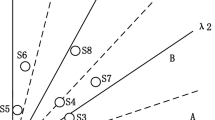
The convergence evaluation metric is denoted as \(\hbox {EC}\), and it is defined as the distance between an individual and an existing elite solution set. Here, the two kinds of distance are plotted in Fig. 1a.

Fig. 1
figure 1

Diagrams of basic concepts in RPE. a \(\hbox {EC}\): the distance between an individual and a solution set. b Intervals in the objective space and the decision space over time

Full size image

The first one is the Euclidean distance from the individual to the ideal point of the solution set in a normalized objective space. Although this distance has been adopted in several studies for convergence measure, it is not quite reasonable for MOP with concave PF. For instance, in Fig. 1a (left), compared to individual \(p_1\), \(p_2\) looks closer to the approximate PF, yet its advantage cannot be reflected. The second distance is calculated by adding a scaling procedure and transforming the PF to the convex shape. The scaling ratio is the length of the normalized objective vector closest to the individual. Assume \({\mathcal {X}}\) is an elite solution set, for individual p, \(\hbox {EC}\) using the second distance is calculated as follows:

$$\begin{aligned}{} & {} p.\hbox {EC} =\frac{\Vert p.{\textbf{f}}'\Vert }{\Vert {\textbf{f}}'({\textbf{x}}^*)\Vert } \nonumber \\{} & {} {\textbf{x}}^* = \arg \min \angle (p.{\textbf{f}},{\textbf{f}}({\textbf{x}})),\quad {\textbf{x}}\in {\mathcal {X}}\nonumber \\{} & {} {\textbf{f}}'({\textbf{x}}^*) =\frac{{\textbf{f}}({\textbf{x}}^*)-{\textbf{z}}^{id}}{{\textbf{z}}^{na}-{\textbf{z}}^{id}}\quad p.{\textbf{f}}' =\frac{p.{\textbf{f}}-{\textbf{z}}^{id}}{{\textbf{z}}^{na}-{\textbf{z}}^{id}}, \end{aligned}$$
(6)

where \(z^{id}_j = \min _{{\textbf{x}} \in {\mathcal {X}}} f_j({\textbf{x}}), j\in \{1,2,\ldots ,M\} \) represents the jth dimension of the ideal point, and \(z_j^{na}\) represents the nadir value. \({\textbf{f}}'\) is the normalized objective vector. Through this \(\hbox {EC}\) metric, the individuals can be distinguished (Fig. 1a (right)).

The diversity evaluation metric is denoted as \(\hbox {ED}\). In this work, \(\hbox {ED}\) has two forms: one evaluates crowding degree in the objective space, termed as \(\hbox {ED}^o\); the other preforms in the decision space, termed as \(\hbox {ED}^d\). In each form, the diversity evaluation for one individual follows two steps, association and quantification. Given an elite set \({\varepsilon }\) and population \({\mathcal {P}}_e\) to be evaluated. First, each individual \(p\in {\mathcal {P}}_e\) is associated with one closet elite in \({\varepsilon }\). Second, the diversity metric is quantified as follows:

$$\begin{aligned} p.\hbox {ED} = \hbox {dist}\times \alpha ^{(c-1)}, \end{aligned}$$
(7)

where, for \(\hbox {ED}^o\), \(\hbox {dist}\) represents one minus the cosine of the included angle between the normalized objective vectors; for \(\hbox {ED}^d\), \(\hbox {dist}\) represents Euclidean distance in the normalized decision space. \(\alpha \) is a penalty factor, \(\alpha \in [0,1]\); c is the index after sorting individual associated with a same elite in descending order with respect to their \(\hbox {dist}\) values.

Based on the above definition, the RPE mechanism transforms a individual’ historical states to the metric intervals over time window K, denoted as \(p.\hbox {EC}^I \triangleq [\underline{\hbox {EC}}({\textbf{x}}_{t-K+1:t}),\overline{\hbox {EC}}({\textbf{x}}_{t-K+1:t})]\), \(p.\hbox {ED}^I \triangleq [\underline{\hbox {ED}}({\textbf{x}}_{t-K+1:t}),\overline{\hbox {ED}}({\textbf{x}}_{t-K+1:t})]\). The diagram of the intervals is displayed in Fig. 1b. The following sections will introduce the RPE-based elite preservation.

Robust performance evaluation-based preservation

This section bases on the RPE metrics in the section “Robust performance evaluation” and the interval Pareto dominance relation in Definition 4.

To incorporate RPE into metaheuristic algorithms, a robust archive (RA) is established to preserve individuals with advantageous intervals in the objective or the decision spaces. These individuals are selected considering convergence as well as diversity performance. Hence, RA consists of two segments with equal capacity, which, respectively, evaluated by interval \([\hbox {EC}^I,-\hbox {ED}^{oI}]\) and interval \([\hbox {EC}^I,-\hbox {ED}^{dI}]\). The intervals are displayed in Fig. 2a. The cylinders represent the convergence intervals quantified by \(\hbox {EC}^I\), and the arcs represent the diversity fluctuation quantified by \(\hbox {ED}^I\). Based on the interval Pareto relation, in the decision space, \(p_1 \prec _{\textrm{IN}} p2\); in the objective space, \(p_3 \prec _{\textrm{IN}} p4\).

Fig. 2
figure 2

Diagrams of a performance intervals in decision space and objective space for individual comparison; b evolving trends corresponding to different \(\varphi \) values: (left) small \(\varphi \); (right) large \(\varphi \)

Full size image

During RA selection, individuals with nondominated intervals have higher preserve priorities; individuals on the same interval nondominated level are selected according to their current convergence degree \(\hbox {EC}_t\). This procedure is described in Algorithm 1.

figure a

Learning-based local search

Solutions selected by RPE metric have strong robustness, which indicate potential convergence areas. However, since interval evaluation has less selection pressure, these solutions are suboptimal and always lag behind the converging process on the basis of the current fitness evaluation, they cannot directly contribute to the approximate Pareto front. Therefore, the utilization of these solutions is to conduct local search that enhances the exploration performance in subregions. The local search is realized by updating the position of individuals in RA.

A learning-based local search (LBLS) is proposed for this purpose. LBLS takes into account the robust solutions’ current state, historical states, and information from the current optimal solutions. It consists of two steps: individual selection and learning-based update.

  1. (1)

    Select individuals from RA and current optimal population separately. For example, in genetic algorithm (GA), the current population is the optimal population, which is updated by environmental selection strategy. The tournament selection mechanism is adopted to determine the mating parents. First, two sets of individuals, \({\mathcal {R}}_1\) and \({\mathcal {R}}_2\), are selected from RA. The individuals’ interval nondominated levels and the maximum crowding distances of the interval in the objective space (for \({\mathcal {R}}_1\)) as well as the decision space (for \({\mathcal {R}}_2\)) determine the selection result. Second, select individuals from the current optimal population \({\mathcal {P}}\). The nondominated levels and the closest distance to the selected robust individuals are considered during the selection. To be noted, the number of selected individuals for LBLS is designed to be adaptive to maintain diversity at the beginning and stability at the end, that is

    $$\begin{aligned} \mid {\mathcal {R}}_1\mid= & {} \left\lceil \frac{N_A}{4}\times \frac{\hbox {Eval}-\hbox {Evaluated}}{\hbox {Eval}} \right\rceil \nonumber \\ \mid {\mathcal {R}}_1\mid= & {} \mid {\mathcal {R}}_2\mid , \quad \mid {\mathcal {P}}\mid = \mid {\mathcal {R}}_1\mid +\mid {\mathcal {R}}_2\mid . \end{aligned}$$
    (8)
  2. (2)

    Update the individuals in RA. LBLS strategy is inspired from PSO [5] and CSO [4] operators. The individual from the elite archive is seen as a leader, and its position is denoted as \({\textbf{x}}_{e}\). Denote at time t, the position and velocity of individuals from robust archive are denoted as \({\textbf{x}}_{r,t}\) and \({\textbf{v}}_{r,t}\). The update formulation is as follows:

    $$\begin{aligned} {\textbf{v}}_{r,t+1}= & {} {\textbf{r}}1\times {\textbf{v}}_{r,t}\nonumber \\{} & {} +{\textbf{r}}2\times ({\textbf{x}}_{e}-{\textbf{x}}_{r,t}) +{\textbf{r}}3\times \varphi \times (\overline{{\textbf{x}}}_{r,T} -{\textbf{x}}_{r,t})\nonumber \\ {\textbf{x}}_{r,t+1}= & {} {\textbf{x}}_{r,t}+{\textbf{v}}_{r,t+1}. \end{aligned}$$
    (9)

    Here, \({\textbf{r}}_1\), \({\textbf{r}}_2\), \({\textbf{r}}_3 \in [0,1]^D\) are randomly generated vectors, \(\overline{{\textbf{x}}}_{r,T}\) is the mean value of the individual’s historical position over time interval T, and \(\varphi \in [0,1]\) is a parameter to control the proportion of the historical information and the elite information. When \(\varphi \) is small, the update operator presents higher convergence strength guided by the elite information; otherwise, when \(\varphi \) is large, the updated individual receives backward strength, remaining exploration in local areas. Trajectories under these two conditions are illustrated in Fig. 2b. To control the influence of local search to the main searching process, \(\varphi \) can be designed adaptive to fit different evolution stages.

Main framework

The main framework of MOEA-RPE is illustrated in Algorithm 2. In the framework, “GA” represents the general evolutionary algorithm including tournament selection, simulated binary crossover, and polynomial mutation. The “EnvironmentalSelection” can refer to any existing selection technique in multiobjective research, such as metric-based sorting, one-by-one selection, etc. Individuals eliminated by “EnvironmentalSelection” are denoted as \({\mathcal {P}}^r\). These individuals will be further evaluated and selected to update RA. At the same time, optimal solutions found by RA will update the population in MOEA.

It can be seen that the proposed framework is a modification of traditional MOEA that appends an external production–selection process to discover robust noninferior solutions. The external process will contribute to the diversity preservation in the objective space and the decision space, as well as enhancing exploration in local regions. The update diagram of the population in MOEA and the external RA is displayed in Fig. 3.

Fig. 3
figure 3

The update diagram of the population and the robust archive in MOEA-RPE

Full size image
figure b

Experiments

In this section, the experiments are arranged to validate the effectiveness of the robust performance evaluation. Problems with complex properties are selected as the test instances, respectively. Several appropriate optimization algorithms for these kinds of problems are selected to compare with the proposed method.

Experiments on problems with biased decision space

Experiment setting

For optimization problems, complexity in the decision space mainly refers to the biased searching space [15]. Bias means that the slopes of objectives are large in the vicinities of some Pareto solutions, that is, a small variation will cause significant deterioration. Therefore, the bias feature presents difficulty in the balance between exploitation and exploration, results in premature during optimization, and also challenges the diversity performance. Benchmarks have been built considering this complexity. Typical benchmark suite is BT [16].

The complexity in decision space challenges the evolution operator. Therefore, in this experiment, MOP methods with different operators are selected, namely genetic operator, particle swarm optimizer, and differential optimizer. Since this part of experiment does not focus on the high dimension in the objective space, the performance of traditional algorithms, such as NSGAII [7], MOPSO [5], and MOEADDE [15], is similar to that of the current new algorithms. Thus, these traditional algorithms are selected as comparisons. Moreover, two algorithms with local search mechanisms are selected, namely, MOEADCMA [16] and NSLS [2]. These algorithms have advantages in dealing with complexity in the decision space. The comparison algorithms are provided by PlatEMO [27].

Elite definition has great influence on the optimization performance. For fair competition, the proposed MOEA-RPE adopts the same environmental selection methods as NSGAII (Algorithm 2, Line 7). The population size N and the maximal number of fitness evaluations are set to be 100 and 1e5 in all runs.

The inverted generational distance (IGD) is used as the performance assess indicators, which is a combinational metric for both convergence and diversity. IGD is the average distance from a uniformly distributed set selected from the true PF to the obtained solution set. The size of the uniform set for calculating IGD is set to be 5000.

Experimental results

The best, medium, and worst IGD values of each algorithm on test instances BT1-5 from 30 independent runs are presented in Table 1. The best IGD value in each row is marked in black. The Wilcoxon’s rank sum test with the significance level 0.05 is performed to show the statistically significant differences between the results; the symbols “\(+\)”, “−”, and “=” in the table, respectively, indicate that the results obtained by the reference algorithms are significantly better than, worse than or equal to the ones obtained by the proposed MOEA-RPE. Also, the Pareto optimal solutions of all runs are plotted in Fig. 4, where the true PFs are marked in red. From the IGD values and the position of the best solutions, it can be observed that MOEA-RPE have achieved most of the best performance. For BTs that have distance-related bias, the convergence difficulty is raised. Here, MOPSO, MOEADDE, MOEADCMA, and NSLS cannot converge to the true PF; NSGAII and MOEA-RPE have competitive performance, while MOEA-RPE shows smaller converge distance and better stability. BT3 and BT4 also have position-related bias. In these cases, compared to the approximate PF of NSGAII, the shape of MOEA-RPE is closer to the true PF. Considering that NSGAII and MOEA-RPE adopt the same environmental selection method, it can be concluded that MOEA-RPE has better exploration ability. The IGD curves within 1e5 fitness evaluations are given in Fig. 5. Compared to NSGAII, MOEA-RPE can further improve the optimization performance. This can be explained by the robust performance evaluation approach that can reserve potential good solutions, thus improving the exploration ability of MOEA.

Table 1 The IGD values (best, medium, and worst) on BTs
Full size table
Fig. 4
figure 4

The obtained solutions from 30 independent runs on BTs

Full size image
Fig. 5
figure 5

The IGD curves with respect to the fitness evaluation times on BT1, BT2, and BT5

Full size image

Experiments on many-objective problems

Experiment setting

Complexity in objective space mainly refers to high-dimensionality, degeneration, and so on. For many-objective optimization, diversity control is essential in objective space as well as decision space. The popular many-objective benchmark test suite MaF is selected as the optimization problem in this section. MaF includes diverse properties in separability, variable linkage, modality, and front geometry. In MaF, the nonlinearity simulated by several transformation functions can examine the convergence ability of the optimization methods. In this section, the objective dimension in MaF suite M is set to be 5.

MaF8 is a multi-point distance minimization problem (MPDMP), which can visually examine the elite distribution in decision space [14]. The difficulty of MaF8 has been raised, and another 3 MPDMPs with disconnected PS, local optima, and shift transformation have been built. These new instances are described in Table 2, where the penalty area \(\Omega _p\) is built in decision space to complicate the fitness landscape; shift transformation in MPDMP4 makes the problem deceptive and multimodal. All these changes require algorithm to have better exploration ability. In MPDMP experiments, the objective dimension M is set to be 10.

For many-objective problems, both evolution operator and environmental selection method are important. Therefore, many-objective algorithms using different operators are selected as the comparison, namely, NSGAIII [6], MyODEMR [8], and NMPSO [19]. The operators adopted are GA, DE, and PSO, respectively. Also, an algorithm for MaOP considering history information, NSGAIII-F1 [11], is also selected, which introduces an information feedback model in updating population. And a newly proposed decomposition-based algorithm MOEA/D-UR [9] is included. All methods adopt the reference-based method and the truncation approach in environmental selection. In this experiment, to adjust the proposed RPE-based method for solving many-objective problem, during the environmental selection (Algorithm 2, Line 7), extreme solution on each objective is first selected; the rest solutions are selected by the truncation approach according to the minimum distance to the neighboring solutions [37]. The population size N is set to be 150 (for NSGAIII, \(N=126\)), and the maximal number of fitness evaluations is 1e5.

Table 2 Definition of the multi-point distance minimization problems (MPDMPs)
Full size table

Experiment result

The IGD performance from 30 independent runs on MaF1-8 and MPDMP2-4 is displayed in Table 3. It can be observed from the IGD values that MOEA-RPE has an obvious advantage on MaF1,2,5,6. For instances with multimodal modality, MOEA-RPE has poor performance on MaF3, which has a large number of local fronts. However, it is competitive on MaF4. It can be concluded that although the robust performance evaluation has the ability to handle local optima, it may not suitable for highly multimodal situation. This limitation can be explained by the leader matching mechanism in LBLS, which can cause fluctuations in exploiting an objective direction. Therefore, the highly multimodal complexity remains a challenge for MOEA-RPE. On MPDMP2-4, MOEA-RPE has achieved the best IGD scores. To observe the effectiveness of integrating historical information, attention should be paid to NSGAIII-F1 and MOEA-RPE. Compared to NSGAIII, NSGAIII-F1 has advantage in solving a few instances, such as MaF8 and MPDMP2, while MOEA-RPE has advantage in most of the instances, except MaF3. Therefore, the robust-based approach has better effectiveness and stability to utilize the historical information.

To study the distribution of the obtained solutions, the solutions with medium performance are given in the parallel coordinates in Fig. 6. It can be seen that MOEA-RPE has advantageous convergence and diversity performance in MaF1,2,4-8; and both NMPSO and MOEA-RPE have competitive performance in MPDMPs. For MaF8 and MPDMPs, the distributions in decision space can reflect the performance visually, which are given in Fig. 7. Since the robust performance evaluation consider the solutions’ historical position in both objective space and decision space, MOEA-RPE can achieve better distribution compared to the other algorithms, including NMPSO and NSGAIII-F1. That is to say, MOEA-RPE can provide more diverse solutions for the decision maker.

Table 3 The IGD values (best, medium, and worst) on MaFs and MPDMPs
Full size table
Fig. 6
figure 6

Solutions with medium performance on MaFs and MPDMPs

Full size image
Fig. 7
figure 7

The distribution of solutions with medium performance on MPDMPs

Full size image

In summary, according to the experiments, the proposed method has advantages in dealing with bias in the decision space, and is competitive in maintaining a uniform distribution in high-dimensional objective space. Since many real-world problems, such as the path planning and crashworthiness optimizations, have the bias characteristics, the proposed mechanism is suitable for solving these cases. To further demonstrate this point, a robotic path planning experiment will be performed in the section “Application on a path planning problem in robotic manipulation system”.

Discussions

In this section, the effectiveness analysis of the applied strategies and the sensitivity analysis of the main parameters are included, followed by a computational complexity analysis of the proposed framework.

Strategy effectiveness analysis

The proposed MOEA-RPE algorithm includes two main operations, RA selection and LBLS. The effectiveness of these two operations is discussed in this section.

Since the LBLS update requires individuals’ historical performance, it cannot work alone without RPE in RA selection. The effectiveness of the combination of LBLS and RA selection will be first discussed. When MOEA-RPE employs the same environmental selection approach as NSGAII, the comparative study between MOEA-RPE and NSGAII will illustrate the differences. The bi-objective benchmark suite BT is selected as the optimization problem. The optimization results are displayed in Table 4, MOEA-RPE is represented by “NSGAII\(+\)RA\(+\)LBLS”, which is significantly better than NSGAII on 2 of the 5 test instances, and has better average performance on 4 instances. This demonstrates that the utilization of historical performance is meaningful.

Moreover, to analyze the effectiveness of LBLS separately, an altered algorithm “NSGAII\(+\)RA\(+\)GA” is generated which adopts GA operation instead of LBLS. Results show that without LBLS, the performance of four instances would be degraded. The phenomenon can beŁ explained by the advantages of the learning-based mechanisms in balancing global exploration and local search.

Table 4 The statistical results (mean and standard deviation) in terms of IGD values in the effectiveness study
Full size table

Sensitivity study on the robust archive capacity

In the proposed method, the robust archive capacity \(N_A\) determines the extent of its influence on MOEA. In previous experiment, \(N_A\) is equal to the population size N. In this section, MOEA-RPE with different \(N_A\) values will be examined and analyzed.

Let \(P=N_A/N\), the IGD performance of \(P \in \{0.2,0.4,0.6,0.8,1.0\}\) from 10 independent runs are plotted in the box diagram Fig. 8. It can be seen that, compared to the performance of NSGAII and NMPSO, the fluctuation in P has no significant impact on MOEA-RPE. In previous experiment, MOEA-RPE has presented better performance on BT1-5, MaF1-2, and MaF5; in this section, the advantage still exists when the proportion of robust solutions is reduced. However, on MaF3 and MaF4, the performance deteriorates when the proportion P is increased. Generally, the performance has better stability when the proportion P is in range [0.2, 0.8]. Thus, \(P=0.6\) is recommended when using the proposed MOEA-RPE.

Fig. 8
figure 8

Sensitivity study on the robust archive capacity

Full size image

Computational complexity analysis

Compared with traditional MOEAs which hold an average time complexity of \(O(MN^2)\), the complexity of MOEA-RPE is mainly increased in processing the RPE-based preservation. In RPE, the number of comparison operation used to obtain a metric interval is equal to the length of time window K, and thus, the complexity in handling historical information is O(KN). The complexity of an interval nondominated sorting operation is \(O(2MN^2)\). Since the sorting operation performs twice in the two-metric-based selection process (according to Algorithm 1), the time consumption will be doubled. Taking all the above considerations and computations into account, the worst-case complexity is \(O(5MN^2)\). When the constant coefficient is not considered, the time complexity becomes \(O(MN^2)\). Meanwhile, since each noninferior individual maintains K historical metrics, the space complexity would increase. In the worst case, it needs K times more memory space than algorithms with no historical records. To be concluded, although the proposed algorithm has the same time complexity as most MOEAs, it requires more sorting operations and read–write operations, so the optimization process will take more time. Figure 9 shows the average runtime of experiments in Table 3. The hardware platform contains an Intel i7-9700K CPU and a memory of 16 GB. The software platform is Matlab. \(K=5\) is adopted in these experiments.

Fig. 9
figure 9

Runtimes on MaFs and MPDMPs

Full size image
Fig. 10
figure 10

The performance of robotic manipulation path planning optimization problem

Full size image

Application on a path planning problem in robotic manipulation system

In this section, the proposed algorithm is adopted and tested in a robotic manipulation scenario. Industrial robots work in environments with many obstacles. In addition to completing a task without collision with obstacles or other manipulators, safety and energy costs should also be considered. Therefore, a multiobjective path planning optimization problem can be built. A manipulator can be described in two spaces, a 6-dimensional task-space illustrating the manipulator’s location and orientation; and a \(N_d\)-dimensional joint-space to record the joint angles of the manipulator motors, where \(N_d\) is the dimension of freedom (DOF). The optimized solution is a trajectory which consists of multiple points in the task-space or the joint-space. Since a small change on the joint angle will cause a significant change in the task-space, the optimizations of the moving safety and the trajectory length have bias features, which present difficulties for evolutionary algorithms.

The manipulator path planning problem under environment with obstacles is defined as follows. The working environment includes a 6-DOF manipulator and a spherical obstacle. The task is to move the manipulator tip from initial position to target position through the stationary obstacle without collision. To optimize the moving path, some points in the path are selected as the control points. During optimization, these control points are first determined by the optimization algorithm, and then, the other points in the path can be determined by interpolation between adjacent control points and endpoints. Each point in the path has two positions, position in the task-space \({\textbf{x}}_{\textrm{op}}\) and position in the joint-space \({\textbf{x}}_{\textrm{jt}}\), respectively.

During path optimization, three objectives are considered. The first objective is the manipulator end-effector/tip travelling length in the task-space. The distance is the summation of the displacements between adjacent points in the task-space. The second objective is the safe distance. It is defined as the minimal distance from the obstacle to the manipulator. The manipulator is simplified as six cylinders, the minimal distance from each cylinder to the obstacle is denoted as \(D_{\textrm{cy}}\). The larger safe distance is, the safer while operating the task. The third objective is the energy cost in the joint-space. It is the summation of angle increments on all joint motors. The objective functions are formulated as follows. To formulate a minimization MOP, a minus sign is added to the safe distance

$$\begin{aligned} f_1= & {} \sum ^{N_p-1}_{i=1} \parallel {\textbf{x}}_{{\textrm{op}},i+1}-{\textbf{x}}_{{\textrm{op}},i}\parallel \nonumber \\ f_2= & {} -\min ^{N_d} D_{{\textrm{cy}}} \nonumber \\ f_3= & {} \sum ^{N_p-1}_{i=1} \sum \mid {\textbf{x}}_{{\textrm{jt}},i+1}-{\textbf{x}}_{{\textrm{jt}},i} \mid \nonumber \\ {\textbf{x}}_{{\textrm{op}}}= & {} \text {forward}({\textbf{x}}_{\textrm{jt}}). \end{aligned}$$
(10)

Here, the number of control points is set to be 10. Thus the dimension of the decision variable is \(10\times N_d\). \(N_p\) is the number of points in the path after interpolation, and the points include start point and target point.

To compare the optimization performance, four algorithms are adopted in this section. The Pareto optimal solutions from 10 independent runs are plotted in Fig. 10. To compare the convergence performance more clearly, the PFs are plotted in the 2D space illustrating the trajectory length (\(f_1\)) and the angle increment (\(f_3\)), and the safe distance (\(-f_2\)) is displayed by the color bar.

It can be seen from the figures that the convergence performance of MOEA-RPE has significant advantage. NSGAIII comes second. From the enlarged views, compared to NSGAIII, the multiple fronts obtained by MOEA-RPE have a similar distribution, which means that MOEA-RPE has better stability in different runs. Therefore, the path planning problem proved that the proposed method has good performance in biased practical problems.

Conclusion

This paper presents a robust performance evaluation approach for multiobjective optimization. Based on this approach, a robust archive has been established to preserve potential solutions for evolution, and an RPE-based MOEA framework has been designed. Experiments have been carried out to examine the effectiveness of the proposed method. Since the RPE considers solutions’ historical performance in decision space and objective space, the RPE-based algorithm can achieve well-distributed solutions with better convergence performance in most test problems. Meanwhile, the proposed method is deeply analyzed in respect of strategy effectiveness and parameter sensitivity, and a recommended range for the robust solution proportion has been given. Finally, the proposed method has been applied to a robotic manipulation system to obtain the optimal path. In conclusion, the RPE approach is a novel and promising technique for multiobjective optimization. However, it still has limitations in highly multimodal environment. In future, the learning-based mechanism will be further studied for multimodal problems, and the RPE-based mechanism will be applied in other complex practical applications.