Abstract
The hesitant fuzzy set has been an important tool to address problems of decision making. There are several various improved hesitant fuzzy sets, such as dual hesitant fuzzy set, hesitant interval-valued fuzzy set, and intuitionistic hesitant fuzzy set, however, no one kind of improved fuzzy sets could reflect attitude characteristics of decision makers on time-sequences. In reality, time-sequence is one important sector to reflect hesitant situations as decision makers might have different knowledges of the same alternative at different moments. To perfect the description of such hesitant situations and obtain more reasonable results of decision making, we define a new kind of hesitant fuzzy set, namely, time-sequential hesitant fuzzy set. Meanwhile, its corresponding basic operators, score function and distance measures are proposed. We also propose the concept of fluctuated hesitant information to describe hesitant degrees of decision makers on time-sequences. By comprehensively utilizing the score function, fluctuated hesitant information and distance measures under time-sequential hesitant fuzzy set, a synthetic decision model is proposed. Two illustrated examples and one real-application are utilized to illustrate the effectiveness and advantage of the synthetic decision model under time-sequential hesitant fuzzy set.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Decision making [1] acts as an important role in science researches [2, 3], energy management and investments [4, 5], manufacturing [6, 7], construction management [8,9,10,11] and so on. In processes of decision making, finding out the finest alternative among feasible ones is the main task. Reasonable decision making not only can bring better incomes but also is more valuable for individuals, organizations, which has attracted attention and researches of many scholars [12]. As an important branch of decision making, multi-attribute decision making (MADM) [13] is popular in various kinds of fields. Usually, due to the complexity and fuzziness of decision problems of MADM, decision makers are faced with challenges in collecting precise data, for that most of the information is either uncertain or imprecise in nature and hence leads to unprecise results. Fuzzy set theory [14] is presented as an effective means to cope with the uncertainty and complexity of decision making [10, 12, 15, 16], especially when decision makers express their opinions in fuzzy linguistic words [17].
Literature review
As ordinary fuzzy linguistic approaches were with the loss of information caused by the need to describe the results in the initial express domain that was discrete via an approximate procedure, Herrera et al. [18] derived the 2-tuple fuzzy linguistic representation model. To cope with the situation that 2-tuple fuzzy linguistic representation model was only suitable for linguistic variables with equidistant labels, Wang et al. [19] induced the symbolic proportion into the 2-tuple fuzzy linguistic representation model and proposed the proportional 2-tuple fuzzy linguistic representation model. Torra introduced possibilities into fuzzy set, and derived hesitant fuzzy set (HFS) [20, 21], which have been developed rapidly and played important roles in the application of decision making [22,23,24,25,26,27,28]. As experts could not easily provide a single term as their own knowledge was limited when faced with decision problems, Rodríguez et al. [28] combined fuzzy linguistic expressions with HFS and proposed hesitant fuzzy linguistic term sets. To assure that linguistic terms in hesitant fuzzy linguistic term sets were consecutive, Wang [29] generalized hesitant fuzzy linguistic term sets into extended hesitant fuzzy linguistic term sets. By inducing proportional information into hesitant fuzzy linguistic term sets to represent important degrees of each linguistic term, Chen et al. [30] presented proportional hesitant fuzzy linguistic term sets and applied which to multiple criteria group decision making. As hesitant fuzzy linguistic term sets could not well describe some more complex linguistic terms, Gou et al. [31] proposed the double hierarchy hesitant fuzzy linguistic term set. To improve properties of dealing with the uncertainty caused by the inherent vagueness of linguistic expressions when utilizing linguistic representation models based on hesitant fuzzy linguistic term sets, Liu et al. [32] introduced type-2 fuzzy envelope into hesitant fuzzy linguistic term sets.
With the convenience of describing hesitance of decision experts, HFSs have been drawing attentions of many researchers. By extending HFEs to be in the same lengths based on arranging values of HFS elements (HFE) in increasing orders or descending orders, Xu et al. [33] defined distance measures and correlation measures for HFSs information. After discussing the relationship between intuitionistic fuzzy set and HFS, Xia et al. [34] introduced a variety of aggregation operators for HFS elements. Farhadinia [35] researched relationships between entropy, distance measure and similarity measure not only for HFSs but also for interval-valued HFSs. After which, new formulas of entropy, distance and similarity measures for HFSs were introduced. Through taking hesitant degrees of HFSs into account, Zeng et al. [36] proposed a series of innovative distance and similarity measures for HFSs. Li et al. [37] presented new distance measure methods, in which lengths of HFEs were taken into account. In the application of MADM, new distance measures could obtain more reasonable ranking results. Chen et al. [38] introduced some correlation coefficient formulas for HFSs and researched corresponding applications to clustering analysis. Wang et al. [39] systematically studied essential characteristics and generation mechanisms of score functions under HFSs environment.
Variants of HFS have been improved to deal with different situations of MADM. Zhu et al. [40] proposed dual hesitant fuzzy set (DHFS), in which several possible non-membership degrees were added to further represent hesitant attitudes of decision experts toward objects based on ordinary hesitant fuzzy set. By adding weights into DHFS, Zeng et al. [41] introduced concepts of weighted dual hesitant fuzzy set and weighted dual hesitant fuzzy set element. To utilize impreciseness and uncertainty properties of soft set under hesitant fuzzy set environment, Babitha et al. [42] introduced the concept of hesitant fuzzy soft set (HFSS) and basic operators. To allow decision makers to describe their attitudes about MADM problems under HFS environment by interval values, Chen et al. [43] induced interval values into HFS and proposed interval-valued hesitant fuzzy set (IVHFS). To depict both preferences and probabilistic information well, Zhu [44] generalized HFS into probabilistic hesitant fuzzy set (PHFS) by including probabilistic knowledge. Peng et al. [45] combined intuitionistic fuzzy set with HFS and proposed intuitionistic hesitant fuzzy set (IHFS), which was applied to multi-criteria decision making. To overcome the problem of loss information under HFS, Zhu et al. [46] introduced the extended hesitant fuzzy set (EHFS) and extended hesitant fuzzy set element. To improve the property of expressing probability information about hesitance, Song et al. [47] presented the interval-valued probabilistic hesitant fuzzy set (IVPHFS) and its corresponding operation laws and aggregation operators.
Motivations
When decision makers evaluate alternatives through corresponding attributes under traditional HFS environments, membership degrees of which always are given one by one. And each membership degree in HFE is given after each certain deep thinking, which is of difference on time-sequences. Then, deserved membership degrees are formed as an HFE. For that, there are kinds of fluctuation information on time-sequences as given membership degrees in HFEs usually are different at different moments, which could be an important index to reflect attitudes of decision makers about MADM problems. Though various kinds of HFS have been proposed to describe attitudes of decision makers more freely and completely, there are hardly any improved HFSs that have been focused on fluctuated influences of membership degrees given by decision makers on time-sequences.
For traditional HFS or variants of HFS mentioned above, there is no time-sequential information in processing membership degrees in HFEs, which neglect fluctuated influences of membership degrees given at different moments. However, if same possible membership degrees in two or more HFEs are given at different moments, namely, same possible membership degrees in the two or more HFEs will be different on time-sequences, the situations of hesitance of decision makers can be different too. For example, assume that there are two HFEs h1 = {0.2, 0.3, 0.6, 0.8, 0.9} and h2 = {0.2, 0.8, 0.6, 0.3, 0.9} given by decision makers about a certain problem of decision making. According to traditional HFS or variants of HFS, h1 and h2 are the same. However, if we fix sequences of membership degrees according to giving moments, h1 and h2 are with different fluctuations, which can represent different hesitant attitudes of decision makers. Detailly, after adding time-sequences, illustrations of h1 and h2 are shown in the Fig. 1. Though h1 and h2 are with the same values of membership degrees, which can reflect different attitudes of decision makers through taking fluctuations of membership degrees on time-sequences into account, and it is obvious that h1 is with fewer fluctuations and more reasonable than h2. Specifically, as time goes on, decision makers should have a deeper knowledge of alternatives, and corresponding given membership degrees of decision making about same alternatives will show smaller and smaller fluctuations on time-sequences. If membership degrees fluctuate acutely on time-sequences, which could reflect the hesitant characteristics of the decision makers are large and hereafter there is the risk of obtaining reasonable and finest alternatives.
To better describe attitudes of decision makers on alternatives when faced with problems of decision making, it is necessary to pay attention to such kind of fluctuations of possible membership degrees on time-sequences. By inducing time-sequences into HFS to perfect descriptions of such situations and to obtain more reasonable results of decision making, we propose the concept of time-sequential hesitant fuzzy set (TSHFS) on the assumption that membership degrees about describing attitudes of decision makers are given one by one on time-sequences, which can well describe fluctuated hesitance of decision makers. Comprehensive and brief comparisons between TSHFS and other variants of HFS are shown in Table 1, from which, TSHFS not only includes characteristics of HFSs but also is with the advantages of reflecting time-sequential information and fluctuated information. The main contributions of our work are as follows. (1) We propose the new concept of TSHFS and define time-sequential hesitant fuzzy set element (TSHFSE) to describe conveniently membership degrees fixed on time-sequences. (2) In order to facilitate calculations on TSHFSEs, basic operators, aggregation operators and basic laws under TSHFS environment are presented. (3) Score function is an important concept coping with decision making problems under fuzzy sets environment, we define the score function under TSHFS environment to compare different TSHFSs. We also define distance measures between different TSHFSs. (4) TSHFS can well describe influences of fluctuations of membership degrees on time-sequences, which is important to reflect fluctuated hesitance of decision makers about decision making problems. To measure such fluctuated hesitance under TSHFS environment, we propose the concept of fluctuated hesitant information and corresponding measuring method. (5) In implementations of MADM, we introduce a synthetic decision model by combing distance measures with score function, fluctuated hesitant information under TSHFS environment.
The rest structure of the paper is organized as follows. “Preliminaries” introduces basic theories of traditional hesitant fuzzy set. The concept, basic operators, aggregation operators and distance measures of TSHFS are proposed in “Time-sequential hesitant fuzzy set”, also the fluctuated hesitant information. “The proposed model for MADM” presents the proposed synthetic decision model. In “Experiments”, to demonstrate effectiveness and advantages of the synthetic decision model in dealing with problems of decision making, we apply which to two illustrated examples of MADM and one real-application under TSHFS environment. “Conclusions” concludes our work and prospects future researches.
Preliminaries
For each element in HFS, a set of membership values are utilized to present its characteristic properties. In this section, the definition of HFS is reviewed, and then several basic operator laws and information measure methods are shown.
Definition 2.1
[20, 21] If X is a reference set, a HFS on X can be represented by a function \(\hbar\) which returns a subset of values in [0,1],
As ordinary fuzzy set is a special case of HFS, a HFS can also be obtained from a family of fuzzy sets. Xia et al. [34] introduced the following mathematical representation of HFS,
where \(h_{E} (x)\) is a set combined by some values in [0,1], which implies possible membership degrees of the element \(x \in X\) to the set E, \(h = h_{E} (x)\) is also called hesitant fuzzy element (HFE).
Definition 2.2
[20, 21] Given an HFE h, its lower and upper bounds are,
Definition 2.3
[20, 21] Let h be an HFE, its complement is defined as,
Definition 2.4
[20, 21] Let h1 and h2 be two HFEs, the union between them is defined as,
Definition 2.5
[20, 21] Let h1 and h2 be two HFEs, the intersection between them is defined as,
To make comparisons between HFEs, Xia et al. [34] introduced a comparison law by defining a score function.
Definition 2.6
[35] Let h be an HFE, the score function of h is defined as follows,
where \(l(h)\) is the length of h.
Distance and similarity measures play important roles in processes of decision making, a series of corresponding methods have been introduced in “Introduction”. In this section, first we give axioms of distance and similarity measures, and then classical measure methods as research foundations are given.
Definition 2.7
[33] Assume that a mapping is \(d:{\text{HFS}}(X) \times {\text{HFS}}(X) \to [0,1],\) P, Q are two HFSs on the reference set, \((P,Q) \to d(P,Q)\) is called the distance measure between P and Q if it satisfies that,
Assume that a mapping is \(s:{\text{HFS}}(X) \times {\text{HFS}}(X) \to [0,1],\) P, Q are two HFSs on reference set, \((P,Q) \to s(P,Q)\) is called the similarity measure between P and Q if it satisfies that,
As s(P,Q) = 1 − d(P,Q), we can obtain a similarity measure if we obtain corresponding distance measure. Therefore, we mainly discuss about distance measure methods in the paper. A general hesitant weighted distance [33] is show as follows,
where \(l_{{x_{i} }}\) denotes the length of \(x_{i}\),\(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). When λ = 1, λ = 2, the well-known Hamming distance and Euclidean distance are formed respectively.
It is noted that, \(h_{P} (x_{i} )\) and \(h_{Q} (x_{i} )\) should be with the same length. When they have different lengths, the shorter one should be extended by adding corresponding values [33]. If decision makers are optimistic about decided objects, the maximum among possible values of HFE will be repeated and added. If decision makers are pessimistic about decided objects, the minimum among possible values of HFE will be repeated and added.
Time-sequential hesitant fuzzy set
To perfect descriptions of hesitant attitudes of decision makers when faced with problems of decision making, and to obtain more reasonable results of decision making, we define time-sequential hesitant fuzzy set as follows on the assumption that membership degrees about describing attitudes of decision makers are given one by one on time-sequences.
Definition 3.1.
Assume X is a reference set, a time-sequential hesitant fuzzy set (TSHFS) on X is defined as follows,
where \(\overrightarrow {{t_{A} }}\) denotes the set of membership degrees among [0,1], which is with fixed sequences according to giving moments of respective membership degrees, and \(\overrightarrow {{t_{A} }} = \left\{ {\gamma_{1}^{(1)} ,\gamma_{2}^{(2)} , \cdots ,\gamma_{m}^{(m)} } \right\}\) is named after time-sequential hesitant fuzzy set element (TSHFSE). In the membership degree \(\gamma_{i}^{(i)}\), (i) denotes the sequence number, \(\gamma_{i}\) is utilized to represent the value of membership degree.
Example 3.1.
If \(\overrightarrow {t} ,\) \(\overrightarrow {{t_{1} }}\) and \(\overrightarrow {{t_{2} }}\) are three TSHFSEs of a TSHFS on reference set X,\(\overrightarrow {t} ,\)\(\overrightarrow {{t_{1} }}\) and \(\overrightarrow {{t_{2} }}\) can be shown as following examples,
Though \(\overrightarrow {{t_{1} }}\) and \(\overrightarrow {{t_{2} }}\) are with same membership degrees, fluctuations on time-sequences are different. Under TSHFS environment,\(\overrightarrow {{t_{1} }}\) and \(\overrightarrow {{t_{2} }}\) are different TSHFSEs, which represent more information compared with traditional HFE under HFS environment.
Basic operators under TSHFS
Definition 3.2.
Given a TSHFSE \(\overrightarrow {t}\) of the TSHFS on reference set X, its lower and higher bounds are defined as,
where m denotes the length of \(\overrightarrow {t}\).
Example 3.2.
Given a TSHFSE \(\overrightarrow {t} = \left\{ {0.2^{(1)} ,0.7^{(2)} ,0.4^{(3)} ,0.8^{(4)} } \right\}\), its lower and higher bounds are,
Definition 3.3.
Given three TSHFSEs \(\overrightarrow {t} ,\) \(\overrightarrow {{t_{1} }} ,\) \(\overrightarrow {{t_{2} }}\) and \(\overrightarrow {{t_{1} }} ,\) \(\overrightarrow {{t_{2} }}\) are with the same length, the basic operators are defined as,
(1) Union operator:
(2) Intersection operator:
(3) Complement operator:
(4) Exponentiation operator:
(5) Number multiplication operator:
(6) Probability sum operator:
(7) Probability product operator:
where \(\lambda > 0\). Little arrows on operators mean that operators need to be executed according to time-sequences of TSHFSEs, and it is easy to obtain that calculated results through above operators are TSHFSEs.
Example 3.3.
As TSHFSEs \(\overrightarrow {t} = \left\{ {0.2^{(1)} ,0.7^{(2)} ,0.4^{(3)} ,0.8^{(4)} } \right\}\), \(\overrightarrow {{t_{1} }} = \left\{ {0.9^{(1)} ,0.5^{(2)} ,0.3^{(3)} ,0.7^{(4)} } \right\}\), \(\overrightarrow {{t_{2} }} = \left\{ {0.5^{(1)} ,0.7^{(2)} ,0.9^{(3)} ,0.3^{(4)} } \right\}\), then,
(1) on union operator:
(2) on intersection operator:
(3) on complement operator:
(4) on exponentiation operator (λ = 2):
\(\begin{aligned}\overrightarrow {t}^{\lambda } = &\mathop \cup \limits_{{\gamma_{{}}^{(i)} \in \overrightarrow {t} }}^{ \to } \left\{ {(\gamma_{{}}^{2} )^{(i)} } \right\} \\ =& \left\{ {0.04^{(1)} ,0.49^{(2)} ,0.16^{(3)} ,0.64^{(4)} }\right\}\end{aligned}\),
(5) on number multiplication operation (λ = 2):
(6) on probability sum operation:
(7) on probability product operation:
The calculated results above also are illustrated in the Fig. 2. In (a) of the Fig. 2, \(\overrightarrow {t}\) is represented by purple dots and curves, green dots and curves denote \(\overrightarrow {{t_{1} }}\), blue dots and curves represent the TSHFE \(\overrightarrow {{t_{2} }}\) in Example 3.3. Compared with \(\overrightarrow { \cap }\) and \(\overrightarrow { \cup } ,\) calculated results of \(\overrightarrow { \otimes }\) and \(\overrightarrow { \oplus }\) are less fluctuated respectively. Meanwhile, \(\overrightarrow {t}\) and its complement are with opposite volatilities.
Property 3.1.
Given two TSHFSEs \(\overrightarrow {t} ,\) \(\overrightarrow {{t_{1} }} ,\) \(\overrightarrow {{t_{2} }}\) and \(\overrightarrow {t} ,\) \(\overrightarrow {{t_{1} }} ,\) \(\overrightarrow {{t_{2} }}\) are with the same length. Operators \(\overrightarrow { \cup } ,\) \(\overrightarrow { \cap }\) satisfy following properties,
(1) commutativity:
(2) associativity:
(3) distributivity:
The proofs are trivial.
Property 3.2.
Given three TSHFSEs \(\overrightarrow {t} ,\) \(\overrightarrow {{t_{1} }} ,\) \(\overrightarrow {{t_{2} }} ,\) and \(\overrightarrow {t} ,\)\(\overrightarrow {{t_{1} }}\),\(\overrightarrow {{t_{2} }}\) are with the same length. Operators \(\overrightarrow { \oplus } ,\)\(\overrightarrow { \otimes }\) satisfy following properties,
(1) commutativity:
(2) associativity:
(3) distributivity:
The proofs are trivial.
Property 3.3.
Given two TSHFSEs \(\overrightarrow {{t_{1} }} = \{ \alpha_{1}^{(1)} ,\alpha_{2}^{(2)} , \cdots ,\alpha_{m}^{(m)} \}\), \(\overrightarrow {{t_{2} }} = \{ \beta_{1}^{(1)} ,\beta_{2}^{(2)} , \cdots ,\beta_{m}^{(m)} \}\),and \(\overrightarrow {{t_{1} }} ,\) \(\overrightarrow {{t_{2} }}\) are with the same length. Operators \(\overrightarrow { \cup } ,\)\(\overrightarrow { \cap }\),\(\overrightarrow { \oplus } ,\) \(\overrightarrow { \otimes }\) satisfy following properties,
Proof.
First, we verify that \(\overrightarrow {{t_{1} }} \mathop \oplus \limits^{ \to } \overrightarrow {{t_{2} }} \ge \overrightarrow {{t_{1} }} \mathop \cup \limits^{ \to } \overrightarrow {{t_{2} }} .\) As \(\overrightarrow {{t_{1} }} \mathop \oplus \limits^{ \to } \overrightarrow {{t_{2} }} = \mathop \cup \limits_{{\alpha_{i}^{(i)} \in \overrightarrow {{t_{1} }} ,\beta_{i}^{(i)} \in \overrightarrow {{t_{2} }} }}^{ \to } \{ \alpha_{i}^{(i)} + \beta_{i}^{(i)} - (\alpha_{i} \beta_{i} )^{(i)} \} ,\) \(\overrightarrow {{t_{1} }} \mathop \cup \limits^{ \to } \overrightarrow {{t_{2} }} = \mathop \cup \limits_{{\alpha_{i}^{(i)} \in \overrightarrow {{t_{1} }} ,\beta_{i}^{(i)} \in \overrightarrow {{t_{2} }} }}^{ \to } \max \{ \alpha_{i}^{(i)} ,\beta_{i}^{(i)} \} ,\) \(0 \le \alpha_{i}^{(i)} \le 1,0 \le \beta_{i}^{(i)} \le 1,\) then,
By combing above two inequalities,
It is obvious that \(\overrightarrow {{t_{1} }} \mathop \cup \limits^{ \to } \overrightarrow {{t_{2} }} \ge \overrightarrow {{t_{1} }} \mathop \cap \limits^{ \to } \overrightarrow {{t_{2} }}\), and \(\overrightarrow {{t_{1} }} \mathop \cap \limits^{ \to } \overrightarrow {{t_{2} }} \ge \overrightarrow {{t_{1} }} \mathop \otimes \limits^{ \to } \overrightarrow {{t_{2} }}\) can be obtained by using the same method above.
The proof is completed.
Theorem 3.1.
Given three TSHFSEs \(\overrightarrow {t} ,\)\(\overrightarrow {{t_{1} }}\),\(\overrightarrow {{t_{2} }} ,\) and \(\overrightarrow {{t_{1} }}\),\(\overrightarrow {{t_{2} }}\) are with the same length. The operators of Definition 3.3 satisfy following properties:
(1)
(2)
(3)
(4)
(5)
(6)
Proof.
(1).
(2)
(3)
(4)
(5)
(6)
Score function and fluctuated hesitant information under TSHFS
Definition 3.4.
Given a TSHFSE \(\overrightarrow {t}\), to compare different TSHFSEs, the score function of \(\overrightarrow {t}\) is defined as,
where \(n(\overrightarrow {t} )\) denotes the length of \(\overrightarrow {t}\), and it is easy to be verified that \(K(\overrightarrow {t} ) \in [0,1].\)
Remark 3.1.
Assume that there are two TSHFSEs \(\overrightarrow {{t_{1} }} ,\) \(\overrightarrow {{t_{2} }} ,\) if \(K(\overrightarrow {{t_{1} }} )\) > \(K(\overrightarrow {{t_{2} }} )\), \(\overrightarrow {{t_{1} }}\) > \(\overrightarrow {{t_{2} }}\) is derived. If \(K(\overrightarrow {{t_{1} }} )\) < \(K(\overrightarrow {{t_{2} }} )\), \(\overrightarrow {{t_{1} }}\) < \(\overrightarrow {{t_{2} }}\) can be derived, and if \(K(\overrightarrow {{t_{1} }} )\) = \(K(\overrightarrow {{t_{2} }} )\), we can achieve that \(\overrightarrow {{t_{1} }}\) = \(\overrightarrow {{t_{2} }}\).
Example 3.4.
Given TSHFSEs \(\overrightarrow {{t_{1} }} = \Big\{ 0.9^{(1)} ,0.5^{(2)} ,0.3^{(3)} ,0.7^{(4)} \Big\}\), \(\overrightarrow {{t_{2} }} = \Big\{ 0.5^{(1)} ,0.7^{(2)} ,0.9^{(3)} ,0.3^{(4)} \Big\}\), we compare \(\overrightarrow {{t_{1} }}\) and \(\overrightarrow {{t_{2} }}\) by using the score function above,
As \(K(\overrightarrow {{t_{1} }} )\) < \(K(\overrightarrow {{t_{2} }} )\), it is derived that \(\overrightarrow {{t_{1} }}\) < \(\overrightarrow {{t_{2} }}\). However, if we do not consider influences of sequences of membership degrees, according to Definition 2.6, \(\overrightarrow {{t_{1} }}\) is equal to \(\overrightarrow {{t_{2} }}\) under HFS environment. The score function of Definition 3.4 not only can reflect attitudes as what usually utilized under traditional HFS environments, but also can imply that deeper understandings of decision makers about alternatives as time goes forwards, which conforms to common senses.
The property of reflecting hesitant attitudes by fluctuated information is the core of TSHFS, and following fluctuated hesitant information is defined to describe such hesitance reflected on time-sequences.
Definition 3.5.
Assume there is a TSHFSE \(\overrightarrow {t} = \Big\{ \gamma_{1}^{(1)} ,\gamma_{2}^{(2)} , \cdots ,\gamma_{m}^{(m)} \Big\}\), it can be transformed into the new form \(\overrightarrow {t^{\prime}} = \Big\{ \{ (\gamma_{i}^{(i)} )^{(1)} ,(\gamma_{j}^{(j)} )^{(2)} , \ldots , (\gamma_{k}^{(k)} )^{(m - 1)} ,(\gamma_{g}^{(g)} )^{(m)} \} \Big| \gamma_{i}^{(i)} \le \gamma_{j}^{(j)} \le \cdots \le \gamma_{k}^{(k)} \le \gamma_{g}^{(g)} ,i \le m,j \le m, \ldots ,k \le m,g \le m \Big\}\) by arranging values of membership degrees of \(\overrightarrow {t}\) from the smallest one to the largest one and \( \overrightarrow {t^{\prime\prime}} = \left\{ \{ (\gamma_{g}^{(g)} )^{(1)} ,(\gamma_{k}^{(k)} )^{(2)} , \ldots , (\gamma_{j}^{(j)} )^{(m - 1)} ,(\gamma_{i}^{(i)} )^{(m)} \} \left| \gamma_{g}^{(i)} \ge \gamma_{k}^{(k)} \right.\right. \break\left.\ge\cdots \ge \gamma_{j}^{(j)} \ge \gamma_{i}^{(i)} ,i \le m,j \le m, \ldots ,k \le m,g \le m \right\}\) by arranging values of membership degrees of \(\overrightarrow {t}\) from the largest one to the smallest one. To describe hesitant degrees induced by fluctuations of membership degrees, the fluctuated hesitant information (FI) of \(\overrightarrow {t}\) is defined as,
Furthermore, it is easy to be verified that \({\text{FI}}(\overrightarrow {t} ) \in [0,1].\)
Example 3.5.
For two TSHFSEs \(\overrightarrow {{t_{1} }} = \{ 0.9^{(1)} ,0.5^{(2)} ,0.3^{(3)} ,0.7^{(4)} \} ,\) \(\overrightarrow {{t_{2} }} = \{ 0.5^{(1)} ,0.7^{(2)} ,0.9^{(3)} ,0.3^{(4)} \} ,\) according to Definition 3.5,
Though \(\overrightarrow {{t_{1} }}\) and \(\overrightarrow {{t_{2} }}\) are with same values of membership degrees, they are with different fluctuations on time-sequences, which reflect important and various kinds of hesitant attitudes of decision makers.
Example 3.6.
If let HFEs h1 = {0.2,0.3,0.6,0.8,0.9} and h2 = {0.2,0.8,0.6,0.3,0.9} be transformed into TSHFSEs in “Introduction”, namely, \(\overrightarrow {{h_{1} }} = \{ 0.2^{(1)} ,0.3^{(2)} ,0.6^{(3)} ,0.8^{(4)} ,0.9^{(5)} \} ,\) \(\overrightarrow {{h_{2} }} = \{ 0.2^{(1)} ,0.8^{(2)} ,0.6^{(3)} ,0.3^{(4)} ,0.9^{(5)} \} .\) Then \(FI(\overrightarrow {{h_{1} }} ) = 0.2538,\) \(FI(\overrightarrow {{h_{2} }} ) = 0.4644,\) which correspond correctly to fluctuations of \(h_{1} ,\) \(h_{2}\) with fixed sequences in Fig. 1.
By combing the score function of Definition 3.4 and the fluctuated hesitant information above, the following method can be more reasonable to compare TSHFSEs.
Remark 3.2.
Given two TSHFSEs \(\overrightarrow {{t_{1} }}\),\(\overrightarrow {{t_{2} }}\) are with the same length. According to Definitions 3.4 and 3.5,
-
1.
if \(K(\overrightarrow {{t_{1} }} )^{{{\text{FI}}(\overrightarrow {{t_{1} }} ) + 1}} < K(\overrightarrow {{t_{2} }} )^{{{\text{FI}}(\overrightarrow {{t_{2} }} ) + 1}} ,\) then \(\overrightarrow {{t_{1} }} < \overrightarrow {{t_{2} }} ;\)
-
2.
if \(K(\overrightarrow {{t_{1} }} )^{{{\text{FI}}(\overrightarrow {{t_{1} }} ) + 1}} > K(\overrightarrow {{t_{2} }} )^{{{\text{FI}}(\overrightarrow {{t_{2} }} ) + 1}} ,\) then \(\overrightarrow {{t_{1} }} > \overrightarrow {{t_{2} }} ;\)
-
3.
if \(K(\overrightarrow {{t_{1} }} )^{{{\text{FI}}(\overrightarrow {{t_{1} }} ) + 1}} = K(\overrightarrow {{t_{2} }} )^{{{\text{FI}}(\overrightarrow {{t_{2} }} ) + 1}} ,\) then \(\overrightarrow {{t_{1} }} = \overrightarrow {{t_{2} }} .\)
Specify \(\overrightarrow {{t_{1} }}\),\(\overrightarrow {{t_{2} }}\) as in Examples 3.4 and 3.5, then \(K(\overrightarrow {{t_{1} }} )^{{{\text{FI}}(\overrightarrow {{t_{1} }} ) + 1}} = 0.56^{1.5058} = 0.4177 < K(\overrightarrow {{t_{2} }} )^{{{\text{FI}}(\overrightarrow {{t_{2} }} ) + 1}} = 0.58^{1.4954} = 0.4428,\) it is derived that \(\overrightarrow {{t_{1} }} < \overrightarrow {{t_{2} }} .\) What’s more, following relationship can be acquired.
Theorem 3.2.
Assume that two TSHFSEs \(\overrightarrow {{t_{1} }}\),\(\overrightarrow {{t_{2} }}\) are with the same length, according to Definitions 3.4 and 3.5, \(K(\overrightarrow {{t_{1} }} ),\) \(K(\overrightarrow {{t_{2} }} ),\) \({\text{FI(}}\overrightarrow {{t_{1} }} )\) and \({\text{FI}}(\overrightarrow {{t_{2} }} )\) are derived. If \(K(\overrightarrow {{t_{1} }} ) \le K(\overrightarrow {{t_{2} }} ),\) and \({\text{FI}}(\overrightarrow {{t_{1} }} ) \ge {\text{FI}}(\overrightarrow {{t_{2} }} ),\) it holds that,
Proof.
It is easy to obtain that \(K(\overrightarrow {{t_{1} }} ) \in [0,1],\) \(K(\overrightarrow {{t_{2} }} ) \in [0,1],\) \({\text{FI}}(\overrightarrow {{t_{1} }} ) \in [0,1],\) and \({\text{FI}}(\overrightarrow {{t_{2} }} ) \in [0,1],\) then,
Namely, \(K(\overrightarrow {{t_{1} }} ) - K(\overrightarrow {{t_{2} }} ) \le K(\overrightarrow {{t_{1} }} )^{{{\text{FI}}(\overrightarrow {{t_{1} }} ) + 1}} - K(\overrightarrow {{t_{2} }} )^{{{\text{FI}}(\overrightarrow {{t_{2} }} ) + 1}}\), the proof is finished.
Theorem 3.2 reflects that after inducing fluctuated hesitant information into the score function, which is with better differential characteristic among TSHFSEs.
Aggregation operators under TSHFS
Definition 3.6.
Assume that there are TSHFSEs \(\{ \overrightarrow {{t_{1} }} ,\overrightarrow {{t_{2} }} , \ldots ,\overrightarrow {{t_{m} }} \}\) with the same length and with respective weights \(\left\{ {w_{j} \left| {0 \le w_{j} \le 1,\sum\nolimits_{1 \le i \le m} {w_{j} } = 1} \right.} \right\}\) need to be aggregated, we defined the weighted averaging operator under TSHFS as follows,
Example 3.7.
Assume that there are two TSHFSEs \(\overrightarrow {{t_{1} }} = \left\{ {0.9^{(1)} ,0.5^{(2)} ,0.3^{(3)} ,0.7^{(4)} } \right\}\),\(\overrightarrow {{t_{2} }} = \left\{ {0.5^{(1)} ,0.7^{(2)} ,0.9^{(3)} ,0.3^{(4)} } \right\}\), with respective weights {0.5,0.5}, then,
Definition 3.7.
Assume that there are TSHFSEs \(\{ \overrightarrow {{t_{1} }} ,\overrightarrow {{t_{2} }} , \cdots ,\overrightarrow {{t_{m} }} \}\) with the same length and with respective weights \(\left\{ {w_{i} \left| {0 \le w_{i} \le 1,\sum\nolimits_{1 \le i \le m} {w_{i} } = 1} \right.} \right\}\) need to be aggregated, the geometric averaging operator under TSHFS is defined as follows,
Example 3.8.
Assume that there are two TSHFSEs \(\overrightarrow {{t_{1} }} = \left\{ {0.9^{(1)} ,0.5^{(2)} ,0.3^{(3)} ,0.7^{(4)} } \right\}\),\(\overrightarrow {{t_{2} }} = \left\{ {0.5^{(1)} ,0.7^{(2)} ,0.9^{(3)} ,0.3^{(4)} } \right\}\), with averaged weights then,
Theorem 3.3.
Assume that there are some TSHFSEs \(\{ \overrightarrow {{t_{1} }} ,\overrightarrow {{t_{2} }} , \ldots ,\overrightarrow {{t_{m} }} \}\) of TSHFS on the reference set with respective weights \(\left\{ {w_{j}| {0 \le| 1},\left|{\sum\nolimits_{1 \le j \le n} {w_{j} = 1} } \right.} \right\}\) need to be aggregated, then,
According to Lemma 1 in Xia et al. [34], the result of Theorem 3.3 is easy to be derived.
Distance measures under TSHFS
Definition 3.8
Given a mapping \(d:{\text{TSHFS}}(X) \times {\text{TSHFS}}(X) \to [0,1],\) given that there are two TSHFSs T, P, \((T,P) \to d(T,P)\) is called distance measure between T and P if it satisfies following conditions for any TSHFS G,
Definition 3.9.
For two TSHFSs T, P on the reference set, \(T = \{ x,\overrightarrow {{t_{1} }} ,\overrightarrow {{t_{2} }} , \ldots ,\overrightarrow {{t_{n} }} \} ,\)\(P = \{ x,\overrightarrow {{p_{1} }} ,\overrightarrow {{p_{2} }} , \ldots ,\overrightarrow {{p_{n} }} \} ,\) \(\{ \overrightarrow {{t_{j} }} |\overrightarrow {{t_{j} }} = \{ \alpha_{j1}^{(1)} ,\alpha_{j2}^{(2)} , \ldots ,\alpha_{jm}^{(m)} \} ,j \in [1,n]\} ,\)\(\{ \overrightarrow {{p_{j} }} |\overrightarrow {{p_{j} }} = \{ \beta_{j1}^{(1)} ,\beta_{j2}^{(2)} , \cdots ,\beta_{jm}^{(m)} \} ,j \in [1,n]\} ,\) according to Definition 3.8, we define distance measures between T, P as follows,
where \(\left\{ {w_{j}| {0 \le| 1},\left|{\sum\nolimits_{0 \in [1,n]} {w_{j} = 1} } \right.} \right\}\) are weights of TSHFSEs,\(\lambda \ge 1,\) and m denotes the length of TSHFSEs.
Example 3.9.
Given two TSHFSs \(T_{1} = \{ x,\{ 0.9^{(1)} ,0.5^{(2)} ,0.3^{(3)} ,0.7^{(4)} \} \} ,\) \(P_{1} = \{ x,\{ 0.5^{(1)} ,0.7^{(2)} ,0.9^{(3)} ,0.3^{(4)} \} \} ,\) according to the Eq. (3.37), the distance between T1 and P1 is,
Theorem 3.4.
Distances measure d1 defined in Definition 3.9 satisfies all conditions of Definition 3.8, distance measures d2 and dλ only satisfy the fore three conditions of Definition 3.8.
Proof.
It is easy to verify that d1, d2 and dλ satisfy the fore three conditions of Definition 3.8, now we just prove that d1 satisfies the fourth condition. Assume that there are three TSHFSs T, P, G on the reference set, \(T = \{ x,\overrightarrow {{t_{1} }} ,\overrightarrow {{t_{2} }} , \ldots ,\overrightarrow {{t_{n} }} \} ,\)\(P = \{ x,\overrightarrow {{p_{1} }} ,\overrightarrow {{p_{2} }} , \ldots ,\overrightarrow {{p_{n} }} \} ,\)\(G = \{ x,\overrightarrow {{g_{1} }} ,\overrightarrow {{g_{2} }} , \ldots ,\overrightarrow {{g_{n} }} \} ,\)\(\{ \overrightarrow {{t_{j} }} |\overrightarrow {{t_{j} }} = \{ \alpha_{j1}^{(1)} ,\alpha_{j2}^{(2)} , \ldots ,\alpha_{jm}^{(m)} \} ,j \in [1,n]\} ,\)\(\{ \overrightarrow {{p_{j} }} |\overrightarrow {{p_{j} }} = \{ \beta_{j1}^{(1)} ,\beta_{j2}^{(2)} , \ldots ,\beta_{jm}^{(m)} \} ,j \in [1,n]\} ,\) \(\{ \overrightarrow {{g_{j} }} |\overrightarrow {{g_{j} }} = \{ \gamma_{j1}^{(1)} ,\gamma_{j2}^{(2)} , \ldots ,\gamma_{jm}^{(m)} \} ,j \in [1,n]\} .\) According to Definitions 3.8 and 3.9,
And,
namely, \(d_{1} (T,P) + d_{1} (P,G) \ge d_{1} (T,G),\) other situations can be proved as the same method. The proof is finished.
Definition 3.10.
For two TSHFSs T, P on the reference set X, \(T = \{ x,\overrightarrow {{t_{1} }} ,\overrightarrow {{t_{2} }} , \ldots ,\overrightarrow {{t_{n} }} \} ,\)\(P = \{ x,\overrightarrow {{p_{1} }} ,\overrightarrow {{p_{2} }} , \ldots ,\overrightarrow {{p_{n} }} \} ,\) \(\{ \overrightarrow {{t_{j} }} |\overrightarrow {{t_{j} }} = \{ \alpha_{j1}^{(1)} ,\alpha_{j2}^{(2)} , \ldots ,\alpha_{jm}^{(m)} \} ,j \in [1,n]\} ,\) \(\{ \overrightarrow {{p_{j} }} |\overrightarrow {{p_{j} }} = \{ \beta_{j1}^{(1)} ,\beta_{j2}^{(2)} , \ldots ,\beta_{jm}^{(m)} \} ,j \in [1,n]\} .\) By adding the fluctuated hesitant information, the following distance measure is defined,
where \(\left\{ {w_{j}| {0 \le| 1},\left|{\sum\nolimits_{1 \le j \le n} {w_{j} = 1} } \right.} \right\}\) are weights of TSHFSEs,\(\lambda \ge 1\).When \(\lambda = 1\),\(\lambda = 2\), the form of Hamming distance and the form of Euclidean distance are obtained respectively.
The proposed model for MADM
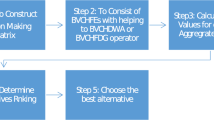
As usual, to solve problems of MADM with several kinds of necessary attributes under traditional HFS environment, a series of alternatives \(\{ A_{1} ,A_{2} , \ldots ,A_{h} \}\) need to be ranked. Each alternative is with n attributes \(\{ t_{i1} ,t_{i2} , \ldots ,t_{in} \}\)(i denotes i-th alternative), which are with weights \(\left\{ {w_{j} \left| {0 \le w_{j} } \right. \le 1,\;\sum\nolimits_{j = 1}^{n} {w_{j} = 1} } \right\}\)). Under TSHFS, attributes are formed as \(\{ \overrightarrow {{t_{i1} }} ,\overrightarrow {{t_{i2} }} , \ldots ,\overrightarrow {{t_{in} }} \}\) (i denotes i-th alternative). We propose following five steps to solve problems of MADM, and final results will be sorted from the best alternative to the worst one, which is also illustrated in Fig. 3.
Assume that alternatives are represented by several attributes under TSHFS as,
The ideal alternative is \(A_{I} = \{ \overrightarrow {{t_{I1} }} ,\overrightarrow {{t_{I2} }} , \ldots ,\overrightarrow {{t_{In} }} \} = \{ \{ \alpha_{I1}^{(1)} ,\alpha_{I2}^{(2)} , \ldots ,\alpha_{Im}^{(m)} \} ,\{ \beta_{I1}^{(1)} ,\beta_{I2}^{(2)} , \ldots ,\beta_{Im}^{(m)} \} , \ldots ,\{ \gamma_{I1}^{(1)} ,\gamma_{I2}^{(2)} , \ldots ,\gamma_{Im}^{(m)} \} \} .\)
Step1: Utilize TSWA of the Eq. (3.34),
\(\overrightarrow {{t_{1} }} = {\text{TSWA(}}\overrightarrow {{t_{11} }} ,\overrightarrow {{t_{12} }} , \ldots ,\overrightarrow {{t_{1m} }} ),\) \(\overrightarrow {{t_{2} }} = {\text{TSWA}}(\overrightarrow {{t_{21} }} ,\overrightarrow {{t_{22} }} , \ldots ,\overrightarrow {{t_{2m} }} ), \ldots ,\) \(\overrightarrow {{t_{h} }} = {\text{TSWA}}(\overrightarrow {{t_{h1} }} ,\overrightarrow {{t_{h2} }} , \ldots ,\overrightarrow {{t_{hm} }} ),\) \(\overrightarrow {{t_{I} }} = {\text{TSWA}}(\overrightarrow {{t_{I1} }} ,\overrightarrow {{t_{I2} }} , \ldots ,\overrightarrow {{t_{Im} }} ).\)
Step 2: Utilize the score function of the Eq. (3.29) and the fluctuated hesitant information of Eq. (3.30–3.32),
Step 3: According to d1 of the Eq. (3.37),
\(D(A_{1} ) = d_{1} (\overrightarrow {{t_{1} }} ,\overrightarrow {{t_{I} }} ),\) \(D(A_{2} ) = d_{1} (\overrightarrow {{t_{2} }} ,\overrightarrow {{t_{I} }} ), \ldots ,\) \(D(A_{h} ) = d_{1} (\overrightarrow {{t_{h} }} ,\overrightarrow {{t_{I} }} ).\)
As d1 satisfies all conditions of definition about distance measure under TSHFS, we choose it in the proposed model. If \(D(A_{i} ) = 0,\) Ai would be the finest alternative.
Step 4: The synthetic values can be achieved,
\(\mathop {A_{1} }\limits^{ \cdot } = \frac{{S(A_{1} )}}{{D(A_{1} ) + 10^{ - 5} }},\) \(\mathop {A_{2} }\limits^{ \cdot } = \frac{{S(A_{2} )}}{{D(A_{2} ) + 10^{ - 5} }} \cdots ,\) \(\mathop {A_{h} }\limits^{ \cdot } = \frac{{S(A_{h} )}}{{D(A_{h} ) + 10^{ - 5} }}.\)
Step 5: According to corresponding synthetic values \(\mathop {A_{1} }\limits^{ \cdot } ,\mathop {A_{2} }\limits^{ \cdot } , \ldots ,\mathop {A_{h} }\limits^{ \cdot }\), arrange \(\{ A_{1} ,A_{2} , \cdots ,A_{h} \}\) from the feast one to the worst one.
Experiments
Illustrated examples
Case 1. MADM of Data association [34]. Data association is an important research topic in multiple objective tracking under complex flight environments. Assume that four different targets (A1, A2, A3, A4) are simultaneously tracking, which are with four categories of attribute-information sampled from four different types of sensors (ti1, ti2, ti3, ti4, i denotes i-th target) under TSHFS. To improve the tracking accuracy, it is needed to categorize certain trajectory points sampled from complex flight environment into the different trajectories of four different targets. Given the sampled information of a trajectory point is AI = {{0.4(1),0.6(2),0.5(3)}, {0.2(1),0.4(2)}, {0.5(1),0.7(2),0.6(3)}, {0.8(1),0.9(2)}}, the weight vector of four sensors is w = (0.25, 0.25, 0.25, 0.25)T, the corresponding decision matrix is shown in Table 2.
To make sure that TSHFEs are in the same length and avoid changing “attitudes” of sensors, inserting “0” at the front of TSHFSEs with shorter lengths is used in the paper. TSHFSEs in Table 2 can be formed as follows,
Step 1: Utilize TSWA of the Eq. (3.34),
Step 2: Utilize the score function of the Eq. (3.29) and the fluctuated hesitant information of Eqs. (3.30–3.32),
Step 3: According to d1 of the Eq. (3.27),
\(D(A_{1} ) = d_{1} (\overrightarrow {{t_{1} }} ,\overrightarrow {{t_{I} }} ) = 0.1283,\) \(D(A_{2} ) = d_{1} (\overrightarrow {{t_{2} }} ,\overrightarrow {{t_{I} }} ) = 0.1433,\) \(D(A_{3} ) = d_{1} (\overrightarrow {{t_{3} }} ,\overrightarrow {{t_{I} }} ) = 0.1183,\) \(D(A_{4} ) = d_{1} (\overrightarrow {{t_{4} }} ,\overrightarrow {{t_{I} }} ) = 0.0050.\)
Step 4: The synthetic values can be achieved,
\(\mathop {A_{1} }\limits^{ \cdot } = \frac{{S(A_{1} )}}{{D(A_{1} ) + 10^{ - 5} }} = 3.6231,\) \(\mathop {A_{2} }\limits^{ \cdot } = \frac{{S(A_{2} )}}{{D(A_{2} ) + 10^{ - 5} }} = 3.3784,\) \(\mathop {A_{3} }\limits^{ \cdot } = \frac{{S(A_{3} )}}{{D(A_{3} ) + 10^{ - 5} }} = 3.9092,\) \(\mathop {A_{4} }\limits^{ \cdot } = \frac{{S(A_{4} )}}{{D(A_{4} ) + 10^{ - 5} }} = 69.1182.\)
Step 5: According to corresponding synthetic values \(\mathop {A_{1} }\limits^{ \cdot } ,\mathop {A_{2} }\limits^{ \cdot } ,\mathop {A_{3} }\limits^{ \cdot } \mathop {,A_{4} }\limits^{ \cdot } ,\) arrange A1, A2, A3, A4 from the feast one to the worst one (Table 3).
Common sense says that the ideal alternative is most similar to A4, all ranking results can find out the feast alternative, though which are with more or less different in arrangements. If let the decision matrix of Case 1 in Table 2 be under HFS environment, similar ranking result \(A_{4} \succ A_{2} \succ A_{3} \succ A_{1}\) can be obtained by dn Xu et al. [33], which is the same with dλ(λ = 2). The influence of parameter λ in dλ and dkfλ on ranking results are shown in Tables 4 and 5. When λ is larger than 2, the ranking results of dλ and dkfλ will be steady. As d1 satisfies the triangle inequality, the ranking result of d1 is more reliable than that of dλ when λ is larger than 2. With combining comprehensively with the score function, fluctuated hesitant information and distance measure d1, ranking result of the proposed decision model is the most reasonable. What’s more, from calculated values of alternatives in above tables, the proposed model can make better differences among alternatives.
Case 2. MADM of supplier selection [48]. An enterprise’s board of directors with five members is to make a plan of the development of following large projects. Four possible large projects (A1, A2, A3, A4) are alternatives, which are with four categories of attributes (ti1: financial perspective, ti2: the customer satisfaction, ti3: internal business process perspective, ti4: learning and growth perspective, all of them are maximization types, i denotes i-th alternative). To select the most appropriate one, the directors should make comparisons between alternatives and rank them. The weight vector of the attributes is supposed as w = (0.25, 0.25, 0.25, 0.25)T. The corresponding decision matrix is shown in Table 6, and the ideal alternative is represented as AI = {{0.4(1),0.6(2),0.8(3)}, {0.1(1),0.2(2),0.4(3),0.6(4)}, {0.3(1),0.4(2),0.6(3),0.8(4),0.9(5)}, {0.1(1), 0.3(2),0.9(3)}} under TSHFS.
To make sure that TSHFEs are in the same length and avoid changing attitudes of decision makers, inserting “0” at the front of TSHFSEs with shorter lengths is used in the paper. TSHFSEs in Table 6 can be formed as follows,
Step 1: Utilize TSWA of the Eq. (3.34),
Step 2: Utilize the score function of the Eq. (3.29) and the fluctuated hesitant information of Eqs. (3.30–3.32),
Step 3: According to d1 of the Eq. (3.27),
\(D(A_{1} ) = d_{1} (\overrightarrow {{t_{1} }} ,\overrightarrow {{t_{I} }} ) = 0.1317,\) \(D(A_{2} ) = d_{1} (\overrightarrow {{t_{2} }} ,\overrightarrow {{t_{I} }} ) = 0.0500,\) \(D(A_{3} ) = d_{1} (\overrightarrow {{t_{3} }} ,\overrightarrow {{t_{I} }} ) = 0.1217,\) \(D(A_{4} ) = d_{1} (\overrightarrow {{t_{4} }} ,\overrightarrow {{t_{I} }} ) = 0.1033.\)
Step 4: The synthetic values can be achieved,
\(\mathop {A_{1} }\limits^{ \cdot } = \frac{{S(A_{1} )}}{{D(A_{1} ) + 10^{ - 5} }} = 2.4902,\) \(\mathop {A_{2} }\limits^{ \cdot } = \frac{{S(A_{2} )}}{{D(A_{2} ) + 10^{ - 5} }} = 7.6812, \cdot\) \(\mathop {A_{3} }\limits^{ \cdot } = \frac{{S(A_{3} )}}{{D(A_{3} ) + 10^{ - 5} }} = 2.9557,\) \(\mathop {A_{4} }\limits^{ \cdot } = \frac{{S(A_{4} )}}{{D(A_{4} ) + 10^{ - 5} }} = 3.4009.\)
Step 5: According to corresponding synthetic values \(\mathop {A_{1} }\limits^{ \cdot } ,\mathop {A_{2} }\limits^{ \cdot } ,\mathop {A_{3} }\limits^{ \cdot } \mathop {,A_{4} }\limits^{ \cdot } ,\) arrange A1, A2, A3, A4 from the feast one to the worst one,
Ranking results of Case 2 are shown in Table 7. As distance measure d1 satisfies the triangle inequality, we choose it as the measure method in the Case 2. From the initiatively stable ranking results of Table 5, λ is set at 3 respectively dkfλ. Common sense says that the ideal alternative is most similar with A2, all ranking results can find out the feast alternative by proposed methods in the paper, though which are with more or less different in arrangements. However, if let the decision matrix in Table 6 be under HFS environment,\(A_{1} \succ A_{2} \succ A_{4} \succ A_{3}\) is obtained by dn Xu et al. [33], which cannot differentialize out the feast alternative. The reason why the method dn Xu et al. [33] could not receive the feast alternative under HFS is that when HFEs are in different length, the shorter ones should be extended by adding value [33] of the biggest membership degree or the smallest membership degree, such operator is with the risk of changing attitudes of decision makers. Faced with the same situation, we adopt it by inserting 0 into the TSHFS decision matrix, which avoids such risk.
Real application to ranking evaluation of world universities
A reasonable evaluation of running level of a university can not only provide guidance for candidates applying for universities, but also help universities realize their own advantages and disadvantages needed to be improved. Every year, some well-known agencies rank and evaluate global universities according to several attributes, usually including Arts and Humanities (A–H), Life Sciences and Medicine (L–M), Engineering and Technology (ENG), Natural Sciences and Mathematics (SCI), and Social Sciences (SOC). There are seven evaluated top universities including Stanford University, Harvard University, Oxford University, Cambridge University, Berkeley University, Princeton University and Yale University, and corresponding decision matrix adopted from [49, 50] is shown in Table 8 according to mentioned five attributes, with weights w = (0.2, 0.2, 0.2, 0.2, 0.2)T. The ideal university is represented as AI = {{1(1),1(2),1(3)}, {1(1),1(2),1(3)}, {1(1),1(2),1(3)}, {1(1), 1(2),1(3)}, {1(1), 1(2),1(3)}}.
Step 1: Utilize TSWA of the Eq. (3.34),
\({\text{Stanford}}:\overrightarrow {{t_{1} }} = \{ 0.9002^{(1)} ,0.8326^{(2)} ,0.9060^{(3)} \} ,\) \({\text{Harvard}}:\overrightarrow {{t_{2} }} = \{ 0.8988^{(1)} ,0.9248^{(2)} ,0.9244^{(3)} \} ,\)
\({\text{Oxford}}:\overrightarrow {{t_{3} }} = \{ 0.8878^{(1)} ,0.6438^{(2)} ,0.9242^{(3)} \} ,\) \({\text{Cambridge}}:\overrightarrow {{t_{4} }} = \{ \{ 0.8750^{(1)} ,0.7550^{(2)} ,0.9280^{(3)} \} ,\)
\({\text{Berkeley}}:\overrightarrow {{t_{5} }} = \{ 0.8608^{(1)} ,0.8018^{(2)} ,0.8874^{(3)} \} ,\) \({\text{Princeton}}:\overrightarrow {{t_{6} }} = \{ 0.7906^{(1)} ,0.6650^{(2)} ,0.8316^{(3)} \} ,\)
\({\text{Yale}}:\overrightarrow {{t_{7} }} = \{ 0.8462^{(1)} ,0.6238^{(2)} ,0.8490^{(3)} \} ,\) \(A_{I} :\overrightarrow {{t_{I} }} = \{ 1^{(1)} ,1^{(2)} ,1^{(3)} \} .\)
Step 2: Utilize the score function of the Eq. (3.29) and the fluctuated hesitant information of Eqs. (3.30–3.32),
Step 3: According to d1 of the Eq. (3.27),
\(D({\text{Stanford}}) = d_{1} (\overrightarrow {{t_{1} }} ,\overrightarrow {{t_{I} }} ) = 0.1194,\) \(D({\text{Harvard}}) = d_{1} (\overrightarrow {{t_{2} }} ,\overrightarrow {{t_{I} }} ) = 0.0797,\) \(D({\text{Oxford}}) = d_{1} (\overrightarrow {{t_{3} }} ,\overrightarrow {{t_{I} }} ) = 0.1753,\) \(D({\text{Cambridge}}) = d_{1} (\overrightarrow {{t_{4} }} ,\overrightarrow {{t_{I} }} ) = 0.1385,\) \(D({\text{Berkeley}}) = d_{1} (\overrightarrow {{t_{5} }} ,\overrightarrow {{t_{I} }} ) = 0.1456,\)
\(D({\text{Ptinceton)}} = d_{1} (\overrightarrow {{t_{6} }} ,\overrightarrow {{t_{I} }} ) = 0.2308,\) \(D({\text{Yale}}) = d_{1} (\overrightarrow {{t_{7} }} ,\overrightarrow {{t_{I} }} ) = 0.2265.\)
Step 4: The synthetic values can be achieved,
\(\mathop {A_{1} }\limits^{ \cdot } = \frac{{S({\text{Stanford}})}}{{D({\text{Stanford}}) + 10^{ - 5} }} = 6.7931,\) \(\mathop {A_{2} }\limits^{ \cdot } = \frac{{{\text{S}}({\text{Harvard}})}}{{D({\text{Harvard}}) + 10^{ - 5} }} = 10.9128,\) \(\mathop {A_{3} }\limits^{ \cdot } = \frac{{{\text{S}}({\text{Oxford}})}}{{D({\text{Oxford}}) + 10^{ - 5} }} = 4.1949,\) \(\mathop {A_{4} }\limits^{ \cdot } = \frac{{{\text{S}}({\text{Cambridge}})}}{{D({\text{Cambridge}}) + 10^{ - 5} }} = 5.6704,\) \(\mathop {A_{5} }\limits^{ \cdot } = \frac{{{\text{S}}({\text{Berkeley}})}}{{D({\text{Berkeley}}) + 10^{ - 5} }} = 5.3232,\) \(\mathop {A_{6} }\limits^{ \cdot } = \frac{{{\text{S}}({\text{Ptinceton)}}}}{{D({\text{Ptinceton)}} + 10^{ - 5} }} = 2.8820,\)
\(\mathop {A_{7} }\limits^{ \cdot } = \frac{{{\text{S}}({\text{Yale}})}}{{D({\text{Yale}}) + 10^{ - 5} }} = 2.9554.\)
Step 5: According to corresponding synthetic values \(\mathop {A_{1} }\limits^{ \cdot } ,\mathop {A_{2} }\limits^{ \cdot } ,\mathop {A_{3} }\limits^{ \cdot } \mathop {,A_{4} }\limits^{ \cdot } ,\mathop {A_{5} }\limits^{ \cdot } \mathop {,A_{6} }\limits^{ \cdot } \mathop {,A_{7} }\limits^{ \cdot } ,\) arrange seven mentioned universities from the best one to the worst one,
Ranking results of Alcantuda et al. [49], Farhadinia et al. [50] and the proposed model are shown in Table 9. It is evident that three different methods obtain the same ranking result, which demonstrates the effectiveness of the proposed model under TSHFS environment in the real-application. What’s more, the same ranking result also can be obtained by proposed d1 and dkfλ(λ = 3) under TSHFS environment. From values of three different methods in Table 9, the proposed model is with higher resolution as various kinds of information are integrated in it, including distance measure information, score information and fluctuated hesitant information.
Conclusions
In this paper, by taking fluctuated hesitance on time-sequences into account, we have proposed the new type of hesitant fuzzy set, namely, time-sequential hesitant fuzzy set (TSHFS). We have also defined basic operators, score function, aggregation operators and a series of distance measures under TSHFS. What’s more, we have proposed the definition of fluctuated hesitant information to measure hesitant degrees brought by fluctuations of membership degrees on time-sequences. By integrating the proposed score function, fluctuated hesitant information and distance measure into a synthetic decision model under TSHFS environment, we have applied which to solve three different decision-making problems and reasonable feast results and ranking results have been obtained.
We put forward TSHFS on the assumption that membership degrees of TSHFSEs are given one by one on time-sequences. If membership degrees of TSHFSEs are simultaneously given almost at one moment or time-sequences are neglected, TSHFS would become into classical HFS. In the proposed decision model, we used the distance measure as the denominator. To avoid the situation that distance measure might be 0, 10–5 was added in the denominator. And the influence of when replace 10–5 with other values on final results should be studied in future. What’s more, ranking results of the proposed model could not always correspond to ones of d1, which is acted as the denominator in the proposed model. We consider ranking results of the proposed model as the accurate ones, for that it consists of not only distance measure information but also score information and fluctuated hesitant information. Compared with other types of HFS, some important concepts are not discussed in the paper, such as entropy measures, cross-entropy measures, correlation coefficients. As another sector reflecting hesitant information through fluctuations of membership degrees on time-sequences, extending which to other types of hesitant fuzzy set would be interesting studies, such as DHFS, IVHFS. In order to dig out better potential meanings of TSHFS, future works will mainly focus on mentioned above.
References
Tversky A, Kahneman D (1974) Utility, probability, and human decision making. Science 185(4157):1124–1131. https://doi.org/10.1126/science.185.4157.1124
Mitchell DGV (2011) The nexus between decision making and emotion regulation: a review of convergent neurocognitive substrates. Behav Brain Res 217:215–231. https://doi.org/10.1016/j.bbr.2010.10.030
Chen Z-S, Liu X-L, Chin K-S et al (2021) Online-review analysis based large-scale group decision-making for determining passenger demands and evaluating passenger satisfaction: case study of high-speed rail system in China. Inf Fusion 69:22–39. https://doi.org/10.1016/j.inffus.2020.11.010
Strantzali E, Aravossis K (2016) Decision making in renewable energy investments: a review. Renew Sustain Energy Rev 55:885–898. https://doi.org/10.1016/j.rser.2015.11.021
Mardania A, Zavadskasb EK, Khalifah Z et al (2017) A review of multi-criteria decision-making applications to solve energy management problems: two decades from 1995 to 2015. Renew Sustain Energy Rev 71:216–256. https://doi.org/10.1016/j.rser.2016.12.053
Liu HC, Chen XQ, Duan CY et al (2019) Failure mode and effect analysis using multi-criteria decision making methods: a systematic literature review. Comput Ind Eng 135:881–897. https://doi.org/10.1016/j.cie.2019.06.055
Rizova MI, Wong TC, Ijomah W (2020) A systematic review of decision-making in remanufacturing. Comput Ind Eng 147:106681. https://doi.org/10.1016/j.cie.2020.106681
Chen Z-S, Zhang X, Pedrycz W et al (2020) Bid evaluation in civil construction under uncertainty: a two-stage LSP-ELECTRE III-based approach. Eng Appl Artif Intell 94:103835
Xiao L, Chen Z-S, Zhang X et al (2020) Bid evaluation for major construction projects under large-scale group decision-making environment and characterized expertise levels. Int J Comput Intell Syst 13(1):1227–1242. https://doi.org/10.2991/ijcis.d.200801.002
Chen L, Pan W (2021) Review fuzzy multi-criteria decision-making in construction management using a network approach. Appl Soft Comput 102:107103. https://doi.org/10.1016/j.asoc.2021.107103
Chen Z-S, Zhang X, Rodríguez RM et al (2021) Expertise-based bid evaluation for construction-contractor selection with generalized comparative linguistic ELECTRE III. Autom Constr 125:103578. https://doi.org/10.1016/j.autcon.2021.103578
Liu W, Liao H (2017) A bibliometric analysis of fuzzy decision research during 1970–2015. Int J Fuzzy Syst 19(1):1–14. https://doi.org/10.1007/s40815-016-0272-z
Chen S-M, Han W-H (2018) An improved MADM method using interval-valued intuitionistic fuzzy values. Inf Sci 467:489–505. https://doi.org/10.1016/j.ins.2018.07.062
Zadeh LA (1965) Fuzzy sets. Inf Control 8(1):338–353. https://doi.org/10.1016/S0019-9958(65)90241-X
Heywood MI, Zincir-Heywood AN, Chatwin CR (2000) Digital library query clearing using clustering and fuzzy decision-making. Inf Process Manage 36:571–583. https://doi.org/10.1016/s0306-4573(99)00074-6
Ganie AH, Singh S (2021) An innovative picture fuzzy distance measure and novel multi-attribute decision-making method. Complex Intell Syst 7:781–805. https://doi.org/10.1007/s40747-020-00235-3
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning–1. Inf Sci 8:199–249
Herrera F, Martínez L (2000) A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans Fuzzy Syst 8(6):746–752. https://doi.org/10.1109/91.890332
Wang J-H, Hao J (2006) A new version of 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans Fuzzy Syst 14(3):435–445. https://doi.org/10.1109/TFUZZ.2006.876337
Torra V (2010) Hesitant fuzzy sets. Int J Intell Syst 25:529–539. https://doi.org/10.1002/int.20418
Rodríguez RM, Martínez L, Torra V et al (2014) Hesitant fuzzy sets: state of the art and future directions. Int J Intell Syst 29:495–524. https://doi.org/10.1002/int.21654
Zeshui Xu, Zhang X (2013) Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl Based Syst 52:53–64. https://doi.org/10.1016/j.knosys.2013.05.011
Wang J-Q, Jia-ting Wu, Wang J et al (2014) Interval-valued hesitant fuzzy linguistic sets and their applications in multi-criteria decision-making problems. Inf Sci 288:55–72. https://doi.org/10.1016/j.ins.2014.07.034
Wang H, Xu Z, Zeng X (2018) Hesitant fuzzy linguistic term sets for linguistic decision making: current developments, issues and challenges. Inf Fusion 43:1–12. https://doi.org/10.1016/j.inffus.2017.11.010
Naz S, Akram M (2019) Novel decision making approach based on hesitant fuzzy sets and graph theory. Comput Appl Math 38:7. https://doi.org/10.1007/s40314-019-0773-0
Feng X, Shang X, Xu Y (2020) A method to multi-attribute decision-making based on interval-valued q-rung dual hesitant linguistic Maclaurin symmetric mean operators. Complex Intell Syst 6:447–468. https://doi.org/10.1007/s40747-020-00141-8
Meng F, Tang J, Pedrycz W (2021) Dual hesitant fuzzy decision making in optimization models. Comput Ind Eng 154:107103. https://doi.org/10.1016/j.cie.2021.107103
Rodríguez RM, Martínez L, Herrera F (2012) Hesitant fuzzy linguistic term sets for decision making. IEEE Trans Fuzzy Syst 20(1):109–119. https://doi.org/10.1109/TFUZZ.2011.2170076
Wang H (2015) Extended hesitant fuzzy linguistic term sets and their aggregation in group decision making. Int J Comput Intell Syst 8(1):14–33. https://doi.org/10.1080/18756891.2014.964010
Chen Z-S, Chin K-S, Li Y-L et al (2016) Proportional hesitant fuzzy linguistic term set for multiple criteria group decision making. Inf Sci 357:61–87. https://doi.org/10.1016/j.ins.2016.04.006
Gou X, Liao H, Xu Z, Herrera F (2017) Double hierarchy hesitant fuzzy linguistic term set and MULTIMOORA method: a case of study to evaluate the implementation status of haze controlling measures. Inf Fusion 38:22–34. https://doi.org/10.1016/j.inffus.2017.02.008
Liu Y, Rodríguez RM, Hagras H et al (2019) Type-2 fuzzy envelope of hesitant fuzzy linguistic term set: a new representation model of comparative linguistic expression. IEEE Trans Fuzzy Syst 27(12):2312–2326. https://doi.org/10.1109/TFUZZ.2019.2898155
Xu Z, Xia M (2011) On distance and correlation measures of hesitant fuzzy information. Int J Intell Syst 26:410–425. https://doi.org/10.1002/int.20474
Xia M, Xu Z (2011) Hesitant fuzzy information aggregation in decision making. Int J Approx Reason 52:395–407. https://doi.org/10.1016/j.ijar.2010.09.002
Farhadinia B (2013) Information measures for hesitant fuzzy sets and interval-valued hesitant fuzzy sets. Inf Sci 240:129–144. https://doi.org/10.1016/j.ins.2013.03.034
Zeng W, Li D, Yin Q (2016) Distance and similarity measures between hesitant fuzzy sets and their application in pattern recognition. Pattern Recogn Lett 84:267–271. https://doi.org/10.1016/j.patrec.2016.11.001
Li D, Zeng W, Li J (2015) New distance and similarity measures on hesitant fuzzy sets and their applications in multiple criteria decision making. Eng Appl Artif Intell 40:11–16. https://doi.org/10.1016/j.engappai.2014.12.012
Chen N, Xu Z, Xia M (2013) Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis. Appl Math Model 37:2197–2211. https://doi.org/10.1016/j.apm.2012.04.031
Wang B, Liang J, Pang J (2019) Deviation degree: a perspective on score functions in hesitant fuzzy sets. Int J Fuzzy Syst 21(7):2299–2317. https://doi.org/10.1007/s40815-019-00722-x
Zhu B, Xu Z, Xia M (2012) Dual hesitant fuzzy sets. J Appl Math. https://doi.org/10.1155/2012/879629
Zeng W, Xi Y, Yin Q et al (2021) Weighted dual hesitant fuzzy set and its application in group decision making. Neurocomputing 458:714–726. https://doi.org/10.1016/j.neucom.2020.07.134
Babitha KV, John SJ (2013) Hesitant fuzzy soft sets. J New Res Sci 3:98–107
Chen Na, Zeshui Xu, Xia M (2013) Interval-valued hesitant preference relations and their applications to group decision making. Knowl-Based Syst 37:528–540. https://doi.org/10.1016/j.knosys.2012.09.009
Zhu B (2014) Decision method for research and application based on preference relation. Southeast University, Nanjing
Peng J, Wang J, Xiao-hui W et al (2015) The fuzzy cross-entropy for intuitionistic hesitant fuzzy sets and their application in multi-criteria decision-making. Int J Syst Sci 46(13):2335–2350. https://doi.org/10.1016/j.cie.2019.106088
Zhu B, Xu ZS (2016) Extended hesitant fuzzy sets. Technol Econ Dev Econ 22:100–121. https://doi.org/10.3846/20294913.2014.981882
Song C, Zhao H, Zeshui X et al (2018) Interval-valued probabilistic hesitant fuzzy set and its application in the Arctic geopolitical risk evaluation. Int J Intell Syst. https://doi.org/10.1002/int.22069
Parreiras RO, Ekel PY, Martini JSC et al (2010) A flexible consensus scheme for multicriteria group decision making under linguistic assessments. Inf Sci 180:1075–1089. https://doi.org/10.1016/j.ins.2009.11.046
Alcantuda JCR, de Andres Calle R, Torrecillas MJM (2016) Hesitant fuzzy worth: an innovative ranking methodology for hesitant fuzzy subsets. Appl Soft Comput 38:232–243
Farhadinia B, Herrera-Viedma E (2019) Multiple criteria group decision making method based on extended hesitant fuzzy sets with unknown weight information. Appl Soft Comput J 78:310–323. https://doi.org/10.1016/j.asoc.2019.02.024
Acknowledgements
We sincerely thank editors and anonymous reviewers, their comments are very helpful to improve our work. This work was supported by the National Natural Science Foundation of China (62171287, 61773267), Science & Technology Program of Shenzhen (Grant no JCYJ20190808120417257).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All the authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meng, L., Li, L. Time-sequential hesitant fuzzy set and its application to multi-attribute decision making. Complex Intell. Syst. 8, 4319–4338 (2022). https://doi.org/10.1007/s40747-022-00690-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-022-00690-0