An iterative approach to unsupervised outlier detection using ensemble method and distance-based data filtering

Abstract

Outlier or anomaly detection is the process through which datum/data with different properties from the rest of the data is/are identified. Their importance lies in their use in various domains such as fraud detection, network intrusion detection, and spam filtering. In this paper, we introduce a new outlier detection algorithm based on an ensemble method and distance-based data filtering with an iterative approach to detect outliers in unlabeled data. The ensemble method is used to cluster the unlabeled data and to filter out potential isolated outliers from the same by iteratively using a cluster membership threshold until the Dunn index score for clustering is maximized. The distance-based data filtering, on the other hand, removes the potential outlier clusters from the post-clustered data based on a distance threshold using the Euclidean distance measure of each data point from the majority cluster as the filtering factor. The performance of our algorithm is evaluated by applying it to 10 real-world machine learning datasets. Finally, we compare the results of our algorithm to various supervised and unsupervised outlier detection algorithms using Precision@n and F-score evaluation metrics.

Introduction

Outliers or anomalies are data objects which show different behavior to the rest of the data in a particular dataset. Outliers are generally caused due to errors that occurred during data entry, data measurement, data sampling, data processing along with natural and experimental errors, and many more. Outlier detection is an important application domain of machine learning and such algorithms are commonly used in fraud detection [1], network industry damage detection [2], healthcare analysis [3], surveillance [4], security [4], intrusion detection [5] and many more.

Detection of outliers is a challenging task as it involves the proper modeling of actual data and outliers. Different flavors of data possess unique challenges. The outlier hypothesis in one domain might not be applicable in another disparate problem. Sometimes, the difference between actual data objects and outliers is minimal, and hence classifying certain abnormalities in data as outliers is quite challenging. The variations on which data objects are classified as outliers vary with the domain of applications [1]. For example, small variations in observed data are neglected in the case of a stock market analysis or fraud detection but in the case of medicinal domains like healthcare such variations cannot be ignored.

The field of outlier detection has been researched extensively in past and various algorithms have been developed to deal with the problem of outlier detection. Such algorithms are generally classified into three common categories namely, supervised method [6], unsupervised method [6], and semi-supervised method [4] with each having its own advantages and disadvantages.

In the supervised method of outlier detection, samples in a dataset are labeled and data is classified into two classes: normal and outlier. Data in the training set are labeled as either normal or as an outlier. A classification model is trained on the training set, and then this model is experimented on the test set (unlabeled data) to predict the outliers. Thus supervised outlier detection methods deal with binary classification problems. Such methods can be further sub-divided into statistical methods [7], decision tree based [8], proximity based approaches [9], etc. The work done in this domain comprises the application of particle swarm optimization algorithms to detect intrusions such as PROBE, R2L, U2R, and DoS. This method was applied for the detection of fraudulent credit cards. In the other work [9], a DBSCAN based outlier detection technique is applied, in combination with Luhn’s and Bayes’ theorem to develop a probability metric that estimates the validity of the credit card.

In cases where labeled data are not available, researchers use unsupervised outlier detection techniques to predict the outliers. In the unsupervised outlier detection approach, the data are assumed to be following a certain pattern that is normal data objects form clusters with high cluster density (i.e., low intra-cluster distance) and high inter-cluster distance. Outliers are detected based on their affinity of belonging to a data cluster. Unsupervised outlier detection methods have been used in various domains such as intrusion detection [10] and sensor networks [11] etc. Zhang et al. [10] develop a random forest based algorithm to identify anomalous patterns in network data. They specifically look at identifying data points that deviate significantly in the same network service and points which belong to other network services. On the other hand, in the work [11], the authors primarily focused on creating an aggregate tree by disseminating beacon information from a sink node and recursively calculating the outlier score for each descending child node.

Semi-supervised learning falls in between supervised and unsupervised methods. The semi-supervised method uses a small amount of labeled data with a very large amount of unlabeled data. In the semi-supervised method of outlier detection, the similar data are first clustered using an unsupervised learning algorithm and then the unlabeled data are labeled based on the existing labeled data into normal and outlier classes. A few of the semi-supervised techniques are followed in the works [12, 13]. Dasgupta and Majumder [12] described a nature inspired censoring process of receptors and apply it to multidimensional personnel data. It is a two-step process wherein given a set of self-strings S and a matching threshold r, the algorithm's first phase finds the total number of unmatched strings for the defined self (S); the second phase selects some of them to build a varied group of detectors for monitoring data patterns.

As elucidated above, both supervised and semi-supervised based outlier detections, depend upon labeling of data, which can be very expensive in certain domains. Furthermore, only unsupervised approaches can classify unknown data into the right bucket of classifiers or not. Our work aims to propose a generic algorithm, which can coherently perform outlier detection on a myriad of data points. This is the major reason for prevailing with unsupervised learning techniques as the underpinning for our research.

Conventional clustering algorithms are insufficient for outlier detection as none of these clustering algorithms provides high accuracy in detecting the actual outliers. Current works in this domain have a multitude of shortcomings [14] that need to be alleviated. To be specific, numerous outlier detection methods (e.g., [15, 16]) require different parameters that are mostly manually tuned. These parameters, if not tuned optimally, are very sensitive to the end outcome. On the contrary, the method we propose here needs only an initial number of clusters and the threshold value as manual parameters. Furthermore, unlike our method, deep learning based outlier detections require a huge number of training samples and have a high time complexity which might not be feasible in terms of real-world data. Furthermore, many existing algorithms do not discount for sparsely arranged or differentiate between the subtle boundaries between two groups. Noting this and the differentiation between noise and outliers, our method intelligently reconsiders all possible candidates, and makes an informed decision. Finally, developing a generalized outlier detection has always been challenging, however, through our application, we go on to validate our results, irrespective of the domains.

Hence, the use of an ensemble method that combines the results obtained from multiple clustering algorithms instead of relying on a single algorithm proves to be a better solution for outlier detection purposes. Furthermore, a distance-based data filtering method has been used as the final layer to further increase the outlier detecting capabilities of the ensemble. Three commonly used clustering techniques: K-means, K-means++, and Fuzzy C-means have been used as the base for our algorithm. All the datasets used in our experiment have been pre-processed, cleaned, and normalized. The ensemble method is used to cluster the unlabeled data and to detect potential isolated outliers based on the cumulative degree of belongingness generated by combining the degree of belongingness scores obtained from each clustering method. An iterative process is designed to maximize the value of the Dunn index (commonly used evaluation metric for clustering methods) which gives us the optimum point. In each step of the iteration, the possible outliers are eliminated from the dataset and the inliers which had been labeled as an outlier in the previous iteration are added to the new dataset based on a cluster membership threshold value. The resultant post-clustered dataset is screened based on a distance-based threshold relative to the center of the majority cluster and further possible outlier points are eliminated. The top N outlier points are chosen based on distance from the majority cluster center. The results have been computed and compared with other outlier detection algorithms for 10 popular machine learning datasets of different sizes and dimensionalities. The contributions of our work are as follows:

• An iterative weighted ensemble of two hard clustering algorithms and one soft clustering algorithm is explored, eliminating bias and introducing agility in terms of a robust search space.

• A Dunn index based thresholding criterion is developed, which ensures that the outlier search is always progressive.

• An intelligent learning step is proposed where previously deemed outliers are also put in contention of being inliers, which removes probabilistic bias present initially and eliminates class imbalance in terms of the number of outliers.

• The results are quantified on 10 openly available datasets and are compared against 12 state-of-the-art algorithms with good results.

Related work

Several solutions have been proposed in the field of outlier detection spanning multiple domains. It has been helpful in intrusion detection, fraud detection, time-series monitoring, and many more. Zhang et al. [10] use the Random Forest algorithm to detect anomalies by building patterns of network intrusion over traffic data. Similarly, fraud detection is dealt with in the work [17], where the authors develop a replicator neural network and apply it to discover oddities across clusters. The work mentioned in [18] tackles several problems which are prevalent in outlier detection of both univariate and multivariate financial time series. It looks at calculating the projections with maximal kurtosis under a finite mixture model which enables separation of outliers from the bulk of the data. Zhang et al. [19] introduce a new factor, Local-Distance-based Outlier Factor (LDOF) which calculates the degrees of outlier-ness of an object in real-world datasets. LDOF is calculated based on the relative location of an object to its neighbors and the false-detection probabilities. The algorithm [20] calculates outliers at a nearly linear time when the dimensionality of the dataset is high. It tracks the nearest neighbors of a point and removes the point from a potential outlier list, using a certain threshold value. At every iteration, the threshold value increases with the pruning efficiency. However, the major disadvantage of this algorithm is that when there are not many outliers in the system, the running time of the algorithm becomes quadratic. To solve this, a two-step algorithm is developed in [21], which tries to solve the bottleneck of high-dimensional data by performing a pre-processing step that allows for fast determination of approximate nearest neighbors. K-means is initially used by Jiang et al. [22] to solve the problem of outlier detection by following a two-phase approach, where they first modify the heuristic of K-means to separate out data points into a new cluster, which are far away from each other, followed by generating a Minimal Spanning Tree (MST) to delete the longest (farthest) edge.

More recently, K-means coupled with a Genetic Algorithm (GA) has been used to solve the said problem. For example, in [23], GA has been used in outlier detection of sparsely populated datasets, where it is used to insert large amounts of relevant data in sparse regions which is then used by the K-means algorithm to solve the interpolation problem. Similarly, Triangle Area-based nearest neighbors are introduced in [24] which works on top of the centroids generated by the K-means algorithm, uses triangular area on each centroid to generate several sets of data, and then uses the k-nearest neighbor (k-NN) algorithm for further analysis. The problem of deriving K, the number of clusters, is done away in [25] where the authors generate a series of local proximity graphs based on a uniform sampling strategy, followed by performing Markovian random walks to detect anomalies across these graphs. Similarly, algorithms have been developed which are built on top of K-means++ and Fuzzy C-means. Feng et al. [26] develop an approximation algorithm for general metric space which uses the K-means++ to sample points from the space and then use them to select centers from them, whereas Fuzzy C-means has been used in [27] to generate clustering extreme classes (highest positive and negative), which are then trained by a Support Vector Machine (SVM) to produce the final classification results. The above works mostly suffer from sensitivity to the initial centroid formation and may not be useful on large scale data.

Ensemble techniques have also been worked upon to solve the problem of outlier detection. For example, Aggarwal in [28] talks about the categorization of outlier ensemble algorithms into sequential or independent ensembles and model-centered or data-centered ensembles; which enables in identifying the metrics behind the ensemble approach. K-means has been used as an ensemble in [29], where the algorithm is used multiple times in tandem to obtain a weighted graph structure equivalent to the averaged co-membership matrix. Neural networks coupled with data and edge sampling have also been used in [30] as an ensemble outlier detection approach, achieved by randomly varying the connectivity architecture of the auto-encoder, obtaining significantly better performance. Most ensemble methods suffer from the problem of either normalization or combination. Given a set of outlier patterns, the problem arises in comparing the different results, since each component of the ensemble might represent its results in a different reference. Similarly, given a normalized set of outlier scores, the technique of combining them together also becomes challenging. For example, if an ensemble has the application of a fuzzy-based and a hard clustering algorithm, combining them so that they can be mapped onto the same proportion is often a tricky problem.

Present work

Our proposed algorithm focuses on the detection of outliers that may be isolated, clustered, or a combination of both. To differentiate between those outliers, we divide our algorithm into two stages. The first stage uses the clustering ensemble which iteratively clusters as well as removes the potential isolated outliers if any from the unlabeled data based on a preset cluster membership threshold value. The second stage uses the distance-based data filtering following a preset distance threshold to filter out the potential outlier clusters if any from the filtered results (post-clustered data) we obtained from the first stage of our algorithm. In this section, we first explain all prerequisites of the proposed method, and then finally we describe the proposed technique.

Clustering algorithms used

As previously mentioned, we use three conventional clustering algorithms: K-means, K-means++, Fuzzy C-means out of which two are hard clustering algorithms and the other follows the soft clustering paradigm. The degree of belongingness scores is not generated by hard clustering algorithms as data objects can only belong to a single cluster (class). Hence, we generate the degree of belongingness scores using the formula described in section “Degree of belongingness score generation for clustering algorithms”. In the case of the soft clustering algorithm, the data objects belong to multiple clusters (classes) with varying degrees of belongingness (i.e., the fuzzy membership values) of the object belonging to each cluster and thus manual generation of the degree of belongingness scores are not required. Below we describe the three algorithms which form our clustering based ensemble.

K-means

K-means [31, 32] is a hard clustering algorithm. It uses an iterative process that partitions data into $K$ non-overlapping clusters whose centroids are chosen randomly at an initial step from the dataset. The K-means algorithm tends to maximize the inter-cluster distance and minimize the intra-cluster distance. A data point is assigned to a cluster that has its centroid at a minimum distance from that data point. The iterations are performed till the algorithm converges (i.e., objective function reaches a satisfactory value). The steps of the K-means algorithm are given below:

• 1. Specify the number of clusters $K$ for a $d$-dimensional dataset.

• 2. Initialize centroids by first shuffling the given dataset and then randomly selecting $K$ points for the cluster centroids from the shuffled dataset without replacement.

• 3. Keep iterating until the algorithm converges.

  • 3.1 Assign each data object ${x}_{i}$ to the cluster whose centroid ${c}_{j}$ is at a minimum distance, ${d}_{ij}=\mathrm{min}\left( \Vert {x}_{i}- {c}_{j}\Vert \right)$ from the data object ${ x}_{i}$, where $j=1, 2, 3, 4, \dots , K$. ||*|| is a norm function.

  • 3.2 Let the number of initial data objects in the ${j}$th cluster be ${N}_{i}$ with its centroid denoted by ${c}_{j}$. Then update the cluster centers using the formula:

    $$ c_{j} = \frac{1}{{N_{j} }}\sum x_{i} \mu_{ij} . $$

    (1)

In Eq. (1), ${\mu }_{ij}=1$ if ${x}_{i}$ belongs to the ${j}$th cluster else ${\mu }_{ij}=0$.

K-means++

Like K-means, K-means++ [33] is also a hard clustering algorithm. It is the modified version of the K-means algorithm which has faster convergence than the conventional K-means algorithm and provides a better clustering of unlabeled data with high inter-cluster distances. It uses a different initial cluster centroid assignment method. The very first cluster centroid is chosen at random from the dataset. Then the remaining $\left(K-1\right)$ cluster centroids are selected based on the principle that a data point from the dataset whose minimum distance to the already selected cluster centroids is the largest is chosen as the new cluster centroid.

Fuzzy C-means

Fuzzy C-means [34] is a soft clustering algorithm. Fuzzy C-means allows data to belong to more than one cluster. It is based on the minimization of the objective function,

$$ J_{m} = { }\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{C} \mu_{ij}^{m} x_{i} - { }c_{j}^{2} ,\quad 1 \le m < \infty . $$

(2)

Here in Eq. (2), $m$ is any real number greater than 1, ${\mu }_{ij}$ is the degree of membership of ${\mathrm{x}}_{\mathrm{i}}$ in the cluster $j$, ${x}_{i}$ is the ${i}$th datum of $d$-dimensional dataset, ${\mathrm{c}}_{\mathrm{j}}$ is the centroid of the ${j}$th cluster in $d$-dimensional space. $N$ is the number of objects in the dataset and $C$ is the number of cluster centers and ||*|| is the norm function. Fuzzy partitioning is carried out through an iterative optimization of the objective function (see Eq. (2)), with the updated membership value (say, ${\mu }_{ij}$) and the cluster centers (say, ${c}_{j}$) defined in Eqs. (3) and (4), respectively:

$${\mu }_{ij}= \frac{1}{\sum_{k=1}^{C}{\left(\frac{\Vert {x}_{i}- {c}_{j}\Vert }{\Vert {x}_{i}- {c}_{k}\Vert }\right)}^{\frac{2}{m-1}}},$$

(3)

$${c}_{j}= \frac{\sum_{i=1}^{N}{\mu }_{ij}^{m}.{x}_{i}}{\sum_{i=1}^{N}{\mu }_{ij}^{m}}.$$

(4)

This iteration will stop when $\mathop {{\text{max}}}\nolimits_{{ij}} \left\{ {\left| {\mu _{{ij}}^{{k + 1}} - \mu _{{ij}}^{k} } \right|} \right\} < \varepsilon$, where $\varepsilon$ is an iteration termination criterion between 0 and 1, and $k$ is the iteration count. This procedure converges to a local minimum of the objective function ${J}_{m}$.

The algorithm can be described by the following steps:

• 1. Initialize $U=\left[{\mu }_{ij}\right]$ matrix, ${U}^{0}$ for $k=0$.

• 2. At ${k}$th-step: calculate the centroid vectors ${C}^{k}=\left[{c}_{j}\right]$, where ${c}_{j}$ is defined using Eq. (4).

• 3. Update ${U}^{k}$ to ${U}^{k+1}$, where each element ${\mu }_{ij}$ in the $U$ matrix is defined using Eq. (3).

• 4. If $\Vert {U}^{k+1}- {U}^{k}\Vert <\varepsilon$ then terminate the process otherwise continue the process to ${\left(k+1\right)}$th step.

Degree of belongingness score generation for clustering algorithms

The degree of belongingness is the scoring scheme we use to assign cluster membership to unlabeled data objects. The hard clustering algorithms in use assign the data objects to a single cluster hence the degree of belongingness is not generated by those algorithms. In the case of soft clustering algorithms, the fuzzy membership values (which are equivalent to the degree of belongingness scores) form an integral part of the algorithm and are crucial for the clustering of unlabeled data. For soft clustering algorithms, a data object belongs to a cluster for which it holds the highest membership value. So, the degree of belongingness scores for a soft clustering algorithm can be represented by its membership values. The degree of belongingness scores for the hard clustering algorithms is defined using the formula:

$${P}_{ij}=1.0-\left(\frac{\Vert {x}_{i}- {c}_{j}\Vert }{\sum_{k}\Vert {x}_{i}- {c}_{k}\Vert }\right).$$

(5)

Here,$j=1, 2,\dots ,K$ and ${P}_{ij}$ represents the degree of belongingness of data object ${x}_{i}$ of belonging to ${j}$th cluster with centroid ${c}_{j}$. From Eq. (5) we observe that degree of belongingness score ${P}_{ij}$ can have a maximum value of $1.0$ and a minimum value of $0.0$. So, we set the scores according to the Euclidean distance of a data point from a cluster centroid. Thus, according to the ratio $\frac{\Vert {x}_{i}-{c}_{j}\Vert }{\sum_{k}\Vert {x}_{i}-{c}_{k}\Vert }$ for larger $\Vert {x}_{i}-{c}_{j}\Vert$ values the overall value will be smaller and hence ${P}_{ij}$ will have a smaller degree of belongingness score for larger distance.

The degree of belongingness scores (equivalent to the fuzzy membership values) for the soft clustering algorithms are generated using the formula:

$${P}_{ij}={\mu }_{ij}= \frac{1}{\sum_{k=1}^{C}{\left(\frac{\Vert {x}_{i}- {c}_{j}\Vert }{\Vert {x}_{i}- {c}_{k}\Vert }\right)}^{\frac{2}{m-1}}}.$$

(6)

In Eq. (6), $j=1, 2, \dots ,K$ and ${P}_{ij}$ represents the degree of belongingness of data object ${x}_{i}$ of belonging to ${j}$th cluster with centroid ${c}_{j}$ and $1<m<\infty$ ($m$ represents the amount of fuzziness in our dataset).

Weighted method of generating the cumulative degree of belongingness scores

In “Degree of belongingness score generation for clustering algorithms” section, we discuss how the degree of belongingness can be generated for the hard clustering algorithms. To combine the degree of belongingness scores we generated for each clustering technique in the ensemble, we use a weighted technique which we represent using the formula provided in Eq. (7):

$${P}_{ij}=\frac{\prod_{y}{P}_{ij}(y)}{\sum_{j}\prod_{y}{P}_{ij}(y)}.$$

(7)

In Eq. (7), $y=\mathrm{1,2},\dots ,m$ and $j=\mathrm{1,2},\dots ,K$. ${P}_{ij}$ is generated for an ensemble of $m$ clustering techniques which is in our case is 3. ${P}_{ij}$ is the combined degree of belongingness of the data object ${x}_{i}$ of belonging to ${j}$th cluster with centroid ${c}_{j}$.

The data object ${x}_{i}$ is assigned to a cluster for which it has the maximum ${P}_{ij}$. Hence, we classify the point ${x}_{i}$ as an outlier if:

$$\mathrm{max}{\{P}_{ij}\}<{P}_{\mathrm{th}}.$$

(8)

In Eq. (8), ${P}_{\mathrm{th}}$ is the cluster membership threshold. Only those data objects with a combined degree of belongingness scores greater than the cluster membership threshold are considered as inliers by our clustering based ensemble method.

Dunn index maximization for convergence of iteration

Different clustering validity indices are used to measure the quality of a clustering algorithm. Dunn index [35, 36] scores are one of the widely used clustering validity indices. It is an internal evaluation scheme. The higher Dunn index indicates greater compactness within clusters and higher inter-cluster separation. Dunn index values are maximized over an iterative process to locate the optimum point (the best quality of clustering). Dunn index values are calculated for each iterative step using Eq. (9):

$${ \mathrm{Dunn}}_{K}^{t}= \frac{{\mathrm{min}}_{i\le i<j\le K}\{d\left({c}_{i},{c}_{j}\right)\}}{{\mathrm{max}}_{l\le p\le K}{\Delta }_{p}}.$$

(9)

In Eq. (9), $t$ is the iterative step count, $\delta \left({c}_{i},{c}_{j}\right)$ is the inter-cluster distance measure between cluster centroids ${c}_{i}$ and ${c}_{j}$ and ${\Delta }_{p}$ is the intra-cluster distance measure for the ${p}$th cluster.

In our algorithm, we use an iterative process to maximize the Dunn index values (maximize the quality of cluster formation). In an iterative step, a selective number of data points with a degree of belongingness less than the threshold level (${P}_{\mathrm{th}}$) are eliminated from the dataset. Then in the next step, the ensemble of the clustering techniques is again applied to the resultant dataset and the degree of belongingness scores for both the previously eliminated data as well as data points in the current dataset are computed. Precisely, we have not considered any data point as an absolute outlier point at any step of the iteration. We consider a data point as an outlier at the end of the iterative process. Based on the new degree of belongingness scores, we perform three operations:

• 1. Some of the previously eliminated data points which have been labeled as outliers in the ${t}$th iteration is again included in the dataset at ${(t+1)}$th iteration based on the assumption that ${{P}_{o}}_{ij}^{t+1}>{P}_{\mathrm{th}}$ i.e., if the data point satisfies the condition to be inlier. Here ${{P}_{o}}_{ij}^{t+1}$ is the updated degree of belongingness scores for the previously eliminated data point in the ${(t+1)}$th iterative step, for $i=1, 2, \dots , M$ (where $M$ is the number of previously eliminated data points), $j=1, 2,\dots , K$ (where $K$ is the number of clusters).

• 2. Data points from the new dataset are eliminated and labeled as outliers in the $(t+1)$-th iteration based on the assumption that ${{P}_{n}}_{ij}^{t+1}<{P}_{\mathrm{th}}$. Here ${{P}_{n}}_{ij}^{t+1}$ is the updated degree of belongingness scores for the new data points in the $(t+1)$-th iterative step, for $i=\mathrm{1,2},\dots , {N}^{^{\prime}}$ (where ${N}^{^{\prime}}$ is the number of data objects in the new dataset), $j=\mathrm{1,2},\dots , K$ (K is the number of clusters).

• 3. We update the current Dunn Index value (i.e., Dunn Index for the $(t+1)$th iterative step) and continue with the next iterative step if ${\mathrm{Dunn}}_{K}^{t+1}>{\mathrm{Dunn}}_{K}^{t}$ where, ${\mathrm{Dunn}}_{K}^{t}$ is the Dunn Index for the $t$th iterative step, else we terminate the iteration.

The resultant Dunn index value after the termination of the iterative process is the maximized Dunn index value (i.e., Dunn index that provides the best quality of clustering) which provides the optimal point of operation of our algorithm. The data points which are eliminated in the final step of the iterative process are labeled as actual outliers.

Distance-based filtering model

Outliers though small in number when compared with the number of actual data points in the dataset may share common traits with other outliers and may form clusters of their own. Let us assume that the outliers form the number of clusters with relatively smaller cluster densities than that of actual ones, but with large inter-cluster distance and small intra-cluster distance. In this scenario, we cannot eliminate those clusters using the iterative ensemble of clustering techniques due to the small intra-cluster distance between outlier points and hence with the degree of belongingness (${P}_{ij}$) greater than that of the fixed threshold (${P}_{\mathrm{th}}$). To eliminate those clusters, we use a distance-based filtering model which performs the following operations on the post-clustered dataset formed using the iterative ensemble method:

• 1. Fix a threshold distance (${d}_{\mathrm{th}}$) for the filter.

• 2. Determine the majority cluster (the cluster with the highest cluster density value) of the post-clustered dataset for each of the clustering techniques (K-means, K-means++, and Fuzzy C-means) used in the ensemble.

• 3. For each of the three clustering techniques compute the distance of each object ${x}_{i}$ in the dataset from the centroid of the majority cluster ${C}_{k}$(centroid for ${k}$th clustering method). Label the object ${x}_{i}$ as an outlier if $\underset{k}{\mathrm{min}}\Vert {x}_{i}- {C}_{k}\Vert >{d}_{\mathrm{th}}$ where $i = 1, 2, \ldots ,N^{\prime \prime }$ and $N^{\prime \prime }$ represents the size of the post-clustered dataset and $k=1, 2, 3$ denotes the number of clustering techniques used in the ensemble. To be specific, for each of the clustering techniques, if an object ${x}_{i}$ is labeled as an outlier, then the point is labeled as an actual outlier despite its belongingness in a formed cluster by present ensemble-based clustering.

Iterative ensemble method with distance-based data filtering

In the previous sections, we discussed in detail the different basics and working principles of our algorithm. In this section, we combine the various steps mentioned in the previous sections and present the overall algorithm. A pictorial description of the proposed method has been shown in Fig. 1 while in Fig. 2, the methodology of the proposed method is shown using a flowchart.

Fig. 1

Pictorial description of the proposed method (iterative ensemble method with distance-based data filtering). The circles with black colored dashed lines show the elimination process of outliers based on a cluster membership threshold (P_th), in which the points outside the dashed circles are eliminated. The concentric blue circles show the process of elimination of outliers in outlier clusters based on a distance threshold (d_th) from the majority cluster center

Fig. 2

Overview of our proposed method (iterative ensemble method with distance-based data filtering) for outlier detection

Given a dataset $X=\left\{{x}_{1},{x}_{2},\dots ,{x}_{n}\right\}$, the number of clusters (say, K), and fixing a cluster membership and distance threshold as ${P}_{\mathrm{th}}$ and ${d}_{\mathrm{th}}$ respectively. The steps of the algorithm are as follows:

• 1. Compute clusters for the given dataset using each of the mentioned three clustering techniques.

• 2. Determine the cluster centroids and degree of belongingness of each of the data point ${x}_{i}$ in the dataset for each of the clustering techniques used. For hard clustering algorithms (i.e., K-means and K-means++) assign the degree of belongingness scores to data points based on the formula defined in Eq. (5). For the soft clustering algorithm use the fuzzy membership values as the degree of belongingness scores for the data points based on the formula defined in Eq. (6).

• 3. Start the iterative process and compute ${\mathrm{Dunn}}_{K}^{t}$ where $t=0$ for the initially computed clusters.

• 4. Generate the cumulative degree of belongingness score for the cluster ensemble using the formula defined in Eq. (7). Eliminate points from the given dataset and label them as possible outliers using Eq. (8) based on the maximum cumulative degree of belongingness score of each data point ${x}_{i}$ of $X$.

• 5. Compute the clusters and centers for each of the clustering techniques for post elimination. Find the updated Dunn index value (${\mathrm{Dunn}}_{K}^{t}$) for updated clusters in the $t$th iterative step.

• 6. In $\left(t+1\right)$th iterative step, check if any of the data points in the updated dataset have a degree of belongingness ${{P}_{n}}_{ij}^{t+1}<{P}_{\mathrm{th}}$ for which those points are eliminated from the dataset. Also, check if any of the previously eliminated possible outliers have a degree of belongingness ${{P}_{o}}_{ij}^{t+1}>{P}_{\mathrm{th}}$ (i.e., satisfies the condition to be inlier) for which those points are included in the updated dataset.

• 7. Check if updated Dunn Index value (i.e., Dunn Index for the $(t+1)$th iterative step) is greater than original Dunn Index value (i.e., Dunn Index for the $t$-th iterative step) ${\mathrm{Dunn}}_{K}^{t+1}-{\mathrm{Dunn}}_{K}^{t}>0$. If true then continue with the next iteration step else we terminate the iteration process

• 8. After termination of the iteration determines the final majority clusters for each of the 3 clustering techniques. Based on the distance threshold ${d}_{\mathrm{th}}$ select points ${x}_{i}$ from the dataset for which $\underset{k}{\mathrm{min}}\Vert {x}_{i}- {C}_{k}\Vert >{d}_{\mathrm{th}}$ where $k=1, 2, 3$ (number of clustering techniques used), ${C}_{k}$ is the majority cluster centroid for the ${k}$th clustering method. If a point ${x}_{i}$ is labeled as an outlier by all three of the clustering methods, then select that point as an outlier and add that point to the list of previously labeled outliers (outliers labeled using the ensemble).

Results and discussion

To assess the performance of our proposed algorithm, we evaluate it on 10 machine learning datasets with different sizes and dimensions and each having a varying number of outliers. Our results have been compared to those obtained from 12 other outlier detection algorithms which demonstrate that our proposed method shows superior or comparable performance on most of the datasets to those existing outlier detection algorithms. In this section, first, we describe different requirements for the experiment and then mention the obtained results.

Database description

The datasets on which our proposed method has been evaluated are shown in Table 1. From Table 1, we observe that the Pima dataset has the largest number of samples (510) and the Parkinson dataset is the smallest sized dataset (50). The Ionosphere dataset has the largest dimension (32), whereas the Glass dataset has the smallest dimension (7). In terms of outlier count Ionosphere, the dataset has the largest number of outliers at 126 (i.e., 35.90% of the entire dataset) with the Pima dataset is having the smallest outlier count at 10 (1.96% of the entire dataset).

Table 1 The datasets used to evaluate the proposed outlier detection method and their properties

Evaluation metrics

We evaluate the performance of our algorithm based on the evaluation metrics described below.

F-score: The F-score [37, 38], also called the F1-score or the F-measure reflects upon a test’s accuracy. It is defined as the harmonic mean of the precision and recall values. This score is calculated according to:

$${{{\text{F-score}}}} = \left( {\frac{{{\text{recall}}^{ - 1} + {\text{precision}}^{ - 1} }}{2}} \right)^{ - 1} = 2 \times \left( {\frac{{{\text{precision}} \cdot {\text{recall}} }}{{{\text{precision}} + {\text{recall}}}}} \right). $$

(10)

With both precision and recall considered for the calculation of the F1-score, it is useful in providing a realistic measure of a test’s performance by balancing both precision and recall. A F-score value ranges from 0 to 1.

Precision@n (P@n): For a classification system P@n [39, 40] is the proportion of relevant output at the top-n selected outputs. For example, if our algorithm returns N number of ranked data points as outliers and out of those N points if we use only the top-n ranked data points as outlier points of which r points are true outliers then we calculate P@n of that algorithm as:

$$P@n=\frac{r}{n}.$$

(11)

Results on the database

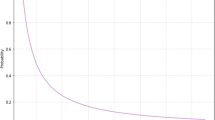
Results have been calculated for the mentioned 10 different datasets. We conduct multiple experiments by setting different parameters, i.e., by setting different cluster membership thresholds (${P}_{\mathrm{th}}$) and varying distance threshold (${d}_{\mathrm{th}}$) and the number of clusters ($K$) over a wide range of values. The parameter values for which we obtain the maximum F-score are considered as the best parameter values (see Table 2). Figure 3 shows the variation of the F-score with the cluster membership threshold (${P}_{th}$) parameter values for the present clustering ensemble method. In Table 2, the mentioned score is obtained using the best parameter values shown therein. $P@n$ scores corresponding to the maximum F-score are considered in the results shown below. Using the parameter values (mentioned in Table 2), we compute the results in terms of F-score and $P@n$ of the proposed algorithm and compare these results with those obtained using only K-means, K-means++, and Fuzzy C-means exclusively in place of the clustering ensemble. The comparative results are shown in Fig. 4. The results of this figure suggest that the present clustering ensemble method performs reasonably better as compared to K-means, K-means++, and Fuzzy C-means individually.

Table 2 Results for the present iterative ensemble method with distance-based filtering. Here, the optimal parameter values are mentioned that we obtain after several experiments

Fig. 3

Variation of F-score with the parameter value (${P}_{\mathrm{th}}$) for the present iterative ensemble method

Fig. 4

Performance of our proposed ensemble method in comparison with K-means, K-means++, and Fuzzy C-means clustering algorithms. The comparisons are made in terms of a F-score and b P@n for all datasets used here. In b, the missing bars indicate zero scores

Dunn Index variation for convergence of iteration

In this subsection, we show the Dunn index variation with each step of the iterative process until the convergence criterion is satisfied (i.e., till the Dunn index gets maximized, see section “Dunn index maximization for convergence of iteration”) for all of the algorithms (i.e., clustering ensemble, K-mean, K-means++, and Fuzzy C-means). The results for which are shown in Fig. 5.

Fig. 5

Dunn index variation for all of the algorithms: a clustering ensemble, b K-means, c K-means++, and d Fuzzy C-means

Performance of alternative ensemble-based outlier detection algorithms

In our proposed work, we have used three clustering algorithms: K-means, K-means++, and Fuzzy C-means. However, to test the performance of the proposed iterative ensemble with distance-based data filtering approach with varying base clustering algorithms we have performed more experiments. For this, we have considered two more clustering techniques namely, Self-Organizing Map (SOM) [41], and Single-Linkage (SL) [42]. We have constructed 4 new iterative ensemble methods with distance-based data filtering approach with the help of the K-means, Fuzzy C-means, SOM, and SL clustering algorithms. The 4 different methods comprising 4 different clustering ensembles are Method 1 (K-means, SOM, and SL), Method 2 (K-means, SOM, and Fuzzy C-means), Method 3 (K-means, SL, and Fuzzy C-means), and Method 4 (SL, SOM, and Fuzzy C-means) have been built. The performances of the 4 alternative methods along with the proposed one (K-means, K-means++, and Fuzzy C-means) are shown in Table 3 (for P@n) and Table 4 (for F-score). These tables also include the performances of K-means, K-means++, Fuzzy C-means, SOM, and SL. From the results it is clear that the performance of the proposed approach is better in most of the cases.

Table 3 Performances in terms of P@n score of different base clustering algorithms and the alternative ensemble methods constructed with varying these base clustering algorithms

Table 4 Performances in terms of F-score of different base clustering algorithms and the alternative ensemble methods constructed with varying these base clustering algorithms

Comparison with other outlier detection algorithms

We compare the performance of our proposed algorithm (iterative ensemble method with distance-based data filtering) with 12 other existing outlier detection algorithms (viz., kth-Nearest Neighbor (kNN), kNN-weight (kNNW), Local Outlier Factor (LOF), Simplified LOF, Local Outlier Probabilities (LoOP), Local Distance-based Outlier Factor (LDOF), Outlier Detection using Indegree Number (ODIN), Fast Angle-Based Outlier Detection (FastABOD), Kernel Density Estimation Outlier Score (KDEOS), Local-Density Factor (LDF), Influenced Outlierness (INFLO) and Connectivity-based Outlier Factor (COF)) the results. The score mentioned for the comparative methods is the experimental outcome of the work mentioned in [43]. The metrics $P@n$ and F-score are only used for the comparative purpose as they are popularly used comparative metrics used for comparing outlier detection algorithms. These comparative results are shown in Fig. 6.

Fig. 6

Performance comparison of the proposed method with state-of-the-art techniques on the 10 datasets used in this work. The missing bars (in f and h) indicate zero scores

As indicative of the results shown in Fig. 6a, we observe that our proposed method outperforms the 12 other outlier detection algorithms on the Glass dataset and our proposed method also registers the highest $P@n$ score and F-score. On the Lymphography dataset (see Fig. 6b for performance results) our proposed method performs comparably to the 12 other outlier detection algorithms. Our proposed method registers the highest $P@n$ score along with a comparable F-score and gives better overall performance than LoOP, LDOF, ODIN, Fast ABOD, KDEOS, and INFLO algorithms. Following a similar trend to the previous results our proposed method registers the highest $P@n$ score on the Ionosphere dataset (see Fig. 6c for performance results) and also shows comparable F-score performance. So, we infer that our proposed method outperforms all of the 12 outlier detection algorithms on the Ionosphere dataset. Only the KNN and KNNW algorithms (both are supervised outlier detection algorithms) show performance comparable to our proposed method on the Ionosphere dataset.

Figure 6d suggests that our proposed method gives better overall performance than the LoOP, LDOF, ODIN, and KDEOS algorithms on the WBC dataset but lags when compared to KNN and LDF algorithms both of which registered the highest F-score. Similar to what we observed before, our proposed method outperforms the KDEOS algorithm on the WDBC dataset and shows performance comparable to the LDF, ODIN, and FastABOD algorithms as evidenced by the results shown in Fig. 6e. The LOF algorithm registers the highest F-score on the WDBC dataset but is outperformed by the LDF algorithm on the $P@n$ results. The performance results on the Heart Disease dataset are shown in Fig. 6f. We observe that the highest $P@n$ scores are registered by our proposed method as well as by LDF and COF algorithms but our method falls behind in the F-score results registering the third highest score (behind COF and LDF algorithms) but in overall performance, our proposed method gives superior results to the rest of the 10 outlier detection algorithms. The results on the Hepatitis dataset shown in Fig. 6g again show that our proposed method shows comparable performance to the other algorithms. Our proposed method registers the highest $P@n$ score along with the LDF, LOF, and COF algorithms.

Also, our proposed method registers the second highest F-score behind the 3 previously mentioned algorithms but shows greater overall performance than the rest of the 12 outlier detection algorithms on the Hepatitis dataset. On the Pima dataset (see Fig. 6h for performance results) our proposed method registers the highest $P@n$ score and a comparable F-score. Only the FastABOD and KDEOS algorithms show similar performance to our method with FastABOD registering the highest F-score with KDEOS following in at a close second with our method falling in at third. So, we infer that our proposed method shows superior performance than the rest of the 10 outlier detection algorithms on the Pima dataset. Comparison results on the Parkinson dataset shown in Fig. 6i show that the LDF algorithm has the best $P@n$ and F-score performance and all the other algorithms (including our proposed method) show exactly similar performance. Finally, in Fig. 6j, we show the performance results of the algorithms on the Stamps dataset. As we see from the comparison results that our proposed method again registers the highest $P@n$ score with F-score comparable to what we observe for the other outlier detection algorithms. Only the COF algorithm shows performance comparable to our proposed method and registers the highest F-score. But all the other outlier detection algorithms fall behind in both the $P@n$ score and F-score performance. Hence, our proposed method shows better overall performance than all the 12 other outlier detection algorithms on the Stamps dataset.

So, the comparison results indicate that our proposed algorithm shows good performance when compared to the said 12 existing outlier detection algorithms (both classification and clustering based) for all of the 10 machine learning datasets from our database. For some of the datasets, our algorithm gives outright better results than all the 12 algorithms whereas on other datasets it gives results comparable to those algorithms. We also infer that irrespective of the outlier type (isolated or clustered) present in the dataset our proposed algorithm has reasonable outlier detection accuracy as evidenced from the comparison results shown above.

Conclusion

In this paper, we propose an algorithm that consists of an iterative clustering ensemble of K-means, K-means++, and Fuzzy C-means clustering algorithms and a distance-based filtering method for outlier detection from unlabeled datasets. We observe that using a clustering ensemble, we obtain results comparable or better than those obtained using individual clustering techniques (i.e., K-means, K-means++, and Fuzzy C-means) in place of the ensemble. Using an ensemble of clustering techniques, we can compensate for the erroneous results that we obtain from any of the individual clustering algorithms. The distance-based filter is effective in removing those outliers that remain undetected by our iterative clustering ensemble. Our results that we have obtained by experimenting on 10 datasets from various application domains infer that the proposed algorithm performs superior to some of the pre-established outlier detection algorithms (both classification and clustering based) on certain datasets. The performance of the proposed algorithm varies depending on the threshold values (cluster membership threshold ${P}_{\mathrm{th}}$ and distance threshold ${d}_{\mathrm{th}}$) chosen. In the future, an intelligent evaluation method can be designed to set the values of ${P}_{\mathrm{th}}$ and ${d}_{\mathrm{th}}$ for better estimation of the outlier data points. A larger clustering ensemble can be used which will combine results from multiple pre-established clustering outlier detection algorithms used for detecting outliers. In place of the distance-based data filtering scheme, a weighted method of data filtering can be used for the detection of possible outlier clusters which remain undetected by the clustering ensemble.