Abstract
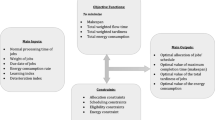
Robotic Mobile Fulfillment System (RMFS) affects the traditional scheduling problems heavily while operating a warehouse. This paper focuses on storage assignment optimization for Fishbone Robotic Mobile Fulfilment Systems (FRMFS). Based on analyzing operation characteristics of FRMFS, a storage assignment optimization model is proposed with the objectives of maximizing operation efficiency and balancing aisle workload. Adaptive Genetic Algorithm (AGA) is designed to solve the proposed model. To validate the effectiveness of AGA in terms of iteration and optimization rate, this paper designs a variety of scenarios with different task sizes and storage cells. AGA outperforms other four algorithm in terms of fitness value and convergence and has better convergence rate and stability. The experimental results also show the advancement of AGA in large size FRMFS. In conclusion, this paper proposes a storage assignment model for FRMFS to reduce goods movement and travel distance and improve the order picking efficiency.
Similar content being viewed by others
Introduction
Robotic technology has made a significant impact on electronics, transportation and logistics [1]. Robotic Mobile Fulfillment System (RMFS), like Amazon Kiva System, is a robot-based and parts-to-picker system which can improves warehouse throughput and reduces operating costs [2]. Robots delivery mobile racks that contain required stock keeping units, SKUs, to the picker or picking stations. The worker can complete order picking processes with no need of tediously lengthy walking, which effectively saves the walking and finding time of picking operators.
The layout of RMFS is complex and flexible. Different from the traditional layout, the fishbone layout breaks the restriction that the aisle must be parallel or vertical, through two diagonal aisles to reach the best theoretically Euclidean distance [3]. The robot can not only pass through the vertical and horizontal aisles, but also the oblique aisles. For fishbone layout, the robot can carry the rack to the work station through the oblique aisle, so the time to complete the rack handling task is different from the time consumed in the traditional layout, and the expected travel distance under a single cycle can be reduced by about 20% [4]. Excellent storage assignment strategy can reduce rack handling time and robot congestion, improve the efficiency of throughout and order picking. The current research directions of storage assignment optimization of RMFS are mainly focused on storage assignment strategy and model solving algorithm.
For storage assignment strategy of RMFS, Weidinger et al. [5] established a model for minimizing robot handling cost for the storage assignment problem, transformed the storage assignment into a special interval scheduling problem and introduced a new adaptive programming algorithm to solve the model. Lamballais et al. [6] established a Semi-Open Queueing Network model, focusing on the study of the number of items stored, the ratio of the number of picking stations to replenishment stations and the impact of replenishment strategies on order throughput time. The result proved that when the items are distributed for multiple shelves, the number of picking stations and replenishing stations are 4 and 2 respectively and the replenishment threshold is set to 50%, the picking efficiency is higher. By analyzing the impact of storage partitions and robot allocation strategies on RMFS throughput, Roy et al. [7] proposed a cross-regional scheduling strategy based on the shortest queue. Hadi et al. [8] considered item relevance, picking distance and item priority to improve system performance. This research adopted a COI-based classification storage strategy to dynamically determine the storage location of products. Based on the traditional human to arrival system, Bahrami et al. [9] proposed a location allocation strategy combining fixed location and free location. According to the order information, he moved the hot SKU to the free location close to the picking station to improve the picking efficiency. Wu et al. [10] proposed a delay factor for the automatic picking system to compare the picking volume of each picking area and achieved a reasonable allocation of goods with the goal of minimizing the total delay factor. He et al. [11] aimed at minimizing the picking distance and the number of rack handling times and established a dynamic inventory allocation strategy considering the turnover rate of items. Xu et al. [12] proposed a location assignment model based on the Dutch Auction mechanism to improve the efficiency of the system’s picking.
The intelligent algorithms commonly used to solve the optimization problem of storage assignment include particle swarm optimization [15,16,17], genetic algorithm [17, 18], ant colony optimization [19] and other neighborhood search heuristic algorithms [20,21,22]. There have been many studies on the improvement of these algorithms. Lee et al. [13] proposed a dual-objective storage allocation optimization model that takes picking efficiency and traffic balance into account and uses a multi-objective evolutionary algorithm to solve it. Different improved particle swarm optimization algorithms and improved genetic algorithms are used to solve the problem of outbound storage assignment and job scheduling [14,15,16,17,18,19]. Ning et al. [20] put forward a method for optimizing the rack location based on item correlation and rack relevance in the fishbone layout. According to the correlation of the items and the order frequency, the item clusters are divided and a storage allocation model aiming at minimizing the picking distance is established. For the target value, a tabu search algorithm based on rack correlation is designed, which effectively reduces the number of moving by 26.3–39.6% and shortens the picking distance by 34.2–48.6%. Zou et al. [21] proposed an assignment rule based on handling speeds of workstations and design a neighborhood search algorithm to find a near optimal assignment rule. Gharehgozli et al. [22] studied the order retrieval problem and developed an adaptive large neighborhood search heuristic to solve the real size instance. Reference [23] solved an item assignment problem of RMFS by maximizing the sum of similarity values of items in each pod and proposed an efficient heuristic algorithm to address it. Many studies have shown that intelligent algorithm or heuristic algorithm has great advantages for storage assignment problems. Some scholars have researched in-depth on the solution of multi-objective optimization. Reference [24] developed a framework for automatic production scheduling problems with genetic programming. Nastasi et al. [25] compared the statistical significance of Nicked Pareto Genetic Algorithm, Non-dominated Sorting Genetic Algorithm 2 and Strength Pareto Genetic Algorithm 2 on the improved model on a steelmaking industry. And result shown that NSGA2 has the best performance. He et al. [26] developed a discrete multi-objective fireworks algorithm to solve multi-objective flow shop scheduling problem. Opposition-based learning and clustering analysis are used to improve the algorithm. And the results show that DMOFWA performs better than four comparison algorithms. Qin et al. [27] improved particle swarm optimization by decomposition with different ideal points. The improved algorithm has better performance in multi-objective optimization and high-dimensional optimization problems. Random immigrant policy is also adopted in [28] and the improved algorithm outperformed than mutation MOPSO.
However, due to the large difference between the traditional RMFS and the FRMFS, the proposed storage assignment strategy and model for traditional RMFS are not completely applicable in this system. The existing storage assignment model needs to be adjusted to adapt to the fishbone layout. This research proposed an optimized model of storage assignment for FRMFS aimed at improving the efficiency of outbound of warehouse and balancing the workload of each aisle by analyzing the layout structure and calculating various rack moving distances. The improved genetic algorithm is used to solve the problem, and the results show that the proposed model is effective. Through the comparison of other algorithms, the optimization efficiency of AGA is higher than that of other intelligent algorithms.
This paper is organized as follows. “System description” describes the operations of the FRMFS. "Performance estimation of FRMFS" analyzes the workflow of FRMFS and a storage assignment model is proposed in "Model of storage assignment in FRMFS". AGA is presented to solve the storage assignment model in "Model-solving algorithm". "Simulation experiment" designs experiments of different algorithm and discusses their results. Lastly, "Conclusion" provides conclusions and suggests some directions for future research.
System description
Fishbone layout
The rack layout of FRMFS is shown in Fig. 1. The entire warehouse space comprises four zones, each being a triangle with equal areas. And between zones there are two diagonal cross aisles which are vertical to each other. Besides, the width of aisles between racks is equal among areas.
RMFS operational procedure
Mobile racks move to the picking station in which workers pick required SKUs for each customer order. Utilizing mobile racks can significantly reduce worker walking time and improve system efficiency, as shown in Fig. 2.
-
(1)
Depending on real-time workload and customer orders, match mobile racks with picking stations.
-
(2)
Assign tasks to idle robots near to the targeted racks, then, determine the optimal travel paths.
-
(3)
Robots move the targeted rack along with predetermined travel paths.
-
(4)
Move rack to picking stations sequentially and await workers to complete order picking. If all required SKUs from this mobile rack have been picked out, continue with Step 5.
-
(5)
If a replenishment task has dispatched, move the rack to replenishment stations. Otherwise, continue with step 6.
-
(6)
Move the rack back to storage location that is determined in real time.
-
(7)
Back to step 2 until there is no customer order in the queue.
Performance estimation of FRMFS
Assumptions
-
(1)
Random storage strategy is applied. The random storage strategy is consistent with the actual storage operating environment.
-
(2)
Picking or replenishment stations are located at the bottom center of the warehouse. According to the fishbone rack layout, placing the work station at the bottom of the warehouse can shorten the robot movement distance and improve order picking efficiency.
-
(3)
Robot with rack must move along the aisles, but idle robot can also pass through the bottom of racks. The robot takes the shortest path.
-
(4)
Travel congestion, turnaround and waiting time at picking stations are not considered in the model. Complex conditions such as congestion and steering may complicate the storage assignment model, and these conditions can be studied in multi-robot path planning problem.
Layout parameters
System parameters of FRMFS are listed in Table 1 and can be calculated according to Fig. 3, separately.
According to these definitions, the gray storage location in Fig. 1 is indicated by \(O_{153}\). The set of all storage locations, D, can be expressed as
Number of storage columns \(w_{ij}\)
Let the number of storage rows in zone 1 or 4 be \(\eta_{1}\,=\,\eta_{4}\,=\,\eta\). As zones 1 and 4 are symmetric, this research takes zone 1 as an example. Definition of I1, I2, r1 and r2 can be found in Fig. 3b. As shown Fig. 3a, warehouse parameter \(\eta\,= 4\), s = 3, I2 = 3, I1 = 1. The slope of diagonal aisle, K, and inclination angle, θ, are shown by Eqs. (2) and (3).
The increment between an odd row and the next adjacent row, I1, is integer and determined by the length of r1-r2 in Fig. 3a and b
The distance between the vertex of zones 1 and 4 and the first storage row is
Suppose \(\eta\) is an even number. The side length and bottom length of zones 1 and 4 are
The overall length and width of the storage space are
Based on the calculation of I1 and I2, the number of rack columns in zones 1 and 4 can be easily obtained. The first row (j = 1) has s rack columns, and the second row (j = 2) has s + I1 rack columns. In the same way, there are s + I1 + (I2−I1) rack columns in the third row (j = 3), and there are s + I1 + (I2−I1) + I1 rack columns in the four row (j = 4) and so on. According to this, the number of rack columns in zones 1 or zone 4 can be calculated by Eq. (10).
Rack layout in zone 2 or zone 3 follows the next rule: place as many two-side racks near to the centered aisle as possible and then place other two-side racks sequentially from the center to the outer siders on the premise of a vertical aisle. There is a local aisle between each rack.
To sum up, the number of rack columns in row j of zone i is
Horizontal coordinate of storage location O ijk
Suppose the point of left and bottom be the coordinate origin. The horizontal and vertical coordinates of storage location Oijk are
The coordinate of picking stations is (xw,0), of which xw is
Rack moving time is one of the key factors of order picking efficiency. High moving efficiency can reduce waiting time and energy consumption. While the picking SKUs are known, the main way to improve the rack moving efficiency is to reduce the moving path length. Therefore, the optimization of storage assignment can start from the travel distance of target rack and picking station.
Travel distance
The operational procedure of the FRMFS can be divided as:
-
(1)
According to the picking task, a robot moves to targeted rack;
-
(2)
Robot with rack moves to the picking stations for order fulfilment;
-
(3)
The robot moves the rack back to the storage location.
The robot moves towards the targeted rack
Suppose the coordinates of idle robot A is (\({x}_{1}\), \({y}_{1}\)) at zone 1 and it will move towards targeted rack B with coordinate (\({x}_{2}\), \({y}_{2}\)), which has four different cases.
(1) Targeted rack B in zone 1.
The robot arrives at rack B in two manners, depending on whether it goes pass via diagonal cross aisle. The two travel distances \({d}_{1}\), \({d}_{2}\) are
The travel path with shorter distance \({\text{d}}_{\text{AB}}\) will be applied in Eq. (18).
(2) Targeted rack B in zone 2.
There are three cases in this scenario. If \({x}_{2}<{x}_{1}\) and \({\text{y}}_{2}\text{<}{\text{y}}_{1}\), rack B is located at the upper left side of rack A and a robot needs to move upper first and then approaches the targeted row via the diagonal cross aisle. The distance \({\text{d}}_{\text{AB}}\) is
If \({x}_{2}>{x}_{1}\) and \({y}_{2}>{y}_{1}\), rack B is located at the upper right side of rack A and a robot directly moves through rack bottom. \({\text{d}}_{\text{AB}}\) is
If \({x}_{2}>{x}_{1}\) and \({y}_{2}<{y}_{1}\), rack B is located at the bottom right side of rack A and the robot moves towards to the diagonal cross aisle and then to the targeted rack. \({\text{d}}_{\text{AB}}\) is
(3) Targeted rack B in zone 3.
There are four cases in this scenario. If \({y}_{2}<{y}_{1}\), rack B is located at the bottom right side of rack A and the robot moves right towards diagonal cross aisle and then to the targeted rack. \({d}_{AB}\) is
Let \({y}={y}_{2}\) and the vertical coordinate of the cross point with diagonal cross aisle be \({y}_{3}\). is
If \({y}_{1}<{y}_{3}\), rack B is located at the upper side of rack A and the robot moves right across zones 2 and 3 and approaches the targeted row via the diagonal cross aisle. \({d}_{AB}\) is
If \({y}_{1}>{y}_{3}\), rack B is located at the bottom side of rack A and the robot moves directly towards the targeted rack. \({d}_{AB}\) is
(4) Targeted rack B in zone 4.
If \({y}_{2}<{y}_{1}\), the robot moves towards the diagonal cross aisle and then approaches the targeted rack via zones 2 and 3. If \({y}_{2}>{y}_{1}\), the robot moves across zones 2 and 3, and approaches the targeted rack via the diagonal cross aisle. \({d}_{AB}\) is
The calculation for other scenarios is similar to previous equations.
Robot moves to picking station
(1) Rack B in zone 1 or 4.
If rack B is at the bottom row in zone 1 or 4, the robot does not need pass across the diagonal cross aisle. \({\text{d}}_{\text{BO}}\) is
If rack B is located between the first row and row \(\eta - 1\), the robot moves to the picking station via the diagonal cross aisle. Assume that rack B is located at row j. \({y}_{l}\) is
\({\text{d}}_{\text{BO}}\) is
(2) Rack B in zone 2 or 3.
If rack B is located at the first row, the robot does not need across the diagonal cross aisle. \({\text{d}}_{\text{BO}}\) is
If rack B is located between row 2 and row c, the robot moves to the picking station via the bottom diagonal cross aisle. Assume that rack B is located at row j. xl is
And \(d_{{BO}} \) is
Robot returns rack back to storage location
If the rack is delivered back to the original location, the distance can be gotten from \( d_{{OB}} = d_{{BO}} \) . Therefore, the entire travel distance is
Robot travel time between two location
In practice, the robot with mobile rack may turn around regularly in the fishbone layout, which will inevitably experience acceleration and deceleration. According to the principle of kinematics, for each travel path a robot can reach the maximum velocity, as shown in Fig. 4b or cannot reach it, as shown in Fig. 4a. Therefore, travel time between locations S1 and S2 is
Workload of each local aisle
While too many inbound/outbound tasks of the warehouse in an aisle need to be processed, robot congestion could occur. Only one or two robots can perform tasks in the aisle, and the rest of the robots need to wait in queue, which will seriously reduce the efficiency of task execution. In order to reduce queuing, tasks should be scattered in different aisles. While robots perform tasks in different aisles, the probability of queuing is reduced and the efficiency of inbound/outbound of warehouse is improved.
The workload of each aisle can be represented by the racks on both sides of the aisle. The racks contained required SKUs are expressed as 1, and others are 0. Multiple racks may leave the storage location at the same time, so the frequency of each item corresponding to each rack should be taken into account. Taking the aisle between the second row and the third row (j = 2 and j = 3) in zone 1 as an example, the sum of inbound/outbound ratio of the local aisle is:
In Eq. (35) \(w_{12}\) and \(w_{13}\) represented the number of rack in row 2 and 3.
Considering the first row in zone 1 and the second row in zone 2 as the same aisle and the first row in zone 4 and the third row in zone 3 as the same aisle, the number of local aisles of the fishbone rack layout is:
The average outbound ratio of each aisle could be calculated by Eq. (37):
Model of storage assignment in FRMFS
Suppose that N items are stored in the warehouse, and the outbound frequency of item n is pn. Decision variables is \({{x}}_{ijk}^{n}\) which represents item n should be put at the rack of row j and column k in zone i. M is the maximum number of categories that can be stored on a movable rack. Other parameters could be found in Table 1.
Improve outbound efficiency
Placing the goods with high outbound frequency on the racks closer to the workstation can reduce the inbound/outbound time of the warehouse and improve the efficiency of goods turnover. Suppose that the distance that the robot carries the rack at the row j and column k of zone i to the workstation is dijk and the time for the robot to transport the rack to the workstation is tijk. The objective function of warehouse throughout efficiency can be calculated as in Eq. (38):
Balance the workload of each local aisle
The workload of each local aisle should be considered. The items with high turnover rate are scattered and stored on the racks in different zones and different aisles to balance the workload to avoid the accumulation of inbound and outbound tasks and robot congestion. The optimization goal of balancing the workload of each local aisle is the minimum sum of square of the difference between the sum of actual throughout ratio of each local aisle and average throughout ratio it should take [29], as in Eq. (39).
Equation (40) represents the value range of the decision variable. When the variable is 1, the item n is stored on the rack in the row j and column k of the zone i. Equations (41) to (44) indicate the limit of the item number and rack coordinates. Equation (45) indicates that the number of storage items at a rack should be less than the maximum number of items that can be stored. Equation (46) indicates that all the item to be store into the warehouse have been allocated a storage location.
Model-solving algorithm
The storage assignment model proposed in this paper is a NP-hard combinatorial optimization problem [5]. At present, most researches use heuristic algorithms to solve it. By comparing with other algorithms (in the next section), this paper uses the improved genetic algorithm to solve the model. Adaptive genetic algorithm (AGA) is an improved algorithm based on genetic algorithm (GA). This algorithm adopts a parameter adaptive strategy, that is, in each iteration, the crossover probability and genetic mutation probability are adaptively set according to the individual fitness value. This makes the adaptive genetic algorithm better efficiency and global optimality [30].
Chromosome coding
In the proposed optimization model, the decision variable \( x_{{ijk}}^{n} \) is related to four dimensions of rack number, rack zone, rack row and column. Higher dimensions are not beneficial to process, so storage locations are numbered according to special rules to simplify decision variables. Using real number coding, the numbering is carried out in the order of increasing rows and columns from zone 1 to zone 4. Assuming there are 10 goods to be put into storage, each chromosome is an array with 10 elements, which represents a storage allocation solution. The element is the storage number and the index of the element is the item number. As shown in Fig. 5, item 1 is allocated to the storage location 6 and item 2 is placed on location 48.
Fitness
Since the dimensions of the two minimized objective functions are different, weighting factors are introduced in Eq. (47) according to the importance of the sub-objectives to form a single-objective optimization problem. And in Eq. (47), fi* represents the current average value in this iteration and ai represents the weight factors.
In the adaptive genetic algorithm, the population fitness function is required to be maximized and is non-negative. The two objective functions of the storage assignment optimization model are both minimized, so the inverse number of the objective function f is taken as the individual fitness value, as shown in Eq. (49):
Crossover and mutation
To generate new chromosomes and obtain the crossover chromosomes, select any gene fragments randomly on the parent chromosomes to interact with each other. The mutation operation adopts the single-locus mutation method, which randomly selects a locus for the chromosome to be mutated, and changes the expression value of the locus.
In the crossover and mutation operation, the adaptive strategy is used to dynamically adjust the parameters. According to Eqs. (50) and (51), the crossover probability pc and the mutation probability pm are calculated respectively, so that the crossover probability and the mutation probability dynamically change with the fitness value. In this way, the algorithm can maintain a strong global search ability in the initial stage and can fully utilize the local search ability in the later stage to accelerate the convergence to find the optimal solution.
In Eqs. (50) and (51), gmax is the maximum value of fitness for the current generation, \(\stackrel{\mathrm{-}}{\text{g}}\) is the average value, and g’ is the individual fitness value. For the maximum fitness individual, pc and pm are 0. To prevent pc and pm exceeding 1, lower limit k3, k4 is set.
The steps of the AGA algorithm are as follows:
Step1: Set parameters and generate the initial population.
Step2: Calculate each objective function f and fitness g.
Step3: Perform selection operation.
Step4: Calculate the crossover probability and mutation probability according to Eqs. (50) and (51) and perform crossover and mutation operations.
Step5: When the algorithm reaches the termination condition, stop the search and output the result, otherwise return to Step2.
Simulation experiment
Basic parameter setting
This experiment uses the improved adaptive genetic algorithm to solve the storage assignment model. The program is compiled by MATLAB (R2017a). First, determine the basic parameters of the fishbone rack layout. In this experiment, the width of the rack d and middle and partial aisles h is 1 m. The width of the diagonal aisle hp is 2 m. The number of racks in the first row of zone 1 (or zone 4) s is 1, the increment number of racks between two adjacent odd-numbered rows in zone 1 (or Zone 4) I2 is 3, and the number of rack rows in zone 1 (or zone 4) \(\eta\) is 8. Through the above basic parameters, the number of rack rows in zones 1 to 4 can be obtained as:
As shown in Fig. 1, the number of racks in each row of racks in zones 1 to 4 is w,
According to the value of w, the warehouse has 120 storage locations totally. If each rack can store 4 kinds of items, the warehouse can store 480 kinds of items. If there are 30 kinds of goods to be put into the warehouse, the outbound frequency and the original storage location coordinates according to the random storage strategy are shown in Table 2.
Under the initial storage solution, the warehousing throughout efficiency f1 is 145.07 and the balance value of aisle workload f2 is 4.16. The storage allocation is unreasonable and may result in an imbalance in local aisle workload and low warehousing efficiency. Therefore, to improve the efficiency of inbound/outbound process and balance the workload of aisles, the storage locations should be optimized.
Firstly, each objective function is simulated to verify the effectiveness of single objective function, so the optimal value of a single objective function is obtained. Then, according to Eq. (47), the multi-objective function is transformed into a single objective function. Set the value of the weight (α1, α2) to (0.5, 0.5) and the simulation is finally performed.
Optimization based on adaptive genetic algorithm
In the experiment, the maximum number of evolutions T is set to 200, the population size J is 200, the parameters of adaptive crossover probability and the mutation probability can be obtained by k1 = 0.5, k3 = 1, k2 = 0.3, k4 = 0.5. When only the warehouse outbound efficiency is considered, the iteration convergence process is shown in Fig. 6a and the optimized storage location coordinates are shown in Table 3. When only the balance of aisle workload is considered, the iteration convergence process is shown in Fig. 6b, and the optimized storage location coordinates are shown in Table 4.
From Fig. 6a, the objective function converges in 80 iterations and the optimized value of the outbound efficiency is 82.11, which is 43.40% lower than optimization before. According to the optimization results, the number of racks occupied by this batch of goods in the warehouse is significantly reduced. The items are placed close to the workstations, which indicate that the optimization goal of improving warehouse outbound efficiency is effective. But almost all items are arranged at the first row of in zone 2 or zone 3 and piled up near the workstations, so the workload of local aisles is unbalanced, which is easy to cause congestion.
From Fig. 6b, the objective function converges in 33 iterations and the optimal target value for balancing the local aisle workload is 0.53, which is 87.26% lower than optimization before. According to the results, items has been scattered in the warehouse zone and the aisle. It shows that the optimization goal of balancing local aisle workload is effective, but most of the goods are far away from the workstation, which is against to improving the efficiency of the warehouse.
Based on the sub-objective simulation, substitute the above optimal value into Eq. (47) to eliminate the influence of different dimensions. A new function is obtained as the objective function for optimization. The iteration convergence process is shown in Fig. 7, and the optimized location coordinates are shown in Table 5.
After 4.67 s the AGA algorithm terminates. The objective function is converged in 84 iterations, and the optimized objective value f is 2.79. In this case, the objective value f1 and f2 are 115.17 and 1.64, respectively. Compared with the random storage assignment solution, the two optimized values of the AGA algorithm are both smaller. The goods are placed in an orderly manner according to the outbound frequency and distance and they are evenly distributed in all zones and aisles, which indicates that both the outbound efficiency and the workload of the balanced aisles have been improved. The optimization rates have reached 20.61% and 60.57%, respectively.
Sensitivity analysis
The AGA algorithm has four key parameters, k1, k2, k3, k4. All the four parameters are associated to the crossover and mutation probability for each child, which should be calculated dynamically in AGA. Unsuitable initial value or default probability will lead to premature convergence or local optimum. The experimental data of four parameters is analyzed, as shown in Fig. 8. It can be seen that the value of k3 fluctuates greatly, followed by k1, k2 and k4. According to Fig. 8 and algorithm tuning experience, the parameter of adaptive crossover and the mutation probability could be set as follows, k1 = 0.5, k3 = 1, k2 = 0.3, k4 = 0.5.
Algorithm adaptability analysis
This combinatorial optimization problem proposed in this paper can be solved by most intelligent algorithms, such as ant colony optimization (ACO) [31], artificial bee colony (ABC) [32], particle swarm optimization (PSO) [33], elephant herding optimization (EHO) [34]. In order to further verify the applicability of the improved algorithm in this research for storage assignment problem on the fishbone layout, it is necessary to compare the differences between the improved algorithm and other algorithms to illustrate the effectiveness of the improved strategy. Therefore, simulation experiments are carried out using different size of examples.
In this section, GA, ACO, ABC, and PSO are used to solve the optimization model of storage assignment problem on the fishbone rack layout. AGA and the simulated annealing particle swarm optimization (SAPSO) are used for comparison. In the experiments, the initial parameters of the similar algorithms (such as the PSO and SAPSO) are set to be the same which is convenient to compare the performance of different algorithm. The results of GA, ACO, ABC, PSO, and SAPSO are shown in Fig. 9.
As shown in Figs. 7 and 9, the objective function values obtained by the six algorithms of GA, ACO, ABC, PSO, AGA, and SAPSO are 3.5, 3.91, 3.58, 3.34, 2.79, 2.78, respectively. And the convergence iterations are 148, 122, 158, 129, 84, and 169. As for the performance of the four traditional algorithms of this model, the optimization value of PSO is the smallest, but GA can better avoid the local extremum. Compared with the former two algorithms, ABC and ACO converges slowly. And the objective value is slightly larger, so the performance of the algorithms for this model is poor. Therefore, PSO algorithm with simulated annealing strategy and AGA are compared to solve the model. In this scale of examples, SAPSO has the smallest optimization result, followed by AGA, and the difference is 0.01. However, AGA has fast convergence speed and better stability. Both improved algorithms are better than the basic algorithms.
In order to further measure the performance of different algorithms, the optimization problem under different scales (N is task number, C is storage location number) is designed. The value of the outgoing efficiency f1, the value of the balanced aisle workload f2 and the mean convergence iterations G are selected as the algorithm performance analysis indicators. In order to avoid the contingency of the experiment, the experimental results of the examples in this paper are the average of 10 times of operation. The results are shown in Tables 6, 7, 8, 9.
According to Table 6, with the expansion of the problem scale, the convergence speed of AGA and SAPSO is obviously faster than the basic algorithm. As a whole, the convergent iterations of ABC and ACO are bigger than others. This result verifies that the improved strategy can improve the local optimization ability at the end stage of the algorithm and accelerate the convergence. The convergence speed of AGA has obvious advantages over SAPSO. And its solution has less fluctuation and stronger stability.
As for optimization value, in most cases the optimization results of AGA and SAPSO are better than the basic algorithm. The larger the scale of the problem, the smaller the objective function value of the solution obtained by AGA and SAPSO compared with the basic algorithm. Although the optimization performance of the algorithm decreases with the increase of the problem scale, all the algorithms still have a large improvement compared with the random allocation strategy. The optimal values of GA, PSO, ACO, ABC are almost the same, but there is a big gap between the results of the improved algorithm and them. Considering the convergence speed and optimal value, GA and PSO are more suitable for solving the model. The CPU time of GA, AGA, PSO, SAPSO is shown in Fig. 10.
Figure 10 shows the execution times of the four algorithms related to the number of tasks. With the number of tasks increasing, the CPU time of all algorithms are growing smoothly. The computing time of AGA and GA algorithms is about the same, because the difference between the two algorithms is whether the probability of crossover and mutation needs to be calculated dynamically. The gap between the CPU time of PSO related algorithm and GA related algorithm is increasing gradually because of the large amount of calculation for PSO potentially. GA algorithm uses less CPU time and takes up less computer resources. As shown in Tables 7, 8, 9, a comparison and analysis of AGA and SAPSO algorithm shows that when the problem size is small, the optimal gap between the two algorithms is acceptable. However, when the problem size is large, the overall optimization ability of AGA is more advantageous. The calculation speed for AGA is faster than SAPSO algorithm and has better solutions. SAPSO algorithm can sometimes obtain solutions better than AGA, but due to the randomness of initial solution generation and the limitation of artificial selection of algorithm parameters, the obtained objective function value fluctuates greatly, and there is a gap in stability compared with AGA. Therefore, the AGA algorithm is more suitable for solving large-scale storage assignment optimization problems.
Conclusions
This paper takes the robot mobile fulfillment system with fishbone rack layout as the research object to establish a storage assignment optimization model with the goal of improving the efficiency of warehouse inbound/outbound and balancing the workload of local aisles. Different intelligent algorithms can give their own better solutions. Compared with other algorithms, genetic algorithm has the lowest probability of falling into local optimization and has a higher degree of optimization. Therefore, the improved adaptive genetic algorithm is used to solve the storage assignment model.
By a series of simulation experiment, the accuracy of the mathematical model and the effectiveness of the algorithm are verified. In order to further illustrate the applicability and superiority of the improved algorithm on fishbone storage assignment problems, the optimization effect and optimization efficiency of the adaptive genetic algorithm, improved particle swarm optimization based on simulated annealing, ant colony optimization, genetic algorithm, particle swarm optimization, and artificial bee colony are compared on the instances of different scales. Result shows that AGA is more suitable for solving large-scale storage assignment optimization problems.
The optimization model proposed in this research only considers the working distance and aisle balance. The influence of the correlation between orders on storage assignment needs focus on further study. And the adaptability of intelligent algorithms for other problems in FRMFS is also worthy for further research.
References
Yang F, Gu S (2021) Industry 4.0, a revolution that requires technology and national strategies. Complex Intell Syst 7(3):1311–1325
Lamballais T, Roy D, De Koster M (2017) Estimating performance in a robotic mobile fulfillment system. Eur J Oper Res 256(3):976–990
Gue R, Meller D (2009) Aisle configurations for unit load warehouses. IIE Trans 41(3):171–182
White J (1972) Optimum design of warehouses having radial aisles. IIE Trans 4(4):333–336
Weidinger F, Boysen N, Briskorn D (2018) Storage assignment with rack-moving mobile robots in KIVA warehouses. Transp Sci 52(6):1479–1495
Lamballais T, Roy D, Koster R (2020) Inventory allocation in robotic mobile fulfillment systems. IISE Trans 52(1):1–17
Roy D, Nigam S, de Koster R, Adan I, Resing J (2019) Robot-storage zone assignment strategies in mobile fulfillment systems. Transp Res Pt e-Logist Transp Rev 122:119–142
Hadi M, Djatna T (2018) A modeling of dynamic storage assignment for order picking in beverage warehousing with Drive-in Rack system. Iop Conference 337(1):12020–12026
Bahrami B, Aghezzaf E, Limère V (2019) Enhancing the order picking process through a new storage assignment strategy in forward-reserve area. Int J Prod Res 57(21):6593–6614
Wu Y, Wu Y (2014) Taboo search algorithm for item assignment in synchronized zone automated order picking system. Chin J Mech Eng 27(4):860–866
He M, Xie F, Li C (2018) Dynamic optimization strategy of KIVA storage location based on T-SKU method. Logist Eng Manag 40(04):47–50
Xu X, He S, Li X (2020) RMFS storage location assignment based on dutch auction. Packag Eng 41(01):128–133
Lee I, Chung S, Yoon S (2020) Two-stage storage assignment to minimize travel time and congestion for warehouse order picking operations. Comput Ind Eng 139:106129
Zhang R, Wang M, Pan X (2019) New model of the storage location assignment problem considering demand correlation pattern. Comput Ind Eng 129:210–219
He Y, Wang A, Su H, Wang M (2019) Particle swarm optimization using neighborhood-based mutation operator and intermediate disturbance strategy for outbound container storage location assignment problem. Math Probl Eng 2019:1–13
Tang H, Yan W, Chen Q, Lu J, Zhan Y (2020) Integrated optimization of location assignment and job scheduling in automated storage and retrieval system. Comput Sci 47(05):204–211
Hu Y (2019) Research on the optimization storage slotting and order picking with non-traditional warehouse. Nanchang University, Nanchang
Cai A, Cai Y, Guo S, Geng C (2019) Ensemble multi-objective genetic algorithm with application to automated warehouse scheduling. Mach Des Manuf 5:95–98
Gonzalez-Pardo A, Del Ser J, Camacho D (2017) Comparative study of pheromone control heuristics in ACO algorithms for solving RCPSP problems. Appl Soft Comput 60:241–255
Ning F, He C, Li T (2017) Study on slotting optimization of fishbone layout based on rack-to- picker mode. J Zhejiang Sci-Tech Univ (Soc Sci Ed) 38(04):293–298
Zou B, Gong Y, Xu X, Yuan Z (2017) Assignment rules in robotic mobile fulfilment systems for online retailers. Int J Prod Res 55(20):6175–6192
Gharehgozli A, Zaerpour N (2020) Robot scheduling for pod retrieval in a robotic mobile fulfillment system. Transp Res Pt e-Logist Transp Rev 142:19
Kim H, Pais C, Shen Z (2020) Item assignment problem in a robotic mobile fulfillment system. IEEE Trans Autom Sci Eng 17(4):1854–1867
Nguyen S, Mei Y, Zhang M (2017) Genetic programming for production scheduling: a survey with a unified framework. Complex Intell Syst 3(1):41–66
Nastasi G, Colla V, Cateni S, Campigli S (2018) Implementation and comparison of algorithms for multi-objective optimization based on genetic algorithms applied to the management of an automated warehouse. J Intell Manuf 29(7):1545–1557
He L, Li W, Zhang Y, Cao Y (2019) A discrete multi-objective fireworks algorithm for flowshop scheduling with sequence-dependent setup times. Swarm Evol Comput 51:100575–110590
Qin S, Sun C, Zhang G, He X, Tan Y (2020) A modified particle swarm optimization based on decomposition with different ideal points for many-objective optimization problems. Complex Intell Syst 6(2):263–274
Unal A, Kayakutlu G (2020) Multi-objective particle swarm optimization with random immigrants. Complex Intell Syst 6(3):635–650
Peng W (2018) Design of automated warehouse and research on the method of intelligent accessing the goods. Jiangsu University of Science and Technology, Zhenjiang
Yu G, Yu X (2015) An improved adaptive genetic algorithm. Math Pract Theory 45(19):259–264
Dorigo M, Stutzle T (2004) Ant colony optimization. MIT Press, Cambridge
Karaboga D, Basturk B (2007) A powerful and efficient algorithm for numerical function optimization: artificial bee colony (abc) algorithm. J Glob Optim 39:459–471
Kennedy J, Eberhart R (1995) Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, IEEE, pp 1942–1948
Wang G, Deb S, Coelho L (2015) Elephant Herding Optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI 2015), IEEE, pp 1–5
Funding
This work was supported by Science, Technology and Innovation Commission of ShenZhen Municipality(No. JCYJ20190807094803721) and Shandong Provincial Natural Science Foundation (No. ZR2020MF085).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All the authors have approved the manuscript for publication, and there is no conflict of interest exists.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Y., Man, R., Zhao, W. et al. Storage assignment optimization for fishbone robotic mobile fulfillment systems. Complex Intell. Syst. 8, 4587–4602 (2022). https://doi.org/10.1007/s40747-021-00597-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-021-00597-2